三角函数与圆中的计算
完整三角函数公式表

完整三角函数公式表三角函数公式表是数学中常用的一个工具,用于计算三角函数的数值。
它包含了各种三角函数的定义和性质,能够帮助我们在解决三角函数相关问题时,快速找到所需的公式和计算方法。
以下是一个完整的三角函数公式表,包含了常见的正弦、余弦、正切、余切、正割和余割函数的公式:1. 正弦函数(sin):- 定义:在单位圆上,从原点到圆上一点与x轴的正角对应的y坐标。
- 基本关系:sin θ = y/r,其中θ是角度,y是对应的y坐标,r是单位圆的半径(常为1)。
- 周期性:sin (θ + 2π) = sin θ。
- 奇偶性:sin (-θ) = -sin θ。
2. 余弦函数(cos):- 定义:在单位圆上,从原点到圆上一点与x轴的正角对应的x坐标。
- 基本关系:cos θ = x/r,其中θ是角度,x是对应的x坐标,r是单位圆的半径(常为1)。
- 周期性:cos (θ + 2π) = cos θ。
- 奇偶性:cos (-θ) = cos θ。
3. 正切函数(tan):- 定义:tan θ = sin θ / cos θ。
- 周期性:tan (θ + π) = tanθ。
- 奇偶性:tan (-θ) = -tan θ。
4. 余切函数(cot):- 定义:cot θ = 1 / tan θ = cos θ / sin θ。
- 周期性:cot (θ + π) = cot θ。
- 奇偶性:cot (-θ) = -cot θ。
5. 正割函数(sec):- 定义:sec θ = 1 / cos θ。
- 周期性:sec (θ + 2π) = sec θ。
- 奇偶性:sec (-θ) = sec θ。
6. 余割函数(csc):- 定义:csc θ = 1 / sin θ。
- 周期性:csc (θ + 2π) = csc θ。
- 奇偶性:csc (-θ) = -csc θ。
此外,三角函数还有一些重要的性质:1. 三角函数的范围:sin、cos、csc、sec的值在[-1, 1]之间,tan、cot的值在整个实数范围内。
单位圆上三角函数值的计算

单位圆上三角函数值的计算三角函数是一门与数学有关的学科,也是数学中的一种重要思想工具。
在三角函数中,常常会涉及单位圆。
单位圆是一个半径为1的圆,其圆心位于坐标系原点处。
在单位圆上,我们可以用三角函数计算出各种角度的正弦、余弦、正切值等。
一、单位圆上的正弦和余弦我们先来看正弦和余弦。
在单位圆上,任意一点(x,y)都可以表示为(x,√(1-x²))或(√(1-y²),y)的形式。
因为单位圆的方程式为x²+y²=1,所以当我们知道了x或y的值,就能算出另外一个未知的值。
因为正弦和余弦都是关于y和x的函数,所以对于一个三角形ABC,如果我们知道了其内角B的度数,就可以根据三角函数计算出BC与AB的比值,也就是正弦值sin(B)和余弦值cos(B)。
在单位圆上,如果一个角的终边与x轴正方向之间的夹角为α,则该角的正弦函数值为sin(α),其余弦函数值为cos(α)。
因为半径为1,所以在单位圆上,正弦和余弦的取值范围都是[-1,1]。
当角度为0度时,终边就在x轴上,此时的正弦函数值和余弦函数值都为1。
当角度为90度时,终边就在y轴上,此时的正弦函数值为1,余弦函数值为0。
类似地,当角度为180度时,终边就在-x轴上,此时的正弦函数值和余弦函数值都为-1;当角度为270度时,终边就在-y轴上,此时的正弦函数值为-1,余弦函数值为0。
二、单位圆上的正切值类似于正弦和余弦函数,正切函数也是与单位圆有关的。
在单位圆上,如果一个角的终边与x轴正方向之间的夹角为α,则该角的正切函数值为tan(α)。
因为正切值的定义是一个比值,所以正切值没有像正弦或者余弦那样有固定的取值范围。
不过,在单位圆的第一象限和第三象限,正切值是正数,而在第二象限和第四象限,正切值是负数。
举个例子,假设终边角度为45度,则终边上的点为(√2/2,√2/2)。
这个点与x轴正方向之间的夹角为45度,所以其正切值为tan(45)=1。
圆中的计算——构造直角三角形转化三角函数
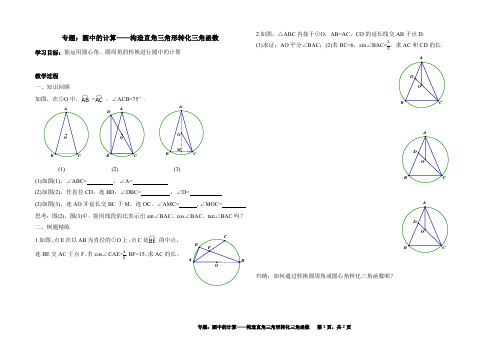
专题:圆中的计算——构造直角三角形转化三角函数学习目标:能运用圆心角、圆周角的转换进行圆中的计算教学过程 一、知识回顾如图,在⊙O 中,⌒AB =⌒AC ,∠ACB=75°.(1) (2) (3) (1)如图(1),∠ABC= ,∠A=(2)如图(2),作直径CD ,连BD ,∠DBC= ,∠D= (3)如图(3),连AO 并延长交BC 于M ,连OC ,∠AMC= ,∠MOC= 思考:图(2),图(3)中,能用线段的比表示出sin ∠BAC 、cos ∠BAC 、tan ∠BAC 吗? 二、例题精练1.如图,点E 在以AB 为直径的⊙O 上,点C 是⌒BE 的中点,连BE 交AC 于点F 。
若cos ∠CAE=45,BF=15,求AC 的长。
2.如图,△ABC 内接于⊙O ,AB=AC ,CO 的延长线交AB 于点D. (1)求证:AO 平分∠BAC ;(2)若BC=6,sin ∠BAC=35,求AC 和CD 的长.归纳:如何通过转换圆周角或圆心角转化三角函数呢?A三、课堂检测1.如图,⊙O 的直径为5,△ABC 为⊙O 的内接三角形,AC =2√6,则tan ∠B=2.如图,△ABC 内接于⊙O ,AB=AC ,若AB=4√3, cos ∠BAC=13,则BC=3.如图,AB 为⊙O 的直径,CD 为⊙O 的弦,AB=10,cos ∠BAC=35,∠BAD=30°,则线段CD 的长是四、巩固练习1.如图,△ABC 内接于⊙O ,E 在⌒AC 上,⌒EC=⌒AB ,AC=BC ,若AB=4,BE=6,求cos ∠EBC.2.如图,△ABC 是⊙O 的内接三角形,AB=AC ,点P 是⌒AB的中点,连接PA 、PB 、PC ,若sin ∠BPC=2425,求tan ∠PAB.AEA。
常用三角函数计算公式

常用三角函数计算公式在数学中,三角函数是一类基础的数学函数,它们与三角形的边长关系密切相关。
常用的三角函数有正弦函数、余弦函数和正切函数。
下面是一些常用的三角函数计算公式。
1. 正弦函数(sin):正弦函数表示一个角的正弦值与其对边与斜边之比。
在单位圆上,一个角对应于圆周上的一个弧,弧的长度即为角的大小。
常用的正弦函数公式如下:- sin(θ + π) = -sin(θ) (正弦函数的周期性)- sin(θ + 2π) = sin(θ)- sin(π/2 - θ) = cos(θ) (正弦函数的补角关系)- sin(θ + π/2) = cos(θ)- sin(π/2 + θ) = cos(θ)- sin(π - θ) = sin(θ) (正弦函数的对称性)- sin(2θ) = 2sin(θ)cos(θ) (正弦函数的倍角公式)2. 余弦函数(cos):余弦函数表示一个角的余弦值与其邻边与斜边之比。
在单位圆上,余弦值等于角对应的点的横坐标。
常用的余弦函数公式如下:- cos(θ + π) = -cos(θ) (余弦函数的周期性)- cos(θ + 2π) = cos(θ)- cos(π/2 - θ) = sin(θ) (余弦函数的补角关系)- cos(θ + π/2) = -sin(θ)- cos(π/2 + θ) = -sin(θ)- cos(π - θ) = -cos(θ) (余弦函数的对称性)- cos(2θ) = cos²(θ) - sin²(θ) (余弦函数的倍角公式)3. 正切函数(tan):正切函数表示一个角的正切值与其对边与邻边之比。
在单位圆上,正切值等于角对应的点的纵坐标与横坐标之比。
常用的正切函数公式如下:- tan(θ) = sin(θ) / cos(θ) (正切函数与正弦、余弦的关系)- tan(θ + π) = tan(θ) (正切函数的周期性)- tan(θ + 2π) = tan(θ)- tan(π/2 - θ) = 1/tan(θ) (正切函数的补角关系)- tan(π/2 + θ) = -1/tan(θ)- tan(π - θ) = -tan(θ) (正切函数的对称性)- tan(2θ) = 2tan(θ) / (1 - tan²(θ)) (正切函数的倍角公式)除了上述的基本公式外,三角函数还有很多推导公式和恒等式,用于推导和证明其他数学问题。
圆和三角函数的知识点总结

圆和三角函数的知识点总结一、圆的基本概念1. 圆的定义圆是由平面上到一点距离等于定值的所有点的集合所构成的图形。
这个定值称为圆的半径,记作R。
圆的中心是到圆上任意一点的距离都等于半径的点。
2. 圆的性质(1)圆的直径是经过圆心并且两端点在圆上的线段,其长度等于半径的两倍,即2R。
(2)圆的周长是圆的边界长度,等于2πR。
(3)圆的面积是圆的内部面积,等于πR²。
3. 圆的相关公式(1)周长的计算公式:C = 2πR(2)面积的计算公式:A = πR²4. 圆的图形圆的图形一般用于图像的绘制、工程设计和数学证明等方面,其圆心和半径都是图形的重要参数。
二、三角函数的基本概念1. 三角函数的定义三角函数是一类反映角度和三角形边长关系的函数,包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数等。
其中,最基本的三角函数是正弦函数和余弦函数。
2. 三角函数的性质(1)正弦函数的性质:周期性、奇偶性、单调性等。
(2)余弦函数的性质:周期性、偶偶性、单调性等。
(3)其他三角函数的性质:正切函数、余切函数、正割函数和余割函数的性质。
3. 三角函数的公式三角函数有一系列的常用公式,如和差公式、倍角公式、半角公式、和角公式等,这些公式能够简化三角函数的计算。
4. 三角函数的图形正弦函数和余弦函数的图形是三角函数中最为常见的图形,它们在数学和物理学中有着广泛的应用。
在图像上,正弦函数是一个周期函数,其图像呈现正弦波形;余弦函数也是一个周期函数,其图像呈现余弦波形。
三、圆和三角函数的关系1. 弧度制和角度制圆和三角函数之间的关系在很大程度上依赖于角度的度量方式。
弧度制是一种更为自然的角度度量方式,而角度制是较为常见的角度度量方式。
弧度制和角度制的关系为:1弧度= 180°/π度。
2. 弧长和扇形面积正弦函数和余弦函数的定义涉及到圆的弧长和扇形面积,它们与三角函数之间有着密切的关系。
三角函数与弧度制角度制的转化表

三角函数与弧度制角度制的转化表一、弧度制与角度制的概念在数学中,我们经常会涉及到角度的计算和转化。
角度的计量方式有两种,一种是角度制,另一种是弧度制。
角度制是以度(°)为单位来度量角度的,一个圆周等于360度,一个直角等于90度。
弧度制是以弧度(rad)为单位来度量角度的,一个圆周等于2π弧度,一个直角等于π/2弧度。
二、角度制转化为弧度制将角度制转化为弧度制,只需将角度除以180,再乘以π即可。
例如,将90度转化为弧度制,计算方法如下:90度÷ 180 × π = π/2弧度同理,将其他角度制转化为弧度制的方法也是一样的。
三、弧度制转化为角度制将弧度制转化为角度制,只需将弧度除以π,再乘以180即可。
例如,将π/2弧度转化为角度制,计算方法如下:π/2弧度÷ π × 180 = 90度同理,将其他弧度制转化为角度制的方法也是一样的。
四、角度制与弧度制之间的转化关系角度制与弧度制是相互转化的,它们之间的转化关系可以通过以下公式表示:角度制 = 弧度制÷ π × 180弧度制 = 角度制× π ÷ 180五、总结通过以上的介绍,我们了解到了角度制与弧度制之间的转化关系。
在实际应用中,我们需要根据具体的问题来选择使用角度制还是弧度制来进行计算和表示。
在数学和物理领域中,弧度制是更为常见和方便的计量方式,因为它与圆的性质更为密切相关。
而在日常生活和一些特定的领域中,角度制更为常用,例如方向、时间和温度等的表示。
希望通过这篇文章,您能够更加清晰地理解三角函数与弧度制角度制的转化关系,为您的学习和工作带来帮助。
单位圆与三角函数的关系解析

单位圆与三角函数的关系解析三角函数是数学中一个重要的概念,它与单位圆之间有着密切的关系。
在解析几何中,单位圆是指半径为1的圆,它在坐标系中的位置为原点(0, 0)。
单位圆上的点(x, y)与三角函数的关系可以通过三角函数的定义来解析。
三角函数包括正弦(sin)、余弦(cos)、正切(tan)、余切(cot)、正割(sec)和余割(csc),它们的值是根据单位圆上的点(x, y)的坐标来确定的。
首先,我们来看正弦(sin)和余弦(cos)函数。
对于单位圆上的任意一点(x, y),其对应的弧度角θ可以通过三角函数的反函数(arcsin和arccos)来计算。
对于正弦函数来说,sinθ = y,而余弦函数则是cosθ = x。
因此,我们可以通过单位圆上的点的y 坐标来计算正弦值,通过点的x坐标来计算余弦值。
接下来是正切(tan)与余切(cot)函数。
正切函数定义为tanθ = sinθ/cosθ,而余切函数则是cotθ = cosθ/sinθ。
我们可以利用单位圆上的点(x, y)和三角函数的关系来计算正切和余切的值。
最后是正割(sec)和余割(csc)函数。
正割函数定义为se cθ = 1/cosθ,而余割函数则是cscθ = 1/sinθ。
我们可以将正割和余割的值与单位圆上的点的x坐标和y坐标来计算。
除了通过三角函数的定义来计算单位圆上的点的三角函数值外,我们还可以利用三角函数图像的周期性来计算。
以sin函数为例,对于单位圆上的第一象限(0 ≤ θ ≤ π/2)上的任意一点(x, y),我们可以发现在π/2的位置上,sin函数的值是最大的,为1。
而在0和π/2之间的位置上,sin函数的值是递增的,也就是说,随着弧度角θ的增大,sin函数的值也增大。
同样的道理,我们可以得到余弦、正切、余切、正割和余割在单位圆上的图像。
总结起来,单位圆与三角函数的关系可以通过三角函数的定义来解析。
我们可以通过单位圆上的点(x, y)的坐标来计算正弦、余弦、正切、余切、正割和余割的值。
三角函数弧度制

三角函数弧度制三角函数是数学中的一种基本函数,它们在三角形的计算中非常有用。
在数学中,三角函数包括正弦函数、余弦函数、正切函数等,它们的定义和性质可以用角度或弧度来表示。
在这里,我们将重点介绍三角函数的弧度制。
弧度制是一种角度的度量方式,它是以圆的半径为单位来度量角度的大小。
具体来说,一个角度的弧度数等于它所对应的圆弧长度与圆的半径之比。
例如,一个角度为60度的圆心角所对应的弧长是圆的周长的1/6,如果圆的半径为1,那么这个角度的弧度数就是1/6π,即约为0.523。
在三角函数中,弧度制的应用非常广泛。
例如,正弦函数的定义是一个角度的正弦值等于它所对应的三角形的对边长度与斜边长度之比。
在弧度制下,正弦函数的定义可以改写为一个角度的正弦值等于它所对应的圆上一点的纵坐标与圆的半径之比。
这个定义可以用下面的公式来表示:sinθ=y/r其中,θ是一个角度,y是它所对应的圆上一点的纵坐标,r是圆的半径。
这个公式可以用来计算任意一个角度的正弦值,只要知道它所对应的圆上一点的坐标即可。
同样地,余弦函数和正切函数的定义也可以用弧度制来表示。
余弦函数的定义是一个角度的余弦值等于它所对应的三角形的邻边长度与斜边长度之比。
在弧度制下,余弦函数的定义可以改写为一个角度的余弦值等于它所对应的圆上一点的横坐标与圆的半径之比。
正切函数的定义是一个角度的正切值等于它所对应的三角形的对边长度与邻边长度之比。
在弧度制下,正切函数的定义可以改写为一个角度的正切值等于它所对应的圆上一点的纵坐标与横坐标之比。
总之,弧度制是一种非常重要的角度度量方式,它在三角函数的计算中起着至关重要的作用。
掌握弧度制的概念和计算方法,可以帮助我们更好地理解三角函数的定义和性质,从而更加熟练地运用它们进行数学计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档,值得拥有
1 / 2
三角函数与圆中的计算
1.(朝阳一模25).如图,△ABC 内接于⊙O ,AB 为直径,点D 在⊙O 上,过点D 作⊙O 切线与AC 的延长线交于点E ,ED ∥BC ,连接AD 交BC 于点F . (1)求证:∠BAD =∠DAE ;
(2)若AB =6,AD =5,求DF 的长.
2.(门头沟一模25).如图,在△ABC 中,AB=AC ,以AC 为直径作⊙O 交BC 于点D ,过点D 作⊙O 的切线EF ,交AB 和AC 的延长线于E 、F .
(1)求证:FE ⊥AB ;
(2)当AE =6,sin ∠CFD =3
5
时,求EB 的长.
3.(丰台一模25).如图,⊙O 的直径AB 垂直于弦CD ,垂足为点E ,过点C 作⊙O 的切线,交AB 的延长线于点P ,联结PD .
(1)判断直线PD 与⊙O 的位置关系,并加以证明; (2)联结CO 并延长交⊙O 于点F ,联结FP 交CD 于点G ,如
果CF =10,4cos 5APC ∠=,求EG 的长.
4.(石景山一模25).如图,AB 是⊙O 的直径,C 是⊙O 上一
点,D
是OB 中点,过点D 作AB 的垂线交AC 的延长线于点F .过点C 作⊙O 的切线交FD 于点E . (1)求证:CE EF =; (2)如果3sin 5F =,2
5
=EF ,求AB 的长.
G
O P
A
B
C
D E F。
