变量与函数1
一次函数-变量与函数

变量与函数(知识讲解)【学习目标】1.知道现实生活中存在变量和常量,变量在变化的过程中有其固有的范围(即变量的取值范围);2.能初步理解函数的概念;能初步掌握确定常见简单函数的自变量取值范围的基本方法;给出自变量的一个值,会求出相应的函数值.【要点梳理】要点一、变量、常量的概念在一个变化过程中,我们称数值发生变化的量为变量.数值保持不变的量叫做常量.要点诠释:一般地,常量是不发生变化的量,变量是发生变化的量,这些都是针对某个变化过程而言的.例如,60s t =,速度60千米/时是常量,时间t 和里程s 为变量.要点二、函数的定义一般地,在一个变化过程中. 如果有两个变量x 与y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是x 的函数.要点诠释:对于函数的定义,应从以下几个方面去理解:(1)函数的实质,揭示了两个变量之间的对应关系;(2)对于自变量x 的取值,必须要使代数式有实际意义;(3)判断两个变量之间是否有函数关系,要看对于x 允许取的每一个值,y 是否都有唯一确定的值与它相对应.(4)两个函数是同一函数至少具备两个条件:①函数关系式相同(或变形后相同);②自变量x 的取值范围相同.否则,就不是相同的函数.而其中函数关系式相同与否比较容易注意到,自变量x 的取值范围有时容易忽视,这点应注意.要点三、函数值y 是x 的函数,如果当x =a 时y =b ,那么b 叫做当自变量为a 时的函数值.要点诠释:对于每个确定的自变量值,函数值是唯一的,但反过来,可以不唯一,即一个函数值对应的自变量可以是多个.比如:2y x =中,当函数值为4时,自变量x 的值为±2.要点四、自变量取值范围的确定使函数有意义的自变量的取值的全体实数叫自变量的取值范围.要点诠释:自变量的取值范围的确定方法:首先,要考虑自变量的取值必须使解析式有意义:(1)当解析式是整式时,自变量的取值范围是全体实数;(2)当解析式是分式时,自变量的取值范围是使分母不为零的实数;(3)当解析式是二次根式时,自变量的取值范围是使被开方数不小于零的实数;(4)当解析式中含有零指数幂或负整数指数幂时,自变量的取值应使相应的底数不为零;(5)当解析式表示实际问题时,自变量的取值必须使实际问题有意义.【典型例题】类型一、变量与函数例1、下列是关于变量x 与y 的八个关系式:① y = x ;② y 2 = x ;③ 2x 2 − y = 0;④ 2x − y 2 = 0;⑤ y = x 3 ;⑥ y =∣x ∣;⑦ x = ∣y ∣;⑧ x =2y .其中y 不是x 的函数的有_____.(填序号)【变式】下列:①2y x ;②21y x =+;③22(0)y x x =≥;④0)y x =≥,具有函数关系(自变量为x )的是______.类型二、函数解析式的取值范围 例2、求出下列函数中自变量x 的取值范围(1)2321y x x =--; (2)2131x y x -=+;(3)y =(4)y =.举一反三:【变式】等腰三角形的周长为10,底边长y 与腰x 的函数关系式是102y x =-,则自变量x 的取值范围是________.类型三、函数解析式例3.如图,一农户要建一个矩形猪舍,猪舍的一边利用住房墙(住房墙的长度大于BC ),另外三边用25m 长的建筑材料围成,为方便进出,在CD 边上留一个1m 宽的门.若设AB 为()y m ,BC 为()x m ,则y 与x 之间的函数关系式为______.【变式】如图,ABC 中,90BAC ∠=,4BC =,BD 是ABC 的角平分线,过点C 作BD 的垂线,交BD 的延长线于点E .若设AB x =,CE y =,则y 关于x 的函数解析式为___________.类型四、函数值例4、 若y 与x 的关系式为306y x =-,当x =时,y 的值为( )A .5B .10C .4D .-413课后练习1.下列式子:①y=3x ﹣5;②y=1x ;③y 2=x ;⑤y=|x|,其中y 是x 的函数的个数是( ) A .2个 B .3个 C .4个 D .5个2.下列说法中,正确的是( )A .对于两个变量x ,y ,若y x =,则y 是x 的函数B .对于两个变量x ,y ,若22016x y +=,则y 是x 的函数C .对于两个变量x ,y ,若2y x =,则y 是x 的函数D .对于两个变量x ,y ,若22y x =,则y 是x 的函数3.函数y =的自变量的取值范围是( ) A .0x B .0x > C .0x ≠ D .0x =4.下列曲线中不能表示y 与x 的函数的是( )A .B .C .D .5.下列图象中,表示y 不是x 的函数的是( )A .B .C .D .6.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了 一觉. 当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终 点……. 用 s 1 、s2 分别表示乌龟和兔子所行的路程, t 为时间,则下列图像中与故事情节相吻合的是( )A .B .C .D .。
变量与函数大一高数知识点

变量与函数大一高数知识点高等数学是大一大二学生必修的一门基础课程,其中包括了许多重要的知识点。
其中,变量与函数是高等数学中最为基础和重要的概念之一。
一、变量变量是数学中使用的一种概念,它可以表示不同数值的符号或字母。
在数学中,我们常常用字母来表示变量,如x、y、z等等。
变量可以代表任意数的集合,也可以代表某一个具体的数值。
在数学中,我们通常用变量来表示未知数,通过解方程等方法来求解变量的数值。
变量在实际问题中也很常见,我们可以通过设定变量来描述实际问题的各种情况,从而得到数学模型并解决问题。
二、函数函数是数学中另一个重要的概念。
函数是一个特殊的关系,它将一个集合的元素(自变量)映射到另一个集合(因变量)。
函数常用符号表示为y = f(x),其中x为自变量,y为因变量,f为函数关系。
函数包含了定义域、值域和对应关系三个重要的概念。
定义域是自变量的取值范围,值域是因变量的取值范围,对应关系是自变量和因变量之间的映射关系。
函数在数学中有着广泛的应用。
它们可以用来描述各种数学模型,如直线方程、曲线方程等等。
通过函数的性质和图像,我们可以研究函数的增减性、极值、导数等,从而了解函数的行为和特点。
函数可以用来解决各种实际问题,如经济学中的生产函数、物理学中的运动方程等等。
因此,对于函数的理解和掌握是我们学习高等数学的基础。
三、变量与函数的关系变量与函数之间有着密切的关系。
在函数中,自变量常常是一个或多个变量,而函数则是对自变量的一种规定或设定。
变量作为函数中的自变量,它的取值范围和变化规律会影响到函数的性质和行为。
因此,变量的取值是函数研究中一个非常重要的问题。
在实际问题中,我们可以通过设定变量来描述问题的各种情况,从而建立函数模型。
通过分析自变量的取值范围和变化规律,我们可以研究函数的图像、性质和规律。
例如,我们可以用变量来表示一个物体的位置,然后建立位置和时间的函数关系,通过分析函数曲线的形状和变化趋势,我们可以了解物体的运动规律和特点。
数学中的变量与函数关系

数学中的变量与函数关系数学中的变量与函数关系是一项基础而重要的概念。
变量和函数是数学中常见的概念,它们用于描述事物之间的关系以及数值的变化规律。
在本文中,将详细探讨数学中的变量与函数关系的基本概念、性质和应用。
一、变量变量是数学中用来表示不确定或可变值的符号。
通常用字母表示,比如x、y或者其他字母。
变量可以代表不同的数值,并且可以随着问题的不同而改变。
例如,当我们要描述一辆汽车的速度时,可以用v表示变量,因为不同的汽车会有不同的速度。
变量可以分为独立变量和因变量。
独立变量是研究中独立选择或设定的变量,它不依赖于其他变量。
而因变量是依赖于其他变量的变量,它的值根据独立变量的取值而改变。
例如,在研究中,以一个人的年龄为独立变量,体重为因变量,我们可以观察到随着年龄的增加,体重也会有相应的变化。
二、函数函数是数学中常见的关系类型,它描述了变量之间的映射关系。
对于给定的输入(自变量),函数会给出相应的输出(因变量)。
函数通常用f(x)来表示,其中,f表示函数名称,x表示自变量的取值。
函数有许多不同的类型,包括线性函数、二次函数、指数函数等。
不同类型的函数具有不同的性质和特点,它们可以用来描述不同类型的变量与变量之间的关系。
函数可以通过图像、表格或者公式来表示,这些表示方式都能够清晰地展示出变量与函数的关系。
三、变量与函数关系的性质在数学中,变量与函数关系具有许多重要的性质,其中包括:1. 单调性:变量与函数关系可以是单调递增的或单调递减的。
当自变量增大时,函数值也增大,则称其为单调递增;当自变量增大时,函数值减小,则称其为单调递减。
2. 奇偶性:变量与函数关系可以是奇函数或偶函数。
当函数满足f(-x) = -f(x)时,称其为奇函数;当函数满足f(-x) = f(x)时,称其为偶函数。
3. 周期性:变量与函数关系可以是周期函数。
周期函数在一定区间内重复出现相同的值。
例如,正弦函数和余弦函数都是周期函数,它们在一定范围内以一定的周期重复出现。
一次函数讲义变量与函数
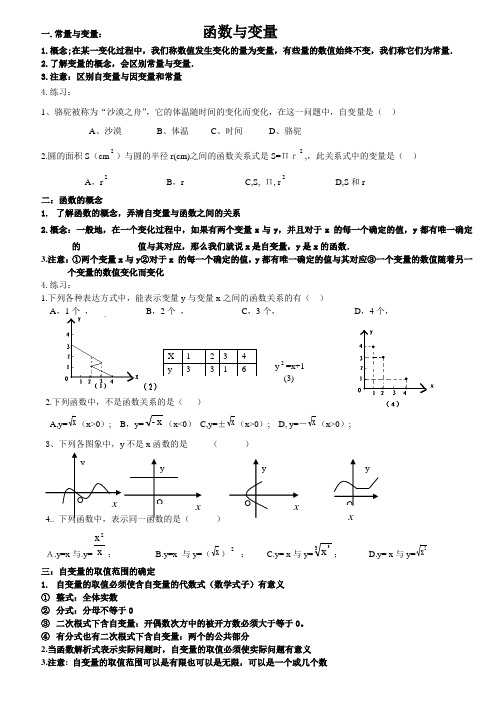
一.常量与变量:函数与变量1.概念;在某一变化过程中,我们称数值发生变化的量为变量,有些量的数值始终不变,我们称它们为常量.2.了解变量的概念,会区别常量与变量.3.注意:区别自变量与因变量和常量4.练习:1、骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一问题中,自变量是( )A 、沙漠B 、体温C 、时间D 、骆驼2.圆的面积S (cm 2)与圆的半径r(cm)之间的函数关系式是S=Πr2,,此关系式中的变量是( )A ,r 2B ,r C,S, Π, r 2D,S 和r二:函数的概念1. 了解函数的概念,弄清自变量与函数之间的关系2.概念:一般地,在一个变化过程中,如果有两个变量x 与y ,并且对于x•的每一个确定的值,y 都有唯一确定的 值与其对应,那么我们就说x 是自变量,y 是x 的函数.3.注意:①两个变量x 与y ②对于x•的每一个确定的值,y 都有唯一确定的值与其对应③一个变量的数值随着另一个变量的数值变化而变化 4.练习:1.下列各种表达方式中,能表示变量y 与变量x 之间的函数关系的有( )A ,1个 ,B ,2个 ,C ,3个,D ,4个,2.下列函数中,不是函数关系的是( )A,y=x (x>0); B ,y=x -(x<0) C,y=±x (x>0); D, y=-x (x>0); 3、下列各图象中,y 不是x 函数的是 ( )4.. 下列函数中,表示同一函数的是( )A.y=x 与.y=x x 2; B.y=x 与y=(x )2; C.y= x 与y=33x ; D.y= x 与y=2x三:自变量的取值范围的确定1. 自变量的取值必须使含自变量的代数式(数学式子)有意义 ① 整式:全体实数 ② 分式:分母不等于0③ 二次根式下含自变量:开偶数次方中的被开方数必须大于等于0。
④ 有分式也有二次根式下含自变量:两个的公共部分2.当函数解析式表示实际问题时,自变量的取值必须使实际问题有意义3.注意: 自变量的取值范围可以是有限也可以是无限,可以是一个或几个数X 1 2 3 4 y33 16O yxOxyOxyxyOy 2=x+1 (3)4.有的要列不等式或不等式组来求5.练习: 1、在函数y=xx 32+中,自变量的取值范围是( )A 、x ≥-2且x ≠0; B 、x ≤2且x ≠0; C 、x ≠0; D 、x ≤-2; 2.、函数212-++=x x y 的自变量x 的取值范围是( ) A 、x ≥-2; B 、x >-2且x ≠2; C 、x ≥0且x ≠2; D 、x ≥-2且x ≠2。
变量与函数的概念1说

数据可视化
函数还可以用于数据可视化,如 绘制图表、直方图和散点图等,
以更好地理解和分析数据。
系统建模
线性模型
线性函数可以用于建立线性模型,以描述两个变量之间的关系。
非线性模型
非线性函数可以用于建立非线性模型,以描述非线性关系。
微分方程
函数还可以用于建立微分方程,以描述动态系统的行为。
3
变量的类型和范围
根据函数的需求,变量可以有不同的数据类型 (如整数、浮点数、字符串等)和范围(如数组、 集合、字典等)。
变量作为函数
函数的结果通过变量返回
01
在函数中,经过计算或处理后,结果通常通过一个或多个变量
返回给调用者。
变量的类型和值
02
根据函数的设计,返回的变量可以有特定的数据类型和值,这
变量的分类
基本数据类型
根据存储的数据类型,变量可以 分为不同的基本数据类型,如整 数类型、浮点数类型、字符类如数 组、字符串、集合等。在这种情 况下,变量实际上存储的是对象 的内存地址,而不是对象本身。
变量的作用域
变量的作用域是指变量在程序中的可见 性和可用性范围。根据作用域的不同, 变量可以分为局部变量和全局变量。
函数可以提高代码的可重用性和可维护性,减少代码冗余。
函数的参数
参数是函数接受输入 的方式,它可以是变 量、常量、表达式等。
参数可以是必需的 (必须提供),也可 以是可选的(可以不 提供)。
参数的作用是传递数 据给函数,以便函数 能够执行所需的操作。
函数的返回值
返回值是函数执行后返回的结果。
返回值可以是任何类型的数据, 如整数、浮点数、字符串、数组
参数传递
在函数调用过程中,变量 可以作为参数传递给函数, 以影响函数的执行行为或 返回结果。
沪科版八年级数学上册第12章教学课件:12.1 第1课时 变量与函数(共23张PPT)

典例精析
例1 指出下列事件过程中的常量与变量注意:π是一个确 定的数,是常量
(1)某水果店橘子的单价为5元/千克,买a千橘子的总 价为m元,其中常量是 5 ,变量是 a,m ;
(2)周长C与圆的半径r之间的关系式是C=2πr,其中常 量是 2,π ,变量是 C, r ;
(3)三角形的一边长5cm,它的面积S(cm2)与这边上的高
第12章 一次函数
12.1 函数
第1课时 变量与函数
学习目标
1.联系自己的学习、生活实际,通过具体情境 领悟函数的概念,了解常量、变量,知道自变量 与函数,能写出简单的函数表达式;
2.探究变量的发现和函数概念的形成,提高学 生分析、解决问题的能力.
导入新课
情境引入
万物皆变
行星在宇宙中的位置随时间而变化
例2 阅读并完成下面一段叙述: ⒈某人持续以a米/分的速度用t分钟时间跑了s米,其中 常量是 a ,变量是 t,s .
⒉s米的路程不同的人以不同的速度a米/分各需跑的时间 为t分,其中常量是 s ,变量是 a,t .
3.根据上面的叙述,写出一句关于常量与变量的结论: 在不同的条件下,常量与变量是相对的 .
(2)y 是n的函数,其中n是自变量. (3)y 不是x的函数.
例如,到原点的 距离为1的点对 应实数1或-1,
课堂小结
常量与变量:在一个变化过程中, 数值发生变化的量为变量,数值 始终不变的量为常量.
变量与函数
函数:一般地,在一个变化过程 中,如果有两个变量x与y,并且 对于x的每个确定值,y都有唯一确 定的值与其对应,那么我们就说x 是自变量,y是x的函数.
自我发生变化的量__t_________; 因别人变化而变化的量___h_______.
14.1变量与函数 (第1课时)变量
第十四章一次函数
14.1变量与函数( 课时) 14.1变量与函数(第1课时) 变量与函数
问题一: 问题一
汽车以60千米 时的速度匀速行驶 千米, 汽车以 千米/时的速度匀速行驶,行驶里程为 s 千米, 千米 时的速度匀速行驶, 小时,先填下面的表,再试用含t的式子表示 的式子表示s. 行驶时间为 t 小时,先填下面的表,再试用含 的式子表示
1 s = x(10 − 2x) = x(5 − x) 2
(1)S = 60t (2) y = 10x ) ) (3)l =10+0.5x
(4)r =
1 (5)ms = x(10 − 2x) = x(5 − x) 2
s π
发生变化的量为变量 1、变量:在一个变化过程中,数值发生变化的量为变量。 变量:在一个变化过程中,数值发生变化的量为变量。 始终不变的量为常量 常量:在一个变化过程中,数值始终不变的量为常量。 2、常量:在一个变化过程中,数值始终不变的量为常量。
y = 10x
问题三: 问题三
在一根弹簧的下端挂重物,改变并记录重物的质量, 在一根弹簧的下端挂重物,改变并记录重物的质量,观 并记录弹簧长度的变化,探索它们的变化规律。 察并记录弹簧长度的变化,探索它们的变化规律。如果 弹簧长原长为10cm,每1千克重物使弹簧伸长 千克重物使弹簧伸长0.5cm,怎 弹簧长原长为 , 千克重物使弹簧伸长 怎 样用含重物质量m(单位: ) 样用含重物质量 (单位:kg)的式子表示受力后的弹 单位: 簧长度 l (单位:cm)? 单位
6a2 , 2、如图 正方体的棱长为 表面积 正方体的棱长为a,表面积 、如图2正方体的棱长为 表面积S=
体积V= 体积
11.1 变量与函数1
11.1 变量与函数第一教时 11.1.1 变 量教学要求:通过课本上的五个问题,引入并理解常量、变量的概念,会求函数自变量的取值范围教学重点:针对具体问题,分清常量与变量教学难点:在不同的变化过程中,常量与变量并不是固定不变的教学过程:一、导入新课:1.有关图形的体积、面积、周长公式:图形的周长:C 圆=2лR ;C 正方形=4a ;图形的面积:S △ABC =21×ah ; S 圆=лR 2;S 梯形=21×(a+b)h ; 图形的体积:V 圆柱=лR 2h , V 圆锥=31лR 2h ;V 正方体=a 3. 2.从实际问题出发,出于从具体到抽象在认识事物的考虑,列举课本上的物理问题、销售问题、几何问题等,要求学生会用填表、求值、写解析式等二、新授:1.常量、变量:在一个变化过程中,数值发生变化的量叫变量;数值不发生变化的量叫常量两个变量之间相互依赖、互相制约、互相转化.如在匀速直线运动中,当速度是常量,时间和路程都是变量,即s=vt ;当路程一定时,速度、时间是变量.例如,v=t s , t=v s.2.共同解答例子:[例1]下表是某市2000年统计的该市男学生各年龄组(岁)的平均身高(cm).(1)从表中你能看出该市14岁的男学生的平均身高是多少吗?(2)该市男学生的平均身高从哪一岁开始迅速增加?(3)上表反映了哪些变量之间的关系?其中哪个是自变量?哪个是函数?[思维点拨] 借助表格,可以直接找到自变量与函数的具体对应值.从中挖掘有用的信息.[解] (1)从表中能看出该市14岁的男学生的平均身高为146.1㎝;(2)该市男学生的平均身高是从14岁开始迅速增加(在14~17岁之间,后一年比上一年的身高分别增加了8.7cm,8.1cm,5.3cm);(3)表中反映了2000年某市男生的平均身高与学生年龄的关系.三、小结:由学生举一实际问题,说明哪些量是变量?哪些量是常量?四、课堂练习:课本18页第1、2、8、9题.五、教学后记:第二教时 11.1.2 函 数教学要求:通过经历从具体到抽象的认识过程,理解函数的概念、函数的单值对应. 教学重点:针对具体问题,利用表格、解析式和图象,体会相关变量之间的对应关系 教学难点:变量之间的单值对应关系教学过程:一、导入新课:从上节课的五个实际问题出发,直接导入新课二、新授:1.理解单值对应:变量之间的单值对应关系,当一个变量取定一个值时,单值对应有两重含义:(一)另一变量有对应值;(二)对应值只有一个2.理解函数的概念一般地,在一个变化过程中,如果有两个变量x 与y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说x 是自变量,y 是x 的函数.函数的定义中包括了对应值的存在性和唯一性,函数是对变量而言的;函数值是对具体数值而言的。
数学的变量与函数
数学的变量与函数数学作为一门精确的科学,扮演着解决问题、推导规律的重要角色。
在数学的世界中,变量和函数是两个基本概念,它们的关系和应用广泛存在于数学的各个领域。
本文将详细介绍数学中的变量与函数,探讨它们的定义、特性及其在数学中的应用。
1. 变量在数学中,变量是指可以取不同值的量。
它是数学中用来表示未知数或可变因素的一个符号。
通常用字母表示变量,如x、y、z等。
变量的值可以随着问题或条件的变化而改变,可以是实数、整数、分数等。
在数学中,我们经常遇到需要利用变量来表示和解决问题的情况。
变量的特性有以下几个方面:首先,变量具有可变性。
它的值没有固定的限制,可以随着问题的不同而取不同的值。
其次,变量的值可以通过计算、观察或实验来确定。
一般来说,变量的值可以通过解方程、代入等方法来求解。
最后,变量可以进行运算。
我们可以对变量进行加减乘除等基本运算,通过这些运算可以得到新的变量或确定变量的取值范围。
2. 函数函数是数学中一个重要的概念,它描述了两个量之间的依赖关系。
函数可以看作是一种特殊的关联,将一个变量的值映射到另一个变量的值。
数学上,函数通常用f(x)或y来表示,其中x是自变量,y是因变量。
函数可以看作是一个规则,它给出了自变量和因变量之间的关系。
函数有以下几个要素:首先,函数有定义域和值域。
定义域是自变量的取值范围,值域是因变量的取值范围。
其次,函数可以用图像来表示。
通过绘制函数的图像,可以更直观地理解函数的性质和关系。
最后,函数可以进行运算和组合。
我们可以对函数进行加减乘除、求导等运算,也可以通过组合两个或多个函数来构造新的函数。
函数在数学中的应用非常广泛。
例如,它可以用来描述物体的运动规律、计算数列的通项公式、解决最优化问题等。
函数的概念在数学分析、微积分、代数等学科中都有重要的应用。
3. 变量与函数的关系变量和函数是数学中密切相关的两个概念。
变量可以看作是函数中的自变量,它决定了函数的取值范围和性质。
19.1.1 变量与函数(1)
初步应用 巩固知识 3、下列关系中,y不是x的函数的是( )
x A. y 2
C.
B. D.
y 2x
2
y x ( x 0)
y x
对于x的每一个值,y 有两个值与它对应, 所以y不是x的函数。
初步应用 巩固知识
4、下列各曲线中哪些表示y是x的函数
x2 对于x的 每一个值, y只有唯 一确定的 值与它应, y才是x 的函数。
找一找
下面问题中变化的量和不变的量: (3)圆形水波慢慢地扩大,在这一过程中,当圆 的半径r 分别为10 cm,20 cm,30 cm 时,圆的面积S 分别为多少?在这个过程中,哪些量是变化的?
找一找
下面问题中变化的量和不变的量: (4)用10 m长的绳子围一个矩形,当矩形的一边 长x 分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分别为多少?在矩形改变形状的变化过程中,哪些量 是变化的?哪些量是固定不变的? D C y
x1
x1
当堂反馈
1.下列问题中哪些量是自变量?哪些量是自变 量的函数?试写出用自变量表示函数的式子
(1)改变正方形的边长x,正方形的面积S随之改变。
____是自变量,___
是___的函数,关系式__________。
(2)秀水村的耕地面积是106 m2 ,这个村人均占有 耕地面积y随这个村人数n的变化而变化。 关系式____________。 ___是自变量,___是___的函数,
万物皆变
量的变化
研究变量之间的关系
把握运动变化规律
观察思考
分析变化
想一想:1前面的每个问题中各有几个变量?
2同一个问题中的变量之间有什么联系? (1)汽车以60 km/h 的速度匀速行驶,行驶的时间 为t h,行驶的路程为s km; S=60t 行驶时间 t/h 行驶里程s/km 1 60 3 180 3. 4 204 4 240 9 540 … …
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
样爱惜美丽? ? 让我们都来力争做一个优秀的女人吧。为了世界更精彩,为了自身更完美,为了和时间对抗,为了使宇宙永恒。 今世的五百次回眸 ? 佛说,前世的500次回眸,才换来今生的擦肩而过。顿生气馁,这辈子是没得指望了,和谁路遇和谁接踵,和谁相亲和谁反目,都是
命定,挣扎不出。特别想到我今世从医,和无数病患咫尺对视。若干垂危之人,我手经治,每日查房问询,执腕把脉,相互间凝望的频率更是不可胜数,如有来世,将必定与他们相逢,赖不脱躲不掉的。于是这一部分只有作罢,认了就是。但余一部分,却留了可以掌握的机缘。一些愿望,
都一古脑地塞进去,然后蒙一块宿命的轻纱。我背着它慢慢地向前
3、如果弹簧原长10cm。每1kg重物使弹簧伸 长0.5cm,怎样用含重物质量(单位:kg)的式 子表示受力后的弹簧长度(单位:cm)?
悬挂重物 的质量(kg) 1 2
3
4
5
弹簧长度
x (cm)
4、用10cm长的绳子围成长方形,试改变长方形 的长度,观察长方形的面积怎样变化。记录不 同的长方形的长度值。计算相应的长方形面积 的值,探索它们的变化规律。设长方形的长为 xcm,面积为S,怎样用含x的式子表示S?
如果今生屡屡瞩目,就埋了一个下辈子擦肩而过的伏笔,待到日后便可再接再厉地追索和厮守。 今世,我将用余生500次眺望高山。我始终认为高山是地球上最无遮掩的奇迹。一个浑圆的球,有不屈的坚硬的骨骼隆起,离太阳更近,离平原更远,它是这颗星球最勇敢最孤独的犄角,
它经历了最残酷的折叠,也赢得了最高耸的荣誉。它有诞生也有消亡,它将被飓风抚平,它将被酸雨冲刷,它将把溃败的肌体化做肥沃的土地,它将在柔和的平坦中温习伟大。我不喜欢任何关于征服高山的言论,以为那是人的菲薄和短视。真正的高山不可能被征服的,它只是在某一个瞬
看到密集的闪电。眼神荒疏了忘却了这人间最滋润的色彩,以为是虚妄的梦境。就在那一瞬,我皈依了绿色。这是最美丽的归宿,有了它,生命才得以繁衍和兴旺。常常听到说地球上的绿地到了年头就全部沙化了,那是多么恐怖的期限。为了人类的长盛不衰,我以目光持久地祷告。
今生,我将一万次目不转睛地注视人群。如果有来生,我期望还将成为他们之中的一员,而不是其他的什么动物或是植物。尽管我知道人类有那么多可怕的弱点和缺陷,我还是为这个物种的智慧和勇敢而赞叹。我做过一次人类了,我知道了怎样才能更好地做人,做人是一门长久的功课,
例如在问题1中,时间t是自变量,里程s是t的函数。 t=1时,其函数值为6ቤተ መጻሕፍቲ ባይዱ,t=2时,其函数值为120。
; https:/// 棋牌游戏网站
;
模糊了她们的眼睛,狭隘的圈子拘谨了她们的想象。她们的嗅觉易在甜蜜的语言中迟钝,她们的脚步易在扑朔的路径中迷离。智慧不单单是天赋的独生女,她还是阅历、经验、胆魄三位共同的学生。智慧是一块璞,需要雕琢。而雕琢需要机遇。不是每一块宝石都会璀璨,不是每一粒树种
美丽的女人应该是持久的。凡稍纵即逝的美丽都不是属于人的,而是属于物的。美丽的女人少年时像露水一样纯洁,年轻时像白桦一样蓬勃,
中年时像麦穗一样端庄,老年时像河流的入海口,舒缓而磅礴。
美丽的女人经得起时间的推敲。时间不是美丽的敌人,而只是美丽的代理人。它让美丽在不同的时刻呈现出不同的状态,从单纯走向深邃。女人的美丽不是只有一根蜡烛的灯笼,它是可以不断燃烧的天然气。时间的掸
地对抗你。这不知是优秀女人的幸还是不幸?善良的智慧的有勇气的女人,要敢在黑暗的旷野独自唱着歌走路,要敢在没有桥没有船也没有乌鸦的野渡口,像美人鱼一般泅过河。
这个比例有多少? 望着越来越稀疏的队伍,我真不忍心将筛孔做得太大。但女人天性胆小,就像
含羞草乐意把叶子合起来一样。你不能苛求她们。现在,在漫长阶梯上行走的女人已经不多了。
游历和瞻仰山的英拔和广博,期望自己也变得如许坚强。喜欢绿色和生命,喜爱人的丰饶和宝贵,就爱惜资源,尊重自己也尊重他人。 活着 ?一个孩子,就像一颗渐渐长大的珍珠,润泽明媚。人们不是以一位老人的逝世当作新的开端,不是偶然的。当我们面对一个婴儿的降临,总是会
以最美好的心态祝福他比以往的任何一代,都更幸运和强大。 生命只是幸福感得以附丽的温床,生命本身是一个中性的存在。它是既可以涂写痛苦也可以泼洒快乐的一幅白绢。在我们的生命里面,寻找安全,是集体无意识的顽强表现。 人的生命是一根链条,永远有比你年轻的孩子和比
间,宽容地接纳了登山者,让你在它头顶歇息片刻,给你一窥真颜的恩赐。如同一只鸟在树梢啼叫,它敢说自己把大树征服了吗?山的存在,让我们永葆谦逊和恭敬的姿态,知道在这个世界上,有一些事物必须仰视。 今生,我将用余生一千次不倦地凝望绿色。我少年戍边,有10年的
时间面对的是皑皑冰雪,看到绿色的时间已经比他人少了许多。若是因为这份不属于我选择的怠慢,罚我下辈子少见绿色,岂不冤枉死了?记得在千百个与绿色隔绝的日子之后,我下了喀喇昆仑山,在新疆叶城突然看到辽阔的幽深绿色之后,第一反应竟是悚然,震惊中紧闭了双眼。如同
例1、写出下列各问题中的关系式,并指出 其中的自变量与函数
(1)正方形的面积S 随边长 x 的变化
S=x2
(2)秀水村的耕地面积是106m2,这个村人均耕 地面积y随着人数的变化而变化
y 106 x
(3)正多边形的内角和度数y随变数n的变化情况
y=180°(n-2)
例2、下列各问题中的变量是否是函数?
优美。甚至缺陷也是一种和谐,犹如月中的桂影。那不是皓月引发无数遐想最确实的物质基础吗?和谐是一种心灵向外散发的光辉,它最终走向圣洁。 ? 美丽其次应该是柔和的。大辛辣太喧嚣的感觉不是美,而是一种刺激。优秀女人的美丽像轻风,给世界以潜移默化的温馨。当然它
也容纳篝火一般的热情。可是你看,跳动的火苗舒卷的舌头是多么的柔和,像嫩红的枫叶,像浸湿的红绸。激情的局部仍旧是细致而绵软的。
11.1.2 函数
作者 爱才
问题1、汽车以60千米/时的速度匀速行驶,行 驶里程为s千米,行驶时间为t小时,先填写下 表,再试着用含t的式子表示s。
问题2、每张电影票的售价为10元,如果早场售出 票150张,日场售出票205张,晚场售出票310张, 三场电影的票房收入各多少元?设一场电影售出票 x张,票房收入为sy元,怎样用含x的式子表示 y?
◆最后让我们来说说美丽吧。
在这样艰苦的跋涉之后再来要求女人的美丽,真是一种残酷。犹如我们在暴风雨以后寻找晶莹的花朵。但女人需要美丽。美丽是女人最初也是最终的
魅力。不美丽的女人辜负了造物主的青睐,她们不是世上的风景,反倒成了污染。
何为美丽?一千个人有一千种说法。我只能扔出我的那一块砖。
美丽的女人首先是和谐的。面容的和谐,体态的和谐,灵与肉的和谐。美丽并非一些精致巧妙的零件的组合,而是一种整体的
别人手里,它只有一个主人,就是你自己。无论你的生命线是长是短,每一笔都由你来涂画。痛苦的人生,没有权利悲哀。苍茫的人生,没有权利渺小。。 生命一定有一个终结,正常的终结都在一天天迫近,何况还有许多意外的终结。我很想让我在有限的时间里做更多有意义的事情。
生命是个人的一种缘分,我们每个人都有开拓它的自由。年轻时谋生的压力可能比较大,选择时会有所勉强,中年往往就不必为生计所累,倒更有可能做自己真正愿意做的事情。。 我喜欢未雨绸缪,在我还能微笑和努力的时候,就把心上的坠累一一摘掉。我不希图来世的天堂,只期待
今生今世此时此刻朝着愉悦和幸福的方向前进。天堂不是目的地,只是一个让我们感到快乐自信的地方。。 一个人就像是一粒种子,天生就有发芽的欲望。只要是一颗健康的种子,哪怕是在地下埋藏千年,哪怕是到太空遨游过一圈,哪怕被冰雪封盖,哪怕经过了鸟禽消化液的浸泡,哪
怕被风剑霜刀连续宰杀,只要那宝贵的胚芽还在,一到时机成熟,它就会在阳光下探出头来,绽开勃勃的生机。 无助无望无用,是人生的大悲凉。 命运是我怯懦时的盾牌,当我叫嚷命运不公最响的时候,正是我预备逃遁的前奏。命运像一只筐,我把对自己的姑息、原谅以及所有的延宕
(1)y 2x 中的y与x
是
(2)初二某班的同学与号次 是
(3)一天中的气温与时刻
是
(4) y x
不是
例3、求出下列函数中自变量的取值范围
(1)y=2x
x为任何实数
(2) m n 1
n≥1
(3)y 3 x2
(4)h 1 k k 1
x≠-2
k≤1且k ≠-1
1、轮船在静水中的速度为x千米/小时,水速为2 千米/小时,A、B两地相距60千米,船在A、B两 地往返一次所需时间y小时,则y与x的函数关系
你年迈的老人。我们每个人都有自己的位置,它是一宗谁也掠夺不去的财宝。不要计较何时年轻,何时年老。只要我们生存一天,青春的财富,就闪闪发光。能够遮蔽它的光芒的暗夜只有一种,那就是你自以为已经衰老。坎坷和顺利,似乎是反义词,其实都是生命的相对状态。……我们
可以在顺利的时候愁容惨淡,也可以在苦难的时候欢颜一笑,关键在于我们把握命运的定力。 生命正是因为种种的不知道和种种的可能性,才变得绚烂多姿和魅力无穷。 生命是美丽的,它无所谓高贵也无所谓谦卑。人类和所有的物种都是自然之子,我们有一座共同的花园。人类自身昌
子轻轻扫去女人脸上的红颜,但它是有教养的,还女人一件永恒的化妆品--叫做气质。可惜有的女人很傻,把气质随手丢掉了。
也许可以说,所有美好的女人都是美丽的。
我在女性的群体里砌了一座金字塔,它是我心目中的女性黄金分割图。这样一路算下来,优秀的女人多
乎哉?不多也。是不是我的比例过于苛刻?是不是我对世界过于悲观?是不是我看女人的暗影太多,是不是优秀和平庸原不该分得太清?
1、都有两个变量
共同特征:2、其中的一个变量取定一个值,另
一个变量的值也唯一确定
在心电图中,时间、心脏电流都是变量
§11.1.2函数(一)
在一个变化过程中,如果有两个变量x与y,并 且对于x的每一个确定的值,y都有唯 一确定的 值与其对应,那么我们就说是x自变量 ,y是x 的函数。如果当x=a时y=b,那么b叫做当自变 量x的值为a时y的函数值
