第22讲 磁感应强度 毕萨定律
毕奥-萨伐尔定律

毕奥—萨伐尔定律1820年,毕奥和萨伐尔通过实验得到了载流导线周围磁场与电流的定量关系,拉普拉斯又以公式的形式概括得出电流元产生磁感强度d B 的规律。
为计算电流为I 的导线在空间某点户产生的磁感强度B ,设想将载流导线分割成许多电流元,用矢量dl I 表示.线元dl的方向与电流流向一致。
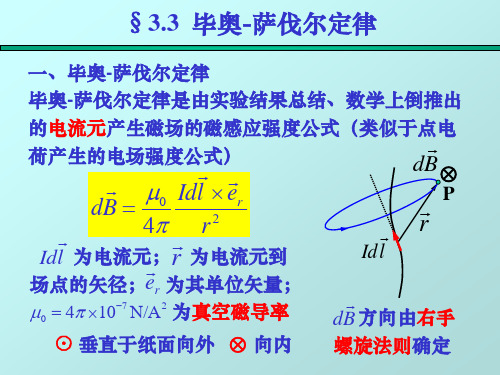
毕奥—萨伐尔定律指出:载流导线上的电流元dl I 在真空中某点P 的磁感度dB 的大小与电流元dl I 的大小成正比,与电流元dl I 和从电流元到P 点的位矢r 之间的夹角θ的正弦成正比,与位矢r 的大小的平方成反比,即20sin 4r dl I dB θπμ= (9-2a ) 上式中,πμ40为比例系数,0μ称为真空磁导率,其值为 270104--∙⨯=A N πμ dB 的方向垂直于dl I 和r 所确定的平面,当右手弯曲,四指从dl I 方向沿小于π角转向r 时,伸直的大姆指所指的方向为dB 的方向, 即dB 、dl I 、r 三个矢量的方向符合右手螺旋法则,如图9—2所示,因此,可将式(9—2a)写成矢量形式204r rdlI dB ⨯=πμ(9-2b)上式中,r0为位矢r的单位矢量.此即毕奥——萨伐尔定律的公式表述。
与点电荷的场强公式相似,毕奥——萨伐尔定律是求电流周围磁感强度的基本公式.磁感强度B也遵从叠加原理.因此,任一形状的载流导线在空间某一点P的磁感强度B,等于各电流元在该点所产生的磁感应强度dB的矢量和,即⎰⎰⨯==L r rIdldBB204πμ(9-3)例9-1例9-1求载流直导线周围的磁场。
解:设有长为L的直导线上通有电流I,求距离此导线为a处一点P的磁感应强度。
在直导线上任取一电流元Idl,它到P点的位矢为r,P点到直线的垂足为O,电流元到O的距离为l,Idl与r的夹角为θ,如左图所示。
根据毕萨定律可得该电流元在P点的磁感应强度dB的大小为20sin 4r l d I dB θπμ= dB 的方向垂直于纸面向里,图中用⊗表示.由于直导线上所有电流元在P 点的磁感应强度dB 的方向度相同,所以, P 点的磁感应强度B 的大小等于各电流元在P 点dB 的大小之和,即20sin 4r l d I B L θπμ⎰= 将上式中l 、r 、θ等变量统一为一个变量,以便积分.由图9-3所得()θπ-=ctg a lθθd adl 2sin =()θθπsin sin a a r =-=于是()2100c o s c o s 4s i n 421θθπμθθπμθθ-==⎰aI d a I B (9-4)式中,θ1和θ2分别为直导线两端的电流元与它到P 点的位矢之间的夹角。
毕萨定律演示文稿

O l
x
θ
θ
1
⊗
P
µ0I = (cosθ1 −cosθ2) 4x π
I dl
r
讨论
µ0I B= (cosθ1 −cosθ2) 4x π
∞ ( x<<L) 0 θ2 π
θ2
1、无限长载流直导线 、
当 L θ1
比较无限长带电 直导线附近场强
λ E= 2πε 0 x
µ0I B= 2x π
l O
x
θ
I dl
y
设圆电流在yz平面内 设圆电流在 平面内
I z
R o
x.
P
x
y
Id l r 组成的平面
Idl r0 ˆ
I z R
o
r
dB
x
.
P
x
第一步: 解:第一步:在圆电流上任取一电流元 Idl 由毕-萨定律知其在场点P 由毕-萨定律知其在场点P产生的磁感强度
dB =
ˆ µ0 Idl × r 0 4πr
2
第二步: 第二步:分析各量关系 明确 dB的方向和大小
毕奥- §11-2 毕奥-萨伐尔定律及其应用
要解决的问题是: 要解决的问题是: 真空中电流与其激发的磁场之间的定量关系 真空中电流与其激发的磁场之间的定量关系 电流与其激发的磁场 方法: 方法:将电流分割成无穷多电流元 Idl 求出电流元产生的磁感强度 应用叠加原理 可得到任一电流所激发的磁场
一 毕奥 – 萨伐尔定律
(4)通电均匀密绕螺线管轴线上 注意: 注意:a、分析B的对称性,建立坐标系,变矢量积分为标量 分析B的对称性,建立坐标系, 积分进行计算; 统一积分变量,给出正确的积分上下限。 积分进行计算;b、统一积分变量,给出正确的积分上下限。 5、用已知典型电流的磁场迭加求出未知磁场的分布
磁学 3-2 毕奥-萨伐尔定律
B
0m 2x3
类似于电偶极子电场强度
m S en
I
B
磁偶极子
E
电偶极子
三、运动电荷产生的磁场
电流是大量电荷定向运动形 成的,所以从本质上说电流 产生的电场就是运动电荷所 产生的磁场。
I
qv
I = nqSv
S
P
在载流 导线中选取一段电流
dl
元 Idl ,其电流 I = nqSv
代入毕奥-萨伐尔定律,得
大小为
dB
0 4
Idl sin
r2
θ2
Id l
θ
r
l
Oa
θ1
B
P
由右手螺旋法则知其方向 垂直于纸面向内。因直导 线上所有电流元在 P 点产 生的磁感应强度方向均相
B
dB
0 4
Idl sin r2
l a cot ( ) a cot
同,故 P 点总的磁感应强
dl ad / sin 2
磁场叠加原理:任意形状的载流导线的磁场是所有
电流元的磁场的矢量和
B dB
0
L
L 4
Idl
r2
er
积分遍及整 个载流导线
实际上不存在孤立的电流元,毕奥-萨伐尔定律是基 于特殊情形的实验结果从数学上倒推出来的。但从 此定律出发推出任意恒定电流的磁场都与实验结果 相符,从而验证了毕奥-萨伐尔定律的正确性。
B 0I 4a
(3)直电流延长线上 B = 0
直线电流的 磁感应线
例 2 载流圆线圈半径为 R,电流强度为 I,求圆线圈 中轴线上与圆心 O 距离为 x 处 P 点的磁感应强度。
解:如图建立坐标 系
任取一电流元 Idl,注意到
大学物理毕萨定律教案

课时:2课时教学目标:1. 理解毕萨定律的基本内容,掌握其应用方法。
2. 能够运用毕萨定律解决实际问题,提高学生的分析问题和解决问题的能力。
3. 培养学生的科学素养,提高学生的科学探究能力。
教学重点:1. 毕萨定律的基本内容2. 毕萨定律的应用教学难点:1. 毕萨定律在解决实际问题中的应用2. 对比毕萨定律与安培定律的区别与联系教学过程:第一课时一、导入1. 引入电磁学的基本概念,激发学生的学习兴趣。
2. 简要介绍毕萨定律的背景和意义。
二、新课讲解1. 介绍毕萨定律的基本内容:电流元在空间某点P处产生的磁感应强度dB与电流元Idl的大小、夹角的正弦成正比,与距离的平方成反比。
2. 解释毕萨定律中的各个物理量:电流元、磁感应强度、夹角、距离。
3. 通过实例说明毕萨定律的应用,如:计算电流元在空间某点产生的磁场。
三、课堂练习1. 计算电流元在空间某点产生的磁场。
2. 分析毕萨定律与安培定律的区别与联系。
四、课堂小结1. 总结本节课所学内容,强调毕萨定律的基本内容和应用。
2. 提出课后作业,巩固所学知识。
第二课时一、导入1. 复习上节课所学内容,检查学生对毕萨定律的掌握情况。
2. 引入毕萨定律在解决实际问题中的应用。
二、新课讲解1. 介绍毕萨定律在解决实际问题中的应用:如计算电流元在空间某点产生的磁场,分析电流分布对磁场的影响等。
2. 通过实例说明毕萨定律在工程、科研等领域的应用。
三、课堂练习1. 计算电流元在空间某点产生的磁场。
2. 分析电流分布对磁场的影响。
四、课堂小结1. 总结本节课所学内容,强调毕萨定律在解决实际问题中的应用。
2. 提出课后作业,巩固所学知识。
教学反思:1. 本节课通过实例讲解毕萨定律的基本内容,帮助学生理解和掌握该定律。
2. 通过课堂练习,提高学生的分析问题和解决问题的能力。
3. 在实际应用中,培养学生的科学素养和科学探究能力。
.毕奥-萨伐尔定律

.毕奥-萨伐尔定律
摘要:
1.毕奥- 萨伐尔定律的定义
2.毕奥- 萨伐尔定律的发现历程
3.毕奥- 萨伐尔定律的数学表达式
4.毕奥- 萨伐尔定律的应用领域
5.毕奥- 萨伐尔定律在我国的研究现状与前景
正文:
毕奥- 萨伐尔定律,又称毕萨定律,是电磁学中的一个基本定律,描述了电流在磁场中受力的规律。
该定律由法国物理学家让- 巴蒂斯特·毕奥(Jean-Baptiste Biot)和法国数学家费尔南德·萨伐尔(Ferdinand de Saussure)在1820 年同时独立发现,故以两位科学家的名字命名。
毕奥- 萨伐尔定律的数学表达式为:F = I * d * B,其中F 表示电流在磁场中受到的安培力,I 表示电流强度,d 表示电流元的长度,B 表示磁感应强度。
根据这个公式,可以计算出电流在磁场中所受的力。
毕奥- 萨伐尔定律在许多领域都有广泛的应用,如电磁制动、电磁起重机、电磁继电器等。
此外,在现代科技领域,如磁悬浮列车、电动汽车、风力发电等方面,毕奥- 萨伐尔定律的应用也越来越重要。
在我国,对毕奥- 萨伐尔定律的研究始于上世纪50 年代。
经过几十年的发展,我国在电磁学领域的研究已经取得了世界领先的成果。
目前,我国正加大对电磁学领域的研究力度,致力于推动电动汽车、磁悬浮列车等新型产业发
展,为我国经济建设和科技进步做出贡献。
总之,毕奥- 萨伐尔定律作为电磁学的基本定律之一,对我国科技发展具有重要意义。
大学物理磁场毕萨定律教案

课时:2课时教学目标:1. 理解毕奥-萨伐尔定律的基本概念和公式。
2. 掌握计算电流元在空间某点产生的磁感应强度的方法。
3. 理解磁感应强度与电流元、距离和夹角之间的关系。
4. 能够运用毕奥-萨伐尔定律解决实际问题。
教学重点:1. 毕奥-萨伐尔定律的基本概念和公式。
2. 磁感应强度的计算方法。
教学难点:1. 理解磁感应强度与电流元、距离和夹角之间的关系。
2. 运用毕奥-萨伐尔定律解决实际问题。
教学准备:1. 教学课件2. 黑板、粉笔3. 学生实验器材(如电流表、磁针、导线等)教学过程:第一课时一、导入1. 回顾电流与磁场之间的关系,引出毕奥-萨伐尔定律。
2. 介绍毕奥-萨伐尔定律的发现背景和意义。
二、基本概念1. 电流元:一段长度为dl、电流为I的导线段。
2. 磁感应强度:描述磁场对电流元的作用力,用B表示,单位为特斯拉(T)。
3. 毕奥-萨伐尔定律:电流元在空间某点P处产生的磁感应强度dB与电流元Idl 的大小、距离r和夹角θ之间的关系。
三、公式推导1. 电流元Idl在空间某点P处产生的磁感应强度dB的公式:dB = (μ0/4π) (Idl × r) / r^3其中,μ0为真空磁导率,r为电流元Idl到点P的距离,θ为电流元Idl与r之间的夹角。
四、例题解析1. 给定一个电流I,求其所在直线段上的磁感应强度。
2. 给定一个圆环电流,求其中心点的磁感应强度。
第二课时一、复习导入1. 回顾上一节课的内容,提问学生毕奥-萨伐尔定律的基本概念和公式。
2. 引导学生思考磁感应强度与电流元、距离和夹角之间的关系。
二、实际应用1. 介绍磁感应强度在生活中的应用,如电流表的制作、磁悬浮列车等。
2. 给出一些实际问题,让学生运用毕奥-萨伐尔定律进行计算。
三、实验演示1. 展示毕奥-萨伐尔定律的实验装置,如电流表、磁针、导线等。
2. 实验操作,观察实验现象,分析实验结果。
四、课堂小结1. 总结毕奥-萨伐尔定律的基本概念和公式。
大学物理磁场与毕萨定理
(x)的磁感应强度。
R
解:任取电流元 Idl
电流元在P点激发的磁 I o
感应强度 dB 的大小为:
dB
0Idl sin 4r 2
90 0
Idl
r
dB
dB
dB x
x P dBx ' x
dB ' dB'
在 x 轴下方找出 dl 关于 x 轴对称的一个电流元 Idl’,
Idl sin r2
为Idl 与 r 之间的夹角。
•方向:由右手螺旋法则确定
dB 的方向垂直于Id
l和r所形
成的平面。
Idl
P
r
dB
dB
Idl
r
一段载流导线产生的磁场:
B dB
L
L
o
Idl
4r 2
er
应用毕萨定律计算一段载流导体的磁场:
(2)具有磁极,分磁北极N 和磁南极S。
司南勺
(3)磁极之间存在相互作用,同性相斥,异性相吸。
(4)磁极不能单独存在。
在磁极区域,磁性较强
地球是一个巨大 的永磁体。
11.5
磁偏角
1820年4月,丹麦物理学家奥 斯特发现了小磁针在通电导 线周围受到磁力作用而发生 偏转。
实验发现: 磁铁对载流导线、载流导线之
的无限长载流直导线;
电流元电流 dI I dx a
o P B x
dB
0dI 2x
0 Idx 2ax
b
B dB ab 0Idx 0 I ln a b
b 2ax 2a b
毕萨定律
r
r
P 点产生的磁场: 在P点产生的磁场: 点产生的磁场
dB 0 qv sin( ∠v.r) B= = 2 dN 4π r
S ++
+
dl + + +
v
I
r B = dB = 0
dN
r
P
在P点产生 点产生 的磁场: 的磁场:
考虑方向: 考虑方向:
0 qv × r B= 2 4π r
0 qv sin 90 B= 2 4π r7BFra bibliotek- v
4π
r
2
1.60×10 ×2.2×10 =10 =13(T) 10 2 (0.53×10 )
6
19
�
电流
磁感应强度的定义
某点磁感应强度数值上等于单 某点磁感应强度数值上等于单 位电荷以单位速率通过该点所 受的最大磁力. 受的最大磁力.
Fm
αB q
v
(F洛 )最大 F洛 B= ====== α等于90 qv sinα (α等于 0) qv
方向:沿小磁针 极方向 方向:沿小磁针N极方向
毕奥--沙伐尔 拉普拉斯定律 毕奥 沙伐尔--拉普拉斯定律 沙伐尔
四)运动电荷的磁场 考虑一段导体,载流子带正电q, 考虑一段导体,载流子带正电 ,以同一平均 运动. 速度 v 运动. + + + ++ + ++ +++++++++++++++++++++++++++++++++++ v +++++++++++++++++++++++ + ++j+++++++ + +++++++++++++++++++++++++++++ +++ ++++++++ + ++ + +
磁场与毕奥萨伐尔定律
解 求出:
:
r dB
=
μ0 4π
Idzerz
×
(
r0 erx r02 +
− zerz z 2 )3 /
2
r Idl
=
Idzerz
,相应的
r dB
用毕—萨定律
∫ ∫ 磁场
r B
=
r dB
=
μ0 4π
Iery
r0
∞ ∞
( r02
dz + z2
)3 / 2
=
μ0 2πr0
Iery
[例
3-2-2]半径为r0的圆形电流I,在轴线上距离为z的P1点的磁场
r H
()之间的关系,然后拉普拉斯
从数学上导出电流
r Idl
及其场强
r dH
(或
r dB
=
r μ 0 dH
)之间的关系,因此(4)式
又称为毕奥—萨伐尔—拉普拉斯(Biot-Sarvart-Laplace)定律。毕奥—萨伐尔 的重要实验是弯折导线的实验,参见图 3.23 实验结果是
H∞ 1 tg a r2
半截导线与上半截导线重合,由这个特点就能推出下半截导线与上半截导线产生
的磁场是相等的,都是H/2。现在A点附近取一点A1(参见图 5 或附图 1),令AA1=dl,
考虑到A1 以上段的半直线电流可以成以A1 为顶点的折线电流的上半段,因它在
P0
点所产生的磁场为
r H
′′
=
r H1 2
=
k1 I 2r1
a
− da 2
)ery
=
k1 2
I[
dr r2
tg
a 2
+
高二物理竞赛电磁学磁场毕萨定律课件
第1节 磁性与磁场
Magnetism and Magnetic Fields
一、磁场
1. 基本的磁现象:
磁铁、磁性、磁极(N、S)、磁力、磁化等
SN
条形磁铁:
S
指南针:
N
最早的指南针——司南 (战国,距今约2500年)
航海使用的罗盘
2.电与磁的联系
1820年,奥斯特发现: 电流旁的小磁针偏转
同年,安培发现: 磁铁旁的载流导线运动
B 磁场对其内的运动电荷有力的作用。
o x I 载流导线——载流导线
P 圆心处: B (下面讨论几种常见的电流结构)
3/2 0
3º 轴线以外的磁场较复杂,
3º 无限长载流直螺线管的磁场 I与B线仍服从右手螺旋关系
(下面讨论几种常见的电流结构) 可定性给出磁感应线,
2R
求载流圆线圈轴线上的磁场B,
SI制 T(特斯拉)
dB
0 4
Idl er r2
毕 — 萨定律
长为L的载流导线, 在P点的磁感应强度
.P
I d l r
用迭加法得:
B
0 4
Idl er r2
I
B x LdB x
B B y LdB y
Bz LdBz
二、毕—萨定律的应用
(下面讨论几种常见的电流结构)
例1. 求长为L的直线电流 I 在周围 空间激发的磁场。
Fq0vB
1ºF(v、B) 决定的平面
F
vB
2ºv B 时,F=Fmax 3ºv ||B 或 vB 及v =0 时, F=0
大小 B Fm ax
B
q0v 方向 Fmaxv
Fm ax B
v
显然比 单位:
