§9.2 毕奥-萨伐尔定律
合集下载
毕奥萨伐尔定律
1820年，法国物理学家比奥特（Biot）和萨瓦特（Savart）通过实验，测量了一条长直电流线附近的小磁针的力定律，并发表了一篇论文，题为“传递给运动中的金属的电的磁化力”。
后来被称为比奥-萨瓦特定律。
后来，在数学家拉普拉斯（Laplace）的帮助下，该定律以数学公式表示。
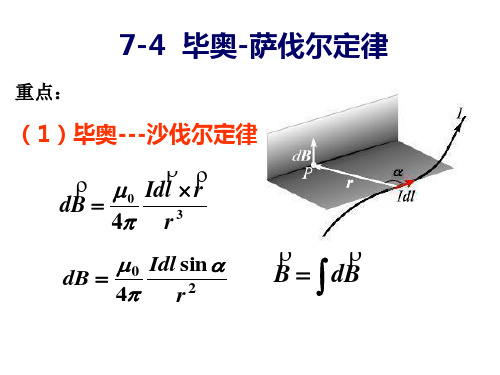
毕奥-萨伐尔定律：载流导线上的电流元Idl在真空中某点P的磁感度dB的大小与电流元Idl的大小成正比，与电流元Idl和从电流元到P点的位矢r之间的夹角θ的正弦成正比，与位矢r的大小的平方成反比。
dB的方向垂直于Idl和r所确定的平面，当右手弯曲，四指从方向沿小于π角转向r时，伸直的大拇指所指的方向为dB的方向，即dB、Idl、r三个矢量的方向符合右手螺旋法则。
叠加原理：
与点电荷的场强公式相似，毕奥——萨伐尔定律是求电流周围磁感强度的基本公式．磁感强度B也遵从叠加原理．因此，任一形状的载流导线在空间某一点P的磁感强度B，等于各电流元在该点所产生的磁感应强度dB的矢量和。
特点：
从课程论和物理学课自身特点的角度来分析毕奥-萨伐尔定律，它体现的学科特点有以下几点：（1）是稳恒电流磁场的关键知识点；（2）具有高度的抽象性；（3）使用数学工具的复杂性；（4）掌握“方法”比掌握“内容”更重要；（5）在探索知识的过程中体现“把握本质联
系，揭示事物发展内在规律性”的唯物辩证法观点。
毕奥---萨伐尔定律
毕奥---萨伐尔定律 毕奥 萨伐尔定律
两电流元之间的安培定律也可表示成 两电流元之间的安培定律也可表示成
u r r uur u r ˆ I1 I 2 dl2 × (dl1 × r12 ) d F12 = k = I 2 dl2 × dB1 2 r 12
电流元 I1d l1产生的磁场
ˆ ˆ Idl × r µ0 Idl × r dB = k = 2 2 r 4π r
• 求二阶导数
d 2B 在O 令x = 0处的 2 = 0 ⇒ 在O点附近磁场最均匀的条件 dx µ0 d 2B 2a 2 − 2 R 2 = 6π R 2 I = 0 ⇒ a2 = R2 7 2 dx 2 x =0 4π 2 a 2 2 R + 4
a=R
例1、无限长载流直导线弯成如图形状
大小
µ0 Idl dB = 4π r2
r r 方向 Idl × r0
分析对称性、 分析对称性、写出分量式
r r B⊥ = ∫ dB = 0
⊥
µ0 Idl sinα Bx = ∫ dBx = ∫ 4π r2
统一积分变量
µ0 Idl sinα Bx = ∫ dBx = ∫ 4π r2 µ0IR µ0IR dl = π = ⋅2 R 3 ∫ 3 4 r 4 r π π
a
•
•
P T
µ0I 3 BL′A = (cos π − cosπ ) 4πa 4
µ0I π BLA = (cos0 − cos ) 方向 ⊗ 4 a 4 π
方向 ⊗
T点
Bp = BLA + BL′A = 2.94×10−5T 方向 ⊗
r 电流元 Idl
——右手定则 右手定则 r r r µ0 Idl ×r 毕奥-萨伐尔定律 毕奥 萨伐尔定律 dB = 4 π r3 r r r r µ0 Idl ×r 对一段载流导线 B = ∫ dB = ∫ 4π L r3
两电流元之间的安培定律也可表示成 两电流元之间的安培定律也可表示成
u r r uur u r ˆ I1 I 2 dl2 × (dl1 × r12 ) d F12 = k = I 2 dl2 × dB1 2 r 12
电流元 I1d l1产生的磁场
ˆ ˆ Idl × r µ0 Idl × r dB = k = 2 2 r 4π r
• 求二阶导数
d 2B 在O 令x = 0处的 2 = 0 ⇒ 在O点附近磁场最均匀的条件 dx µ0 d 2B 2a 2 − 2 R 2 = 6π R 2 I = 0 ⇒ a2 = R2 7 2 dx 2 x =0 4π 2 a 2 2 R + 4
a=R
例1、无限长载流直导线弯成如图形状
大小
µ0 Idl dB = 4π r2
r r 方向 Idl × r0
分析对称性、 分析对称性、写出分量式
r r B⊥ = ∫ dB = 0
⊥
µ0 Idl sinα Bx = ∫ dBx = ∫ 4π r2
统一积分变量
µ0 Idl sinα Bx = ∫ dBx = ∫ 4π r2 µ0IR µ0IR dl = π = ⋅2 R 3 ∫ 3 4 r 4 r π π
a
•
•
P T
µ0I 3 BL′A = (cos π − cosπ ) 4πa 4
µ0I π BLA = (cos0 − cos ) 方向 ⊗ 4 a 4 π
方向 ⊗
T点
Bp = BLA + BL′A = 2.94×10−5T 方向 ⊗
r 电流元 Idl
——右手定则 右手定则 r r r µ0 Idl ×r 毕奥-萨伐尔定律 毕奥 萨伐尔定律 dB = 4 π r3 r r r r µ0 Idl ×r 对一段载流导线 B = ∫ dB = ∫ 4π L r3
毕奥萨伐尔定律
• 我们只计算了轴线上的磁场分布,轴线以外磁场分布的计算比 较复杂, 略。为了给同学们一个较全面的印象，下左图显示 了通过圆线圈轴线的平面上磁感应线的分布图。可以看出， 磁感应线是一些套连在圆电流环上的闭合曲线。
• 下右图给出另一个右手定则，用它可以判断载流线 圈的磁感应线方向。这右手定则是：用右手弯曲的 四指代替圆线圈中电流的方向,则伸直的姆指将沿着 轴线上Ｂ的方向。
生的磁感应强度的大小 • 与电流元Idl的大小成正比， • 与电流元和从电流元到Ｐ点的位矢之间的夹
角θ的正弦成正比， • 与位矢r的大小的平方成反比。即：
一、毕奥－－－萨伐尔定律
dB的方向 垂直于dl和r所确定的平面，沿
dl×r的方向，用右手螺旋法 则来判定。
矢量表示为： d B 0 Id l r 4 r 3
• 其中：S=πR2为圆线圈的面积。
三、载流圆环导线轴线上的磁场
• 圆线圈轴线上各点的磁感应强度都沿着轴线方向， 与电流方向组成右手螺旋关系。
• 下面讨论两种特殊的情况： • 1、在圆心Ｏ处，即a=0处的磁感应强度为： •
• 2、在远离线圈处，即 a>>R，轴线上各点的磁感 应强度约为：
三、载流圆环导线轴线上的磁场
• 由图
cos 1
x L 2
R2 (x L )2 2
cos 2
x L 2
R2 (x L)2 2
代入即得螺线管轴线上任一点P的磁感应强度。
B随x变化关系见上图中的曲线，由这曲线可以看出，当 L>>R时，在螺线管内部很大一个范围内磁场近于均匀， 只在端点附近B值才显著下降。
• 其中 40为比例系数， • μ0 称 为 真 空 磁 导 率 ， ：
• 下右图给出另一个右手定则，用它可以判断载流线 圈的磁感应线方向。这右手定则是：用右手弯曲的 四指代替圆线圈中电流的方向,则伸直的姆指将沿着 轴线上Ｂ的方向。
生的磁感应强度的大小 • 与电流元Idl的大小成正比， • 与电流元和从电流元到Ｐ点的位矢之间的夹
角θ的正弦成正比， • 与位矢r的大小的平方成反比。即：
一、毕奥－－－萨伐尔定律
dB的方向 垂直于dl和r所确定的平面，沿
dl×r的方向，用右手螺旋法 则来判定。
矢量表示为： d B 0 Id l r 4 r 3
• 其中：S=πR2为圆线圈的面积。
三、载流圆环导线轴线上的磁场
• 圆线圈轴线上各点的磁感应强度都沿着轴线方向， 与电流方向组成右手螺旋关系。
• 下面讨论两种特殊的情况： • 1、在圆心Ｏ处，即a=0处的磁感应强度为： •
• 2、在远离线圈处，即 a>>R，轴线上各点的磁感 应强度约为：
三、载流圆环导线轴线上的磁场
• 由图
cos 1
x L 2
R2 (x L )2 2
cos 2
x L 2
R2 (x L)2 2
代入即得螺线管轴线上任一点P的磁感应强度。
B随x变化关系见上图中的曲线，由这曲线可以看出，当 L>>R时，在螺线管内部很大一个范围内磁场近于均匀， 只在端点附近B值才显著下降。
• 其中 40为比例系数， • μ0 称 为 真 空 磁 导 率 ， ：
毕奥-萨伐尔定律公式
毕奥-萨伐尔定律公式
毕奥-萨伐尔定律公式是描述电磁感应现象的重要公式之一，它是由法国物理
学家毕奥和英国物理学家萨伐尔分别独立提出的，因此也被称为毕萨定律。
该定律表述了当一个闭合电路中的磁通量发生变化时，该电路内会产生电动势。
具体来说，如果一个电磁感应器中的磁通量Φ发生变化，那么在该感应器两端就
会产生一个电动势E，其大小与磁通量变化率的绝对值成正比。
毕奥-萨伐尔定律公式可以用一个简单的公式来表达：
E = -dΦ/dt
其中，E是感应电动势的大小，Φ是穿过感应电路的磁通量，t是时间，d/dt表示对时间的导数运算。
公式中的负号表示感应电动势的方向与磁通量变化的方向相反。
需要注意的是，该定律只适用于闭合电路中的感应电动势。
对于非闭合电路，根据法拉第电磁感应定律，产生的感应电动势大小与闭合电路中的相同，但方向可能不同。
总的来说，毕奥-萨伐尔定律公式是电磁学中一个非常重要的公式，广泛应用
于各种电磁感应现象的分析和设计中。
毕奥-萨伐尔定律
结果对比
将实验结果与毕奥-萨伐尔定律的理论值进行对比，评估定律的准确性。
结果分析
分析实验误差来源，如设备精度、环境干扰等，提高实验的可靠性和准确性。
05
毕奥-萨伐尔定律的扩展与 推广
对三维空间的推广
总结词
毕奥-萨伐尔定律最初是在二维空间中 推导出来的，但通过引入矢量运算， 该定律可以扩展到三维空间中。
Idl
电流元，表示电流的一 部分。
r
观察点到电流元的径矢 ，表示观察点与电流元
之间的距离。
03
毕奥-萨伐尔定律的应用场 景
电场与磁场的关系
磁场是由电流产生的，而电场是由电 荷产生的。毕奥-萨伐尔定律描述了 电流和磁偶极子产生的磁场，以及变 化的电场产生的磁场。
毕奥-萨伐尔定律揭示了电场和磁场之 间的相互关系，表明它们是电磁场的 两个方面，而不是独立存在的。
THANKS
对微观尺度的适用性问题
毕奥-萨伐尔定律在描述微观尺度的电磁场时，其精确度受 到限制。在量子尺度下，电磁场的涨落和量子效应可能导 致定律的不适用。
未来研究需要进一步探索毕奥-萨伐尔定律在微观尺度下 的适用性和修正，以更好地描述量子电磁场的行为。
对超导态物质的适用性问题
毕奥-萨伐尔定律在描述超导态物质的 电磁场时，可能存在局限性。超导态 物质的电磁行为与常规物质有所不同， 需要更复杂的理论模型来描述。
电流与磁场的相互作用
根据毕奥-萨伐尔定律，电流产生磁场，而磁场对电流有作用 力。这种作用力被称为洛伦兹力，它描述了电流在磁场中所 受到的力。
毕奥-萨伐尔定律是电动机和发电机等电气设备工作的基础， 它解释了电流如何在磁场中受到作用力，从而产生旋转或线 性运动。
磁力线的描绘
将实验结果与毕奥-萨伐尔定律的理论值进行对比，评估定律的准确性。
结果分析
分析实验误差来源，如设备精度、环境干扰等，提高实验的可靠性和准确性。
05
毕奥-萨伐尔定律的扩展与 推广
对三维空间的推广
总结词
毕奥-萨伐尔定律最初是在二维空间中 推导出来的，但通过引入矢量运算， 该定律可以扩展到三维空间中。
Idl
电流元，表示电流的一 部分。
r
观察点到电流元的径矢 ，表示观察点与电流元
之间的距离。
03
毕奥-萨伐尔定律的应用场 景
电场与磁场的关系
磁场是由电流产生的，而电场是由电 荷产生的。毕奥-萨伐尔定律描述了 电流和磁偶极子产生的磁场，以及变 化的电场产生的磁场。
毕奥-萨伐尔定律揭示了电场和磁场之 间的相互关系，表明它们是电磁场的 两个方面，而不是独立存在的。
THANKS
对微观尺度的适用性问题
毕奥-萨伐尔定律在描述微观尺度的电磁场时，其精确度受 到限制。在量子尺度下，电磁场的涨落和量子效应可能导 致定律的不适用。
未来研究需要进一步探索毕奥-萨伐尔定律在微观尺度下 的适用性和修正，以更好地描述量子电磁场的行为。
对超导态物质的适用性问题
毕奥-萨伐尔定律在描述超导态物质的 电磁场时，可能存在局限性。超导态 物质的电磁行为与常规物质有所不同， 需要更复杂的理论模型来描述。
电流与磁场的相互作用
根据毕奥-萨伐尔定律，电流产生磁场，而磁场对电流有作用 力。这种作用力被称为洛伦兹力，它描述了电流在磁场中所 受到的力。
毕奥-萨伐尔定律是电动机和发电机等电气设备工作的基础， 它解释了电流如何在磁场中受到作用力，从而产生旋转或线 性运动。
磁力线的描绘
毕奥-萨伐尔定律 磁通量 磁场的高斯定理
0 Idz sin B dB 4 r2
解：（1）判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解： dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的，所以只能用它的矢量表示：
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体，其截面积为S，其 中载流子的密度为n，载流子带电 q，以漂移速度 v 运动。
毕奥—萨伐尔定律：
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
解：（1）判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解： dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的，所以只能用它的矢量表示：
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体，其截面积为S，其 中载流子的密度为n，载流子带电 q，以漂移速度 v 运动。
毕奥—萨伐尔定律：
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
毕奥萨伐尔定律
电磁炉具有加热速度快、热效率高、安全可靠等优点，广泛 应用于家庭和餐饮行业。
磁力发电机
磁力发电机是一种利用磁场产生电能的装置。根据毕奥萨 伐尔定律，当导体在磁场中运动时，会在导体中产生感应 电流。磁力发电机通过转子产生的旋转磁场与定子绕组相 对运动，使定子绕组中产生感应电流，实现发电的目的。
磁力发电机广泛应用于风力发电、水力发电、汽车发动机 等领域，为可再生能源的开发和节能减排做出了重要贡献 。
06
毕奥萨伐尔定律的未来研 究与展望
磁场产生的原因与机制
磁场产生的原因
毕奥-萨伐尔定律指出，运动电荷或电流会产生磁场，这是磁场产生的根本原因。
磁场产生的机制
磁场的产生与电荷或电流的运动有关，当电荷或电流运动时，会激发周围的磁场 ，磁场的大小和方向与电荷或电流的运动状态有关。
磁场对物质的作用与影响
核磁共振成像等磁现象在医疗领域具有广泛的应用前景，同时磁 约束核聚变等前沿技术也在积极探索中。
磁现象在太阳能领域的应用
太阳能电池板在吸收太阳能时，利用磁性原理可以提高太阳能利 用率。
感谢您的观看
THANKS
磁场强度的方向与单位
磁场强度的方向
在右手螺旋定则中，拇指指向电流的方向 ，四指环绕的方向就是磁场的方向。
VS
磁场强度的单位
安培/米(A/m)，国际单位制中，磁场强度 的单位是安培/米。
03
毕奥萨伐尔定律的实验验 证
实验设计思路
确定实验目标
验证毕奥萨伐尔定律在特定情况下 的适用性，即通过实验手段测量物 理量以验证理论的准确性。
总结词
描述电磁场基本规律的方程组。
详细描述
麦克斯韦方程组是描述电磁场基本规律的方程组，其 中包括了电场、磁场和电荷密度等物理量的关系。毕 奥萨伐尔定律是麦克斯韦方程组的一个推论，它描述 了磁场与电流之间的关系。此外，麦克斯韦方程组还 预言了电磁波的存在，即光、无线电波等。
磁力发电机
磁力发电机是一种利用磁场产生电能的装置。根据毕奥萨 伐尔定律，当导体在磁场中运动时，会在导体中产生感应 电流。磁力发电机通过转子产生的旋转磁场与定子绕组相 对运动，使定子绕组中产生感应电流，实现发电的目的。
磁力发电机广泛应用于风力发电、水力发电、汽车发动机 等领域，为可再生能源的开发和节能减排做出了重要贡献 。
06
毕奥萨伐尔定律的未来研 究与展望
磁场产生的原因与机制
磁场产生的原因
毕奥-萨伐尔定律指出，运动电荷或电流会产生磁场，这是磁场产生的根本原因。
磁场产生的机制
磁场的产生与电荷或电流的运动有关，当电荷或电流运动时，会激发周围的磁场 ，磁场的大小和方向与电荷或电流的运动状态有关。
磁场对物质的作用与影响
核磁共振成像等磁现象在医疗领域具有广泛的应用前景，同时磁 约束核聚变等前沿技术也在积极探索中。
磁现象在太阳能领域的应用
太阳能电池板在吸收太阳能时，利用磁性原理可以提高太阳能利 用率。
感谢您的观看
THANKS
磁场强度的方向与单位
磁场强度的方向
在右手螺旋定则中，拇指指向电流的方向 ，四指环绕的方向就是磁场的方向。
VS
磁场强度的单位
安培/米(A/m)，国际单位制中，磁场强度 的单位是安培/米。
03
毕奥萨伐尔定律的实验验 证
实验设计思路
确定实验目标
验证毕奥萨伐尔定律在特定情况下 的适用性，即通过实验手段测量物 理量以验证理论的准确性。
总结词
描述电磁场基本规律的方程组。
详细描述
麦克斯韦方程组是描述电磁场基本规律的方程组，其 中包括了电场、磁场和电荷密度等物理量的关系。毕 奥萨伐尔定律是麦克斯韦方程组的一个推论，它描述 了磁场与电流之间的关系。此外，麦克斯韦方程组还 预言了电磁波的存在，即光、无线电波等。
毕奥撒法尔定律
毕奥撒法尔定律
毕奥-萨伐尔定律（也被称为电场定律）是电学中的一个重要定律，它描述了电荷之间的相互作用力与它们所带电荷量的乘积以及它们之间距离之间的关系。
具体来说，毕奥-萨伐尔定律表明在真空中，静止的点电荷所产生的电场强度与它们所带电荷量成正比，与它们之间的距离的平方成反比。
公式表示为：$\frac{E}{q} = \frac{k}{r^{2}}$，其中E是电场强度，q是源电荷的电荷量，k是常数，r是源电荷与试探电荷之间的距离。
这个定律是英国物理学家约瑟夫·安培的学生，法国物理学家奥古斯汀·毕奥和其时的科学家萨伐尔共同发现的。
他们在研究电流产生的磁场时，通过实验和理论推导得出了这个定律。
这个定律不仅适用于点电荷产生的电场，还适用于任何形状的电荷分布产生的电场，以及多个电荷共同产生的电场。
需要注意的是，毕奥-萨伐尔定律是在静止电荷产生的电场中得出的，对于随时间变化的磁场，需要使用麦克斯韦方程组来描述。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B
0 I
2π r
I B
电流与磁感强度 成右螺旋关系
I
X
B
(3)、半长直电流的磁场 半长直电流：垂足与电流的一端重合，而直电流的另一段是无限长。
P P
1
0
2
2 , 2
I
1
1 0, 2
1 I B 2 2a
重庆邮电大学理学院
2
I
0
2
1
1 I B 2 2a 2016/10/19
解： 旋转带电球面
等效
许多环形电流
o dI
取半径
r 的环带
dq dS 2rRd
等效圆电流：
2016/10/19
dq dI R 2s i n d 2
重庆邮电大学理学院 20
x
dB
0 r 2 dI
2(r x )
2 2
3 2
r dB
R
0 Idl
4π R
0
2
+ 3
2、 4、 6、 8 点 ：
+4
dB
B dB
L
0 Idl
4π R
2
sin 45
5 任意载流导线在点 P 处的磁感强度 磁感强度叠加原理
L
ˆ o Idl r 4r 2
注意：任意载有恒定电流的导线，在空间产生稳恒电场和稳恒 2016/10/19 2 重庆邮电大学理学院 磁场的磁感强度
1
x 2
2 2
2
d cot csc2 d
x2 x
2
1 cot csc x
2 2
×× × ×× × ×× × ×× ×× ×
cot x / R
dx R csc2 d
x Rcot
B
R x R csc
2
0 nI
2
2
1
R csc d 0 nI 3 3 R csc 2
圆弧 bc 产生的磁场 B2 2R 3 6R
向里
2016/10/19
B B1 B2 B3
0 I 3 0 I (1 ) R 2 6R 重庆邮电大学理学院
12
类似题目：
O
I
O
R
I
BO
0 I
8R
R
3 0 I 0 I BO 8R 4R
IIΒιβλιοθήκη 0 I BO 8 R 2R
r2
4π
z Idz
x
r
*
dB
方向：沿负x 各电流元在P 点
I
o r0
1
P
y
B dB
统一变量
4 π CD
0
dB 同向
Idz sin r2
C
sin( ) sin r0 / r cot( ) cot z / r0
重庆邮电大学理学院 4
dI I Id Rd R
0 dI 0 Id dB 2R 2 2 R
方向如图由对称性：
B y dB y 0
2016/10/19
B Bx dB sin
0 重庆邮电大学理学院 0
I sin d 0 I 2 2 2 R R
§9.2 毕奥-萨伐尔定律 一 、毕奥—萨伐尔定律
电流元 Idl
（实验）
元电流的磁场具有轴 对称性（不具有柱对 称性）！
大小: Idl
方向:该点电流的方向 电流元在空间产生的磁场
Idl
dB
r
0 Idl r dB 4 π r3 7 2 4 π 10 N A 真空磁导率 0
0 R 2sin 2 R 2sind
2R3
o dI
R 0 sin 3d 2
方向如图
2 B dB R sin d 0 R 2 3 0
3
0
写成矢量式：
2016/10/19
2 B 0 R 3
重庆邮电大学理学院 21
B Bx i By j Bz k ,
2 2 B Bx By Bz2
2016/10/19
重庆邮电大学理学院
3
例1:一段有限长载流直导线,通有电流为I ,求距r0处的P点磁感 应强度。 解:建立直角坐标系如图所示 分割电流元
z
D
2
Idz
( )
dB
0 Idz sin
点）
1 , 2 0 2
则有A1、A2点磁感应强度
π 1 π, 2 2 1 B 0 nI
2
1 0 nI 2
B O
0 nI
x
19
2016/10/19
重庆邮电大学理学院
[例6]均匀带电球面( R , ), 绕直径以 匀速旋转
求球心处 B0
x
r
R
3 2
2
1
sin d
B
2016/10/19
0 nI
2
cos 2 cos 1
重庆邮电大学理学院 18
讨论：
1、无限长的螺线管轴线上的磁感应强度
1 π, 2 0
B 0 nI
根据对称性：轴上各点磁感应强度相同。 2、对长直螺线管的端点（上图中
x1、x2
6
(4)、任意形状直导线
半无限长载流直导线
B1 0
B2
(cos 900 cos180 0 ) 0 I 4a 4a
0 I
2
P r
B
I
1
区别：电流元与电流管（积分元， 又叫元电流）
a
练习：半径R ，无限长半圆柱金属面通电流I，求轴线上磁感应强度 解：通电半圆柱面 —电流管（无限长直电流）集合
S Idl ( j S )dl ( qnv)Sdl r dl I d l 0 nSdlqv r dB 4π r3 dV内电子数 : dN ndV n( Sdl ) j qnv
一个运动电荷激发的磁场： 0 qv r dB B 4 π r3 dN
0
2 dr
0, B
B
2016/10/19
0
dr
0 R
2
23
重庆邮电大学理学院
一.用毕 — 沙定律求 B 分布
小结：
（1）将电流视为电流元集合（或典型电流集合）
2016/10/19
z r0 cot , r r0 / sin
2 r dz r0 d / sin 2 dz d r0 0 0 I 2 Idz sin B sin d 2 CD 4π r 4 π r0 1
0 I B (cos1 cos 2 ) 4 π r0
二 毕奥---萨伐尔定律应用举例 应用毕萨定律解题的方法 计算一段载流导体的磁场
1.建立坐标系;将电流视为电流元（或典型电流）的集合 2. 确定电流元的磁场（做示意图分析几何、对称关系） 3.求 B 的分量 Bx 、By 、Bz ;
Bx
dB
x
, By
dB
y
, Bz
dB
z
4.求总场。
o
P
x
b
x
a
B dB
2016/10/19
a b
b
0 Idx 0 I a b ln 2a b 2ax
重庆邮电大学理学院 8
例3：一载流圆环半径为R 通有电流为I，求圆环轴线上一点的磁感 应强度B。 解：将圆环分割为无限多个电流元；电流元在轴线上产生的 磁感应强度dB 为： 0Idl sin Idl 0 dB ,
a
B1
0 0 (cos 0 cos 30 ) 0 4 R sin 30
0 I
I b
300
c
1200
I
d
o
R
0 I 3 (1 ) 向里 2 R 2 0 I 0 I 3 0 0 (cos 150 cos180 ) (1 ) Cd 段： B3 0 4 R sin 30 2 R 2 0 I 1 0 I
1， 2 0或
dB 0
B
的方向沿 x 轴的负方向
讨论： （1）、直导线延长线上点
具有柱对称性！
I
2
B 1 r0
5
B0
（2）、无限长直导线 1 0 2 0 I B 方向：右螺旋法则 2 r
2016/10/19 重庆邮电大学理学院
P
无限长载流长直导线的磁场
7 沿 x 方向
例2：一宽为 a 无限长载流平面，通有电 流 I , 求距平面左侧为 b 与电流共面 的 P 点磁感应强度 B 的大小。
区别：电流元与元电流
解：以 P 点为坐标原点，向右为坐标正向； 分割电流为无限多宽为dx的无限长载流直导线；
I
dI dx
I 元电流 dI dx a 0dI 0 Idx dB 2x 2ax
圈数ndx
R
p dB * x
dx
x
×× × ×× × ×× × ×× ×× ×
dB
0 R 2 I ndx
2 R x
2
2 3/ 2
0 nI x 2 R 2dx B dB 3/ 2 2 2 x 1 2 R x