2考点分析与举例
2020中考语文一轮复习课件第三部分现代文阅读专题一记叙文考点2 分析人物及作用

考点探源 考向2 次要人物作用 (统编九下教参《蒲柳人家(节选)》“问题探究”)何满子是个怎样的形象? 这一人物在文中起什么作用? 【解题思路】解答时结合关键语句“整天在运河滩上野跑”“何满子也真是 聪慧灵秀,脑瓜儿记性好”“小嘴噘得能挂个油瓶儿”等分析何满子的形象。 作用方面可结合何满子这一人物贯穿全文始终、推动小说情节的发展分析。 【参考答案】六岁男孩何满子,一个机灵顽皮、充满稚气的孩子。他是小 说的线索人物,作者正是通过他串起了后面的人物和故事,推动了小说情 节的发展。
【方法总结】 第一步:审题。此考点的题干一般包括两部分:一是对人物形象的概括,
需要写出品质特征;二是简要分析,需写出具体的依据。 第二步:梳理与人物相关的情节、描写、评价等。 ①理情节。在情节发展、矛盾冲突中,看人物所作所为、价值取向、性
格特点、内心状态。 ②看描写。找出文中描写人物的句子,对描述人物言谈举止、外貌神态、
语言动作、内心波动的信息进行整合。 ③找评价。找出作者或他人对该人物的介绍或评价,进而辨析“真伪”,
合理利用反语、他人衬托的语句或情节。
第三步:结合文章中的社会背景进行分析。(若文章社会背景因素不强,则 可省略此步骤)把人物形象放置到特定的历史时代、社会环境中去,分析人物 命运和性格形成的根源,从而做出合理的分析。
【方法总结】 (1)从人物描写入手。抓住描写人物语言、动作、神态、心理的句子,
联系上下文把握人物内心情感,结合语境和人物的性格特点揣摩人物心理 活动。
(2)从关键词语入手。人物的心理往往是有一个据此可揣摩人 物心理。
(3)联系上下文,结合情节发展揣摩人物心理、情感变化。 注:补写人物心理描写时,可依据上述方法揣摩出人物心理进行解答, 补写完之后,可将所补写内容代入原文,看是否符合人物的性格特点。
真核细胞和原核细胞考点综合分析
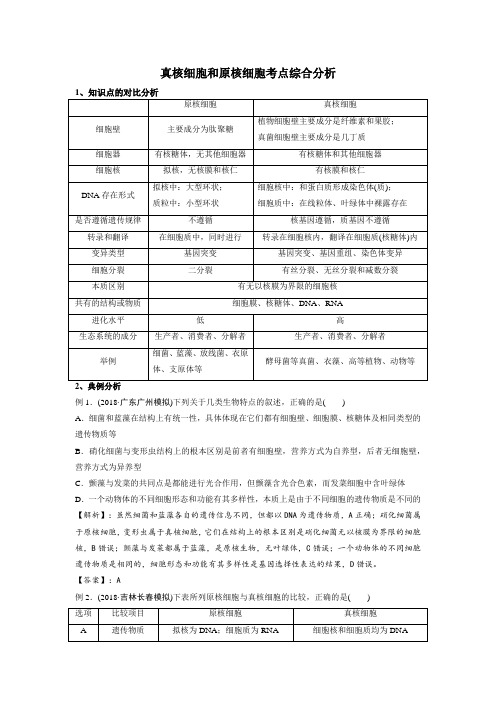
真核细胞和原核细胞考点综合分析例1.(2018·广东广州模拟)下列关于几类生物特点的叙述,正确的是()A.细菌和蓝藻在结构上有统一性,具体体现在它们都有细胞壁、细胞膜、核糖体及相同类型的遗传物质等B.硝化细菌与变形虫结构上的根本区别是前者有细胞壁,营养方式为自养型,后者无细胞壁,营养方式为异养型C.颤藻与发菜的共同点是都能进行光合作用,但颤藻含光合色素,而发菜细胞中含叶绿体D.一个动物体的不同细胞形态和功能有其多样性,本质上是由于不同细胞的遗传物质是不同的【解析】:虽然细菌和蓝藻各自的遗传信息不同,但都以DNA为遗传物质,A正确;硝化细菌属于原核细胞,变形虫属于真核细胞,它们在结构上的根本区别是硝化细菌无以核膜为界限的细胞核,B错误;颤藻与发菜都属于蓝藻,是原核生物,无叶绿体,C错误;一个动物体的不同细胞遗传物质是相同的,细胞形态和功能有其多样性是基因选择性表达的结果,D错误。
【答案】:A例2.(2018·吉林长春模拟)下表所列原核细胞与真核细胞的比较,正确的是()传定律,B错误;原核细胞无核膜,蛋白质合成时转录和翻译可以同时进行,C正确;原核生物无染色体,不会发生染色体变异,D错误。
【答案】:C例3.(2018·北京东城区检测)下列关于原核生物的叙述,不正确的是()A.蓝藻虽不含叶绿体,但能进行光合作用B.乳酸菌无核膜、核仁,但能进行转录和翻译C.硝化细菌虽不能进行光合作用,但属于自养生物D.醋酸菌不含线粒体,故不能进行有氧呼吸【解析】:蓝藻没有叶绿体,但含有光合色素,能进行光合作用;乳酸菌没有核膜和核仁,但能进行转录和翻译过程;硝化细菌虽不能进行光合作用,但能通过化能合成作用合成有机物,属于自养生物;醋酸菌不含线粒体,但能进行有氧呼吸,因为其体内含有与有氧呼吸有关的酶。
【答案】:D。
高考上海语文卷现代文第二篇的解题指导

标题的作用(看标题,略知行文要点)
1.点明主旨《跨越百年的美丽》
2.概括内容《故都的秋》(揭示写作对象)
副标题的作用:
3.引起注意《我们为什么会愉快》
补充说明标题,
4.表达情感《想北平》(点明主旨) 5.展示思路《晨昏诺日朗》 6.表明线索《项链》
对标题的提示、 解说。
7.增加文采《南州六月荔子丹》
⑥评价作品使用的手法。
⑦评价作品内容、思想的意义和价值。
⑧根据作品内容,进行联想、想象 ⑨探究作品内涵,形成自己的见解。
2020/12/29
(二)文学类现代文阅读
经典题型
评价要点
简析修辞的表达作用
修辞对象的把握及特征的描述,修辞手法的效果
赏析有表现力的词句
词句在文本中的运用及其对修辞对象的表达效果
3.造句特点(句式):①整散结合②长短结合③常式句变式结合 整句:节奏鲜明.音韵和谐.语势强烈,适于表达丰富的感情 散句:自由活泼.富于变化.错落有致(只举整.短句作分析)
4.修辞特点:多种修辞手法的综合运用;使描写更生动形象(写出有修辞句子 写表达作用)
5、答题格式:采用总分总形式(总--表明观点分--举例分析[用引号];总--这样写作用.意义)
2020/12/29
9.本文是抒情散文,第⑪段却用了若干数据和年份,有何效果?
在抒情散文中列举数据和年份,能具体确切地表现出湖泊消失数量 之多、速度之快、地域之集中,更好地抒发了作者痛苦无奈之情, 也能带给读者触目惊心之感。
考点:③赏析作品使用的表现手法的特点及其表达效果
解析:要联系说明文的“列数字”的作用,结合具体内容分析说明 ①比较文中各数字的差距,年份间相隔的时间长短。②分析这样写 对表达作品的主题及作者情感的作用。
2018年高考数学热门考点与解题技巧:考点2-函数的概念、定义域、值域(含解析)

题型1 函数与映射的概念例1 (1)下列对应是否是从集合A 到B 的映射,能否构成函数? ①A ={1,2,3},B =R ,f(1)=f(2)=3,f(3)=4. ②A ={x|x≥0},B =R ,f :x→y,y 2=4x. ③A =N ,B =Q ,f :x→y=1x2.④A ={x|x 是平面α内的矩形},B ={y|y 是平面α内的圆},对应关系f :每一个矩形都对应它的外接圆.【解题技巧】判断一个对应是不是映射,应紧扣映射的定义,即在对应法则f 下对应集合A 中的任一元素在B 中都有唯―的象,判断一个对应是否能构成函数,应判断:(1)集合A 与是否为非空数集;(2)f :A →B 是否为一个映射.变式1. (2015浙江理7) 存在函数()f x 满足:对任意x ∈R 都有( ). A. (sin 2)sin f x x = B. 2(sin 2)f x x x =+ C. 2(1)1f x x +=+ D. 2(2)1f x x x +=+ 解析 本题考查函数的定义,即一个自变量只能对应一个函数值. 对A ,取sin 20x =,则当0x =时,()00f =;当π2x =时,()01f =.所以A 错; 同理B 错;对C ,取1x =±,()22f =且()20f =,所以C 错.故选D.题型2 求函数的解析式 例2 求下列函数的解析式:(1)已知f(1-sinx)=cos 2x ,求f(x)的解析式; (2) 已知x x x f 2)1(+=+,求函数)(x f 的解析式;(3)已知f(x)是一次函数且3f(x +1)-2f(x -1)=2x +17,求f(x)的解析式; (4) 已知函数()x f 满足:()x x f x f 312=⎪⎭⎫ ⎝⎛+()0≠x ,求函数()x f 的解析式.(5)已知函()()()()2021,,10x x f x x g x x ⎧≥⎪=-=⎨-≤⎪⎩求()(),f g x g f x ⎡⎤⎡⎤⎣⎦⎣⎦ 的表达式.解法一(换元法):令1+x =t (1≥t ),则,1-=t x 得)1()1(2≥-=t t x ,所以2)1()(-=t t f ()11)1(22≥-=-+t t t ,即()().112≥-=x x x f解法二(配凑法):()()1112-+=+x x f,即)(x f ().112≥-=x x(3)(待定系数法)因为f(x)是一次函数,可设f(x)=ax +b(a≠0), ∴3[a(x +1)+b]-2[a(x -1)+b]=2x +17.即ax +(5a +b)=2x +17,因此应有⎩⎪⎨⎪⎧a =2,5a +b =17,解得⎩⎪⎨⎪⎧a =2,b =7.故f(x)的解析式是f(x)=2x +7.(4)分析 本题中除了所要求取的()x f 形式,同时还存在另个形式⎪⎭⎫⎝⎛x f 1,应通过方程消元的思想,消去⎪⎭⎫⎝⎛x f 1的形式,故只需寻求另一个关于()x f 和⎪⎭⎫⎝⎛x f 1的等量关系式即可. 解析 由()x x f x f 312=⎪⎭⎫⎝⎛+,① 以1x代替x 得到()132f f x x x ⎛⎫+= ⎪⎝⎭,②由①②联立,求得()()20.f x x x x=-≠ (5)分析 本题考查分段函数的概念,根据函数对复合变量的要求解题.解析 由()()()2010x x g x x ⎧≥⎪=⎨-≤⎪⎩可得()()()()221021,30x x f g x g x x ⎧-≥⎪=-=⎡⎤⎨⎣⎦-<⎪⎩当()21,f x x o =-≥ 即12x ≥时,()()221g f x x =-⎡⎤⎣⎦ ;当()0,f x <即12x < 时,g () 1.g f x =-⎡⎤⎣⎦ 因此()()21212.132x x g f x x ⎧⎛⎫-≥ ⎪⎪⎪⎝⎭=⎡⎤⎨⎣⎦⎛⎫⎪-≤ ⎪⎪⎝⎭⎩【解题技巧】求函数解析式的常用方法如下: (1)当已知函数的类型时,可用待定系数法求解.(2)当已知表达式为()[]x g f 时,可考虑配凑法或换元法,若易将含x 的式子配成()x g ,用配凑法.若易换元后求出x ,用换元法. 利用换元法求函数解析式时,应注意对新元t 范围的限制.(3)若求抽象函数的解析式,通常采用方程组法. 若一个方程中同时出现()f x 与其他形式()f x ϕ⎡⎤⎣⎦(如()0a f a x ⎛⎫≠ ⎪⎝⎭或()f a x - 等)时,可用()x ϕ 代替两边所有的x ,得到关于()f x 与()f x ϕ⎡⎤⎣⎦的另一个方程组,解方程程组即可求出()f x 的解析式,常称这种方法为方程组法. (4)求函数解析式要注意定义域(5)对于分段函数的形式,不论是求值还是求分段函数表达式,一定要注意复合变量的要求. 变式1. 已知函数()x f 满足⎪⎭⎫ ⎝⎛+x x f 1221xx +=,则()x f 的表达式为________.变式2. 已知实数a ≠0函数(),1,2,1x a x f x x a x +<⎧=⎨--≥⎩若()()11,f a f a -=+ 则a 的值为______.解析 当a >0时,1-a <1.1+a >1.得()()2112a a a a -+=--- 解得32a =-.(不符,故舍去); 当a <0时,1-a >1,1+a <1 ,得2(1+a )+a =-(1-a )-2a .解得34a =-.综上,34a =- .变式3.(2015全国II 理5)设函数()()2111log 2,12,x x x f x x -⎧+-<⎪=⎨⎪⎩…,则()()22log 12f f -+=( )A.3B.6C.9D.12 解析 由题意可得,2(2)1log 4123f -=+=+=.又由22log 12log 21>=, 故有2222212log log 121log 12log 2log 622(log 12)22226f --=====,所以有2(2)(log 12)369f f -+=+=.故选C.题型3 求函数的定义域 例3 函数ln 1x y +=的定义域为().A.(-4,-1)B.(-4,1)C.(-1,1)D.(-1,1] 分析 本题考查对数、分式根式有关的函数定义域的求解【解题技巧】对求函数定义域问题的思路是:(1)先列出使式子()f x 有意义的不等式或不等式组; (2)解不等式组;(3)将解集写成集合或区间的形式.变式1.(2016江苏5)函数y =的定义域是 . 解析 由题意得2320x x --…,解得31x -剟,因此定义域为[]3,1-.例4 (1)若函数f(x)的定义域为[0,1],求f(2x -1)的定义域. (2)若函数f(2x -1)的定义域为[0,1],求f(x)的定义域.(3)已知函数y =f(2x +1)的定义域为[1,2],求函数y =f(2x -1)的定义域. 【解析】 (1)由0≤2x-1≤1,得12≤x ≤1,∴函数f(2x -1)的定义域为[12,1].(3)因为函数y =f(2x +1)的定义域为[1,2],即1≤x≤2,所以3≤2x+1≤5,所以函数y =f(x)的定义域为[3,5].由3≤2x-1≤5,得2≤x≤3,所以函数y =f(2x -1)的定义域为[2,3]. 【解题技巧】抽象函数定义域的求法(1)若已知y =f(x)的定义域为[a ,b],则y =f[g(x)]的定义域由a≤g(x)≤b,解出. (2)若已知y =f[g(x)]的定义域为[a ,b],则y =f(x)的定义域即为g(x)的值域.变式 1.(2017全国I 理5)函数()f x 在(,)-∞+∞单调递减,且为奇函数.若(11)f =-,则满足21()1x f --≤≤的x 的取值范围是( )A .[2,2]-B . [1,1]-C . [0,4]D . [1,3]【解析】因为()f x 为奇函数,所以()()111f f -=-=,于是()121f x --≤≤,等价于()()()121f f x f --≤≤,又()f x 在()-∞+∞,单调递减,121x ∴--≤≤,3x ∴1≤≤,故选D .题型4 求函数的值域 1.直接法对于常见的基本初等函数,可以根据其性质直接求出其函数的值域. 一次函数y kx b =+的定义域为R ,值域为R ; 反比例函数(0)ky k x=≠的定义域为{|0}x x ≠,值域为{|0}y y ≠; 二次函数2()(0)f x ax bx c a =++≠的定义域为R ,当0a >时,值域为24{|}4ac b y y a -≥;当0a <时,值域为24{|}4ac b y y a-≤. 【例1】(1)已知函数225,[1,2]y x x x =-+∈-,则该函数的值域为________. (2)求函数2()21,[0,2]f x x ax x =--∈的最大值和最小值.【解析】(1)2(1)4y x =-+,因为12x -≤≤. 所以当1x =-时,max 8y =;当1x =时,min 4y =. 所以所给函数的值域为[4,8].(2)22()()1f x x a a =---,对称轴为x a =.综上所述,当0a <时,min ()1f x =-,max ()34f x a =-; 当0≤a <1时,2min ()1f x a =--,max ()34f x a =-; 当1≤a ≤2时,2min ()1f x a =--,max ()1f x =-;当2a >时,min ()34f x a =-,min ()(2)34f x f a ==-,max ()(0)1f x f ==-. 【评注】二次函数2y ax bx c=++在闭区间],[n m 上的值域要同时考虑最大值和最小值,一般是通过讨论对称轴与区间的左右位置关系,来确定函数在区间上的大致图像,结合图像寻找函数的最高点与最低点,进一步确定最大值和最小值,一般需要分四种情况讨论,即;2m a b ≤-;22n m a b m +≤-<;22n a b n m ≤-<+n a b>-22.单调性法【例2】已知函数1-+=x x y ,则该函数的值域是 .【解析】此函数的定义域为),1[+∞,且是增函数,当1=x 时,1min =y ,函数的值域为[)+∞,1.【评注】函数解析式中的每个部分的函数在同一区间上同增同减,这个时候可以利用单调性求函数的值域.【变式】已知函数23y x =-则该函数的值域是 . 【解析】函数在其定义域5(,]2-∞上是减函数,∴当52x =时,min 112y =-.故所求函数的值域是11,2⎡⎫-+∞⎪⎢⎣⎭.3.分离常数法 【例3】求函数511x y x -=+的值域. 【解析】515(1)6655111x x y x x x -+-===-≠+++,值域为{|5}y y ≠. 【评注】形如)0(≠++=c d cx b ax y 可用分离常数法求值域,值域是}|{c a y y ≠;dc b a y xx ++=或b x ax y ++=sin sin 的函数可用分离常数法求值域.对于分子、分母均为二次式的分式函数求值域,也常用分离常数法,将分子降次为一次式后求解.若函数化为反比例型函数(0)ky a k x=+≠,由于0k x≠,则直接知y a ≠. 【变式】已知函数22311x y x -=+,则该函数的值域为 .【解析】2223(1)44311x y x x +-==-++,∵22411041x x +≥⇒<≤+,∴值域是[1,3)-.4.换元法【例4】已知函数y x =________.5.三角换元法【例5】已知函数234x x y -+=,则该函数的的值域是 .【解析】y x =x =, 可设αsi n 32=x ,[,]22ππα∈-,∴α=,∴2cos )y ααα+)3sin(334πα+=,∵5636πππα-≤+≤,∴所给函数的值域为[.【评注】对于被开方数含有平方的模式,可以利用三角函数知识进行三角换元,换元的目的是让式子中的根号去掉,简化式子,方便求解范围,常见的是利用平方关系换元, 其中换元后α的范围的限定要以不影响x 的取值,运算方便为原则.【变式】已知函数y x =则该函数的值域是 . 【解析】设αcos =x []πα,0,∈,则)4sin(2cos sin πααα+=+=y ,∵4544,0ππαππα≤+≤∴≤≤,∴1)4sin(22≤+≤-πα,即值域为[-.6.有界性法【例6】求函数2211x y x -=+的值域.【解析】由2211x y x-=+,得211y x y -=+.∵02≥x ,∴011≥+-y y .∴11≤<-y ,即函数值域为(-1,1]. 【评注】在式中只.出现2x 或x a 或sin x 或cos x 型,可以反解出x ,即用含y 的表达式来表述出2x 或x a 或sin x 或cos x 等,然后利用其范围得到关于y 的不等式,通过解不等式得到求其值域【变式】已知函数2sin 3sin 2x y x -=+;则该函数的值域是 .【解析】由2sin 3sin 2x y x -=+,得32sin 2y x y +=-.∵1|s i n |≤x ,∴3212y y +≤-.∴153y -≤≤-.即函数值域为1[5,]3--.7.平方法【例7】已知函数y =M ,最小值为m ,则mM 的值为 .【评注】注意根式的结构特征,平方后根式外边的x 能抵消,根号里是一个二次函数,可用二次函数求出最值,或由用均值不等式求最大值,典型特征是两个根式被开方数之和为定值,如134x x -++=.【变式1】已知函数y =则该函数的值域为________.【解析】易知11≤≤-x,∴22[2,4]y =+,又0y ≥,故函数的值域是]2,2[.8.判别式法【例8】求函数22221x x y x x -+=++的值域.【评注】原分式函数定义域是全体实数,即对任何实数x 都是等式成立,等价于一元二次方程总有两个实数解,只需要判别式为非负数即可;特别应注意的是,关于x 的方程2(1)(1)20y x y x y -+-++=是类二次方程,只有一元二次方程在实数范围内有解,才能使用判别式,这就是判别式法的基本原理. 【变式】已知函数432+=x xy ,则该函数的值域 . 【解析】:2233404xy yx x y x =⇔-+=+.若20,340y yx x y ≠-+=有两个实数解,29160y ∆=-≥,解得3344y -≤≤且0.y ≠ 若0,y =230.4xy x ==+0x =,符合题意 ∴函数432+=x x y 的值域是]43,43[-。
初三数学《二次函数》考点整理与例题解析

初三数学《二次函数》考点整理与例题解析二次函数重难点分析:1、二次函数的图像2、二次函数的性质以及性质的综合应用3、二次函数的应用性问题:①面积最值问题②高度、长度最值问题③利润最大化问题④求近似解知识点归纳:1、二次函数的概念y=ax2+bx+c(a≠0)2、求二次函数的解析式一般式y=ax2+bx+c、顶点式y=a(x+m)2+k交点式y=a(x-x1)(x-x2)3、二次函数的图像和性质当a>0时,图像开口向上,有最低点,有最小值当a<0时,图像开口向下,有最高点,有最大值顶点式对称轴:直线x=-m一般式对称轴:直线x=-b/2a交点式对称轴:直线x=(x1+x2)/24.二次函数图像的平移函数y=a(x+m)2+k的图像,可以由函数y=ax2的图像先向右(当m<0时)或向左(m>0时)平移|m|个单位,再向上(当k>0时)或向下(当k<0时)平移|k|个单位得到5、抛物线与系数的关系二次项系数a决定抛物线的开口方向和大小。
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口。
|a|越大,则抛物线的开口越小。
一次项系数b和二次项系数a共同决定对称轴的位置。
当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右。
常数项c决定抛物线与y轴交点抛物线与y轴交于(0,c)抛物线与x轴交点个数?= b2-4ac>0时,抛物线与x轴有2个交点。
?= b2-4ac=0时,抛物线与x轴有1个交点。
?= b2-4ac<0时,抛物线与x轴没有交点知识拓展:初中数学最重要的部分,在中考中占的比重大,跟其他知识点联系多,以数形结合的题型考查几何,解方程、代数等都相互联系,知识点多题型多变,压轴题多以此为出题点1、考查形式:以选择题、填空题形式考察二次函数图像的性质,以解答题形式考察以二次函数为载体的综合题。
2、考察趋势:二次函数图像与系数的关系,二次函数的应用仍是重点3、二次函数求最值的应用:依据实际问题中的数量关系,确定二次函数的解析式,结合方程、一次函数等知识解决实际问题(对于二次函数最大(小)值的确定,一定要注意二次函数自变量的取值范围,同时兼顾实际问题中对自变量的特殊约定,结合图像进行理解)经典例题。
专题二 词语的理解与运用

河南省2005~2008年试题类型、分值比重分析表
年份 试题类型 所占分值 分值比重 卷面总分
2005年 课标卷 结合语境解释 2分 1.67% 120分
大纲卷 结合语境解释 2分 2% 100分
2006年 课标卷 结合字形析字义 3分 2.5% 120分
大纲卷 结合语境解释 2分 2% 100分
【知识梳理】
一、 正确理解词义
词有单义和多义之分。单义词大多是表示事物名称的词、科学术语、外来词和新造词。汉语中大量的词是多义词。
凡是表示多种相互联系的不同意义的词叫多义词。一个多义词不论它的义项有多少个,其中必有一个是本义,其它的意义是从这个本义发展变化而来。意义发展变化的途径有两种:引申和比喻。
专题二 词语的理解与运用
【复习要点】
1.掌握课文中常用词语的书写;
2.理解重要词语在具体语境中的含义,并能根据语境进行揣摩,理解词语的比喻义、引申义;
3.能根据语境需要正确选用词语,并能根据语境辨析词语(或成语)运用的正误;
4.能根据语境准确、得体、连贯运用词语(或成语);
5.能根据语境正确运用关联词。
2.从色彩方面来辨析
感情色彩不同:如“爱护”是褒义词,“庇护”是贬义词。
语体色彩不同:如“出租车”适用于书面语,“的士”适用于口语。
3.从用法方面来辨析
搭配对象不同:如“爱戴”适用于对长辈、上级,“爱护”适用于对晚辈、下属。
语法功能不同:如“公然”在句中只能作状语,如“公然侵入”,“公开”在句中还可以作谓语和定语,如“事件的真相早已公开了”,“公开的秘密”。
1.所填关联词语要适应语句表达的具体内容,语句结构所表达的是怎样的意义关系,就选取与之相应的关联词语。
高中数学二次函数的极值情况及拐点的意义分析

高中数学二次函数的极值情况及拐点的意义分析二次函数是高中数学中的重要内容,它在数学建模、物理、经济等领域都有广泛应用。
在学习二次函数时,我们经常会遇到求极值和拐点的问题。
本文将通过具体的题目举例,分析这些问题的考点和解题技巧,并探讨拐点的意义。
一、极值问题求二次函数的极值是我们经常遇到的问题之一。
下面以一个例题来说明。
例题:已知函数f(x) = -2x^2 + 4x + 3,求f(x)的极值。
解析:要求函数f(x)的极值,首先需要求出函数的导数f'(x)。
对于二次函数来说,导数是一个一次函数,其系数即为二次函数的一次项系数。
对于本例中的函数f(x),它的导数f'(x) = -4x + 4。
当导数等于零时,函数取得极值。
因此,我们可以将f'(x) = -4x + 4置为零,解得x = 1。
将x = 1代入原函数f(x)中,可以求得f(1) = 5。
所以,函数f(x)的极大值为5,极大值点为(1, 5)。
通过这个例题,我们可以总结出求二次函数极值的一般步骤:求导,令导数等于零,解方程,求得极值点。
二、拐点问题拐点是二次函数图像上的一个特殊点,它的意义在于函数在该点处由凸变凹或由凹变凸。
下面以一个例题来说明。
例题:已知函数g(x) = x^3 - 3x^2 + 2x,求g(x)的拐点。
解析:要求函数g(x)的拐点,首先需要求出函数的二阶导数g''(x)。
对于二次函数来说,二阶导数是一个常数,其值即为二次函数的二次项系数的两倍。
对于本例中的函数g(x),它的二阶导数g''(x) = 2。
由于二阶导数为常数,它不存在零点,因此,函数g(x)没有拐点。
通过这个例题,我们可以总结出求二次函数拐点的方法:求二阶导数,判断二阶导数的符号。
如果二阶导数大于零,则函数凹;如果二阶导数小于零,则函数凸;如果二阶导数等于零,则函数既不凹也不凸,不存在拐点。
三、拐点的意义拐点在二次函数图像上的位置和性质具有一定的意义。
高中数学二次方程根的性质分析

高中数学二次方程根的性质分析高中数学中,二次方程是一个非常重要的概念,它在各个数学领域都有广泛的应用。
掌握二次方程根的性质对于解题非常有帮助。
本文将从不同角度分析二次方程根的性质,并通过具体题目举例,说明其考点和解题技巧,帮助高中学生更好地理解和应用二次方程。
一、二次方程的根的个数对于一元二次方程ax^2 + bx + c = 0,其中a、b、c为实数且a ≠ 0,根据判别式Δ=b^2-4ac的值可以判断方程的根的个数。
当Δ>0时,方程有两个不相等的实根;当Δ=0时,方程有两个相等的实根;当Δ<0时,方程没有实根。
例如,考虑方程x^2 - 3x + 2 = 0。
可以计算出Δ=9-4*1*2=1,由于Δ>0,所以该方程有两个不相等的实根。
可以通过因式分解或求根公式等方法求得方程的解为x=1和x=2。
这个例子展示了如何通过计算判别式Δ来确定方程的根的个数,并通过具体计算得到解的过程。
二、二次方程的根的和与积对于一元二次方程ax^2 + bx + c = 0,根据韦达定理可以得到方程的根的和和根的积与系数的关系。
根的和为-x_1 - x_2 = -b/a,根的积为x_1 * x_2 = c/a。
例如,考虑方程2x^2 - 5x + 2 = 0。
根据韦达定理,可以得到根的和为-x_1 -x_2 = 5/2,根的积为x_1 * x_2 = 1。
通过计算可以求得方程的解为x=1/2和x=2。
这个例子展示了如何通过韦达定理来确定方程的根的和与积,并通过具体计算得到解的过程。
三、二次方程根的关系对于一元二次方程ax^2 + bx + c = 0,根据根的关系定理可以得到方程的根之间的关系。
设x_1和x_2是方程的两个根,则有x_1 + x_2 = -b/a,x_1 * x_2 = c/a。
例如,考虑方程x^2 - 5x + 6 = 0。
根据根的关系定理,可以得到方程的两个根之和为x_1 + x_2 = 5,根的积为x_1 * x_2 = 6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
环评案例百川模块模拟试题2考点分析第1题考点分析与举例(举一反三)【考点分析】1.项目现有主要环境问题有哪些?确定项目主要环境保护目标及影响因素。
《环境影响评价案例分析》考试大纲中“四、环境影响识别、预测与评价(2)判断建设项目影响环境的主要因素及分析产生的主要环境问题;(4)确定评价工作等级、评价范围及各环境要素的环境保护要求”。
2.生态环境调查除一般需调查的外,还需重点注意哪些问题的调查?《环境影响评价案例分析》考试大纲中“三、环境现状调查与评价(1)判定评价范围内环境敏感区与环境保护目标;(2)制定环境现状调查与监测方案”。
举一反三:水利水电项目生态环境调查内容大致包括以下几点,需要根据项目具体特点进行分析和取舍。
(1)森林调查:类型、面积、覆盖率、生物量、组成的物种等;评价生物量损失、物种影响、有无重点保护物种、有无重要功能要求(如水源林等)。
(2)陆生和水生动物:种群、分布、数量;评价生物量损失、物种影响、有无重点保护物种。
(3)农业生态调查与评价:占地类型、面积,占用基本农田数量,农业土地生产力,农业土地质量。
(4)水土流失调查与评价:侵蚀面积、程度,侵蚀量及损失,发展趋势及造成的生态环境问题,工程与水土流失的关系。
(5)景观资源调查与评价:水库周边景观敏感点段,主要景观保护目标及保护要求,水库建设与重要景观景点的关系。
现状调查方法有:现有资料收集、分析,规划图件收集;植被样方调查,主要调查物种、覆盖率及生物量;现场勘查景观敏感点段;也可以利用遥感信息测算植被覆盖率、地形、地貌及各类生态系统面积、水土流失情况等。
3.水电运行期对环境的主要影响有哪些?《环境影响评价案例分析》考试大纲中“四、环境影响识别、预测与评价(2)判断建设项目影响环境的主要因素及分析产生的主要环境问题”。
举一反三:水利水电项目运营期间的主要环境影响大致包括以下几点。
(1)水环境影响。
①对水文情势的影响:对库区水文情势的影响(水位变幅、水库内流速减缓);减水河段内的流量变化;厂房下游水文情势分析。
②对泥沙情势的影响。
③对水温的影响:水库水温结构的变化等。
④对水质的影响:重点分析对减水河段的影响,一般减水河段自净能力下降。
(2)生态环境影响。
①对局地气候的影响(可通过类比分析)。
②对水生生物多样性的影响(对库区鱼类等水生生物;减水河段鱼类等水生生物;产卵场、索饵场、越冬场的影响)。
③对陆生生物多样性的影响。
④大坝建设对河流廊道的生态功能的影响(分析大坝建设导致的淹没、阻隔、径流变化对河流生态系统的影响)。
⑤新增水土流失预测(主要为工程永久占地、渣场、料场、施工公路占地、施工辅助企业占地、围堰、暂存表土等引起的水土流失)。
(3)社会环境影响。
①对用水的影响:减水河段用水、下游用水。
②对社会经济的影响。
③对人群健康的影响。
(4)对移民安置区的影响(新的移民搬迁后,其生活对周围环境的影响)。
(5)对环境地质的影响(主要是渔场等是否会引起滑坡、塌陷、泥石流等灾害,是否会引发地震等)。
4.弃渣场位置是否合理?拟采取什么措施(现有电站整改措施)?《环境影响评价案例分析》考试大纲中“六、环境保护措施分析(3)分析生态影响防护、恢复与补偿措施及其技术经济可行性”。
第2题考点分析与举例(举一反三)【考点分析】1.判定该项目地下水评价等级,并给出判定依据。
(说明:地下水环境导则判据见附1)《环境影响评价案例分析》考试大纲中“四、环境影响识别、预测与评价(4)确定评价工作等级、评价范围及各环境要素的环境保护要求”。
举一反三:2011年新发布了《环境影响评价技术导则一地下水环境》(HJ610—2011),注意该导则规定对建设项目分类进行评价等级判定,其中I类项目评价等级判定有关规定如本题附1所示,建设项目分类和II类项目评价等级判定有关规定如下:4.1建设项目分类根据建设项目对地下水环境影响的特征,将建设项目分为以下三类:I类:指在项目建设、生产运行和服务期满后的各个过程中,可能造成地下水水质污染的建设项目;II类:指在项目建设、生产运行和服务期满后的各个过程中,可能引起地下水流场或地下水水位变化,并导致环境水文地质问题的建设项目;III类:指同时具备I类和II类建设项目环境影响特征的建设项目。
根据不同类型建设项目对地下水环境影响程度与范围的大小,将地下水环填影响评价工作分为一、二、三级。
具体分级的原则与判据见第6章。
6.1划分原则I类和II类建设项目,分别根据其对地下水环境的影响类型、建设项目所处区域的环境特征及其环境影响程度划定评价工作等级。
III类建设项目应根据建设项目所具有的I类和E类特征分别进行地下水环境影响评价工作等级划分,并按所划定的最高工作等级开展评价工作。
……6.3II类建设项目工作等级划分6.3.1划分依据6.3.1.1II类建设项目地下水环境影响评价工作等级的划分,应根据建设项目地下水供、排水(或注水)规模、引起的地下水水位变化范围、建设项目场地的地下水环境敏感程度以及可能造成的环境水文地质问题的大小等条件确定。
6.3.1.2建设项目供水、排水(或注水)规模建设项目地下水供水、排水(或注水)规模按水量的多少可分为大、中、小三级,分级标准见表7。
6.3.1.3建设项目引起的地下水水位变化区域范围建设项目引起的地下水水位变化区域范围可用影响半径来表示,分为大、中、小三级,分级标准见表8。
影响半径的确定方法可参见附录C。
6.3.1.4建设项目场地的地下水环境敏感程度建设项目场地的地下水环境敏感程度可分为敏感、较敏感、不敏感三级,分级原则见表9。
注:如建设项目场地的含水层(含水系统)处于补给区与径流区或径流区与排泄区的边界时,则敏感程度上调一级。
a“地质灾害”是指因水文地质条件变化发生的地面沉降、岩溶塌陷等。
b“环境敏感区”是指《建设项目环境影响评价分类管理名录》中所界定的涉及地下水的环境敏感区。
6.3.1.5建设项目造成的环境水文地质问题建设项目造成的环境水文地质问题包括:区域地下水水位下降产生的土地次生荒漠化、地面沉降、地裂缝、岩溶塌陷、海水入侵、湿地退化等,以及灌溉导致局部地下水位上升产生的土壤次生盐渍化、次生沼泽化等,按其影响程度大小可分为强、中等、弱三级,分级原则见表10。
6.3.2 II类建设项目评价工作等级II类建设项目地下水环境影响评价工作等级的划分见表11。
2.该项目排入开发区污水处理厂的废水水质执行《污水综合排放标准》三级标准(COD500mg/L、BOD5300mg/L、SS400mg/L、石油类20mg/L、总镍1.0mg/L六价铬0.5mg/L),请评价该项目废水是否达标排放。
为确保该项目污水达标排放,主要应监控哪些污染因子?请给出监测点位建议。
《环境影响评价案例分析》考试大纲中“六、环境保护措施分析(1)分析污染物达标排放情况;(5)制订环境管理与监测计划”。
举一反三:《污水综合排放标准》(GB8978—1996)规定:4.2.1本标准将排放的污染物按其性质及控制方式分为两类。
4.2.1.1第一类污染物:不分行业和污水排放方式,也不分受纳水体的功能类别,一律在车间或车间处理设施排放□采样,其最高允许排放浓度必须达到本标准要求(采矿行业的尾矿坝出水□不得视为车间排放口)。
4.2.1.2第二类污染物:在排污单位排放口采样,其最高允许排放浓度必须达到本标准要求。
应熟悉该标准中第一类污染物名称,了解其标准值,具体见该标准表1:3.根据《制定地方大气污染物排放标准的技术方法》(GB/T13201—91)中的公式计算出该项目二甲苯卫生防护距离为533m,请确定该项目厂区的卫生防护距离。
《环境影响评价案例分析》考试大纲中“六、环境保护措施分析(2)分析污染控制措施及其技术经济可行性”。
举一反三:卫生防护距离的设定是一类特殊的污染控制措施,一方面要会利用专门的卫生防护距离标准判断卫生防护距离;另一方面还要就项目的特殊性,根据环评预测结果,合理确定推荐的卫生防护距离。
了解《制定地方大气污染物排放标准的技术方法》(GB/T13201—91)中有害气体无组织排放控制与工业企业卫生防护距离标准的制定方法规定:7.3卫生防护距离在100m以内时,级差为50m;超过100m,但小于或等于1OOOm时,级差为100m;超过1000m,级差为200m。
7.4各类工业、企业卫生防护距离按下式计算:式中:C m——标准浓度限值,mg/m³;L——工业企业所需卫生防护距离,m;r——有害气体无组织排放源所在生产单位的等效半径,m,根据该生产单元占地面积S(m²)计算,r=√S/π;A,B,C,D——卫生防护距离计算系数,无因次,根据工业企业所在地区近五年平均风速及工业企业大气活染源构成类别从表5査取;Q c——工业企业有害气体无组织排放置可以达到的控制水平,kg/h。
Q c取同类企业中生产工艺流程合理,生产管理与设备维护处于先进水平的工业企业,在正常运行时的无组织排放量。
4.根据附2中该项目水平衡图,计算项目工艺水回用率、间接冷却水循环率、全厂水重复利用率。
《环境影响评价案例分析》考试大纲中“二、项目分析(2)从生产工艺、资源和能源消耗指标等方面分析建设项目清洁生产水平”。
制浆项目清洁生产专题应重点阐述拟建项目生产工艺和技术来源,评价工艺技术与装备水平的先进性。
分别给出单位产品物耗、能耗、水耗、污染物产生量、污染排放量以及全厂水的重复利用率等指标,体现循环经济理念,量化评价项目的清洁生产水平,由此提出提高清洁生产水平的措施及方案。
本题主要考查新水用量指标的计算,其他指标的计算方法也应有所了解。
5.根据附3中《大气污染物综合排放标准》,计算该项目二甲苯最高允许排放速率(kg/h),并分析该项目二甲苯有组织排放是否满足排放标准要求。
《环境影响评价案例分析》考试大纲中“四、环境影响识别、预测与评价(3)选用评价标准”。
举一反三:熟悉《大气污染物综合排放标准》(GB16297-1996)中关于最高允许排放速率计算的规定:7.3若某排气筒的高度处于本标准列出的两个值之间,其执行的最高允许排放速率以内插法计算,内插法的计算式见本标准附录B;当某排气筒的高度大于或小于本标准列出的最大或最小值时,以外推法计算其最高允许排放速率,外推法计算式见本标准附录B。
7.4新污染源的排气筒一般不应低于15m。
若新源的排气筒必须低于15 m,其排放速率标准值按7.3的外推计算结果再严格50%执行。
附录B (标准的附录)确定某排气筒最高允许排放速率的内插法和外推法Bl某排气筒高度处于表列两高度之间,用内插法计算其最高允许排放速率’按下式计算:Q=Q a+ (Q a+1-Q a) (h-h a) / (h a+1-h a)式中:Q——某排气筒最高允许排放速率;Q a——比某排气筒低的表列限值中的最大值;Q a+1——比某排气筒高的表列限值中的最小値;h——某排气筒的几何高度;h a——比某排气筒低的表列高度中的最大值;h a+1——比某排气筒高的表列高度中的最小值。
