成都市高2013届三诊文科数学试题及答案
成都市高2013级高三三诊文综答案

成都市高2013级高中毕业班第三次诊断性检测文科综合参考答案及评分标准一㊁选择题(共140分)1.C2.B3.A4.C5.D6.A7.B8.D9.A 10.C11.B12.A13.C14.C15.B16.D17.C18.B 19.B20.A21.B22.D23.A24.B25.C26.D27.D 28.B29.C30.C31.B32.C33.A34.A35.B二㊁非选择题(共160分)36.(22分)(1)位于长江中下游平原地区,地势平坦,水流平稳(2分);亚热带季风气候,降水丰富,河流水量大(2分);冬季气温高,河流终年不冻,通航时间长(2分);毗邻长江三角洲地区,人口密集,城市众多,经济发达,客货运输量大(2分)㊂(2)劳动力价格上涨,生产成本提高(2分);土地㊁能源等资源短缺(2分);环境污染日益加重(2分);产业结构调整与产业升级的需要(2分)(3)赞同,理由:①促进基础设施建设;②促进产业结构调整与升级;③提高城市等级和城市化水平;④增加当地就业机会;⑤促进区域经济发展㊂(每点2分,任答3点给6分㊂)不赞同,理由:①占用耕地;②土地㊁住房等价格上升;③增大交通运输压力;④加剧环境污染㊂(每点2分,答对3点得6分㊂)37.(24分)(1)地形以平原和(低缓)高原为主,地势平坦(2分);大部分地区属热带季风气候,水热条件好(2分);河流众多,水资源丰富,灌溉便利(2分);人口众多,劳动力资源丰富(2分);农产品市场需求量大(2分)㊂因此,该国耕地比重大㊂(2)年平均气温更低(2分);气温日较差和年较差更小(2分);年降水总量更大(2分);降水季节变化更小(2分)㊂(3)①加强水库㊁排灌水渠等水利工程设施建设;②调整农业生产结构和布局,积极发展旱地农业;③培育耐旱的农作物品种;④发展节水农业等㊂(每点2分,任答3点给6分㊂)文科综合 三诊 考试题答案第1㊀页(共4页)38.(26分)(1)①增值税对货物和服务的全覆盖,有利于避免重复征税,促进社会分工,能有力地支持服务业发展和制造业转型升级㊂(4分)②企业税负减轻,生产和经营成本降低,能增强创新创业活力㊂(4分)③将不动产纳入抵扣,有利于调动投资积极性,培育新的经济增长点㊂(3分)④税收制度的优化和完善,有利于形成公平的市场竞争环境,推动经济持续健康发展㊂(3分)(2)①坚持民主集中制,合理确定中央和地方对增值税的分成比例,保障地方政府的财力㊂(4分)②坚持求真务实,科学民主决策,制定公平合理的征税方案,以实现减轻税负的目的㊂(4分)③依法行政,坚持税收法定原则,依法推进 营改增 ㊂(4分) 39.(26分)(1)①传统建筑是展现传统文化的重要标志㊂城市建设要注重对传统建筑的保护,为继承传统文化提供物质载体㊂(3分)②传统文化具有相对稳定性和鲜明民族性㊂城市建设要注重保护本地历史和文化特色,以增强人们的认同感㊂(3分)③对传统文化要批判继承㊁古为今用,同时要体现时代精神㊂城市建设既要不失传统风格,又要与现代化建设相协调㊂(4分)(2)①为提高城市发展持续性宜居性,着眼于事物的整体性,统筹生产㊁生活㊁生态三大布局㊂(4分)②增强城市内部布局的合理性,推动城市发展由外延扩张式向内涵提升式转变,遵循了系统内部结构的有序性和优化趋向㊂(4分)③按照绿色循环低碳的理念进行规划建设城市基础设施,坚持了用综合的思维方式来认识事物㊂(4分) (3)示例:(1)赞成㊂这样可以缓解交通拥堵;能促进土地节约利用;倡导共享理念㊂(2)不赞成㊂这样会带来安全㊁卫生等问题;会缩小人们的休闲空间,居住环境可能会变差㊂(任选一个角度,符合题意言之成理即可,每个要点2分㊂)40.(25分)(1)双林镇:农业和手工业专业化和商品化程度高;商帮㊁会馆对促进市镇发展作用大;外来商人融入当地社会,基层社会关系变动;初具地方自治功能,士绅占据主导地位㊂(每点2分,任答三点6分)威尼斯:典型的商业城市,金融业发达;产生了近代意义的商业组织形式和商业习惯法;城市独立自治;城市公共设施和公共服务功能比较完善㊂(每点2分,任答三点6分) (2)中国:江南市镇商品经济虽有发展,但不足以对中国传统自然经济造成重大冲击;商人没有转化为资产阶级,士绅化的商人成为封建王朝强化社会治理的力量,维护了封建统治;晚明虽在商品经济发展基础上出现了反传统思潮,但仍未超出传统儒家思想的范畴㊂(共7分,答出一点2分,两点4分,三点7分)文科综合 三诊 考试题答案第2㊀页(共4页)意大利:促进了资本主义萌芽产生和发展;促使新兴资产阶级形成和壮大;推动文艺复兴兴起和扩展,形成了近代欧洲第一次思想解放运动㊂(每点2分,共6分)41.(12分)答案示例(本示例只作阅卷参考用,其他合理的答案可以酌情给分)修改1:将第②项中的 电 更改为 发电机 ㊂说明: 电 是一种自然现象,并非创造的成果,该学生把 电 归入 发明创造 是不科学的;第二次工业革命注重科学和技术的结合,法拉第发现电磁感应现象为西门子发明发电机提供了科学理论基础㊂发电机的发明使得电作为高效率的新能源逐步应用于工业㊁照明及城市公共事业等领域,大大提高了生产效率,使人类由蒸汽时代步入电气时代㊂所以应将 电 改为 发电机 ㊂修改2:第③项中的 产业结构 存在不完整和分类逻辑混乱的问题,应增加第一产业和第二产业,并进行重新分类合并㊂说明:首先,产业结构应该包括第一㊁第二和第三产业三个部分,所以应该增加第一产业(农业)和第二产业;其次, 电力㊁汽车㊁飞机和钢铁工业 与 重工业 是从属关系,并非并列关系,应将前者合并到后者中,并归属于第二产业㊂再次, 电信服务业 与 第三产业 也是从属关系,并非并列关系,应将前者归于后者当中㊂(每项修改意见中,观点2分,理由4分,共6分,两项共12分)42.(10分)独特的地理位置,是我国大陆最北点(3分);独特的天文现象,是我国观赏北极光和白夜胜景的最佳地点(3分);独特的气候,冬季可赏冰雪奇景,夏季凉爽可避暑(2分);与俄罗斯隔江相望,具有独特的民族人文风情(2分)㊂43.(10分)降水量大,集中夏季(2分);支流众多,汇水量大(2分);河流含沙量大,淤塞严重(2分);流经平原,地势低平,雨季河流排水不畅(2分);缺少直接的天然入海河道(2分)㊂44.(10分)原因:面积广大,地域辽阔(2分);地处我国地势一㊁二级阶梯交界处(有高原㊁山地㊁丘陵㊁盆地和平原等地形),地形类型多种多样,高差大(2分);位于亚热带季风气候向高山(高原)气候过渡地带,气候类型复杂多样(2分)㊂措施:①建立自然保护区,保护野生动植物生存环境;②严格执法,严禁滥捕乱杀㊁乱砍滥伐;③严禁向环境排放 三废 ,防治环境污染㊂(每点2分,答对两点得4分㊂其它合理答案可酌情给分,但总分不能超过4分)文科综合 三诊 考试题答案第3㊀页(共4页)45.(15分)(1)放宽入学资格,降低年龄㊁父祖官阶和经学功底等要求,省试不第者也可入选;改革选才方式,从单一的考查经义到兼及文辞史学;扩大招生人数,从500人扩大到1300人㊂(每点3分,其中概括2分,说明1分,三点共9分)(2)关照了中下层官吏的利益,缓和了官僚集团内部的矛盾;推动了庶族精英阶层的崛起,有利于抑制门阀士族;促进了文学㊁史学等各项文化事业的繁荣昌盛;促进了中外文化交流,扩大了唐文化在东亚地区的影响㊂(6分,任答三点即可)46.(15分)(1)中共在长期革命斗争中习惯于运用阶级斗争的思维方式;但基于统一战线的成功经验,建立和建设新中国需要与中间党派继续合作;如何组建 民主联合政府 ,中共没有可资借鉴的理论与经验㊂(每点2分,共6分)(2)理论创新:中共七届二中全会的决议和毛泽东提出人民民主专政理论;法律依据:中国人民政治协商会议制定并通过‘共同纲领“;制度保障:建立中共领导的多党合作与政治协商制度㊂(每点3分,共9分)47.(15分)(1)变化:20世纪20年代到30年代前半期,以美英日为主导;20世纪30年代末,苏联加入,日本受到孤立㊂(4分)原因:日本走向全面侵华,威胁英美等国利益,促使其对日政策从绥靖转向遏制,并逐渐加大对中国抗战的援助;日本与德㊁意结成法西斯同盟,威胁世界安全㊂(5分㊂答出一点3分,答出两点5分)(2)客观上改善了中国抗战的国际处境,提升了中国的国际地位;加速了太平洋战争的爆发,导致了华盛顿体系的最终解体;促成了世界反法西斯同盟的建立;最终改变了世界格局㊂(每点2分,任答三点6分)48.(15分)(1)纳粹德国实行的 统制经济 政策扭曲了市场功能;战胜国的严格监控进一步削弱了市场的作用;二战后,国家垄断资本主义盛行,德国处在探索建立何种市场经济模式的历史关口㊂(每点2分,共6分)(2)特点:以市场经济为基础,同时强调国家干预㊂(2分)影响:抑制了垄断,保护了竞争,增强了市场的活力;推动了经济的高速发展,使联邦德国重新成为世界经济大国;提高了其国际地位;促进了社会的稳定和发展㊂(7分㊂答出一点2分;答出两点4分;答出三点6分;答出四点7分)文科综合 三诊 考试题答案第4㊀页(共4页)。
2013年普通高等学校招生全国统一考试(四川卷)数学试题 (文科) word解析版

2013年普通高等学校招生全国统一考试(四川卷)数 学(文史类)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)。
第Ⅰ卷1至2页,第Ⅱ卷3至4页,共4页。
考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上大题无效。
满分150分。
考试时间120分钟。
考试结束后,将本试题卷和答题卡上一并交回。
第Ⅰ卷 (选择题 共50分)注意事项: 必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1、设集合{1,2,3}A =,集合{2,2}B =-,则A B =( )(A )∅ (B ){2} (C ){2,2}- (D ){2,1,2,3}-1.【答案】B 【解析】本题考查用列举法表示的集合的交运算.∵A ={1,2,3},B ={-2,2},∴A ∩B ={1,2,3}∩{-2,2}={2}.选B. 【易错点】看清题!求交集不是求并集! 【难易度评价】★送分题2.一个几何体的三视图如图所示,则该几何体可以是( )A .棱柱B .棱台C .圆柱D .圆台答案 D解析 根据三视图可知,此几何体是圆台,选D.3.如图,在复平面内,点A 表示复数z ,由图中表示z 的共轭复数的点是( )A .AB .BC .CD .D 答案 B解析 表示复数z 的点A 与表示z 的共轭复数的点关于x 轴对称,∴B 点表示z .选B.4、设x Z ∈,集合A 是奇数集,集合B 是偶数集。
若命题:,2p x A x B ∀∈∈,则( ) (A ):,2p x A x B ⌝∃∈∈ (B ):,2p x A x B ⌝∃∉∈ (C ):,2p x A x B ⌝∃∈∉ (D ):,2p x A x B ⌝∀∉∉答案 C解析 命题p :∀x ∈A,2x ∈B 是一个全称命题,其命题的否定綈p 应为∃x ∈A,2x ∉B ,选C.5.抛物线y 2=8x 的焦点到直线x -3y =0的距离是( ) A .2 3 B .2 C. 3 D .1 答案 D解析 抛物线y 2=8x 的焦点为F (2,0),由点到直线的距离公式得F (2,0)到直线x -3y =0的距离d =|2-3×0|12+(-3)2=22=1.选D.6.函数f (x )=2sin(ωx +φ)(ω>0,-π2<φ<π2)的部分图象如图所示,则ω,φ的值分别是( )A .2,-π3B .2,-π6C .4,-π6D .4,π3答案 A解析 由图象知f (x )的周期T =2⎝⎛⎭⎫11π12-5π12=π,又T =2πω,ω>0,∴ω=2.由于f (x )=2sin(ωx +φ)(ω>0,-π2<φ<π2)的一个最高点为⎝⎛⎭⎫5π12,2,故有2×5π12+φ=2k π+π2,k ∈Z .即φ=2k π-π3,又-π2<φ<π2,∴φ=-π3,选A.7.某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示,以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的概率分布直方图是( )答案 A解析 由于频率分布直方图的组距为5,去掉C 、D ,又[0,5),[5,10)两组各一人,去掉B ,应选A.8.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤8,2y -x ≤4,x ≥0,y ≥0,且z =5y -x 的最大值为a ,最小值为b ,则a -b 的值是( )A .48B .30C .24D .16答案 C解析 画出可行域如图阴影部分(包括边界)易解得A (4,4),B (8,0),C (0,2).对目标函数令z =0作出直线l 0,上下平移易知过点A (4,4),z 最大=16,过点B (8,0),z 最小=-8,即a =16,b =-8, ∴a -b =24.选C.9.从椭圆x 2a 2+y 2b2=1(a >b >0)上一点P 向x 轴作垂线,垂足恰为左焦点F 1,A 是椭圆与x 轴正半轴的交点,B 是椭圆与y 轴正半轴的交点,且AB ∥OP (O 是坐标原点),则该椭圆的离心率是( )A.24B.12C.22D.32解析 由题意可设P (-c ,y 0)(c 为半焦距),k OP =-y 0c ,k AB =-b a ,由于OP ∥AB ,∴-y 0c =-b a ,y 0=bca,把P ⎝⎛⎭⎫-c ,bc a 代入椭圆方程得(-c )2a 2+⎝⎛⎭⎫bc a 2b 2=1,而⎝⎛⎭⎫c a 2=12,∴e =c a =22.选C.10.设函数f (x )=e x +x -a (a ∈R ,e 为自然对数的底数),若存在b ∈[0,1]使f (f (b ))=b 成立,则a 的取值范围是( )A .[1,e]B .[1,1+e]C .[e,1+e]D .[0,1] 答案 A解析 由于f (x )=e x +x -a 在其定义域上单调递增,且y ≥0,∴y =f (x )存在反函数y =f -1(x ),又存在b ∈[0,1]使f (f (b ))=b ,则f -1[f (f (b ))]=f -1(b ),即f (b )=f -1(b ),∴y =f (x )与y =f -1(x )的交点在直线y =x 上,所以e x +x -a =x 在[0,1]上有解.由e x +x -a =x 得a =e x +x -x 2,当x ∈(0,1)时,a ′=e x -2x +1>e x -2+1>0,∴a =e x +x -x 2在[0,1]上单调递增,∴当x =0时,a 最小=e 0=1,当x =1时,a 最大=e ,故a 的取值范围是[1,e].选A.第二卷二、填空题11.lg 5+lg 20的值是________. 答案 1解析 lg 5+lg 20=lg(5·25)=lg 10=1.12.如图,在平行四边形ABCD 中,对角线AC 与BD 交于点O ,AB →+AD →=λAO →,则λ=________. 答案 2解析 由于ABCD 为平行四边形,对角线AC 与BD 交于点O ,∴AB →+AD →=AC →=2AO →,∴λ=2.13.已知函数f (x )=4x +ax(x >0,a >0)在x =3时取得最小值,则a =________. 答案 36解析 ∵x >0,a >0,∴f (x )=4x +a x ≥24x ·a x =4a ,当且仅当4x =a x (x >0)即x =a2时f (x )取得最小值,由题意得a2=3,∴a =36.14.设sin 2α=-sin α,α∈⎝⎛⎭⎫π2,π,则tan 2α的值是________. 答案 3解析 ∵sin 2α=-sin α,∴sin α(2cos α+1)=0,又α∈⎝⎛⎭⎫π2,π,∴sin α≠0,2cos α+1=0即cos α=-12,sin α=32,tan α=-3,∴tan 2α=2tan α1-tan 2α=-231-(-3)2= 3. 15.在平面直角坐标系内,到点A (1,2),B (1,5),C (3,6),D (7,-1)的距离之和最小的点的坐标是________.解析 直线AC 的方程为y -2=2(x -1),直线BD 的方程为y -5=-(x -1),由⎩⎪⎨⎪⎧y -2=2(x -1)y -5=-(x -1)得M (2,4).三、解答题16.在等比数列{a n }中,a 2-a 1=2,且2a 2为3a 1和a 3的等差中项,求数列{a n }的首项、公比及前n 项和.解 设该数列的公比为q .由已知,可得 a 1q -a 1=2,4a 1q =3a 1+a 1q 2,所以,a 1(q -1)=2,q 2-4q +3=0,解得q =3或q =1. 由于a 1(q -1)=2,因此q =1不合题意,应舍去. 故公比q =3,首项a 1=1.所以,数列{a n }的前n 项和S n =3n -12.17.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos(A -B )cos B =sin(A -B )sin(A +C )=-35.(1)求sin A 的值;(2)若a =42,b =5,求向量BA →在BC →方向上的投影.解 (1)由cos(A -B )cos B -sin(A -B )sin(A +C )=-35,得cos(A -B )cos B -sin(A -B )sin B =-35.则cos(A -B +B )=-35,即cos A =-35.又0<A <π,则sin A =45.(2)由正弦定理,有 a sin A =b sin B ,所以,sin B =b sin A a =22. 由题知a >b ,则A >B ,故B =π4.根据余弦定理,有(42)2=52+c 2-2×5c ×⎝⎛⎭⎫-35, 解得c =1或c =-7(负值舍去).故向量BA →在BC →方向上的投影为|BA →|cos B =22.18.某算法的程序框图如图所示,其中输入的变量x 在1,2,3,…,24这24个整数中等可能随机产生.(1)分别求出按程序框图正确编程运行时输出y 的值为i 的概率P i (i =1,2,3);(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n 次后,统计记录了输出y 的值为i (i =1,2,3)的频数,以下是甲、乙所作频数统计表的部分数据. 甲的频数统计表(部分)当n =2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y 的值为i (i =1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.解 (1)变量x 是在1,2,3,…,24这24个整数中随机产生的一个数,共有24种可能.当x 从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时,输出y 的值为1,故P 1=12;当x 从2,4,8,10,14,16,20,22这8个数中产生时,输出y 的值为2,故P 2=13;当x 从6,12,18,24这4个数中产生时,输出y 的值为3,故P 3=16.所以,输出y 的值为1的概率为12,输出y 的值为2的概率为13,输出y 的值为3的概率为16.(2)当n =2 100时,甲、乙所编程序各自输出y 的值为i (i =1,2,3)的频率如下:比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大.19.如图,在三棱柱ABCA 1B 1C 1中,侧棱AA 1⊥底面ABC ,AB =AC =2AA 1=2,∠BAC =120°,D ,D 1分别是线段BC ,B 1C 1的中点,P 是线段AD 上异于端点的点.(1)在平面ABC 内,试作出过点P 与平面A 1BC 平行的直线l ,说明理由,并证明直线l ⊥平面ADD 1A 1; (2)设(1)中的直线l 交AC 于点Q ,求三棱锥A1QC 1D 的体积.(锥体体积公式:V =13Sh ,其中S 为底面面积,h 为高)解:(1)如图,在平面ABC 内,过点P 作直线l ∥BC ,因为l 在平面A 1BC 外,BC 在平面A 1BC 内,由直线与平面平行的判定定理可知,l ∥平面A 1BC . 由已知,AB =AC ,D 是BC 的中点, 所以,BC ⊥AD ,则直线l ⊥AD .因为AA 1⊥平面ABC ,所以AA 1⊥直线l .又因为AD ,AA 1在平面ADD 1A 1内,且AD 与AA 1相交, 所以直线l ⊥平面ADD 1A 1. (2)过D 作DE ⊥AC 于E ,因为AA 1⊥平面ABC ,所以DE ⊥AA 1.又因为AC ,AA 1在平面AA 1C 1C 内,且AC 与AA 1相交,所以DE ⊥平面AA 1C 1C .由AB =AC =2,∠BAC =120°,有AD =1,∠DAC =60°,所以在△ACD 中,DE =32AD =32,又S △A 1QC 1=12A 1C 1·AA 1=1,所以VA 1QC 1D =VDA 1QC 1=13DE ·S △A 1QC 1=13×32×1=36.故三棱锥A 1QC 1D 的体积是36.20.已知圆C 的方程为x 2+(y -4)2=4,点O 是坐标原点,直线l :y =kx 与圆C 交于M ,N 两点. (1)求k 的取值范围;(2)设Q (m ,n )是线段MN 上的点,且2|OQ |2=1|OM |2+1|ON |2,请将n 表示为m 的函数.解 (1)将y =kx 代入x 2+(y -4)2=4中,得(1+k 2)x 2-8kx +12=0.(*) 由Δ=(-8k )2-4(1+k )2×12>0,得k 2>3.所以,k 的取值范围是(-∞,-3)∪(3,+∞).(2)因为M 、N 在直线l 上,可设点M 、N 的坐标分别是(x 1,kx 1),(x 2,kx 2),则|OM |2=(1+k 2)x 21,|ON |2=(1+k 2)x 22, 又|OQ |2=m 2+n 2=(1+k 2)m 2.由2|OQ |2=1|OM |2+1|ON |2,得2(1+k 2)m 2=1(1+k 2)x 21+1(1+k 2)x 22, 即2m 2=1x 21+1x 22=(x 1+x 2)2-2x 1x 2x 21x 22. 由(*)式可知,x 1+x 2=8k 1+k 2,x 1x 2=121+k 2,所以m 2=365k 2-3.因为点Q 在直线y =kx 上,所以k =n m ,代入m 2=365k 2-3中并化简,得5n 2-3m 2=36.由m 2=365k 2-3及k 2>3,可知0<m 2<3,即m ∈(-3,0)∪(0,3).根据题意,点Q 在圆C 内,则n >0,所以n =36+3m 25=15m 2+1805.于是,n 与m 的函数关系为n =15m 2+1805(m ∈(-3,0)∪(0,3)).21.已知函数f (x )=⎩⎪⎨⎪⎧x 2+2x +a ,x <0,ln x ,x >0,其中a 是实数,设A (x 1,f (x 1)),B (x 2,f (x 2))为该函数图象上的两点,且x 1<x 2.(1)指出函数f (x )的单调区间;(2)若函数f (x )的图象在点A ,B 处的切线互相垂直,且x 2<0,证明:x 2-x 1≥1; (3)若函数f (x )的图象在点A ,B 处的切线重合,求a 的取值范围.(1)解 函数f (x )的单调递减区间为(-∞,-1),单调递增区间为[-1,0),(0,+∞).(2)证明 由导数的几何意义可知,点A 处的切线斜率为f ′(x 1),点B 处的切线斜率为f ′(x 2). 故当点A 处的切线与点B 处的切线垂直时, 有f ′(x 1)·f ′(x 2)=-1,当x <0时,对函数f (x )求导,得f ′(x )=2x +2, 因为x 1<x 2<0,所以,(2x 1+2)(2x 2+2)=-1, 所以2x 1+2<0,2x 2+2>0.因此x 2-x 1=12[-(2x 1+2)+2x 2+2]≥[-(2x 1+2)](2x 2+2)=1.(当且仅当-(2x 1+2)=2x 2+2=1,即x 1=-32且x 2=-12时等号成立)所以,函数f (x )的图象在点A 、B 处的切线互相垂直时,有x 2-x 1≥1. (3)解 当x 1<x 2<0或x 2>x 1>0时,f ′(x 1)≠f ′(x 2), 故x 1<0<x 2.当x 1<0时,函数f (x )的图象在点(x 1,f (x 1))处的切线方程为y -(x 21+2x 1+a )=(2x 1+2)(x -x 1),即y =(2x 1+2)x -x 21+a .当x 2>0时,函数f (x )的图象在点(x 2,f (x 2))处的切线方程为y -ln x 2=1x 2(x -x 2),即y =1x 2·x +ln x 2-1.两切线重合的充要条件是 ⎩⎪⎨⎪⎧1x 2=2x 1+2, ①ln x 2-1=-x 21+a ②由①及x 1<0<x 2知,0<1x 2<2.由①②得,a =ln x 2+⎝⎛⎭⎫12x 2-12-1=-ln 1x 2+14⎝⎛⎭⎫1x 2-22-1. 令t =1x 2,则0<t <2,且a =14t 2-t -ln t .设h (t )=14t 2-t -ln t (0<t <2)则h ′(t )=12t -1-1t =(t -1)2-32t<0,所以h (t )(0<t <2)为减函数,则h (t )>h (2)=-ln 2-1,所以a >-ln 2-1. 而当t ∈(0,2)且t 趋近于0时,h (t )无限增大, 所以a 的取值范围是(-ln 2-1,+∞),故当函数f (x )的图象在点A 、B 处的切线重合时,a 的取值范围为(-ln 2-1,+∞).。
四川省成都市2013届高三数学第一次诊断考试试题 文(含解析)新人教A版

2013年四川省成都市高考数学一诊模拟试卷(一)(文科)参考答案与试题解析一、选择题(每小题5分,共50分)1.(5分)(2013•成都一模)不等式的解集是()A、(﹣∞,﹣8)∪(﹣3,+∞)B、(﹣∞,﹣8]∪[﹣3,+∞)C、[﹣3,2]D、(﹣3,2]考点:其他不等式的解法.专题:不等式的解法及应用.分析:把2移到左边后通分,再把分式不等式转化为整式不等式,进而即可求出其解集.解答:解:∵不等式,∴,化为(x+3)(x+8)≥0,且x≠﹣3,解得x>﹣3或x≤﹣8.∴原不等式的解集为{x|x≤﹣8或x>﹣3}.故无答案.点评:正确把分式不等式转化为整式不等式是解题的关键.注意,若利用去分母的方法去解,则必须就x+3的正负讨论,否则可能会出错.2.(5分)(2005•天津)若复数(a∈R,i为虚数单位位)是纯虚数,则实数a的值为()A.﹣2 B.4C.﹣6 D.6考点:复数代数形式的乘除运算;复数的代数表示法及其几何意义.分析:化简复数为a+bi(a、b∈R)的形式,让其实部为0,虚部不为0,可得结论.解答:解:复数=,它是纯虚数,则a=﹣6.故选C.点评:本题考查复数代数形式的乘除运算,复数的分类,是基础题.3.(5分)(2013•甘肃三模)(文)公差不为零的等差数列第2、3、6项构成等比数列,则公比为()A.1B.2C.3D.4考点:等比数列的性质;等差数列的通项公式.专题:计算题.分析:等差数列的第2、3、6项依次成等比数列,所以a32=a2•a6,设此等差数列的首项为a1,公差为d,通项即为a1+(n﹣1)d,得a2=a1+d,a3=a1+2d,a6=a1+5d,代入可得a1和d的关系式,求出公比即可.解答:解:设此等差数列的首项为a1,公差为d,通项即为a1+(n﹣1)d,得a2=a1+d,a3=a1+2d,a6=a1+5d,又因为等差数列的第2、3、6项依次成等比数列,所以a32=a2•a6,,把a2,a3,a6代入可得2a1=﹣d,d=﹣2a1所以公比==把d=﹣2a1代入得公比为3.故选C.点评:考查学生会求等差数列通项公式的能力,会求等比数列公比的能力,以及利用等差、等比数列性质的能力.4.(5分)(2013•成都一模)已知平面向量,满足,与的夹角为,则“m=1”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:平面向量及应用.分析:根据向量垂直的充要条件,直接代入向量数量积公式易构造方程,解方程即可求出未知参数m的值,从而判断出正确选项.解答:解:∵平面向量,满足,与的夹角为,∴=1×2×=1,又若“”,∴=0,即1﹣m=0解得m=1,则“m=1”是“”的充要条件.故选C.点评:本题考查的知识点为平面向量的数量积运算,⊥⇔x1•x2+y1y2=0.即:两个向量若垂直,对应相乘和为0.5.(5分)(2013•成都一模)关于命题p:A∪∅=∅,命题q:A∪∅=A,则下列说法正确的是()A.(¬p)∨q为假B.(¬p)∧(¬q)为真C.(¬p)∨(¬q)为假D.(¬p)∧q为真考点:复合命题的真假.专题:计算题.分析:利用集合知识,先判断出命题p:A∩∅=∅是真命题,命题q:A∪∅=A是真命题,再判断复合命题的真假.解答:解:∵命题p:A∩∅=∅是真命题,命题q:A∪∅=A是真命题,∴(¬p)∨q为真命题,(¬p)∧(¬q)为假命题,(¬p)∨(¬q)为假命题,(¬p)∧q为假命题,故选C.点评:本题考查复合命题的真假判断,是基础题.解题时要认真审题,仔细解答.[“命题p:A∩ϕ=ϕ,命题q:A∪ϕ=A”应该更正为:“命题p:A∩∅=∅,命题q:A∪∅=A”]6.(5分)(2005•江西)设函数f(x)=sin3x+|sin3x|,则f(x)为()A.周期函数,最小正周期为B.周期函数,最小正周期为C.周期函数,数小正周期为2πD.非周期函数考点:三角函数的周期性及其求法.专题:计算题.分析:可把四个选项中的最小正周期代入f(x+T)=f(x)检验,即可得到答案.解答:解:先将周期最小的选项A和C的周期T=和2π代入f(x+)=﹣sin3x+|sin3x|≠f(x),f(x+2π)=﹣sin3x+|sin3x|≠f(x),故排除A和C;再检验(B)f(x+)=sinx+|sin3x|=f(x),成立,可推断函数为周期函数排除D.故选B点评:本题主要考查了三角函数的周期性及其求法.对于选择题可用逆向法,把选项中的值代入题设条件中逐一检验获得答案.有时也能收到事半功倍的效果.7.(5分)(2013•成都一模)下列类比推理命题(其中Q为有理数集,R为实数集,C为复数集):①“若a,b∈R,则a﹣b=0⇒a=b”类比推出“若a,b∈C,则a﹣b=0⇒a=b”;②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”类比推出“若a,b,c,d∈Q,则”;③“若a,b∈R,则a﹣b>0⇒a>b”类比推出“若a,b∈C,则a﹣b>0⇒a>b”.其中类比结论正确的个数是()A.0B.1C.2D.3考点:归纳推理.专题:证明题;探究型.分析:在数集的扩展过程中,有些性质是可以传递的,但有些性质不能传递,因此,要判断类比的结果是否正确,关键是要在新的数集里进行论证,当然要想证明一个结论是错误的,也可直接举一个反例,要想得到本题的正确答案,可对3个结论逐一进行分析,不难解答.解答:解:①在复数集C中,若两个复数满足a﹣b=0,则它们的实部和虚部均相等,则a,b相等.故①正确;②在有理数集Q中,若,则(a﹣c)+(b﹣d)=0,易得:a=c,b=d.故②正确;③若a,b∈C,当a=1+i,b=i时,a﹣b=1>0,但a,b 是两个虚数,不能比较大小.故③错误故3个结论中,有两个是正确的.故选C点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).但类比推理的结论不一定正确,还需要经过证明.8.(5分)(2013•成都一模)如图,在三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则BB1与平面AB1C1所成的角是()A.B.C.D.考点:直线与平面所成的角.专题:计算题.分析:以B为坐标原点,建立空间直角坐标系,利用与平面AB1C1所的一个法向量的夹角,求出则BB1与平面AB1C1所成的角.解答:解:以B为坐标原点,以与BC垂直的直线为x轴,BC为y轴,建立空间直角坐标系,则A(,1,0),B1(0,0,3),C1(0,2,3),=(﹣,﹣1,3),=(0,2,0),=(0,0,3).设平面AB1C1所的一个法向量为=(x,y,z)则即,取z=1,则得=(﹣,0,1),∵cos<,>===,∴BB1与平面AB1C1所成的角的正弦值为,∴BB1与平面AB1C1所成的角为故选A.点评:本题考查线面角的计算,利用了空间向量的方法.要注意相关点和向量坐标的准确性,及转化时角的相等或互余关系.9.(5分)(2013•成都一模)设集合A=[0,),B=[,1],函数f (x)=若x0∈A,且f[f (x0)]∈A,则x0的取值范围是()A.(0,] B.[,]C.(,)D.[0,]考点:函数的值;元素与集合关系的判断.专题:计算题;压轴题;不等式的解法及应用.分析:利用当 x0∈A时,f[f (x0)]∈A,列出不等式,解出 x0的取值范围.解答:解:∵0≤x0<,∴f(x0)=x0 +∈[,1]⊆B,∴f[f(x0)]=2(1﹣f(x0))=2[1﹣(x0+)]=2(﹣x0).∵f[f(x0)]∈A,∴0≤2(﹣x0)<,∴<x0≤.又∵0≤x0<,∴<x0<.故选C.点评:本题考查求函数值的方法,以及不等式的解法,属于基础题.10.(5分)(2013•成都一模)定义在(﹣1,1)上的函数;当x∈(﹣1,0)时,f(x)>0,若,,则P,Q,R的大小关系为()A.R>Q>P B.R>P>Q C.P>R>Q D.Q>P>R考点:不等关系与不等式.专题:新定义.分析:在已知等式中取x=y=0,可求得f(0)=0,取﹣1<x<y<1,能说明,所以说明,从而说明函数f(x)在(﹣1,1)上为减函数,再由已知等式把化为一个数的函数值,则三个数的大小即可比较.解答:解:取x=y=0,则f(0)﹣f(0)=f(0),所以,f(0)=0,设x<y,则,所以所以f(x)>f(y),所以函数f(x)在(﹣1,1)上为减函数,由,得:取y=,,则x=,所以,因为0<,所以所以R>P>Q.故选B.点评:本题考查了不等关系与不等式,考查了特值思想,解答此题的关键是能够运用已知的等式证出函数是给定区间上的减函数,同时需要借助于已知等式把P化为一个数的函数值,是中等难度题.二、填空题(每小题5分,共25分)11.(5分)(2013•成都一模)若x=log43,(2x﹣2﹣x)2= .考点:有理数指数幂的化简求值.专题:计算题.分析:根据题目给出的x的值,首先化为以2为底数的对数,然后代入要求的式子,运用公式计算.解答:解:因为,所以=.故答案为.点评:本题考查了有理指数幂的化简求值,解答此题的关键是熟记公式,是基础题.12.(5分)(2013•成都一模)某程序的框图如图所示,若执行该程序,则输出的i值为7 .考点:循环结构.专题:计算题.分析:根据题意,该算法流程图是要我们求出等比数列{2n﹣1}的前n项和,并且找到使这个和大于100的最小正整数n的值,由此再结合等比数列的求和公式,不难得到本题的答案.解答:解:根据题意,列出如下表格该算法流程图的作用是计算1+21+22+…+2n﹣1的和,并且求出使这个和大于2012的最小n的值∵1+21+22+…+2n﹣1=2n﹣1,且26﹣1=63,27﹣1=127∴S=1+21+22+…+2n﹣1,使S>100的最小正整数n的值为7.故答案为:7点评:本题以循环结构的算法流程图为载体,求满足条件的最小正整数n,着重考查了等比数列的求和公式和循环结构等知识,属于基础题.13.(5分)(2013•成都一模)在正方体ABCD﹣A1B1C1D1中,M、N、P、Q分别是AB、AA1、C1D1、CC1的中点,给出以下四个结论:①AC1⊥MN;②AC1∥平面MNPQ;③AC1与PM相交;④NC1与PM异面.其中正确结论的序号是①③④.考点:空间中直线与平面之间的位置关系.专题:计算题;空间位置关系与距离.分析:①要证A1C⊥MN,由于AD1∥MN,则只需证A1C⊥AD1,即只需证AD1⊥面A1CD即可;②由于A1C与MP交于一点,则A1C与平面MNPQ相交;③④判定空间中直线与直线之间的位置关系,要紧扣定义来完成.解答:解:在正方体ABCD﹣A1B1C1D1中,∴A1D⊥AD1,∵CD⊥面AA1D1D,AD1⊂面AA1D1D,∴CD⊥AD1,∴AD1⊥面A1CD,∴A1C⊥AD1∵M,N分别是AA1,A1D1的中点,∴AD1∥MN,即A1C⊥MN,故①正确;由于M,N,P,Q分别是AA1,A1D1,CC1,BC的中点,则A1C与PM相交,故②不正确,③正确;∵N∉面ACC1A1,而M,P,C∈面ACC1A1,∴NC与PM异面,故④正确;故答案为:①③④.点评:本题考查的知识点是,判断命题真假,同时考查了空间中直线与直线,直线与平面的位置关系,我们可以根据空间几何中的定义,定理及常用结论对四个结论逐一进行判断,可以得到正确的结果.14.(5分)(2013•成都一模)已知函数f(x)=|x﹣3|﹣2|x﹣1|,则其最大值为 2 .考点:带绝对值的函数.专题:不等式的解法及应用.分析:通过去掉绝对值符号得出函数解析式,进而画出图象,即可得出最大值.解答:解:∵函数f(x)=|x﹣3|﹣2|x﹣1|=,根据解析式画出图象:由图象可以看出:当且仅当x=0时,函数f(x)取得最大值2.故答案是2.点评:正确去掉绝对值符号并画出图象是解题的关键.15.(5分)(2013•成都一模)设两个向量=(λ+2,λ2﹣cox2α)和=(m,+sinα),其中λ,m,α为实数.若=2,则的取值范围是[﹣6,1] .考点:平面向量共线(平行)的坐标表示.专题:计算题.分析:根据向量相等的概念,向量相等,即向量的横纵坐标相等,可哪λ用m表示,所以可化简为2﹣,所以只需求的范围即可,再利用向量相等得到的关系式,把m 用α的三角函数表示,根据三角函数的有界性,求出m的范围,就可得到的范围.解答:解:∵=2,∴λ+2=2m,①λ2﹣cox2α=m+2sinα.②∴λ=2m﹣2代入②得,4m2﹣9m+4=cox2α+2sinα=1﹣sin2α+2sinα=2﹣(sinα﹣1)2∵﹣1≤sinα≤1,,∴0≤(sinα﹣1)2≤4,﹣4≤﹣(sinα﹣1)2≤0∴﹣2≤2﹣(sinα﹣1)2≤2∴﹣2≤4m2﹣9m+4≤2分别解4m2﹣9m+4≥﹣2,与4m2﹣9m+4≤2,得,≤m≤2∴≤≤4==2﹣∴﹣6≤2﹣≤1∴的取值范围是[﹣6,1]故答案为[﹣6,1]点评:本题考查了向量相等的坐标表示,以及利用三角函数有界性求范围.属于综合题.三、解答题(第16-第19题每小题12分,20题13分,21题14分.共75分)16.(12分)(2013•成都一模)为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从A、B、C三个区中抽取6个工厂进行调查.已知A、B、C区中分别有18,27,9个工厂.(1)求从A、B、C区中应分别抽取的工厂个数;(2)若从抽得的6个工厂中随机地抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率.考点:列举法计算基本事件数及事件发生的概率;分层抽样方法.专题:概率与统计.分析:(1)先计算A,B,C区中工厂数的比例,再根据比例计算各区应抽取的工厂数.(2)本题为古典概型,先将各区所抽取的工厂用字母表达,分别计算从抽取的6个工厂中随机抽取2个的个数和至少有1个来自A区的个数,再求比值即可.解答:解:(1)工厂总数为18+27+9=54,样本容量与总体中的个体数的比为=,所以从A,B,C三个区中应分别抽取的工厂个数为2,3,1.…(5分)(2)设A1,A2为在A区中抽得的2个工厂,B1,B2,B3为在B区中抽得的3个工厂,C1为在C区中抽得的1个工厂.在这6个工厂中随机地抽取2个,全部可能的结果有:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2,B2),(A2,B3),(A2,C1),(B1,B2),(B1,B3),(B1,C1),(B2,B3),(B2,C1),(B3,C1)共15种.随机地抽取的2个工厂至少有1个来自A区(记为事件X)的结果有:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2,B2),(A2,B3),(A2,C1)共9种.所以这2个工厂中至少有1个来自A区的概率为P(X)=.…(11分)答:(1)从A,B,C三个区中应分别抽取的工厂个数为2,3,1.(2)这2个工厂中至少有1个来自A区的概率为.…(12分)点评:本题主要考查分层抽样、古典概型的基本运算.属于基础知识、基本运算的考查.17.(12分)(2013•成都一模)已知向量=(sin,1),=(cos,cos2),f(x)=•.(1)若f(x)=1,求cos(x+)的值;(2)在△ABC中,角A,B,C的对边分别是a,b,c且满足acosC+c=b,求函数f(B)的取值范围.考点:余弦定理;平面向量数量积的运算;三角函数的化简求值.专题:计算题.分析:(1)由两向量的坐标,利用平面向量的数量积运算法则列出f(x)的解析式,再利用二倍角的正弦、余弦函数公式及两角和与差的正弦函数公式化为一个角的正弦函数,由f(x)=1,得出sin(+)的值,最后将所求的式子中的角提取2,利用二倍角的余弦函数公式化简后,将sin(+)的值代入即可求出值;(2)利用余弦定理表示出cosC,代入已知的等式,整理后代入利用余弦定理表示出的cosA中,得出cosA的值,由A为三角形的内角,利用特殊角的三角函数值求出A的度数,进而确定出B的范围,得出+的范围,利用正弦函数的图象与性质得出此时正弦函数的值域,即为f(B)的范围.解答:解:(1)∵=(sin,1),=(cos,cos2),∴f(x)=•=sin cos+cos2=sin+cos+=sin(+)+,又f(x)=1,∴sin(+)=,(4分)∴cos(x+)=cos2(+)=1﹣2sin2(+)=;(6分)(2)∵cosC=,acosC+c=b,∴a•+c=b,即b2+c2﹣a2=bc,∴cosA==,又∵A∈(0,π),∴A=,(10分)又∵0<B<,∴<+<,∴f(B)∈(1,).(12分)点评:此题考查了余弦定理,平面向量的数量积运算,二倍角的正弦、余弦函数公式,两角和与差的正弦函数公式,以及正弦函数的定义域与值域,熟练掌握定理及公式是解本题的关键.18.(12分)(2013•成都一模)一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点(1)求证:GN⊥AC;(2)当FG=GD时,在棱AD上确定一点P,使得GP∥平面FMC.并给出证明.考点:直线与平面平行的判定;简单空间图形的三视图.专题:计算题;证明题.分析:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC,则(1)连接DB,我们易得FD⊥AD,FD⊥CD,由线面垂直的判定定理,可得FD⊥面ABCD,进而得到AC⊥面FDN,由线面垂直的定义,即可得到GN⊥AC;(2)由图分析得,点P与点A重合时,GP∥面FMC,取DC中点S,连接AS、GS、GA 由三角形中位线宣,我们易证明出面GSA∥面FMC,根据面面平行的性质,我们易得GA∥面FMC,即P与A重合.解答:证明:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC (1)连接DB,可知B、N、D共线,且AC⊥DN又FD⊥AD,FD⊥CD,∴FD⊥面ABCD∴FD⊥AC∴AC⊥面FDN,GN⊂面FDN∴GN⊥AC(2)点P与点A重合时,GP∥面FMC证明:取DC中点S,连接AS、GS、GA∵G是DF的中点,∴GS∥FC,A S∥CM∴面GSA∥面FMCGA⊂面GSA∴GA∥面FMC 即GP∥面FMC点评:本题考查的知识点是直线与平面平行的判定,简单空间图形的三视图,其中根据三视图,判断出该几何体为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC,是解答本题的关键.19.(12分)(2013•长宁区一模)某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元.(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:Q(x)=170﹣0.05x,试问生产多少件产品,总利润最高?(总利润=总销售额﹣总的成本)考点:基本不等式在最值问题中的应用;根据实际问题选择函数类型.专题:应用题.分析:(1)根据每件产品的成本费P(x)等于三部分成本和,建立函数关系,再利用基本不等式求出最值即可;(2)设总利润为y元,根据总利润=总销售额﹣总的成本求出总利润函数,利用二次函数的性质求出取最值时,x的值即可.解答:解:(Ⅰ)根据某工厂生产一种产品的成本费由三部分组成,①职工工资固定支出12500元;②原材料费每件40元;③电力与机器保养等费用为每件0.05x元,可得由基本不等式得当且仅当,即x=500时,等号成立∴的最小值为90元.∴每件产品的最低成本费为90元(Ⅱ)设总利润为y元,∵每件产品的销售价Q(x)与产品件数x有如下关系:Q(x)=170﹣0.05x∴总销售额=xQ(x)=170x﹣0.05x2,则y=xQ(x)﹣xP(x)=﹣0.1x2+130x﹣12500=﹣0.1(x﹣650)2+29750当x=650时,y max=29750答:生产650件产品时,总利润最高,最高总利润为29750元.点评:本题主要考查了基本不等式在最值问题中的应用,以及二次函数的性质,同时考查了建模的能力,属于中档题20.(13分)(2013•成都一模)已知一非零向量列{a n}满足:a1=(1,1),a n=(x n,y n)=(1)证明:{|a n|}是等比数列;(2)设θn=<a n﹣1,a n>(n≥2),b n=2nθn﹣1,S n=b1+b2+…+b n,求S n;(3)设c n=|a n|log2|a n|,问数列{c n}中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.考点:数列与函数的综合;数列的函数特性;等比关系的确定.专题:综合题;压轴题.分析:(1)先利用向量模的计算公式得出的表达式,发现得出=利用等比数列定义判定是等比数列.(2)根据向量夹角公式可以求出θn =,b n=2nθn﹣1=.分组后结合等差数列求和公式计算.(3)由上可得出c n =•,可利用作商法研究数列{c n}的单调性,确定最小项存在与否.解答:解:(l )证明:===(n≥2)又=∴数列是以为首项,公比为的等比数列.…(4分)(2)∵===2∴cosθn ==,∴θn =,∴b n=2nθn﹣1=.Sn=b1+b2+…+b n ==…(8分)(3)假设存在最小项,不防设为cn ,∵==,∴c n=|a n|log2|a n |=•,由c n≤c n+1得≤即(2﹣n)≤1﹣n ,∴(﹣1)n≥2﹣1.∴n≥=3+,∵n为正整数,∴n≥5.由c n≤c n﹣1得n≤4+,n≤5.,∴n=5故存在最小项,最小项为c5=…(12分)点评:本题考查数列的函数性质,等比数列的判定,数列求和,向量数量积、夹角的计算,是数列与不等式的综合.所涉及的知识、方法均为高中学段基本要求.21.(14分)(2013•牡丹江一模)已知函数f(x)=xlnx.(Ⅰ)求函数f(x)的极值点;(Ⅱ)若直线l过点(0,﹣1),并且与曲线y=f(x)相切,求直线l的方程;(Ⅲ)设函数g(x)=f(x)﹣a(x﹣1),其中a∈R,求函数g(x)在区间[1,e]上的最小值.(其中e为自然对数的底数)考点:利用导数研究曲线上某点切线方程;利用导数求闭区间上函数的最值.专题:综合题.分析:(I)先对函数求导,研究函数的单调区间,根据F′(x)>0求得的区间是单调增区间,F′(x)<0求得的区间是单调减区间,求出极值.(II)求出曲线方程的导函数,利用导函数中即可求出切线方程的斜率,根据求出的斜率和已知点的坐标写出切线方程即可;(III)求导:g'(x)=lnx+1﹣a解g'(x)=0,得x=e a﹣1,得出在区间(0,e a﹣1)上,g(x)为递减函数,在区间(e a﹣1,+∞)上,g(x)为递增函数,下面对a进行讨论:当e a﹣1≤1,当1<e a﹣1<e,当e a﹣1≥e,从而得出g(x)的最小值.解答:解:(Ⅰ)f'(x)=lnx+1,x>0,…(2分)由f'(x)=0得,…(3分)所以,f(x)在区间上单调递减,在区间上单调递增.…(4分)所以,是函数f(x)的极小值点,极大值点不存在.…(5分)(Ⅱ)设切点坐标为(x0,y0),则y0=x0lnx0,…(6分)切线的斜率为lnx0+1,所以,,…(7分)解得x0=1,y0=0,…(8分)所以直线l的方程为x﹣y﹣1=0.…(9分)(Ⅲ)g(x)=xlnx﹣a(x﹣1),则g'(x)=lnx+1﹣a,…(10分)解g'(x)=0,得x=e a﹣1,所以,在区间(0,e a﹣1)上,g(x)为递减函数,在区间(e a﹣1,+∞)上,g(x)为递增函数.…(11分)当e a﹣1≤1,即a≤1时,在区间[1,e]上,g(x)为递增函数,所以g(x)最小值为g(1)=0.…(12分)当1<e a﹣1<e,即1<a<2时,g(x)的最小值为g(e a﹣1)=a﹣e a﹣1.…(13分)当e a﹣1≥e,即a≥2时,在区间[1,e]上,g(x)为递减函数,所以g(x)最小值为g(e)=a+e﹣ae.…(14分)综上,当a≤1时,g(x)最小值为0;当1<a<2时,g(x)的最小值a﹣e a﹣1;当a≥2时,g(x)的最小值为a+e﹣ae.点评:本题考查了导数的应用:利用导数判断函数的单调性及求单调区间;函数在区间上的最值的求解,其一般步骤是:先求极值,比较函数在区间内所有极值与端点函数.若函数在区间上有唯一的极大(小)值,则该极值就是相应的最大(小)值.。
2013成都三诊文科数学答案

* B HCDEF# " " ?
! I JKE !"#%$" %! % $# $ $ $ $ # # & 0 ! # ! & # % # $ & # # ) & % # % & & ! + L;E %% $# ! # " $ L &"1 ($ # , ! #'" $ # ! 2 ) 0 ! 1 , # ! #1 #1 #1 #! " " 0 # " 0 # # &" !'" $ # # ! 2 )0 ! 2 ) 1 ! 2 ) ! " 1 "0 " 0 #1 $ &"1 #')*+"
!"# ! " # $ $%&'()*+,-./01 23 45678 9:;<=>?@A
* B CDEF% " ?
! G CDE !"#%$" %% " $# # & '$ ! & '$ $ & ($ ) & *$ % & +$ , & ($ & +$ . & *$ / & +$ # " & (&
! ! !" $8 $ 0 ! ¢567¬! 78$ $0 $ 0 ! ! ! ! ! # ! ! ! !
! 槡 '& 槡
#
!
!
$ ! " i@! -# 1 ! 0 ! $ -8 #4®¯°-1 (0 # ! # " # " Q±0 @! 0 # 1 $ 8 ! $( " @! " 1 # " # " ! % ( !( " ' , # " # '" 3&-'& 0 # " $# 1 -# @ A 0 # " ! A! ,! ,! ,! ? @ A1? ! # ! # " ! # ! # " V, " 1 4 ;0 $ ,0 #1 # 8 4 ;0 # 0 $ 0 B" B # # " # # q,,! ²0 ,! X*+! " 0 # $% ! " # % 0 %0 % ,! ,! B 0 # B 0 # # ! ! # ¡¢$³Q" $# 1 0 # 1 # 8 4 ; 0 # 0 $# $&0 ! ! A! ,! ! " " ' # ,! &$10 & ¢3Oª©,! !'" -# 0 # " 0 # 1 # ! # # ,! ! " ' " " ! # (&-'& ' 0 #" $10 ! -8 4 ;-8 !& # ! " 8 # " 0 # " " ' -8 _-10 ! 1 0 # " ! '! " " "0 #! "8 # 3 8 4 ; # ! ( " " "8 # ! # (# "8 # ! 3 4 ; 4 ; ( 0 !! !8 ( ! " " " " " "
成都市高2013级第一次诊断考试数学文科及答案
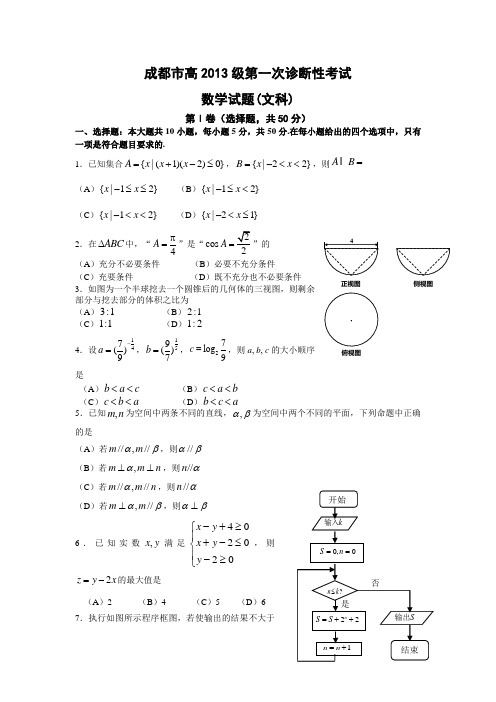
成都市高2013级第一次诊断性考试数学试题(文科)第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|(1)(2)0}A x x x =+-≤,{|22}B x x =-<<,则A B = (A ){|12}x x -≤≤ (B ){|12}x x -≤< (C ){|12}x x -<< (D ){|21}x x -<≤ 2.在ABC ∆中,“4A π=”是“cos A = (A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件 3.如图为一个半球挖去一个圆锥后的几何体的三视图,则剩余部分与挖去部分的体积之比为 (A )3:1 (B )2:1 (C )1:1 (D )1:24.设147()9a -=,159()7b =,27log 9c =,则a , b , c 的大小顺序是(A )b a c << (B )c a b <<(C )c b a << (D )b c a <<5.已知n m ,为空间中两条不同的直线,βα,为空间中两个不同的平面,下列命题中正确的是(A )若βα//,//m m ,则βα//(B )若,m m n α⊥⊥,则//n α(C )若n m m //,//α,则α//n (D )若βα//,m m ⊥,则βα⊥6.已知实数,x y 满足402020x y x y y -+≥⎧⎪+-≤⎨⎪-≥⎩,则2zy x =-的最大值是(A )2 (B )4 (C )5 (D )6 7.执行如图所示程序框图,若使输出的结果不大于正视图侧视图俯视图50,则输入的整数k 的最大值为(A )4 (B )5 (C )6 (D )78.已知菱形A B C D 边长为2,3B π∠=,点P 满足A P A B λ= ,λ∈R .若3BD CP ⋅=-,则λ的值为(A )12 (B )12- (C )13 (D ) 13- 9.已知双曲线2222:1(0,0)x y E a b a b-=>>的左右焦点分别为1F ,2F ,若E 上存在点P 使12F F P ∆为等腰三角形,且其顶角为23π,则22a b的值是(A )43 (B)3 (C )34 (D)210.已知函数232log (2),0()33,x x k f x x x k x a-≤<⎧=⎨-+≤≤⎩ .若存在实数k 使得函数()f x 的值域为[1,1]-,则实数a 的取值范围是(A)3[,12+ (B)[2,1 (C )[1,3] (D ) [2,3]第Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分. 11.设复数z 满足i (32i)(1i)z -=+-(其中i 为虚数单位),则z = . 12.已知函数3()sin 1f x x x -=++.若()3f a =,则()f a -= .13.甲、乙两人在5次综合测评中成绩的茎叶图如图所示,其中一个数字被污损,记甲,乙的平均成绩分别为x 甲,x 乙.则x >甲x 乙的概率是 .14. 已知圆422=+y x ,过点(0,1)P 的直线l 交该圆于B A ,两点,O 为坐标原点,则OAB ∆面积的最大值是 .15.某房地产公司要在一块矩形宽阔地面(如图)上开发物业 ,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线2413y x =-的一部分,栏栅与矩形区域边界交于点M ,N .则当能开发的面积达到最大时,OM 的长为 .三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)已知等比数列{}n a 的公比1q >,且212()5n n n a a a +++=. (Ⅰ)求q 的值;(Ⅱ)若2510a a =,求数列{}3nna 的前n 项和n S . 17.(本小题满分12分)有编号为,,,A A A 的9道题,其难度系数如下表:(Ⅰ)从上述9道题中,随机抽取1道,求这道题为难题的概率; (Ⅱ)从难题中随机抽取2道,求这两道题目难度系数相等的概率. 18.(本小题满分12分)已知函数2251()cos cos sin 424f x x x x x =--. (Ⅰ)求函数()f x 取得最大值时x 取值的集合;(Ⅱ)设A ,B ,C 为锐角三角形ABC 的三个内角.若3cos 5B =,1()4f C =-,求sin A 的值.19.(本小题满分12分)如图,菱形ABCD 与正三角形BCE 的边长均为2,它们所在平面互相垂直,FD ⊥平面A B C D ,且FD =(Ⅰ)求证://EF 平面ABCD ;(Ⅱ)若60CBA ∠=︒,求几何体EFABCD 的体积. 20.(本小题满分13分)已知椭圆22:132x y E +=的左右顶点分别为A ,B ,点P 为椭圆上异于,A B 的任意一点.(Ⅰ)求直线PA 与PB 的斜率之积;(Ⅱ)过点(Q 作与x 轴不重合的任意直线交椭圆E 于M ,N 两点.证明:以MN 为直径的圆恒过点A .21.(本小题满分14分)已知函数21()(1)ln ()2f x ax a x x a =-++-∈R . (Ⅰ)当0a >时,求函数()f x 的单调递减区间;(Ⅱ)当0a =时,设函数()()(2)2g x xf x k x =-++.若函数()g x 在区间1[,)2+∞上有两个零点,求实数k 的取值范围.数学(文科)参考答案及评分意见第I 卷(选择题,共50分)一、选择题:(本大题共10小题,每小题5分,共50分)1.B ; 2.B ; 3.C ; 4.C ; 5.D ; 6.D ; 7.A ; 8.A ; 9.D ; 10.B .第II 卷(非选择题,共100分)二.填空题:(本大题共5小题,每小题5分,共25分) 11.15i +; 12.-1; 13.25; 14.3; 15.1. 三、解答题:(本大题共6小题,共75分) 16.解:(Ⅰ) 212()5,n n n a a a +++=22()5.n n n a a q a q ∴+= 由题意,得0n a ≠,∴22520.q q -+=2q ∴=或1.21q >,2.q ∴= ……………………6分 (Ⅱ)2510,a a = 42911().a q a q ∴=12a ∴=.∴112.n n n a a q -==∴2().33nn n a = ∴122[1()]2332.2313n n n n S +-==--……………………12分 17.解:(Ⅰ)记“从9道题中,随机抽取1道为难题”为事件M ,9道题中难题有1A ,4A ,6A ,7A 四道.∴4().9P M =……………6分 (Ⅱ)记“从难题中随机抽取2道难度系数相等”为事件N ,则基本事件为:14{,}A A ,16{,}A A ,17{,}A A ,46{,}A A ,47{,}A A ,67{,}A A 共6个;难题中有且仅有6A ,7A 的难度系数相等. ∴1().6P N =……………12分 18.解:(Ⅰ)2251()cos cos sin 44f x x x x x =-5sin 231cos 242222x x -=--⨯13(cos 22)24x x =--+1).23x π=--……………………3分 要使()f x 取得最大值,须满足sin(2)3x π-取得最小值.∴22,32x k k ππ-=π-∈Z. ∴,12x k k π=π-∈Z.……………………5分 ∴当()f x 取得最大值时,x 取值的集合为{|,}.12x x k k π=π-∈Z ……………………6分(Ⅱ)由题意,得sin(2)3C π-= (0,),2C π∈ 22(,).333C πππ∴-∈-3C π∴=. ………………9分(0,)2B π∈ ,4sin .5B ∴=sin sin()sin cos cos sin A B C B C B C ∴=+=+413525=⨯+=………………12分 19.解:(Ⅰ)如图,过点E 作EH BC ⊥于H ,连接.HDEH ∴平面ABCD ⊥平面BCE ,EH ⊆平面BCE , 平面ABCD 平面BCE 于BC ,∴EH ⊥平面.ABCD又FD ⊥ 平面ABCD,FD =//.FD EH ∴ ∴四边形EHDF 为平行四边形.//.EF HD ∴EF ⊄ 平面ABCD ,HD ⊆平面,ABCD//EF ∴平面.ABCD ………6分(Ⅱ)连接,CF HA .由题意,得HA BC ⊥.HA ⊆平面,ABCD 平面ABCD ⊥平面BCE 于BC ,∴HA ⊥平面BCE .//FD EH ,EH ⊆平面BCE ,FD ⊄平面BCE ,//FD ∴平面.BCE同理,由//HB DA 可证,//DA 平面.BCEFD DA 于D ,FD ⊆平面ADF ,DA ⊆平面ADF , ∴平面BCE //平面.ADFF ∴到平面BCE 的距离等于HA 的长. FD 为四棱锥F ABCD -的高, EFABCD F BCE F ABCD V V V --∴=+1133BCE ABCD S HA S FD =⨯+⨯1133=⨯3.= ……………………………12分20.解:(Ⅰ)(A B .设点(,)P x y (0)y ≠.则有22132x y +=,即22222(1)(3).33x y x =-=-223PA PBy k k x ∴⋅==-222(3)23.33x x -==-- ……………………4分(Ⅱ)设11(,)M x y ,22(,)N x y , MN 与x 轴不重合,∴设直线:)MN l x ty t =∈R .由22,2360x ty x y ⎧=⎪⎨⎪+-=⎩得22144(23)0.525t y +--= 由题意,可知0∆>成立,且122122523.1442523y y t y y t ⎧⎪+=⎪⎪+⎨⎪-⎪=⎪+⎩ ……(*)11221212()()(AM AN x y x y ty ty y y ⋅=+=+++2121248(1)().525t y y y y =++++ 将(*)代入上式,化简得2222214414448484823482525250.2325252325t t t AM AN t t --++⋅=+=-⨯+=++ ∴AM AN ⊥,即以MN 为直径的圆恒过点A . ………………13分21.解:(Ⅰ)()f x 的定义域为(0,)+∞,(1)(1)()(0).ax x f x a x--'=-> ①当(0,1)a ∈时,11a >.由()0f x '<,得1x a >或1x <.∴当(0,1)x ∈,1(,)x a∈+∞时,()f x 单调递减.∴()f x 的单调递减区间为(0,1),1(,)a+∞.②当1a =时,恒有()0f x '≤,∴()f x 单调递减. ∴()f x 的单调递减区间为(0,)+∞.③当(1,)a ∈+∞时,11a<.由()0f x '<,得1x >或1x a <.∴当1(0,)x a ∈,(1,)x ∈+∞时,()f x 单调递减.∴()f x 的单调递减区间为1(0,)a,(1,)+∞.综上,当(0,1)a ∈时,()f x 的单调递减区间为(0,1),1(,)a+∞;当1a =时,()f x 的单调递减区间为(0,)+∞;当(1,)a ∈+∞时,()f x 的单调递减区间为1(0,)a ,(1,)+∞. ………6分(Ⅱ)2()ln (2)2g x x x x k x =--++在1[,)2x ∈+∞上有零点,即关于x 的方程2ln 22x x x k x -+=+在1[,)2x ∈+∞上有两个不相等的实数根.令函数2ln 21(),[,)22x x x h x x x -+=∈+∞+. 则2232ln 4()(2)x x x h x x +--'=+. 令函数21()32ln 4,[,)2p x x x x x =+--∈+∞. 则(21)(2)()x x p x x -+'=在1[,)2+∞上有()0p x '≥.故()p x 在1[,)2+∞上单调递增.(1)0p = ,∴当1[,1)2x ∈时,有()0p x <即()0h x '<.∴()h x 单调递减;当(1,)x ∈+∞时,有()0p x >即()0h x '>,∴()h x 单调递增.19ln 2()2105h =+ ,(1)1,h =10210ln 21021023(10)12123h --=>=>1()2h , ∴k 的取值范围为9ln 2(1,].105+…………14分。
成都市2013届高中毕业班第一次诊断性检测文科数学试卷

成都市2013届高中毕业班第一次诊断性检测数学(文史类)本试卷分选择题和非选择题两部分。
第I卷(选择题)1至2页,第II卷(非选择题)3至4页,共4页,满分150分,考试时间120分钟。
注意事项:1. 答题前,务必将自己的姓名、考籍号填写在答题卡规定的位置上。
2. 答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3. 答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4. 所有题目必须在答题卡上作答,在试题卷上答题无效。
5. 考试结束后,只将答题卡交回。
第I卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,有且 只有一项是符合题目要求的.1. 已知集合P={1,2},,则集合Q为(A){1,2,3} (B){2,3,4} (C){3,4,5} (D){2,3}2. 复数(i为虚数单位)的虚部为(A)1 (B)i (C)-2i (D)—23.某校在一年一度的“校园十佳歌手”比赛中,9位评委为参赛选手A给出的分数的茎叶图如图所示.在去掉一个最高分和一个最低分后,得出选手A得分的中位数是(A)93 (B)92(C)91 (D) 904.已知,则M a r的值是(A)2 (B)-2 (C) 3 (D)-35. 函数f(x)=e2x+1的大致图象为6. —空间几何体的三视图如图所示,则此空间几何体的直观图为7. 在ΔABC中,若 sinA—sinAcosC=cosAsinC,则ΔABC 的形状是(A)正三角形(B)等腰三角形(C)直角三角形(D)等腰直角三角形8. 已知直线l丄平面a,直线平面,则“”是“”的(A)充要条件(B)必要条件(C)充分条件(D)既不充分又不必要条件9. 如图,在三棱锥S—ABC中,SA丄平面ABC,SA = 3,AC=2, AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为(A)(B)(C)(D)10. 已知数列{a n}满足.一颗质地均匀的正方体骰子,其六个面上的点数分别为1,2,3,4,5,6.将这颗骰子连续抛掷两次,得到的点数分别记为a,b则满足集合()的概率是(A) (B) (C) (D)第II卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.某学校高中三个年级的学生人数分别为:高一 950人,髙二1000人,高三1050人.现要调查该校学生的视力状况,考虑采用分层抽样的方法,抽取容量为60的样本,则应从高三年级中抽取的人数为______12.已知某算法的程序框图如图所示,当输入x的值为13时,则输出y的值为______.13.当x〉l时,的最小值为____.14. 已知角构成公差为的等差数列.若,贝丨J= .15.如图,在ΔABC中,且AH=1,G为4BC的重心,则=____三、解答题:本大题共6小题,共75分.16. (本小题满分12分)已知向量,设..(I )化简函数f(x)的解析式并求其最小正周期;(II)当.时,求函数f(x)的最大值及最小值.17. (本小题满分12分)如图,矩形 ABCD中,BC=2,AB=1,PA丄平面 ABCD,BE//PA,B E=PA,F为PA的中点.(I)求证:DF//平面PEC(II)记四棱锥C一PABE的体积为V1,三棱锥P—ACD的体积为V2,求的值.18. (本小题满分12分)已知函数(I)解关于x的不等式:—;(II)若,判断函数的零点个数,并说明理由.19. (本小题满分12分)某工厂在政府的帮扶下,准备转型生产一种特殊机器,生产需要投入固定成本500万元,生产与销售均以百台计数,且每生产100台,还需增加可变成本1000万元.若市场对该产品的年需求量为500台,每生产m百台的实际销售收入近似满足函数R(m)=5000m-(I)试写出第一年的销售利润y(万元)关于年产量x单位:百台,)的函数关系式;(说明:销售利润=实际销售收人一成本)(II)因技术等原因,第一年的年生产量不能超过300台,若第一年人员的年支出费用(万元)与年产量x(百台)的关系满足,问年产量X为多少百台时,工厂所得纯利润最大?20. (本小题满分13分)在数列{a n}中,a1=2,a2=4,且当时,.(I)求数列{a n}的通项公式a n(II)若,求数列{b n}的前n项和Sn(III)是否存在正整数对(m,n),使等式成立?若存在,求出所有符合条件的(m,n);若不存在,请说明理由.21. (本小题满分14分)已知函数(I)若a = 1,求函数h(x)的极值;(II )若函数Y=H (x)在上单调递增,求实数A的取值范围;(III)在函数:y=f(x)的图象上是否存在不同的两点,使线段AB 的中点的横坐标与直线AB的斜率k之间满足?若存在,求出x 0;若不存在,请说明理由.。
成都七中高2013级3月月考文科数学答案

成都七中高2013级3月月考数学试题(文史类)参数答案一、选择题:本大题共10小题,每小题5分,共50分.二、填空题:本大题共5小题,每小题5分,共25分.11. 4 .12.3-.13. 4,0a a ==或.14.247-. 15. ①②④ .三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)解:(I )由余弦定理:cos .2S ab C =联立(1)(202C π<< 3C π⇒∠=.所以,角C 的值为3π……………6分 (II )因为A 为三角形内角,所以203A π<<,由正弦定理得:a =,B sin 334b =,……7分 所以, 2sin()34sin(A )6a b A ππ+==+-=+………9分2(0,)3A π∈ ,1sin()(,1]62A π∴+∈,(2,4]a b ∴+∈,所以b c +的取值范围为(2,4] …………12分17.(本小题满分12分)提示(1)略…………6分(2)由题意,可补成正方体,如图所示,易证:四边形ABEF 与四边形''EFD B 面积相等, 即''ABEF EFD B S S =梯梯所以,几何体'ABCDEC F 的体积V :''''''127.22A BDFE BCDEC FC BD FE BCDECF AC V V V V V V --=+=+==正方体 …………12分18.(本小题满分12分)解:(Ⅰ)由题设可知,第3组的频率为0.0650.3⨯=,第4组的频率为0.0450.2⨯=,第5组的频率为0.0250.1⨯=. ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅3分第3组的人数为0.310030⨯=,第4组的人数为0.210020⨯=,第5组的人数为0.110010⨯=.因为第3,4,5组共有60名应聘者,所以利用分层抽样在60名应聘者中抽取6名,每组抽取的人数分别为第3组:306360⨯=,第4组:206260⨯=,第5组:106160⨯=. 所以第3,4,5组分别抽取3人,2人,1人. ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅6分(Ⅱ)设第3组的3位应聘者为123,,A A A ,第4组的2位应聘者为12,B B ,第5组的1位应聘者为C .则从六位应聘者中抽两名有:121311121232122231(,),(,),(,),(,),(,),(,),(,),(,),(,),(,),A A A A A B A B A C A A A B A B A C A B3231212(,),(,),(,),(,),(,)A B A C B B B C B C ,共15种可能. ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅9分其中第4组的2位为12,B B 至少有一位应聘者入选的有:1112212231321212(,),(,),(,),(,),(,),(,),(,),(,),(,)A B A B A B A B A B A B B B B C B C ,共9种可能.所以第4组至少有一名应聘者被甲考官面试的概率为93155=. ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅12分 19.(本小题满分12分)解:(Ⅰ)因为点(,)()nS n n N n*∈均在函数()y f x =的图像上,所以n S =3n 2-2n. 当n =1时,a 1=S 1=3×12-2=1,当n ≥2时,a n =S n -S n -1=(3n 2-2n )-[])1(2)132---n n (=6n -5. 所以,a n =6n -5 (n N *∈)⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅6分(Ⅱ)由(Ⅰ)得知13+=n n n a a b =[]5)1(6)56(3---n n =)161561(21+--n n , 故T n =∑=ni i b 1=21⎥⎦⎤⎢⎣⎡+--++-+-)161561(...)13171()711(n n =21(1-161+n )361n n =+ (n N *∈).⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅12分 20.(本小题满分13分)解:解:(1)设椭圆的标准方程为12222=+by a x ,焦点坐标为(c ,0),由题知:⎪⎩⎪⎨⎧=+=,,53322b a a c 结合a 2=b 2+c 2,解得:a 2=3,b 2=2, ∴ 椭圆E 的标准方程为12322=+y x . ………………………………………4分(2)设M (x 1,y 1),N (x 2,y 2),H (x 0,y 0), 由已知直线MN 的方程为y =kx +3k +4,联立方程⎩⎨⎧++==+,,)43(63222k kx y y x消去y ,得0)427227()43(6)32(222=++++++k k x k k x k ,于是x 1+x 2=232)43(6k k k ++-,x 1x 2=2232427227k k k +++.① ………………………7分又P ,M ,H ,N 四点共线,将四点都投影到x 轴上,02102133x x x x x x --=++,整理得:)(6)(322121210x x x x x x x ++++=. …10分 将①代入可得=++-+++-⨯++++⨯=2222032)43(6632)43(63324272272k k k k k k k k k x k k 2176-+, …… 12分 ∴ kk k k k kk kx y 2142)43(2176)43(00-+=++-+=++=, 消去参数k 得01200=+-y x ,即H 点恒在直线012=+-y x 上. ………13分21.(本小题满分14分)解:(Ⅰ) ∵ xx a x a x x x f 2)1()1(2)(2++-=+-+='(0)x > , ∴(1)02f a '=⇒=.………………………3分(Ⅱ) ∵ 函数()f x 在区间23(,)上单调递减'()0f x ⇔≤在区间23(,)上恒成立.即22(1)20(1)20x a x x a x x-++≤⇔-++≤上恒成立. …5分设2()(1)2g x x a x =-++,则只需(2)=42(+1)+20(3)93(1)20g a g a -≤⎧⎨=-++≤⎩,解得 :83a ≥(或: 22()(1)01()max f x x a a x x x'=+-+≤⇔+≥+恒成立) ∴实数a 的取值范围83a ≥.………8分 (Ⅲ)证明:m a m m n a n n m f n f )1(21ln 2)1(21ln 2)()(22++--+-+=- ))(()(21ln222m n n m m n m n -+--+=)(21ln 222m n m n --=, 由已知有m ,n 是方程x 2-(a +1)x +2=0的两个根,所以2=mn ⇒ m =n2, 于是,2224212ln2)()(nn n m f n f +-=-. …………………………………10分 由 0<m <n ,可得n 2>2,解得n >2.∵ a ≥122-+ee , ∴ m +n =a +1≥e e 22+,即n 2+n ≥ee 22+, 可解得0<n ≤e2(舍去),或n ≥e 2. ……………………………………11分 令22n =t ,则n 2=2t ,且t ≥e ,t t t m f n f 1ln 2)()(+-=-,令g (t )=2lnt ﹣t+,则g ′(t )=﹣1﹣=﹣<0;故g (t )=2lnt ﹣t+在[e ,+∞)上单调递减,∴g max (t )=2﹣e+;故f (n )﹣f (m )≤2﹣e+.…………14分。
成都市2013届毕业班零诊试题数学一文数

成都市2013届毕业班摸底检测模拟试题(文数)数学注意事项:本试卷分选择题和非选择题两部分。
第I卷(选择题)1至4页,第II卷(非选择题)4至6页,共6页,满分150分,考试时间120分钟。
1. 答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2. 答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3. 答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4. 所有题目必须在答题卡上作答,在试题卷上答题无效。
5. 考试结束后,只将答题卡交回。
参考公式如果事件A、B互斥,那么球的表面积公式P(A+B)=P(A)+ P(B)如果事件A、B相互独立,那么其中R表示球的半径P(A • B) =P(A) • P(B) 球的体积公式如果事件A在一次试验中发生的概率是P,那么N次独立重复试验中恰好发生A次的概率其中R表示球的半径第I卷(选择题,共60分)一、选择题:(本大题共12小题,每小题5分,共60分)在每小题给出的四个选项中,有且只有一项是符合题目要求的.x 处连续的是(1)下列四个图像所表示的函数,在点0(A)(B)(C)(D)(2)552log 10log 0.25+= (A )0(B )1(C ) 2 (D )4(3)函数2()1f x x mx =++的图像关于直线1x =对称的充要条件是 (A )2m =-(B )2m =(C )1m =-(D )1m =(4)设点M 是线段BC 的中点,点A 在直线BC 外,216,BC AB AC AB AC =∣+∣=∣-∣,则AM ∣∣=(A )8(B )4(C ) 2 (D )1(5)将函数sin y x =的图像上所有的点向右平行移动10π个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是 (A )sin(2)10y x π=- (B )sin(2)5y x π=-(C )1sin()210y x π=-(D )1sin()220y x π=-(6)某加工厂用某原料由甲车间加工出A 产品,由乙车间加工出B 产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A 产品,每千克A 产品获利40元,乙车间加工一箱原料需耗费工时6小时可加工出4千克B 产品,每千克B 产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为 (A )甲车间加工原料10箱,乙车间加工原料60箱 (B )甲车间加工原料15箱,乙车间加工原料55箱 (C )甲车间加工原料18箱,乙车间加工原料50箱(D )甲车间加工原料40箱,乙车间加工原料30箱 (7)椭圆22221()x y a b a b+=>>0的右焦点F ,其右准线与x 轴的交点为A ,在椭圆上存在点P 满足线段AP的垂直平分线过点F ,则椭圆离心率的取值范围是(A )⎛⎝⎦(B )10,2⎛⎤⎥⎝⎦(C ) )1,1(D )1,12⎡⎫⎪⎢⎣⎭(8) 已知函数,,当x=a 时,取得最小值b ,则函数的图象为(9)设F 1,F 2分别为双曲线)0,0(12222>>=-b a by a x 的左、右焦点。
