第四节 物质波.不确定关系
《波粒二象性》3光的波动性 4、概率波 5、不确定性关系

电子枪
U K
D
电子束
探测器
B
G
戴维逊和革末的实验是用 电子束垂直投射到镍单晶, 电子束被散射。其强度分布 可用德布罗意关系和衍射理 论给以解释,从而验证了物 质波的存在。
镍单晶
2. 电子衍射实验2
电子束在穿过细晶体粉末或薄 金属片后,也象X射线一样产生 衍射现象。
1927年 G.P.汤姆逊(J.J.汤姆逊 之子) 也独立完成了电子衍射实 验。
微观粒子单缝衍射时,屏上各点的亮度同样是反映 了粒子到达这点的概率,如果把这个概率的分布在坐标 表示出来,就是图中红色曲线。
b
微观粒子 狭缝
微观粒子(光子)单缝衍射
实验中发现,狭缝的宽度决定了粒子位置的不确定范 围,越宽位置的不确定越大,中央亮条纹的宽度决定了粒 子 的动量的不确定 范围,条纹越宽则动量的不确定越大。
我们可以尝试做以下实验: (1)当入射缝较大时,发现中央亮条纹的宽度较小, 很 大时,没有条纹了,成为一个点了。 说明如果粒子的位置不确定范围大,动量不确定范围小。
(2)当入射缝较小时,发现中央亮条纹宽度大,狭缝越 窄,中央亮条纹则越大,
说明粒子的位置不确定范围小的话,动量的不确定范围大。
结论: 粒子的位置不确定越大,那么其动量的不确定越小 粒子的位置不确定越小,那么其的动量不确定越大
h h h p mv m0v
v2 1 c2
(v:物体运动速度;m0:物体的静质量)
当实物粒子运动速度远小于光速(v<<c)时,公式退化为: h h
m0v p
一、德布罗意波(物质波)
每一个运动的粒子都与一个对应的波相联系,而且粒子的
能量E、动量p与它所对应的波的频率v、波长之间,遵从以下
物质波;不确定关系 人教版

物质波;不确定关系【基础知识导引】1.知道实物粒子和光子一样具有波粒二象性.2.知道德布罗意波长和粒子动量的关系.3.了解牛顿力学的局限性.物理学把物质分为两大类,一类是实物,另一类是场.光既具有粒子性,又具有波动性,那么我们就提出这样的问题:质子、电子以至原子、分子等实物粒子是否在一定条件下会表现出波动性?德布罗意认为,任何一个运动着的物体,小到电子、质子,大到行星、太阳,都有一种波与它对应,波长ph =λ,其中P 是运动物体的动量,h 是普朗克常量.1927年两位美国物理学家在实验室里观察到了电子束的衍射图案,证实了德布罗意的假设.我们把这样的波叫物质波.物质波的存在,进一步论证了波粒二象性和概率波,在这儿,牛顿力学已不适用于微观粒子的运动.对微观粒子而言,确定的坐标已不能描述它们在原子中的位置,因此,电子在原子中运动的“轨道”已没有意义,我们只能知道电子在原子核附近各点出现概率的大小.当原子处于不同的能级时,电子在各处出现的概率是不一样的,如果用疏密不同的点来表示电子在各个位置出现的概率,画出来就像云雾一样,可以形象称为电子云.1.根据ph =λ可知,德布罗意波长与粒子的动量成反比,所以电子的德布罗意波长较短. 2.解:根据p h =λ,德布罗意波长与粒子的动量成反比,银原子的质量较大,动量也大,所以它的德布罗意波长较短.【教材内容全解】在经典力学中,描述粒子的运动状态在于确定任一时刻粒子的位置和动量.这种描述,在宏观领域是可行的,而在微观世界就根本不适用.原因在于粒子具有波粒二象性.在同一时刻,粒子的坐标和动量就不可能都具有确定的值.从光的单缝衍射实验可以看出,屏上的亮点实际反映了粒子(光子)到达该点的概率,入射的粒子可以认为有确定的动量,但它们可以处于挡板左侧的任何位置,粒子在挡板左侧的位置是完全不确定的.对于通过挡板的粒子来说,它们的位置被狭缝限定了,它们的位置不确定量减小了,不过我们仍不能准确地说出射到屏上的粒子在通过狭缝时的准确位置,因为狭缝有一定的宽度a ,从这儿可以看出,粒子动量的不确定性增加了.利用数学方法可以对微观粒子的运动进行分析,如果以Δx 表示粒子的位置的不确定性,用Δp 表示粒子动量的不确定性,可以得出π4h p x ≥∆∆,式中的h 是普朗克常量.这就是著名的不确定关系. 在微观物理学中,除了位置和动量外,还有一些成对的物理量具有不确定关系,时间和能量就是经常用到的一对:π4h t E ≥∆∆ 理论的分析说明,时间和能量间的不确定关系以及其他几对物理量之间的不确定关系都可以从位置和动量的不确定关系推导出来,它们是等价的.【课本习题解答】A 组1.紫外线光子的能量最大.(点拨:根据E =hv)2.不能.(点拨:因为白光是复色光)3.钙:Hz 14105.6⨯镁: Hz 14109.8⨯铍:Hz 14104.9⨯钛:Hz 14109.9⨯金:Hz 14106.11⨯ (点拨:0hv W =).4.由△E=hv 和λcv =得λhcE =∆,把题中所给波长代人,得:eV J E 108.21073.3191=⨯=∆-,eV J E 111.210377.3192=⨯=∆-。
量子力学4-不确定关系

dxdydz
空间某点附近单位体积内出现粒子的概率 概率密度: 空间某点附近单位体积内出现粒子的概率, 而粒子出现在整个空间内的概率应等于1,即:
*
2
归一化条件:
整个空间
2
dv 1
另外 波 数还应该满足如下的标准条件 另外,波函数还应该满足如下的标准条件: (1) 单值: 单值 任意时刻,一个粒子只能出现在一个地方。 (2) 有限: 粒子出现在空间某处的概率不可能大于1。 (3) 连续。 粒子运动过程中概率密度不可能发生突变。
1 sin 0 . 777 50 . 9 极大值出现在 的方 向,与实验符合的很好。
k 1
德布罗意波
例题18-10 电子在铝箔上散射时,第一级最大(k=1)的偏转角 10m,求电子速度。 为 2 ,铝的晶格常数a为4.05 4 05×10-10 求电子速度 解: 参看图示,第 第一级最大的条件是: 级最大的条件是:
3.3 10 8 eV
对氢原子光谱,当 对氢原子光谱 当n不是很大时,这一能级宽度是很小的。所以氢原子谱线系中 不是很大时 这一能级宽度是很小的 所以氢原子谱线系中 的各分立谱线是相当细的。
(2) 由
E h
hc 得: hc E 2
所以 该激发态的平均寿命为 所以,该激发态的平均寿命为:
P Px P sin 1 x
代入德布罗意关系:
h Px 即 x p x h x
考虑到更高级的衍射图样,则应有:
h p
得出:
h Px P sin 即 x
x p x h
上述讨论只是反映不确定关系的实质,并了一条重要的物理规律: 不确定关系揭示了一条重要的物理规律
高三物理最新教案-第二十章四、物质波不确定关系 精品

物质波、不确定关系教学目标一、知识目标1、了解物质波的概念;2、知道波粒二象醒性十物质的共性,物质波也是概率波;3、了解牛顿力学对微观粒子不适用.二、能力目标通过了解物质波帮助学生进一步认识波粒二象性和概率波.三、情感目标培养学生对问题的分析理解能力,分析微观粒子运动与宏观质点运动时需要掌握的思想方法,尤其是不确定理论思想的建立.教学建议教材分析分析:本节内容首先介绍了物质波的概念以及其普遍性,再简单介绍了有关物质波的计算,最后提出牛顿力学的局限性。
教法建议建议:本节内容要求不高,只要求学生对物质波有所了解,开拓视野,因此完全可以由学生自学。
典型例题关于物质波长的计算例题:某电视机显像管中电子的运动速度为4.0×107m/s;质量为10g的子弹运动速度为200m/s.分别计算它们的德布罗意波长.答案:根据公式计算得1.8×10-11m和3.3×10-34m.扩展资料德布罗意和物质波理论的诞生——纪念德布罗意高高诞辰110周年1924年11月,巴黎大学举行了一场不同寻常的博士考试.尽管应试的年轻人发表了令人难以接受的新见解,但考试委员会成员们被应试者的聪明和勇气所感动,为他的大胆假设—物质波理论打开了绿灯.众所周知,物质波就是德布罗意波,这位应试者的名字将永远和物质波紧紧联系在一起.1、出击之前路易斯·德布罗意(Louis de Broglie,1892~1987)出生于法国迪埃普的公爵门庭,父亲曾担任法国首相等要职.他在德赛利中学读书时,就显示了出众的文学才华而引人注目.18岁时获得巴黎大学历史学士学位,接着又学习法律.年青有为的德布罗意尚无一点迹象表明他日后会成为著名的物理学家.但在20世纪初物理学界一个又一个重大发现,首先吸引他的哥哥莫里斯·德布罗意(Mauricede Broglie)献身于实验物理学.在哥哥的影响下,他拜读了彭加勒、洛伦兹和朗之万等人的科学著作.后来他对普朗克、爱因斯坦和玻尔等人的工作发生了兴趣,逐步为之神往.大约20岁时,德布罗意放弃了关于18世纪初期法国内政问题的学位考试,转而学习理科.不出两年,即已成为理科学士(1913年).特别要提到一件事情,它对德布罗意坚定学习物理学的决心起着至关重要的作用.1911年秋,首届索尔维(Solvay)会议在布鲁塞尔召开,莫里斯是这次世界著名科学家盛会的秘书之一.该会的议题是“辐射理论和量子”,普朗克、爱因斯坦等一批物理学大师在会上作了精彩的报告,并进行了热烈的讨论.会后,莫里斯协助朗之万(Paul Largevin,1872~1946)把这些报告和讨论编辑成册,用法文出版.德布罗意得天独厚地享读了这些报告和讨论记录,特别是普朗克和爱因斯坦分别作的关于黑体辐射、固体比热的研究报告给他留下了难以忘怀的印象.40多年后,德布罗意仍念念不忘地谈及这一点:“在我血气方刚的岁月里,非常热衷于那些曾被讨论的问题,决心尽我毕生精力去解开迷人的量子之谜.这量子之谜早在那10年之前就曾被普朗克引入到理论物理学中,然而,它的深刻内涵还没有被掌握”.大幕笼罩的物理世界,迷雾重重.道道难题,对勇敢的年轻人是多大的诱惑!德布罗意自度“有纯理论家的气质,而不是实验工作者和工程师的材料……”,他有志于探索物理学的纯概念王国,但是第一次世界大战的爆发,却把他从物理学的理论天地推向了技术舞台.大战期间,他在埃菲尔铁塔上的军用无线电报站里服役了6年.这样,他的物理学的理想与思考就不以他个人意志为转移地暂时中断了6年.战争结束后,德布罗意立即投身于物理学研究之中.在1920~1924年期间,他主要跟随朗之万攻读理论物理学博士学位,此外还抽出部分时间到哥哥的实验室从事X射线的实验研究这些实验工作为德布罗意的抽象思维提供了必要的实验基础.2、迈出重要的一步曾在第一次世界大战期间,德布罗意就同哥哥莫里斯一道参与了军用无线电的技术研究工作,掌握了较强的物理实验技能也是在这一时期,莫里斯受W·H·布拉格(W.H.Bragg,1862~1942)的影响,把其私人实验室的主攻方向定在X射线的实验研究上.在战争末期,莫里斯因关于X射线的卓越实验研究业绩而蜚声物理学界.大战结束后,德布罗意经常抽出部分时间到哥哥的实验室从事X射线的研究.在X射线的实验方面德布罗意发表了一系列研究报告,为他在法国物理界赢得了一点名声.但更有意义的东西却在于,他和哥哥通过实验得出的不可避免的结论:X射线既是波又是粒子,即X射线具有波粒双重本质.X射线所表现出的双重本质深深地震动了德布罗意兄弟俩.为此他们进行了长期热烈的讨论.作为实验物理学家的莫里斯认为:X射线应当是波和粒子的一种“组合”(combination).但具有理论家气质的德布罗意认为哥哥的观点并不准确也不具体.他在回忆他们的讨论时说:“我哥哥认为X射线是波和粒子的一种组合,但是,作为一个非理论家,他对它没有特别清楚的认识.”“同我哥哥进行的这些长期讨论……对我非常有益,这些讨论使我深深考虑将波的观点和粒子的观点必须综合在一起的必要性.”1921年4月,第三届索尔维会议在布鲁塞尔召开,莫里斯应邀到会报告了他刚完成的X射线在重核上漫射实验研究,这个实验再次证实了辐射是按量子一份份地被吸收的.德布罗意也希望参加这次会议,但他未被邀请.这一次拒绝对他刺激较大,他发誓一定要用自己的发现去争取以后会议的请贴.果然,在1927年召开的第五届索尔维会议上,他如愿以偿.为寻找一个综合波粒两方面的“辐射的综合理论”,德布罗意仔细研究了爱因斯坦的有关经典论文,并于1922年11月发表了一篇题为《黑体辐射与光量子》的论文,这是波相理论诞生的先声.这标志着德布罗意向前迈出重要的一步.值得庆幸的是,对量子论的兴趣引导他朝着将物质波动方向和粒子方向统一起来的正确方向继续前进.41年后的1963年,功成名就的德布罗意回忆往事,曾向科学史家T·S·库恩(T.S.Kuhn)披露说:“(那时候)我开始有了那种想法—不过它尚未诞生,我可能不敢讲出来—但我心中已开始孕育它.”从1922年底到1923年夏,德布罗意一直在深思这个问题:到底可否将他的光量子所暗示的波粒二象性推广到一般物质,特别是电子之上?这是一个重大而独创的问题,也是一个从来未被任何实验揭示的问题,它将关系到~般物质是否都具有波粒二象性这一史无前例的答案.1923年夏末,德布罗意终于跨越了革命性的一步.用他自己的话讲:“我不能记起它产生的确切日期,但它的确是产生于1923的夏天—那时,我突然有一个想法,即把波粒二象性扩展到物质粒子,特别是电子上去.”3、通过类比建立理论关于光是粒子还是波的历史争论,自牛顿、惠更斯各树一帜后,菲涅耳、麦克斯韦和赫兹等人的工作,有力地支持了波动说;而1905年爱因斯坦对赫兹所发现的光电效应的解释,又使光的微粒说夺回了部分阵地.虽然爱因斯坦等物理学家还没有发现波粒二象性的真谛,但光的波粒二象性已经是毋容置疑的了.物理学界前辈们的辛勤劳动,为后继者的探索扫清了道路.爱因斯坦的光量子理论通过密立根、康普顿等研究得到证实,德布罗意对此发生了很大兴趣.他认为在研究光的理论中,必须“同时引进粒子概念和周期性概念.”光本身必须同时考虑粒子性和波动性.他进一步研究了几何光学和经典力学的对应性,几何光学中费马(P.de Fermat 1601-1665)原理:和经典力学中莫培丢(Mauoertuis,1698-1759)变分原理类似:他大胆设想,不仅光有粒子和波动两种性质,而且“一般的”物质也具有这两种性质.德布罗意认为:既然粒子概念在波的领域里成功地解释了令人困惑的康普顿效应.那么,波动概念也能解释粒子领域令人困惑的定态.1923年9月至10月间,德布罗意连续在《法国科学院通报》上发表了三篇有关波和量子的论文.第一篇的题目是《辐射—波与量子》,提出了实物粒子也有波粒二象性,认为与运动粒子相应的还有—正弦波,两者总是保持相同的位相.后来他把这种假想的非物质波称为相波.他考虑一个静质量为的运动粒子的相对论效应,把相应的内在能量视为一种频率为简单周期性现象.他把相波概念应用到以闭合轨道绕核运动的电子,推出玻尔量子化条件.在第二篇题为《光学—光量子、衍射和干涉》的论文中,德布罗意提出了如下设想:“在一定情形中,任一运动质点能够被衍射.穿过一个相当小的开孔的电子群会表现出衍射现象.正是在这一方面,有可能寻得我们观点的实验验证.”在第三篇题为《量子、气体分子运动论和费马原理》的论文中,他进一步提出,“只有满足相波谐振,才是稳定的轨道.”在第二年的博士论文中,他更明确地写下了:“谐振条件是,即电子轨道的周长是位相波波长的整倍数.”他再次详细地给出了有关几何光学和经典力学的类比,在给出费马原理和莫培丢变分原理一致性后,德布罗意说:“几何光学和动力学的两条伟大原理之间的基本联系由此而得以明朗化.”从这篇论文的内容来看,德布罗意不仅完善了他的物质波理论,而且通过费马原理与莫培丢原理之间的类比暗示了:未来的波动力学与经典力学的关系类似于波动光学与几何光学的关系.这种类比性的思想方法与后来薛定谔在创立波动力学时的思想方法不谋而合.这正是他对波动力学的建立所作的主要贡献.1924年,德布罗意将这三篇文章合在一起成为他的博士论文.他在文中进一步指出:“我们认为几何光学和动力学的这两个重要原理之间的深刻关系的这个思想,可以作为将波和量子综合起来的重要指南.”在这篇文章中还得到了以后以他的名字命名的波长与动量的关系式:这个式子和一起,就是我们熟知的爱因斯坦德布罗意关系式.同年11月,德布罗意向巴黎大学科学院提交了博士论文《量子理论研究》.在这篇长达100余页的不朽论文里,他系统整理并完善了物质波理论.德布罗意的导师朗之万把这篇博士论文寄给了爱因斯坦.爱因斯坦高度赞扬了德布罗意的工作,称赞说:“瞧瞧吧,看来疯狂,可真是站得住脚呢!”爱因斯坦在物理上非常喜欢对称性,现在德布罗意实物粒子和光一样具有波粒二象性,显然是又一个自然界对称性的表现.爱因斯坦高兴地赞赏道:“序幕的一角被德布罗意揭开了!”经过爱因斯坦的推荐,德布罗意的工作立即获得大家的注意.物质波理论的诞生,标志着波和粒子概念的一次伟大综合的胜利.不仅如此,它还启发了玻色、爱因斯坦去完成玻色爱因斯坦量子统计,照亮了薛定谔(E.Schrodinger)创立波动力学的道路,激励了狄拉克(P.A.Dirac)和约当(P.Jordan)等人去构筑量子场论.1927年,美国物理学家戴维孙(C.J.Davisson,1881~1958)和助手革末(L.H.Germer,1896~1971)用低速电子进行实验,获得了电子衍射图样;同年英国人G.P.汤姆孙(G.P.Thomson,1892~1975)用高速电子进行实验,也获得了电子衍射图样.这两个实验得出的结果,完全证实了电子波的存在.电子具有和X射线一样的性质,在晶体表面会发生衍射现象,而且证实了德布罗意关系.4、有益的启示回顾德布罗意提出物质波假设的过程,值得我们深思的是德布罗意从几何光学和经典力学的类比,又从爱因斯坦光的彼粒二象性得到启示,提出了一个如此大胆的假设.这说明利用类比的方法,了解事物的历史发展过程,对于物理学研究的重要性.德布罗意早年对历史研究的兴趣也许还有某种潜移默化的影响,促进了德布罗意物质波假设的提出.德布罗意因提出了物质波理论荣获1929年度诺贝尔物理奖,成为第一个以学位论文获得诺贝尔奖的人.物质波干涉现象虽然肉眼无法看见,但当分子和分子碰撞时,也会像光波一样发生干涉现象……在不久前的实验中,我国科学家观察到了这种现象.专家认为,作为分子的物质波特性的表现,这不仅使国外科学家10多年前的理论预测得到证实,而且进一步丰富了量子理论.从1983年起,中国科学院化学物理研究所的一个研究小组瞄准这一国际前沿进行了坚持不懈的研究.他们发展了一种新的非常灵敏的激光光谱方法来测量一氧化碳分子碰撞传能的截面.通过碰撞,分子之间可以传递能量.但令科学家们困惑不解的是,在有些情况下,能量传递的测量结果与前人的传能理论很不相符.为什么?经过反复实验和理论上的研究,科研人员最终推导出一个新公式,与实验结果非常符合,证明了量子干涉效应对分子碰撞传能的重要影响.“这是物质的波粒二象性在分子碰撞传能中产生的一种新效应.如果不考虑这种效应,能量传递的理论将不精确.这对于激光、光化学、光物理、光合作用等研究具有重要意义.”这一成果发表在《美国化学物理》等国际权威杂志上,受到国际同行的关注和高度评价,甚至还成为一次著名国际会议的中心议题.科学家还在实验中进一步发现,不同的碰撞条件,干涉相位角也不一样.最近,我国科学家在钠分子碰撞实验中也观察到了这一效应.受到鼓舞的科学家将进一步在分子束中进行研究,以期对这一现象有更深入的了解并建立一个更为精确的理论系统.量子论探索微观粒子运动所遵从的量子规律的初步理论,是量子力学的先驱.是从普朗克在物理学中引入量子概念(1900年)开始,特别是在玻尔提出他的氢原子理论(1913年)以后发展起来的.量子论仍然以经典物理规律为基础,但加上了一些反映微观运动具有量子特性的附加条件(量子条件).它指出,在物体大、运动范围广(相当于量子数很大)的极限情形下,微观运动规律应该趋近于宏观运动规律,并且两种运动规律应该具有相互对应的关系(对应原理).量子论能够解释一些简单的原子、分子所发射的光谱和黑体辐射等现象,但由于它的半经典性质,其结果在数量方面往往不能与实验符合.量子论本身还包含着很大矛盾,在解释许多实验事实时都遇到严重困难.它的进一步发展导致量子力学的建立(1924~1926年),现在这一理论已被量子力学所代替,故有时称之为旧量子论,但由于它的直观性强,在解释某些现象(如复杂的光谱)时,还常被采用.人们有时也把研究微观运动的整个学科统称为量子论或量子物理学.习题精选习题精选1、电子甲的速度是乙的2倍,哪个电子的德布罗意波长短?2、同样速度的氢原子和银原子,哪种原子的德布罗意波长短?答案:1、甲 2、银原子。
人教版高中物理课件-不确定关系

0
外 力 場
說明
的
勢
(1)求解
E (粒子能量)
能
( r ) (定態波函數)
函
數
(2)勢能函數 V 不隨時間變化。
一維定態薛定諤方程(粒子在一維空間運動)
d
2Ψ( x) dx2
2m 2
E
V
Ψx
0
四.用薛定諤方程解一維無限深勢阱
若品質為m的粒子,在保守力場的作用下,被限
制在一定的範圍內運動,其勢函數稱為勢阱。
就表示t時刻,粒子在空間r 處的單位體積中出現的
概率,又稱為概率密度.
即波函數的物理意義:
|
Ψ(r ,
t
)
|2
——
t
時刻,粒子在空間
r
處
的單位體積中出現的概率,又稱為概率密度
單個粒子在哪一處出現是偶然事件; 大量粒子的分佈有確定的統計規律。
電 子 雙 縫 干 涉 圖 樣
出現概率小
電子數 N=71320000
即:
Ψ 2dV 1
波函數歸一化條件
波函數滿足的條件:單值、有限、連續、歸一
波函數統計詮釋涉及對世界本質的認識爭論至今未息
哥本哈根學派
愛因斯坦
三. 薛定諤方程 (1926年)
描述微觀粒子在外力場中運動的微分方程 。
品質 m 的粒子在外力場中運動,勢能函數 V ( r , t ) ,
薛定諤方程為
2 2m
----------微觀粒子的“波粒二象” 性的具體體現
例 設子彈的品質為0.01㎏,槍口的直徑為0.5㎝。 試求子彈射出槍口時的橫向速度的不確定量。
解 : 槍口直徑可以當作子彈射出槍口時位置的不確定
高中物理 第四章 波粒二象性 4、5 实物粒子的波粒二象性 不确定关系教案 教科版选修3-5-教科版

4 实物粒子的波粒二象性5 不确定关系一、德布罗意物质波 1.粒子的波动性(1)德布罗意波:任何运动着的物体,小到电子、质子,大到行星、太阳,都有一种波与它相对应,这种波叫物质波,又叫德布罗意波.(2)德布罗意波波长、频率的计算公式为λ=h p ,ν=E h.(3)我们之所以看不到宏观物体的波动性,是因为宏观物体的动量太大,德布罗意波长太小的缘故.2.电子波动性的实验验证(1)实验探究思路:干涉、衍射是波特有的现象,如果实物粒子具有波动性,则在一定条件下,也应该发生干涉或衍射现象.(2)实验验证:1926年戴维孙观察到了电子衍射图样,1927年汤姆孙得到了电子的衍射图样,证实了电子的波动性.(3)说明①人们陆续证实了质子、中子以及原子、分子的波动性,对于这些粒子,德布罗意给出的ν=E h 和λ=h p关系同样正确.②德布罗意波也是一种概率波.德布罗意认为任何运动着的物体均有波动性,可是我们观察运动着的汽车(如图所示),并未感到它的波动性.你如何理解该问题?请与同学交流自己的看法.提示:一切微观粒子都存在波动性,宏观物体(汽车)也存在波动性,只是因为宏观物体质量大、动量大、波长短,难以观测.二、氢原子中的电子云1.定义用点的多少表示的电子出现的概率分布.2.电子的分布某一空间X围内电子出现概率大的地方点多,电子出现概率小的地方点少.电子云反映了原子核外的电子位置的不确定性,说明电子对应的波也是一种概率波.三、不确定关系1.定义在经典物理学中,可以同时用质点的位置和动量精确描述它的运动,在微观物理学中,要同时测出微观粒子的位置和动量是不太可能的.2.微观粒子运动的位置不确定量Δx和动量的不确定量Δp x的关系式Δx·Δp x≥h4π,其中h是普朗克常量,这个关系式叫不确定关系.3.不确定关系告诉我们,如果要更准确地确定粒子的位置(即Δx更小),那么动量的测量一定会更不准确(即Δp x更大),也就是说,不可能同时准确地知道粒子的位置和动量,也不可能用“轨迹”来描述粒子的运动.单个粒子的运动情况可否预知?粒子出现的位置是否无规律可循?提示:由不确定性关系可知,我们不能准确预知单个粒子的实际运动情况,但粒子出现的位置也并不是无规律可循,我们可以根据统计规律知道粒子在某点出现的概率.考点一对德布罗意波的理解1.物质的分类:物理学中把物质分为两类,一类是分子、原子、电子、质子及由这些粒子组成的物质;另一类是场,像电场、磁场、电磁场这种看不见的,不是由实物粒子组成的,而是一种客观存在的特殊物质.2.任何物体,小到电子、质子,大到行星、太阳都存在波动性,我们之所以观察不到宏观物体的波动性,是因为宏观物体对应的波长太小的缘故.3.德布罗意波是一种概率波,粒子在空间各处出现的概率受波动规律支配,不要以宏观观点中的波来理解德布罗意波.4.德布罗意假说是光子的波粒二象性的一种推广,使之包括了所有的物质粒子,即光子与实物粒子都具有粒子性,又都具有波动性,与光子对应的波是电磁波,与实物粒子对应的波是物质波.5.对于光,先有波动性(即ν和λ),再在量子理论中引入光子的能量ε和动量p来补充它的粒子性.反之,对于实物粒子,则先有粒子概念(即ε和p),再引入德布罗意波(即ν和λ)的概念来补充它的波动性.不过要注意这里所谓波动性和粒子性,仍然都是经典物理学的概念,所谓补充仅是形式上的.综上所述,德布罗意的推想基本上是爱因斯坦1905年关于光子的波粒二象性理论(光粒子由波伴随着)的一种推广,使之包括了所有的物质微观粒子.【例1】某某综合新闻网2010年8月21日报道:近日,一种发源于南亚没有抗生素可以抵御的“超级细菌”成为社会关注的热点.假若一个细菌在培养器皿中的移动速度为3.5μm/s,其德布罗意波长为1.9×10-19m ,试求该细菌的质量.【解析】 由公式λ=h p得该细菌的质量为m =p v =h vλ= 6.626×10-343.5×10-6×1.9×10-19kg =1.0×10-9kg. 【答案】 1.0×10-9kg德布罗意认为,任何一个运动着的物体,都有一种波与它对应,波长是λ=h p,式中p 是运动物体的动量,h 是普朗克常量.已知某种紫光的波长是440 nm ,若将电子加速,使它的德布罗意波长是这种紫光波长的1104.求: (1)电子的动量大小;(2)试推导加速电压跟德布罗意波长的关系,并计算加速电压的大小(电子质量m =9.1×10-31kg ,电子电荷量e =1.6×10-19C ,普朗克常量h =6.6×10-34J·s,加速电压的计算结果取1位有效数字).答案:(1)1.5×10-23kg·m/s(2)U =h 22emλ2 8×102V解析:(1)由λ=h p得电子的动量大小p =h λ= 6.6×10-34440×10-9×10-4kg·m/s =1.5×10-23kg·m/s(2)设加速电压为U ,由动能定理得eU =12mv 2而12mv 2=p 22m ,所以U =p 22em =h 22emλ2 代入数据得加速电压的大小U =8×102V考点二 对不确定关系的理解在经典力学概念中,一个粒子的位置和动量是可以同时精确测定的.在量子理论发展后,揭示出要同时测出微观物体的位置和动量,其精确度是有一定限制的.由不确定性关系Δx Δp x ≥h4π可知,微观粒子的位置和动量是不能同时被确定的,这也就决定了不能用“轨道”的观点来描述粒子的运动,因为“轨道”对应的粒子某时刻应该有确定的位置和动量,但这是不符合实验规律的.微观粒子的运动状态,不能像宏观物体的运动那样通过确定的轨迹来描述,而是只能通过概率波进行统计性的描述.【例2】 已知h4π=5.3×10-35J·s,试求下列情况中速度测定的不确定量,并根据计算结果,讨论在宏观和微观世界中进行测量的不同情况.(1)一个球的质量m =1.0 kg ,测定其位置的不确定量为10-6m. (2)电子的质量m e =9.0×10-31kg ,测定其位置的不确定量为10-10m(即原子的数量级).根据不确定性关系Δx ·Δp x ≥h4π,先求动量的不确定性关系,再由Δp =m Δv ,计算速度测量的不确定性关系.【解析】 (1)m =1.0 kg ,Δx 1=10-6m , 由Δx Δp x ≥h4π,Δp =m Δv 知Δv 1≥h4πΔx 1m =5.3×10-3510-6×1.0 m/s =5.3×10-29m/s.(2)m e =9.0×10-31kg ,Δx 2=10-10mΔv 2≥h4πΔx 2m e = 5.3×10-3510-10×9.0×10-31 m/s =5.89×105m/s.在宏观世界中物体的质量与微观世界中粒子的质量相比较,相差很多倍.根据计算的数据可以看出,宏观世界中物体的质量较大,位置和速度的不确定量较小,可同时精确地测出物体的位置和动量.在微观世界中,粒子的质量较小,不能同时精确地测出粒子的位置和动量,不能准确地把握粒子的运动状态.【答案】 见解析总结提能 ①不确定性关系不是说微观粒子的坐标测不准,也不是说微观粒子的动量测不准,更不是说微观粒子的坐标和动量都测不准,而是说微观粒子的坐标和动量不能同时测准.②普朗克常量是不确定性关系中的重要角色,如果h 的值可忽略不计,这时物体的位置、动量可同时有确定的值,如果h 不能忽略,这时必须考虑微粒的波粒二象性.h 成为划分经典物理学和微观物理学的一个界线.(多选)关于不确定性关系Δx Δp x ≥h4π有以下几种理解,其中正确的是( CD )A .微观粒子的动量不可能确定B .微观粒子的坐标不可能确定C .微观粒子的动量和坐标不可能同时确定D .不确定性关系不仅适用于电子和光子等微观粒子,也适用于其他宏观粒子 解析:不确定性关系Δx Δp x ≥h4π表示确定位置、动量的精度互相制约,此消彼长,当粒子位置不确定性变小时,粒子动量的不确定性变大;粒子位置不确定性变大时,粒子动量的不确定性变小.故不能同时准确确定粒子的动量和坐标.不确定性关系也适用于其他宏观粒子,不过这些不确定量微乎其微.故C 、D 正确.重难疑点辨析运用不确定性关系解题的方法1.运用不确定性关系ΔxΔp x≥h4π时,应明确两点:(1)位置不确定量Δx,在单缝衍射中,Δx为狭缝的宽度,也可以是光子或电子偏离中心的距离.子弹射出枪口时,Δx为枪口的直径,也可以认为是子弹偏离中心的距离.电子在晶体中衍射时,Δx为晶体中原子间的距离,其单位必须化为国际单位米(m),Δx同时也可以是粒子打在屏上偏离中心的距离.(2)动量的不确定量Δp x:①对宏观的运动物体,Δp x=mΔv,其中Δv为子弹射出枪口时横向速度的确定量,而m为物体的质量,单位应统一为国际单位.②对微观粒子如光子,Δp x=hλ.2.使用ΔxΔp x≥h4π可以求Δx≥h4πΔp x①Δp x≥h4πΔx②Δv≥h4πmΔx③由③式可知,在单缝衍射中狭缝越窄,即Δx越小,粒子通过狭缝时横向速度的不确定量Δv越大,反之当Δp x=mΔv或Δp x=hλ越大时,Δx越小而横向位置的不确定量越小.【典例】已知h4π=5.3×10-35J·s,试求下列两种情况中位置的不确定量.(1)一电子具有200 m/s的速率,动量的不确定X围为0.01%.(2)一颗质量为10 g的子弹,具有200 m/s的速率,动量的不确定量为0.01%. 【解析】(1)电子的动量为p=mv=9.1×10-31kg×200 m·s-1=1.8×10-28kg·m·s-1.动量的不确定X围为Δp x =0.01%p =1.0×10-4×1.8×10-28kg·m·s -1=1.8×10-32kg·m·s -1,由不确定性关系式Δx Δp x ≥h4π,得电子位置的不确定X 围为Δx ≥h4πΔp x,所以Δx ≥5.3×10-351.8×10-32 m =2.9×10-3m. (2)子弹的动量为p =mv =10×10-3 kg×200 m·s -1=2 kg·m·s -1动量的不确定X 围为Δp x =0.01%p =1.0×10-4×2 kg·m·s -1=2×10-4kg·m·s -1, 由不确定性关系式Δx Δp x ≥h4π,得子弹位置的不确定X 围为Δx ≥h4πΔp x,所以Δx ≥5.3×10-352×10-4 m =2.65×10-31m. 【答案】 (1)大于或等于2.9×10-3m (2)大于或等于2.65×10-31m宏观世界中的物体质量比微观世界中的物质(粒子)质量大许多倍,正是因为宏观物体质量较大,其位置和速度的不确定量极小,通常不计,可以认为其位置和速度(动量)可精确测定;而微观粒子由于其质量极小,其位置和动量的不确定性特明显,不可忽略,故不能准确把握粒子的运动状态.1.(多选)在用单缝衍射实验验证光的波粒二象性实验中,下列说法正确的是( AD ) A .使光子一个一个地通过狭缝,如果时间足够长,底片上将会显示衍射图样 B .单个光子通过狭缝后,底片上会出现完整的衍射图样 C .光子通过狭缝的运动轨迹是直线 D .光的波动性是大量光子运动的规律2.下列说法正确的是( B ) A .概率波就是机械波 B .物质波是一种概率波C .概率波和机械波的本质是一样的,都能发生干涉和衍射现象D .在光的双缝干涉实验中,若有一个光子,则能确定这个光子落在哪个点上 解析:概率波与机械波是两个概念,本质不同;物质波是一种概率波,符合概率波的特点;光的双缝干涉实验中,若有一个光子,这个光子的落点是不确定的,但有几率较大的位置.3.(多选)在光的双缝干涉实验中,在光屏上放上照相底片并设法减弱光子流的强度,尽可能使光子一个一个地通过狭缝,在曝光时间不长和曝光时间足够长的两种情况下,其实验结果是( ABC )A .若曝光时间不长,则底片上出现一些无规则的点B .若曝光时间足够长,则底片上出现干涉条纹C .这一实验结果证明了光具有波动性D .这一实验结果否定了光具有粒子性解析:实验表明,大量光子的行为表现为波动性,个别光子的行为表现为粒子性.上述实验表明光具有波粒二象性,故A 、B 、C 正确,D 错误.4.(多选)关于光的波动性与粒子性,下列说法正确的是( ABCD )A .大量光子的行为能明显地表现出波动性,而个别光子的行为往往表现出粒子性B .频率越低、波长越长的光子波动性明显,而频率越高、波长越短的光子粒子性明显C .光在传播时往往表现出波动性,而光在与物质相互作用时往往显示出粒子性D .光子的能量是与频率成正比的,这说明了光的波动性与光的粒子性是统一的 5.一辆摩托车以20 m/s 的速度向墙冲去,车身和人共重100 kg ,则车撞墙时的不确定X 围是Δx ≥2.64×10-38_m.解析:根据不确定关系Δx Δp x ≥h4π得:Δx ≥h4πΔp x = 6.63×10-344×3.14×100×20 m =2.64×10-38m.。
波函数不确定度关系
p mv 0.01300 波长小到实验难以测量的程度(足球也如此), 它们只表现出粒子性,并不是说没有波动性。
<< a : 波动光学 几何光学
h 量子物理 经典物理
7
注意1: 物质波的波速 u 并不等于相应粒子的
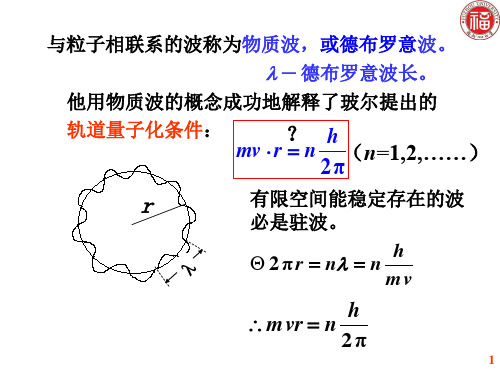
与粒子相联系的波称为物质波,或德布罗意波。
─ 德布罗意波长。
他用物质波的概念成功地解释了玻尔提出的
轨道量子化条件:
mv
r
? n
2hπ(n=1,2,……)
r
有限空间能稳定存在的波
必是驻波。
2 π r n n h
mv
m vr n h 2π
1
导师朗之万把德布洛意的文章寄给爱因斯坦, 爱因斯坦对此论文评价极高,说:
9
注意3: 在有些情况下,我们可由粒子的动能求 德布洛意波长。可利用相对论公式
E 2 = E02 + p2c2; E = Ek + E0
E
pc
相对论情况 h hc
p
E 2 E02
hc
(Ek E0 )2 E02
非相对论情况
Ek
≈ p2 2m0
=h≈ h
p 2m0Ek
运动速度v,它们之间的关系是
c2 u
证明: 波的相速度为 u , v
根据德布洛意公式,相应粒子有
h ,
mc 2
mv
h
两式相乘得
u
h
mc 2 c2
mv h v
德布洛意证明:物质波的群速度为相应粒子的运动
速度v。
德布罗意物质波 不确定关系

3 ε kT 2
1961年,C.约恩孙让电子 束通过单缝、多缝的衍 射图样.
代入数据: 3 ε kT 6.17 10 21 J 2 3.85 10 2 eV
中子的质量为 m =1.67×10-27kg ,
例3. 试计算温度为25时慢中子 的德布罗意波长. 解: 慢中子指处于热平衡 下的中子按能均分定理, 慢中子的平均平动动能为:
h 2 m0 E k
2Ek m0
h h 2 m0 E k 2em0U
1.22 h 1 nm 2em0 U U
如U=200V,则
例1.电子经电势差为U的电 场加速,在v << c下, 求此电 子的德布罗意波长.
1.22 1.22 nm nm U 200 8.63 10 nm
在电子衍射实验中,电子总是 作为整体出现的,它出现的概 率与空间波的强度成正比. 作为粒子具有“整体性”, 即不可分性.不是经典粒子, 因此玻恩认为: 在某处德布 没有“轨道”概念. 罗意波的强度是与粒子在该 处邻近出现的概率成正比. 1. 微观粒子的粒子性
h 0.146nm p
4. 电子双缝衍射实验分析 2. 微观粒子的波动性 (1)只开一缝,屏上电子累积 具有“弥散性”“可叠加 成单缝衍射图样—波动性. 性” “干涉”“衍射”“偏振 ”,具有频率和波长,不 是经典的波 不代表实在 的物理量的波动。 3. 德布罗意的统计解释 (2) 在屏上信号接收器,每 在电子衍射实验中,电子总是 作为整体出现的,它出现的概 次只能接收一个完整的 率与空间波的强度成正比. 电子—粒子性. (3) 打开双缝,屏上呈双缝 因此玻恩认为: 在某处德布 干涉图样—电子的波动性. 罗意波的强度是与粒子在该 处邻近出现的概率成正比.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四节物质波.不确定关系
【基础知识训练】
1.关于物质波下列说法不正确的是
A.实体物质是没有波动性的
B.场类物质既有波动性又有粒子性
C.实体物质也有波动性的,只是波长太小,不易表现出来而已
D.物质波就是概率波
2.下列说法正确的是
A.电子的衍射实验证实物质波的假设是正确的
B.牛顿定律适用于一切实物粒子的运动
C.X光的衍射实验证实物质波的假设是正确的
D.光子和实物粒子在空间分布的概率是受波动规律支配的
3.下列理解正确的是
A.氢原子的电子运行轨道实质上是电子出现概率大的地方
B.我们能用确定的坐标描述电子在原子中的位置
C.在微观领域,不可能同时准确第知道粒子的位置和动量
D.由于微观粒子的轨迹无法描述,所以微观粒子运动规律是无法认识的
4.法国物理学家__________首先提出了物质波,物质波是___________
5.质量5t的汽车,当它以20m/s的速度运动时,其德布罗意波长为_________.
【能力技巧训练】
6.电视机中电子的加速电压为20000v,求电子击中荧光屏的德布罗意波长是多少?
7.一个质子的动能是9.1ev,如果一个电子的德布罗意波长和该质子的德布罗意波长相等,求
该电子的动能?
【探究创新训练】
8.质量为10g的子弹以300m/s的速度在空中飞行,其德布罗意波长是多少?为什么我们无法
观察出其波动性?此过程中子弹的波动性是否表现在子弹的上下或左右颤动前进中,为什么?
(答案和提示见章末…)
1。
