分层法例题(力矩分配法)
第八章 力矩分配法

第八章 力矩分配法1. 图中结构中固定端弯矩 为: ( )2.在力矩分配中等截面杆的远端固定,杆传递系数C等于: ______3.图中结构中固定端弯矩 =_______4.在力矩分配法中杆端的转动刚度与杆另一端的支撑情况有关。
( )5.图中结构中力矩分配系数 =_______6.单独使用力矩分配法,只能解算连续梁和无侧移刚架。
( )7.图a和图b的A端转动刚度相同。
( )8.一个刚结点无论连接多少个杆件,这些杆件的力矩分配系数之和总等于( )9.在力矩分配法中已知某杆一端的分配力矩M,若该杆另端为滑动支座,则传递力矩为M。
( )10.力矩分配法中的传递系数等于传递力矩与分配力矩之比,它与荷载作用无关。
( )11.对图示结构,力矩分配系数 和固端弯矩 分别为:( )A.0.238, -41.67 KN·mB.0.238, 41.67 KN·mC.0.294, -41.67 KN·mD.0.294, 41.67 KN·m12.图示结构中,各杆i等于常数,欲使结点产生顺时针转角,即 =1,要在结点A上施加(顺时针)外力偶为:( )A.8iB.8iC. 11iD.9i13.用力矩分配法计算图示结构,结点A的不平衡力矩为:( )A.-16 KN·mB. 16 KN·mC. 0D.-64 KN·m14.图示连续梁,已知 =1/2,则杆端弯矩 为: ( )A.8 KN·mB.-8 KN·mC.16 KN·mD.-16 KN·m15.用力矩分配法计算图示结构,分配系数 和为4/7和3/7,则杆端弯矩分别为: ( )A.80 KN·m, 60 KN·mB.-80 KN·m,60 KN·mC.80 KN·m,-60 KN·mD.-80 KN·m,-60 KN·m16.AB杆的弯矩传递系数 与: ( )A.杆AB的A端支承情况有关B. 杆AB的两端支承情况有关C. 杆AB的B端支承情况有关D. 杆AB的两端支承情况无关17.在力矩分配法中,某杆端分配系数与该杆的转动刚度: ( )A.成正比B.有时成正比,有时成反比C.无关系D.成反比18.取左半部为如图示对称结构的等代结构,在等代结构中分配系数 等于:( )A.1/3B.4/11C.2/5D.2/719.用力矩分配法计算图示结构,分配系数 、分别等于: ( )A.0.5 0.333B.0.25 0.5C.0.25 0.333D.0.50.57120.如图连续梁中,已知 =4/7,则 等于: ( )A.4/7(-M+Pd/6)B. 4/7(M+Pd/8)C.4/7(-M+Pd/8)D. 4/7(M-Pd/8)。
混凝土-分层法-弯矩分配法计算题

分层法与弯矩分配法的优缺点比较
可以考虑杆件之间的相互作用; 可以方便地进行优化设计和调整。 弯矩分配法的缺点
分层法与弯矩分配法的优缺点比较
计算过程相对复杂;
需要对杆件进行编号和线刚度计算。
05 计算题解析
计算题一:简支梁的弯矩计算
总结词
简支梁的弯矩计算是混凝土结构分析中的基础问题,主要涉及到均布荷载和集 中荷载的作用。
弯矩分配法的应用范围
01
弯矩分配法适用于各种类型的结构,包括梁、板、 壳等。
02
弯矩分配法可以用于计算结构的静力弯矩和动力弯 矩,也可以用于分析结构的稳定性。
03
弯矩分配法可以用于单层结构和多层结构的设计计 算,也可以用于大型复杂结构的分析和设计。
03 混凝土结构分析
混凝土结构的分类
01
02
03
01
分层法的优点
02
可以单独对每一层进行分析,计算简单明了;
03
可以考虑每一层的材料和尺寸差异;
分层法与弯矩分配法的优缺点比较
需要将结构分层,可能会 影响计算的精度;
分Байду номын сангаас法的缺点
可以适用于各种水平结构 的计算。
01
03 02
分层法与弯矩分配法的优缺点比较
对于复杂结构,分层可能会比较困难。 弯矩分配法的优点 可以适用于各种竖向结构的计算;
感谢您的观看
将各层的内力进行汇总,得到整个结 构的内力。
分层法与弯矩分配法的计算步骤
弯矩分配法
1
2
确定结构的杆件和节点,并对其进行编号;
计算各杆件的线刚度;
3
分层法与弯矩分配法的计算步骤
进行弯矩分配,将各杆件的弯矩按照一定的规则进行分配;
【精选】《分层法》例题详解
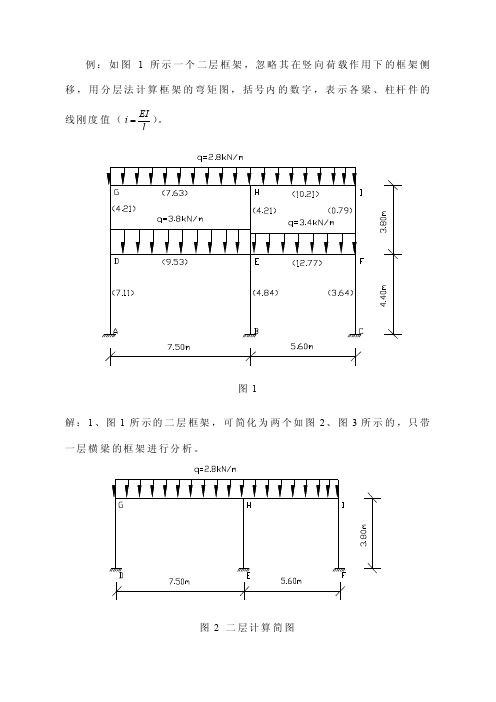
例:如图1所示一个二层框架,忽略其在竖向荷载作用下的框架侧移,用分层法计算框架的弯矩图,括号内的数字,表示各梁、柱杆件的线刚度值(EIil )。
图1解:1、图1所示的二层框架,可简化为两个如图2、图3所示的,只带一层横梁的框架进行分析。
图2 二层计算简图图3 底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数采用分层法计算时,假定上、下柱的远端为固定,则与实际情况有出入。
因此,除底层外,其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为12,其余各层柱的弯矩传递系数为13。
各层梁的弯矩传递系数,均为12。
图4 修正后的梁柱线刚度图5 各梁柱弯矩传递系数3、计算各节点处的力矩分配系数计算各节点处的力矩分配系数时,梁、柱的线刚度值均采用修正后的结果进行计算,如:G节点处:7.630.6687.63 3.79GH GHGHGH GDGjGi ii iiμ====++∑GD3.790.3327.63 3.79GD GDGH GDGjGi ii iiμ====++∑H节点处:7.630.3537.63 3.7910.21H G H GHGHG HE HIHjHi ii i iiμ====++++∑3.790.1757.63 3.7910.21HI HIHIHG HE HIHjHi ii i iiμ====++++∑10.210.4727.63 3.7910.21HE HEHEHG HE HIHjHi ii i iiμ====++++∑同理,可计算其余各节点的力矩分配系数,计算结果见图6、图7。
图6 二层节点处力矩分配系数图7 底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩(1)第二层:①计算各梁杆端弯矩。
先在G、H、I节点上加上约束,详见图8图8 二层计算简图计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号),写在各梁杆端下方,见图9:213.13kN m 12FGHql M =-=-⋅213.13kN m 12F HGql M ==⋅ 27.32kN m 12F HIql M=-=-⋅27.32kN m 12F IHql M==⋅ 在节点G 处,各梁杆端弯矩总和为:13.13kN m FG GH M M ==-⋅在节点H 处,各梁杆端弯矩总和为:13.137.32 5.81kN m F F H HG HI M M M =+=-=⋅在节点I 处,各梁杆端弯矩总和为:7.32kN m F I IH M M ==⋅②各梁端节点进行弯矩分配,各两次,详见图9 第一次弯矩分配过程:放松节点G ,即节点G 处施加力矩13.13kN m ⋅,乘以相应分配系数0.668和0.332,得到梁端+8.76k N m ⋅和柱端+4.37kN m ⋅,+8.76kN m ⋅按12传到GH 梁H 端;放松节点I ,即在节点I 处施加力矩7.32kN m -⋅,乘以相应分配系数0.935和0.065,得到梁端 6.32kN m -⋅和柱端+1.00kN m ⋅, 6.32kN m -⋅按12传到IH 梁H 端;放松节点H ,相应的在节点H 处新加一个外力偶矩,其中包括GH 梁右端弯矩、IH 梁左端弯矩、GH 梁和IH 梁传来的弯矩。
8-3 力矩分配法应用

3.计算杆端弯矩
M
F BA
16kN.m
M
F BC
12kN.m
例3.1 作图示结构的弯矩图。
3.计算过程列表表示
AB 分配系数μ 固端弯矩
分配弯矩 传递弯矩 0 杆端弯矩 0
BA BC 0.5 0.5 16 12 -14 -14
2 -2
M (kN.m)
CB -24 0 -24
例3.2 作图示结构的弯矩图。 解:1.本题可用力矩分配法。
M
F CB
600kN.m
M
F CD
400kN.m
4.计算过程列表表示
结点
A
杆端
AB
分配系数μ
固端弯矩 0
分配传递
杆端弯矩 0
B BA BE BC
0.32 0.36 0.32 0 0 -600
216 192 192 -47.36
C
D
CB CF CD
DC
0.32 0.36 0.32
600 0
-400 0
内力图
不平衡
4.依次类推,再重复第2步和第3步,即轮 流去掉结点B和结点C的约束。连续梁的变 形和内力很快趋于实际情况。
每次只放松一个结点,故每一步均为 单结点的分配与传递。
5.作弯矩图。 将各杆端的固端弯矩、分配弯矩和传
递弯矩累加,即得杆端的最终弯矩。
1.约束可动结点,计算固端弯矩。2.逐个放松可动结点。每次只放松一个结点,故每一 步 均为单结点的分配与传递。3.计算精度(或计算轮次)未达到要求,重复第2步, 进行新 一轮分配计算。4.计算精度(或计算轮次)达到要求,将各杆端的固 端弯矩、分配弯矩和 传递弯矩累加,即得杆端的最 终弯矩。
结构力学——力矩分配法

结构力学——力矩分配法结构力学是研究物体在外力作用下的变形和破坏行为的学科。
其中,力矩分配法是一种求解结构梁的内力和变形的常用方法之一、本文将介绍力矩分配法的基本理论和应用。
首先,对于结构力学的研究,我们需要了解一些基本概念。
力矩是由力的作用点与旋转轴之间的距离和力的大小决定的。
在结构力学中,我们通常考虑作用在梁上的力和力矩。
梁是一种常见的结构元件,可以将其看作是在两个固定点之间作用的力的集合。
在力矩分配法中,我们将梁分割成若干个小段,然后逐段计算每个小段的内力和变形。
假设有一根长度为L,截面形状均匀的梁,并且在两个固定点之间施加了一系列分布力。
我们可以将梁分割成n个小段,每个小段的长度为Δx=L/n。
接下来,我们需要计算每个小段的内力和变形。
首先,我们可以根据材料力学的基本原理得出梁的拉伸、压缩和弯曲的力学方程。
然后,我们可以根据小段的切线方向和切线上的任意一点来推导出该小段的内力和弯曲方程。
最后,我们将内力分量在小段两端的力矩分配系数和位置矩分配系数进行合成,从而得出该小段的内力和弯曲方程。
在力矩分配法中,一个重要的概念是力矩分配系数。
力矩分配系数是一个无量纲的参数,用来表示力和力矩在小段两端分配的比例。
在计算力矩分配系数时,我们可以根据梁的几何形状和分布力的位置,利用力矩的基本原理进行推导。
力矩分配系数是力矩分配法的核心,它可以帮助我们计算出每个小段的内力和变形。
在实际应用中,力矩分配法通常用于求解多跨梁的内力和变形。
我们可以将多跨梁分割成若干个小段,并根据力矩分配法计算出每个小段的内力和变形。
然后,我们可以将各个小段的内力和变形进行叠加,得出整个多跨梁的内力和变形。
需要注意的是,力矩分配法具有一定的局限性。
首先,它只适用于存在弯曲变形的梁,对于其他类型的结构,如框架和板,需要采用其他的分析方法。
其次,力矩分配法仅适用于分布力作用在梁的直线部分上,对于弯曲部分或非均匀分布力的情况,需要采用其他的方法进行分析。
分层法例题(力矩分配法)资料讲解
五、创业机会和对策分析
10、如果学校开设一家DIY手工艺制品店,你希望_____
情感性手工艺品。不少人把自制的手机挂坠作为礼物送给亲人朋友,不仅特别,还很有心思。每逢情人节、母亲节等节假日,顾客Байду номын сангаас别多。
在调查中我们注意到大多数同学都比较注重工艺品的价格,点面氛围及服务。
加拿大beadworks公司就是根据年轻女性要充分展现自己个性的需求,将世界各地的珠类饰品汇集于“碧芝自制饰品店”内,由消费者自选、自组、自制,这样就能在每个消费者亲手制作、充分发挥她们的艺术想像力的基础上,创作出作品,达到展现个性的效果
据调查统计在对大学生进行店铺经营风格所考虑的因素问题调查中,发现有50%人选择了价格便宜些,有28%人选择服务热情些,有30%人选择店面装潢有个性,只有14%人选择新颖多样。如图(1-5)所示
1、你一个月的零用钱大约是多少?可见“体验化消费”广受大学生的欢迎、喜欢,这是我们创业项目是否成功的关键,必须引起足够的注意。
300-400元1632%
力矩分配法
第八章 力矩分配法1. 图中结构中固定端弯矩 为: -533.33KN·m2.在力矩分配中等截面杆的远端固定,杆传递系数C等于: 0.53.图中结构中固定端弯矩 = -10KN·m4.在力矩分配法中杆端的转动刚度与杆另一端的支撑情况有关。
( )5.图中结构中力矩分配系数 = 0.7066.单独使用力矩分配法,只能解算连续梁和无侧移刚架。
( )7.图a和图b的A端转动刚度相同。
( )8.一个刚结点无论连接多少个杆件,这些杆件的力矩分配系数之和总等于( )9.在力矩分配法中已知某杆一端的分配力矩M,若该杆另端为滑动支座,则传递力矩为M。
( )10.力矩分配法中的传递系数等于传递力矩与分配力矩之比,它与荷载作用无关。
( )11.对图示结构,力矩分配系数 和固端弯矩 分别为:( A )A.0.238, -41.67 KN·mB.0.238, 41.67 KN·mC.0.294, -41.67 KN·mD.0.294, 41.67 KN·m12.图示结构中,各杆i等于常数,欲使结点产生顺时针转角,即 =1,要在结点A上施加(顺时针)外力偶为:( A )A.8iB.8iC. 11iD.9i13.用力矩分配法计算图示结构,结点A的不平衡力矩为:( A )A.-16 KN·mB. 16 KN·mC. 0D.-64 KN·m14.图示连续梁,已知 =1/2,则杆端弯矩 为: ( A )A.8 KN·mB.-8 KN·mC.16 KN·mD.-16 KN·m15.用力矩分配法计算图示结构,分配系数 和为4/7和3/7,则杆端弯矩分别为: ( A )A.80 KN·m, 60 KN·mB.-80 KN·m,60 KN·mC.80 KN·m,-60 KN·mD.-80 KN·m,-60 KN·m16.AB杆的弯矩传递系数 与: ( C )A.杆AB的A端支承情况有关B. 杆AB的两端支承情况有关C. 杆AB的B端支承情况有关D. 杆AB的两端支承情况无关17.在力矩分配法中,某杆端分配系数与该杆的转动刚度: ( A )A.成正比B.有时成正比,有时成反比C.无关系D.成反比18.取左半部为如图示对称结构的等代结构,在等代结构中分配系数 等于:( D )A.1/3B.4/11C.2/5D.2/719.用力矩分配法计算图示结构,分配系数 、分别等于: ( D )A.0.5 0.333B.0.25 0.5C.0.25 0.333D.0.50.57120.如图连续梁中,已知 =4/7,则 等于: ( D )A.4/7(-M+Pd/6)B. 4/7(M+Pd/8)C.4/7(-M+Pd/8)D. 4/7(M-Pd/8)。
1《分层法》例题详细讲解
例:如图1所示一个二层框架,忽略其在竖向荷载作用下的框架侧移,用分层法计算框架的弯矩图,括号的数字,表示各梁、柱杆件的线。
图1解:1、简化为两个图:图2、图3所示图2 第二层计算简图图3 底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数除底层外,其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为1/2,其余各层柱的弯矩传递系数为1/3。
各层梁的弯矩传递系数,均为1/2.图4 修正后的梁柱线刚度图5 各梁柱弯矩传递系数3、计算各节点处的力矩分配系数 如:G 节点处:7.630.6687.63 3.79GHGH GH GH GD GjGi i i i iμ====++∑ GD 3.790.3327.63 3.79GDGD GH GD GjGi i i i iμ====++∑H 节点处:7.630.3537.63 3.7910.21HGHG HG HG HE HI HjHi i i i i iμ====++++∑3.790.1757.63 3.7910.21HIHI HI HG HE HI HjHi i i i i iμ====++++∑10.210.4727.63 3.7910.21HEHE HE HG HE HI HjHi i i i i iμ====++++∑其余各节点的力矩分配系数见图6、图7。
图6 二层节点处力矩分配系数图7 底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩(1)第二层: ①计算各梁杆端弯矩。
将各杆变成单跨梁,刚节点看成是固定端。
图8 二层计算简图计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号左负右正),213.13kN m 12F GHql M=-=-⋅ 213.13kN m 12F HGql M ==⋅ 27.32kN m 12F HIql M=-=-⋅ 27.32kN m12F IH ql M ==⋅ ②各梁端节点进行负弯矩分配和传递,各两次,第一次负弯矩分配与传递后再进行第二次负弯矩分配与传递:③计算各柱的杆端弯矩。
竖向荷载作用下的近似计算-分层力矩分配法
力矩的分配系数是根据各层之间 的相对刚度确定的,相对刚度越
大,所分配到的力矩越大。
分层力矩分配法的应用场景
分层力矩分配法适用于多层框架、剪力墙、框架-剪力墙等结构体系的分析和计算。
该方法特别适用于高度超过30m的高层建筑结构,以及需要进行整体性能分析的大 型复杂结构。
分层力矩分配法在工程实践中得到了广泛应用,为多层和高层建筑结构的分析和设 计提供了重要的理论依据和计算工具。
分层力矩分配法在桥梁工程中的应用
总结词
灵活、适用性强
详细描述
分层力矩分配法在桥梁工程中具有灵活和适用性强的特点。该方法可以根据桥梁的结构 形式和跨度大小,灵活地选择合适的分层方式和计算模型,适用于各种类型的桥梁结构, 如梁式桥、拱桥、斜拉桥等。通过分层力矩分配法,可以准确地计算桥梁在不同荷载作
用下的内力和变形,为桥梁的优化设计和安全评估提供依据。
02
分层力矩分配法的计算步骤
确定各层的自重力和各层楼面的可变荷载
确定各层的自重力和各层楼面的可变荷载是进行分层力矩分配法计算的基础步骤 。自重力包括结构自重和填充墙自重,可变荷载包括楼面活荷载、屋面活荷载等 。
在计算过程中,需要将各层的自重力和可变荷载分别乘以相应的楼层高度,得到 每层的竖向荷载。
竖向荷载作用下的近似计算分层力矩分配法
• 分层力矩分配法概述 • 分层力矩分配法的计算步骤 • 分层力矩分配法的优缺点 • 分层力矩分配法的实际应用案例
01
分层力矩分配法概述
分层力矩分配法的定义
1
分层力矩分配法是一种竖向荷载作用下的近似计 算方法,用于计算多层结构的内力和位移。
2
该方法基于分层法的基本原理,将多层结构按照 竖向荷载进行分层,并对每一层进行独立的分析 和计算。
3、恒载作用下分层力矩分配法
99.64 109.5 -209 上柱 下柱 梁 0.431 0.431 0.138 38.81 -16.7 -16.7 -5.36 6 -16.7 22.08 -5.36
22.4 6.43 -16 6.04 1.74
198.4 24.4 28.8 -265 8.15 梁 上柱 下柱 梁 0.149 0.37 0.37 0.11 190.7 9.59 -257 -3.62 8.937 2.417
21 -6
-0.07 -0 0.031 0.01 116 87.36 -204 39 上柱 下柱 梁 0.4 0.431 0.138 29 -232 87 87.34 27.97 5
1.251 -0.15 0.46 -0.46 -0.19 239.8 -17 -5.5 梁 上柱 0.118 0.37 231.8 -6.6 13.93 -5.72 -13 -19.7 -197 下柱 梁 0.367 0.148 -191 -17.8 -7.17
7 -17 2.503 -6.2 6.25 1.8
240.9 -30.5 -5.27 -193 梁 上柱 下柱 梁 0.118 0.367 0.367 0.15 -6.26 0.739 2.299 2.299 0.93 0.739 2.299 4.598 0.93
3.5 -33.6 -116.5 -115
261.7 -116.5 -144 -48 梁 下柱 上柱 0.126 0.437 0.44 291.8 -39
1.209 -0.14 0.44 -0.44 -0.18 239.8 -19 -18.4 -197 -6.2 梁 上柱 下柱 梁 0.118 0.37 0.367 0.148 231.8 -6.1 -191 13.98 -5.78 -13 -18 -7.24
