2.1.1指数与指数幂的运算(二) (2)
【成才之路】2014-2015学年高中数学 2.1.1 指数与指数幂的运算 第2课时 分数指数幂课件 新人教A版必修1

4
B. a-1 D. 1 4 a-1
[答案] B
[解析] 要使原式有意义,则 a-1>0 . 4 1-a ·
2
①
3 1 - (a - 1) 4 = (a - 1)· (a - 1) 3 = |1 - a|· a-1
-
3 4
=(a-1)
1 4
= a-1.
4
随堂测评
1. 若 a>0, 且 m, n 为整数, 则下列各式中正确的是( A.a ÷ a =a
1 -22=(-2)3 3 x3y3=xy4
2 2
)
4 3
(x>0,y>0)
1 -b 3
C. a -b
1 =a3
3 x y 1 - D. y=(x) 3
(x≠0,y≠0)
[答案] D
5.若10x=3,10y=4,则10x-y=________.
[答案] 3 4
x 10 3 x-y [解析] 10 =10y=4.
m n
m n
)
B.am· an=am+n D.1-an=a0-n
C.(am)n=am+n
[答案] B
2. a-2可化为( A.a
-
5
)
5 B.a2 5 D.-a2
2 5
2 C.a5
[答案] A
4 3.a5
的根式为(
4 4
) B. a5
5
A. a C.
5
4
a5
D.
a4
[答案] A
4.下列各式中正确的是( A. B. 6
规律总结: 在将根式化分数指数幂的形式时,关键
是分清指数中分子、分母的位置.
1
将下列根式与分数指数幂进行互化.
2.1.1指数与指数幂的运算(2)

§2.1.1指数与指数幂的运算(2)学习目标1. 理解分数指数幂的概念;2. 掌握根式与分数指数幂的相互转化; 3 掌握有理数指数幂的运算.预习案预习课本P 50—P 52 页内容 1.正数a 的正分数指数幂=n ma (),,0*N n m a ∈> 2.正数a 的负分数指数幂=-nm a(),,0*N n m a ∈>3.s r a a ⋅= (其中),,0Q s r a ∈> 4.s r a )( = (其中),,0Q s r a ∈> 5.s b a )(⋅= (其中),0,Q s b a ∈> 预习自测1. 求下列各式的值:(1)328 (2)21100-(3)239-2.用分数指数幂的形式表示并计算下列各式(式中字母都是正数):(1)a a ⋅2 (2)323a a ⋅ (3)a a3.计算下列各式(式中字母都是正数):(1)(2a 32b 21)(-6a 21b 31)÷(-3a 61b 65); (2)(m 41n 83-)8.我的疑问探究案自主探究一:(1)观察以下式子,并总结出规律:a >0,①510a =552)(a =a 2=a 510; ②8a =24)(a =a 4=a 28; ③412a =443)(a =a 3=a 412; ④210a =225)(a =a 5=a 210. (2)利用(1)的规律,你能表示下列式子吗?435,357,57a ,n m x (x>0,m,n∈+N ,且n>1).(3)你能用方根的意义来解释(3)的式子吗?(4)0的正分数指数幂等于多少?0有负指数幂吗? (5)负整数指数幂的意义是怎样规定的?合作探究例1. 已知231211322[()()]a b a b ab a ------==求的值.变题1:已知31=+-x x ,求下列各式的值:(1)2121-+x x例2. 比较63123,11,5的大小.例3.求下列各式的值:(1)432981⨯; (2)23×35.1×612.总结提升※ 学习小结:1. 分数指数幂nm a 不可理解为nm个a 相乘,它是根式的一种新写法 2. 0的正分数指数幂是0,0的负指数幂没有意义3. 负数的分数指数幂是否有意义,应视指数的分子、分母的具体数值而定※ 当堂检测: 1. 235.0322901.0)833(5.1)8.1(+-⋅+---=2. 求下列各式的值(其中各式字母均为正数):(1)23)425(-= ; (2)()551.0-=__________;(3)()24-π=________ (4)()66y x -()y x >=_______;(5)834121-a a a = ; (6)3163)278(--ba =3. 用根式的形式表示下列各式(a >0)(1).21a (2).43a (3).53-a(4).32-a训练案1. 计算下列各式的值: (1)[(a 23-b 2)-1·(ab -3)21(b 21)7]31(2)1112121-+-++--a a a aa(3)14323)(---÷a b b a2.用分数指数幂表示下列各式(1).32x (2).43)(b a + (3).4)(n m - (4).mm 33.下列运算中,正确的是( )A .a 2·a 3=a 6B .(-a 2)3=(-a 3)2C .(a -1)0=0 D .(-a 2)3=-a 64.下列各式①42)4(n -,②412)4(+-n ③54a ,④45a (各式的n∈N ,a∈R )中,有意义的是( )A.①②B.①③C.①②③④D.①③④5. 设x 5=4,y 5=2,则y x -25=________.思考题:设n n n x x a a x a )1(),(21,0211++-=>-求的值.。
高一数学必修一第二章基本初等函数知识点总结
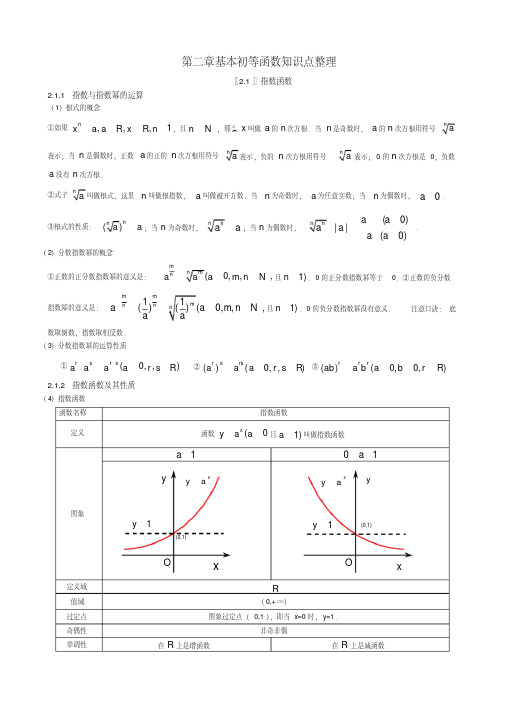
在 R 上是减函数
函数值的 变化情况
a 变化对
图象的影 响
y>1(x > 0), y=1(x=0), 0 < y<1(x < 0)
y> 1(x < 0), y=1(x=0), 0 < y< 1(x > 0)
在第一象限内, a 越大图象越高,越靠近 y 轴; 在第一象限内, a 越小图象越高,越靠近 y 轴; 在第二象限内, a 越大图象越低,越靠近 x 轴. 在第二象限内, a 越小图象越低,越靠近 x 轴.
y
f ( x) 中反解出 x
1
f ( y) ;
③将 x f 1( y ) 改写成 y f 1 ( x) ,并注明反函数的定义域.
( 8)反函数的性质
①原函数 y
f (x) 与反函数 y
1
f ( x) 的图象关于直线 y
x 对称.
②函数 y f ( x) 的定义域、值域分别是其反函数 y f 1 (x ) 的值域、定义域. ③若 P(a,b) 在原函数 y f (x ) 的图象上,则 P' (b, a) 在反函数 y f 1(x ) 的图象上.
③根式的性质: (n a )n a ;当 n 为奇数时, n an
a ;当 n 为偶数时, n an | a |
a (a 0)
.
a (a 0)
( 2)分数指数幂的概念
m
①正数的正分数指数幂的意义是: a n n a m (a 0, m, n N , 且 n 1) . 0 的正分数指数幂等于 0.②正数的负分数
设一元二次方程 ax 2 bx c 0( a 0) 的两实根为 x1, x2 ,且 x1 x2 .令 f ( x) ax 2 bx c ,从以下四个方
面来分析此类问题:①开口方向: a ②对称轴位置: x
人教高中数学必修1课件:2.1.1 指数与指数幂的运算 第2课时 指数幂及运算 探究导学课型

⇓
用符号语言描述:_______(a>0,m,n∈N*且n>1).
m
n am a n
⇓ 分数指数幂的意义:(1)正数的正分数指数幂的意义: __m _____(a>0,m,n∈N*,且n>1). a n n am (2)正数的负分数指数幂的意义:
_a_mn____1m_(a>0,m,n∈N*,且n>1). (3)0的a n正分数指数幂等于0,0的负分数指数幂________.
3111 1121
a2 6 3b 3 3
ab1
a.
b
6.计算
(a
2 3
b
3
)
(
1
a
1 6
b
5 6
).
(仿照教材P52例4的解析3 过程)
【解析】 (a
2 3
b
1 2
)(3a
1 2
1
b3
)
(
1
a
1 6
b
5 6
)
3
211 115
3 3a 3 2 6b2 3 6 9a.
提示:(1)若a=0,因为0的负数指数幂无意义,所以
a≠0.
(2)若a<0,(ar)s=ars也不一定成立,如
1
1
所以a<0不成立.因此不适用于a=0或a<[(04的)2]情4 况(.4)2 ,
3.公式am÷an=am-n(a>0,m,n∈N*)成立吗?请用有
理数指数幂的运算性质加以证明,并说明是否要限
[3 ,) 2
所以2a-3≠0,即(2a
1
3) 3
3
1 2a 3
,
故a的取值范围为a 3 , 2
课件11:2.1.1 指数与指数幂的运算

1
=x+yx--2yxy 2 ,①
又∵x+y=12,xy=9,②
∴(x-y)2=(x+y)2-4xy=122-4×9=108.
∵x<y,∴x-y=-6 3.③
将②、③代入①式得
1
1
1
x x
2
1 2
-y +y
2
1 2
=12--26×39
2
=-
3 3.
【跟踪训练3】
已知a
1 2
-
+a
1 2
=3,求下列各式的值.
2.根式一般先转化成分数指数幂,然后再利用有理数指数幂的运算性质进行运算,在将根式化为分数指 数幂的过程中,一般采用由内到外逐层变换为指数的方法,然后运用运算性质准确求解.
3.对于含有字母的化简求值结果,一般用分数指数幂的形式表示.
[走出误区]
易错点⊳因忽略幂指数的范围而导致错误
11
[典例] 化简(1-a)[(a-1)-2(-a) 2 ] 2 =________.
2.1 指数函数
2.1.1 指数与指数幂的运算
第2课时 指数幂及运算
[问题提出]
1.有理数指数幂的运算性质与整数指数幂的运算性质是否相同? 2.无理数指数幂的运算性质与有理数指数幂的运算性质是否相同?
[基础自学]
1.有理数指数幂的运算性质 (1)ar·as= ar+s (a>0,r,s∈Q); (2)(ar)s= ars (a>0,r,s∈Q); (3)(ab)r= arbr (a>0,b>0,r∈Q).
[解]
(1)令2x=t,则2-x=t-1,∴t+t-1=a.①
由①两边平方得t2+t-2=a2-2,
∴8x+8-x=t3+t-3=(t+t-1)(t2-t·t-1+t-2)
学案6:2.1.1 指数与指数幂的运算

当x≥y时,原式=x-y+y-x=0;
当x<y时,原式=y-x+y-x=2(y-x).
所以原式=
例2(1) (2)a (3)①a3· =a3·a =a =a .
【解析】(1)a = =
(2)(a2· )÷( · )=(a2·a )÷(a ·a )=a ÷a =a =a
(4)2 ÷4 ·3 .
方法归纳
利用指数幂的运算性质化简求值的方法
(1)进行指数幂的运算时,一般化负指数为正指数,化根式为分数指数幂,化小数为分数,同时兼顾运算的顺序.
(2)在明确根指数的奇偶(或具体次数)时,若能明确被开方数的符号,则可以对根式进行化简运算.
(3)对于含有字母的化简求值的结果,一般用分数指数幂的形式表示.
当堂检测
[基础巩固]
一、选择题
1.B
【解析】 =(-2 ) =(-2×2 ) =(-2 ) =-2 .
2.D
【解析】要使原式有意义,只需 ,
∴a≥0且a≠2.
3.A
【解析】依题意知x<0,所以 =- =- .
4.D
【解析】原式= =a =a .
5.C
【解析】( )4·( )4
=( ) ·( )
=(a ) ·(a ) =a ·a =a4.
3.化简 的结果是()
A.- B.
C.- D.
4. (a>0)的值是()
A.1B.a
C.a D.a
5.化简( )4·( )4的结果是()
A.a16B.a8
C.a4D.a2
二、填空题(每小题5分,共15分)
6. -2+(1- )0- -160.75=________.
课件12:2.1.1 指数与指数幂的运算

对于这一理论,其学派中的一个成员希帕索斯考虑了一个 问题:边长为 1 的正方形其对角线长度是多少呢?他发现这一 长度既不能用整数,也不能用分数表示,而只能用一个新数来 表示.希帕索斯的发现导致了数学史上第一个无理数 2 的诞 生.小小 2的出现,却在当时的数学界掀起了一场巨大的风 暴.史称“第一次数学危机”.希帕索斯也因发现了根号 2, 憾动了学派的基石而被扔进大海.
跟踪训练 1. 计算下列各值: (1)27 的立方根是________; (2)256 的四次算术方根是________; (3)32 的五次方根是________.
[答案] (1)3 (2)4 (3)2 [解析] (1)∵33=27,∴27的立方根是3. (2)∵(±4)4=256,∴256的四次算术方根为4. (3)∵25=32,∴32的五次方根为2.
∴ x2-2x+1- x2+6x+9
=--24x-2
-3<x<1 1≤x<3 .
命题方向4.根式的运算技巧
例 4.计算 5-2 6+ 5+2 6.
[分析] 注意 a+2 b的配方或整体考虑运用方程思想. [解析] 解法一:原式= 2- 32+ 2+ 32= 3- 2+ 3+ 2=2 3. 解法二:设 x= 5-2 6+ 5+2 6,则 x>0. 平方得 x2=(5-2 6)+(5+2 6)+ 2 5+2 65-2 6 即 x2=12,∵x>0,∴x=2 3.∴原式=2 3.
新知导学
1.n次方根
一般地,如果 xn=a,那么__x__叫做 a 的_n_次__方__根__, 定义>0 奇数 a<0 x<0
x 仅有一个值,记为n a
个数 n 是 a>0 x 有两个值,且互为相反数,记为±n a
最新人教必修一数学导学案:2.1.1 指数与指数幂的运算(2)

最新人教版数学精品教学资料§2.1.1 指数与指数幂的运算(2)班级 姓名 学号1. 理解分数指数幂的概念;2. 掌握根式与分数指数幂的互化;3. 掌握有理数指数幂的运算.一、课前准备(预习教材P 50~ P 53,找出疑惑之处)复习1:一般地,若n x a =,则x 叫做a 的 ,其中1n >,n *∈N .简记为: .的式子就叫做 ,具有如下运算性质:n = ;= ;= .复习2:整数指数幂的运算性质.(1)m n a a = ;(2)()m n a = ; n※ 学习探究 探究任务:分数指数幂引例:a >01025a a ==,则类似可得 ;23a = .新知:规定分数指数幂如下*(0,,,1)m n a a m n N n =>∈>;*1(0,,,1)mnm n a a m n N n a -==>∈>. 试试:(1)将下列根式写成分数指数幂形式:= ; = ;= (0,)a m N *>∈.(2)求值:238; 255; 436-; 52a -.反思:① 0的正分数指数幂为 ;0的负分数指数幂为 .② 分数指数幂有什么运算性质?小结:规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理数指数,那么整数指数幂的运算性质也同样可以推广到有理数指数幂.指数幂的运算性质: (0,0,,a b r s Q >>∈)r a ·r r s a a +=; ()r s rs a a =; ()r r s ab a a =.※ 典型例题例1 求值:2327;4316-; 33()5-;2325()49-.例2 用分数指数幂的形式表示下列各式(0)b >:(1)2b b ; (2)533b b ; (3.例3 计算(式中字母均正): (1)211511336622(3)(8)(6)a b a b a b -÷-; (2)311684()m n .例4 计算:(1334a a (0)a >; (2)312103652(2)()m n m n --÷- (,)m n N *∈;(3)小结:在进行指数幂的运算时,一般地,化指数为正指数,化根式为分数指数幂,对含有指数式或根式的乘除运算,还要善于利用幂的运算法则.反思:①结论:无理指数幂.(结合教材P 53利用逼近的思想理解无理指数幂意义)② 无理数指数幂(0,)a a αα>是无理数是一个确定的实数.实数指数幂的运算性质如何?三、总结提升※ 学习小结①分数指数幂的意义;②分数指数幂与根式的互化;③有理指数幂的运算性质.※ 知识拓展放射性元素衰变的数学模型为:0t m m e λ-=,其中t 表示经过的时间,0m 表示初始质量,衰减后的质量为m ,λ为正的常数.1. 若0a >,且,m n 为整数,则下列各式中正确的是( ).A. m m n n a a a ÷=B. m n mn a a a ⋅=C. ()nm m n a a += D. 01n n a a -÷= 2. 化简3225的结果是( ).A. 5B. 15C. 25D. 1253. 计算(122--⎡⎤⎢⎥⎣⎦的结果是( ).A B . D . 4. 化简2327-= . 5. 若102,104m n ==,则3210m n -= .1. 化简下列各式:(1)3236()49; (2.2. 1⎛÷- ⎝.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
班主任: 我觉得何旋今天取得这样的成绩, 我觉得,很重要的是,何旋是土生土长的北京 二中的学生,二中的教育理念是综合培养学生 的素质和能力。我觉得何旋,她取得今天这么 好的成绩,一个来源于她的扎实的学习上的基 础,还有一个非常重要的,我觉得特别想提的, 何旋是一个特别充满自信,充满阳光的这样一 个女孩子。在我印象当中,何旋是一个最爱笑 的,而且她的笑特别感染人的。所以我觉得她 很阳光,而且充满自信,这是她突出的这样一 个特点。所以我觉得,这是她今天取得好成绩 当中,心理素质非常好,是非常重要的。
x 1
1
3, 求x 2
x
1
2的
值.
课堂小结
1. 分数指数幂的意义; 2. 分数指数幂与根式的互化; 3. 有理数指数幂的运算性质.
课后作业
1.阅读教材P.50-P.52; 2.《习案》作业十六.
语文
小魔方站作品 盗版必究
湖南省长沙市一中卫星远程学校
谢谢您下载使用!
更多精彩内容,微信扫描二维码获取 扫描二维码获取更多资源
2.1.1指数与指数幂 的运算
复习引入
1. 整数指数幂的运算性质:
复习引入
1. 整数指数幂的运算性质:
am an amn (m, n Z ), (a m )n a mn (m, n Z ), (ab)n an bn (n Z ).
复习引入
2. 根式的运算性质:
讲授新课
1. 正数的正分数指数幂的意义:
m
a n n a m (a>0, m, n∈N*, 且n>1).
注意两点: (1)分数指数幂是根式的另一种表示形式; (2)根式与分数指数幂可以进行互化.
2. 对正数的负分数指数幂和0的分数指数 幂的规定:
2. 对正数的负分数指数幂和0的分数指数 幂的规定:
湖南省长沙市一中卫星远程学校
高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校: 北京大学光华管理学院
北京市理科状元杨蕙心
湖南省长沙市一中卫星远程学校
班主任 孙烨:杨蕙心是一个目标高远 的学生,而且具有很好的学习品质。学 习效率高是杨蕙心的一大特点,一般同 学两三个小时才能完成的作业,她一个 小时就能完成。杨蕙心分析问题的能力 很强,这一点在平常的考试中可以体现。 每当杨蕙心在某科考试中出现了问题, 她能很快找到问题的原因,并马上拿出 解决办法。
100 2 ,
( 1 )3 ,
(
16
)
3 4
.
4 81
4. 例题与练习: 例2 用分数指数幂的形式表示下列各式 (其中a>0):
a2 a; a3 3 a2; a a .
4. 例题与练习: 例2 用分数指数幂的形式表示下列各式 (其中a>0):
a2 a; a3 3 a2; a a .
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
青 春 风 采
湖南省长沙市一中卫星远程学校
高考总分:
692分(含20分加分) 语文131分 数学145分 英语141分 文综255分
毕业学校:北京二中 报考高校:
北京大学光华管理学 院
北京市文科状元 阳光女孩--何旋
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
曹杨二中高三(14)班学生
班级职务:学习委员
高考志愿:北京 大学中文系
高考成绩:语文121分数学146分
英语146分历史134分
综合28分总分
575分
(另有附加分10
分)
上海高考文科状元--常方舟
湖南省长沙市一中卫星远程学校
“我对竞赛题一样发怵”
总结自己的成功经验,常方舟认为学习的高 效率是最重要因素,“高中三年,我每天晚 上都是10:30休息,这个生活习惯雷打不动。 早晨总是6:15起床,以保证八小时左右的睡 眠。平时功课再多再忙,我也不会‘开夜 车’。身体健康,体力充沛才能保证有效学 习。”高三阶段,有的同学每天学习到凌晨 两三点,这种习惯在常方舟看来反而会影响 次日的学习状态。每天课后,常方舟也不会 花太多时间做功课,常常是做完老师布置的 作业就算完。
湖南省长沙市一中卫星远程学校
“用好课堂40分钟最重要。我的经验是,哪怕 是再简单的内容,仔细听和不上心,效果肯 定是不一样的。对于课堂上老师讲解的内容, 有的同学觉得很简单,听讲就不会很认真, 但老师讲解往往是由浅入深的,开始不认真, 后来就很难听懂了;即使能听懂,中间也可 能出现一些知识盲区。高考试题考的大多是 基础知识,正就是很多同学眼里很简单的内 容。”常方舟告诉记者,其实自己对竞赛试 题类偏难的题目并不擅长,高考出色的原因 正在于试题多为基础题,对上了自己的“口 味”。
湖南省长沙市一中卫星远程学校
孙老师说,杨蕙心学习效率很高,认真执行老师 的复习要求,往往一个小时能完成别人两三个小 时的作业量,而且计划性强,善于自我调节。此 外,学校还有一群与她实力相当的同学,他们经 常在一起切磋、交流,形成一种良性的竞争氛围。
谈起自己的高考心得,杨蕙心说出了“听话” 两个字。她认为在高三冲刺阶段一定要跟随老师 的脚步。“老师介绍的都是多年积累的学习方法, 肯定是最有益的。”高三紧张的学习中,她常做 的事情就是告诫自己要坚持,不能因为一次考试 成绩就否定自己。高三的几次模拟考试中,她的 成绩一直稳定在年级前5名左右。
当n为偶数时, n
an
| a |
a(a 0) a(a 0).
② 当n为任意正整数时,(n a )n a.
ห้องสมุดไป่ตู้习引入
3. 引例:当a>0时,
10
① 5 a10 5 (a 2 )5 a 2 a 5 ; ②
③
④
是否可以呢?
讲授新课
1. 正数的正分数指数幂的意义:
m
a n n a m (a>0, m, n∈N*, 且n>1).
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
上海 2006 高考 理科 状元-武亦 文
武亦文 格致中学理科班学生 班级职务:学习委员 高考志愿:复旦经济 高考成绩:语文127分 数学142分 英语144分
物理145分 综合27分 总分585分
湖南省长沙市一中卫星远程学校
“一分也不能少”
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
附赠 中高考状元学习方法
湖南省长沙市一中卫星远程学校
湖南省长沙市一中卫星远程学校
前言
高考状元是一个特殊的群体,在许多 人的眼中,他们就如浩瀚宇宙里璀璨夺目 的星星那样遥不可及。但实际上他们和我 们每一个同学都一样平凡而普通,但他们 有是不平凡不普通的,他们的不平凡之处 就是在学习方面有一些独到的个性,又有 着一些共性,而这些对在校的同学尤其是 将参加高考的同学都有一定的借鉴意义。
an
(2) 0的正分数指数幂等于0;
(3) 0的负分数指数幂无意义.
3. 有理数指数幂的运算性质:
am an amn (m, n Q), (a m )n a mn (m, n Q), (ab)n an bn (n Q).
4. 例题与练习:
例1 求值:
2
83 ,
1
练习:教材P.54练习第2题.
4. 例题与练习:
例3 计算下列各式(式中字母都是正数)
21
11
15
(1) (2a 3b 2 )(6a 2b 3 ) (3a 6b 6 );
(
2)
(
m
1 4
n
3 8
)8
;
(3) (3 25 125 ) 4 5 ;
a2
( 4)
.
a 3 a2
4. 例题与练习:
an
| a |
a(a 0) a(a 0).
复习引入
2. 根式的运算性质:
① 当n为奇数时, n a n a;
当n为偶数时, n
an
| a |
a(a 0) a(a 0).
② 当n为任意正整数时,
复习引入
2. 根式的运算性质:
① 当n为奇数时, n a n a;
“我坚持做好每天的预习、复习,每 天放学回家看半小时报纸,晚上10: 30休息,感觉很轻松地度过了三年 高中学习。”当得知自己的高考成 绩后,格致中学的武亦文遗憾地说 道,“平时模拟考试时,自己总有 一门满分,这次高考却没有出现, 有些遗憾。”
湖南省长沙市一中卫星远程学校
坚持做好每个学习步骤
武亦文的高考高分来自于她日常严谨的学习 态度,坚持认真做好每天的预习、复习。 “高中三年,从来没有熬夜,上课跟着老师 走,保证课堂效率。”武亦文介绍,“班主 任王老师对我的成长起了很大引导作用,王 老师办事很认真,凡事都会投入自己所有精 力,看重做事的过程而不重结果。每当学生 没有取得好结果,王老师也会淡然一笑,鼓 励学生注重学习的过程。”
例3 计算下列各式(式中字母都是正数)
21
11
15
(1) (2a 3b 2 )(6a 2b 3 ) (3a 6b 6 );
(
2)
(
m
1 4
n
3 8
)8
;
(3) (3 25 125 ) 4 5 ;
a2
( 4)
.
a 3 a2
练习:教材P.54练习第3题.
4. 例题与练习:
例4
已 知x
(1)
m
an
1
m
(a>0, m, n∈N*, 且n>1).
