几何证明题专项训练系列4
几何证明练习题带答案

几何证明练习题带答案一、选择题1. 已知三角形ABC中,AB=AC,点D在BC上,且BD=DC。
求证:∠BAD=∠CAD。
A. 利用等腰三角形性质B. 利用角平分线定理C. 利用等边三角形性质D. 利用相似三角形性质答案:B2. 已知线段AB和CD平行,且M是线段AB上的一点,N是线段CD上的一点,MN与AB、CD不平行。
求证:∠AMN≠∠CNM。
A. 利用平行线性质B. 利用内错角定理C. 利用同位角定理D. 利用补角定理答案:A二、填空题1. 在三角形ABC中,若∠A=90°,AB=AC,那么∠B=∠C=______。
答案:45°2. 已知三角形ABC中,AB=5,AC=7,BC=6,根据勾股定理可知这是一个______三角形。
答案:直角三、简答题1. 如何证明三角形内角和定理?答案:在三角形ABC中,延长BC至点D,根据外角定理,∠ACD=∠A+∠B。
又因为∠ACD+∠C=180°,所以∠A+∠B+∠C=180°,证明了三角形内角和为180°。
2. 如何证明圆内接四边形的对角互补?答案:设圆内接四边形ABCD,连接对角线AC和BD,由于AC和BD 都是圆的直径,根据圆周角定理,∠A+∠C=90°,∠B+∠D=90°。
因此,对角互补。
四、证明题1. 已知三角形ABC中,AB=AC,点D在BC上,且BD=DC。
证明∠BAD=∠CAD。
证明:由于AB=AC,根据等腰三角形性质,∠ABC=∠ACB。
又因为BD=DC,根据等边三角形性质,∠ABD=∠ACD。
因此,∠BAD=∠ABC-∠ABD=∠ACB-∠ACD=∠CAD。
2. 已知圆O中,弦AB和CD相交于点P,PA=PB,PC=PD。
证明:OP垂直于AB和CD。
证明:由于PA=PB,根据圆周角定理,∠APB=∠PBA。
同理,∠CPD=∠PDC。
因为∠APB+∠CPD=180°,所以∠OPB+∠OPD=90°。
八年级上册几何证明题

八年级上册几何证明题一、三角形内角和定理相关证明题。
1. 已知:在△ABC中,∠A = 50°,∠B = 60°,求证:∠C = 70°。
解析:根据三角形内角和定理,三角形内角和为180°。
在△ABC中,因为∠A+∠B +∠C=180°,已知∠A = 50°,∠B = 60°,所以∠C=180°∠A ∠B = 180°-50° 60° = 70°。
2. 如图,在△ABC中,AD是∠BAC的平分线,∠B = 70°,∠C = 30°,求∠ADC的度数。
解析:根据三角形内角和定理,在△ABC中,∠BAC=180°∠B ∠C = 180°-70° 30° = 80°。
因为AD是∠BAC的平分线,所以∠BAD = 1/2∠BAC = 40°。
在△ABD中,根据三角形外角性质,∠ADC = ∠B+∠BAD,所以∠ADC = 70°+40° = 110°。
二、等腰三角形性质证明题。
3. 已知:在等腰△ABC中,AB = AC,∠A = 80°,求∠B和∠C的度数。
解析:因为AB = AC,所以△ABC是等腰三角形,根据等腰三角形两底角相等的性质,设∠B =∠C=x。
根据三角形内角和定理,∠A+∠B +∠C = 180°,即80°+x + x = 180°,2x=180° 80°,2x = 100°,x = 50°,所以∠B =∠C = 50°。
4. 如图,在等腰三角形ABC中,AB = AC,BD⊥AC于点D,求证:∠CBD=(1)/(2)∠A。
解析:设∠A=x。
因为AB = AC,所以∠ABC =∠ACB=(1)/(2)(180° x)=90°-(x)/(2)。
第19章 几何证明(常考、易错必刷30题14种题型专项训练)(原卷版)

第19章几何证明(常考、易错必刷30题14种题型专项训练)一.平行线的判定与性质(共2小题)1.(2023春•浦东新区校级期末)若两条平行线被第三条直线所截,则下列说法错误的是( )A.一对同位角的平分线互相平行B.一对内错角的平分线互相平行C.一对同旁内角的平分线互相平行D.一对同旁内角的平分线互相垂直2.(2023秋•浦东新区期中)如图,点C,D在直线AB上,∠ACE+∠BDF=180°,EF∥AB.(1)求证:CE∥DF.(2)∠DFE的角平分线FG交AB于点G,过点F作FM⊥FG交CE的延长线于点M.若∠CMF=55°,再求∠CDF的度数.二.三角形内角和定理(共1小题)3.(2022秋•庐阳区校级月考)如图,BD,CE分别是△ABC的高线和角平分线,且相交于点O,若∠BCA =70°,则∠BOE的度数是( )A.60°B.55°C.50°D.40°三.直角三角形全等的判定(共1小题)4.(2021秋•徐汇区校级期末)下列条件中,不能判定两个直角三角形全等的是( )A.一锐角和斜边对应相等B.两条直角边对应相等C.斜边和一直角边对应相等D.两个锐角对应相等四.全等三角形的判定与性质(共5小题)5.(2023秋•闵行区期中)如图在△ABC中,AB=AC,BF=CD,BD=CE,∠FDE=70°,那么∠A= .6.(2023秋•浦东新区期中)如图,△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,且ED ⊥AB于点F,且AB=DE.(1)求证:BD=2EC;(2)若BD=10cm,求AC的长.7.(2022秋•杨浦区期中)如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC 于E,BF交AC于F,过点O作OD⊥BC于D,下列三个结论:①∠AOB=90°+∠C;②当∠C=60°=ab.其中正确的个数是( )时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S△ABCA.1个B.2个C.3个D.0个8.(2023秋•闵行区期中)如图,在△ABC中,AD平分∠BAC,E是BC的中点,过点E作FG⊥AD交AD的延长线于H,交AB于F,交AC的延长线于G.求证:(1)AF=AG;(2)BF=CG.9.(2022秋•静安区校级期中)如图,已知在△ABC中,AB=AC,点O是△ABC内部的一点,OD⊥AB,OE⊥AC,垂足分别为点D、E,且AD=AE.求证:OB=OC.五.角平分线的性质(共2小题)10.(2022秋•杨浦区期中)如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S=26,DE=△ABC 4,AB=7,则AC长是( )A.5B.6C.7D.811.(2022秋•黄浦区校级月考)如图,点P是∠BAC平分线AD上的一点,AC=9,AB=5,PB=3,则PC 的长不可能是( )A.4B.5C.6D.7六.线段垂直平分线的性质(共4小题)12.(2022秋•栾城区期末)如图所示,在△ABC中,AB的垂直平分线交AC于点E,若AE=,则BE 两点间的距离是( )A.B.C.D.13.(2022秋•杨浦区期末)如图,已知在等腰△ABC中,如果AB=AC,∠A=40°,DE是AB的垂直平分线,那么∠DBC= 度.14.(2022秋•翔安区期末)如图,在△ABC中,BC=AC,∠ACB=90°,D是AC上一点,AE⊥BD交BD 的延长线于点E,且AE=BD,求证:BD是∠ABC的角平分线.15.(2022秋•松江区校级月考)如图,△ABC中,BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=85°,则∠BDC= .七.等腰三角形的性质(共1小题)16.(2023秋•闵行区期中)如图,在Rt△ABC中,∠BAC=90°,D是BC上的一点,AD=AB.求证:∠BAD=2∠C.八.含30度角的直角三角形(共2小题)17.(2021秋•普陀区期末)如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于H,如果CH=AC,那么∠B= 度.18.(2022秋•杨浦区期末)已知,如图,在△ABC中,AD为BC边上的中线,且AD=BC,AE⊥BC.(1)求证:∠CAE=∠B;(2)若∠CAE=30°,CE=2,求AB的长.九.勾股定理(共3小题)19.(2023秋•宝山区校级月考)△ABC中,AB=13,AC=15,BC边上的高AD=12,则BC = .20.(2022秋•徐汇区期末)一个直角三角形两条直角边的比是3:4,斜边长为10cm,那么这个直角三角形面积为 .21.(2022秋•徐汇区期末)如图,在△ABC中,∠C=90°,AB=2BC,BD平分∠ABC,BD=2,则以下结论错误的是( )A.点D在AB的垂直平分线上B.点D到直线AB的距离为1C.点A到直线BD的距离为2D.点B到直线AC的距离为一十.勾股定理的证明(共2小题)22.(2022秋•宝山区期末)如图,直角三角形ACB,直角顶点C在直线l上,分别过点A、B作直线l的垂线,垂足分别为点D和点E.(1)求证:∠DAC=∠BCE;(2)如果AC=BC.①求证:CD=BE;②若设△ADC的三边分别为a、b、c,试用此图证明勾股定理.23.(2022秋•青浦区校级期末)在证明“勾股定理”时,可以将4个全等的直角三角形和一个小正方形拼成一个大正方形(如图所示,AB<BC).如果小正方形的面积是25,大正方形的面积为49,那么= .一十一.勾股定理的逆定理(共2小题)24.(2021秋•浦东新区期末)下列三个数为边长的三角形不是直角三角形的是( )A.3,3,3B.4,8,4C.6,8,10D.5,5,525.(2022秋•青浦区校级期末)如图,在△ABC中,AB=AC,点D为AB上一点,联结CD,BD=5,DC =12,BC=13,则AB= .一十二.勾股定理的应用(共1小题)26.(2022秋•宝山区校级期末)如图是一块四边形绿地的示意图,其中AB=24,BC=15,CD=20,DA=7,∠C=90°.求此绿地ABCD的面积.一十三.命题与定理(共2小题)27.(2023秋•闵行区期中)下列命题中是真命题的是( )A.有两边和其中一边的对角对应相等的两个三角形全等B.两条平行直线被第三条直线所截,则一组同旁内角的平分线互相垂直C.三角形的一个外角等于两个内角的和D.等边三角形既是中心对称图形,又是轴对称图形28.(2023秋•普陀区期中)将命题“等角对等边”改写成“如果…,那么…”的形式: .一十四.轨迹(共2小题)29.(2022秋•徐汇区期末)到点P的距离等于4cm的点的轨迹是 .30.(2022秋•杨浦区期末)经过定点A且半径为2cm的圆的圆心的轨迹是 .。
初中几何证明练习题含答案
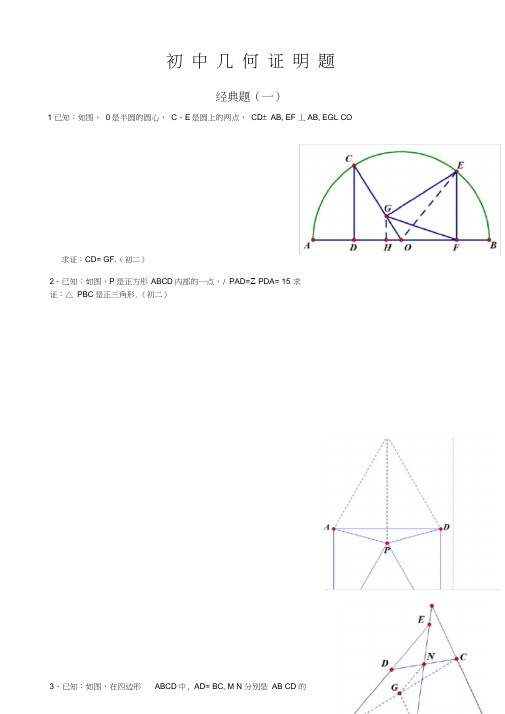
初中几何证明题经典题(一)1 已知:如图,0是半圆的圆心,C、E是圆上的两点,CD± AB, EF丄AB, EGL CO求证:CD= GF.(初二)2、已知:如图,P是正方形ABCD内部的一点,/ PAD=Z PDA= 15 求证:△ PBC是正三角形.(初二)3、已知:如图,在四边形ABCD中, AD= BC, M N 分别是AB CD 的中点,AD BC的延长线交MN于E、F.求/ DEN=Z F.证:经典题(二)1 已知:△ ABC中,H为垂心(各边高线的交点),0为外心,且OM L BC于M(1)求证:AH= 20M(2)若/ BAC= 600,求证:AH= AO (初二)2、设MN是圆O外一条直线,过0作OAL MN于A,自A引圆的两条割线交圆0于B、C及D、E,连接CD并延长交MN于Q,连接EB并延长交MN于P.求证:AP= AQ3、如图,分别以△ ABC的AB和AC为一边,在厶ABC的外侧作正方形ABFG和正方形ACDE点0是DF的中点,OPL BC求证:BC=20P(初二)L、MN证明:分别过F、A D作直线BC的垂线,垂足分别是•/ OF=OD DIN/ OP// FL••• PN=PL••• OP是梯形DFLN的中位线• DN+FL=2OP•/ ABFG是正方形•••/ ABM丄FBL=90°又/ BFL+Z FBL=90°•••/ ABM2 BFL又/ FLB=Z BMA=90 , BF=AB•△BFL^A ABM• FL=BM同理△ AMC^A CND• CM=DN• BM+CN=FL+DN• BC=FL+DN=2OP经典题(二)1如图,四边形ABCD为正方形, 于F .求证:CE= CF.(初二)DE// AC, AE= AC, AE 与CD相交证明:连接 BD 交AC 于0。
过点E 作EGL AC 于G •/ ABCD 是正方形 ••• BD L AC 又 EGL AC ••• BD// EG 又 DE// AC • 0DEG 是平行四边形 又/ COD=90 • 0DEG1矩形1 1 1 • EG=OD= BD=丄 AC )AE222• / EAG=30 •/ AC=AE• / ACE 玄 AEC=75 又/ AFD=90 -15 ° =75° • / CFE=/ AFD=75 =Z AEC • CE=CF• AE=AF3、设P 是正方形 求证:PA = PF.证明:过点F 作FGL CE 于G, ••• CD L CG ,. HCGF 是矩形•••/ HCF 玄 GCF\ FH=FG • HCGF 是正方形 •CG=GF -AP L FP• / APB+/ FPG=90 -/ APB+/ BAP=90° • / FPG 玄 BAP 又/ FGP 玄 PBA• △ FGP^A PBA 设 AB=x , BP=y , CG=z z : y= (x-y+z ): x 化简得(x-y )• y = (x-y )-x-y 丰 0• y=z 即 BP=FG • △ ABP ^^ PGF2、如图,四边形 ABCD 为正方形,DE// AC 且CE= CA 直线EC 交DA 延长线于F . 求证:AE = AF.(初二) 证明:连接BD,过点E 作EGL AC 于G •/ ABCD 是正方形 • B D L AC,又 EGL AC • B D// EG 又 DE// AC • ODEG!平行四边形 又/ COD=90 • ODEG !矩形 o-/ FAC-/ ACF o1• / CAE / CEA 「/ GCE=152在厶AFC 中/ F =180• EG =OD =丄 BD=! AC 」CE 2 22• / GCE=30 =180 =180 • / F=/ CEA-/ FAC-/ GCE-135 ° -30 ° =15•/ AC=EC ABC [一边BC 上的任一点, PF L AP, CF 平分/ DCE (初二)FH 丄 CD 于 H••• FG: PB=PG AB4、如图,PC 切圆O 于C , AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于 B D. 求证:AB= DC, BC = AD.(初三)..—../证明:过点 E 作EK// BD,分别交 连接OH MH EC •/ EH=FH• OHL EF ,「./ PHO=90 又 PC L OC POC=90• P 、C H O 四点共圆 •••/ HCO M HPO 又 EK// BD HPO M HEK• / HCM N HEM • H C E 、M 四点共圆 • / ECM M EHM 又/ ECM M EFA • / EHM M EFA • HIM/ AC •/ EH=FH经典题(四)1已知:△ ABC 是正三角形,P 是三角形内一点, PA = 3, 求/ APB 的度数.(初二)解:将△ ABP 绕点B 顺时针方向旋转 60°得厶BCQ 连接 则厶BPQ 是正三角形• / BQP=60 , PQ=PB=3在厶 PQC 中, PQ=4, CQ=AP=3 PC=5 • △ PQC 是直角三角形 • / PQC=90• / BQC 2 BQP+Z PQC=60 +90° =150 °• / APB=/ BQC=150 2、设P 是平行四边形 ABCD 内部的一点,且/ PBA=/ PDA求证:/ PAB=/ PCB (初二) 证明:过点P 作AD 的平行线,过点 两平行线相交于点 E ,连接BE•/ PE// AD, AE// PD • ADPE 是平行四边形 • PE=AD又ABCD 是平行四边形 • AD=BC \• PE=BC又 PE// AD AD// BC \• PE// BC• BCPE 是平行四边形 ; • / BEP=/ PCB ••• ADPE 是平行四边形; AC AF 于M K ,取EF 的中点H,1• EM=KM I•/ EK// BD\ • OB竺EM AM KM•OB=ODI又 AO=CO•四边形ABCD 的对角线 ;互相平分•ABCD 是平行四边又/ ADP 玄 ABP •/ AEP=Z ABP • A 、E 、B 、P 四点共圆 •/ BEP=Z PABC•/ ADP玄AEP '3、设ABCD 为圆内接凸四边形,求证: AB- CD+ AD- BC = AC- BD.(初三) 证明:在 BD 上去一点 E ,使/ BCE=/ ACD •/ CD=CD •••/ CAD 2 CBD• B£ BC _AD AC• AD- BC=BE- ACBCE 玄 ACDBCE+Z ACE=/ ACD y ACEBCA=/ ECD • AB AC"DE CD• AB- CD=DE AC4、平行四边形 ABCC 中,设E 、F 分别是BC AB 上的一点,AE 与CF 相交于P,且AE = CF.求证:/ DPA=Z DPC (初二)证明:过点 D 作DGL AE 于G 作DH1 FC 于H,连接DF 、 1 1• S A ADE =2AE • DG S A FDc FqFC • DH 又 AE=CF • DG=DH•••点D 在/ APC 的角平分线上•••/ DPA=Z DPC经典题(五)证明:(1)将厶BPC 绕B 点顺时针旋转60°的厶BEF 连接 •/ BP=BE / PBE=60 • △ PBE 是正三角形。
平行线与相交线几何证明题专项训练及答案

平行线与相交线几何证明题专项训练及答案证明题1:平行线与等角线的性质问题描述在平面内给出一组平行线和一条相交线,证明以下性质:如果该相交线与任意一条平行线均成相等角,则该相交线与其它平行线也成相等角。
证明过程已知条件设给出的平行线为l1 和 l2,给出的相交线为l3。
根据已知条件,相交线l3与平行线l1成相等角,即∠A = ∠D(角度A在l1上,角度D在l3上)。
证明目标要证明相交线l3与平行线l2成相等角,即∠B = ∠E(角度B在l2上,角度E在l3上)。
证明过程1.假设相交线l3与平行线l2不成相等角,即∠B ≠ ∠E。
2.在l2上取一点F,并作垂线FG与l1相交于G点。
3.连接点E和G,并延长线段EG与l1和l2相交于H 点。
4.根据平行线的性质,得到∠D = ∠F(对应角相等)和∠A = ∠G(同旁内角相等)。
5.在△DGF和△AEG中,根据三角形内角和定理,得到∠D + ∠F + ∠G = 180°和∠A + ∠E + ∠G = 180°。
6.结合前述结果,得到∠D + ∠F = ∠A + ∠E。
7.根据已知条件,得到∠A = ∠D。
8.结合步骤6和7的结果,得到∠F = ∠E。
9.根据角度相等的定义,得到∠B = ∠E,即相交线l3与平行线l2也成相等角,证明完毕。
答案根据以上证明过程,可以得出结论:如果相交线与一组平行线成等角,那么相交线与其它平行线也成等角。
证明题2:平行线的封闭性问题描述在平面内给出一组平行线,证明以下性质:如果两条平行线的一个夹角与另外一条平行线的一个角相等,则这两条平行线也相等。
证明过程已知条件设给出的平行线为l1 和 l2,给出的夹角为∠A(角度A在l1和l2之间)。
根据已知条件,∠A = ∠B(角度B在l1和另外一条平行线l3之间)。
证明目标要证明l1 = l2,即两条平行线相等。
证明过程1.假设l1 ≠ l2,即l1和l2不相等。
八年级几何证明专题训练(50题)
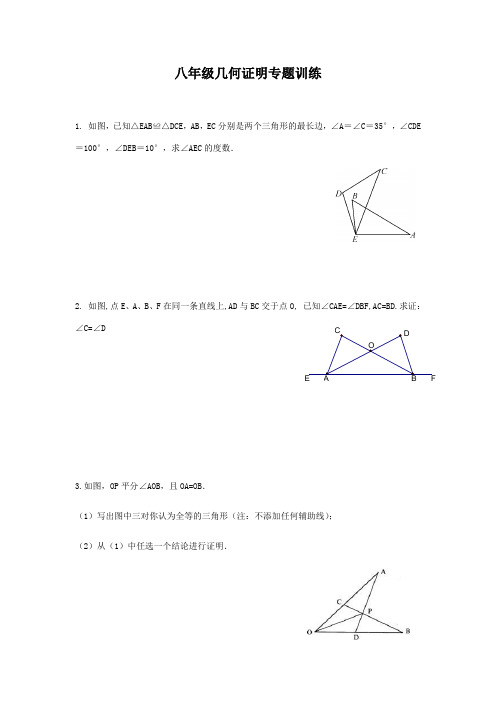
(2) 当取何值时, 与 全等.
38. 如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点 重合,AE为折痕,求 的长度
39. 如图,已知ΔABC是等腰直角三角形,∠C=90°.
(1)操作并观察,如图,将三角板的45°角的顶点与点C重合,使这个角落在∠ACB的内部,两边分别与斜边AB交于E、F两点,然后将这个角绕着点C在∠ACB的内部旋转,观察在点E、F的位置发生变化时,AE、EF、FB中最长线段是否始终是EF写出观察结果.
源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯网wwwzxxkcom源户卷件材源载丰讯
(3)试探索CF、GF和BG之间的等量关系,并证明你的结论.
28. 如图,在在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一单,点E在BC上,且AE=CF。
(1)求证:
(2)若∠CAE=30°,求∠ACF的度数
29. 如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE,AE于点G、H. 试猜测线段AE和BD数量关系,并说明理由.
(2)求证:CF=EF.
36.在 中, 平分 ,点 为直线 上一动点, 于点 .
(1)如图1 ,当 , ,点 与点 重合时,求 的度数;
(2)如图2,当点 在 延长线时, 求证: ;
[必刷题]2024七年级数学下册几何证明专项专题训练(含答案)
![[必刷题]2024七年级数学下册几何证明专项专题训练(含答案)](https://img.taocdn.com/s3/m/e2aed845c4da50e2524de518964bcf84b8d52d05.png)
[必刷题]2024七年级数学下册几何证明专项专题训练(含答案)试题部分一、选择题:1. 在下列几何图形中,哪一个图形可以通过旋转90度后与自身重合?()A. 矩形B. 等边三角形C. 正方形D. 梯形2. 下列哪个条件可以证明两个三角形全等?()A. 两边和其中一边的对角相等B. 两角和其中一角的对边相等C. 两边和它们的夹角相等D. 两角和其中一边相等3. 在直角坐标系中,点A(2,3)关于原点对称的点是()A. (2,3)B. (2,3)C. (2,3)D. (3,2)4. 下列哪个条件可以证明两个角相等?()A. 两角的度数相等B. 两角的对边相等C. 两角的邻边相等D. 两角的余角相等5. 若一个等腰三角形的底边长为10cm,腰长为13cm,则该三角形的周长为()A. 32cmB. 42cmC. 46cmD. 52cm6. 在平行四边形ABCD中,若AB=6cm,BC=8cm,则对角线AC的取值范围是()A. 2cm < AC < 14cmB. 2cm < AC < 6cmC. 2cm < AC < 8cmD. 6cm < AC < 14cm7. 下列哪个条件可以证明两个平行四边形全等?()A. 一组对边平行且相等B. 两组对边平行C. 一组对边平行,另一组对边相等D. 一组对边平行且相等,另一组对边也相等8. 在三角形ABC中,若AB=AC,∠B=60°,则三角形ABC的周角为()A. 120°B. 180°C. 240°D. 360°9. 下列哪个图形是轴对称图形?()A. 等腰梯形B. 直角梯形C. 等腰三角形D. 一般四边形10. 若一个正方形的对角线长为10cm,则该正方形的面积是()A. 50cm²B. 100cm²C. 200cm²D. 500cm²二、判断题:1. 若两个三角形的两边和夹角分别相等,则这两个三角形全等。
初中经典几何证明练习题(含答案)
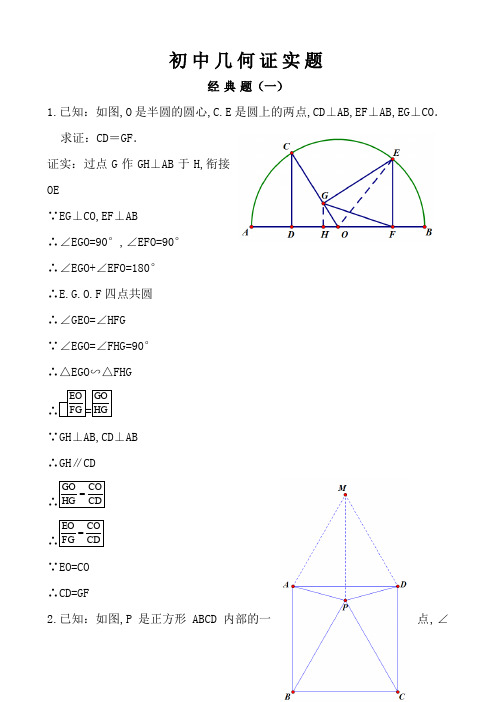
初中几何证实题经典题(一)1.已知:如图,O 是半圆的圆心,C.E 是圆上的两点,CD ⊥AB,EF ⊥AB,EG ⊥CO . 求证:CD =GF .证实:过点G 作GH ⊥AB 于H,衔接OE∵EG ⊥CO,EF ⊥AB∴∠EGO=90°,∠EFO=90°∴∠EGO+∠EFO=180°∴E.G.O.F 四点共圆∴∠GEO=∠HFG∵∠EGO=∠FHG=90°∴△EGO ∽△FHG ∴FG EO =HG GO∵GH ⊥AB,CD ⊥AB∴GH ∥CD∴CD CO HG GO = ∴CD CO FG EO = ∵EO=CO∴CD=GF2.已知:如图,P 是正方形ABCD 内部的一点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)证实:作正三角形ADM,衔接MP∵∠MAD=60°,∠PAD=15°∴∠MAP=∠MAD+∠PAD=75°∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75°∴∠BAP=∠MAP∵MA=BA,AP=AP∴△MAP≌△BAP∴∠BPA=∠MPA,MP=BP同理∠CPD=∠MPD,MP=CP∵∠PAD=∠PDA=15°∴PA=PD,∠BAP=∠CDP=75°∵BA=CD∴△BAP≌∠CDP∴∠BPA=∠CPD∵∠BPA=∠MPA,∠CPD=∠MPD∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP,MP=CP ∴BP=CP ∴△BPC是正三角形3.已知:如图,在四边形ABCD中,AD=BC,M.N分离是AB.CD的中点,AD.BC的延伸线交MN于E.F.求证:∠DEN =∠F .证实:衔接AC,取AC 的中点G,衔接NG.MG∵CN=DN,CG=DG∴GN ∥AD,GN=21AD∴∠DEN=∠GNM∵AM=BM,AG=CG∴GM ∥BC,GM=21BC∴∠F=∠GMN∵AD=BC∴GN=GM∴∠GMN=∠GNM∴∠DEN=∠F经典题(二)1.已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM;(2)若∠BAC =600,求证:AH =AO .(初二)证实:(1)延伸AD 交圆于F,衔接BF,过点O作OG ⊥AD 于G∵OG ⊥AF∴AG=FG∵AB ⌒ =AB ⌒∴∠F=∠ACB又AD ⊥BC,BE ⊥AC∴∠BHD+∠DBH=90°∠ACB+∠DBH=90°∴∠ACB=∠BHD∴∠F=∠BHD∴BH=BF 又AD ⊥BC∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD又AD ⊥BC,OM ⊥BC,OG ⊥AD∴四边形OMDG 是矩形∴OM=GD ∴AH=2OM(2)衔接OB.OC∵∠BAC=60∴∠BOC=120°∵OB=OC,OM ⊥BC∴∠BOM=21∠BOC=60°∴∠OBM=30°∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2.设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A,自A 引圆的两条割线交圆O 于B.C 及D.E,衔接CD 并延伸交MN 于Q,衔接EB 并延伸交MN 于P. 求证:AP =AQ .证实:作点E 关于AG 的对称点F,衔接AF.CF.QF∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF即∠PAE=∠QAF∵E.F.C.D 四点共圆∴∠AEF+∠FCQ=180°∵EF ⊥AG,PQ ⊥AG∴EF ∥PQ∴∠PAF=∠AFE∵AF=AE∴∠AFE=∠AEF∴∠AEF=∠PAF∵∠PAF+∠QAF=180°∴∠FCQ=∠QAF∴F.C.A.Q 四点共圆∴∠AFQ=∠ACQ又∠AEP=∠ACQ∴∠AFQ=∠AEP3.设MN 是圆O 的弦,过MN 的中点A 任作两弦BC.DE,设CD.EB 分离交MN 于P.Q .求证:AP =AQ .(初二)证实:作OF ⊥CD 于F,OG ⊥BE 于G,衔接OP.OQ.OA.AF.AG∵C.D.B.E 四点共圆∴∠B=∠D,∠E=∠C∴△ABE ∽△ADC 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ∴DF BG FD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF∴∠AGB=∠AFD∴∠AGE=∠AFC∵AM=AN,∴OA ⊥MN又OG ⊥BE,∴∠OAQ+∠OGQ=180°∴O.A.Q.E 四点共圆∴∠AOQ=∠AGE同理∠AOP=∠AFC∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA∴△OAQ ≌△OAP∴AP=AQ4.如图,分离以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证实:分离过F.A.D 作直线BC 的垂线,垂足分离是L.M.N∵OF=OD,DN ∥OP ∥FL∴PN=PL∴OP 是梯形DFLN 的中位线∴DN+FL=2OP∵ABFG 是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB∴△BFL ≌△ABM∴FL=BM同理△AMC ≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题(三)1.如图,四边形ABCD 为正方形,DE ∥AC,AE =AC,AE 与CD 订交于F . 求证:CE =CF .(初二)证实:衔接BD 交AC 于O.过点E 作EG ⊥AC于G∵ABCD 是正方形∴BD ⊥AC 又EG ⊥AC∴BD ∥EG 又DE ∥AC∴ODEG 是平行四边形又∠COD=90°∴ODEG 是矩形∴EG=OD=21BD=21AC=21AE∴∠EAG=30°∵AC=AE∴∠ACE=∠AEC=75°又∠AFD=90°-15°=75°∴∠CFE=∠AFD=75°=∠AEC∴CE=CF2.如图,四边形ABCD 为正方形,DE ∥AC,且CE =CA,直线EC 交DA 延伸线于F .求证:AE =AF .(初二)证实:衔接BD,过点E 作EG ⊥AC 于G∵ABCD 是正方形∴BD ⊥AC,又EG ⊥AC∴BD ∥EG 又DE ∥AC∴ODEG 是平行四边形又∠COD=90°∴ODEG 是矩形∴EG =OD =21BD=21AC=21CE∴∠GCE=30°∵AC=EC3.设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP,CF 等分∠DCE . 求证:PA =PF .(初二)证实:过点F 作FG ⊥CE 于G,FH ⊥CD 于H∵CD ⊥CG ∴HCGF 是矩形∴∠CAE=∠CEA=21∠GCE=15° 在△AFC 中∠F =180°-∠FAC-∠ACF =180°-∠FAC-∠GCE =180°-135°-30°=15° ∴∠F=∠CEA ∴AE=AF∵∠HCF=∠GCF ∴FH=FG∴HCGF 是正方形∴CG=GF∵AP ⊥FP∴∠APB+∠FPG=90°∵∠APB+∠BAP=90°∴∠FPG=∠BAP又∠FGP=∠PBA∴△FGP ∽△PBA∴FG :PB=PG :AB4.如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE.AF 与直线PO 订交于B.D .求证:AB =DC,BC =AD .(初三)证实:过点E 作EK ∥BD,分离交AC.AF 于M.K,取EF 的中点H,衔接OH.MH.EC∵EH=FH∴OH ⊥EF,∴∠PHO=90°又PC ⊥OC,∴∠POC=90°∴P.C.H.O 四点共圆∴∠HCO=∠HPO又EK ∥BD,∴∠HPO=∠HEK∴∠HCM=∠HEM∴H.C.E.M 四点共圆 设AB=x ,BP=y ,CG=z z :y=(x-y+z ):x 化简得(x-y )·y =(x-y )·z ∵x-y ≠0 ∴y=z 即BP=FG ∴△ABP ≌△PGF ∴EM=KM ∵EK ∥BD ∴KM OD AM AO EM OB == ∴OB=OD 又AO=CO ∴四边形ABCD 的对角线互相等分 ∴ABCD 是平行四边形B ∴∠ECM=∠EHM又∠ECM=∠EFA∴∠EHM=∠EFA∴HM ∥AC∵EH=FH经典题(四)1.已知:△ABC 是正三角形,P 是三角形内一点求∠APB 的度数.(初二)解:将△ABP 绕点B 顺时针偏向扭转60°得△则△BPQ 是正三角形∴∠BQP=60°,PQ=PB=3在△PQC 中,PQ=4,CQ=AP=3,PC=5∴△PQC 是直角三角形∴∠PQC=90°∴∠BQC=∠BQP+∠PQC=60°+90°=150°∴∠APB=∠BQC=150°2.设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二) 证实:过点P 作AD 的平行线,两平行线订交于点E,衔接BE∵PE ∥AD,AE ∥PD∴ADPE 是平行四边形∴PE=AD,又ABCD 是平行四边形 ∴AD=BC ∴PE=BC又PE ∥AD,AD ∥BC ∴PE ∥BC∴BCPE 是平行四边形 ∴∠BEP=∠PCB ∵ADPE 是平行四边形 ∴∠ADP=∠AEP3.设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三) 证实:在BD 上去一点E,使∠BCE=∠ACD ∵CD ⌒ =CD⌒ ∴∠CAD=∠CBD ∴△BEC ∽△ADC∴AD ·BC=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BCA=∠ECD∵BC ⌒=BC ⌒,∴∠BAC=∠BDC △BAC ∽△EDC∴AB ·CD=DE ·AC ……………………②又∠ADP=∠ABP∴∠AEP=∠ABP ∴A.E.B.P 四点共圆 ∴∠BEP=∠PAB ∴∠PAB=∠PCB①+②得AB ·CD+ AD ·BC =DE ·AC+ BE ·AC=(DE+BE )·AC =BD ·AC4.平行四边形ABCD 中,设E.F 分离是BC.AB 上的一点,AE 与CF 订交于P,且AE =CF .求证:∠DPA =∠DPC .(初二)证实:过点D 作DG ⊥AE 于G,作DH ⊥FC 于∴S △ADE =12AE ·DG,S △FDC =12FC ·DH又S △ADE =S △FDC =12S □ABCD∴AE ·DG=FC ·DH 又AE=CF ∴DG=DH∴点D 在∠APC 的角等分线上 ∴∠DPA =∠DPC经典题(五)1.设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC,L <2. 证实:(1)将△BPC 绕B 点顺时针扭转60°的△BEF,衔接PE,∵BP=BE,∠PBE=60° ∴△PBE 是正三角形.∴PE=PB 又EF=PC ∴L=PA+PB+PC=PA+PE+EF当PA.PE.EF 在一条直线上的时刻,L=PA+PE+EF 在△ABF 中,∠ABP=120°∴∴L=PA+PB+PC (2)过点P 作BC 的平行线分离交AB.AC 于D.G 则△ADG 是正三角形BGB∴∠ADP=∠AGP,AG=DG ∵∠APD >∠AGP ∴∠APD >∠ADP∴AD >PA …………………………① 又BD+PD >PB ……………………② CG+PG >PC ……………………③ ①+②+③得AD+BD+CG+PD+PG >PA+PB+PC ∴AB+CG+DG=AB+CG+AG=AB+AC >PA+PB+PC=L ∵AB=AC=1∴L <2由(1)(2L <2.2.已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB 解:将△BCP 绕点B 顺时针扭转60°得△BEF,衔接PE, 则△BPE 是正三角形 ∴PE=PB∴PA +PB +PC=PA+PE+EF∴要使PA +PB +PC 最小,则PA.PE.EF 此时AF=PA+PE+EF过点F 作FG ⊥AB 的延伸线于G则∠GBF=180°-∠ABF=180°-150°=30° ∴GF=12,BG=∴C∴PA +PB +PC3.P 为正方形ABCD 内的一点,并且PA =a,PB =2a,PC =3a,求正方形的边长.证实:将△ABP 绕点B 顺时针扭转90°得△BCQ,则△BPQ 是等腰直角三角形, ∴又QC=AP=a∴QP 2+QC 22+a 2=9a 2=PC 2∴△PQC 是直角三角形 ∴∠BQC=135°∵BC 2=BQ 2+CQ 2-2BQ ·CQ ·cos ∠BQC =PB 2+PA 2-2PB ·PAcos135° =4a 2+a 2-2×2a ×a ×解得4.如图,△ABC 中,∠ABC =∠ACB =80°,D.E 分离是AB.AC 上的点,∠DCA =30°,∠EBA =20°,求∠BED 的度数.解:在AB 上取一点F,使∠BCF=60°,CF 交BE 于G,衔接∵∠ABC=80°,∠ABE=20°,∴∠EBC=60°,又∠BCG=60° ∴△BCG 是正三角形∴BG=BC∵∠ACB=80°,∠BCG=60°∴∠FCA=20°∴∠EBA=∠FCA 又∵∠A=∠A,AB=AC ∴△ABE ≌ACF ∴AE=AF ∴∠AFE=∠AEF=12(180°-∠A )=80°又∵∠ABC=80°=∠AFE ∴EF ∥BC ∴∠EFG=∠BCG=60° ∴△EFG 是等边三角形∴EF=EG,∠FEG=∠EGF=∠EFG=60° ∵ACB=80°,∠DCA=30°∴∠BCD=50°∴∠BDC=180°-∠BCD-∠ABC=180°-50°-80°=50° ∴∠BCD=∠BDC ∴BC=BD 前已证BG=BC ∴BD=BG ∠BGD=∠BDG=12(180°-∠ABE )=80°∴∠FGD=180°-∠BGD-∠EGF=180°-80°-60°=40° 又∠DFG=180°-∠AFE-∠EFG=180°-80°-60°=40° ∴∠FGD=∠DFG ∴DF=DG 又EF=EG,DE=DE ∴△EFD ≌△EGD ∴∠BED=∠FED=12∠FEG=12×60°=30°5.如图,△ABC 内接于⊙O,且AB 为⊙O 的直径,∠ACB 的等分线交⊙O 于点D,过点D 作⊙O 的切线PD 交CA 的延伸线于点P,过点A 作AE ⊥CD 于点E,过点B 作BF ⊥CD 于点F,若AC=6,BC=8,求线段PD 的长. 解:∵∠ACD=∠BCD ∴AD ⌒=BD ⌒∴AD=BD ∵AB 为⊙O 的直径∴∠ADB=90° ∴△ABD 是等腰直角三角形∵∠ACB=90°,AC=6,BC=8 ∴AB=10 ∴AD=AB ·cos ∠DAB=10×22=52又AE ⊥CD,∠ACD=45°∴△ACE 是等腰直角三角形∴CE=AE=AC ·cos ∠CAE=6×22=32在△ADE 中,DE 2=AD 2-AE 2∴DE2=32232522 )()(-∴DE=24∴∵∠PDA=∠PCD,∠P=∠P ∴△PDA∽△PCD∴∵PC=PA+AC解得。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明题专项训练系列4
1、已知在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.
(1)求证:CD=BE;
(2)若AD=3,DC=4,求AE.
2、如图,在梯形ABCD中,AD∥BC,AB⊥AC,∠B=45°,AD=1,BC=4,求DC的长.
3、已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且.
(1)求证:BF=EF﹣ED;
(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.
4、如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,且AF⊥AB,连接EF.
(1)若EF⊥AF,AF=4,AB=6,求AE的长.
(2)若点F是CD的中点,求证:CE=BE﹣AD.
5、如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.(1)求证:DH=(AD+BC);
(2)若AC=6,求梯形ABCD的面积.
6、已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE,BD.
(1)求证:△AGE≌△DAB;
(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.
7、如图,梯形ABCD中,AD∥BC,DE=EC,EF∥AB交BC于点F,EF=EC,连接DF.
(1)试说明梯形ABCD是等腰梯形;
(2)若AD=1,BC=3,DC=,试判断△DCF的形状;
(3)在条件(2)下,射线BC上是否存在一点P,使△PCD是等腰三角形,若存在,请直接写出PB的长;若不存在,请说明理由.
8、如图,在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,AD=DC,E、F分别在AD、DC的延长线上,且DE=CF.AF交BE于P.
(1)证明:△ABE≌△DAF;
(2)求∠BPF的度数.
几何证明题专项训练系列4
参考答案
1、如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.
(1)求证:CD=BE;
(2)若AD=3,DC=4,求AE.
(1)证明:∵AD∥BC,
∴∠DAC=∠BCE,而BE⊥AC,
∴∠D=∠BEC=90°,AC=BC,
∴△BCE≌△CAD.
∴CD=BE.
(2)解:在Rt△ADC中,根据勾股定理得AC==5,
∵△BCE≌△CAD,
∴CE=AD=3.
∴AE=AC﹣CE=2.
2、如图,在梯形ABCD中,AD∥BC,AB⊥AC,∠B=45°,AD=1,BC=4,求DC的长.
解:如图,过点D作DF∥AB,分别交AC,BC于点E,F.(1分)
∵AB⊥AC,
∴∠AED=∠BAC=90度.
∵AD∥BC,
∴∠DAE=180°﹣∠B﹣∠BAC=45度.
在Rt△ABC中,∠BAC=90°,∠B=45°,BC=4,∴AC=BC•sin45°=4×=2(2分)
在Rt△ADE中,∠AED=90°,∠DAE=45°,AD=1,∴DE=AE=.∴CE=AC﹣AE=.(4分)在Rt△DEC中,∠CED=90°,∴DC==.(5分)
3、已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且.
(1)求证:BF=EF﹣ED;
(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.
证明:∵FC=F′C,EC=EC,∠ECF'=∠BCF+∠DCE=∠ECF,
∴△FCE≌△F′CE,
∴EF′=EF=DF′+ED,
∴BF=EF﹣ED;
(2)解:∵AB=BC,∠B=80°,
∴∠ACB=50°,
由(1)得∠FEC=∠DEC=70°,
∴∠ECB=70°,
而∠B=∠BCD=80°,
∴∠DCE=10°,
∴∠BCF=30°,
∴∠ACF=∠BCA﹣∠BCF=20°.
4、如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,且AF⊥AB,连接EF.
(1)若EF⊥AF,AF=4,AB=6,求AE的长.
(2)若点F是CD的中点,求证:CE=BE﹣AD.
解:(1)作EM⊥AB,交AB于点M.∵AE=BE,EM⊥AB,
∴AM=BM=×6=3;
∵∠AME=∠MAF=∠AFE=90°,
∴四边形AMEF是矩形,
∴EF=AM=3;
在Rt△AFE中,AE==5;
(2)延长AF、BC交于点N.
∵AD∥EN,
∴∠DAF=∠N;
∵∠AFD=∠NFC,DF=FC,
∴△ADF≌△NCF(AAS),
∴AD=CN;
∵∠B+∠N=90°,∠BAE+∠EAN=90°,
又AE=BE,∠B=∠BAE,
∴∠N=∠EAN,AE=EN,
∴BE=EN=EC+CN=EC+AD,
∴CE=BE﹣AD.
5、如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.(1)求证:DH=(AD+BC);
(2)若AC=6,求梯形ABCD的面积.
解:(1)证明:过D作DE∥AC交BC延长线于E,(1分)
∵AD∥BC,
∴四边形ACED为平行四边形.(2分)
∴CE=AD,DE=AC.
∵四边形ABCD为等腰梯形,
∴BD=AC=DE.
∵AC⊥BD,
∴DE⊥BD.
∴△DBE为等腰直角三角形.(4分)
∵DH⊥BC,
∴DH=BE=(CE+BC)=(AD+BC).(5分)
(2)∵AD=CE,
∴.(7分)
∵△DBE为等腰直角三角形BD=DE=6,
∴.
∴梯形ABCD的面积为18.(8分)
注:此题解题方法并不唯一.
6、已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE,BD.
(1)求证:△AGE≌△DAB;
(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.
(1)证明:∵△ABC是等边三角形,DG∥BC,
∴∠AGD=∠ABC=60°,∠ADG=∠ACB=60°,且∠BAC=60°,
∴△AGD是等边三角形,
AG=GD=AD,∠AGD=60°.
∵DE=DC,∴GE=GD+DE=AD+DC=AC=AB,
∵∠AGD=∠BAD,AG=AD,
∴△AGE≌△DAB;
(2)解:由(1)知AE=BD,∠ABD=∠AEG.
∵EF∥DB,DG∥BC,
∴四边形BFED是平行四边形.
∴EF=BD,
∴EF=AE.
∵∠DBC=∠DEF,
∴∠ABD+∠DBC=∠AEG+∠DEF,即∠AEF=∠ABC=60°.
∴△AFE是等边三角形,∠AFE=60°.
7、如图,梯形ABCD中,AD∥BC,DE=EC,EF∥AB交BC于点F,EF=EC,连接DF.
(1)试说明梯形ABCD是等腰梯形;
(2)若AD=1,BC=3,DC=,试判断△DCF的形状;
(3)在条件(2)下,射线BC上是否存在一点P,使△PCD是等腰三角形,若存在,请直接写出PB的长;若不存在,请说明理由.
解:(1)证明:∵EF=EC,
∴∠EFC=∠ECF,
∵EF∥AB,
∴∠B=∠EFC,
∴∠B=∠ECF,∴梯形ABCD是等腰梯形;
(2)△DCF是等腰直角三角形,
证明:∵DE=EC,EF=EC,∴EF=CD,
∴△CDF是直角三角形(如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形),∵梯形ABCD是等腰梯形,
∴CF=(BC﹣AD)=1,
∵DC=,
∴由勾股定理得:DF=1,
∴△DCF是等腰直角三角形;
(3)共四种情况:
∵DF⊥BC,
∴当PF=CF时,△PCD是等腰三角形,
即PF=1,
∴PB=1;
当P与F重合时,△PCD是等腰三角形,
∴PB=2;
当PC=CD=(P在点C的左侧)时,△PCD是等腰三角形,
∴PB=3﹣;
当PC=CD=(P在点C的右侧)时,△PCD是等腰三角形,
∴PB=3+.
故共四种情况:PB=1,PB=2,PB=3﹣,PB=3+.(每个1分)
8、如图,在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,AD=DC,E、F分别在AD、DC的延长线上,且DE=CF.AF交BE于P.
(1)证明:△ABE≌△DAF;
(2)求∠BPF的度数.
解答:(1)证明:∵在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,
∴AB=CD,
∵AD=DC,
∴BA=AD,∠BAE=∠ADF=120°,
∵DE=CF,
∴AE=DF,
在△BAE和△ADF中,
,
∴△ABE≌△DAF(SAS).
(2)解:∵由(1)△BAE≌△ADF,
∴∠ABE=∠DAF.
∴∠BPF=∠ABE+∠BAP=∠BAE.
而AD∥BC,∠C=∠ABC=60°,
∴∠BPF=120°.。
