第十七届华罗庚金杯少年数学邀请赛初一决赛B试卷答案及其详细解析
第十七届华杯赛决赛初一笔试A答案

第十七届华罗庚金杯少年数学邀请赛决赛笔试试题A 参考答案(初一组)一、填空(每题 10 分, 共80分)一、填空题(每小题 10分, 共80分)1. 计算:=-⨯-+⎪⎭⎫⎝⎛-⨯-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--÷---⨯-)]21(31[81221|10|)1()2(22334 . 原式=43210219122--⨯++=31226-⨯=4216-=-2. 一串有规律排列的数, 从第二项起每一项都等于1加前一项的倒数之和.当第五项是0时, 第一项是 .分析:设这列数从第一项起依次为12345,,,,a a a a a 根据题意4101a =+,可以得出41a =-。
倒推可以得到135a =-3. 如图, AB=BC=CA=AD , 则∠BDC= .解:设AC 与BD 的交点是E∵AB=BC=CA=AD∴△ABC 是正三角形,每个内角为600,△ABD 和△ACD 是等腰三角形。
∴∠ABD =∠ADB ,∠ACD =∠ADC∵∠ABE +∠BAE +∠BEA =∠EDC +∠DCE+∠CED 。
∵∠BEA=∠CED∴∠ABE +∠BAE =∠EDC +∠DCE 。
∵∠DCE=∠EDC+∠ADB∴∠ABE +∠BAE=∠EDC+∠EDC+∠ADB 。
∴∠BAE=∠EDC+∠EDC ,即600=2∠EDC ∴∠EDC =3004. 已知c b a 2+=, c b 3=, 207--=a b c , 那么b =_______. 解:∵c b a 2+=, c b 3=∴5a c =把a ,b 的值代入207--=a b c ,得21520c c c =--,得解方程得c =43把解方程得c =43带入c b 3=,得4b =分析:根据c b a 2+=, c b 3=,得到5a c =。
把a ,b 的值代入207--=a b c ,得到关于c 的一元一次方程。
21520c c c =--,解方程得c =43,4b =。
第十七届华罗庚金杯少年数学邀请赛_试题及答案_小学高年级组

第十五届华罗庚金杯少年数学邀请赛初赛试卷(小学组)一、选择题(每小题10分,满分60分。
以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内。
)1.如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的()。
2.两条纸带,较长的一条为23cm,较短的一条为15 cm。
把两条纸带剪下同样长的一段后,剩下的两条纸带中,要求较长的纸带的长度不少于较短的纸带长度的两倍,那么剪下的长度至少是()cm。
(A)6 (B)7 (C)8 (D)93.两个水池内有金鱼若干条,数目相同。
亮亮和红红进行捞鱼比赛,第一个水池内的金鱼被捞完时,亮亮和红红所捞到的金鱼数目比是3:4;捞完第二个水池内的金鱼时,亮亮比第一次多捞33条,与红红捞到的金鱼数目比是5:3。
那么每个水池内有金鱼()条。
(A)112 (B)168 (C)224 (D)3364.从中去掉两个数,使得剩下的三个数之和与最接近,去掉的两个数是()。
5.恰有20个因数的最小自然数是()。
(A)120 (B)240 (C)360 (D)4326.如图的大正方形格板是由81个1平方厘米的小正方形铺成,B,C是两个格点。
若请你在其它的格点中标出一点A,使得△ABC的面积恰等于3平方厘米,则这样的A点共有()个。
(A)6 (B)5 (C)8 (D)107.算式的值为,则m+n 的值是 。
8.“低碳生活”从现在做起,从我做起。
据测算,1公顷落叶阔叶林每年可吸收二氧化碳14吨。
如果每台空调制冷温度在国家提倡的26℃基础上调到27℃,相应每年减排二氧化碳21千克。
某市仅此项减排就相当于25000公顷落叶阔叶林全年吸收的二气化碳;若每个家庭按3台空调计,该市家庭约有 万户。
(保留整数)9.从0、1、2、3、4、5、6、7、8、9这十个数字中,选出九个数字,组成一个两位数、一个三位数和一个四位数,使这三个数的和等于2010,那么其中未被选中的数字是 。
2020年第十七届“无悔金杯”少年数学邀请赛决赛试卷(小高组b卷)

2012年第十七届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B卷)一、填空题(每小题10分,共80分)1.(10分)算式÷()的值为.2.(10分)设a△b和a▽b分别表示取a和b两个数的最小值和最大值,如,3△4=3,3▽4=4,那么对于不同的数x,5▽[4▽(x△4)]的取值共有个.3.(10分)里山镇到省城的高速路全长189千米,途经县城,里山镇到县城54千米.早上8:30,一辆客车从里山镇开往县城,9:15到达,停留15分钟后开往省城,11:00到达.另有一辆客车于同天早上8:50从省城径直开往里山镇,每小时行驶60千米.那么两车相遇的时间为.4.(10分)有高度相同的一段方木和一段圆木,体积之比是1:1.如果将工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得圆柱体积和长方体的体积的比值为.5.(10分)用[x]表示不超过x的最大整数,记{x}=x﹣[x],则算式{}+{}+{}+…+{}的值为.6.(10分)某个水池存有其容量的十八分之一的水.两条注水管同时向水池注水,当水池的水量达到九分之二时,第一条注水管开始单独向水池注水,用时81分钟,所注入的水量等于第二条注水管已注入水池内的水量.然后第二条注水管单独向水池注水49分钟,此时,两条注水管注入水池的总水量相同.之后,两条注水管都继续向水池注水.那么两条注水管还需要一起注水分钟,方能将水池注满.7.(10分)有16位选手参加象棋晋级赛,每两人都只赛一盘.每盘胜者积1分,败者积0分.如果和棋,每人各积0.5分.比赛全部结束后,积分不少于10分者晋级.那么本次比赛后最多有位选手晋级.8.(10分)平面内有5个点,其中任意3个点均不在同一条直线上,以这些点为端点连接线段,则除这5个点外,这些线段至少还有个交点.二、解答下列各题(每题10分,共40分,要求写出简要过程)9.(10分)能否用540个图所示的1×2的小长方形拼成一个6×180的大长方形,使得6×180的长方形的每一行、每一列都有奇数个星?请说明理由.10.(10分)已知100个互不相同的质数p1,p2,…,p100,记N=p12+p12+…+p1002,问:N被3除的余数是多少?11.(10分)王大妈拿了一袋硬币去银行兑换纸币,袋中有一分、二分、五分和一角四种硬币,二分的枚数是一分的,五分硬币的枚数是二分的,一角硬币的枚数是五分的少7枚.王大妈兑换到的纸币恰好是大于50小于100的整元数.问这四种硬币各有多少枚?12.(10分)右图是一个三角形网格,由16个小的等边三角形构成.网格中由3个相邻的小三角形构成的图形称为“3﹣梯形”.如果在每个小三角形内填上数字1﹣9中的一个,那么能否给出一种填法,使得任意两个“3﹣梯形”中的3个数之和均不相同?如果能,请举出一例;如果不能,请说明理由.三、解答下列各题(每小题15分,共30分,要求写出详细过程)13.(15分)请写出所有满足下面三个条件的正整数a和b;(1)a≤b;(2)a+b是个三位数,且三个数字从小到大排列等差;(3)a×b是一个五位数,且五个数字相同.14.(15分)记一百个自然数x,x+1,x+2,…,x+99的和为a,如果a的数字和等于50,则x最小为多少?2012年第十七届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B卷)参考答案与试题解析一、填空题(每小题10分,共80分)1.(10分)算式÷()的值为.【分析】先算小括号里面的加法,再算除法,最后算减法.【解答】解:÷(),=÷,=,=.故答案为:.2.(10分)设a△b和a▽b分别表示取a和b两个数的最小值和最大值,如,3△4=3,3▽4=4,那么对于不同的数x,5▽[4▽(x△4)]的取值共有1个.【分析】分x>4和x≤4两种情况进行讨论,据此解答.【解答】解:分情况讨论:①x≤4时,x△4=x,4▽x=4,5▽4=5;②x>4时,x△4=4,4▽4=4,5▽4=5.所以5▽[4▽(x△4)]的取值共有1种.故答案为:1.3.(10分)里山镇到省城的高速路全长189千米,途经县城,里山镇到县城54千米.早上8:30,一辆客车从里山镇开往县城,9:15到达,停留15分钟后开往省城,11:00到达.另有一辆客车于同天早上8:50从省城径直开往里山镇,每小时行驶60千米.那么两车相遇的时间为10:08.【分析】此题应先求出甲车在县城开往省城的速度和所用时间,速度是(189﹣54)÷1.5=90(千米/小时),所用的时间(189﹣54﹣60×40÷60)÷(90+60),再求出两车相遇的时间,解决问题.【解答】解:甲车在县城开往省城的速度是:(189﹣54)÷1.5,=135÷1.5,=90(千米/小时);甲车在县城开往省城所用的时间:(189﹣54﹣60×40÷60)÷(90+60),=95÷150,=(小时),=38(分钟);两车相遇的时间:15+15=30(分钟),9点30分+38分=10时8分.答:两车在10:08相遇.故答案为:10:08.4.(10分)有高度相同的一段方木和一段圆木,体积之比是1:1.如果将工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得圆柱体积和长方体的体积的比值为.【分析】方木与圆木的体积和高度都相等,说明底面积也相等,要求加工成的圆柱体积和长方体的体积的比,就是比较底面积的比,所以只要求出底面积即可,然后按正方形的内接圆和外接圆考虑即可.【解答】解:(1)设圆的半径为r,圆的面积与正方形的面积比是:(πγ2):(2γ×2γ)=,(2)设圆的半径为r,正方形的面积与圆的面积比是:(2γ×γ):(π×γ2)=,因为,方木与圆木的体积和高度都相等,说明底面积也相等,即图(1)的大正方形面积等于图(二)的大圆的面积,所以,现在的圆柱体积和长方体的体积的比值是::=;答:圆柱体积和长方体的体积的比值为.故答案为:5.(10分)用[x]表示不超过x的最大整数,记{x}=x﹣[x],则算式{}+{}+{}+…黑豆网https://黑豆网涵盖电影,电视剧,综艺,动漫等在线观看资源!金马医药招商网:金马医药招商网是专业提供医药代理招商的资讯信息发布平台,科技新闻网:科技新闻网每天更新最新科技新闻,这里有最权威的科技新闻资料。
“华罗庚金杯”少年数学邀请赛1-9届试题及详解

1 63 =1 64 64 63 米。 64
答:七根竹竿的总长是1
【分析与讨论】 中国古代就有 “一尺之棰, 日取其半, 万世不竭” 这样一个算术问题。就是说,有一根一尺长的短棍,每天截去它的一 半,永远也截不完。那么,每天剩下多少呢?第七天剩下多少呢? 用上面的解法计算七根竹竿的总长,时间是绰绰有余的。但如果 先把每根竹竿都算出来再相加,需要通分,时间恐怕就来不及了。同 学们不妨试一试。 有三条线段 A、B、C,A 长 2.12 米,B 长 2.71 米,C 长 3.53 米, 以它们作为上底、下底和高,可以作出三个不同的梯形。问:第几个 梯形的面积最大? 【解法】首先注意,梯形的面积=(上底+下底)×高÷2。但 我们现在是比较三个梯形面积的大小, 所以不妨把它们的面积都乘以 2,这样只须比较(上底+下底)×高的大小就行了。我们用乘法分配 律: 第一个梯形的面积的 2 倍是: (2.12+3.53)×2.71=2.12×2.17+3.53×2.71
而王师傅从甲地到乙地的实际行驶速度只有55公里小时这样一来实际行驶1公里所花费的时间是55小时为了能按时返回甲地王师傅从乙地返回甲地时行驶1公里所花的时间必须比原计划时间少55小时
历年华罗庚金杯试题 第一届“华罗庚金杯”少年数学邀请赛
初赛试题
1.1966、1976、1986、1996、2006 这 5 个数的总和是多少? 2.每边长是 10 厘米的正方形纸片,正中间挖一个正方形的洞, 成为一个宽度是 1 厘米的方框。把 5 个这样的ቤተ መጻሕፍቲ ባይዱ框放在桌面上,成为 这样的图案。 问桌面上被这些方框盖住的部分面积是多少平方厘米?
的时间。这样一来,问题就化为求 9 和 33 的最小公倍数的问题了。 不难算出 9 和 33 的最小公倍数是 99,所以答案为 99÷9=11。 答:小圆上的蚂蚁爬了 11 圈后,再次碰到大圆上的蚂蚁。 【分析与讨论】这个题目的关键是要看出问题实质是求最小公倍 数的问题。注意观察,看到生活中的数学,这 是华罗庚教授经常启发青少年们去做的。 图 33 是一个跳棋棋盘, 请你算算棋盘上共 有多少个棋孔? 【解法】这个题目的做法很多。由于时间 所限,直接数是来不及的,而且容易出错。下 图(图 34)给出一个较好的算法。把棋盘分 割成一个平行四边形和四个小三角形,如图 34。平行四边形中的棋孔数为 9×9=91,每个 小三角形中有 10 个棋孔。所以棋孔的总数是 81+10×4=121 个 答:共有 121 个棋孔。 【分析与讨论】 玩过跳棋的同学们, 你们以前数过棋孔的数目吗? 有兴趣的同学在课余时都可以数一数,看谁的方法最巧? 有一个四位整数。在它的某位数字前面加上一个小数点,再和这 个四位数相加,得数是 2000.81。求这个四位数。 【解法 1】由于得数有两位小数,小数点不可能加在个位数之前。 如果小数点加在十位数之前,所得的数是原米四位数的百分之一,再 加上原来的四位数,得数 2000.81 应该是原来四位数的 1.01 倍,原来 的四位数是 2000.81÷1.01=1981。 类似地,如果小数点加在百位数之前,得数 2000.81 应是原来四
2020年第十七届“无悔金杯”少年数学邀请赛决赛试卷(小高组b卷)(1)

2012年第十七届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B卷)一、填空题(每小题10分,共80分)1.(10分)算式÷()的值为.2.(10分)设a△b和a▽b分别表示取a和b两个数的最小值和最大值,如,3△4=3,3▽4=4,那么对于不同的数x,5▽[4▽(x△4)]的取值共有个.3.(10分)里山镇到省城的高速路全长189千米,途经县城,里山镇到县城54千米.早上8:30,一辆客车从里山镇开往县城,9:15到达,停留15分钟后开往省城,11:00到达.另有一辆客车于同天早上8:50从省城径直开往里山镇,每小时行驶60千米.那么两车相遇的时间为.4.(10分)有高度相同的一段方木和一段圆木,体积之比是1:1.如果将工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得圆柱体积和长方体的体积的比值为.5.(10分)用[x]表示不超过x的最大整数,记{x}=x﹣[x],则算式{}+{}+{}+…+{}的值为.6.(10分)某个水池存有其容量的十八分之一的水.两条注水管同时向水池注水,当水池的水量达到九分之二时,第一条注水管开始单独向水池注水,用时81分钟,所注入的水量等于第二条注水管已注入水池内的水量.然后第二条注水管单独向水池注水49分钟,此时,两条注水管注入水池的总水量相同.之后,两条注水管都继续向水池注水.那么两条注水管还需要一起注水分钟,方能将水池注满.7.(10分)有16位选手参加象棋晋级赛,每两人都只赛一盘.每盘胜者积1分,败者积0分.如果和棋,每人各积0.5分.比赛全部结束后,积分不少于10分者晋级.那么本次比赛后最多有位选手晋级.8.(10分)平面内有5个点,其中任意3个点均不在同一条直线上,以这些点为端点连接线段,则除这5个点外,这些线段至少还有个交点.二、解答下列各题(每题10分,共40分,要求写出简要过程)9.(10分)能否用540个图所示的1×2的小长方形拼成一个6×180的大长方形,使得6×180的长方形的每一行、每一列都有奇数个星?请说明理由.10.(10分)已知100个互不相同的质数p1,p2,…,p100,记N=p12+p12+…+p1002,问:N被3除的余数是多少?11.(10分)王大妈拿了一袋硬币去银行兑换纸币,袋中有一分、二分、五分和一角四种硬币,二分的枚数是一分的,五分硬币的枚数是二分的,一角硬币的枚数是五分的少7枚.王大妈兑换到的纸币恰好是大于50小于100的整元数.问这四种硬币各有多少枚?12.(10分)右图是一个三角形网格,由16个小的等边三角形构成.网格中由3个相邻的小三角形构成的图形称为“3﹣梯形”.如果在每个小三角形内填上数字1﹣9中的一个,那么能否给出一种填法,使得任意两个“3﹣梯形”中的3个数之和均不相同?如果能,请举出一例;如果不能,请说明理由.三、解答下列各题(每小题15分,共30分,要求写出详细过程)13.(15分)请写出所有满足下面三个条件的正整数a和b;(1)a≤b;(2)a+b是个三位数,且三个数字从小到大排列等差;(3)a×b是一个五位数,且五个数字相同.14.(15分)记一百个自然数x,x+1,x+2,…,x+99的和为a,如果a的数字和等于50,则x最小为多少?2012年第十七届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B卷)参考答案与试题解析一、填空题(每小题10分,共80分)1.(10分)算式÷()的值为.【分析】先算小括号里面的加法,再算除法,最后算减法.【解答】解:÷(),=÷,=,=.故答案为:.2.(10分)设a△b和a▽b分别表示取a和b两个数的最小值和最大值,如,3△4=3,3▽4=4,那么对于不同的数x,5▽[4▽(x△4)]的取值共有1个.【分析】分x>4和x≤4两种情况进行讨论,据此解答.【解答】解:分情况讨论:①x≤4时,x△4=x,4▽x=4,5▽4=5;②x>4时,x△4=4,4▽4=4,5▽4=5.所以5▽[4▽(x△4)]的取值共有1种.故答案为:1.3.(10分)里山镇到省城的高速路全长189千米,途经县城,里山镇到县城54千米.早上8:30,一辆客车从里山镇开往县城,9:15到达,停留15分钟后开往省城,11:00到达.另有一辆客车于同天早上8:50从省城径直开往里山镇,每小时行驶60千米.那么两车相遇的时间为10:08.【分析】此题应先求出甲车在县城开往省城的速度和所用时间,速度是(189﹣54)÷1.5=90(千米/小时),所用的时间(189﹣54﹣60×40÷60)÷(90+60),再求出两车相遇的时间,解决问题.【解答】解:甲车在县城开往省城的速度是:(189﹣54)÷1.5,=135÷1.5,=90(千米/小时);甲车在县城开往省城所用的时间:(189﹣54﹣60×40÷60)÷(90+60),=95÷150,=(小时),=38(分钟);两车相遇的时间:15+15=30(分钟),9点30分+38分=10时8分.答:两车在10:08相遇.故答案为:10:08.4.(10分)有高度相同的一段方木和一段圆木,体积之比是1:1.如果将工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得圆柱体积和长方体的体积的比值为.【分析】方木与圆木的体积和高度都相等,说明底面积也相等,要求加工成的圆柱体积和长方体的体积的比,就是比较底面积的比,所以只要求出底面积即可,然后按正方形的内接圆和外接圆考虑即可.【解答】解:(1)设圆的半径为r,圆的面积与正方形的面积比是:(πγ2):(2γ×2γ)=,(2)设圆的半径为r,正方形的面积与圆的面积比是:(2γ×γ):(π×γ2)=,因为,方木与圆木的体积和高度都相等,黑豆网https://黑豆网涵盖电影,电视剧,综艺,动漫等在线观看资源!金马医药招商网:金马医药招商网是专业提供医药代理招商的资讯信息发布平台,科技新闻网:科技新闻网每天更新最新科技新闻,这里有最权威的科技新闻资料。
第17届“华杯赛”笔试决赛初一组试题B及参考答案

三、解答下列各题(每题 15 分, 共 30 分, 要求写出详细过程)
13. 答案:最大值为 503,最小值为 14. 罗庚金杯少年数学邀请赛
决赛笔试试题 B 参考答案 (初一组) 一、填空(每题 10 分, 共 80 分)
题号 答案 1 2 2 3 93.75 4 805.4 5 40 6 671 7 4 8 4396
88 211
二、解答下列各题(每题 10 分, 共 40 分, 要求写出简要过程) .
.
5. 如右图,四边形 MAOB 与 NAOB, 且 S 四边形 MAOB
=40, 点 P 在线段 MN 上, 则 S 四边形 PAOB 的面积等
=S 四边形 NAOB 于 .
6. 设 m 2 n n 2 . 当 n 取 1, 2, , 2012 时, 能被 6 整除的 m 有
个.
7. 一个学校选出 5 个年级共 8 个班, 从每个班至少选出一名学生, 则在这些选出的学生中 , 至少有 名学生 , 他们的同班同学比他们的同年级同学少.
第十七届华罗庚金杯少年数学邀请赛决赛笔试试题 B(初一组)
第十七届华罗庚金杯少年数学邀请赛
决赛笔试试题 B(初一组)
(时间: 2012 年 4 月 21 日 10:00~11:30)
一、填空题(每小题 10 分, 共 80 分)
1 2 (2) (1) | 12 | 2 = 1. 计算: 1 2 2 [1 3 2 (2)] 4
1 . 两台抽水机同时向水池注水, 当水池的 18
2 时, 第一台抽水机开始单独向水池注水, 用时 81 分钟, 所注入的 9
17th华杯赛初一试题及解答

1
初一竞赛数学(上)
竞赛题讲解
课件
第十七届全国华杯赛初赛试题 (初一组笔试)答案
选择题 题号 答案 1 B 2 A 3 C 4 D 5 D 6 B
T1:两点确定一条直线,另外两点在该直线的同侧或异侧,分情况讨论,如图是最少三角形个数情形,为 4 个。
A
D C
B
T2: 173+286=459; 观察发现: (1) 因为 H=4,I=5,所以还剩下 1,2,3,6,7,8,9;百位数 A 和 D 只能是 1 和 2,反之如果 是 1 和 3,则十位数只能是 2 和 6 或 2 和 7,不能进位,它们的和分别为 8 和 9,最多再增加 各位的进位 1,始终到不了 5,与 I=5 矛盾; (2) 剩下 5 个数 3,6,7,8,9,又十位两个数之和进位,其和必定为 14 或 15,有 3 种可能: (6, 8) , (6,9) , (7,8) ; (3) 还剩下 3 个数字之和的末尾数字为另外一个数字,可知当且仅当十位数字为 7 和 8,末位数字 为 3 和 6 时,J=9 才成立; (4) 综上所述,结论为 173+286=273+186=183+276=……=459. (100+200)+(70+80)+(3+6) =459,共有 2×2×2=8 种可能的情形,但是最小和只有一个 459。 T3: 首先,内角都小于 180 度的角有钝角、直角和锐角,其次钝角小于 180 度,直角和锐角小于等于 90 度。 根据多边形内角和公式可知,这个七边形内角和为 180°×(7-2)=900°, 设这个七变形有 x 个钝角,则 900 < 180x+90(7-x) ; 解这个不等式 90x+630>900, x+7>10, x>3, 又因为 x 为整数, 所以 x 最小为 4 答:内角都小于 180 度的七边形的内角至少有 4 个钝角. 另外 :七边形的内角中,最多有 3 个锐角,最多有 7 个钝角(正七边形的内角都为 900°/7,是钝角) 。 T4: 四队进行单循环赛,共赛 6 场,每场比赛无论输赢,得分都是 3 分,所以 6 场比赛的总分是 6×3=18 分,即比赛后四个队的总得分是 18 分,因为比赛后各队得分恰好是四个连续的自然数,所以,设最高分 为 x, 则第二名得分为 x-1, 第三名得分为 x-2, 第四名得分为 x-3, 且 x+(x-1)+ (x-2) + (x-3) =18, 4x-6=18,x=6,所以选 D. 只有 6+5+4+3=18 满足条件。 注:关键是每场比赛得分总数总是 3 分。 T5:因为 ABCD 是平行四边形,故 AB∥CN,∴ △ABM △NCM
第17届“华杯赛”网上决赛试题以及答案(小中组)
3. 鸡兔同笼, 共有头 51 个, 兔的总脚数比鸡的总脚数的 3 倍多 4 只, 那么笼中 共有兔子 只.
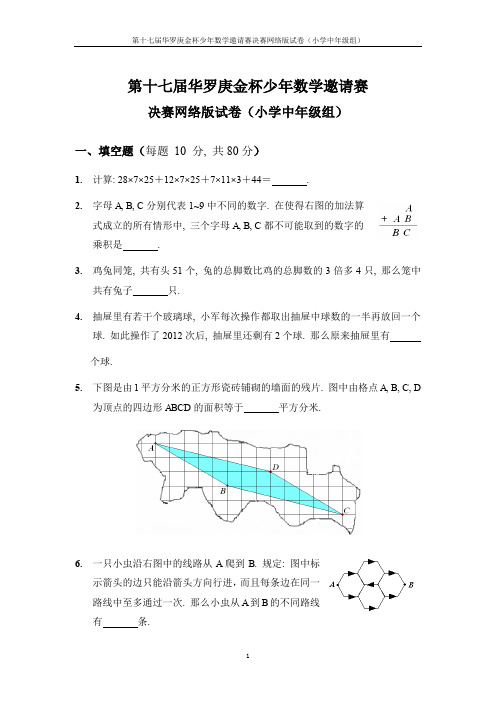
4. 抽屉里有若干个玻璃球, 小军每次操作都取出抽屉中球数的一半再放回一个 球. 如此操作了 2012 次后, 抽屉里还剩有 2 个球. 那么原来抽屉里有 个球. 5. 下图是由 1 平方分米的正方形瓷砖铺砌的墙面的残片. 图中由格点 A, B, C, D 为顶点的四边形 ABCD 的面积等于 平方分米.
6. 一只小虫沿右图中的线路从 A 爬到 B. 规定: 图中标 示箭头的边只能沿箭头方向行进, 而且每条边在同一 路线中至多通过一次. 那么小虫从 A 到 B 的不同路线 有 条.
1
第十七届华罗庚金杯少年数学邀请赛决赛网络版试卷(小学中年级组)
7. 有一些自然数, 它们中的每一个与 7 相乘, 其积的末尾四位数都为 2012, 那 么在这些自然数中, 最小的数是 .
8. 将棱长为 1 米的正方体木块分割成棱长为 1 厘米的小正方体积木, 设想孙悟 空施展神力将所有的小积木一个接一个地叠放起来, 成为一根长方体 “神棒”, 直指蓝天. 已知珠穆朗玛峰的海拔高度为 8844 米, 则“神棒”的高度超过珠 穆朗玛峰的海拔高度 米.
二、回答下列各题(每题 10 分, 共 40 分, 写出答案即可)
第十七届华罗庚金杯少年数学邀请赛决赛网络版试卷(小学中年级组)
第十届华罗庚金杯少年数学邀请赛
决赛网络版试卷(小学中年级组)
一、填空题(每题 10 分, 共 80 分)
1. 计算: 28× 7× 25+12× 7× 25+7× 11× 3+44= .
2. 字母 A, B, C 分别代表 1~9 中不同的数字. 在使得右图的加法算 式成立的所有情形中, 三个字母 A, B, C 都不可能取到的数字的 乘积是 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十七届华罗庚金杯少年数学邀请赛决赛笔试试题B (初一组)(时间:2012年4月21日10:00~11:30)一、填空题(每小题10分,共80分) 1.计算:()()()234221-2-1--12--2=1-2-+1-3-24⎡⎤⎛⎫⨯÷⎢⎥⎪⎝⎭⎢⎥⎣⎦⎛⎫⎡⎤⨯⨯ ⎪⎣⎦⎝⎭解析: []3422211(2)(1)12()8112()84840242111(118)202()13(2)4()19(2)44⎡⎤-⨯---÷---⨯-÷-⎢⎥-+⎣⎦====++⎡⎤-⨯-+-⨯--⨯-+-⨯-⎣⎦2. 一串有规律排列的数,从第二项起每一项都是2加前一项的倒数之和,当第五项是20时,第一项是 解析:154321111111181351882,1,1,20118352202183588211222183588n nnn a n a n a a a a a a a ++-=+≥⇒=≥=⇒==⇒==-⇒==-⇒==-------3.两条直角边相差5分米,且斜边为20分米的直角三角形面积为( 93.75 )平方分米。
解析:22222211,5,(5)(5)223751375(5)205(5)93.75224x x x x x x x x x x x x ++=+++=⇒+=+==设较短的直角边为分米则另一直角边为分米所求面积S=由勾股定理得:,从而S=4.令[x]表示不大于x 的最大整数,{x}=x-[x],则20121201222012+320122012+++...+5555+++⎧⎫⎧⎫⎧⎫⎧⎫⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭的值为(505.4)解析:2012120122201232012201220103201042010520102014......55555555201032010320104201042010520105555555++++++++⎧⎫⎧⎫⎧⎫⎧⎫⎧⎫⎧⎫⎧⎫⎧⎫++++=++++⎨⎬⎨⎬⎨⎬⎨⎬⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭⎩⎭⎩⎭⎩⎭⎩⎭⎛++⎫⎛++⎫++⎡⎤⎡⎤⎡=-+-+-⎪ ⎪⎢⎥⎢⎥⎢⎣⎦⎣⎦⎣⎝⎭⎝⎭2010201420102014...5520103201032010420104201052010520106201062010920109...55555555552010105⎛⎫⎛++⎫⎤⎡⎤++- ⎪ ⎪⎥⎢⎥⎦⎣⎦⎝⎭⎝⎭⎛++⎫⎛++⎫⎛++⎫⎛++⎫⎛++⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=-+-+-+-++- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭++201010201011201011201014201014......55555201020102010201020102011201020112010201420102014...555555345⎛+⎫⎛++⎫⎛++⎫⎡⎤⎡⎤⎡⎤-+-++-+ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎝⎭⎝⎭⎝⎭⎛++⎫⎛++⎫⎛++⎫⎡⎤⎡⎤⎡⎤+-+-++- ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎝⎭⎝⎭⎝⎭=+14141471470...0......0...0...4022402805.455555555555⎛⎫+++++++++++++=++++⨯=+⨯= ⎪⎝⎭5如右图,四边形MAOB 与NAOB ,且S 四边形MAOB =S 四边形NAOB =40,点P 在线段MN 上,则S 四边形PAOB 的面积等于解析:连接AB ,由S 四边形MAOB =S 四边形NAOB 知S 三角形ABN =S 三角形ABM , 所以 AB//NM 所以S 三角形ABP =S 三角形ABN ,所以S 四边形PAOB =S 四边形MAOB =406.设m=2n -n 2.当n 取1,2,…,2012时,能被6整除的m 有(671)个。
解析:2n ≡n 2 (mod 6),则n 必须为偶数,且2n ≡n 2 (mod 3)2n (mod 3): 2, 1, 2, 1, 2, 1, 2, 1, 2, …,n 2 (mod 3): 1, 1, 0, 1, 1, 0, 1, 1, 0, …以6个为周期重复,符合条件的n=6k+2, 6k+4,2012=335*6+2, 所以共有335组,最后还多一个符合条件的2012,总数为335*2+1=6717. 一个学校选出5个年级共8个班,从每个班至少选出一名学生,则在这些选出的学生中,至少有(4)名学生,他们的同班同学比他们的同年级同学少。
解析:“同班同学比同年级同学少”意味着该年级选了不止一个班,每班只选1人,先在每个年级选1个班级,还差3个班级,易知这3个班级应该从同一年级选,所以某年级共选了4个班级。
分布为:4,1,1,1,1,所以符合条件的共4名学生8.在乘法算式:草绿X 花红了=春光明媚,中,汉字代表非零数字,不同汉字代表不同数字,那么 春光明媚 所代表的四位数最小是(4396)解析:容易猜测:草=2,花=1,春=4 考察个位,绿*了 = X 媚,在剩下的数字中符合这个关系的组合有3*6=18,3*9=27,7*8=56,7*9=63,由于要求四位数最小,所以我们对于乘数从大到小尝试 对于7*9=63,红=5,6,8,经验证均不合条件。
对于7*8=56,红=3,5,9,经验证,当红=5时,有:157*28=4396,所以最小的四位数是 4396二、解答下列各题(每题10分,共40分,要求写出简要过程)9.能否用500个右图所示的1X2的小长方形拼成一个5X200的大长方形,使得5X200的每一行都有奇数个星、每一列都有偶数个星?说明理由。
解析:因为有奇数行, 奇数⨯奇数=奇数. 有偶数列, 偶数⨯偶数=偶数, 奇数不等于偶数, 因此不可能。
10.从1到1000中最多可以选出多少个数,满足:这些数中任意两个数的差都不整除它们的和? 解析:构造抽屉, (1,2,3)(4,5,6)(7,8,9)……(997, 998,999)(1000), 共334组, 前面333组中, 每组的数满足任意两个数的差整除它们的和, 故每组取一个, 最多取334个.取:1,4, 7, ⋯, 1000, 因为这些数中任意两个数的差是3的倍数, 任意两个数的和被3除余2. 因此满足题目的要求.11.某个水池存有的水量是其容量的118,两台抽水机同时向水池注水,当水池的水量达到29时,第一台抽水机开始单独向水池注水,用时81分钟,所注入的水量等于第二台抽水机已注入水池内的水量,然后第二台抽水机单独向水池注水49分钟,此时,两台抽水机注入水池的总水量相同,之后,两台抽水机都继续向水池注水,那么两台抽水机还需要一起注水多少分钟,方能将水池注满。
解析:由题意可知:两台抽水机第一次同时向水池注水的水量是6118192=-.设水池容量为1, 两台抽水机单独向水池注水的水量为61时所需时间分别为1V 和2V , 两台抽水机一起向水池注水的水量为61时,设所需时间为t, 则有下列方程:221249,81V V t V V t ==.所以, 6397,9712=⨯==t V V .由题意可知:两台抽水机单独向水池注水的水量之和也是61, 两台抽水机都继续向水池注水, 还需要注水18111816121=-⨯-方能将水池注满水, 故有23163611811=⨯⎪⎭⎫⎝⎛÷(分钟).12.小李和小张在一个圆形跑道上匀速跑步,两人同时同地出发,小李顺时针跑,每72秒跑一圈;小张逆时针跑,每80秒跑一圈,在跑道上划定起点为中点的1/4圆弧区间,那么两人同时在划定的区间内所持续的时间为多少秒?解析: 设起跑时间为0秒时刻, 则小李和小张在划定区间跑的时间段分别为]9,0[, ]972,972[+-k k ,,3,2,1=k ,和]10,0[, ]1080,1080[+-m m , ,3,2,1=m .其中 [a, b] 表示第a 秒时刻至第b 秒时刻. 显然 ]9,0[ 即前9秒里两类时间段的公共部分. 此外, 考虑]972,972[+-k k 和]1080,1080[+-m m 的公共区间, m k ,为正整数, 分两种情况:1) m k 8072=, 即小李和小张分别跑了k 圈和m 圈同时回到起点, 他二人同时在划定区域跑18秒. 2) m k 8072≠, 例如10809721080972+≤+≤-≤-m k m k ⇔1972801≤-≤k m ①.两人同时在划定区域内跑了)1080(972--+m k )7280(19k m --=. 由①知87280=-k m , 16. 于是两人同时在划定区域内跑持续时间为11秒或3秒. 其它情况类似可得同样结果.综上, 答案为18,11,9,3.三、解答下列各题(每小题15分,共30分,要求写出详细过程)13.实数x,y,z,w 满足x ≥y ≥z ≥w ≥0,且5x+4y+3z+6w=2012,求x+y+z+w 的最大值和最小值。
解析:设z=w+a, y=w+a+b, x=w+a+b+c.则b,c ≥0, 且x+y+z+w=4w+3a+2b+c. 2012=5(w+a+b+c)+4(w+a+b)+3(w+a)+6w=18w+12a+9b+5c=4⨯(4w+3a+2b+c)+(2w+b+c) ≥4(x+y+z+w). 因此, x+y+z+w ≤503. 当x=y=z=503/3, w=0时, 上式等号成立.故x+y+z+w 的最大值为503又2012=18w+12a+9b+5c=5⨯ (4w+3a+2b+c)-(2w+3a+b)≤5(x+y+z+w), 则 x+y+z+w ≥2012/5. 当x=2012/5, y=z=w=0时, 上式等号成立.故x+y+z+w 的最小值为2012/5.14. 平面上有从1到n 编了号的n 个点,每个点与另外k 个点连有直线段,若一个点连的k 条直线段的另外k 个端点的编号中有多于一半的编号小于它自身的编号,这个点就称为“好点”。
若恰有5个好点,问:n 的最小值是多少?解析:一个点连的线段的另一端点的编号小于它的编号, 我们称这条线段为该点发出的“好线”. 每个好点, 发出的“好线”的条数不小于12+⎥⎦⎤⎢⎣⎡k ,令][x 表示不大于x 的最大整数, ][}{x x x -=。
编号为n 的点发出的连线都是好线,其它4个好点发出的连线的条数大于等于22214124+=+⨯≥⎪⎪⎭⎫ ⎝⎛+⎥⎦⎤⎢⎣⎡⨯k k k 由于5个好点发出的好线的条数小于所有的连线数2nk ,所以222nkk k <++,(*))6(4-<n k 另外,设好点中最小编号为m ,则编号为1,2,…,1-m 的点都不是好点, 而非好点的总数是5-n , 所以, 1 5.m n -≤-此外, 第m 号点最多只能发出1-m 条好线, 因此,[]11 5.2km n +≤-≤-{}152221151, 211. (**)222 k kn k k n n k n -+≤--⎧⎫≤--+≤≤-⎨⎬⎩⎭由(*)和(**), 4(211)(6),,8.n n n <--≥不难验证不等式才能成立 下面例子说明,n=8是可以达到的. 现设n=8,取k=3,有*表示编号等于行号和列号的两个点连线.。
