网络计划优化案例-费用优化
网络计划费用优化中的线性规划数学模型

[] 王 赫 , 玉琬 , 玉仙 . 5 金 贺 建筑工程 事故 分析 [ ]北 京 : M . 中
国建 筑 工 业 出版 社 ,0 1 20 .
、
Fa t r nfu n i h e i biiy o c o s i l e c ng t e r la lt f
计划 方案 , 工程项 目施工 中 , 在 分为工期优 化 、 资源优 化及费用优
化, 在工程项 目建设 中 , 工程周 期 的长短 直接关 系到 工程成本 的
本文就 网络计划 的费用 优化 进行 论述 即网络计划 时间成本优 在工程项目 施工管理中, 于施工环境、 由 地质, 网络计 划, 数学模 型, 工程项 目
中图分类号 : 7 1 TU 2 文献标识码 : A
0 引言
件的变化 , 据工程项 目的实 施方 案 , 根 编制 的项 目初始 网络 计划 不能满 足实际需要 , 要使其满 足工期合理 、 人力和物力科学 配置 , 工程成本最小 , 必须 随时对 网络 计划进行 多 目标优化 配置 。在满
网络 计 划 费 用优 化 中 的线 性 规 划 数 学模 型
张奎 俊 尚 书 河 时 美荣
摘 要: 介绍 了线性规划数学模型建立 的方 法和步骤 , 运用 Mal 优 化工具箱进行分析计算 , tb a 并通过具体 实例对模 型进 行检验 , 计算结果与纯压缩 网络计划 的结果进行 了对比分析, 出运用数 学模 型对网络计划优 化配置更加简单、 靠。 将 指 可
侧压力 以及施工荷载 。因此模 板工 程 的安全性 对结 构施 工期 的 安全起着 重要 作用。模 板及其支撑应 根据工程结 构形式 、 荷载大 新技术 、 新材料 的应用 。
57-网络计划的优化依据和优化方法

网络计划的优化分为工期优化、费用优化和资源优化三种。
•已知某工程双代号网络计划如图所示,图中箭线下方括号外数字为工作的正常时间,括号内数字为最短持续时间;•箭线上方括号外数字为工作按正常持续时间完成时所需的直接费,括号内数字为工作按最短持续时间完成时所需的直接费。
•该工程的间接费用率为0.8万元/天,试对其进行费用优化。
(1)根据各项工作的正常持续时间,用标号法确定网络计划的计算工期和关键线路,如图。
计算工期为19天,关键线路有两条,即:①—③—④—⑥和①—③—④—⑤—⑥。
•(2)计算各项工作的直接费用率:•△C1-2=(7.4-7.0)∕(4-2)=0.2万元∕天•△C1-3=(11.0-9.0)∕(8-6)=1.0万元∕天•△C1-2=(7.4-7.0)∕(4-2)=0.2万元∕天=0.3万元∕天•△C2-3•△C2-4=0.5万元∕天•△C3-4=0.2万元∕天•△C3-5=0.8万元∕天•△C4-5=0.7万元∕天•△C4-6=0.5万元∕天•△C5-6=0.2万元∕天•(3)计算工程总费用:•①直接费总和:C d=7.0+9.0+5.7+5.5+8.0+8.0+5.0+7.5+6.5=62.2万元;•②间接费总和:C i=0.8×19=15.2万元;•③工程总费用:C t= C d+C i=62.2+15.2=77.4万元。
←1)第一次压缩←从图可知,该网络计划中有两条关键线路,为了同时缩短两条关键线路的总持续,有以下四个压缩方案:←压缩工作B,直接费用率为1.0万元/天;←压缩工作E,直接费用率为0.2万元/天;←同时压缩工作H和工作I,组合直接费用率为:0.7+0.5=1.2万元/天;←同时压缩工作I和工作J,组合直接费用率为:0.5+0.2=0.7万元/天。
•在上述压缩方案中,由于工作E的直接费用率最小,故应选择工作E为压缩对象。
•工作E的直接费用率0.2万元/天,小于间接费用率0,8万元/天,说明压缩工作E可使工程总费用降低。
网络计划费用优化方法的讨论

+ 2=O
t 一 l 3+ + 3=0 t 一 2 3+ + =0 t 一 2 5+ + =0 5 t 一 3 4+ + =0 6 t 一 3 5+ + =0 7 t 一 4 6+ + =0 8
次缩短工作 时间的限度受以下 3 个条件 限制 : () 1 需要缩短 的时间, 即计划工期减去规定工
然, 解如下模型即可一次得到 :
体 目标最佳的线性规划解法 。
m x = ∑c l¥ l t
2 例 证
给定 网络如图 1 所示 ( 参数 :d ' IC) 。 ( IDi i ) j ,i
’
iti ≥- dj。 i jD 二 < -j i <
收稿 日期 :05. .2 20 .91 0
‘
—
—
要求工期( ; 日)
间, 使工期缩短的代价最小 , 同时 , 再考虑缩短工期
所带来的间接费节约或工程提前投产效益 , 根据费
D ——工作 i y - 的正常时间( ; 日) d——工作 f - “ 一 的压 限时间( ; 『 日)
用与爱益相抵后 的净效果来确定成本最低的最佳工 期或指定工期 的最低成本¨ 引。当然 , 更一般意义的 费用优化应是先求 出不同工期下最低 直接费用 , 然
网络计划 费用优化的方法有多种 , 如直观判断 法、 流量法( 又称最大流最小割法) 线性规划解 法、 、 标记法等。其 中, 流量法得 到工期缩短而代价最小 的过程为: 逐次选取增加直 接费用最小 的工作来压 缩其持续 时间 , 如可能工期或指定工期为 2 , 0d 流量 法可能经过 3 —2 —2 共两次压缩 。流量法 0d 5d 0d 是逐次选取增加直接费用 ( 或组合 费用率) 小的 最
lO 2 O 2 0= 2 0元 。
运用时标网络实现工期成本优化
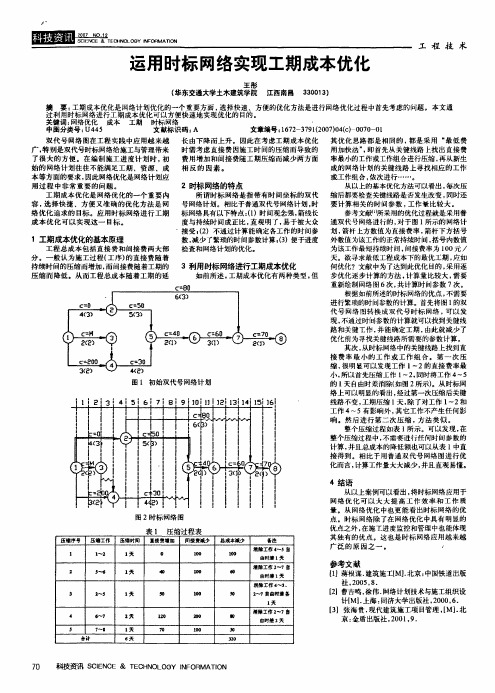
4 结语
从以上案例可以看出, 将时标网络应用于 网络优化可以大大提高工作效率和工作质 量。从网络优化中也更能看出时标网络的优 点。时标网络除了 在网络优化中 具有明显的 优点之外, 在施工进度监控和管理中也能体现 其独有的优点。这也是时标网络应用越来越 广泛的原因之一。
图2 时标网络图
表1
压怕序号
l
C二 0 8
王彤
重新绘制网络图6 次, 共计算时间参数 7 次。
根据如前所述的时标网 络的优点, 不需要 进行繁琐的时间参 数的计算。 首先将图1的双
代号网络图转换成双代号时标网络 , 可以发 现, 不通过时间参数的计算就可以找到关键线
3‘ 己)
4 (己 )
图 1
初始双代号网络计划
路和关键工作, 并能确定工期, 此就减少了 由 优化前为寻找关键线路所需要的参数计算。 其次, 从时标网络中的关键线路上找到直 接费率最小的工作或工作组合。第一次压 缩, 很明显可以发现工作 1一 的直接费率最 2 小, 所以首先压缩工作1一 , 2 同时将工作4 一 5 的 1 天自由 时差消除(如图2 所示)。 从时标网 络上可以明显的看出, 经过第一次压缩后关键 线路不变, 工期压缩 1天, 除了对工作 1一2 和 工作4 一 有影响外, 5 其它工作不产生任何影 响。然后进行第二次压缩, 方法类似。 整个压缩过程如表 1 所示。可以发现, 在 整个压缩过程中, 不需要进行任何时间参数的 计算, 并且总成本的降低额也可以从表 1 中 直 接得到。相比于用普通双代号网 络图进行优 化而言, 计算工作量大大减少, 并且直观易懂。
S C } 干 E & 丁 J 利O L以〕 INF 臼书 A T 1 N 〔忆 〔 丫 幼 0
网络计划优化工期

4
2(1) 2
1
7
32
4
6
6(5)
3(2)
1
3
5
6(3)
3(2)
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第一次:选择工作③-⑤,压缩2天,成为4天;
参考答案:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8
6
3(2)
4(2)
4
2(1) 2
1
7
32
4
6
6(5)
1
3
5
3(3)
3(2)
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第二次:选择工作③-④和③-⑤,同时压缩1天,③- ④成为2天,③-⑤成为3天 ;
工期变为12天,关键工作没有变化。
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8
6
3(2)
4(2)
4
2(1) 2
3
20(15)
4 2
3
10(8) 30(18)
2
1
3
40(20)
3 60(30)
1
4
50(30)
5
2 30(20)
8 6
50(25)
(4)选择关键工作压缩时间,并重新计算工期Tc′; 第一次:选择工作①-③ ,压缩10天,成为40天;
工期变为150天,①-②和②-③也变为关键工作。
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160
6
4(2)
3
5
3(2)
第3章 网络进度计划的优化

项目进度计划的优化
主讲: 谢雪梅 主讲:
内容
• 3.1 工期优化 • 3.2 费用优化 • 3.3 资源优化
项目进度计பைடு நூலகம்的优化
• 网络计划的优化,就是在满足既定的约束 条件下,按某一目标,对网络计划进行不 断检查、评价、调整和完善,以寻求最优 网络计划方案的过程。网络计划的优化有 工期优化、费用优化和资源优化三种 • 费用优化又叫工期成本优化 • 资源优化分为资源有限-工期最短的优化 和工期固定-资源均衡的优化
• 3.2 费用优化
• 在一定范围内,工程的施工费用随着工期的 变化而变化,在工期与费用之间存在着最优 解的平衡点。费用优化就是寻求最低成本时 的最优工期及其相应进度计划,或按要求工 期寻求最低成本及其相应进度计划的过程。 因此费用优化又叫工期-成本优化。
工期-成本优化
1、时间和费用的关系 工程的成本由直接费和间接费组成。 直接费:由人工费、材料费及机械使用费等构成。 与所采用的施工方案有关。 间接费:包括施工组织和经营管理的全部费用。
• 3.1 工期优化
工期优化是在网络计划的工期不满足要求时, 通过压缩计算工期以达到要求工期目标,或在一定 约束条件下使工期最短的过程。 • 在确定需缩短持续时间的关键工作时,应按以下几 个方面进行选择: (1)缩短持续时间对质量和安全影响不大的工作; (2)有充足备用资源的工作; (3)缩短持续时间所需增加的工人或材料最少的工 作; (4)缩短持续时间所需增加的费用最少的工作。 •
• 1. 资源有限─工期最短优化(ResourceScheduling)。 是通过调整计划安排以满足资源限制条件,并 使工期延长最少。其优化步骤如下: 1)计算网络计划每天资源的需用量; 2)从计划开始日期起,逐日检查每天资源需用量 是否超过资源的限量,如果在整个工期内每天 均能满足资源限量的要求,可行优化方案就编 制完成。否则必须进行计划调整; 3)调整网络计划。对资源有冲突的活动做新的顺 序安排。顺序安排的选择标准是工期延长的时 间最短; 4)重复上述步骤,直至出现优化方案为止。
工期优化(例题)

1
10 10
2
3 20(15)
2
3
40(20) 40 40
3 30(30)
70 70
5
8 50(25)
6 120 120
1 30(30)
4
70
70
2 30(20)
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 选择关键工作压缩作业时间,并重新计算工期T 第四次:选择工作① 同时压缩10 10天 第四次:选择工作①-③和②-③,同时压缩10天, 成为30 30天 成为20 20天 ①-③成为30天, ②-③ 成为20天;
4 2(1) 7 6(5)
2 6
2
8 3(2) 2 3(2) 1 4(3)
9 9
4
0 0
1
3
6 4(2) 3 3(2)
13 13
6
6 6
5
10 10
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 选择关键工作压缩作业时间,并重新计算工期T 第二次:选择工作③ 同时压缩1 第二次:选择工作③-④和③-⑤,同时压缩1天,③ 成为2 成为3 -④成为2天,③-⑤成为3天 ; 工期变为12 12天 关键工作没有变化。 工期变为12天,关键工作没有变化。
6 10
×
1
12
4
4 4
7 9
6 2 6
5
2
× 5
2
3
10
× 5
8
11
6
12
7
× 7
× 2
× 2
例题2 例题
请用关键节点法判断关键线路: 请用关键节点法判断关键线路:
网络计划的调整与优化

10.2 网络计划技术
• 1.关键路径法 • 关键路径法是美国杜邦公司和兰德公司于1957 年联合研究提出
的。1956—1957 年,美国杜邦公司在新建生产线时,为了 使该项目能够及时竣工投产,请兰德咨询公司研究开发了一种新的计 划管理方法,即关键路径法。关键路径技术是一套用于计划和控制项 目实施的图形技术。在任何给定的项目中,项目管理者需要考虑三个 因素:工期、成本和资源。关键路径技术用图形描述一项工程的全貌 ,并强调将注意力集中于关键路径上的活动,因为关键路径决定了项 目的最终完工时间。 • 关键路径技术最适合用于具有以下特点的项目:
上一页 下一页 返回
10.1 项目管理概述
• 项目的全过程质量管理,指的是从项目的立项开始、可行性研究、决 策、规划设计、项目采购、施工、调试、试运转,到正式投产的整个 项目管理过程中,都要保证质量第一。
• 项目的全员质量管理指的是参与项目建设的每一个人,从项目经理到 专业技术人员到普通人员,都要对本岗位以及整个项目的工作质量负 责。
• 纯项目组织结构就是半永久性的相对独立的工作机构。在这种结构形 式中,由一个装备齐全的项目小组负责该项目全部的工作,如图10 -1 所示。纯项目组织结构的优缺点如表10-1 所示。
上一页
返回
10.2 网络计划技术
• 10.2.1 网络计划技术概述
• 网络计划技术是项目计划管理的重要方法,它是伴随着建设和管理庞 大、复杂的项目的需要而产生的。由于项目具有任务繁多、协作面广 的特点,常常需要动用大量的人力、物力和财力,因此,如何合理而 有效地组织项目的各项具体任务,使之相互协调,在有限的资源约束 条件下,以最短的工期和最少的费用,最佳地完成整个项目,是项目 管理者所面临的一个重要挑战。网络计划技术就是在这种背景下产生 的。其中,关键路径法(Critical PathMethod ,CPM)和计划评审技术(Program Evaluation Technique,PERT)是两种主要形式的网络计划技术。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、费用优化示例
已知某工程双代号网络计划如图7所示,图中箭线下方括号外数字为工作的正常时间,括号内数字为最短持续时间;箭线上方括号外数字为工作按正常持续时间完成时所需的直接费,括号内数字为工作按最短持续时间完成时所需的直接费。
该工程的间接费用率为0.8万元/天,试对其进行费用优化。
图7 初始网络计划
(1)根据各项工作的正常持续时间,用标号法确定网络计划的计算工期和关键线路,如图8所示。
计算工期为19天,关键线路有两条,即:①—③—④—⑥和①—③—④—⑤—⑥。
(①,4)
(③,13) Array (①,8)(④,15)
图8 初始网络计划中的关键线路
(2)计算各项工作的直接费用率:
△C1-2=(7.4-7.0)∕(4-2)=0.2万元∕天
△C1-3=(11.0-9.0)∕(8-6)=1.0万元∕天
△C1-2=(7.4-7.0)∕(4-2)=0.2万元∕天
△C2-3=0.3万元∕天
△C2-4=0.5万元∕天
△C3-4=0.2万元∕天
△C3-5=0.8万元∕天
△C4-5=0.7万元∕天
△C4-6=0.5万元∕天
△C5-6=0.2万元∕天
(3)计算工程总费用:
①直接费总和:C
d
=7.0+9.0+5.7+5.5+8.0+8.0+5.0+7.5+6.5=62.2万元;
②间接费总和:C
i
=0.8×19=15.2万元;
③工程总费用:C
t = C
d
+C
i
=62.2+15.2=77.4万元。
(4)通过压缩关键工作的持续时间进行费用优化(优化过程见表1):
1)第一次压缩
从图8可知,该网络计划中有两条关键线路,为了同时缩短两条关键线路的总持续,有以下四个压缩方案:
①压缩工作B,直接费用率为1.0万元/天;
②压缩工作E,直接费用率为0.2万元/天;
③同时压缩工作H和工作I,组合直接费用率为:0.7+0.5=1.2万元/天;
④同时压缩工作I和工作J,组合直接费用率为:0.5+0.2=0.7万元/天。
在上述压缩方案中,由于工作E的直接费用率最小,故应选择工作E为压缩对象。
工作E的直接费用率0.2万元/天,小于间接费用率0,8万元/天,说明压缩工作E可使工程总费用降低。
将工作E的持续时间压缩至最短持续时间3天,利用标号法重新确定计算工期和关键线路,如图9所示。
此时,关键工作E 被压缩成非关键工作,故将其持续时间延长为4天,使成为关键工作。
第一次压缩后的网络计划如图10所示。
图中箭线上方括号内数字为工作的直接费用率。
(①,8)(④,14)
图9 工作E压缩至最短时的关键线路
(③,12)
(①,4)
图10 第一次压缩后的网络计划
2)第二次压缩
从图3-44可知,该网络计划中有三条关键线路,即:①—③—④—⑥、①—③—④—⑤—⑥和①—③—⑤—⑥。
为了同时缩短三条关键线路的总持续时间,有以下五个压缩方案:
①压缩工作B,直接费用率为1.0万元/天;
②同时压缩工作E和工作G,组合直接费用率为0.2+0.8=1.0万元/天;
③同时压缩工作E和工作J,组合直接费用率为:0.2+0.2=0.4万元/天;
④同时压缩工作G、工作H和工作J,组合直接费用率为:0.8+0.7+0.5=2.0万元/天;
⑤同时压缩工作I和工作J,组合直接费用率为:0.5+0.2=0.7万元/天。
在上述压缩方案中,由于工作E和工作J的组合直接费用率最小,故应选择工作E和工作J作为压缩对象。
工作E和工作J的组合直接费用率0.4万元/天,小于间接费用率0.8万元/天,说明同时压缩工作E和工作J可使工程总费用降低。
由于工作E的持续时间只能压缩1天,工作J的持续时间也只能随之压缩1天。
工作E和工作J的持续时间同时压缩1天后,利用标号法重新确定计算工期和关键线路。
此时,关键线路由压缩前的三条变为两条,即:①—③—④—⑥和①—③—⑤—⑥。
原来的关键工作H未经压缩而被动地变成了非关键工作。
第二次压缩后的网络计划如图11所示。
此时,关键工作E的持续时间已达最短,不能再压缩,故其直接费用率变为无穷大。
(①,8)(③,14)
图11 第二次压缩后的网络计划
3)第三次压缩
从图11可知,由于工作E不能再压缩,而为了同时缩短两条关键线路①—③—④—⑥和①—③—⑤—⑥的总持续时间,只有以下三个压缩方案:
①压缩工作B,直接费用率为1.0万元/天;
②同时压缩工作G和工作I,组合直接费用率为0.8+0.5 =1.3万元/天;
③同时压缩工作I和工作J,组合直接费用率为:0.5+0.2=0.7万元/天。
在上述压缩方案中,由于工作I和工作J的组合直接费用率最小,故应选择工作I和工作J作为压缩对象。
工作I和工作J的组合直接费用率0.7万元∕天,小于间接费用率0.8万元∕天,说明同时压缩工作I和工作J可使工程总费用降低。
由于工作J的持续时间只能压缩1天,工作I的持续时间也只能随之压缩1天。
工作I和工作J的持续时间同时压缩l天后,利用标号法重新确定计算工期和关键线路。
此时,关键线路仍然为两条,即:①—③—④—⑥和①—③—⑤—⑥。
第三次压缩后的网络计划如图12所示。
此时,关键工作/的持续时间也已达最短,不能再压缩,故其直接费用率变为无穷大。
(①,4)
(③,11) Array (①,8)(③,14)
图12 第三次压缩后的网络计划
4)第四次压缩:
从图3-46可知,由于工作E和工作/不能再压缩,而为了同时缩短两条关
键线路①—③—④—⑥和①—③—⑤—⑥的总持续时间,只有以下两个压缩方案:
①压缩工作B,直接费用率为1.O万元/天;
②同时压缩工作G和工作I,组合直接费用率为0.8+0.5=1.3万元∕天。
在上述压缩方案中,由于工作B的直接费用率最小,故应选择工作B作为压缩对象。
但是,由于工作B的直接费用率1.O万元∕天,大于间接费用率0.8万元/天,说明压缩工作B会使工程总费用增加。
因此,不需要压缩工作B,优化方案已得到,优化后的网络计划如图13所示。
图中箭线上方括号内数字为工作的直接费。
(①,4)
(①,8)(③,14)
(③,11)
图13 费用优化后的网络计划
(5)计算优化后的工程总费用
①直接费总和:C
d0
=7.0+9.0+5.7+5.5+8.4+8.0+5.0+8.0+6.9= 63.5万元;
②间接费总和:C
i0
=0.8×16=12.8万元;
③工程总费用:C
t0 = C
d0
+ C
iO
= 63.5+12.8=76.3万元。
