2018秋新人教版九年级数学上册第二十三章旋转章末检测题B有答案
2018年秋九年级数学上册第23章旋转单元测试卷(含解析)(新版)新人教版

第23章旋转考试时间:120分钟;满分:150分学校:___________姓名:___________班级:___________考号:___________题号一二三总分得分评卷人得分一.选择题(共10小题,满分40分,每小题4分)1.(4分)下列运动属于旋转的是()A.滚动过程中的篮球的滚动B.钟表的钟摆的摆动C.气球升空的运动D.一个图形沿某直线对折的过程2.(4分)如图,△ODC是由△OAB绕点O顺时针旋转40°后得到的图形,若点D恰好落在AB上,且∠AOC=105°,则∠DOB的度数是()A.40° B.30° C.25° D.20°3.(4分)正五边形绕着它的中心旋转后与它本身重合,最小的旋转角度数是()A.36° B.54° C.72° D.108°4.(4分)在平面直角坐标系中,把点P(﹣5,4)向右平移9个单位得到点P1,再将点P1绕原点顺时针旋转90°得到点P2,则点P2的坐标是()A.(4,﹣4) B.(4,4) C.(﹣4,﹣4) D.(﹣4,4)5.(4分)在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O 称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是()A.Q(3,240°)B.Q(3,﹣120°) C.Q(3,600°) D.Q(3,﹣500°)6.(4分)在平面直角坐标系中,点P(﹣3,﹣5)关于原点对称的点的坐标是()A.(3,﹣5) B.(﹣3,5)C.(3,5) D.(﹣3,﹣5)7.(4分)下列各图,均是圆与等边三角形的组合,则不是轴对称图形的是()A.B. C. D.8.(4分)将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是()A. B.C.D.9.(4分)已知正方形的一条对角线长为2,把正方形经过某种图形变换后的面积为4,则图形变换是()A.相似变换 B.旋转变换 C.轴对称变换 D.平移变换10.(4分)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,从一个格点移动到与之相距5的另一个格点的运动称为一次跳马变换,例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.現有10×10的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是()A.7 B.8 C.9 D.10二.填空题(共4小题,满分20分,每小题5分)11.(5分)如图,将Rt △ABC 绕直角顶点C 顺时针旋转90°,得到△DEC ,连接AD ,若∠BAC=25°,则∠BAD= .12.(5分)如图,在矩形ABCD 中,AD=3,将矩形ABCD 绕点A 逆时针旋转,得到矩形AEFG ,点B 的对应点E 落在CD 上,且DE=EF ,则AB 的长为 .13.(5分)在平面直角坐标系中,点A 的坐标为(a ,3),点B 的坐标是(4,b ),若点A 与点B 关于原点O 对称,则ab= .14.(5分)如图,点O 是▱ABCD 的对称中心,AD >AB ,E 、F 是AB 边上的点,且EF=21AB ;G 、H 是BC 边上的点,且GH=31BC ,若S 1,S 2分别表示△EOF 和△GOH 的面积,则S 1与S 2之间的等量关系是 .三.解答题(共9小题,满分90分)15.(8分)如图所示,将△AOB绕着点O旋转180度得到△DOC,过点O的一条直线分别交BA、CD 的延长线于点E、F,求证:AE=DF.16.(8分)如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE,求证:FD=BE.17.(8分)在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1,P1关于原点的对称点是点P2,求点P2的坐标及P2到原点的距离.18.(8分)如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.(1)在图1中,画出一个与△ABC成中心对称的格点三角形;(2)在图2中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;(3)在图3中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.19.(10分)如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM.(1)求证:EF=MF;(2)当AE=1时,求EF的长.20.(10分)如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.(1)求证:四边形ABEF是平行四边形;(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.21.(12分)如图,在△ABC中,∠ABC=90°,∠BAC=60°,AC绕点C顺时针旋转60°至CD,F是CD的中点,连接BF交AC于点E,连接AD.求证:(1)AC=BF;(2)四边形ABFD是平行四边形.22.(12分)如图,已知A(2,3)和直线y=x.(1)分别写出点A关于直线y=x的对称点B和关于原点的对称点C的坐标.(2)若点D是点B关于原点的对称点,判断四边形ABCD的形状,并说明理由.23.(14分)如图,矩形ABCD中,AC=2AB,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B'落在AC上,B'C'交AD于点E,在B'C′上取点F,使B'F=AB.(1)求证:AE=C′E.(2)求∠FBB'的度数.(3)已知AB=2,求BF的长.2018年九年级上学期 第23章 旋转 单元测试卷参考答案与试题解析一.选择题(共10小题,满分40分,每小题4分)1.【分析】根据旋转变换的概念,对选项进行一一分析,排除错误答案.【解答】解:A 、滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属旋转;B 、钟表的钟摆的摆动,符合旋转变换的定义,属于旋转;C 、气球升空的运动是平移,不属于旋转;D 、一个图形沿某直线对折的过程是轴对称,不属于旋转.故选:B .【点评】本题考查旋转的概念.旋转变换:一个图形围绕一个定点旋转一定的角度,得到另一个图形,这种变换称为旋转变换.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.2.【分析】根据旋转的性质求出∠AOD 和∠BOC 的度数,计算出∠DOB 的度数.【解答】解:由题意得,∠AOD=∠BOC=40°,又∠AOC=105°,∴∠DOB=105°﹣40°﹣40°=25°.故选:C .【点评】本题考查的是旋转的性质,掌握旋转角的概念是解题的关键.3.【分析】根据旋转的定义,最小旋转角即为正五边形的中心角.【解答】解:正五边形绕着它的中心旋转后与它本身重合,最小的旋转角度数是5360=72度. 故选:C .【点评】考查图形的旋转与重合,理解旋转对称图形的定义是解决本题的关键.【链接】旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.4.【分析】首先利用平移的性质得出P1(4,4),再利用旋转变换的性质可得结论;【解答】解:∵P(﹣5,4),点P(﹣5,4)向右平移9个单位得到点P1∴P1(4,4),∴将点P1绕原点顺时针旋转90°得到点P2,则点P2的坐标是(4,﹣4),故选:A.【点评】本题考查坐标与图形变化﹣旋转以及平移,解题的关键是理解题意,熟练掌握基本知识,属于中考基础题.5.【分析】根据中心对称的性质解答即可.【解答】解:∵P(3,60°)或P(3,﹣300°)或P(3,420°),由点P关于点O成中心对称的点Q可得:点Q的极坐标为(3,240°),(3,﹣120°),(3,600°),故选:D.【点评】此题考查中心对称的问题,关键是根据中心对称的性质解答.6.【分析】根据关于原点对称的点的坐标特点解答.【解答】解:点P(﹣3,﹣5)关于原点对称的点的坐标是(3,5),故选:C.【点评】本题考查的是关于原点的对称的点的坐标,平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),即关于原点的对称点,横纵坐标都变成相反数.7.【分析】根据轴对称图形的概念对各选项分析判断即可得解.【解答】解:A、是轴对称图形,故本选项错误;B、不是轴对称图形,故本选项正确;C、是轴对称图形,故本选项错误;D、是轴对称图形,故本选项错误.故选:B.【点评】本题考查了利用轴对称设计图案,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.8.【分析】根据旋转的性质,△AOB 绕点O 旋转180°得到△DOE ,点A 与点D 、B 与E 关于点O 成中心对称解答.【解答】解:∵△AOB 绕点O 旋转180°得到△DOE ,∴作图正确是C 选项图形.故选:C .【点评】本题考查了利用旋转变换作图,熟记旋转的性质,判断出对应点关于点O 对称是解题的关键.9.【分析】根据正方形的性质利用勾股定理可求得其边长,从而就不难求得其面积,根据其面积不变解答即可.【解答】解:由题意得,正方形的边长为2,故面积为2,把正方形经过某种图形平移变换后的面积为4,故选:D .【点评】主要考查到正方形的性质和面积的求法.要注意:正方形的对角线和正方形的两条相邻的边构成等腰直角三角形.10.【分析】根据从一个格点移动到与之相距5的另一个格点的运动称为一次跳马变换,计算出按A ﹣D ﹣F 的方向连续变换4次后点M 的位置,再根据点N 的位置进行适当的变换,即可得到变换总次数.【解答】解:如图1,连接AD ,DF ,则AF=32,∴两次变换相当于向右移动3格,向上移动3格,又∵MN=102,∴102÷32=310,(不是整数) ∴按A ﹣D ﹣F 的方向连续变换4次后,相当于向右移动了4÷2×3=6格,向上移动了4÷2×3=6格, 此时M 位于如图2所示的正方形网格的点G 处,再按如图所示的方式变换4次即可到达点N 处,∴从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是4+4=8次,故选:B.【点评】本题主要考查了几何变换的类型以及勾股定理的运用,解题时注意:在平移变换下,对应线段平行且相等,两对应点连线段与给定的有向线段平行(共线)且相等.解决问题的关键是找出变换的规律.二.填空题(共4小题,满分20分,每小题5分)11.【分析】根据旋转的性质可得AC=CD,再判断出△ACD是等腰直角三角形,然后根据等腰直角三角形的性质求出∠CAD=45°,由∠BAD=∠BAC+∠CAD可得答案.【解答】解:∵Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,∴AC=CD,∴△ACD是等腰直角三角形,∴∠CAD=45°,则∠BAD=∠BAC+∠CAD=25°+45°=70°,故答案为:70°.【点评】本题考查了旋转的性质,等腰直角三角形的判定与性质,熟记各性质并准确识图是解题的关键.12.【分析】由旋转的性质得到AD=EF,AB=AE,再由DE=EF,等量代换得到AD=DE,即三角形AED为等腰直角三角形,利用勾股定理求出AE的长,即为AB的长.【解答】解:由旋转得:AD=EF,AB=AE,∠D=90°,∵DE=EF,∴AD=DE ,即△ADE 为等腰直角三角形,根据勾股定理得:AE=2233+=32,则AB=AE=32,故答案为:32【点评】此题考查了旋转的性质,矩形的性质,熟练掌握旋转的性质是解本题的关键.13.【分析】直接利用关于原点对称点的性质得出a ,b 的值,进而得出答案.【解答】解:∵点A 的坐标为(a ,3),点B 的坐标是(4,b ),点A 与点B 关于原点O 对称, ∴a=﹣4,b=﹣3,则ab=12.故答案为:12.【点评】此题主要考查了关于原点对称点的性质,正确得出a ,b 的值是解题关键.14.【分析】根据同高的两个三角形面积之比等于底边之比得出AOB S S ∆1=AB EF =21,BOC S S ∆2=BC GH =31,再由点O 是▱ABCD 的对称中心,根据平行四边形的性质可得S △AOB =S △BOC =41S ▱ABCD ,从而得出S 1与S 2之间的等量关系.【解答】解:∵AOB S S ∆1=AB EF =21,BOC S S ∆2=BC GH =31, ∴S 1=21S △AOB ,S 2=31S △BOC . ∵点O 是▱ABCD 的对称中心, ∴S △AOB =S △BOC =41S ▱ABCD , ∴21S S =3121=23. 即S 1与S 2之间的等量关系是21S S =23.故答案为21S S =23. 【点评】本题考查了中心对称,三角形的面积,平行四边形的性质,根据同高的两个三角形面积之比等于底边之比得出AOB S S ∆1=AB EF =21,BOC S S ∆2=BC GH =31是解题的关键.三.解答题(共9小题,满分90分)15.【分析】先利用旋转的性质得OB=OC ,AB=CD ,∠B=∠C ,再证明△OBE ≌△OCF 得到BE=CF ,从而可判断AE=DF .【解答】证明:∵△AOB 绕着点O 旋转180度得到△DOC ,∴OB=OC ,AB=CD ,∠B=∠C ,在△OBE 和△OCF 中⎪⎩⎪⎨⎧∠=∠=∠=∠COF BOE OCOB C B , ∴△OBE ≌△OCF ,∴BE=CF ,∴BE ﹣AB=CF ﹣CD ,即AE=DF .【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质.16.【分析】根据中心对称的性质可得BO=DO ,AO=CO ,再利用等式的性质可得FO=EO ,然后再证明△FOD ≌△EOB ,利用全等三角形的性质可得DF=BE .【解答】证明:∵△ABO 与△CDO 关于O 点中心对称,∴BO=DO ,AO=CO ,∵AF=CE ,∴AO ﹣AF=CO ﹣CE ,∴FO=EO ,在△FOD 和△EOB 中⎪⎩⎪⎨⎧=∠=∠=DO BO EOB FOD EO FO ,∴△FOD ≌△EOB (SAS ),∴DF=BE .【点评】此题主要考查了中心对称以及全等三角形的判定和性质,关键是掌握关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.17.【分析】先利用点平移的坐标规律,把点P 的横坐标加上8,纵坐标不变可得到P 1点的坐标,再利用关于原点对称的点的坐标特征写出P 2点的坐标,然后利用两点间的距离公式计算点P 2到原点的距离.【解答】解:∵点P (﹣5,3)向右平移8个单位得到点P 1,∴P 1点的坐标为(3,3),∵,P 1关于原点的对称点是点P 2,∴P 2点的坐标为(﹣3,﹣3),P 2到原点的距离=2233+=32.【点评】本题考查了关于原点对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x 轴对称的点,横坐标相同,纵坐标互为相反数;关于y 轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.18.【分析】(1)根据中心对称的性质即可作出图形;(2)根据轴对称的性质即可作出图形;(3)根据旋转的性质即可求出图形.【解答】解:(1)如图所示,△DCE为所求作(2)如图所示,△ACD为所求作(3)如图所示△ECD为所求作【点评】本题考查图形变换,解题的关键是正确理解图形变换的性质,本题属于基础题型.19.【分析】(1)由旋转的性质可得DE=DM,∠EDM为直角,可得出∠EDF+∠MDF=90°,由∠EDF=45°,得到∠MDF为45°,可得出∠EDF=∠MDF,再由DF=DF,利用SAS可得出三角形DEF与三角形MDF 全等,由全等三角形的对应边相等可得出EF=MF;(2)由第一问的全等得到AE=CM=1,正方形的边长为3,用AB﹣AE求出EB的长,再由BC+CM求出BM的长,设EF=MF=x,可得出BF=BM﹣FM=BM﹣EF=4﹣x,在直角三角形BEF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为EF的长.【解答】(1)证明:∵△DAE绕点D逆时针旋转90°得到△DCM,∴DE=DM,∠EDM=90°,∴∠EDF=∠FDM .又∵DF=DF ,DE=DM ,∴△DEF ≌△DMF ,∴EF=MF ;(2)解:设EF=MF=x ,∵AE=CM=1,AB=BC=3,∴EB=AB ﹣AE=3﹣1=2,BM=BC+CM=3+1=4,∴BF=BM ﹣MF=4﹣x .在Rt △EBF 中,由勾股定理得EB 2+BF 2=EF 2,即22+(4﹣x )2=x 2, 解得:x=25, 则EF 的长为25.【点评】此题考查了旋转的性质,正方形的性质,全等三角形的判定与性质,以及勾股定理,利用了转化及方程的思想,熟练掌握性质及定理是解本题的关键.20.【分析】(1)根据旋转得出CA=CE ,CB=CF ,根据平行四边形的判定得出即可;(2)根据等边三角形的判定得出△ABC 是等边三角形,求出AE=BF ,根据矩形的判定得出即可.【解答】(1)证明:∵将△ABC 绕点C 顺时针旋转180°得到△EFC ,∴△ABC ≌△EFC ,∴CA=CE ,CB=CF ,∴四边形ABEF 是平行四边形;(2)解:当∠ABC=60°时,四边形ABEF 为矩形,理由是:∵∠ABC=60°,AB=AC ,∴△ABC是等边三角形,∴AB=AC=BC,∵CA=CE,CB=CF,∴AE=BF,∵四边形ABEF是平行四边形,∴四边形ABEF是矩形.【点评】本题考查了旋转的性质和矩形的判定、平行四边形的判定、等边三角形的性质和判定等知识点,能综合运用知识点进行推理是解此题的关键.21.【分析】(1)连接AF,由旋转的旋转得到AC=DC,∠ACD=60°,进而△ACD是等边三角形,再证四边形ADCF是矩形,根据矩形的对角线相等即可得到AC=BF.(2)根据△ACD是等边三角形,得到AC=AD,进一步证明AD=BF,再证明AB=DF,即可得到四边形ABFD是平行四边形.【解答】解:(1)如图,连接AF,∵AC绕点C顺时针旋转60°至CD,∴AC=DC,∠ACD=60°,∴△ACD是等边三角形,∵F是CD的中点,∴AF⊥CD,∴∠AFC=90°,∵在△ABC中,∠ABC=90°,∠BAC=60°,∴∠ACD=30°,∵∠ACD=60°,∴∠BCD=90°,又∵∠ADC=90°,∴AC=BF.(2)∵△ACD是等边三角形,∴AC=AD,∵AC=BF,∴AD=BF,∵四边形ABCF是矩形,∴AB=CF,∵F是CD的中点,∴DF=CF,∴AB=DF,∴四边形ABFD是平行四边形.【点评】本题考查了旋转的旋转,解决本题的关键是熟记矩形、平行四边形的性质定理与判定定理.22.【分析】(1)依据关于直线y=x的对称点的坐标特征以及关于原点的对称点的坐标特征,即可得到B(3,2),C(﹣2,﹣3);(2)先依据轴对称和中心对称的性质,得到四边形ABCD是平行四边形,再依据AC=BD,即可得出四边形ABCD是矩形.【解答】解:(1)∵A(2,3),∴点A关于直线y=x的对称点B和关于原点的对称点C的坐标分别为:B(3,2),C(﹣2,﹣3);(2)四边形ABCD是矩形.理由如下:∵B(3,2)关于原点的对称点为D(﹣3,﹣2),又∵点B点D关于原点对称,∴BO=DO.同理AO=DO,∴四边形ABCD是平行四边形.∵A关于直线y=x的对称点为B,点A关于原点的对称点C,∴AC=BD,∴四边形ABCD是矩形.【点评】本题主要考查了关于原点对称的点的坐标特征以及矩形的判定,解题时注意:对角线相等23.【分析】(1)在直角三角形ABC 中,由AC=2AB ,得到∠ACB=30°,再由折叠的性质得到一对角相等,利用等角对等边即可得证;(2)由(1)得到△ABB′为等边三角形,利用矩形的性质及等边三角形的内角为60°,即可求出所求角度数;(3)法1:由AB=2,得到B′B=B′F=2,∠B′BF=15°,过B 作BH ⊥BF ,在直角三角形BB′H 中,利用锐角三角函数定义求出BH 的长,由BF=2BH 即可求出BF 的长;法2:连接AF ,过A 作AM ⊥BF ,可得△AB′F 是等腰直角三角形,△AB′B 为等边三角形,分别利用三角函数定义求出MF 与AM ,根据AM=BM ,即BM+MF=BF 即可求出.【解答】(1)证明:∵在Rt △ABC 中,AC=2AB ,∴∠ACB=∠AC′B′=30°,∠BAC=60°,由旋转可得:AB′=AB,∠B′AC=∠BAC=60°,∴∠EAC′=∠AC′B′=30°,∴AE=C′E;(2)解:由(1)得到△ABB′为等边三角形,∴∠AB′B=60°,∴∠FBB′=15°;(3)法1:解:由AB=2,得到B′B=B′F=2,∠B′BF=15°,过B 作B′H⊥BF ,在Rt △BB′H 中,cos15°=BB BH ',即BH=2×426+=226+, 则BF=2BH=6+2(cos15°=cos(45°﹣30°)=cos45°cos30°+sin45°sin30°=22×23+22×21=226+); 法2:连接AF ,过A 作AM ⊥BF ,(2)可得△AB′F 是等腰直角三角形,△AB′B 为等边三角形,∴∠AFB′=45°,∴∠AFM=30°,∠ABF=45°,在Rt △AMF 中,AM=BM=AB•cos∠ABM=2×22=2, 在Rt △AMF 中,MF=AFM AM tan =332=6, 则BF=2+6.【点评】此题考查了旋转的性质,矩形的性质,锐角三角函数定义,等边三角形、直角三角形的性质,熟练掌握旋转的性质是解本题的关键.。
人教版九年级数学上册第二十三章旋转单元复习与检测(含答案解析)

人教版九年级数学上册第二十三章旋转单元复习与检测(含答案)一、选择题1、如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°,得到△AB'C',过点B'作B'D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )A.2B.3C.2D.32、下列说法中,正确的有( )①线段两端点关于它的中点对称;②菱形的一组对边关于对角线的交点对称;③成中心对称的两个图形一定全等;④如果两个图形全等,那么这两个图形一定关于某点成中心对称;⑤如果两个三角形的对应点连线都经过一点,那么这两个三角形成中心对称.( )A.2个B.3个C.4个D.5个3、在等腰三角形、平行四边形、直角梯形和圆中,既是轴对称图形又是中心对称图形的是( )A.等腰三角形B.平行四边形C.直角梯形D.圆4、一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )A.是轴对称图形,但不是中心对称图形B.是中心对称图形,但不是轴对称图形C.既是轴对称图形,又是中心对称图形D.既不是轴对称图形,也不是中心对称图形5、如图是由五个形状、大小相同的正方形组成的图形,如果去掉其中一个正方形,使得剩下的图形是一个中心对称图形,那么不同的方法有( )A.1种B.2种C.3种D.4种6、如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③△ABF与△DAE成中心对称.其中正确的结论有( )A.0个B.1个C.2个D.3个7、平面直角坐标系内,把一个三角形的各顶点的横、纵坐标都乘以-1,则以这三个新坐标为顶点的三角形与原三角形( )A.关于x轴对称B.关于y轴对称C.关于坐标原点对称D.关于直线y=x对称8、如图,△ABC与△A'B'C'成中心对称,下列说法不正确的是( )A.S△ACB=S△A'B'C'B.AB=A'B'C.AB∥A'B',A'C'∥AC,BC∥B'C'D.S△A'B'O=S△ACO9、如图,在平面直角坐标系中,等边三角形OAB的顶点A在x轴上,顶点B在第一象限,若OA=2,则点B关于原点的对称点坐标为( )A.(1,)B.(,1)C.(-1,-)D.(-,-1)10、在平面直角坐标系中,把一个三角形的各顶点的横、纵坐标都乘-1,则以这三个新坐标为顶点的三角形与原三角形( )A.关于x轴对称B.关于y轴对称C.关于坐标原点对称D.关于直线y=x对称二、填空题11、如图,在△ABC中,AC=BC=8,∠C=90°,点D为BC的中点,将△ABC绕点D逆时针旋转45°,得到△A'B'C',B'C'与AB交于点E,则S四边形ACDE= .12、在一次数学社团活动上,小明设计了一个社团标识,如图所示,正方形ABCD与折线D-E-F-B构成了中心对称图形,且DE⊥EF,AD=50,DE比EF长25,那么EF的长是.13、下列图形:角、线段、等边三角形、长方形、平行四边形、圆,其中既是轴对称图形又是中心对称图形的有.14、如图,已知矩形ABCD,AB在y轴上,AB=2,BC=3,点A的坐标为(0,1),在AD边上有一点E(1,1),过点E的直线平分矩形ABCD的面积,则此直线的解析式为.15、四边形ABCD中,AD∥BC,E是CD的中点,连接AE并延长交BC的延长线于点F,连接BE,则点C与点关于点E对称,△ADE与△FCE成对称;若AB=AD+BC,则△ABF 是三角形,BE是△ABF的(将你认为正确的结论填上一个即可).16、已知a<0,则点P(-a2,-a+1)关于原点的对称点P'在第象限.17、如图,P为正方形ABCD内的一点,PC=1,将△CDP绕点C逆时针旋转得到△CBE,则PE= .18、如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC 绕点C逆时针旋转60°得到FC,连接DF,则在点E运动过程中,DF的最小值是.19、已知平面直角坐标系中点A、B、C的坐标分别为(0,-1)、(0,2)、(3,0),若从四个点M(3,3)、N(3,-3)、P(-3,1)、Q(-3,0)中选一个,分别与点A、B、C一起作为顶点组成四边形,则组成的四边形是中心对称图形的个数为( )A.4B.3C.2D.120、在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出旋转后的点关于原点的对称点,称为一次变换.已知点A的坐标为(-1,0),则点A经过连续2 019次这样的变换后得到的点A2 019的坐标是.三、解答题21、如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上的一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,求AP的长.22、如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O对称.求证:BF=DE.23、如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的格点上.(1)在图甲中作出的四边形是中心对称图形但不是轴对称图形;(2)在图乙中作出的四边形是轴对称图形但不是中心对称图形;(3)在图丙中作出的四边形既是轴对称图形又是中心对称图形.24、如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.25、如图,在正方形网格上有A、B、O三点,用(3,3)表示A点的位置,用(1,1)表示B点的位置,O点也在网格格点上.(1)作出点B关于直线OA的对称点C,写出点C的坐标(不写作法,但要在图中标出字母);(2)作出△ABC关于点O的中心对称图形△A'B'C',写出A'、B'、C'三点的坐标(不写作法,但要标出字母);(3)若网格上的最小正方形边长为1,求出△A'B'C'的面积.参考答案一、1、答案 D 在等腰直角△ABC中,AB===6,由旋转的性质知AB'=AB=6,∠BAB'=75°.在直角△B'AD中,∠B'AD=180°-∠BAC-∠BAB'=180°-45°-75°=60°,则AD=6×=3.故选D.2、答案 B ①正确;②正确;③正确;两个图形全等,这两个图形不一定关于某点成中心对称,但关于某点中心对称的两个图形一定全等,故④错误;如果两个三角形的对应点连线都经过一点,那么这两个三角形位似,但不一定全等,故这两个三角形不一定成中心对称,故⑤错误.故选B.3、答案 D 由轴对称图形与中心对称图形的概念知,圆既是轴对称图形又是中心对称图形.故选D.4、答案 C ∵一个正多边形绕它的中心旋转45°后,能与原正多边形第一次重合,又∵360°÷45°=8,∴这个正多边形是正八边形.正八边形既是轴对称图形,又是中心对称图形.故选C.5、答案 B 去掉一个正方形,得到中心对称图形的情况如下图所示,共2种方法.故选B.6、答案 C ∵四边形ABCD为正方形,∴AB=DA=DC,∠D=∠BAD=90°,∵CE=DF,∴DE=AF,∴△DEA≌△AFB,∴AE=BF,∠DEA=∠AFB,又∠DEA+∠DAE=90°,∴∠AFB+∠DAE=90°,∴∠AOF=90°,即AE⊥BF,∴①②正确.∵△ABF 绕对角线的交点,顺时针旋转90°可得△DAE,∴△ABF与△DAE不成中心对称,故③错误.故选C.7、答案 C 一个三角形的各顶点的横、纵坐标都乘以-1,则新图形的各顶点的横、纵坐标与原图形的相应顶点的横、纵坐标互为相反数,∴以这三个新坐标为顶点的三角形与原三角形关于坐标原点对称.故选C.8、答案y=x-1解析∵抛物线y=-x2的顶点为(0,0),抛物线y=x2-2的顶点为(0,-2),∴点A的坐标为(0,-1).把y=0代入y=x2-2,得x2-2=0,解得x=±,∴点B的坐标为(,0).设直线AB的解析式为y=kx+b,把(0,-1)和(,0)代入可得解得∴直线AB的解析式为y=x-1.9、答案C如图,过点B作BC⊥x轴于C,∵△OAB是等边三角形,OA=2,∴OC=OA=×2=1,OB=OA=2,由勾股定理得BC=-=-=,∴点B的坐标为(1,),∴点B关于原点的对称点坐标为(-1,-).故选C.10、答案 C ∵一个三角形的各顶点的横、纵坐标都乘-1,∴以这三个新坐标为顶点的三角形与原三角形关于坐标原点对称.故选C.二、11、答案4+2解析如图,连接MN,过N作NH⊥OA于H,∵线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点,∴∠MPN=90°,PN=PM=,∴△PMN为等腰直角三角形,∴MN===2,在Rt△OHN中,∵∠NOH=30°,ON=8,∴NH=ON=4,OH=-=-=4.在Rt△MNH中,∵NH=4,MN=2,∴MH=-=2,∴OM=OH+MH=4+2.12、答案10解析连接BD,与EF交于点O,∵正方形ABCD与折线D-E-F-B构成了中心对称图形,∴OE=EF,OD=BD.∵AD=50,∴BD==50,∴OD=25.设EF=2x,则OE=x,DE=2x+25,在Rt△DOE中,x2+(2x+25)2=(25)2,解得x=5或x=-25(舍去),则EF=5×2=10.13.答案线段、长方形、圆解析由轴对称图形和中心对称图形的概念可知,线段、长方形、圆既是轴对称图形又是中心对称图形.14、答案y=-2x+3解析易知矩形是中心对称图形,且对称中心是对角线的交点.由题意可得矩形ABCD的对角线交于点F(1.5,0),∵过对称中心的直线把矩形分成面积相等的两个图形,∴直线EF平分矩形ABCD的面积.设直线EF的解析式为y=kx+b,则解得∴直线EF的解析式为y=-2x+3.15、答案D;中心;等腰;高(或中线或角平分线)16、答案四解析∵点P(-a2,-a+1)关于原点的对称点为P',∴P'(a2,a-1),∵a<0,∴a-1<0,a2>0,∴P'在第四象限.17、答案解析∵△CDP绕点C逆时针旋转得到△CBE,∴其旋转中心是点C,旋转角度是90°,∴∠PCE=90°,EC=PC,∵PC=1,∴EC=PC=1,∴△CPE是等腰直角三角形,∴PE===.18、答案 1.5解析如图,取AC的中点G,连接EG,∵旋转角为60°,∴∠ECD+∠DCF=60°.又∵∠ECD+∠GCE=∠ACB=60°,∴∠DCF=∠GCE.∵AD是等边△ABC的对称轴,∴CD=BC,∴CD=CG.又∵CE旋转到CF,∴CE=CF,∴△DCF≌△GCE,∴DF=EG,根据垂线段最短知EG⊥AD时,EG最短,即DF最短,此时,∵∠CAD=×60°=30°,AG=AC=×6=3,∴EG=AG=×3=1.5,∴DF=1.5.19、答案 B 如图所示,组成的四边形有4个,其中四边形BACM、四边形BANC和四边形ACBP 都是平行四边形,都是中心对称图形.故选B.20、答案-解析由题意知第一次变换后的坐标为,第二次变换后的坐标为(0,-1),第三次变换后的坐标为-,第四次变换后的坐标为(1,0),第五次变换后的坐标为--,第六次变换后的坐标为(0,1),第七次变换后的坐标为-,第八次变换后的坐标为(-1,0),回到变换前A的位置,说明8次变换为一个循环.因为2 019÷8=252……3,所以把点A经过连续2 019次这样的变换后得到的点A2 019的坐标是-.三、21、解析如图,∵AC=9,AO=3,∴CO=6.∵△ABC为等边三角形,∴∠A=∠C=60°.∵线段OP绕点O逆时针旋转60°得到线段OD,且点D恰好落在BC上,∴OD=OP,∠POD=60°.∵∠1+∠2+∠A=180°,∠1+∠3+∠POD=180°,∴∠1+∠2=120°,∠1+∠3=120°,∴∠2=∠3.在△AOP和△CDO中,∴△AOP≌△CDO,∴AP=CO=6.即AP的长为6.22、证明如图,连接AD、BC,∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,∴BO=DO,∵点E、F关于点O对称,∴OF=OE,在△BOF和△DOE中,∴△BOF≌△DOE(SAS),∴BF=DE.23.解析(1)如图甲所示.(2)如图乙所示.(3)如图丙所示.24、解析(1)如图所示.(2)如图所示.(3)点P的坐标为(2,0).25、解析(1)如图所示:点C即为所求,C(5,1).(2)如图所示:△A'B'C'即为所求,A'(3,-3),B'(5,-1),C'(1,-1).(3)△A'B'C'的面积S△A'B'C'=×4×2=4.。
2018年秋人教版九年级数学上《第23章旋转》单元测试题(含答案解析)

2018年秋人教版九年级上册数学《第23章旋转》单元测试题一.选择题(共10小题)1.下列各图中,既可经过平移,又可经过旋转,由图形①得到图形②的是()A.B.C.D.2.若干个正方形按如图方式拼接,三角形M经过旋转变换能得到三角形N,下列四个点能作为旋转中心的是()A.点A B.点B C.点C D.点D3.下列图形绕某点旋转90°后,不能与原来图形重合的是()A.B.C.D.4.如图,已知A(2,1),现将A点绕原点O逆时针旋转90°得到A1,则A1的坐标是()A.(﹣1,2)B.(2,﹣1)C.(1,﹣2)D.(﹣2,1)5.下列四组图形中,左边的图形与右边的图形成中心对称的有()A.1组B.2组C.3组D.4组6.如图图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.7.已知点A(a,﹣1)与B(2,b)是关于原点O的对称点,则()A.a=﹣2,b=﹣1 B.a=﹣2,b=1 C.a=2,b=﹣1 D.a=2,b=1 8.如图,是用围棋子摆出的图案,围棋子的位置用有序数对表示,如:A点在(5,1),若再摆放一枚黑棋子,要使8枚棋子组成的图案是轴对称图形,则下列摆放错误的是()A.黑(2,3)B.黑(3,2)C.黑(3,4)D.黑(3,1)9.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是()A.B.C.D.10.如图,将△ABC绕点A逆时针旋转100°,得到△ADE,若点D在线段BC的延长线上,则∠B的大小为()A.60°B.50°C.45°D.40°二.填空题(共8小题)11.如图,等边△AOB绕点O逆时针旋转到△A′OB′的位置,∠A′OB=80°,则△AOB旋转了度.12.时钟上的分针匀速旋转一周需要60分钟,则经过10分钟,分针旋转了度.13.已知点A(a,b)绕着(0,﹣1)旋转180°得到B(﹣4,1),则A点坐标为.14.在平面直角坐标系中,设点P到原点的距离为ρ(希腊字母读作“柔”),OP看作由x轴的正半轴逆时针旋转而成的夹角α,则用[ρ,α]表示点P的雷达坐标,则点P(﹣7,7)的雷达坐标为.15.已知点A(a,1)与点A(4,b)关于原点对称,则a+b=.16.若点P(m+1,8﹣2m)关于原点的对称点Q在第三象限,那么m的取值范围是.17.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有个.18.一个正n边形绕它的中心至少旋转18°才能与原来的图形完全重合,则n的值为.三.解答题(共7小题)19.如图,△AEC绕A点顺时针旋转60°得△APB,∠PAC=20°,求∠BAE.20.如图所示,点D是等边△ABC内一点,DA=13,DB=19,DC=21,将△ABD 绕点A逆时针旋转到△ACE的位置,求△DEC的周长.21.如图,△ABC中,AD是中线,将△ACD旋转后与△EBD重合.(1)旋转中心是点,旋转了度;(2)如果AB=7,AC=4,求中线AD长的取值范围.22.如图,在△ABC中,∠C=90°,AC=2cm,AB=3cm,将△ABC绕点B顺时针旋转60°得到△FBE,求点E与点C之间的距离.23.如图,△A1AC1是由△ABC绕某点P按顺时针方向旋转90°得到的,△ABC的顶点坐标分A(﹣1,6),B(﹣5,0),C(﹣5,6).(1)求旋转中心P和点A1,C1的坐标;(2)在所给网格中画出△A1AC1绕点P按顺时针方向旋转90°得到的图形;(3)在所给网格中画出与△A1AC1关于点P成中心对称的图形.24.如图,在平面直角坐标系内,边长为4的等边△ABC的顶点B与原点重合,将△ABC绕顶点C顺时针旋转60°得到△ACA1,将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,请回答:(1)点A的坐标为;点A1的坐标为.(2)A2018的坐标为.25.如图,AM∥BN,∠MAB和∠NBA的角平分线相交于点P,过点P作直线EF分别交AM、BN于F、E.(1)求证:AB=AF+BE;(2)若EF绕点P旋转,F在MA的延长线上滑动,如图,请你测量,猜想AB、AF、BE之间的关系,写出这个关系式,并加以证明.2018年秋人教版九年级上册数学《第23章旋转》单元测试题参考答案与试题解析一.选择题(共10小题)1.下列各图中,既可经过平移,又可经过旋转,由图形①得到图形②的是()A.B.C.D.【分析】此题是一组复合图形,根据平移、旋转的性质解答.【解答】解:A、B、C中只能由旋转得到,不能由平移得到,只有D可经过平移,又可经过旋转得到.故选:D.【点评】本题考查平移、旋转的性质:①平移不改变图形的形状和大小;经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.②旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,两组对应点连线的交点是旋转中心.2.若干个正方形按如图方式拼接,三角形M经过旋转变换能得到三角形N,下列四个点能作为旋转中心的是()A.点A B.点B C.点C D.点D【分析】直接利用旋转的性质结合正方形的性质进而分析得出答案.【解答】解:如图所示:三角形M绕点C经过逆时针旋转变换能得到三角形N,故选:C.【点评】此题主要考查了旋转的性质以及正方形的性质,正确把握旋转的性质是解题关键.3.下列图形绕某点旋转90°后,不能与原来图形重合的是()A.B.C.D.【分析】根据旋转对称图形的概念作答.【解答】解:A、绕它的中心旋转90°能与原图形重合,故本选项不合题意;B、绕它的中心旋转90°能与原图形重合,故本选项不合题意;C、绕它的中心旋转90°能与原图形重合,故本选项不合题意;D、绕它的中心旋转120°才能与原图形重合,故本选项符合题意.故选:D.【点评】本题考查了旋转对称图形的知识,如果某一个图形围绕某一点旋转一定的角度(小于360°)后能与原图形重合,那么这个图形就叫做旋转对称图形.4.如图,已知A(2,1),现将A点绕原点O逆时针旋转90°得到A1,则A1的坐标是()A.(﹣1,2)B.(2,﹣1)C.(1,﹣2)D.(﹣2,1)【分析】将A点绕原点O逆时针旋转90°得到A1,相当于将Rt△OBA点绕原点O 逆时针旋转90°得到Rt△OB1A1,如图,然后根据旋转的性质得OB1=OB=2,A1B1=AB=1,从而得到点A1的坐标.【解答】解:将A点绕原点O逆时针旋转90°得到A1,即将Rt△OBA点绕原点O逆时针旋转90°得到Rt△OB1A1,如图,所以OB1=OB=2,A1B1=AB=1,所以点A1的坐标是(﹣1,2).故选:A.【点评】本题考查了坐标与图形变化﹣旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.5.下列四组图形中,左边的图形与右边的图形成中心对称的有()A.1组B.2组C.3组D.4组【分析】欲分析两个图形是否成中心对称,主要把一个图形绕一个点旋转180°,观察是否能和另一个图形重合即可.【解答】解:根据中心对称的概念,知②③④都是中心对称.故选:C.【点评】本题重点考查了两个图形成中心对称的定义.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.如果一个图形绕某一点旋转180°后能够与自身重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.6.如图图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念进行判断即可.【解答】解:A、是轴对称图形,不是中心对称图形,不合题意;B、不是轴对称图形,是中心对称图形,不合题意;C、是轴对称图形,不是中心对称图形,不合题意;D、是轴对称图形,也是中心对称图形,符合题意.故选:D.【点评】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.7.已知点A(a,﹣1)与B(2,b)是关于原点O的对称点,则()A.a=﹣2,b=﹣1 B.a=﹣2,b=1 C.a=2,b=﹣1 D.a =2,b=1【分析】平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),记忆方法是结合平面直角坐标系的图形记忆.根据条件就可以求出a,b的值.【解答】解:∵点A(a,﹣1)与点B(2,b)是关于原点O的对称点,∴a=﹣2,b=1,故选:B.【点评】此题考查关于原点对称的点的坐标,关于原点对称的点坐标的关系,是需要识记的基本问题.根据对称点坐标之间的关系可以得到方程或方程组问题.8.如图,是用围棋子摆出的图案,围棋子的位置用有序数对表示,如:A点在(5,1),若再摆放一枚黑棋子,要使8枚棋子组成的图案是轴对称图形,则下列摆放错误的是()A.黑(2,3)B.黑(3,2)C.黑(3,4)D.黑(3,1)【分析】根据轴对称图形定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【解答】解:要使8枚棋子组成的图案是轴对称图形,则黑子可以摆放在横坐标为3的格点上,故摆放错误的是A,故选:A.【点评】此题主要考查了轴对称图形,关键是掌握轴对称图形定义.9.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是()A.B.C.D.【分析】根据旋转的性质,△AOB绕点O旋转180°得到△DOE,点A与点D、B与E关于点O成中心对称解答.【解答】解:∵△AOB绕点O旋转180°得到△DOE,∴作图正确是C选项图形.故选:C.【点评】本题考查了利用旋转变换作图,熟记旋转的性质,判断出对应点关于点O对称是解题的关键.10.如图,将△ABC绕点A逆时针旋转100°,得到△ADE,若点D在线段BC的延长线上,则∠B的大小为()A.60°B.50°C.45°D.40°【分析】根据旋转的性质可得出AB=AD、∠BAD=100°,再根据等腰三角形的性质可求出∠B的度数,此题得解.【解答】解:根据旋转的性质,可得:AB=AD,∠BAD=100°,∴∠B=∠ADB=×(180°﹣100°)=40°.故选:D.【点评】本题考查了旋转的性质以及等腰三角形的性质,根据旋转的性质结合等腰三角形的性质求出∠B的度数是解题的关键.二.填空题(共8小题)11.如图,等边△AOB绕点O逆时针旋转到△A′OB′的位置,∠A′OB=80°,则△AOB旋转了140度.【分析】∠AOA′就是旋转角,根据等边三角形的性质得出∠AOB等于60°,再根据∠BOA′等于90°,从而求出∠AOA′的度数.【解答】解:旋转角∠AOA′=∠AOB+∠BOA′=60°+80°=140°.∴△AOB旋转了140度.故答案为:140.【点评】本题主要考查了旋转的性质,正确理解旋转角是解题的关键;此题较简单,解题时要能根据等边三角形的性质求出角的度数.12.时钟上的分针匀速旋转一周需要60分钟,则经过10分钟,分针旋转了60度.【分析】先求出时钟上的分针匀速旋转一分钟时的度数为6°,再求10分钟分针旋转的度数即可.【解答】解:∵时钟上的分针匀速旋转一周的度数为360°,时钟上的分针匀速旋转一周需要60分钟,则时钟上的分针匀速旋转一分钟时的度数为:360÷60=6°,那么10分钟,分针旋转了10×6°=60°,故答案为:60.【点评】本题主要考查了旋转,解决本题的关键是求出时钟上的分针匀速旋转一分钟时的度数.13.已知点A(a,b)绕着(0,﹣1)旋转180°得到B(﹣4,1),则A点坐标为(4,﹣3).【分析】利用旋转的性质得到点(0,﹣1)为AB的中点,利用线段中点坐标公式得到0=,1=,然后求出a、b即可得到A点坐标.【解答】解:∵点A(a,b)绕着(0,﹣1)旋转180°得到B(﹣4,1),∴点(0,﹣1)为AB的中点,∴0=,1=,解得a=4,b=﹣3,∴A点坐标为(4,﹣3).故答案为(4,﹣3).【点评】本题考查了坐标与图形变化:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.14.在平面直角坐标系中,设点P到原点的距离为ρ(希腊字母读作“柔”),OP看作由x轴的正半轴逆时针旋转而成的夹角α,则用[ρ,α]表示点P的雷达坐标,则点P(﹣7,7)的雷达坐标为[7,135°].【分析】先计算出点P(﹣7,7)到原点的距离,再求出点P(﹣7,7)与x轴的正半轴的夹角,然后利用新定义表示出雷达坐标.【解答】解:点P(﹣7,7)到原点的距离为7,因为点P(﹣7,7)在第二象限的角平分线上,所以点P(﹣7,7)与x轴的正半轴的夹角为135°,所以点P(﹣7,7)的雷达坐标为[7,135°].故答案为[7,135°].【点评】本题考查了坐标与图形变化﹣旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.15.已知点A(a,1)与点A(4,b)关于原点对称,则a+b=﹣5.【分析】根据“两点关于原点对称,则两点的横、纵坐标都是互为相反数”解答.【解答】解:∵点A(a,1)与点A′(4,b)关于原点对称,∴a、b的值分别为﹣4,﹣1.所以a+b=﹣1﹣4=﹣5,故答案为:﹣5【点评】本题考查了关于原点对称的点的坐标:两点关于原点对称,则两点的横、纵坐标都是互为相反数.16.若点P(m+1,8﹣2m)关于原点的对称点Q在第三象限,那么m的取值范围是﹣1<m<4.【分析】根据关于原点对称的点的坐标特点求出点Q的坐标,根据第三象限点的坐标特征列出不等式组,解不等式组即可.【解答】解:点P(m+1,8﹣2m)关于原点的对称点Q的坐标为(﹣m﹣1,﹣8+2m),由题意得,,解得,﹣1<m<4,故答案为:﹣1<m<4.【点评】本题考查的是关于原点对称的点的坐标特点和点的坐标,掌握两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点是P′(﹣x,﹣y)是解题的关键.17.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.【分析】利用轴对称图形的性质分别得出符合要求的答案即可.【解答】解:如图所示:与△ABC成轴对称的有△ACG、△AFE、△BFD、△CHD、△CGB一共有5个.故答案为:5.【点评】此题主要考查了利用轴对称设计图案,根据已知得出所有符合要求的答案注意不要漏解.18.一个正n边形绕它的中心至少旋转18°才能与原来的图形完全重合,则n的值为20.【分析】直接利用旋转图形的性质结合正多边形中心角相等进而得出答案.【解答】解:∵一个正n边形绕它的中心至少旋转18°才能与原来的图形完全重合,∴n的值为:=20.故答案为:20.【点评】此题主要考查了旋转对称图形,正确把握正多边形的性质是解题关键.三.解答题(共7小题)19.如图,△AEC绕A点顺时针旋转60°得△APB,∠PAC=20°,求∠BAE.【分析】充分运用旋转的性质,旋转前后三角形全等,即△ABP≌△ACE,根据对应角相等,三角形内角和定理,对应边的夹角为旋转角,通过计算解答题目问题.【解答】解:根据旋转的性质可得△ABP≌△ACE,AC与AB是对应边,∠BAC=∠BAP+∠PAC=60°,∵∠PAC=20°,∴∠CAE=∠BAP=40°,∴∠BAE=∠BAC+∠CAE=100°.【点评】本题考查旋转的性质,旋转变化前后,对应角分别相等,结合三角形内角和定理求出相关的角.20.如图所示,点D是等边△ABC内一点,DA=13,DB=19,DC=21,将△ABD 绕点A逆时针旋转到△ACE的位置,求△DEC的周长.【分析】先根据等边三角形的性质得∠BAC=60°,AB=AC,再根据旋转的性质得到AD=AE,CE=BD=19,∠DAE=∠BAC=60°,则可判断△ADE为等边三角形,从而得到DE=AD=13,然后计算△DEC的周长.【解答】解:∵△ABC为等边三角形,∴∠BAC=60°,AB=AC,∵△ABD绕点A逆时针旋转到△ACE的位置,∴AD=AE,CE=BD=19,∠DAE=∠BAC=60°,∴△ADE为等边三角形,∴DE=AD=13,∴△DEC的周长=DE+DC+CE=13+21+19=53.【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质.21.如图,△ABC中,AD是中线,将△ACD旋转后与△EBD重合.(1)旋转中心是点D,旋转了180度;(2)如果AB=7,AC=4,求中线AD长的取值范围.【分析】(1)根据旋转的性质填空即可;(2)根据三角形的任意两边之和大于第三边,两边之差小于第三边求出AE的取值范围,再根据旋转的性质可得DE=AD,然后求解即可.【解答】解:(1)∵将△ACD旋转后能与△EBD重合,∴旋转中心是点D,旋转了180度;故答案为:D,180;(2)∵将△ACD旋转后能与△EBD重合,∴BE=AC=4,DE=AD,在△ABE中,由三角形的三边关系得,AB﹣BE<AE<AB+BE,∵AB=7,∴3<AE<11,即3<2AD<11,∴1.5<AD<5.5,即中线AD长的取值范围是1.5<AD<5.5.【点评】本题考查了旋转的性质,三角形的三边关系,熟记各性质并准确识图是解题的关键.22.如图,在△ABC中,∠C=90°,AC=2cm,AB=3cm,将△ABC绕点B顺时针旋转60°得到△FBE,求点E与点C之间的距离.【分析】连接EC,即线段EC的长是点E与点C之间的距离,根据题意可得BC=,根据旋转的性质可证△EBC是等边三角形,即可求EC的长.【解答】解:连接EC,即线段EC的长是点E与点C之间的距离,在Rt△ACB中,由勾股定理得:BC===将△ABC绕点B顺时针旋转60°得到△FBE,∴BC=BE,∠CBE=60°∴△BEC是等边三角形∴EC=BE=BC=【点评】本题考查旋转的性质,等边三角形的判定和性质,熟练运用旋转的性质解决问题是本题的关键.23.如图,△A1AC1是由△ABC绕某点P按顺时针方向旋转90°得到的,△ABC的顶点坐标分A(﹣1,6),B(﹣5,0),C(﹣5,6).(1)求旋转中心P和点A1,C1的坐标;(2)在所给网格中画出△A1AC1绕点P按顺时针方向旋转90°得到的图形;(3)在所给网格中画出与△A1AC1关于点P成中心对称的图形.【分析】(1)利用网格特点和性质的性质,作AA1和CC1的垂直平分线,它们的交点即为P点,然后旋转中心P和点A1,C1的坐标;(2)利用网格特点和性质的性质作出A1、C1的对应点A2、C2,A点的对应点为A1,从而得到△A2A1C2;(3)根据中心对称的性质作出C关于P点的对应点C3,从而得到△BA2C3.【解答】解:(1)如图,点P为所作,P点坐标为(0,1),A1的坐标为(5,6);(2)如图,△A2A1C2为所作;(3)如图,△BA2C3为所作.【点评】本题考查了作图﹣旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.24.如图,在平面直角坐标系内,边长为4的等边△ABC的顶点B与原点重合,将△ABC绕顶点C顺时针旋转60°得到△ACA1,将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,请回答:(1)点A的坐标为(2,2);点A1的坐标为(6,2).(2)A2018的坐标为(8074,2).【分析】(1)过点A作AD⊥x轴于点D,根据等边三角形的性质可求出AD,BD的长度,进而可得出点A的坐标,再由旋转的性质可得出四边形ABCA1是平行四边形,结合点A的坐标及BC的值,即可得出点A1的坐标;(2)根据平移的性质可找出点A2,A3,…的坐标,进而可得出点A2018的坐标.【解答】解:(1)∵边长为4的等边△ABC的顶点B与原点重合,∴OA=BC=4,∠AOC=60°.如图,过点A作AD⊥x轴于点D,∴BD=DC=BC=2,AD=2,∴点A的坐标为(2,2).∵将△ABC绕顶点C顺时针旋转60°得到△ACA1,∴四边形ABCA1是平行四边形,∴AA1=BC=4,AA1∥BC,∴点A1的坐标为(2+4,2),即(6,2).故答案为:(2,2);(6,2).(2)∵将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,∴点A2的坐标为(2+4×2,2),即(10,2);点A3的坐标为(2+4×3,2),即(14,2);……;∴点A2018的坐标为(2+4×2018,2),即(8074,2).故答案为:(8074,2).【点评】本题考查了利用旋转设计图案、等边三角形、平行四边形的判定与性质、规律型:点的坐标、旋转及平移,解题的关键是:(1)利用等边三角形的性质求出点A的坐标;(2)根据平移的性质,找出点A2018的坐标.25.如图,AM∥BN,∠MAB和∠NBA的角平分线相交于点P,过点P作直线EF分别交AM、BN于F、E.(1)求证:AB=AF+BE;(2)若EF绕点P旋转,F在MA的延长线上滑动,如图,请你测量,猜想AB、AF、BE之间的关系,写出这个关系式,并加以证明.【分析】(1)求出AB=BQ,根据等腰三角形性质求出AP=PQ,推出AF=EQ,即可得出答案;(2)①求出AB=BQ,根据等腰三角形性质求出AP=PQ,推出AF=EQ,即可得出答案;②延长AC交N于点F,同①可得AB=BQ,再求出AF=EQ,即可得出答案.【解答】(1)证明:延长AP交BE于Q,∵AP平分∠MAB,∴∠MAP=∠BAP,∵AM∥BN,∴∠MAP=∠AQB,∴∠BAP=∠AQB,∴AB=BQ,∵BP平分∠ABE,∴AP=PQ,∵AM∥BN,∴==1,∴AF=EQ,∴AB=AF+BE;(2)①成立,证明:如图2,延长AP交BE于Q,∵AP平分∠MAB,∴∠MAP=∠BAP,∵AM∥BN,∴∠MAP=∠AQB,∴∠BAP=∠AQB,∴AB=BQ,∵BP平分∠ABE,∴AP=PQ,∵AM∥BN,∴==1,∴AF=EQ,∴AB=AF+BE;②不同,猜想:AF+AB=BE,证明:延长AP交BE于Q,∵AP平分∠MAB,∴∠MAP=∠BAP,∵AM∥BN,∴∠MAP=∠AQB,∴∠BAP=∠AQB,∴AB=BQ,∵BP平分∠ABE,∴AP=PQ,∵AM∥BN,∴==1,∴AF=EQ,∴AF+AB=BE.【点评】本题考查了的是平行线的性质,等腰三角形的性质等知识点的应用,主要考查学生的推理能力.。
新人教版数学九年级上册第二十三章旋转单元达标检测试题及其答案

新人教版数学九年级上册第二十三章旋转单元达标检测试题一、单项选择题:(本大题共10个小题,每小题3分,共30分,每小题给出的四个选项中,只有一项是符合题目要求的,将此选项的字母填在答题卡上)1. 下列图形是中心对称图形的是( )A. B. C. D.2.晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中是中心称图形但是不是轴对称图形的是()3.有6个相同的立方体搭成的几何体如图所示,则它的主视图是()4.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.5.如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是()A.(,1)B.(1,﹣)C.(2,﹣2)D.(2,﹣2)5题图6题图7题图8题图6.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有()A.2种B.3种C.4种D.5种7.如图,在正方形网格中,将△绕点旋转后得到△,则下列旋转方式中,符合题意的是()A.顺时针旋转90°B.逆时针旋转90°C.顺时针旋转45°D.逆时针旋转45°8.如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC 经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是()A.△ABC绕点C顺时针旋转90°,再向下平移3B.△ABC绕点C顺时针旋转90°,再向下平移1C.△ABC绕点C逆时针旋转90°,再向下平移1D.△ABC绕点C逆时针旋转90°,再向下平移39.下面图形中,既是轴对称图形又是中心对称图形的是()10.如图,将四个“米”字格的正方形内涂上阴影,其中既是轴对称图形,又是中心对称图形的是()A.B.C.D.二、填空题:(本大题共10小题,每小题3分,共30分.把答案写在答题卡中的横线上11.如图所示,把一个直角三角尺ACB绕着30角的顶点B顺时针旋转,使得点A落在CB的延长线上的点E处,则∠BDC的度数为_____ .12.正方形是中心对称图形,它绕它的中心旋转一周和原来的图形重合______次.13.等边三角形绕着它的三边中线的交点旋转至少______度,能够与本身重合.14.点P(-3,4)关于原点对称的点Q的坐标为______.15.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为.15题图16题图17题图16.如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= .17.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是.18.如图,△ABO中,AB⊥OB,AB=,OB=1,把△ABO绕点O旋转120°后,得到△A1B1O,则点A1的坐标为.18题图 19题图 20题图19.如图,平面直角坐标系的原点O是正方形ABCD的中心,顶点A,B的坐标分别为(1,1)、(-1,1),把正方形ABCD绕原点O逆时针旋转45°得到正方形A′B′C′D′则正方形ABCD与正方形A′B′C′D′重叠部分形成的正八边形的边长为_____________.20.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE=.三、解答题(每小题10分,共90分)21.如图1,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.(1)求证:CF=CH;(2)如图2,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.22.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.23.如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(2,﹣4),B(4,﹣4),C(1,﹣1).(1)画出△ABC关于y轴对称的△A1B1C1,直接写出点A1的坐标;(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).24.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).(1)在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2,点C2在AB上.①旋转角为多少度?②写出点B2的坐标.25.在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F.(1)若点B的坐标是(-4,0),请在图中画出△AEF,并写出点E,F的坐标;(2)当点F落在x轴上方时,试写出一个符合条件的点B的坐标.26.矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.(1)求AD的长;(2)求阴影部分的面积和直线AM的解析式;(3)求经过A、B、D三点的抛物线的解析式;(4)在抛物线上是否存在点P,使S△PAM=?若存在,求出P点坐标;若不存在,请说明理由.27.找出图中的旋转中心,说出旋转多少度能与原图形重合?并说出它是否是中心对称图形.28.如图所示,已知是△的中线,画出以点为对称中心,与△•成中心对称的三角形.29.如图所示,在正方形中,,点在上,且,点是上一动点,连接,将线段绕点逆时针旋转90°得到线段.要使点恰好落在上,求的长。
人教版九年级上册数学第二十三章旋转单元达标测试题(含答案)

人教版九年级上册数学第二十三章旋转单元达标测试题(含答案)一、选择题1.下列图形中,是中心对称图形的是()A. 圆B. 等边三角形C. 直角三角形D. 正五边形2.如图,将绕点逆时针旋转70°到的位置,若,则()A. 45°B. 40°C. 35°D. 30°3.如图,已知△ADE是△ABC绕点A逆时针旋转所得,其中点D在射线AC上,设旋转角为α,直线BC与直线DE交于点F,那么下列结论不正确的是()A. ∠BAC=αB. ∠DAE=αC. ∠CFD=αD. ∠FDC=α4.将下列图形绕着直线旋转一周正好得到如图所示的图形的是()A. B. C. D.5.下列图形,可以看作中心对称图形的是()A. B. C. D.6.如图,将Rt△ABC(∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于()A. 55°B. 70°C. 125°D. 145°7.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为()A. 30°B. 90°C. 120°D. 180°8.在平面直角坐标系中,点P(-3,m2+1)关于原点对称点在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限9.在平面直角坐标系中,已知点A(﹣4,3)与点B关于原点对称,则点B的坐标为()A. (﹣4,﹣3)B. (4,3)C. (4,﹣3)D. (﹣4,3)10.在平面直角坐标系xOy中,已知点A(2,3).若将OA绕原点O逆时针旋转180°得到OA’,则点A’在平面直角坐标系中的位置是在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限11.如图,将线段AB 先向右平移5 个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段AB ,则点 B 的对应点B′的坐标是()A. (-4 , 1)B. (-1, 2)C. (4 ,- 1)D. (1 ,- 2)12.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点的坐标是()A. B. C. D.二、填空题(共10题;共11分)13.在“线段、等腰三角形、四边形、圆”这几个图形中,中心对称图形是________.14.点P(-2,3)关于原点的对称点Q的坐标为________.15.如图,在正方形网格中,格点绕某点顺时针旋转角得到格点,点与点,点与点,点与点是对应点,则________度.16.一副三角板如图放置,将三角板ADE绕点A逆时针旋转,使得三角板ADE 的一边所在的直线与BC垂直,则的度数为________.17.如图,在中,,在同一平面内,将绕点逆时针旋转得到,连接,则的值是________.18.如图,点A、B、C、D 都在方格纸的格点上,若△AOB 绕点O 按逆时针方向旋转到△COD 的位置,则旋转角为________.19.在平面直角坐标系xOy中,若点B与点A(-2,3) 关于点O中心对称,则点B 的坐标为________.20.如图,点C是线段AB的中点,点B是线段CD的中点,线段AB的对称中心是点________,点C关于点B成中心对称的对称点是点________.21.如图,在数轴上,点A表示的数为﹣1,点B表示的数为4,C是点B关于点A的对称点,则点C表示的数为________.22.平面直角坐标系中,点P(-2,1)绕点O(0,0)顺时针旋转90°后,点P的对应点将落在第________象限.三、解答题23.直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y 的值.24.如果B(m+1,3m﹣5)到x轴的距离与它到y轴的距离相等,求:(1)m的值;(2)求它关于原点的对称点坐标.25.如图,△ABC中,∠BAC=120o,以BC为边向外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60o后到△ECD的位置。
人教版2018-2019学年九年级上册数学第二十三章《旋转》单元检测卷(有答案)

第二十三章检测卷(120分钟150分)一、选择题(本大题共10小题,每小题4分,满分40分)1.下列图形,既是轴对称图形,又是中心对称图形的是2.将大写字母E绕点P按顺时针方向旋转90°得到的图形是3.下列说法中,正确的有①平行四边形是中心对称图形;②两个全等三角形一定成中心对称;③中心对称图形的对称中心是连接两对称点的线段的中点;④一个图形若是轴对称图形,则一定不是中心对称图形;⑤一个图形若是中心对称图形,则一定不是轴对称图形.A.1个B.2个C.3个D.4个4.如图,已知点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,则下列说法正确的是A.△ODE绕点O顺时针旋转60°得到△OBCB.△ODE绕点O逆时针旋转120°得到△OABC.△ODE绕点F顺时针旋转60°得到△OABD.△ODE绕点C逆时针旋转90°得△OAB5.在直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度,得到的点的坐标是A.(4,-3)B.(-4,3)C.(0,-3)D.(0,3)6.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A'BC'的位置,则AA'的长为A.10B.10C.20D.527.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为A.30,2B.60,2D.60,3C.60,328.如图,在平面直角坐标系中,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为A.(-a,-b)B.(-a,-b-1)C.(-a,-b+1)D.(-a,-b+2)9.有两个完全重合的直尺,将其中一个始终保持不动,另一个直尺绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,…,则第10次旋转后得到的图形与图①~④中相同的是A.图①B.图②C.图③D.图④10.Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点.下列结论:①(BE+CF )= 22BC ;②S △AEF ≤14S △ABC ;③S 四边形AEDF =AD ·EF ;④AD ≥EF ;⑤AD 与EF 可能互相平分,其中正确结论的个数是A.1个B.2个C.3个D.4个二、填空题(本大题共4小题,每小题5分,满分20分)11.已知a<0,则点P (-a 2,-a+1)关于原点的对称点P'在第 象限.12.如图所示,把一个直角三角尺ACB 绕着30°角的顶点B 顺时针旋转,使得点A 落在CB 延长线上的点E 处,则∠BDC= .13.如图,在Rt △ABC 中,∠ACB=90°,∠BAC=60°,AB=6,Rt △AB'C'可以看作是由Rt △ABC 绕点A 逆时针方向旋转60°得到的,则线段B'C 的长为 .14.如图,在Rt △ABC 中,∠ACB=90°,∠A=30°,AC=6 3,BC 的中点为D ,将△ABC 绕点C 顺时针旋转任意一个角度得到△FEC ,EF 的中点为G ,连接DG 在旋转过程中,DG 的最大值是 .15.如图,四边形ABCD绕点O旋转后,顶点A的对应点为点E.试确定旋转后的四边形.AB,请你用旋转16.如图,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,且AF=12的方法说明线段BE和DF之间的关系.四、(本大题共2小题,每小题8分,满分16分)17.△ABC在平面直角坐标系中的位置如图所示,A,B,C三点在格点上.(1)作出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标;(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.18.已知点P(x+1,2x-1)关于原点的对称点在第一象限,试化简:|x-3|-|1-x|.19.如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上的一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,求AP的长.20.在平面直角坐标系中,O为原点,B(0,6),A(8,0),以点B为旋转中心把△ABO逆时针旋转,得△A'BO',点O,A旋转后的对应点为O',A',记旋转角为β.(1)如图1,若β=90°,求AA'的长;(2)如图2,若β=120°,求点O'的坐标.六、(本题满分12分)21.如图,在等腰△ABC中,∠CAB=90°,P是△ABC内一点,PA=1,PB=3,PC=7,将△APB绕点A 逆时针旋转后与△AQC重合.求:(1)线段PQ的长;(2)∠APC的度数.七、(本题满分12分)22.如图,▱ABCD中,AB⊥AC,AB=1,BC=5,对角线BD,AC交于点O.将直线AC绕点O顺时针旋转分别交BC,AD于点E,F.(1)试说明在旋转过程中,AF与CE总保持相等;(2)证明:当旋转角为90°时,四边形ABEF是平行四边形;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能请说明理由;如果能,求出此时AC绕点O顺时针旋转的角度.八、(本题满分14分)23.如图1,在正方形ABCD中,点M,N分别在AD,CD上,若∠MBN=45°,易证MN=AM+CN.∠(1)如图2,在梯形ABCD中,BC∥AD,AB=BC=CD,点M,N分别在AD,CD上,若∠MBN=12 ABC,试探究线段MN,AM,CN有怎样的数量关系?请写出猜想,并给予证明.(2)如图3,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M,N分别在DA,CD的延长线上,若∠MBN=1∠ABC,试探究线段MN,AM,CN又有怎样的数量关系?请直接写出猜想,不需2证明.第二十三章检测卷(120分钟150分)一、选择题(本大题共10小题,每小题4分,满分40分)1.下列图形,既是轴对称图形,又是中心对称图形的是2.将大写字母E绕点P按顺时针方向旋转90°得到的图形是3.下列说法中,正确的有①平行四边形是中心对称图形;②两个全等三角形一定成中心对称;③中心对称图形的对称中心是连接两对称点的线段的中点;④一个图形若是轴对称图形,则一定不是中心对称图形;⑤一个图形若是中心对称图形,则一定不是轴对称图形.A.1个B.2个C.3个D.4个4.如图,已知点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,则下列说法正确的是A.△ODE绕点O顺时针旋转60°得到△OBCB.△ODE绕点O逆时针旋转120°得到△OABC.△ODE绕点F顺时针旋转60°得到△OABD.△ODE绕点C逆时针旋转90°得△OAB5.在直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度,得到的点的坐标是A.(4,-3)B.(-4,3)C.(0,-3)D.(0,3)6.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A'BC'的位置,则AA'的长为A.102B.10C.20D.527.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为A.30,2B.60,2C.60,3D.60,328.如图,在平面直角坐标系中,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为A.(-a,-b)B.(-a,-b-1)C.(-a,-b+1)D.(-a,-b+2)9.有两个完全重合的直尺,将其中一个始终保持不动,另一个直尺绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,…,则第10次旋转后得到的图形与图①~④中相同的是A.图①B.图②C.图③D.图④10.Rt △ABC 中,AB=AC ,点D 为BC 中点.∠MDN=90°,∠MDN 绕点D 旋转,DM ,DN 分别与边AB ,AC 交于E ,F 两点.下列结论:①(BE+CF )= 22BC ;②S △AEF ≤14S △ABC ;③S 四边形AEDF =AD ·EF ;④AD ≥EF ;⑤AD 与EF 可能互相平分,其中正确结论的个数是A.1个B.2个C.3个D.4个二、填空题(本大题共4小题,每小题5分,满分20分)11.已知a<0,则点P (-a 2,-a+1)关于原点的对称点P'在第 四 象限.12.如图所示,把一个直角三角尺ACB 绕着30°角的顶点B 顺时针旋转,使得点A 落在CB 延长线上的点E 处,则∠BDC= 15° .13.如图,在Rt △ABC 中,∠ACB=90°,∠BAC=60°,AB=6,Rt △AB'C'可以看作是由Rt △ABC 绕点A 逆时针方向旋转60°得到的,则线段B'C 的长为 3 7 .14.如图,在Rt △ABC 中,∠ACB=90°,∠A=30°,AC=6 3,BC 的中点为D ,将△ABC 绕点C 顺时针旋转任意一个角度得到△FEC ,EF 的中点为G ,连接DG 在旋转过程中,DG 的最大值是 9 .三、(本大题共2小题,每小题8分,满分16分)15.如图,四边形ABCD绕点O旋转后,顶点A的对应点为点E.试确定旋转后的四边形.解:如图所示,四边形EB'C'D'即为四边形ABCD绕点O旋转后的四边形.AB,请你用旋转16.如图,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,且AF=12的方法说明线段BE和DF之间的关系.AB,∴AE=AF,解:∵四边形ABCD为正方形,∴AD=AB,∠BAD=90°,∵E是AD的中点,AF=12∴△DFA≌△BEA,∴把△ABE绕点A逆时针旋转90°可得到△ADF,∴BE=DF,BE⊥DF.四、(本大题共2小题,每小题8分,满分16分)17.△ABC在平面直角坐标系中的位置如图所示,A,B,C三点在格点上.(1)作出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标;(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.答案图解:(1)如图,C1(-3,2).(2)如图,C2(-3,-2).18.已知点P(x+1,2x-1)关于原点的对称点在第一象限,试化简:|x-3|-|1-x|.解:∵点P(x+1,2x-1)关于原点的对称点P'的坐标为(-x-1,-2x+1),点P'在第一象限,∴-x-1>0,-2x+1>0,∴x<-1,∴|x-3|-|1-x|=-x+3-1+x=2.五、(本大题共2小题,每小题10分,满分20分)19.如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上的一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,求AP的长.解:如图,∵AC=9,AO=3,∴OC=6,∵△ABC为等边三角形,∴∠A=∠C=60°,∵线段OP绕点D逆时针旋转60°得到线段OD,要使点D恰好落在BC上,∴OD=OP,∠POD=60°,∵∠1+∠2+∠A=180°,∠1+∠3+∠POD=180°,∴∠1+∠2=120°,∠1+∠3=120°,∴∠2=∠3,在△AOP和△CDO中,∠A=∠C,∠2=∠3, OP=OD,∴△AOP≌△CDO,∴AP=CO=6.20.在平面直角坐标系中,O为原点,B(0,6),A(8,0),以点B为旋转中心把△ABO逆时针旋转,得△A'BO',点O,A旋转后的对应点为O',A',记旋转角为β.(1)如图1,若β=90°,求AA'的长;(2)如图2,若β=120°,求点O'的坐标.解:(1)∵β=90°,∴∠A'BA=90°,∵A(8,0),B(0,6),∴OA=8,OB=6,根据勾股定理得,AB=2+OB 2= 82+62=10, 由旋转的性质得,A'B=AB=10,在Rt △A'BA 中,根据勾股定理得,AA'= AB 2+A 'B 2= 102+102=10 2. (2)如图,过点O'作O'C ⊥y 轴于点C , 由旋转的性质得,O'B=OB=6,∵β=120°,∴∠OBO'=120°,∴∠O'BC=180°-120°=60°, ∴BC=12O'B=12×6=3,CO'= O 'B 2-BC 2= 62-32=3 3,∴OC=OB+BC=6+3=9,∴点O'的坐标为(3 3,9).六、(本题满分12分)21.如图,在等腰△ABC 中,∠CAB=90°,P 是△ABC 内一点,PA=1,PB=3,PC= 7,将△APB 绕点A 逆时针旋转后与△AQC 重合.求: (1)线段PQ 的长;(2)∠APC的度数.解:(1)∵△APB绕点A旋转与△AQC重合,∴AQ=AP=1,∠QAP=∠CAB=90°,∴在Rt△APQ中,PQ= AQ22=2.(2)∵∠QAP=90°,AQ=AP,∴∠APQ=45°.∵△APB绕点A旋转与△AQC重合,∴CQ=BP=3.在△CPQ中,PQ=,CQ=3,CP=7,∴CP2+PQ2=CQ2,∴∠CPQ=90°,∴∠APC=∠CPQ+∠APQ=135°.七、(本题满分12分)22.如图,▱ABCD中,AB⊥AC,AB=1,BC=5,对角线BD,AC交于点O.将直线AC绕点O顺时针旋转分别交BC,AD于点E,F.(1)试说明在旋转过程中,AF与CE总保持相等;(2)证明:当旋转角为90°时,四边形ABEF是平行四边形;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能请说明理由;如果能,求出此时AC绕点O顺时针旋转的角度.解:(1)在▱ABCD中,AD∥BC,OA=OC,∴∠1=∠2,在△AOF和△COE中,∠1=∠2,OA=OC,∠3=∠4,∴△AOF≌△COE(ASA),∴AF=CE.(2)由题意,∠AOF=90°(如图1), 又∵AB ⊥AC ,∴∠BAO=90°,∴∠BAO=∠AOF ,∴AB ∥EF ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,即AF ∥BE , ∵AB ∥EF ,AF ∥BE ,∴四边形ABEF 是平行四边形.(3)当EF ⊥BD 时,四边形BEDF 是菱形(如图2).由(1)知,AF=CE ,∵▱ABCD ,∴AD=BC ,AD ∥BC ,∴DF ∥BE ,DF=BE ,∴四边形BEDF 是平行四边形,又∵EF ⊥BD ,∴▱BEDF 是菱形,∵AB ⊥AC ,∴在△ABC 中,∠BAC=90°,∴BC 2=AB 2+AC 2, ∵AB=1,BC= ,∴AC= BC 2-AB 2= ( 2-12=2, ∵四边形ABCD 是平行四边形,∴OA=12AC=12×2=1, ∵在△AOB 中,AB=AO=1,∠BAO=90°, ∴∠1=45°,∵EF ⊥BD ,∴∠BOF=90°,∴∠2=∠BOF-∠1=90°-45°=45°,即旋转角为45°. 八、(本题满分14分)23.如图1,在正方形ABCD 中,点M ,N 分别在AD ,CD 上,若∠MBN=45°,易证MN=AM+CN.(1)如图2,在梯形ABCD 中,BC ∥AD ,AB=BC=CD ,点M ,N 分别在AD ,CD 上,若∠MBN=12∠ABC ,试探究线段MN ,AM ,CN 有怎样的数量关系?请写出猜想,并给予证明.(2)如图3,在四边形ABCD 中,AB=BC ,∠ABC+∠ADC=180°,点M ,N 分别在DA ,CD 的延长线上,若∠MBN=12∠ABC ,试探究线段MN ,AM ,CN 又有怎样的数量关系?请直接写出猜想,不需证明.解:(1)MN=AM+CN.理由如下:如图2,∵BC ∥AD ,AB=BC=CD ,∴梯形ABCD 是等腰梯形,∴∠A+∠BCD=180°,把△ABM 绕点B 顺时针旋转使AB 边与BC 边重合,则△ABM ≌△CBM',∴AM=CM',BM=BM',∠A=∠BCM',∠ABM=∠M'BC , ∴∠BCM'+∠BCD=180°,∴点M',C ,N 三点共线,∵∠MBN=12∠ABC ,∴∠M'BN=∠M'BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=12∠ABC ,∴∠MBN=∠M'BN ,在△BMN 和△BM'N 中, BM =BM ',∠MBN =∠M 'BN ,BN =BN ,∴△BMN ≌△BM'N (SAS),∴MN=M'N ,又∵M'N=CM'+CN=AM+CN ,∴MN=AM+CN.(2)MN=CN-AM.。
人教版 九年级数学上册第二十三章 旋转 单元检测(含答案)

人教版九年级数学上册第二十三章旋转单元检测(含答案)一、单选题1.下面说法正确的是()A.全等的两个图形成中心对称B.能够完全重合的两个图形成中心对称C.旋转后能重合的两个图形成中心对称D.旋转180°后能重合的两个图形成中心对称2.下列图案中,是中心对称图形的是( )A.B.C.D.3.如图,△DEF是△ABC经过某种变换后得到的图形.△ABC内任意一点M的坐标为(x,y),点M经过这种变换后得到点N,点N的坐标是()A.(﹣y,﹣x)B.(﹣x,﹣y)C.(﹣x,y)D.(x,﹣y)4.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是A.(﹣3,2)B.(﹣1,2)C.(1,2)D.(1,﹣2)5.如图所示,ABC V 中,5AC =,中线7AD =,EDC V 是由ADB V 旋转180o 所得,则AB 边的取值范围是( )A .1<AB<29B .4<AB<24C .5<AB<19D .9<AB<196.如图,将△ABC 绕点B 顺时针旋转60°得△DBE ,点C 的对应点E 恰好落在AB 延长线上,连接AD .下列结论一定正确的是( )A .△ABD =△EB .△CBE =△C C .AD △BC D .AD =BC 7.下列图形是中心对称图形,但不是轴对称图形的是( )A .正方形B .等边三角形C .圆D .平行四边形8.如图,将△AOB 绕点O 按逆时针方向旋转45︒后得到△COD ,若15AOB ∠=︒,则AOD ∠的度数是( )A .75︒B .60︒C .45︒D .30°9.如图所示,△ABC 与△A′B′C′是成中心对称的两个图形,则下列说法不正确的是( )A .AB=A′B′,BC=B′C′B .AB△A′B′,BC△B′C′C .S △ABC =S △A′B′C′D .△ABC△△A′OC′10.如图,在Rt 直角△ABC 中,△B =45°,AB =AC ,点D 为BC 中点,直角△MDN 绕点D 旋转,DM ,DN 分别与边AB ,AC 交于E ,F 两点,下列结论:△△DEF 是等腰直角三角形;△AE =CF ;△△BDE△△ADF ;△BE+CF =EF ,其中正确结论是( )A .△△△B .△△△C .△△△D .△△△△二、填空题 11.如图,在正方形网格中,格点ABC ∆绕某点顺时针旋转角()0180αα<<︒得到格点111A B C ∆,点A 与点1A ,点B 与点1B ,点C 与点1C 是对应点,则α=_____度.12.如图,将△ABC 绕点A 逆时针旋转的到△ADE ,点C 和点E 是对应点,若△CAE=90°,AB=1,则BD=_________.13.如图,直线443y x =+与x 轴轴分别交于A ,B 两点,把AOB ∆绕点A 逆时针旋转90︒后得到''AO B ∆,则点'B 的坐标是______.14.如图所示,一段抛物线:()()303y x x x =--≤≤,记为1C ,它与x 轴交于点O ,1A ; 将1C 绕点1A 旋转180︒得2C ,交x 轴于点2A ;将2C 绕点2A 旋转180︒得3C ,交x 轴于点3A ;⋅⋅⋅如此进行下去,直到13C .若()37,P m 在第13段抛物线13C 上,则m =______.三、解答题15.如图,在平面直角坐标系中,ABC ∆的三个顶点的坐标分别为(1,1)A 、(5,1)B 、(4,4)C .(1)按下列要求作图:△将ABC ∆向左平移5个单位得到111A B C ∆,并写出点1A 的坐标;△将ABC ∆绕原点O 逆时针旋转90°后得到222A B C ∆,并写出点2B 的坐标;(2)111A B C ∆与222A B C ∆重合部分的面积为 (直接写出答案).16.如图,在平面直角坐标系网格中,△ABC 的顶点都在格点上,点C 坐标(0,﹣1).(1)作出△ABC 关于原点对称的△A 1B 1C 1,并写出点A 1的坐标;(2)把△ABC 绕点C 逆时针旋转90°,得△A 2B 2C ,画出△A 2B 2C ,并写出点A 2的坐标;(3)直接写出△A 2B 2C 的面积.17.如图,已知点A(1,0),B(0,3),将△AOB绕点O逆时针旋转90°,得到△COD,设E为AD的中点.(1)判断AB与CD的关系并证明;(2)求直线EC的解析式.18.操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.(1)连接AE,求证:△AEF是等腰三角形;猜想与发现:(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.结论1:DM、MN的数量关系是;结论2:DM、MN的位置关系是;拓展与探究:(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由答案1.D2.D3.B4.C 。
人教版数学九年级上册 第二十三章 旋转(包含答案)
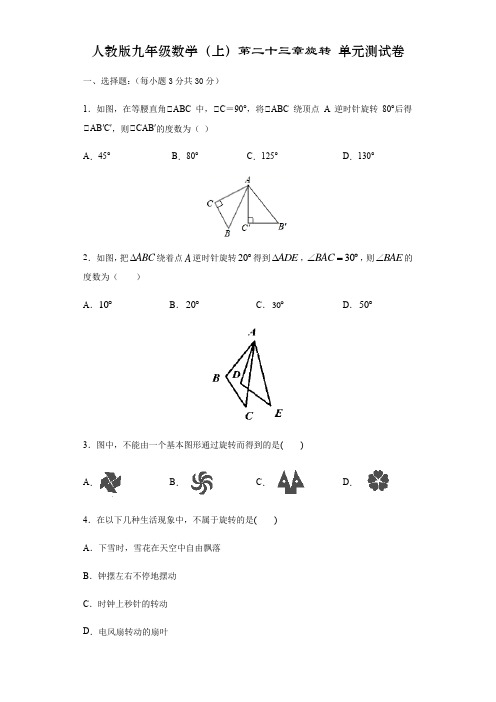
人教版九年级数学(上)第二十三章旋转 单元测试卷一、选择题:(每小题3分共30分)1.如图,在等腰直角△ABC 中,∠C =90°,将△ABC 绕顶点 A 逆时针旋转 80°后得△AB′C′,则∠CAB′的度数为( )A .45°B .80°C .125°D .130°2.如图,把ABC ∆绕着点A 逆时针旋转20︒得到ADE ∆,30BAC ∠=︒,则BAE ∠的度数为( ) A .10︒B .20︒C .30°D .50︒3.图中,不能由一个基本图形通过旋转而得到的是( )A .B .C .D .4.在以下几种生活现象中,不属于旋转的是( ) A .下雪时,雪花在天空中自由飘落 B .钟摆左右不停地摆动 C .时钟上秒针的转动 D .电风扇转动的扇叶5.下列图形中,既是中心对称图形又是轴对称图形的是()A. B. C. D.6.下列图形中,既是轴对称图形,又是中心对称图形的是()A.等边三角形B.等腰直角三角形C.平行四边形D.菱形7.如图,将绕点逆时针旋转一定的角度,得到,且.若,,则的大小为()A. B. C. D.8.如图①,在△AOB 中,∠AOB=90°,OA=3,OB=4,AB=5.将△AOB 沿x 轴依次绕点A、B、O 顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为()A.(30,0)B.(32,0)C.(34,0)D.(36,0)△绕点B顺时针旋转60 得到DBE,点C的对应点E落在AB的9.如图,将ABCAD AC与DE相交于点F.则下列结论不一定正确的是()延长线上,连接,A .60ABD CBE ︒∠=∠=B .ADB △是等边三角形C .BC DE ⊥D .60EFC ︒∠=10.在等边△ABC 中,D 是边AC 上一点,连接BD ,将△BCD 绕点B 逆时针旋转60°,得到△BAE ,连接ED ,若BC=5,BD=4,则以下四个结论中: ①△BDE 是等边三角形; ②AE ∥BC ; ③△ADE 的周长是9; ④∠ADE=∠BDC .其中正确的序号是( )A .②③④B .①②④C .①②③D .①③④二、填空题:(每小题3分共18分)11.在平面直角坐标系中,点(45)P -,与点Q(4,1m -+)关于原点对称,那么m =_____;12.如图,等腰△ABC 中,∠BAC =120°,点D 在边BC 上,等腰△ADE 绕点A 顺时针旋转30°后,点D 落在边AB 上,点E 落在边AC 上,若AE =2cm ,则四边形ABDE 的面积是__________.13.如图,在ΔABC 中,AB=8,AC=6,∠BAC=30°,将ΔABC 绕点A 逆时针旋转60°得到△AB 1C 1,连接BC 1,则BC 1的长为________.14.如图,两块相同的三角板完全重合在一起,30,10A AC ∠==,把上面一块绕直角顶点B 逆时针旋转到''A BC ∆的位置,点'C 在AC 上,''A C 与AB 相交于点D ,则'BC =______.15.如图,在矩形ABCD 中,3AD =,将矩形ABCD 绕点A 逆时针旋转,得到矩形AEFG ,点B 的对应点E 落在CD 上,且60DAG ∠=︒,若EC =AB =__.16.如图,点D 是等边ABC △内部一点,1BD =,2DC =,AD =ADB∠的度数为=________°.三、解答题:(共72分)17.如图,已知△ABC 的顶点A ,B ,C 的坐标分别是A (-1,-1),B (-4,-3),C (-4,-1).(1)作出△ABC关于原点O中心对称的图形△A’B’C’;(2)将△ABC绕原点O按顺时针方向旋转90°后得到△A1B1C1,画出△A1B1C1,并写出点A1的坐标.18.已知,P为等边三角形内一点,且BP=3,PC=4,将BP绕点B顺时针旋转60°至BP′的位置.(1)试判断△BPP′的形状,并说明理由;(2)若∠BPC=150°,求PA的长度.19.如图,在平面直角坐标系中,直线:l y=+与x轴、y轴分别交于点A, B,将点B绕坐标原点O顺时针旋转60︒得点C,解答下列问题:(1)求出点C的坐标,并判断点C是否在直线l上;(2)若点P在x轴上,坐标平面内是否存在点Q,使得以P、C、Q、A为顶点的四边形是菱形?若存在,请直接写出Q点坐标;若不存在,请说明理由.20.在Rt△ABC中,∠ACB=90°,,点D是斜边AB上一动点(点D与点A、B不重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接AE,DE.(1)求△ADE的周长的最小值;(2)若CD=4,求AE的长度.21.四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=3,AB=7,求(1)指出旋转中心和旋转角度;(2)求DE的长度;(3)BE与DF的位置关系如何?请说明理由.22.如图所示:已知∠ABC=120°,作等边△ACD,将△ACD旋转60°,得到△CDE,AB=3,BC=2,求BD和∠ABD.23.如图,把一副三角板如图①放置,其中,∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm ,DC=7cm .把三角板DCE 绕点C 顺时针旋转15°得到△D 1CE 1(如图②). (1)求∠OFE 1的度数; (2)求线段AD 1的长.24.如图,在正方形ABCD 中,点M 、N 是BC 、CD 边上的点,连接AM 、BN ,若BM=CN(1)求证:AM ⊥BN(2)将线段AM 绕M 顺时针旋转90°得到线段ME ,连接NE ,试说明:四边形BMEN 是平行四边形;(3)将△ABM 绕A 逆时针旋转90°得到△ADF ,连接EF ,当1BM BC n时,请求出四边形四边形ABCDAMEFS S 的值。
