2017年初中学业水平考试数学全真模拟试题三
山东省潍坊诸城市2017届九年级第三次模拟考试数学试题

2017年初中学业水平模拟考试(三)数学试题注意事项:本试题共120分,考试时间为120分钟,答卷前务必将试题密封线内及答题卡上面的项目填涂清楚,所有答案都必须涂,写在答题卡相应位置,答在本试卷上一律无效。
一、选择题(本大题共12小题,每小题四个选项只有一项是正确的,每小题选对得3分) 1.下列计算正确的是( )A. 030=B. 33-=--C. 331-=-D. 39±= 2.下列运算正确的是( )A.53255x x x =∙B.xy y x 532=+C. 428224x x x =÷ D. 523)(x x =-3.下列图形中,既是轴对称图形又是中心对称图形的是( )A. 4个B. 3个C. 2个D. 1个4.如图,是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么该班40名同学一周体育锻炼时间的众数、中位数分别是( )A. 16、10.5B. 8、9C. 16、8.5D. 8、8.55.方程0411)1(2=+---x k x k 有两个实数根,则k 的取值范围是( ) A. 1≥k B. 1≤k C. 1<k D. 1>k 7.如图是五个相同的正方体组成的一个几何体,它的左视图是( )正面 A B C D 8.函数a ax y -=与)0(≠=a xay 在同一直角坐标系中的图象可能是( )A B C D 8.A 若关于x 的一元一次不等式组⎩⎨⎧>+<-22m x m x 有解,则m 的取值范围为( )A 32->m B 32≤m C 32>m D 32-≤m9.如图,边长为1的小正方形构成的网络中,半径为1的⊙O 的圆心O 在格点上,则∠AED 的正切值等于( ) A55 B 552 C 2 D 2110.已知二次函数)0(2≠++=a c bx ax y 的图象如图所示,则下列结论中正确的是( )A a>0B x=3是方程02=++c bx ax 的一个根C 0=++c b aD 当x<1时,y 随x 的增大而减小11.如图,正方形ABCD 的边长为4,点P 、Q 分别是CD 、AD 的中点,动点E 从点A 向点B 运动,到点B 时停止运动;同时,动点F 从点P 出发,沿P →D →Q 运动,点E 、F 的运动速度相同,设点E 的运动路程为x ,△AEF 的面积为y,能大致刻画y 与x 的函数关系的图象是( )A B C二、填空题(本大题共6小题,共18分,只填写最后结果,每小题填对得3分)13.若分式12323-+-x xx x 的值为零,则x=14.已知x 、y 是二元一次方程组⎩⎨⎧=+=-54232y x y x 的解,则代数式224y x -的值为15.如图,在△ABC 中,AB=AC=10,以AB 为直径的⊙O 与BC 交于点D,与AC 交于点E ,连接OD 交BE 于点M,且MD=2,则BE 长为第15题图 第16题图 第17题图16.如图,在平面直角坐标系中xOy 中,多边形OABCDE 的顶点坐标分别是O (0,0),A (0,6),B (4,6),C (4,4)D (6,4)E (6,0)。
2017年中考数学三模试卷

中考数学三模试卷一、选择题(本大题共16小题,1-10题,每小题3发,11-16小题,每小题3分,共42分)1.(3分)下面的数中,与﹣2的和为0的是()A.2 B.﹣2 C.D.2.(3分)把x3﹣9x分解因式,结果正确的是()A.x(x2﹣9)B.x(x﹣3)2C.x(x+3)2D.x(x+3)(x﹣3)3.(3分)下列说法正确的是()A.为了审核书稿中的错别字,选择抽样调查B.为了了解春节联欢晚会的收视率,选择全面调查C.“射击运动员射击一次,命中靶心”是随机事件D.“经过有交通信号灯的路口,遇到红灯”是必然事件4.(3分)某种电子元件的面积大约为0.00000069平方毫米,将0.00000069这个数用科学记数法表示正确的是()A.0.69×10﹣6B.6.9×10﹣7C.69×10﹣8D.6.9×1075.(3分)一个正多边形的内角和是外角和的2倍,则这个正多边形的每个外角为()A.50°B.60°C.45°D.120°6.(3分)如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是()A.B.C.D.7.(3分)下列说法正确的是()A.若a<0,则<0 B.x实数,且x2=a,则a>0C.有意义时,x≤0 D.0.1的平方根是±0.018.(3分)化简÷的结果是()A. B.C. D.2(x+1)9.(3分)当0<x<1时,x2、x、的大小顺序是()A.x2B.<x<x2C.<x D.x<x2<10.(3分)如图,直线l1∥l2,等腰直角△ABC的两个顶点A、B分别落在直线l1、l2上,∠ACB=90°,若∠1=15°,则∠2的度数是()A.35°B.30°C.25°D.20°11.(2分)如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为()A.(2,1) B.(2,0) C.(3,3) D.(3,1)12.(2分)如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是()A.AD平分∠MAN B.AD垂直平分BCC.∠MBD=∠NCD D.四边形ACDB一定是菱形13.(2分)木杆AB斜靠在墙壁上,当木杆的上端A沿墙壁NO竖直下滑时,木杆的底端B也随之沿着射线OM方向滑动.下列图中用虚线画出木杆中点P随之下落的路线,其中正确的是()A. B. C.D.14.(2分)已知反比例函数y=,当1<x<2时,y的取值范围是()A.0<y<5 B.1<y<2 C.5<y<10 D.y>1015.(2分)施工队要铺设一段全长2000米的管道,因在中考期间需停工两天,实际每天施工需比原计划多50米,才能按时完成任务,求原计划每天施工多少米.设原计划每天施工x米,则根据题意所列方程正确的是()A.﹣=2 B.﹣=2C.﹣=2 D.﹣=216.(2分)如图,⊙O的弦BC长为8,点A是⊙O上一动点,且∠BAC=45°,点D,E分别是BC,AB的中点,则DE长的最大值是()A.4 B.4 C.8 D.8二、填空题(本大题共3个小题,共10分,17-18小题各3分,19小题共4分)17.(3分)计算:(+1)(3﹣)=.18.(3分)一只不透明的袋子中装有红球和白球共30个,这些球除了颜色外都相同,校课外学习小组做摸球实验,将球搅匀后任意摸出一个球,记下颜色后放回,搅匀,通过多次重复试验,算得摸到红球的频率是0.2,则袋中有个红球.19.(4分)如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM 交x轴于点N(n,0),设点M转过的路程为m(0<m<1).(1)当m=时,n=;(2)随着点M的转动,当m从变化到时,点N相应移动的路径长为.三、解答题(本大题共7小题,共68分)20.(9分)定义新运算:对于任意实数a、b,都有a⊕b=a﹣2b,等式右边是通常的减法及乘法运算.例如:3⊕2=3﹣2×2=﹣1.(1)计算:3⊕(﹣2);(2)若3⊕x的值小于1,求x的取值范围,并在如图所示的数轴上表示出来.21.(9分)如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC ⊥ON.(1)求∠ACD度数;(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)22.(9分)为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:(1)本次调查属于调查,样本容量是;(2)请补全频数分布直方图中空缺的部分;(3)求这50名学生每周课外体育活动时间的平均数;(4)估计全校学生每周课外体育活动时间不少于6小时的人数.23.(9分)教室内的饮水机接通电源进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(分钟)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为30℃时,接通电源后,水温y(℃)和时间x(分钟)的关系如图.(1)a=;(2)直接写出图中y关于x的函数关系式;(3)饮水机有多少时间能使水温保持在70℃及以上?(4)若饮水机早上已加满水,开机温度是20℃,为了使8:40下课时水温达到70℃及以上,并节约能源,直接写出当它上午什么时间接通电源比较合适?24.(10分)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.25.(10分)某电子厂生产一种新型电子产品,每件制造成本为20元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;(2)当销售单价为多少元时,厂商每月获得的利润为400万元?(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过520万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?26.(12分)平面上,Rt△ABC与直径为CE的半圆O如图1摆放,∠B=90°,AC=2CE=m,BC=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转且∠ECD始终等于∠ACB,旋转角记为α(0°≤α≤180°)(1)当α=0°时,连接DE,则∠CDE=°,CD=;(2)试判断:旋转过程中的大小有无变化?请仅就图2的情形给出证明;(3)若m=10,n=8,当α=∠ACB时,求线段BD的长;(4)若m=6,n=4,当半圆O旋转至与△ABC的边相切时,直接写出线段BD 的长.2017年河北省唐山市路北区中考数学三模试卷参考答案一、选择题(本大题共16小题,1-10题,每小题3发,11-16小题,每小题3分,共42分)1.A;2.D;3.C;4.B;5.B;6.D;7.C;8.A;9.A;10.B;11.A;12.AD;13.D;14.C;15.A;16.B;二、填空题(本大题共3个小题,共10分,17-18小题各3分,19小题共4分)17.2;18.6;19.﹣1;;三、解答题(本大题共7小题,共68分)20.;21.;22.抽样;50;23.7;24.;25.;26.90;;。
2017年陕西省初中毕业学业数学模拟试卷3(有答案)

2017年陕西省初中毕业学业数学模拟试卷3(有答案)2017年陕西省初中毕业学业模拟考试(三)数学本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷2至6页,全卷共120分。
考试时间为120分钟。
第Ⅰ卷(选择题共30分)注意事项:1.答第Ⅰ卷前,请你千万别忘了将自己的姓名、准考证号、考试科目用2B铅笔和钢笔准确涂写在答题卡上;并将本试卷左侧的项目填写清楚。
2.当你选出每小题的答案后,请用2B铅笔把答题卡上对应题号的答案标号涂黑。
如需改动,请用橡皮擦干净后,再选涂其它答案标号。
把答案填在试题卷上是不能得分的。
3.考试结束,本卷和答题卡一并交给监考老师收回。
一、选择题(共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的)1.有理数-1,-2,0,3中,最小的数是( B )A.-1B.-2.0D.32.图中几何体的俯视图是( D )3.下列计算正确的是( D )A.2a2-a2=1 B.(a+b)2=a2+b2.(3b3)2=6b6 D.(-a)÷(-a)3=a24.将一副三角板如图放置,使点A在DE上,B∥DE,则∠AE的度数为( B )A.10° B.1°.20° D.2°,第4题图),第6题图),第8题图).若正比例函数的图象经过点(2,-3),则这个图象必经过点( D ) A.(-3,-2) B.(2,3).(3,-2) D.(-4,6)6.如图,在平行四边形ABD中,对角线A,BD相交于点,点E,F 分别是边AD,AB的中点,EF交A于点H,则AH的值为( B ) A.1 B12 13 D147.一元二次方程2x2-3x+1=0的根的情况是( B )A.有两个相等的实数根B.有两个不相等的实数根.只有一个实数根D.没有实数根8.如图,已知平行四边形ABD中,对角线A,BD相交于点,过点的直线分别交AD,B于点E,F,则图中的全等三角形共有( )A.2对B.4对.6对D.8对9如图,圆内接四边形ABD的两组对边的延长线分别相交于点E,F,若∠A=°,∠E=30°,则∠F的度数为( )A.2° B.30°.40° D.°,第9题图),第10题图)10.如图是二次函数=ax2+bx+(a≠0)的图象的一部分,给出下列命题:①a+b+=0;②b>2a;③ax2+bx+=0的两根分别为-3和1;④a-2b+>0其中正确的命题是( )A.①②B.②③.①③D.①②③④点拨:∵x=1时,=0,∴a+b+=0,所以①正确;∵x=-b2a=-1,∴b=2a,所以②错误;∵点(1,0)关于直线x=-1对称的点的坐标为(-3,0),∴抛物线与x轴的交点坐标为(-3,0)和(1,0),∴ax2+bx+=0的两根分别为-3和1,所以③正确;∵抛物线与轴的交点在x轴下方,∴<0,而a+b+=0,b=2a,∴=-3a,∴a-2b +=-3b,∵b>0,∴-3b<0,所以④错误.故选第Ⅱ卷(非选择题共90分)注意事项:1.请用0毫米黑色墨水签字笔直接答在答题卡上。
【首发】广东省2017年初中毕业生学业考试数学预测卷(三)【word版,含答案】

2017年广东省初中毕业生学业考试数学预测卷(三)(满分:120分时间:100分钟)一、选择题(本大题10小题,每小题3分,共30分)1.在-1和2之间的数是()A. -3B.-2C.0D.32.如图3 - 1所示的几何体的左视图是()3.下列运算正确的是()A. a+2a=3a2B. 3a3·2a2=6a6C.a8÷a2=a4D.(2a)3=8a34.下面关于永洁环保、绿色食品、节能、绿色环保的四个标志中,是轴对称图形的是()5.有一组数据为88, 96, 109, 109, 122, 141,则这组数据的众数和中位数分别是()A. 122, 109B.109, 122C.109, 109D. 141,1096.如图3-2, AB//CD,CB平分∠ABD.若∠C=40°,则∠D的度数为()A. 90°B.100°C.110°D.120°的结果是()7.a,b在数轴上的位置如图3-3所示,化简a bA. –a-bB.a + bC.a-bD. b-a8.已知线段AB=8cm,点C是直线AB上一点,BC=2cm,若点M是AB的中点,点N是BC 的中点,则线段MN的长度为()A. 5 cmB.5 cm或 3 cmC.7 cm或3cmD.7 cm9.如图3-4是二次函2y ax bx c =++(0)a ≠的图象,下列说法错误的是( ) A.函数y 的最大值是4B.函数的图象关于x =-1对称C.当x<-1时,y 随x 的增大而增大D.当-4<x<1时,函数值y>010.如图3-5, AB 是⊙O 的直径,⊙O 的半径为5,⊙O 上有定点C 和动点P ,它们位于直径AB 的异侧,过点C 作CP 的垂线,与PB 的延长线交于点Q,若tan ∠ABC=34,则线段CQ 的长度的最大值为( )A.10B.152C.403D.203二、填空题(本大题6小题,每小题4分,共24分) 11.因式分解:2x y y -=.12.x 的取值范围是.13.已知点P 坐标为(1,1),将点 P 绕原点逆时针旋转45°得点P 1,则点P 1的坐标为.14.关于x 的一元二次方程2210ax x -+=有实数根,则a 的取值范围是 .15.在△ABC 中,点D,E 分別是AB,AC 的中点,AC= 10.点F 是DE上一点.连接AF,CF,DE=1,若∠AFC=90°,则BC 的长度为.16.如图3-6,是正六边形硬纸片ABCDEF 在桌面上的起始位置,它的边长为 2cm,若它沿直线l 不滑行地翻滚一周,则正六边形的中心O 运动的路程为cm.三、解答题(一)(本大题3小题,每小题6分,共18分) 17.解分式方程:352x x =-.18.已知:如图3-7,AB=AC,∠DBC=∠DCB,求证:∠BAD=∠CAD.19.如图3-8,已知△ABC,利用尺规完成下列作图(不写画法,保留作图痕迹).(1)作△ABC的外接圆;(2)若△ABC所在平面内有一点D,满足∠CAB=∠CDB,BC=BD,求作点D.四、解答题(二)(本大题3小题,每小题7分,共21分)20.我区某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球,为关注儿童成长的健康,实施“关注肥胖儿童计划”,某校结合全校各班肥胖儿童的人数情况进行了统计,发现各班肥胖儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,如下两幅不完整的统计图:(1)求全校班级的个数,并该条形统计图补充完整;(2)为了了解肥胖儿童的饮食情况,某校决定从只有2名肥胖儿童的这些班级中,任选两名进行调查,请用列表法或画树形图的方法,求出所选两名儿童来自同一个班级的概率.21.某中学开学初到商场购买A,B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元,购买一个B种品牌的足球比购买一个A种品牌的足球多花30元.(1)求购买一个A种品牌、一个B种品牌的足球各需多少元;(2)学校为了响应习总书记“足球进校园”的号召,决定再次购进A,B两种品牌足球共50个,正好赶上商场对商品价格进行调整,A种品牌足球售价比第一次购买时提高4元,B种品牌足球按第一次购买时售价的9折出售,如果学校此次购买A,B两种品牌足球的总费用不超过第一次花费的70%,且保证这次购买的B种品牌足球不少于23个,则这次学校有哪几种购买方案?(3)请你求出学校在第二次购买活动中最多需多少资金?22.已知反比例函数:1k y x=与一次函数y=k 2x+b 的图象交于点A ((1,8),),B (-4,m ). (1)分别求反比例函数和一次函数的解析式; (2)若M(x 1,y 1),N(x 2,y 2)是反比例函数1k y x=图象上的两点,且x 1<x 2,y 1<y 2,指出点M ,N 各位于哪个象限,并简要说明理由.五、解答题(三)(本大题3小题,每小题9分,共27分)23.如图3-10,AB 为⊙O 的直径,直线CD 切⊙O 于点M ,BE 丄CD 于点E. (1)求证:∠BME=∠MAB ; (2)求证:BM 2=BE •AB ; (3)若BE=185,sin ∠BAM=35,求线段AM 的长.24. 如图3-11,已知拋物线2y x bx c =++经过A (-1,0),B(3,0)两点,与y 轴相交于点C ,该拋物线的顶点为点D.(1)求该拋物线的解析式及点D 的坐标;(2)连接AC,CD,DB,BC ,设△AOC,△BOC,△BCD 的面积分别为S 1,S 2,S 3,求证:231S S S =. (3)点M 是线段AB 上一动点(不包括点A 和点B ),过点M 作MN//BC 交AC 于点N,连接MC ,是否存在点M 使∠AMN=∠ACM ?若存在,求出点M 的坐标和此时直线MN 的解析式;若不存在,请说明理由.25.如图3-12,在矩形ABCD中,AD=4,点M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.(1)如图3-12①,求证:AE = DF;(2)如图3-12②,若AB=2,过点M作MG丄EF交线段BC于点G,连接EG,GF,求证△GEF 是等腰直角三角形;(3)如图3-12③,若AB=,过点M作MG丄EF交线段BC的延长线于点G,求线段AE长度的取值范围.2017年广东省初中毕业生学业考试数学预测卷(三)参考答案1.C2.C3. D4. B5. C6. B7. A8. B9. D 10.C 11.y(x+l)(x-l) 12. x ≥14. a ≤1且a ≠0 15. 12 14.4π 17.解:原方程两边乘x(x-2),得3x-6=5x. 解得x= -3.经检验x= -3是分式方程的解。
2017年数学中考三模检测试题
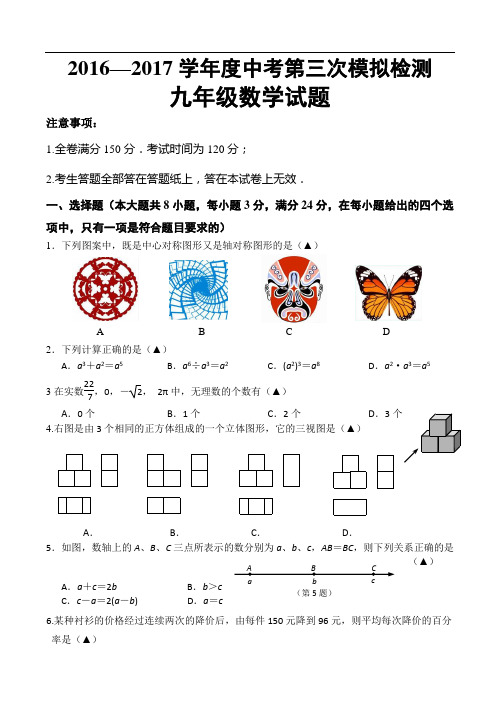
(第5题)c BA C 2016—2017学年度中考第三次模拟检测九年级数学试题注意事项:1.全卷满分150分.考试时间为120分;2.考生答题全部答在答题纸上,答在本试卷上无效.一、选择题(本大题共8小题,每小题3分,满分24分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列图案中,既是中心对称图形又是轴对称图形的是(▲)A B C D 2.下列计算正确的是(▲) A .a 3+a 2=a 5B .a 6÷a 3=a 2C .(a 2)3=a 8D .a 2·a 3=a 53在实数227,0,-2, 2π中,无理数的个数有(▲)A .0个B .1个C .2个D .3个 4.右图是由3个相同的正方体组成的一个立体图形,它的三视图是(▲)A .B .C .D .5.如图,数轴上的A 、B 、C 三点所表示的数分别为a 、b 、c ,AB =BC ,则下列关系正确的是 (▲)A .a +c =2bB .b >cC .c -a =2(a -b )D .a =c 6.某种衬衫的价格经过连续两次的降价后,由每件150元降到96元,则平均每次降价的百分 率是(▲)A.10%B.15%C.20%D.30%7.如图,AB是半圆O直径,半径OC⊥AB,连接AC,∠CAB的平分线AD 交OC于点E,交BC︵于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD 是CE与CO的比例中项.其中,所有正确结论的序号是(▲)A.①②B.①③C.②③D.①②③8.如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数kyx=的图象经过点D,四边形BCFG的面积为8,则k的值为(▲)A.16 B.20 C.24 D.28二、填空题(本大题共8小题,每小题3分,共24分,不需写出解答过程,请把答案直接写在答题纸相应的位置上)9.分解因式:ax2-2ax+a=________.10.抛物线y=(x+1)2﹣2的顶点坐标是.11.若(7x﹣a)2=49x2﹣bx+9,则|a+b|的值为________.12.如图,直线a∥b,三角板的直角顶点A落在直线a上,两条直角边分别交直线b于B、C 两点.若∠1=50°,则∠2的度数是°.13.第12题图第13题图如图,每个小正方形的边长为l,A、B、C是小正方形的顶点,则sin∠ABC的值等于____________.14.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为 cm2.15.如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为度.16. 如图,直线y=34x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心、1为半径的圆上一动点,连接PA、PB,则△PAB面积的最大值是三、解答题(本大题共11小题,共102分.请在答题纸指定区域内作答,解答时写出必要的文字说明、证明过程或演算步骤)17.(本题共6分)计算:()112322sin60.2π-⎛⎫--+︒⎪⎝⎭18.(本题共6分)解不等式组()()4132142x xxx⎧-≤+⎪⎨--⎪⎩19.(本题共6分)先化简,再求值:22144(1)1-+-÷--a aa a a,其中-2<a ≤2,请选择一个a的合适整数代入求值.20.(本题共8分)某校举行春季运动会,需要在初三年级选取1或2名同学作为志愿者,初三(5)班的小熊、小乐和初三(6)班的小矛、小管4名同学报名参加.(1)若从这4名同学中随机选取1名志愿者,则被选中的这名同学恰好是初三(5)班同学的概率是 ;(2)若从这4名同学中随机选取2名志愿者,请用列举法(画树状图或列表)求这2名同学恰好都是初三(6)班同学的概率.21.(本题共10分)在平面直角坐标系x O y ,直线y =x -1与y 轴交于点A ,与双曲线=ky x交于点B (m ,2).(1)求点B 的坐标及k 的值;(2)将直线AB 平移,使它与x 轴交于点C ,与y 轴交于点D ,若△ABC 的面积为6,求直线CD 的表达式.22.(本题共10分)某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分步直方图.组别 次数 频数 (人数)A 80≤x <100 6B 100≤x <120 8C 120≤x <140 mD 140≤x <160 18 E160≤x <1806(1)表中的m=______;(2)请把频数分布直方图补完整;(3)这个样本数据的中位数落在第________组;(4)若九年级学生一分钟跳绳次数(x )合格要求是x ≥120,请估计九年级学生中一分钟跳绳成绩不合格的人数.跳绳次数频数(人数)18016014012010080681815126323.(本题共10分)如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC.(1)求证:△ABD≌△ECB;(2)若∠EDC=65°,求∠ECB的度数;(3)若AD=3,AB=4,求DC的长.24.(本题共10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.(1)求证:EF⊥AB;(2)若∠C=30°,6,求EB的长.25.(本题共10分)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:3AB=10米,AE=15米.(i=1:3BH与水平宽度AH的比)(1)求点B距水平面AE的高度BH;(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:2≈1.414,3≈ 1.732)26.(本题共12分)如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过y O D Q EC B AxE 作直线l //BC ,交直线CD 于点F .将直线l 向右平移,设平移距离BE 为t (t ≥0),直角梯形ABCD 被直线l 扫过的面积(图中阴影部份)为S ,S 关于t 的函数图象如图②所示,OM 为线段,MN 为抛物线的一部分,NQ 为射线,N 点横坐标为4.信息读取(1)梯形上底的长AB= ;(2) 直角梯形ABCD 的面积= ; 图象理解(3)写出图②中射线NQ 表示的实际意义;(4) 当42<<t 时,求S 关于t 的函数关系式; 问题解决(5)当t 为何值时,直线l 将直角梯形ABCD 分成的两部分面积之比为1: 3.27.(本题共14分)如图,抛物线y =ax 2-2ax+c (a ≠0)与y 轴交于点C (0,4),与x 轴交于点A 、B ,点A 的坐标为(4,0). (1)求该抛物线的解析式;(2)点Q 是线段AB 上的动点,过点Q 作QE ∥AC ,交线段BC 于点E ,连接CQ ,当△CQE 的面积为3时,求点Q 的坐标;(3)若平行于x 轴的动直线l 与该抛物线交于点P ,与直线AC 交于点F ,点D 的坐标为 (2,0).问:是否存在这样的直线l ,使得△ODF 是等腰三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.2016—2017学年度中考第三次模拟检测九年级数学答题纸一、选择题(本大题共8小题,每小题3分,满分24分,在每小题给出的四个选项中,只有一项是符合题目要求的)二、填空题(本大题共8小题,每小题3分,共24分,不需写出解答过程,请把答案直接写在答题纸相应的位置上)9. 10. 11. 12.13. 14. 15. 16. 三、解答题(本大题共11小题,共102分.请在答题纸指定区域内作答,解答时写出必要的文字说明、证明过程或演算步骤)17.(本题共6分)计算:()101222sin60.2π-⎛⎫--+︒ ⎪⎝⎭18.(本题共6分)解不等式组()()4132142x x x x ⎧-≤+⎪⎨--⎪⎩19.(本题共6分)先化简,再求值:22144(1)1-+-÷--a a a a a,其中-2<a ≤2,请选择一个a 的合适整数代入求值.20.(本题8分)(1);(2)21.(本题共10分)(1)(2)22.(本题共10分)(1)表中的m=______;(2)请把频数分布直方图补完整;(3)这个样本数据的中位数落在第________组;(4)23.(本题共10分)(1)(2)(3)24.(本题共10分)跳绳次数频数(人数)180160140120100806818151263(2)25.(本题共10分) (1) (2)26.(本题共12分)(1) ;(2) ; (3) (4) (5)27.(本题共14分)(2)(3)2016—2017学年度中考第三次模拟检测九年级数学答案一、选择题(本大题共8小题,每小题3分,满分24分,)题号 1 2 3 4 5 6 7 8 选项 A D C A A C B B二、填空题(本大题共8小题,每小题3分,共24分,)9. a(x-1)210. (-1,-2)11. 4512. 4013.14. 16 \ 15. 40 16.三、解答题(本大题共11小题,共102分.)17.解:原式=2-1+2- +2×·········································· 2分=3-+···································································4分=3 ··································································································6分18.解:解4(x-1)≤3(x+2)得:x≤10··························································· 2分解得:x>7·····························································4分所以不等式组的解集为7<x≤10·····························································6分19.解:原式, ··········································3分∵-2<a ≤2,a-1≠0.a-2≠0,a≠0∴a≠1,a≠2.a≠0∴当a=-1时,原式==··························································· 6分21.(1);·· ······················································· 2分(2)列表如下(小熊记作A,小乐记作B,小矛记作C,小管记作D),A B C DA ﹣﹣﹣﹣(B,A)(C,A)(D,A)B (A,B)﹣﹣﹣﹣(C,B)(D,B)C (A,C)(B,C)﹣﹣﹣﹣(D,C)D (A,D)(B,D)(C,D)﹣﹣﹣﹣·····································6分所有等可能的情况数有12种,其中这2名同学恰好都是初三(6)班同学的情况有2种,则P==.·····································8分21.(1)将点B(m,2)代入y=x-1得:m=3,∴点B的坐标为(3,2),将点B(3,2)代入y=,得k=6. ·····································4分(2)方法一:设将直线AB平移m个单位,则设平移后直线CD的表达式为y=x-1+m,∵△ABC的面积为6,∴∣m∣×2×+∣m∣×1×=6解得:m= 4∴将直线AB向左或向右平移4个单位∴直线CD的表达式为y=x+3或y=x-5 ·····································10分方法二:当y=0时,x-1=0,x=1,所以直线y=x-1与x轴的交点坐标为(1,0),∵将直线AB平移,∴设平移后直线CD的表达式为y=x+b设平移后C点坐标为(m,0)∵△ABC的面积为6,∴∣m-1∣×2×+∣m-1∣×1×=6解得:m=5或-3此时C点坐标为(5,0)或(-3,0),代入y=x+b得,b=3或b=-5∴直线CD的表达式为y=x+3或y=x-522.(1)表中的m=___12___;············· 2分(2)请把频数分布直方图补完整;·········· 5分(3)这个样本数据的中位数落在第___三_组;·····································7分(4)=126 人························· 10分23.解:(1)证明:, ,,在△ABD与△ECB中,, ∴△ABD≌△ECB································· 3分(2)由(1)证得△ABD≌△ECB,∴BD=BC,,,; (6)分(3)由(1)证得△ABD≌△ECB,,,,,····································· 10分24.(1)证明:连接OD,∵AB=AC, ∴∠B=∠C,∵OC=OD ∴∠C=∠ODC∴∠B=∠ODC, 是的切线, ,; ·····································5分(2), ,,,, , ,,,,.·······························10分25.(1)根据题意可知,即,所以,故。
2017年初中学业数学模拟试卷及答案

2017年初中学业模拟考试数学试题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共8页.满分120分.考试时间120分钟.考试结束后,将本试卷和答题卡一并交回.注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将区县、毕业学校、姓名、考试号、座号填写在答题卡和试卷规定的位置上,并核对监考教师粘贴的考号条形码是否与本人信息一致.2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能写在试卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;需要在答题卡上作图时,可用2B铅笔,但必须把所画线条加黑.4.答案不能使用涂改液、胶带纸、修正带修改.不按以上要求作答的答案无效.不允许使用计算器.第Ⅰ卷(选择题共48分)一、选择题:本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项选出来.每小题4分,共48分,错选、不选或选出的答案超过一个,均记0分.1、观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有A .1个B .2个C .3个D .4个2、小明将一个直角三角板(如左图)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是A .B .C .D . 3、下列计算正确的是A .+=B .1)(11=C . 1211()()24xy xy xy -=D .﹣(﹣a )4÷a 2=a 24、如图,一束光线与水平面成︒60 的角度照射地面,现在地面AB 上支放一个平面镜CD ,使这束光线经过平面镜反射后成水平光线,则平面镜CD 与地面AB 所成角DCB ∠的度数等于A .︒30B .︒45C .︒50D .︒60 5、甲、乙两人5次射击命中的环数如下:则以下判断中,正确的是 A .‾x 甲=‾x 乙,S 甲2=S 乙2 B .‾x 甲=‾x 乙,S 甲2>S 乙2C .‾x 甲=‾x 乙,S 甲2 <S 乙2D .‾x 甲<‾x 乙,S 甲2<S 乙26、一只盒子中有红球m 个,白球8个,黑球n 个,每个球除颜色外都相同,从中任取一个球,取得是白球的概率与不是白球的概率相同,那么m 与n 的大小关系是 A .m + n = 8 B .m + n = 4 C . m = n = 4 D . m = 3,n =57、在下图4×4的正方形网格中,△MNP 绕某点旋转一定的角度,得到△M 1N 1P 1,则其旋转中心可能是A .点AB .点BC .点CD .点D 8、用计算器计算时,下列说法错误的是A .“计算431-21B .“计算281035-⨯C .“已知SinA=0.3,求锐角AD .“计算521⎪⎭⎫ ⎝⎛”的按键顺序是9、如图,AB 是⊙的直径,弦CD 垂直平分OB ,则∠BDC 的度数为A .15°B .20°C .30°D .45°10、已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:第1行 1 第2行 -2 3第3行 -4 5 -6第4行 7 -8 9 -10 第5行 11 -12 13 -14 15 …… ……按照上述规律排下去,那么第100行从左边数第5个数是 A .-4955 B .4955 C .-4950 D .495011、函数x y 4=和x y 1=在第一象限内的图象如图,点P 是xy 4=的图象上一动点,PC ⊥x 轴于点C ,交x y 1=的图象于点A ,PD ⊥y 轴于D ,交xy 1=的图象于点B ,给出如下4个结论:①△ ODB 与△OCA 的面积相等;②线段PA 与PB 始终相等;③四边形PAOB 的面积大小不会发生变化;④CA=31AP .其中正确的结论是A .①②③B .①②④C .②③④D .①③④12、如图,在矩形ABCD 中,BC=8,AB=6,经过点B 和点D 的两个动圆均与AC 相切,且与AB 、BC 、AD 、DC 分别交于点G 、H 、E 、F ,则EF+GH 的最小值是A .6B .8C .9.6D .10第Ⅱ卷(非选择题 共72分)二、填空题:本题共5小题,每小题4分,共20分,只要求填写最后结果. 13、分解因式()()11+---++b a b a b a =.14、已知022=--a a ,则代数式111--a a 的值为. 15、 如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若ABC ∆与△111A B C 是位似图形,且顶点都在格点上,则位似中心的坐标是.16、如图,三角板ABC 的两直角边AC ,BC 的长分别为40cm 和30cm ,点G 在斜边A B 上,且BG =30cm ,将这个三角板以G 为中心按逆时针旋转90°至△A′B′C′的位置,那么旋转前后两个三角板重叠部分(四边形EFGD )的面积为____________.17、如图,在以AB 为直径的半圆中,有一个边长为1的内接正方形CDEF ,则以AC 和BC 的长为两根的二次项为1的一元二次方程是 .三、解答题:本大题共7小题,共52分.解答要写出必要的文字说明、证明过程或演算步骤.18、(本题满分5分)如图,直线a ∥b ,RtABC 的顶点B 在直线a 上,∠C =90°, ∠β=55°,求∠α的度数.19、(本题满分6分)某校对九年级学生进行了一次数学学业水平测试,成绩评定分为A、B、C、D四个等级(注:等级A、B、C、D分别代表优秀、良好、合格、不合格),学校从九年级学生中随机抽取50名学生的数学成绩进行统计分析,并绘制成扇形统计图(如图所示).根据图中所给的信息回答下列问题:(1)随机抽取的九年级学生数学学业水平测试中,D等级人数的百分率和D等级学生人数分别是多少?(2)这次随机抽样中,学生数学学业水平测试成绩的中位数落在哪个等级?(3)若该校九年级学生有800名,请你估计这次数学学业水平测试中,成绩达合格以上(含合格)的人数大约有多少人?20、(本题满分6分)已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.(1)求证:△ABD≌△CAE;(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.21、(本题满分8分) 已知:一元二次方程04522=--x x 的某个根,也是一元二次方程 049)2(2=++-x k x 的根,求k 的值.22、(本题满分8分)如图,王刚在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB 为3.2m ,在入口的一侧安装了停止杆CD ,其中AE 为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C 恰好与地面接触,此时CA 为0.7m .在此状态下,若一辆货车高3m ,宽2.5m ,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过计算说明.(参考数据:3≈1.7)23、(本题满分9分)已知抛物线的顶点为(1,0),且经过点(0,1).(1)求该抛物线对应的函数的解析式; (2)将该抛物线向下平移个单位,设得到的抛物线的顶点为A ,与轴的两个交点为B 、C ,若△ABC 为等边三角形.①求的值;②设点A 关于轴的对称点为点D ,在抛物线上是否存在点P ,使四边形CBDP 为菱形?若存在,写出点P 的坐标;若不存在,请说明理由.24、(本题满分10分)在Rt △ABC 中,∠ACB =90°,BC =30,AB =50.点P 是AB 边上任意一点,直线PE ⊥AB ,与边AC 或BC 相交于E .点M 在线段AP 上,点N 在线段BP 上,EM =EN ,sin ∠EMP =1213. (1)如图1,当点E 与点C 重合时,求CM 的长;(2)如图2,当点E 在边AC 上时,点E 不与点A 、C 重合,设AP =x ,BN =y ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)若△AME ∽△ENB ,求AP 的长.图1 图2 备用图初中学业模拟考试数学参考答案及评分标准一.选择题(每小题4分,共48分) 1--12:BDCAB ABDCB DC 二.填空题(每小题4分,共20分) 13、 (a +b -1)214、2115、 (9,0) 16、 144cm 217、x 2﹣5x+1=0 三.解答题18、解:过点C作CE∥a,……………………………………………………………………………………1分∵a∥b,∴CE∥a∥b,∴∠BCE=∠α,∠ACE=∠β=55°,………………………………………………………………………3分∵∠C=90°,∴∠α=∠BCE=∠ABC﹣∠ACE=35°.…………………………………………………………………5分19、解:(1)∵1-30%-48%-18% = 4%,∴D等级人数的百分率为4%,………………………………………………………………………………1分∵4%×50 = 2,∴D等级学生人数为2人,…………………………………………………………………2分(2) ∵A等级学生人数为30%×50 = 15人,B等级学生人数为48%×50 = 24人,C等级学生人数为18%×50 = 9人,D等级学生人数为4%×50 = 2人,∴中位数落在B等级.………………………………………………………………………………………4分(3) 800×(30%+48%+18%)= 768,∴成绩达合格以上(含合格)的人数大约有768人.………………………………………………………6分20、解:(1)证明:∵AB=AC,AD是BC边上的中线,∴AD⊥BC,BD=CD.∵AE∥BC,CE⊥AE,∴四边形ADCE是矩形.∴AD=CE.在Rt△ABD与Rt△CAE中,AD CEAB CA=⎧⎨=⎩, ∴Rt △ABD ≌Rt △CAE (HL).………………………………………………………………………………3分 (2) DE ∥AB ,DE=AB .………………………………………………………………………………4分 证明:∵四边形ADCE 是矩形, ∴AE=CD=BD ,AE ∥BD , ∴四边形ABDE 是平行四边形,∴DE ∥AB ,DE=AB .……………………………………………………………………………………………6分 21、解:由25204x x --=,得212951(1),,422x x x -===-,………………………………………………2分 当152x =是29(2)04x k x -++=的根时, 21119204x x kx --+=,11404kx -+=,5722k =,75k =…………………………………………………………………………………………………5分 当212x =-是29(2)04x k x -++=的根时,22229204x x kx --+=, 21404kx -+=, 1722k -=,7k =-. ……………………………………………………………………………………………8分 22、解:如图,在AB 之间找一点F ,使BF =2.5m ,过点F 作GF ⊥AB 交CD 于点G ,…………………………………2分∵AB =3.2m ,CA =0.7m ,BF =2.5m ,∴CF =AB -BF +CA =1.4m ,………………………………………………………………………………4分分 ∵2.38<3,∴这辆货车在不碰杆的情况下,不能从入口内通过.………………………………………… 8分(或者设GF=3,求出BF ,再与2.5去比较)23.解:(1)由题意可得,解得∴抛物线对应的函数的解析式为.…………………………….…………….……3分 (2)①将向下平移个单位得:-=,可知A (1,-),B (1-,0),C (1+,0),BC =2.………………………………….……….…….……5分 由△ABC 为等边三角形,得,由>0,解得=3.…………….……….……6分 ②不存在这样的点P .………….………………………………………….………………………7分∵点D 与点A 关于轴对称,∴D (1,3).由①得BC =2.要使四边形CBDP 为菱形,需DP ∥BC ,DP =BC .由题意,知点P 的横坐标为1+2, 当=1+2时-m ==,故不存在这样的点P .………….……………………….…………………9分24、解:(1)如图1,∵∠ABC=90°,BC=30,AB=50,∴AC=40,∵PE ⊥AB ,∴∠EPM=90°,∴sin ∠A=AB BC =AC CP ,∴405030CP =,∴24=CP , ∴在RT ΔCMP 中,sin ∠EMP=CM CP ,即131224=CM ,∴CM=26.…………………2分图1 图2(2)如图2,∠EPM=90°,∠ABC=90°∴tan ∠A=AC BC =APEP , ∴x EP =4030,∴x EP 43=, ∴在RT ΔEMP 中,sin ∠EMP=EM EP ,即131243=EM x , ∴x EM 4839=,∴x PM 4815=,∵EM=EN ,∴x PM PN 4815==, ∴x x y 481550--==x 162150-…………………………………………….…4分 如图1,点E 与点C 重合时,32==x AP ,又∵点E 不与点A 、C 重合∴320<<x ……………5分(3)∵EM=EN ,∴∠EMP=∠ENP ,∴∠EMA=∠ENB ,当点E 在线段AC 上,∴如图3,△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应,图3 图4 ∴BNEM EN AM =, ∴(x x 4815-):(x 4839)=(x 4839):(x 162150-) ∴22=x ,………………………………………………………………………………7分当点E 在线段BC 上,∴如图4,△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应, ∴BNEM EN AM =, ∵BP=x -50,∴EP=)50(34x -∴EM=)50(913x -,MP=)50(95x -, ∴BN=)50(9550x x ---,∴[)50(95x x --]:)50(913x -=)50(913x -:[)50(9550x x ---], ∴42=x . ……………………………………………………………………………9分 综上AP 的长为22或42.…………………………………………………………10分。
潍坊市2017年初中学业水平模拟第三次考试数学试题有答案

潍坊市初中学业水平模拟考试(三)数 学 试 题一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分. 错选、不选或多选均记0分.) 1.-2的绝对值是( )A.-2B. 12C. 12- D.22. tan30°的值等于( )A.B. 3C.D.3. 下列图形中,既是轴对称图形又是中心对称图形的是( )4. 下列运算正确的是( )A .3﹣1=﹣3 B .=±3 C .(ab 2)3=a 3b 6 D . a 6÷a 2=a 35. 某生态示范园,计划种植一批核桃,原计划总产量达36万千克.为了满足市场需求,现决定改良核桃品种,改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万千克,种植亩数减少了20亩.则原计划和改良后平均每亩产量各多少万千克?设原计划每亩平均产量x 万千克,则改良后平均亩产量为1.5x 万千克.根据题意列方程为( ). A .20365.1936=-+x x B .205.13636=-x x C .205.193636=+-x x D .205.193636=++xx 6. 某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30,则这组数据的众数与中位数分别是( ) A .30,29 B .30,27 C .29,30 D .30,287. 如图,在△ABC 中,∠CAB=65°,将△ABC 在平面内绕点A 旋转到△AB′C′的位置,使CC′∥AB ,则旋转角的度数为( ) A.35° B.40° C.45° D.50° 8.已知反比例函数(0)ky k x=<的图象上两点112212A(,)B(,)0,x y x y x x <<、,且则下列不等式恒成立的是( )A. 12y y 0⋅<B. 12y y 0-<C. 12y y 0->D. 12y y 0+<9. 如图①是一个直角三角形纸片,∠A=30°,将其折叠,使点C 落在斜边上的点C′处,折痕为BD ,如图②,再将②沿DE 折叠,使点A 落在DC′的延长线上的点A′处,如图③.若折痕DE 的长是38cm ,则BC 的长是( ) A .3 cm B .4cm C . 5cm D . 6cm10. 已知6是关于x 的方程27240x mx m -+=的一个根,并且这个方程的两个根恰好是菱形ABCD 两条对角线的长,则菱形ABCD 的周长为( )A.20B.24C.32D.56 11.如图,在圆心角为90°的扇形OAB 中,半径OA=4cm ,C 为弧AB 的中点,D 、E 分别是OA 、OB 的中点,则图中阴影部分的面积为 ( ) cm 2.A. 42π-B. 42π-C. 22π+D. 2π+12.已知二次函数y =ax 2+bx +c 的图象如图所示.下列结论: ①abc >0;②2a ﹣b <0;③4a ﹣2b +c <0;④(a +c )2<b 2 ⑤2b -4ac 0>. 其中正确的个数有( ) A.5 B.4 C.3 D.2二、填空题(本大题共6小题,共18分. 只要求填写最后结果,每小题填对得3分.) 13.如图,已知在梯形ABCD 中,AD ∥BC ,∠B =30°, ∠C =75°,AD =2,BC =7,那么AB =_________. 14. 分解因式:3231215x x x --= .15.一个几何体的三视图如图所示,根据图示的数据计算该几何体的表面积是 .(结果保留π)16. 已知关于x 的一元二次方程042=+-m x x .方程两实数根分别为1x ,2x ,且满足22521=+x x ,则m -2的最后结果是 .17. 在平面直角坐标系中,点A 、B 的坐标分别是(m,5)、(3m-1,5).若直线y=2x+1不经过点A 和点B 但与线段AB 相交,则m 的取值范围是__________.18.如图,双曲线y=xk(x >0)经过△OAB 的顶点A 和OB 的中点C ,AB ∥x 轴,点A 的坐标为(2,3).求△OAC 的面积是 .三、解答题(本大题共6小题,共66分.解答要写出必要的文字说明、证明过程或演算步骤)19.(本题满分10分)某中学在实施快乐大课间之前组织过“我最喜欢的球类”的调查活动,每个学生仅选择一项,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.(1)求出被调查的学生人数; (2)把折线统计图补充完整;(3)小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.如果确定小亮打第一场,其余三人用“手心、手背”的方法确定谁获胜谁打第一场.若三人中有一人出的与其余两人不同则获胜;若三人出的都相同则平局.已知大刚出手心,请用树状图分析大刚获胜的概率是多少?20. (本题满分10分)某商场门前的台阶截面如图中阴影部分所示.已知台阶有四级小台阶且每一级小台阶高度相等,台阶高度EF为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为1米的不锈钢架杆AD和BC(杆子的低端分别为D,C),且∠DAB=66.5°(cos66.5°≈0.4).(1)求点D与点C的高度差DH;(2)求所用不锈钢材料的总长度(即AD+AB+BC的长).21. (本题满分10分)如图,AC是⊙O的直径,PA切⊙O于点A,点B在⊙O上,PA=PB,PB的延长线与AC的延长线交于点M.(1)求证:PB是⊙O的切线;(2)当AC=6,PA=8时,求MB的长.22.(本题满分11分)某文具专卖店专销某种品牌的钢笔,进价12元/支,售价20元/支.为了促销,专卖店决定:凡是一次性购买超过10支的,每超过一支,所购钢笔每支售价就降低0.20元,但是每支售价不能低于16元.如图线段AB和BC是购买钢笔的单价y(元/支)与购买数量x(支)的函数图象的一部分.(1)顾客要想以最低价购买,需要一次至少购买支(填最后结果);(2)当顾客一次购买x支时,求专卖店的利润w(元)与购买数量x(支)之间的函数关系式;(3)求顾客一次购买多少支时,专卖店的利润是123.2元?23. (本题满分12分)如图,已知锐角△ABC中,边BC长为6,高AD长为8,两动点M、N分别在边AB、AC 上滑动,且MN∥BC,以MN为边向下作正方形MPQN.设正方形的边长为x.(1)若正方形MPQN的顶点P、Q在边BC上,求MN的长;(2)设正方形MPQN与△ABC公共部分的面积为y(y>0),当x是多少时,公共部分的面积y最大?最大值是多少?24. (本题满分13分)已知:抛物线y=﹣x2+bx+c交y轴于点C(0,3),交x轴于点A,B,(点A在点B的左侧),其对称轴为x=1,顶点为D.(1)求抛物线的解析式及A,B两点的坐标;(2)若⊙P经过A,B,C三点,求圆心P的坐标;(3)求△BDC的面积S△DCB;并探究抛物线上是否存在点M,使S△MCB=S△DCB,若存在,求出M 点的坐标,若不存在,说明理由.初中学业水平模拟考试(三)数学试题答案及评分标准二、填空题(每小题3分,共18分.)13.5 14. ()()315x x x +- 15. 16)π 16.114417. 1m 2<< 18. 4.5 三、解答题(共6小题,共66分.)19.(本题满分10分)解:(1)由篮球所占比例及相应人数可求出被调查的学生数是:40÷20%=200(人);………………………3分(2)喜欢足球的人数为:200×15%=30(人);……4分 喜欢羽毛球人数为:200-70-20-40-30=40(人);……5分 折线统计图如图所示……6分(3)……8分由树状图可知:三人伸手的情况有(手心,手心,手心)、(手心,手心,手背)、(手心,手背,手心)、(手心,手背,手背)、4种,每种情况出现的可能性都是相同的,其中大刚伸手心与其他两人不同的情况有1种,所以P (大刚)=14所以大刚打第一场的概率为14.……10分20. (本题满分10分) 解:(1)DH=1.6×43=1.2(米);……2分 (2)连接CD∵AD ∥BC ,AD=BC ,∴四边形ABCD 为平行四边形. ∴AB ∥CD ,AB=CD ,∴∠HDC=∠DAB=66.5°,……5分 Rt △HDC 中,∵cos ∠HDC=CDDH, ∴CD=︒5.66cos DH ≈34.02.1=(米),……8分∴m=AD+AB+BC ≈1+3+1=5(米),即所用不锈钢材料的总长度约为5米. ……10分21. (本题满分10分)(1)证明:连接OB 、OP.∵PA=PB ,OP=OP,OA=OB. ∴PAO PBO ∆∆≌. ∴∠OBP=∠OAP . ∵PA 切⊙O 于A , ∴∠OAP=90°.∴∠OBP=∠OAP=90° ,即OB ⊥PB ∵OB 是⊙O 的半径,∴PB 是⊙O 的切线. ……………………………………………………4分 (2)解:∵PA 切⊙O 于点A ,PB 切⊙O 于点B , ∴∠OBM=∠PAM=90°. ∵∠M=∠M .∴△MBO ∽△MAP . ∴MB OBMA PA=∵AC =6,∴OB=3. ∵PA =8, ∴38MB MA =,∴83MA MB =.…………………………………………………………6分 ∵在直角三角形MAP 中,222+MA AP MP =,又∵PA=PB=8, ∴2228()8(8)3MB MB +=+, 即55(-16)09MB MB =,∴MB=0(舍去),55-1609MB =,MB=14455.…………………………10分 22. (本题满分11分)解:(1)30…………2分(2)购买数量x 决定利润w (元)与购买数量x (支)的函数关系式,有3种情况: ①当10x 0≤<时, w =(20-12)x=8x ;②当30x 10≤<时, w =[]x 1210x 0.220---)(=x 10x 2.02+-; ③当30x >时, w =4x综上所述⎪⎩⎪⎨⎧>≤<+-≤<=)30x (4 )3010x10x 2.010x 0x8w 2x x ()(…………8分 (3)专卖店的利润w =123.2元时,不可能是(2)中的①和③,只能为第②情况, 故x 10x 2.02+-=123.2,即0616x 50x 2=+-,解得.28x 22x 21==,所以,顾客一次购买22支或28支时,此时专卖店的利润为123.2元. ……11分23. (本题满分12分)证明:(1)如图,∵MN ∥B C ∴AMN ∆∽ABC ∆,又∵AD 是ABC ∆的高,AK 是AMN ∆的高, ∴AK MNAD BC=. ∵BC=6,AD=8,∴8x x86-=, ∴24x=7.即MN 的长是247.…………4分(2)公共部分分为三种情形:在三角形内;一边在BC 上;正方形有一部分在三角形外,此时 为矩形.显然在内部时的面积比刚好在边上时要小,所以需比较后两种情形时的面积大小.…………6分①当PQ 边在BC 上时,根据(1)得正方形的边长为247,所以此时公共部分的面积y=224576=749(). …………7分 ②如图,当正方形有一部分在三角形外时,由题意和(1)知:正方形边长x 的取值范围为724<x <6 . ∵AMN ∆∽ABC ∆,∴AK MNAD BC =,即8-x86KD =, ∴48x 3KD =-,∴公共部分的面积y=244x 8x = -x +8x 33-()=12)3(342+--x …………10分∴当724<x <6时,y 随x 的增大而减小,y 无最大值. 若当x=724时,y=49576综①②知,当正方形的边长为724时,公共部分面积最大,最大面积为49576. …………12分24. (本题满分13分)解:(1)∵抛物线:y=﹣x 2+bx+c 的对称轴为x=1,∴﹣=1,解得b=2,又∵过点C (0,3),∴c=3∴抛物线的解析式为y=﹣x 2+2x+3,令y=0,可得﹣x 2+2x+3=0,解得x=﹣1或x=3, ∴A 点坐标为(﹣1,0),B 点坐标为(3,0)…………3分(2)∵点P 到A,B 的距离相等,∴点P 一定在直线x=1上,设P 点坐标为(1,y ), ∴PC 2=12+(y ﹣3)2=y 2﹣6y+10,PA 2=22+y 2=y 2+4, 又∵PC=PA ,∴y 2﹣6y+10=y 2+4,解得y=1, ∴P 点坐标为(1,1);…………7分(3)①当x=1时,y=4,∴点D 的坐标为(1,4), 设直线BC 的解析式为y=kx+m ,由题意得⎩⎨⎧+==m k 30m 3解之得:⎩⎨⎧-==13m k ,∴直线BC 的解析式为y=-x+3, 设直线BC 与对称轴x=1交于点E,则E (1,2),∴DE=2.S △DCB =3212121=⋅=⋅+⋅OB DE FB DE OF DE …………9分②存在.过点D 作直线1l ∥BC,可以求出其解析式为5+-=x y ,⎩⎨⎧++-=+-=3252x x y x y 解之得⎩⎨⎧==41x 11y ,⎩⎨⎧==32x 22y ∴点M 坐标为M 1(2,3) 又∵DE=EF, ∴过点F 做直线2l ∥BC,可以求出其解析式为1+-=x y ,⎩⎨⎧++-=+-=3212x x yx y解之得⎪⎪⎩⎪⎪⎨⎧=+=217-1-2173x 11y ,⎪⎪⎩⎪⎪⎨⎧+==2171-217-3x 22y ∴点M 坐标为M 2(2173+,2171--),M 3(2173-,2171+-) ∴符合条件的点共有3个,M 1(2,3);M 2(2173+,2171--);M 3(2173-,2171+-). …13分。
2017年初中毕业班模拟测试题数学(三)汇总

2017 年初中毕业班模拟测试题数学 (三)第一部分 选择题(共 30 分)一、选择题 (本大题共 10 小题,每题 3 分,满分 30 分。
在每题给出的四个选项中,只有一项吻合题目要求的。
1、实数1)的相反数是(3A.3B.31 1C.D.332、以下运算正确的选项是()A. 4a a3 B. ab 5ab 6ab C. a 2 a0 D. ab 3 2ab 63、下面的几何体中,主(正)视图为三角形的是()A.B. C. D.4、某校九年级( 3)班“环保小组”的5 位同学在一次活动中捡荒弃塑料袋的个数分别为:4,6,8,16,16. 这组数据的中位数、众数分别为 ()A. 16,16B. 10,16C. 8,8D. 8,165、 以下交通标志中,是轴对称图形的是()A.B. C. D.6、使分式x )有意义的 x 的取值范围是(2x 4A . x = 2B . x ≠2C . x =- 2D . x ≠- 2 7、实数 a 在数轴上的地址以下列图,则 a 3()A. a 3B.a 3C.a 3D.a 38、已知反比率函数 yk(k 0) 的图象上两点 A(x 1 , y 1 ) 、B( x 2 , y 2 ) ,且 x 1 x 2 0 ,则 y 1x与 y 2 的大小关系是()A. y 1 y 2B.y 1 y 2C.y 1 y 2D.不能够确定9、已知cos A2),则 tan A 的值为(22B.1C.3D.3BA.3 210、以下列图,已知在三角形纸片ABC中,∠BCA=90°,C A∠ BAC=30°, AB=6,在 AC上取一点 E,以 BE为折痕,E使 AB的一部分与 BC重合, A与 BC延长线上的点 D重合,则 DE的长度为()DA. 6B.3 C .2 3 D .3第 10 题图第二部分非选择题(共120 分)二、填空题(本大题共 6 小题,每题 3 分,满分 18 分)11、如图,ABP 绕点B逆时针旋转获得A1BP1,若 P 95 ,A135 ,则 A1 BP1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密★启用前试卷类型:A 2017年初中学业水平考试全真模拟试题
数学试题(三)
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题,36分;第Ⅱ卷为非选择题,84
分;共120分.考试时间为120分钟.
2.答卷前务必将试题密封线内和答题卡上的项目填写清楚.所有答案均填写在答题卡
上,答在本试卷上一律无效.
第Ⅰ卷(选择题共36分)
一、选择题(本大题共12小题,每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。
每小题选对得3分,选错、不选或选出的答案超过一个均记0分)
1.的立方根是()
2.下列标志中不是中心对称图形的是()
A
第4题图
5.若代数式有意义,则实数x 的取值范围是( )
则∠ADC
的度数是( )
7.若不等式组无解,则实数
a 的取值范围是( ) 8.如图,已知矩形ABCD 的长AB 为5,宽BC 为4,E 是BC 边上的一个动点,AE ⊥EF ,EF 交CD 于点F .设BE=x ,FC=y ,则点E 从点B 运动到点C 时,能表示y 关于x 的函数关系
的大致图象是( )
9.等腰三角形一条边的边长为3,它的另两条边的边长是关于x
的一元二次方程x 2
﹣10.已知一次函数y 1=kx+b (k <0)与反比例函数y 2=
x
m
(m≠0)的图象相交于A 、B 两点,其横坐标分别是﹣1和3,当y 1>y 2时,实数x 的取值范围是( )
第6题图
第7题图
11.如图是某市7月1日至10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择7月1日至7月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间有且仅有1天空气质量优良的概率是()
形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为()
第Ⅱ卷(非选择题共84分)
说明:第Ⅱ卷请用0.05mm的黑色中性笔直接在试卷上作答.
二、填空题(本大题共6小题,共18分.只要求填写最后结果,每小题填对得3分)13.分解因式:2x(x﹣3)﹣8= .
14.计算:82014×(﹣0.125)2015= .
15.如图,两个半径均为的⊙O1与⊙O2相交于A、B两点,
且每个圆都经过另一个圆的圆心,则图中阴影部分的面积
为.(结果保留π)
16.已知一组数据﹣3,x,﹣2,3,1,6的中位数为1,则其方差为.17.如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔50米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆
CD后退2米到点G处,在G处测得建筑物顶端A
和标杆顶端C在同一条直线上;从标杆FE后退4米
到点H处,在H处测得建筑物顶端A和标杆顶端E
在同一条直线上,则建筑物的高是米.
18.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是尺.
三、解答题(本大题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤)19.(9分)今年我市把男生“引体向上”项目纳入学业水平体育考试内容,考试前某校为了解该项目的整体水平,从九年级220名男生中,随机抽取20名进行“引体向上”测试,测试成绩(单位:个)如图1:
其中有一数据被污损,统计员只记得11.3是这组样本数据的平均数.
(1)求该组样本数据中被污损的数据和这组数据的极差;
(2)请补充完整下面的频数、频率分布表和频数分布直方图(如图2);
(3)(包含11个)“引体向上”?
20.(10分)如图,在梯形ABCD中,AD∥BC,∠B=90°,以AB为直径作⊙O,恰与另一腰CD相切于点E,连接OD、OC、BE.
(1)求证:OD∥BE;
(2)若梯形ABCD的面积是48,设OD=x,OC=y,且x+y=14,求CD的长.
21.(10分)如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.新-课- 标-第一-网
22.(12分)如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP到BA的延长线于点Q,求sin ∠BQP的值;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.
23.(12分)经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.
(1)求大桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时,应控制大桥上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.
24.(13分)如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
2017年初中学业水平考试全真模拟试题
数学试题(三)答题卡
试题编辑:王欣武。
