中考数学全真模拟试题(5)浙教版
2024-2025学年浙教版中考数学模拟试卷及答案
2024-2025学年浙教版中考数学模拟试卷班级：____________________ 学号：____________________ 姓名：____________________一、单选题（每题3分）1.若函数y=2x+1与直线y=−x+5相交，则交点的坐标是：A.(2,5)B.(1,3)C.(3,7)D.(−1,−1)答案：BBC，连接AE并延长至F，使2.已知正方形ABCD的边长为a，点E在BC上，且BE=13EF=AE。
则△AEF的面积与正方形ABCD面积之比为：A.1:2B.1:3C.1:4D.1:6答案：D3.下列哪个数是方程x2−9x+20=0的一个根？A. 4B. 5C. 6D. 7答案：B4.若tanθ=3，则sin2θ的值为：4A.2425B.1225C.1625D.725答案：A5.在半径为r的圆中，弦AB的长度为r，则∠AOB（O为圆心）的度数为：A. 30°B. 45°C. 60°D. 90°答案：C二、多选题（每题4分）1.【函数】问题描述：这里是关于函数的一个问题…•选项A: 描述A•选项B: 描述B•选项D: 描述D•选项E: 描述E答案：选项A: 描述A, 选项B: 描述B2.【几何】问题描述：这里是关于几何的一个问题…•选项E: 描述E•选项D: 描述D•选项A: 描述A•选项C: 描述C•选项B: 描述B答案：选项C: 描述C, 选项B: 描述B3.【几何】问题描述：这里是关于几何的一个问题…•选项E: 描述E•选项C: 描述C•选项A: 描述A•选项D: 描述D答案：选项B: 描述B, 选项A: 描述A, 选项C: 描述C4.【函数】问题描述：这里是关于函数的一个问题…•选项C: 描述C•选项E: 描述E•选项D: 描述D•选项A: 描述A•选项B: 描述B答案：选项A: 描述A, 选项C: 描述C5.【概率统计】问题描述：这里是关于概率统计的一个问题…•选项B: 描述B•选项D: 描述D•选项A: 描述A•选项C: 描述C•选项E: 描述E答案：选项A: 描述A, 选项B: 描述B, 选项C: 描述C三、填空题（每题3分）1.若一个正方形的对角线长为(8√2)厘米，则该正方形的面积为________平方厘米。
浙教版中考数学模拟试卷
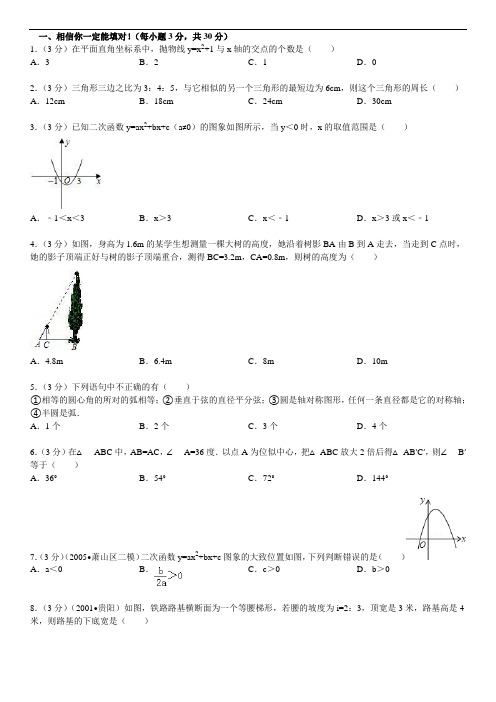
一、相信你一定能填对！（每小题3分，共30分）23．（3分）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，当y＜0时，x的取值范围是（）4．（3分）如图，身高为1.6m的某学生想测量一棵大树的高度，她沿着树影BA由B到A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m，CA=0.8m，则树的高度为（）5．（3分）下列语句中不正确的有（）①相等的圆心角的所对的弧相等；②垂直于弦的直径平分弦；③圆是轴对称图形，任何一条直径都是它的对称轴；6．（3分）在△ABC中，AB=AC，∠A=36度．以点A为位似中心，把△ ABC放大2倍后得△ AB′C′，则∠B′2C8．（3分）（2001•贵阳）如图，铁路路基横断面为一个等腰梯形，若腰的坡度为i=2：3，顶宽是3米，路基高是4米，则路基的下底宽是（）9．（3分）已知，直角坐标系中，点E（﹣4，2），F（﹣1，﹣1），以O为位似中心，按比例尺2：1把△ EFO缩小，则点E的对应点E′的坐标为（）10．（3分）如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2，则该半圆的半径为（）．cm cm D．cm二、你能填得又快又对吗？（每小题5分，共30分）11．（5分）在平面内，⊙O的半径为5cm，点P到圆心O的距离为3cm，则点P与⊙O的位置关系是_________．12．（5分）如果一条抛物线的形状与y=﹣x2+2的形状相同，且顶点坐标是（4，﹣2），则它的解析式是_________．13．（5分）如图，AB是⊙O的直径，AC是弦，D是AC弧的中点，若∠BAC=30°，则∠DCA=_________．14．（5分）计算：tan230°﹣sin60°﹣2sin45°=_________．15．（5分）二次函数y=ax2+bx+c的图象如图所示，则①abc，②b2﹣4ac，③2a+b，④a+b+c这四个式子中，值为正数的有_________（填序号）．16．（5分）将一副三角板如图叠放，则左右阴影部分积之比等于_________．三、认真解答，一定要细心哟！17．（10分）已知在平面直角坐标系中，Rt△ABC的位置如图所示（方格小正方形的边长为1）．（1）把△ABC绕原点O逆时针方向旋转90°得△A1B1C1，A、B、C的对应点分别为A1、B1、C1．请画出△A1B1C1，并直接写出点A1、B1、C1的坐标：A1_________，B1_________，C1_________；（2）线段AB、A1B1的中点分别为M、N，则△OMN的面积为_________平方单位．18．（10分）如图，点A、B为地球仪的南、北极点，直线AB与放置地球仪的平面交于点D，所成的角度约为67°，半径OC所在的直线与放置平面垂直，垂足为点E．DE=15cm，AD=14cm．求半径OA的长．（精确到0.1cm）（参考数据：sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）19．（10分）已知梯形ABCD中，AB∥ CD，AC与BD交于O点，AB=2cm，CD=4cm，S△ AOB=1cm2，求梯形ABCD的面积．20．（12分）反比例函数与一次函数y2=kx+b的图象交于两点A（﹣2，1），B（1，﹣2）．（1）求反比例函数的解析式；（2）求一次函数y2=kx+b的解析式；（3）在下图的同一直角坐标系中，画出反比例函数和一次函数的图象，并根据图象回答：当x为何值时，y1＜y2？21．（12分）已知等腰三角形的周长为20，其中一内角的余弦值是，求这个等腰三角形的腰长．22．（12分）如图，锐角三角形ABC中，CD，BE分别是AB，AC边上的高，垂足为D，E．（1）证明：△ACD ∽△ABE．（2）若将D，E连接起来，则△AED与△ABC能相似吗？说说你的理由．23．（14分）如图，抛物线y=x2﹣2x﹣3与x轴交A、B两点（A点在B点左侧），与y轴交于点D．（1）求点A、B、D的坐标；（2）若点C在该抛物线上，使△ABD≌△BAC．求点C的坐标，及直线AC的函数表达式；（3）P是（2）中线段AC上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值．浙教版中考数学模拟试卷参考答案与试题解析一、相信你一定能填对！（每小题3分，共30分）23．（3分）（2008•达州）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，当y＜0时，x的取值范围是（）4．（3分）（2005•南京）如图，身高为1.6m的某学生想测量一棵大树的高度，她沿着树影BA由B到A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m，CA=0.8m，则树的高度为（）米，则=，=5．（3分）下列语句中不正确的有（）①相等的圆心角的所对的弧相等；②垂直于弦的直径平分弦；③圆是轴对称图形，任何一条直径都是它的对称轴；6．（3分）（2005•扬州）在△ABC中，AB=AC，∠A=36度．以点A为位似中心，把△ ABC放大2倍后得△AB′C′，2C，错误，对称轴为直线x=，8．（3分）（2001•贵阳）如图，铁路路基横断面为一个等腰梯形，若腰的坡度为i=2：3，顶宽是3米，路基高是4米，则路基的下底宽是（）9．（3分）（2007•泰州）已知，直角坐标系中，点E（﹣4，2），F（﹣1，﹣1），以O为位似中心，按比例尺2：1把△EFO缩小，则点E的对应点E′的坐标为（）10．（3分）（2008•芜湖）如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2，则该半圆的半径为（）．cm cm D．cmR=二、你能填得又快又对吗？（每小题5分，共30分）11．（5分）（2008•重庆）在平面内，⊙O的半径为5cm，点P到圆心O的距离为3cm，则点P与⊙O的位置关系是点P在⊙O内．12．（5分）如果一条抛物线的形状与y=﹣x2+2的形状相同，且顶点坐标是（4，﹣2），则它的解析式是y=﹣x2+8x ﹣18或y=x2﹣8x+14．=413．（5分）如图，AB是⊙O的直径，AC是弦，D是AC弧的中点，若∠BAC=30°，则∠DCA=30°．14．（5分）计算：tan230°﹣sin60°﹣2sin45°=﹣﹣．××﹣﹣﹣﹣15．（5分）二次函数y=ax2+bx+c的图象如图所示，则①abc，②b2﹣4ac，③2a+b，④a+b+c这四个式子中，值为正数的有①②（填序号）．＜对称轴﹣16．（5分）将一副三角板如图叠放，则左右阴影部分积之比等于．，，=EF==故答案为：三、认真解答，一定要细心哟！17．（10分）已知在平面直角坐标系中，Rt△ABC的位置如图所示（方格小正方形的边长为1）．（1）把△ABC绕原点O逆时针方向旋转90°得△A1B1C1，A、B、C的对应点分别为A1、B1、C1．请画出△A1B1C1，并直接写出点A1、B1、C1的坐标：A1（﹣5，1），B1（﹣1，5），C1（﹣1，1）；（2）线段AB、A1B1的中点分别为M、N，则△OMN的面积为9平方单位．×18．（10分）如图，点A、B为地球仪的南、北极点，直线AB与放置地球仪的平面交于点D，所成的角度约为67°，半径OC所在的直线与放置平面垂直，垂足为点E．DE=15cm，AD=14cm．求半径OA的长．（精确到0.1cm）（参考数据：sin67°≈0.92，cos67°≈0.39，tan67°≈2.36），≈19．（10分）已知梯形ABCD中，AB∥CD，AC与BD交于O点，AB=2cm，CD=4cm，S△AOB=1cm2，求梯形ABCD 的面积．，20．（12分）反比例函数与一次函数y2=kx+b的图象交于两点A（﹣2，1），B（1，﹣2）．（1）求反比例函数的解析式；（2）求一次函数y2=kx+b的解析式；（3）在下图的同一直角坐标系中，画出反比例函数和一次函数的图象，并根据图象回答：当x为何值时，y1＜y2？点坐标代入的解析式为，解得：．21．（12分）已知等腰三角形的周长为20，其中一内角的余弦值是，求这个等腰三角形的腰长．来求解，若底角的余弦值是，若顶角的余弦值是2x+若底角的余弦值是cosB=AB+BD=，且=若顶角的余弦值是cosA=x xx=x x．22．（12分）如图，锐角三角形ABC中，CD，BE分别是AB，AC边上的高，垂足为D，E．（1）证明：△ACD∽△ABE．（2）若将D，E连接起来，则△AED与△ABC能相似吗？说说你的理由．23．（14分）如图，抛物线y=x2﹣2x﹣3与x轴交A、B两点（A点在B点左侧），与y轴交于点D．（1）求点A、B、D的坐标；（2）若点C在该抛物线上，使△ABD≌△BAC．求点C的坐标，及直线AC的函数表达式；（3）P是（2）中线段AC上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值．﹣x==。
浙江省杭州市2020年初中毕业生学业考试仿真考试数学试题(五)含答案
2020年初中毕业生学业考试仿真卷(五)数 学(满分：120分 考试时间：120分钟)一、选择题(每小题3分，共30分，在每小题给出的四个选项中，只有一项符合题目要求) 1．实数8可以化为( D ) A ．42B ．24C ．32D ．23[命题考向：本题考查整数指数幂的意义．] 2．把a 2－b 2分解因式，结果为( A ) A ．(a ＋b )(a －b ) B ．(a ＋b )2 C ．(a －b )2D ．2(a －b )[命题考向：本题考查用公式法分解因式．]3．已知A 在B 的北偏东30°方向，则B 在A 的( A ) A ．南偏西30°方向 B ．南偏西60°方向 C ．南偏东30°方向D ．南偏东60°方向[命题考向：本题考查在平面上，用方位角刻画两个物体的相对位置．] 4．下表是某市部分行政区陆地面积统计表：(单位：平方公里)行政区 A B C D E F 面积1 4001 300600600400200这六个行政区陆地面积的中位数是( C ) A ．1 400平方公里 B ．750平方公里 C ．600平方公里D ．200平方公里[命题考向：本题考查中位数的概念．] 5．不等式组⎩⎨⎧x －3＜0，－x ＞2的解为( D )A ．x ＜3B ．x ＞－2C ．－2＜x ＜3D ．x ＜－2[命题考向：本题考查解由两个一元一次不等式组成的不等式组．]6．在下列各组视图中，能正确表示由立方体搭成几何体的是(C)(第6题图)A．①②B．①③C．②③D．①②③[命题考向：本题考查根据视图描述简单的几何体．]7．如图，四边形ABCD是轴对称图形，对角线BD所在的直线是它的对称轴，∠A＝∠C＝90°，AB≠AD，若把这个轴对称图形沿对角线BD剪开成两个三角形后，再把这两个三角形的一边完全重合在一起，重新拼成一个中心对称图形，则拼法共有(D)(第7题图)A．0种B．1种C．2种D．3种[命题考向：本题考查轴对称的性质，中心对称图形的概念．]8．甲、乙两人跑步，他们所在的位置y(m)和时间x(min)之间的关系如图所示，已知甲的跑步速度比乙快，则下列说法正确的是(B)(第8题图)A．甲每分钟跑200 m，乙每分钟跑100 mB．甲每跑100 m时，乙只能跑60 mC．相遇时，甲、乙两人都跑了500 mD ．经过4 min 时，甲、乙两人都跑了800 m[命题考向：本题考查用一次函数解决问题，理解函数图象表示的实际意义．]9．机器人从甲地出发，先向前走10 m ，再向右转140°，又向前走10 m ，再向右转140°，接下来继续以这种方式行走，…当它第1次回到出发地时共走了( B ) A ．90 m B ．180 m C ．270 mD ．360 m[命题考向：本题考查圆的基本性质．理解题意，准确画出运动轨迹，找到运动规律是解题关键．解析：如答图，机器人从A 出发，直走10 m 到B ，向右转140°(∠PBC ＝140°)直走10 m 到C ，再走CD ，DE ，…AB ＝BC ＝CD ＝DE ＝10，∠ABC ＝∠CDE ＝180°－140°＝40°，AC ＝CE ，点A ，B ，C ，D ，E ，…在同一个圆O 上．∵∠AOC ＝2∠ABC ＝80°，而80°×9＝720°＝360°×2，∴OA 绕点O 逆时针转9个80°第1次回到原位置，即机器人走18个AB 第1次回到A ，故共走了18×10＝180(m)．](第9题答图)10．如图，在△ABC 中，∠C ＝90°，∠B ＝45°，O 是AB 边上一点，以O 为圆心，以OA 为半径的圆过BC 边的中点D ，交BC 于另一点E ，交AC 于点F ，交AB 于点G ，则在①S △BGD ＝32S △EFC ，②EF ︵＝DG ︵，③DE ＝FC ，④EF AB ＝56这四个结论中，正确的为( C ) A ．①② B ．③④ C ．①②③D ．①②③④(第10题图)(第10题答图)[命题考向：本题考查圆的基本性质，相似、全等三角形的判定与性质．解析： 如答图，连结AD ，GF ，作GH ⊥BC 于点H ，则∠ADG ＝∠AFG ＝90°，∠GHB ＝∠GHC ＝90°.∵四边形AFED 内接于⊙O ， ∴∠CEF ＝∠CAD ，∠CFE ＝∠ADC ， ∵∠C ＝90°，∴△CEF ∽△CAD ， ∴CE ∶CF ＝CA ∶CD ， ∵∠B ＝45°，∴AC ＝BC ， 又∵D 是BC 边中点， ∴AC ＝2CD ，CE ＝2CF . ∵GF ∥BC ，∴GH ＝CF ，∵∠BDG ＋∠ADC ＝90°，∴∠BDG ＝∠CEF ， ∴△GHD ≌△FCE ，∴DH ＝CE ＝2CF ， ∵BH ＝GH ＝CF ，∴BD ＝3CF ， ∴S △BGD ＝32S △EFC ，①正确； ∴EF ＝DG ，∴EF ︵＝DG ︵，②正确； ∵CD ＝DE ＋CE ，BD ＝BH ＋HD ， ∴DE ＝BH ＝GH ＝FC ，③正确；设CF ＝a ，则EF ＝5a ，BC ＝6a ，AB ＝62a ， ∴EF AB ＝5a 62a ＝1012，④不正确．]二、填空题(每小题4分，共24分)11．若x 2＝－x ，则x 的取值范围是__x ≤0__． [命题考向：本题考查二次根式的非负性．]12．举一个能证明命题“若x ，y 都是实数，则1x ＋2y ≠12”是假命题的反例：__答案不唯一，合理即可，如x ＝4，y ＝8__．[命题考向：本题考查理解命题，利用反例证明命题错误．]13．如图，从⊙O 外一点A 引⊙O 的切线，切点为B ，OA 交⊙O 于点C ，CD ⊥OA 交AB 于点D ，若OC AC ＝23，则BD AD 的值为__25__．(第13题图)[命题考向：本题考查圆的基本性质，切线的性质，相似三角形的判定与性质．]14．已知点O(0，0)，点A(0，－1)，点B(2，－1)，点C(2，0)，把抛物线y＝－x2＋2x＋1向下平移n(0≤n≤4)个单位后，它的顶点正好落在四边形OABC内的概率为__14__．[命题考向：本题考查根据二次函数表达式确定顶点坐标，计算简单事件发生的概率．]15．如图，在△ABC中，AB＝AC，∠BAC＝90°，延长CB至D，使BD＝CB，以点A为旋转中心，把线段AD绕顺时针方向旋转90°，得线段AE，则tan∠EDC的值为__12__．(第15题图)[命题考向：本题考查旋转的基本性质，全等三角形的判定与性质．] 16．如图，已知正方形ABCD的顶点A(1，1)，B两点都在反比例函数y＝kx的图象上，并且点B在第三象限，点C在x轴的负半轴上，则点C的坐标为__(－5－1，0)__．(第16题图) (第16题答图)[命题考向：本题考查正方形的性质，反比例函数的性质．用代数表示出在函数图象上的点的坐标，再根据线段的等量关系建立方程求解．解析：如答图，AE⊥BE，BF⊥OC，∵四边形ABCD是正方形，可证△ABE≌△CBF，∴AE＝CF，BE＝BF，∵点A(1，1)，B在y＝kx上，∴k＝1，设B ⎝ ⎛⎭⎪⎫b ，1b (b ＜0)，由BF ＝BE ，得－1b ＝1－b ，解得b ＝12－52(正值舍去)，∴CF ＝AE ＝1－1b ＝52＋32，∴OC ＝5＋1， 即点C 的坐标为(－5－1，0)．]三、解答题(本题有7小题，共66分．解答应写出文字说明，证明过程或演算步骤) 17．(本题6分)(1)计算：32＋|－4|＋3－8； (2)解方程：2x 2－3x ＝0.[命题考向：本题考查实数的运算，解一元二次方程．] 解：(1)原式＝3＋4－2＝5； (2)x (2x －3)＝0，x 1＝0，x 2＝32.18．(本题8分)为积极响应教育部关于足球进校园的号召，某校在足球课上让同学们训练点球，有两名同学各进行了5组练习，每组练习各射门10次，结果统计如下：组别 第1组 第2组 第3组 第4组 第5组 甲进球次数 6 7 5 7 5 乙进球次数58548(1)计算这两名同学每组射门的平均进球数； (2)通过计算说明哪位同学射门技术的稳定性更好？ [命题考向：本题考查读取表格数据，计算平均数、方差．] 解：(1)15(6＋7×2＋5×2)＝6，15(5×2＋8×2＋4)＝6. 答：这两名同学每组射门的平均进球数都是6个． (2)S 2甲＝15[(6－6)2＋2×(5－6)2＋2×(7－6)2]＝0.8， S 2乙＝15[2×(5－6)2＋2×(8－6)2＋(4－6)2]＝2.8， ∵S 2甲＜S 2乙，∴甲同学射门技术的稳定性更好．19．(本题8分)如图，抛物线y 1＝－x 2－x ＋c 与直线y 2＝12x ＋b 交于A ，B (1，0)两点． (1)分别求出c ，b 的值；(2)求y 1－y 2的最大值；(3)求点A 的坐标，并根据图象判断，当x 取何值时y 1＞y 2?(第19题图)[命题考向：本题考查二次函数、一次函数的图象与性质．联立函数表达式、解方程组即可得两函数的交点坐标．]解：(1)－12－1＋c ＝0，c ＝2，12×1＋b ＝0，b ＝－12. (2)y 1－y 2＝(－x 2－x ＋2)－⎝ ⎛⎭⎪⎫12x －12＝－x 2－32x ＋52＝－⎝ ⎛⎭⎪⎫x ＋342＋4916，y 1－y 2的最大值为4916.(3)∵点A 是y 1＝－x 2－x ＋2，y 2＝12x －12的交点， ∴y 1＝y 2，解得⎩⎪⎨⎪⎧x ＝－52，y ＝－74，⎩⎨⎧x ＝1，y ＝0，(舍去) ∴点A 的坐标为⎝ ⎛⎭⎪⎫－52，74，当－52＜x ＜1时y 1＞y 2.20．(本题10分)从A 地出发去B 地，以前只有两种走法，第一种：从A 地出发向西走6 km 后再向北走到B 地；第二种：从A 地出发向东走2.4 km 后再沿另一直路走到B 地，他们行驶的路程刚好相等，为缓解“出行难”的问题，A ，B 两地之间新建了一条笔直的地铁，求这条地铁的长度． [命题考向：本题考查利用勾股定理解决实际问题．根据题意画出示意图便于分析问题．] 解：设按以前的走法，从A 地到B 地的路程为x km. (x －6)2＋8.42＝(x －2.4)2，解得x ＝14. ∴AB ＝（14－6）2＋62＝10.答：这条地铁的长度为10 km.21．(本题10分)如图，已知A(0，1)，B(0，－1)，点C在x轴上，把线段CA绕点C沿顺时针方向旋转90°得线段CD，直线DB交x轴于点E.(1)求证：AE⊥BD；(2)求点E的坐标；(3)若点C的坐标为(－2，0)，求四边形ACDE的面积．(第21题图) (第21题答图)[命题考向：本题考查旋转的性质，四边形的内角和，全等三角形的判定与性质．]解：(1)证明：如答图，连结CB，∵A，B两点关于x轴对称，∴∠CAE＝∠CBE，CA＝CB，∵CA＝CD，∴CB＝CD，∴∠CDB＝∠CBD，∵∠CBD＋∠CBE＝180°，∴∠CDB＋∠CAE＝180°，在四边形ACDE中，∠ACD＝90°，∴∠AED＝90°，∴AE⊥BD.(2)在Rt△ABE中，OA＝OB，∴OE＝12AB＝1，∴点E的坐标为(1，0)．(3)如答图，延长BD至点F，使DF＝AE，∵CA＝CD，∠CAE＝∠CDF，AE＝DF，∴△CAE≌△CDF，∴∠ACE＝∠DCF，在等腰直角三角形CEF中，CE＝3，∴S四边形ACDE ＝S△CEF＝92.22．(本题12分)定义：如果一个四边形的两条对角线都能把它分割成两个等腰三角形，那么这样的四边形叫优美四边形．(1)在矩形，菱形，正方形中哪些是优美四边形，哪些不是优美四边形？(2)如图，四边形ABCD 是优美四边形，其中AB ＝AC ＝AD ，BC ＝CD ，E 是AC 与BD 的交点． ①求证：AC ⊥BD ；②若AC ＝BD ＝a ，CE ＝1，求a 的值；(3)请找出一个对角线相等且不互相垂直的优美四边形，并求出它的四个内角的度数．(第22题图)(第22题答图)[命题考向：本题考查等腰三角形的性质，勾股定理及四边形内角和．] 解：(1)正方形和菱形都是优美四边形，矩形不是优美四边形． (2)①证明：∵AB ＝AD ，BC ＝CD ， ∴A ，C 两点都是线段BD 的中垂线上的点， ∴AC ⊥BD .②∵AC ⊥BD ，AB ＝AD ，∴AC 平分BD ， 在Rt △AEB 中，AB 2＝AE 2＋BE 2， ∴a 2＝(a －1)2＋⎝ ⎛⎭⎪⎫12a 2，解得a ＝4±23，∵a －1＞0，而4－23－1＝3－23＜0， ∴a ＝4＋2 3.(3)如答图，∠ABC ＝∠BCD ＝72°，∠BAD ＝∠CDA ＝108°.23．(本题12分)如图1，AB 是⊙O 的直径，点C 在⊙O 上，AC ︵＝2BC ︵，点D 是线段AB 上的动点，线段CD 的延长线交⊙O 于点E . (1)求∠BEC 的度数；(2)若AD ＝2DB ，BE ＝63，求直径AB 的长； (3)当△BDE 是等腰三角形时，求CD的值；(4)如图2，以OE 为一边，在CE 的左侧作正方形OFGE ，连结GD ，把线段GD 绕点G 按逆时针方向旋转90°，得线段GH ，连结FH ，当AB ＝1，CD ⊥AB 时，求△GFH 的面积．(第23题图)[命题考向：本题考查圆的基本性质，旋转的性质，正方形的性质以及全等三角形的判定与性质．利用三角形全等可将线段、面积作相等代换．] 解：(1)∵AB 是⊙O 的直径，∴AB ︵＝180°，(第23题答图①)∵AC ︵＝2BC ︵，∴BC ︵＝60°， ∴∠BEC ＝30°.(2)如答图①，作OQ ⊥BE 于点Q ，DP ⊥BE 于点P ，这时EQ ＝QB ， ∵AD ＝2DB ，∴OD DB ＝12， ∵OQ ∥DP ，∴QP PB ＝OD DB ＝12，∵BE ＝63，∴EQ ＝33，QP ＝3，PB ＝23， ∴DP ＝EP tan 30°＝43×33＝4，∴BD ＝DP 2＋PB 2＝16＋（23）2＝27， ∴AB ＝67.(3)当DE ＝DB 时，D 与O 重合，CD＝1，∵C ，B ，E 三点不共线，∴∠ABE 不会等于120°，∴BE ≠BD ；当ED ＝EB 时，如答图②，连结OC ，OE ，作CF ⊥AB 于点F ，EG ⊥AB 于点G ，这时∠BOE ＝30°， ∵∠COE ＝60°＋30°＝90°，由AAS 可得△OCF ≌△EOG ，∴CF ＝OG ，∵△CDF ∽△EDG ，∴CD DE ＝CF EG ＝OG EG ＝tan 60°＝ 3.综上所述，CD DE ＝1或3.(第23题答图②) (第23题答图③)(4)如答图③，作GP ⊥CE ，垂足为P ，延长DG 至Q ，使GQ ＝DG ，连结EQ ，∵△EGP ≌△OED ，∴GP ＝DE ，∴S △DGE ＝12DE 2，∵△GFH ≌△GEQ ，∴S △GFH ＝S △DGE ＝12DE 2＝12×⎝ ⎛⎭⎪⎫342＝332.。
2024-2025学年浙教版中考数学模拟试卷及答案
2024-2025学年浙教版中考数学模拟试卷一、单选题（每题3分）1. 题目： 解方程组：1.(2x +3y =12)2.(x −y =1)答案：(x =3,y =2)2. 题目： 解二次方程：(x 2−5x +6=0)答案：(x =2)或(x =3)3. 题目： 解方程组：1.(3x −4y =16)2.(2x +y =10)答案：(x =5611),(y =−211)4. 题目： 解二次方程：(4x 2−9=0)答案：(x =−32)或(x =32)5. 题目： 解三次方程：(x 3−2x 2−x +2=0)答案：(x =−1),(x =1), 或(x =2)二、多选题（每题4分）题目1 (4分):下列哪些选项是代数式的正确表述？(A)3x + 4y - z (B) 5 * 6 + 2 / x (C) 2x^2 - 3x + 4 (D) a / b + c答案: (A), (C)题目2 (4分):下面哪一组线性方程有唯一解？(A)x + y = 3; x - y = 1 (B) 2x + 3y = 5; 4x + 6y = 10 (C) x + y = 2; 2x + 2y = 4 (D) 3x - 2y = 1;6x - 4y = 2答案: (A)题目3 (4分):在等腰三角形ABC中，AB=AC，角B和角C的度数可能是什么？(A)50°和 50° (B) 45°和 45° (C) 60°和 60° (D) 70°和 70°答案: (A), (B), (C), (D)题目4 (4分):抛掷一枚公平的骰子两次，得到两个点数之和为7的概率是多少？(A)1/6 (B) 1/9 (C) 1/12 (D) 1/18答案: (A)题目5 (4分):下列哪些变换可以保持图形的形状和大小不变？(A) 平移 (B) 旋转 (C) 缩放 (D) 反射答案: (A), (B), (D)请仔细审题并作答，祝你考试顺利！三、填空题（每题3分）1. 计算：((23)2−4×6)，答案：402. 解方程：(2x +3=7)，求 x 的值，答案：23. 若 a:b = 3:4，且 b = 12，求 a 的值，答案：94. 一个正方形的周长是 20 厘米，求它的面积，答案：25 平方厘米5. 在直角三角形中，一条直角边长为 3 厘米，另一条直角边长为 4 厘米，求斜边长，答案：5 厘米四、解答题（每题8分）题目1已知函数(f (x )=2x 2−3x +4)，求函数的最小值及对应的(x )值。
初中数学浙江省杭州市中考模拟数学模拟考试卷及答案5.docx
xx学校xx 学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）试题1:下面是一位同学做的四道题：①；②；③；④.其中做对了几道题（）A.0B.1C.2D.3试题2:如图,BC∥DE,∠1=117°, ∠AED=77°, 则∠A的大小是（）A．25° B．35° C．40° D．60°试题3:相邻两边长分别为2和3的平行四边形，若边长保持不变，则它可以变为（）A. 矩形B. 菱形C. 正方形D. 梯形试题4:如图①，有6张写有实数的卡片，它们的背面都相同，现将它们背面朝上洗匀后如图②摆放，从中任意翻开两张都是无理数的概率是（）评卷人得分（A）（B）（C）（D）试题5:两圆的半径分别为，圆心距为4．若，则两圆（）A．内含B．相交C．外切D．外离试题6:如图，一块直角三角板ABC的斜边AB与量角器的直径重合，点D对应54°，则∠BCD的度数为（）A. 27°B. 54°C. 63°D. 36°试题7:已知a＞b，则下列不等式中，错误的是（）A、3a＞3bB、-<-C、4a-3＞4b-3D、(c-1)2a＞(c-1)2b关于分式，有下列说法，错误的有（）个：（1）当x取1时，这个分式有意义，则a≠3；（2）当x=5时，分式的值一定为零；（3）若这个分式的值为零，则a≠-5；（4）当x取任何值时，这个分式一定有意义，则二次函数y=x2-4x+a与x轴没有交点。
A. 0B. 1C. 2D. 3试题9:如图，设三角形ABC为一等腰直角三角形，角ABC为直角，D为AC中点。
以B为圆心，AB为半径作一圆弧AFC，以D为中心，AD为半径，作一半圆AGC，作正方形BDCE。
初中数学浙江省杭州市中考模拟数学模拟考试卷5.docx
xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）试题1:的平方根是（）A. 4B. 2C. ±4D.±2试题2:估算的值（）A．在2和3之间 B．在3和4之间 C．在4和5之间 D．在5和6之间试题3:若反比例函数的图象经过点，其中，则此反比例函数的图象在（）A．第一、二象限 B．第一、三象限 C．第二、四象限 D．第三、四象限试题4:由两块大小不同的正方体搭成如图所示的几何体，它的主视图是（）试题5:评卷人得分把二次根式中根号外的因式移到根号内，结果是（）A． B． C． D．试题6:如图，是⊙O的直径，点在的延长线上，切⊙O于若则等于（）A． B． C． D．试题7:函数中自变量x的取值范围是（）A．x≤3 B．x＝4 C．x＜3且x≠4 D．x≤3且x≠4试题8:函数在同一直角坐标系内的图象大致是（）试题9:如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个锐角为60°的菱形，剪口与折痕所成的角a的度数应为（）A．15°或30° B．30°或45° C．45°或60° D．30°或60°试题10:正方形、正方形和正方形的位置如图所示，点在线段上，正方形的边长为4，则的面积为（）Ａ、10 Ｂ、12 Ｃ、14 Ｄ、16试题11:一条弦把圆分成2:3两部分，那么这条弦所对的圆周角的度数为__________.试题12:一串有趣的图案按一定的规律排列(如图)：按此规律在右边的圆中画出的第2011个图案：。
试题13:与的比例中项是 .试题14:已知，则代数式的值为_________.试题15:如图所示，正方形的面积为12，是等边三角形，点在正方形内，在对角线上有一点，使的和最小，则这个最小值为 .试题16:如图，n+1个上底、两腰长皆为1，下底长为2的等腰梯形的下底均在同一直线上，设四边形P1M1N1N2面积为S1，四边形P2M2N2N3的面积为S2，……，四边形P n M n N n N n+1的面积记为S n，则S n= ▲试题17:；试题18:试题19:已知关于的函数的图像与坐标轴只有2个交点，求的值.试题20:“知识改变命运，科技繁荣祖国”．我区中小学每年都要举办一届科技比赛．下图为我区某校2010年参加科技比赛（包括电子百拼、航模、机器人、建模四个类别）的参赛人数统计图：（1）该校参加机器人、建模比赛的人数分别是人和人；（2）该校参加科技比赛的总人数是人，电子百拼所在扇形的圆心角的度数是°，并把条形统计图补充完整；（3）从全区中小学参加科技比赛选手中随机抽取80人，其中有32人获奖. 今年我区中小学参加科技比赛人数共有2485人，请你估算今年参加科技比赛的获奖人数约是多少人?试题21:如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.(1)尺规作图：过A，D，C三点作⊙O（只要求作出图形，保留痕迹，不要求写作法）；(2)求证：BC是过A，D，C三点的圆的切线；试题22:如图，一艘渔船位于海洋观测站P的北偏东60°方向，渔船在A处与海洋观测站P的距离为60海里，它沿正南方向航行一段时间后，到达位于海洋观测站P的南偏东45°方向上的B处。
初中数学浙江省杭州中考模拟数学模拟命题比赛考试题5考试卷及答案.docx
xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）试题1:下列运算正确的是（）A.6a－5a＝1B.a＋2a2＝3a3C.－(a－b)＝-a＋bD.2(a＋b)＝2a＋b试题2:在下列四个图案中，既是轴对称图形，又是中心对称图形的是( )A B C D试题3:一个盒子中放着三种颜色的球，每个球除颜色外都相同，红球x个，白球7个，黑球y个，如果从中任取一个球，取得的白球的概率与取得非白球的概率相同，那么x与y的关系是（）A. x+y=7B. x+y=14C. x=y=7D. x-y=7试题4:如图，矩形OABC的边OA长为2 ，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是( )评卷人得分A.2.5B.2C.D.试题5:九年级（10）班数学进行了六次测试，其中李明六次成绩分别为：110、98、97、103、105、105，则他的中位数和众数分别是( )Ａ．100、105 Ｂ．104、105 Ｃ．105、105 Ｄ．103、105试题6:正方形具有而矩形不一定具有的性质是( )A. 对角线互相垂直B. 四个角都是直角C. 对角线相等D. 两对角线将其分割的四个三角形面积相等试题7:如图，在菱形ABCD中，DE⊥AB，，BE=2，则tan∠DBE的值是（）A． B．2 C．D．试题8:如图三棱柱ABC-A1B1C1的侧棱长和底面边长均为2，且侧棱AA1⊥底面ABC，其主视图是边长为2的正方形，则此三棱柱左视图的面积为（）A. B. C. 2 D. 4试题9:学校大门出口处有一自动感应栏杆，点是栏杆转动的支点，当车辆经过时，栏杆AE会自动升起，某天早上，栏杆发生故障，在某个位置突然卡住，这时测得栏杆升起的角度，已知⊥，支架AB高1.2米，大门BC打开的宽度为2米，以下哪辆车可以通过（栏杆宽度，汽车反光镜忽略不计） ( )A.宝马Z4（）B.奇瑞QQ（)B.大众朗逸（)D.奥迪A4（）（参考数据：sin 37°≈ 0.60，cos 37°≈ 0.80，tan 37°≈ 0.75．车辆尺寸：）试题10:在直角梯形中，，为边上一点，，且．连接交对角线于，连接．下列结论：①；②为等边三角形；③；④．其中结论正确的是（）A．只有①② B．只有①②④C．只有③④ D．①②③④试题11:因式分解：=试题12:用一个半径为㎝的半圆围成一个圆锥的侧面，则这个圆锥的高为㎝试题13:一次函数y=ax+b与反比例函数,x与y的对应值如下表：x -3 -2 -1 1 2 3y=ax+b 4 3 2 0 -1 -21 2 -2 -1方程ax+b=－的解为___ __；不等式ax+b>－的解集为___ __.试题14:某居民区一处圆形下水管道破裂，修理人员准备更换一段与原管道同样粗细的新管道。
2022年浙江省杭州市中考数学全真模拟试卷附解析
2022年浙江省杭州市中考数学全真模拟试卷 学校：__________ 姓名：__________ 班级：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1．如图，在高楼前D 点测得楼顶的仰角为30︒，向高楼前进60米到C 点，又测得仰角为45︒，则该高楼的高度大约为（ ）A ．82米B ．163米C ．52米D ．70米2．抛物线2y ax bx c =++的图象如图所示，则不等式0bx a +>的解是（ ）A ．a x b >-B ．a x b >C ．a x b <-D ．a x b< 3．一个样本的频数分布直方图如图所示，则样本的中位数约为（ ）A ．10．5B ．14．5C ．12．5D ．8．5 4．232x x -+ =2(___)x -（ ）5．如图，在△ABC 中，AD ⊥BC ，CE ⊥AB ，垂足分别为 D ，E ，AD ，CE 交于点H ，已知 EH=EB= 6，AE=8，则CH 的长是（ ）A ．5B ．4C ．3D ．26．如图，a ∥b ，若∠1=120°，则∠2 的度数是（ ）A ．l20°B ．70°C ．60°D ． 507．24a x +可表示为（ ）A ．24a x x +B ．24a x x x ⋅⋅C ．22a x x +⋅D ．24()a x x ⋅8．下面的图表是护士统计的一位病人一天的体温变化情况：时间6:0010:0014:0018:0022:00体温/℃37.638.338.039.137.9通过图表，估计这个病人下午16:00时的体温是（）A．38.0℃B．39.1℃C．37.6℃D．38.6℃9．火车票上的车次号有两个意义：（1）数字越小表示车速越快，如 1~98次为特快列车，101~198次直快列车，301~398次为普快列车，401~498次为普客列车；（2）奇数与偶数表示不同的行驶方向，例如：奇数表示从北京开出，偶数表示开往北京. 根据以上规定，杭州开往北京的某一直快列车的车次号可能是（）A． 20 B．119 C．120 D．319二、填空题10．如图，已知正方形ABCD的边长为2.如果将线段BD 绕着点B旋转后，点D落在CB的延长线上的D′点处，那么tan BAD∠′等于__________．11．如图，D、E两点分别在△ABC 的边AB、AC上，DE与BC不平行，当满足条件（写出一个即可）时，△ADE∽△ACB．12．把一张矩形的纸片对折，若对折后的矩形与原矩形相似，则原矩形纸片的宽与长之比为．13．已知等腰梯形的上、下底边长分别是2，10，腰长是5，则这个梯形的面积是 . 14．已知直角梯形的一腰长为10㎝，这条腰与底所成的角为30°，那么另一腰的长是_________cm..a a+=．15．若a是11的小数部分，则(6)16．如图，梯形AOCD中，AD∥0C，AD=3，点；A到x轴的距离为4，到y 轴的距离为3，则点D的坐标为．17．一次函数(26)5=-+中，y随x增大而减小，则m的取值范围是．y m x18．观察图形：其中是轴对称图形的是 (填序号) .19．某商品原价为a元，若按此价的8折出售，仍获利 b%，则此商品进价是元.20．袋中装有 4 个白球和 8 个红球，每个球除颜色外完全相同，从袋中任意摸一球，则P(摸到红球)= ，P(摸到黑球)= ．21．早上8：15分．钟面上的时针与分针所夹的角的度数是．A B C D F E 22．(1)7点整，分针和时针之间的夹角的度数是 ．(2)从午夜0时到早上8时，时针所转过的角度是 ．23．计算： (-0.1)× (-0.001) ×(-100)×1000= ．三、解答题24．如图是某几何体的展开图．(1）这个几何体的名称是 ； (2）画出这个几何体的三视图；(3）求这个几何体的体积．（ 取3.14）25．如图所示的相似四边形中，求未知边 x 、y 的长度和角度α的大小.26．已知：如图，E ，F 分别是□ABCD 的边AD ，BC 的中点，求证：DE ＝DF.20127．甲、乙两人参加某体育训练项目，近期的五次测试成绩得分情况如图．(1)分别求出两人得分的平均数与方差；(2)根据图和上面算得的结果，对两人的训练成绩作出评价．28．计算：(1）)1)(1()2(2-+-+x x x (2）)()23(3223ab ab b a b a ÷+- (3）262--x x ÷ 4432+--x x x29．如图所示，已知△ABC 中，D 是AB 的中点，过D 点作DE ∥BC 交AC 于E ．(1)从△ABC 到△ADE 是什么变换?(2)经过这一变换，△ABC 的角分别变为哪些角?它们的大小改变吗?(3)经过这一变换，△ABC 的边分别变为哪些边?它们的大小改变吗?30．一个圆柱体的体积是60立方米，底面圆的直径与圆柱的高相等，求这个圆柱的底面圆半径(π取 3.14，结果精确到 0.01 米).【参考答案】学校：__________ 姓名：__________ 班级：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1．A2．C3．C4．9 16，345．D6．C7．D8．D9．C二、填空题10．2 11．∠ADE=∠ACB （或∠AED=∠ABC 或AD AE AC AB =）12． 1:213．1814．2015．216．(6，4)17．m ＜318．①②③④⑥19．80100ab +20．23，021．157．5°22．(1)150°(2)240°23．-10三、解答题24．（1）圆柱；(2）三视图为：(3）体积为:2πr h =23.14520⨯⨯=1570． 25．由于两个四边形相似，它们的对应边成比例，对应角相等， 所以18467y x ==,解得 x=31.5，y=27. α= 360°- (77°+83°+ 117°) =83°.26．提示：四边形BEDF 是平行四边形．27． (1)13.5x =甲，21S =甲；13.5x =乙，20S =乙.2；(2)乙较为稳定28．（1）54+x ；（2）2223b ab a +-；（3）42-x ．29．(1)相似变换；(2)∠A ，∠B ，∠C 分别变为∠A ，∠ADE ，∠AED ，它们的大小没有改变；(3)AB ，BC ，CA 分别变为AD ，DE ，AE 它们的大小改变，AB=2AD ，BC=2DE ，AC=2AE 30．2.12≈(米)。
浙教版中考数学模拟试卷
浙教版中考数学模拟试卷浙教版中考数学模拟试卷一、选择题1、在的展开式中，的系数为____________.2、一个三角形的边长分别为3，4，5，它的面积是____________.3、一个扇形的半径是10，圆心角是120°，则此扇形的面积是____________.4、若是关于的方程，则它的解为____________.5、若分式，则 ______.二、填空题6、已知，则 ______.61、已知是方程的解，则 ______.611、已知，则 ______.6111、已知，则 ______.61111、已知，则 ______.三、解答题11、已知，求的值.111、已知是方程的两个根，求的值.1111、已知，求的值.11111、已知，求的值.111111、已知，求的值.四、综合题16、已知，求的值.161、已知是方程的两个根，求的值.1611、已知，求的值.16111、已知，求的值.161111、已知，求的值.五、应用题21、某市为了鼓励市民节约用水，采用分段计费的方法计算水费，每月用水量不超过6m³时，每立方米收费1元；超过6m³时，超过部分按每立方米2元收费.某月甲用户比乙用户多交4元，则甲、乙该月的水费分别为多少元？211、已知某市居民生活用电的电价为每度0.56元（即每千瓦时0.56元），每月用电量实行阶梯式电价：每月用电量不超过100度的部分，按每度0.56元计费；超过100度但不超过200度的部分，按每度0.60元计费；超过200度的部分，按每度0.80元计费.若该市某户居民这个月交电费用了78元，则该户这个月用电多少度？2111、在平面直角坐标系中，、、分别表示三角形ABC三边的中点坐标，若三角形ABC的顶点坐标为（2,4）、（5,2）、（1,0），则三角形ABC的三边中点的坐标分别为多少？并请说明原因。
21111、一个三位数是一个整数和一个两位数的和，且三位数恰好有三个不同的质因数，两位数是质数，且质因数是这三个质因数的唯一一个。
2012年浙教版中考数学模拟试卷(5)及答案
2012年中考数学模拟试卷5一．选择题（本题有10个小题，每小题3分，共30分．）1．下面四个数中比－2小的数是………………………………………………………（ ）A .1B .0C .－1D .－32. 如图中几何体的主视图是............................................. （ ）Ａ． Ｂ． Ｃ．Ｄ．3．下列运算正确．．的是........................................................................................................（ ） A ． B ．C ．D ．4. 不等式组的解集为 ......................（ ） Ａ．Ｂ．Ｃ．Ｄ．5．如图，⊙O 是等边ABC △的外接圆，P 是⊙O 上一点，则CPB ∠等于............（ ） Ａ．30Ｂ．45Ｃ．60 Ｄ．906.那么该公司员工月工资的平均数和众数分别是..........（ ）Ａ．1600，1500 Ｂ．2000，1000Ｃ．1600，1000 Ｄ．2000，1500 7. 方程的解是..............................................（ ）Ａ．4Ｂ．5 Ｃ．6Ｄ．88. 如图，四边形ABCD 的对角线互相平分，要使它变为菱形，需要添加的条件是.（ ） A ．AB ﹦CD B. AD ﹦BCC. AB ﹦BCD. AC ﹦BD9．如图、在Rt △ABC 中，∠C=90°，AC=8，BC=6，两等圆⊙A ，⊙B 外切，那么 图中两个 扇形（即阴影部分）的面积之和为........（ ）B CDA ．B ．C ．D ．10. 如图1，在直角梯形ABCD 中，∠B =90°，DC ∥AB ，动点P 从B 点出发，沿折线 B →C →D →A 运动，点P 运动的速度为2个单位长度/秒，若设点P 运动的时间为x 秒， △ABP 的面积为y ，如果y 关于x 的函数图像如图2所示，则M 点的纵坐标为.（ ）A ．16B ．48C ．24D ．64卷Ⅱ二、填空题 (本题有6小题,每小题4分,共24分) 11. 分解因式：．12．已知整式-x 2+4x 的值为6，则2X 2-8X+4的值为13．一个不透明的袋中装有除颜色外其他均相同的2个红球和3个黄球，从中随机摸出两个 都是黄球的概率是 ．14. 圆锥底面半径为4cm ，高为3cm ，则它的侧面积是 15. 定义：是不为1的有理数，我们把a -11称为a 的衍生数．．．．如：2的衍生数是1211-=-， 的衍生数是21)1(11=--．已知311-=a ，2a 是1a 的衍生数，3a 是2a 的衍生数，4a 是3a 的衍生数，……，依此类推，则=2012a ．16. 如图，在平面直角坐标系中，O 为坐标原点，点A 的坐标为（－8，0），直线BC 经过点B （－8，6），C （0，6），将四边形OABC 绕点O 按顺时针方向旋转α度（0＜α ≤180°）得到四边形OA ′B ′C ′，此时直线OA ′、直线B ′C ′分别与直线BC 相交于P 、Q ．在四边形OABC 旋转过程中，若BP ＝BQ ，则点P 的坐标为___ ▲ __．三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程) 17（本题满分6分）计算．18. (本题6分)如图，菱形ABCD 的边长为2，对角线BD ＝2，E 、F 分别是AD 、CD 上的两个动点且满足AE ＋CF ＝2．(1) 由已知可得，∠BDA 的度数为 ▲ ；(2) 求证：△BDE ≌△BCF ．19﹒（本题6分）如图所示，某市的A 、B 两地相距20km ，B 在A 的北偏东45°方向上，一高新技 术园区P 在A 的北偏东30°和B 的正西方向上.现计划修建的一条高速铁路将经过AB （线段），已知高新技术园区的范围在以点P 为圆心，半径为4km 的圆形区域内.速铁路会不会穿越高新技术园区？（参考数据：sin150≈0.2588，cos150≈0.9659，20．(本题8分)某公司专销产品A ，第一批产品A 上市40天内全部售完．该公司对第一批产品A 上 市后市场销售情况进行了跟踪调查，调查结果如图所示：其中，图①中的折线表示的是市场日销售量与上市时间的关系，图②中的折线表示的是每件产品A 的销售利润与上市时间的关系．(1)试写出第一批产品A 的市场日销售 量y 与上市时间t 的关系式，(2)第一批产品A 上市后，哪一天这家公司市场日销售利润最大?最大日销售利润是多少万元?21.(本题8分)“校园手机”现象越来越受到社会的关注﹒春节期间，小明随机调查了城区若干名同学和家长对中学生带手机现象的看法．统计整理并制作了如下的统计图：（第2２（1）这次的调查对象中，家长有 ▲ 人；（2）图②中表示家长“赞成”的圆心角的度数为 ▲ 度；（3）开学后，甲、乙两所学校对各自学校所有学生带手机情况进行了统计，发现两校共 有2384名学生带手机，且乙学校带手机的学生数是甲学校带手机学生数的 53，求甲、乙两校中带手机的学生数各有多少？22、(本题10分)如图,AB 是⊙O 的直径,点P 是AB 延长线上一点,PC 切⊙O 于点C ,连结AC ,过点O 作AC 的垂线交AC 于点D ,交⊙O 于点E .已知AB ﹦8,∠P=30°. (1) 求线段PC 的长；（2）求阴影部分的面积.23.（本题10分） 已知：△ABC 中，AB ＝10；⑴如图①，若点D 、E 分别是AC 、BC 边的中点，求DE 的长；⑵如图②，若点A 1、A 2把AC 边三等分，过A 1、A 2作AB 边的平行线，分别交BC 边于点 B 1、B 2，求A 1B 1＋A 2B 2的值；⑶如图③，若点A 1、A 2、…、A 10把AC 边十一等分，过各点作AB 边的平行线，分别交BC 边于点B 1、B 2、…、B 10。
浙江省杭州余杭区2024届中考数学全真模拟试卷含解析
浙江省杭州余杭区2024届中考数学全真模拟试卷考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。
考试结束后，请将本试卷和答题卡一并交回。
一、选择题（共10小题，每小题3分，共30分）1．下列图形中，是中心对称图形但不是轴对称图形的是（）A．B．C．D．2．某工厂现在平均每天比原计划多生产50台机器，现在生产600台所需时间与原计划生产450台机器所需时间相同．设原计划平均每天生产x台机器，根据题意，下面所列方程正确的是（）A．60050x-＝450xB．60050x+＝450xC．600x＝45050x+D．600x＝45050x-3．计算（﹣12）﹣1的结果是（）A．﹣12B．12C．2 D．﹣24．数据”1,2,1,3,1”的众数是( )A．1 B．1.5 C．1.6 D．35．下列运算中，正确的是（）A．（ab2）2=a2b4B．a2+a2=2a4C．a2•a3=a6D．a6÷a3=a26．如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF 的长为（）A．95B．185C．165D．1257．若10，则实数a在数轴上对应的点的大致位置是（）A ．点EB ．点FC ．点GD ．点H8．一个不透明的布袋里装有5个红球，2个白球，3个黄球，它们除颜色外其余都相同，从袋中任意摸出1个球，是黄球的概率为（ ）A ．310B ．15C ．12D ．710 9．如图钓鱼竿AC 长6m ，露在水面上的鱼线BC 长32m ，钓者想看看鱼钓上的情况，把鱼竿AC 逆时针转动15°到AC ′的位置，此时露在水面上的鱼线B 'C '长度是（ ）A ．3mB ．33 mC ．23 mD ．4m10．关于的一元二次方程有两个不相等的实数根，则的取值范围为（ ） A ． B ． C ． D ．二、填空题（本大题共6个小题，每小题3分，共18分）11．一只不透明的袋子中装有红球和白球共30个，这些球除了颜色外都相同，校课外学习小组做摸球实验，将球搅匀后任意摸出一个球，记下颜色后放回，搅匀，通过多次重复试验，算得摸到红球的频率是0.2，则袋中有________个红球．12．如果一个三角形有一条边上的高等于这条边的一半，那么我们把这个三角形叫做半高三角形．已知直角三角形ABC 是半高三角形，且斜边AB=5，则它的周长等于_____．132(2)-14．若代数式5x x +有意义，则实数x 的取值范围是____. 15．一个几何体的三视图如左图所示，则这个几何体是( )A．B．C．D．16．电子跳蚤游戏盘是如图所示的△ABC，AB=AC=BC=1．如果跳蚤开始时在BC边的P0处，BP0=2．跳蚤第一步从P0跳到AC边的P1（第1次落点）处，且CP1= CP0；第二步从P1跳到AB边的P2（第2次落点）处，且AP2= AP1；第三步从P2跳到BC边的P3（第3次落点）处，且BP3= BP2；…；跳蚤按照上述规则一直跳下去，第n次落点为P n （n为正整数），则点P2016与点P2017之间的距离为_________．三、解答题（共8题，共72分）17．（8分）为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件元,出厂价为每件元,每月销售量（件）与销售单价（元）之间的关系近似满足一次函数:．李明在开始创业的第一个月将销售单价定为元,那么政府这个月为他承担的总差价为多少元?设李明获得的利润为（元）,当销售单价定为多少元时,每月可获得最大利润?物价部门规定,这种节能灯的销售单价不得高于元．如果李明想要每月获得的利润不低于元,那么政府为他承担的总差价最少为多少元?18．（8分）某中学为了考察九年级学生的中考体育测试成绩（满分30分），随机抽查了40名学生的成绩（单位：分），得到如下的统计图①和图②．请根据相关信息，解答下列问题：（1）图中m 的值为_______________.（2）求这40个样本数据的平均数、众数和中位数：（3）根据样本数据，估计该中学九年级2000名学生中，体育测试成绩得满分的大约有多少名学生。
浙教中考模拟数学试卷
一、选择题（每小题3分，共30分）1. 下列各数中，无理数是（）A. √4B. √9C. √16D. √252. 已知一元二次方程x²-5x+6=0，则方程的解是（）A. x₁=2，x₂=3B. x₁=3，x₂=2C. x₁=-2，x₂=-3D. x₁=-3，x₂=-23. 在平面直角坐标系中，点A（-1，2）关于原点的对称点是（）A. （1，-2）B. （-1，-2）C. （-1，2）D. （2，-1）4. 若a，b是方程2x²-5x+2=0的两根，则a²+b²的值是（）A. 9B. 7C. 5D. 45. 在△ABC中，∠A=45°，∠B=90°，∠C=45°，那么△ABC是（）A. 等腰直角三角形B. 等边三角形C. 钝角三角形D. 锐角三角形6. 下列函数中，y是x的一次函数是（）A. y=√xB. y=x²C. y=2x+1D. y=x³7. 下列命题中，正确的是（）A. 所有的平行四边形都是矩形B. 所有的等腰三角形都是等边三角形C. 所有的直角三角形都是等腰三角形D. 所有的等边三角形都是直角三角形8. 下列图形中，对称轴是直线y=x的是（）A. 等腰三角形B. 正方形C. 圆D. 梯形9. 下列数列中，下一项是16的是（）1，3，6，10，（）A. 15B. 16C. 17D. 1810. 下列关于三角形的外接圆的叙述中，正确的是（）A. 三角形的外接圆半径一定小于三角形的高B. 三角形的外接圆半径一定等于三角形的中线长度C. 三角形的外接圆半径一定等于三角形的斜边长度D. 三角形的外接圆半径一定等于三角形的三边之和的一半二、填空题（每小题5分，共50分）11. 已知等差数列的前三项分别为2，5，8，则该数列的公差是______。
12. 在△ABC中，∠A=30°，∠B=45°，则∠C的度数是______。
浙江省杭州地区达标名校2024届中考数学全真模拟试卷含解析
浙江省杭州地区达标名校2024学年中考数学全真模拟试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题（共10小题，每小题3分，共30分）1．如图，菱形ABCD的对角线交于点O，AC=8cm，BD=6cm，则菱形的高为（）A．485cm B．245cm C．125cm D．105cm2．如图，△ABC在平面直角坐标系中第二象限内，顶点A的坐标是（﹣2，3），先把△ABC向右平移6个单位得到△A1B1C1，再作△A1B1C1关于x轴对称图形△A2B2C2，则顶点A2的坐标是（）A．（4，﹣3）B．（﹣4，3）C．（5，﹣3）D．（﹣3，4）3．13-的相反数是（）A．13B．13-C．3 D．-34．如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y=6x在第一象限的图象经过点B，则△OAC与△BAD的面积之差S△OAC﹣S△BAD为（）A ．36B ．12C ．6D ．35．若一个函数的图象是经过原点的直线，并且这条直线过点（-3,2a ）和点（8a ，-3），则a 的值为（ ）A ．B ．C ．D ．±6．已知一次函数3y kx =-且y 随x 的增大而增大，那么它的图象不经过（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限7．下列运算正确的是（ ） A ．5ab ﹣ab=4 B ．a 6÷a 2=a 4 C ．112a b ab+= D ．（a 2b ）3=a 5b 38．如图，⊙O 是等边△ABC 的外接圆，其半径为 3，图中阴影部分的面积是（ ）A ．πB ．32π C ．2π D ．3π9．某反比例函数的图象经过点（-2,3），则此函数图象也经过（ ） A ．（2，-3）B ．（-3,3）C ．（2,3）D ．（-4,6）10．下列计算正确的是（ ）A ．2224()39b b c c =B ．0.00002=2×105C ．2933x x x -=--D ．3242·323x y y x x =二、填空题（本大题共6个小题，每小题3分，共18分）11．如图，在直角坐标系中，⊙A 的圆心A 的坐标为（1，0），半径为1，点P 为直线y =34x +3上的动点，过点P 作⊙A 的切线，切点为Q ，则切线长PQ 的最小值是______________．12．有四张质地、大小、反面完全相同的不透明卡片，正面分别写着数字1，2，3，4，现把它们的正面向下，随机摆放在桌面上，从中任意抽出一张，则抽出的数字是奇数的概率是 ． 13．4的平方根是 ．14．2017年5月5日我国自主研发的大型飞机C919成功首飞，如图给出了一种机翼的示意图，用含有m 、n 的式子表示AB 的长为______．15．分解因式：4a 2-4a+1=______．16．如图，已知点E 是菱形ABCD 的AD 边上的一点，连接BE 、CE ，M 、N 分别是BE 、CE 的中点，连接MN ，若∠A=60°，AB=4，则四边形BCNM 的面积为_____．三、解答题（共8题，共72分）17．（8分）在Rt ABC ∆中，90ACB ∠=，CD 是AB 边的中线，DE BC ⊥于E ，连结CD ，点P 在射线CB 上（与B ，C 不重合）（1）如果30A ∠=①如图1，DCB ∠=②如图2，点P 在线段CB 上，连结DP ，将线段DP 绕点D 逆时针旋转60，得到线段DF ，连结BF ，补全图2猜想CP 、BF 之间的数量关系，并证明你的结论；（2）如图3，若点P 在线段CB 的延长线上，且()090A αα∠=<<，连结DP ，将线段DP 绕点逆时针旋转2α得到线段DF ，连结BF ，请直接写出DE 、BF 、BP 三者的数量关系（不需证明）18．（8分）定义：若四边形中某个顶点与其它三个顶点的距离相等，则这个四边形叫做等距四边形，这个顶点叫做这个四边形的等距点．（1）判断：一个内角为120°的菱形 等距四边形．（填“是”或“不是”）（2）如图2，在5×5的网格图中有A 、B 两点，请在答题卷给出的两个网格图上各找出C 、D 两个格点，使得以A 、B 、C 、D 为顶点的四边形为互不全等的“等距四边形”，画出相应的“等距四边形”，并写出该等距四边形的端点均为非等距点的对角线长．端点均为非等距点的对角线长为 端点均为非等距点的对角线长为（3）如图1，已知△ABE 与△CDE 都是等腰直角三角形，∠AEB=∠DEC=90°，连结A D ，AC ，BC ，若四边形ABCD 是以A 为等距点的等距四边形，求∠BCD 的度数． 19．（8分）关于x 的一元二次方程ax 2+bx+1=1． （1）当b=a+2时，利用根的判别式判断方程根的情况；（2）若方程有两个相等的实数根，写出一组满足条件的a ，b 的值，并求此时方程的根． 20．（8分）如图，在△ABC 中，∠ABC=90°，BD 为AC 边上的中线．（1）按如下要求尺规作图，保留作图痕迹，标注相应的字母：过点C 作直线CE ，使CE ⊥BC 于点C ，交BD 的延长线于点E ，连接AE ；（2）求证：四边形ABCE 是矩形．21．（8分）如图，在平面直角坐标系中，矩形DOBC 的顶点O 与坐标原点重合，B 、D 分别在坐标轴上，点C 的坐标为（6，4），反比例函数y=1k x（x ＞0）的图象经过线段OC 的中点A ，交DC 于点E ，交BC 于点F ． （1）求反比例函数的解析式； （2）求△OEF 的面积；（3）设直线EF 的解析式为y=k 2x+b ，请结合图象直接写出不等式k 2x+b ＞1k x的解集．22．（10分）如图，已知△ABC 中，∠ACB ＝90°，D 是边AB 的中点，P 是边AC 上一动点，BP 与CD 相交于点E ．（1）如果BC ＝6，AC ＝8，且P 为AC 的中点，求线段BE 的长； （2）联结PD ，如果PD ⊥AB ，且CE ＝2，ED ＝3，求cos A 的值； （3）联结PD ，如果BP 2＝2CD 2，且CE ＝2，ED ＝3，求线段PD 的长．23．（12分）已知关于 x 的一元二次方程 x 2﹣2(k ﹣1)x+k(k+2)＝0 有两个不相等的实数根．求 k 的取值范围；写出一个满足条件的 k 的值，并求此时方程的根．24．鄂州某个体商户购进某种电子产品的进价是50元/个，根据市场调研发现售价是80元/个时，每周可卖出160个，若销售单价每个降低2元，则每周可多卖出20个．设销售价格每个降低x 元（x 为偶数），每周销售为y 个． （1）直接写出销售量y 个与降价x 元之间的函数关系式；（2）设商户每周获得的利润为W 元，当销售单价定为多少元时，每周销售利润最大，最大利润是多少元？ （3）若商户计划下周利润不低于5200元的情况下，他至少要准备多少元进货成本？参考答案一、选择题（共10小题，每小题3分，共30分） 1、B 【解题分析】试题解析：∵菱形ABCD 的对角线86AC cm BD cm ==，，114322AC BD OA AC cm OB BD cm ∴⊥====，，，根据勾股定理，5AB cm ===， 设菱形的高为h ， 则菱形的面积12AB h AC BD =⋅=⋅， 即15862h =⨯⨯， 解得24.5h = 即菱形的高为245cm ． 故选B ． 2、A 【解题分析】直接利用平移的性质结合轴对称变换得出对应点位置． 【题目详解】 如图所示：顶点A2的坐标是（4，-3）．故选A．【题目点拨】此题主要考查了轴对称变换和平移变换，正确得出对应点位置是解题关键．3、B【解题分析】先求13-的绝对值，再求其相反数：根据数轴上某个数与原点的距离叫做这个数的绝对值的定义，在数轴上，点13-到原点的距离是13，所以13-的绝对值是13；相反数的定义是：如果两个数只有符号不同，我们称其中一个数为另一个数的相反数，特别地，1的相反数还是1．因此13的相反数是13-．故选B．4、D【解题分析】设△OAC和△BAD的直角边长分别为a、b，结合等腰直角三角形的性质及图象可得出点B的坐标，根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论．解：设△OAC和△BAD的直角边长分别为a、b，则点B的坐标为（a+b，a﹣b）．∵点B在反比例函数6yx=的第一象限图象上，∴（a+b）×（a﹣b）=a2﹣b2=1．∴S△OAC﹣S△BAD=12a2﹣12b2=12（a2﹣b2）=12×1=2．故选D．点睛：本题主要考查了反比例函数系数k的几何意义、等腰三角形的性质以及面积公式，解题的关键是找出a2﹣b2的值．解决该题型题目时，要设出等腰直角三角形的直角边并表示出面积，再用其表示出反比例函数上点的坐标是关键．5、D【解题分析】根据一次函数的图象过原点得出一次函数式正比例函数，设一次函数的解析式为y＝kx，把点（−3，2a）与点（8a，−3）代入得出方程组，求出方程组的解即可．【题目详解】解：设一次函数的解析式为：y＝kx，把点（−3，2a）与点（8a，−3）代入得出方程组，由①得：，把③代入②得：，解得：.故选：D.【题目点拨】本题考查了用待定系数法求一次函数的解析式，主要考查学生运用性质进行计算的能力．6、B【解题分析】根据一次函数的性质：k＞0，y随x的增大而增大；k＜0，y随x的增大而减小，进行解答即可．【题目详解】解：∵一次函数y=kx-3且y随x的增大而增大，∴它的图象经过一、三、四象限，∴不经过第二象限，故选：B．【题目点拨】本题考查了一次函数的性质，掌握一次函数所经过的象限与k、b的值有关是解题的关键.7、B【解题分析】由整数指数幂和分式的运算的法则计算可得答案.【题目详解】A项, 根据单项式的减法法则可得:5ab-ab=4ab,故A项错误;B 项, 根据“同底数幂相除,底数不变,指数相减”可得: a 6÷a 2=a 4，故B 项正确;C 项,根据分式的加法法则可得:11a ba b ab++=,故C 项错误; D 项, 根据 “积的乘方等于乘方的积” 可得:2363()a b a b =,故D 项错误; 故本题正确答案为B. 【题目点拨】 幂的运算法则:(1) 同底数幂的乘法: ·m n m n a a a +=(m 、n 都是正整数) (2)幂的乘方:()m n mn a a =(m 、n 都是正整数) (3)积的乘方:()n n n ab a b = (n 是正整数)(4)同底数幂的除法:m n m n a a a -÷=(a≠0,m 、n 都是正整数,且m>n) (5)零次幂:01a =(a≠0) (6) 负整数次幂: 1ppa a -=(a≠0, p 是正整数). 8、D 【解题分析】根据等边三角形的性质得到∠A=60°，再利用圆周角定理得到∠BOC=120°，然后根据扇形的面积公式计算图中阴影部分的面积即可． 【题目详解】∵△ABC 为等边三角形， ∴∠A=60°，∴∠BOC=2∠A=120°，∴图中阴影部分的面积= 21203360π⨯=3π．故选D ． 【题目点拨】本题考查了三角形的外接圆与外心、圆周角定理及扇形的面积公式，求得∠BOC=120°是解决问题的关键． 9、A 【解题分析】 设反比例函数y=kx（k 为常数，k≠0），由于反比例函数的图象经过点（-2，3），则k=-6，然后根据反比例函数图象上点的坐标特征分别进行判断． 【题目详解】 设反比例函数y=kx（k 为常数，k≠0）， ∵反比例函数的图象经过点（-2，3）， ∴k=-2×3=-6，而2×（-3）=-6，（-3）×（-3）=9，2×3=6，-4×6=-24， ∴点（2，-3）在反比例函数y=-6x的图象上． 故选A ． 【题目点拨】本题考查了反比例函数图象上点的坐标特征：反比例函数y=kx（k 为常数，k≠0）的图象是双曲线，图象上的点（x ，y ）的横纵坐标的积是定值k ，即xy=k ． 10、D 【解题分析】在完成此类化简题时，应先将分子、分母中能够分解因式的部分进行分解因式．有些需要先提取公因式，而有些则需要运用公式法进行分解因式．通过分解因式，把分子分母中能够分解因式的部分，分解成乘积的形式，然后找到其中的公因式约去． 【题目详解】解：A 、原式=2249b c；故本选项错误；B 、原式=2×10-5；故本选项错误；C 、原式=()()3333x x x x +-=+- ；故本选项错误；D 、原式=223x ；故本选项正确； 故选：D ． 【题目点拨】分式的乘除混合运算一般是统一为乘法运算，如果有乘方，还应根据分式乘方法则先乘方，即把分子、分母分别乘方，然后再进行乘除运算．同样要注意的地方有：一是要确定好结果的符号；二是运算顺序不能颠倒．二、填空题（本大题共6个小题，每小题3分，共18分）11、【解题分析】分析：因为BP ＝22PA AB -，AB 的长不变，当PA 最小时切线长PB 最小，所以点P 是过点A 向直线l 所作垂线的垂足，利用△APC ≌△DOC 求出AP 的长即可求解. 详解：如图，作AP ⊥直线y ＝34x ＋3，垂足为P ，此时切线长PB 最小，设直线与x 轴，y 轴分别交于D ，C . ∵A 的坐标为(1，0)，∴D (0，3)，C (﹣4，0)，∴OD ＝3，AC ＝5，∴DC ＝22OD OC ＋＝5，∴AC ＝DC ，在△APC 与△DOC 中，∠APC ＝∠COD ＝90°，∠ACP ＝∠DCO ，AC ＝DC ，∴△APC ≌△DOC ，∴AP ＝OD ＝3，∴PB ＝2231-＝22．故答案为22.点睛：本题考查了切线的性质，全等三角形的判定性质，勾股定理及垂线段最短，因为直角三角形中的三边长满足勾股定理，所以当其中的一边的长不变时，即可根据另一边的取值情况确定第三边的最大值或最小值.12、21 【解题分析】试题分析：这四个数中，奇数为1和3，则P （抽出的数字是奇数）=2÷4=12． 考点：概率的计算．13、±1． 【解题分析】试题分析：∵2(2)4±=，∴4的平方根是±1．故答案为±1． 考点：平方根．14、33m n n +- 【解题分析】过点C 作CE ⊥CF 延长BA 交CE 于点E,先求得DF 的长,可得到AE 的长,最后可求得AB 的长.【题目详解】解：延长BA 交CE 于点E ，设CF ⊥BF 于点F ，如图所示．在Rt △BDF 中，BF ＝n ，∠DBF ＝30°， ∴3tan 3DF BF DBF n =⋅∠=． 在Rt △ACE 中，∠AEC ＝90°，∠ACE ＝45°，∴AE ＝CE ＝BF ＝n ，∴33AB BE AE CD DF AE m n n =-=+-=+-． 故答案为：33m n n +-．【题目点拨】此题考查解直角三角形的应用,解题的关键在于做辅助线.15、2(21)a -【解题分析】根据完全平方公式的特点：两项平方项的符号相同，另一项是两底数积的2倍，本题可用完全平方公式分解因式．【题目详解】解：22441(21)a a a -+=-．故答案为2(21)a -．【题目点拨】本题考查用完全平方公式法进行因式分解，能用完全平方公式法进行因式分解的式子的特点需熟练掌握． 16、3【解题分析】如图，连接BD ．首先证明△BCD 是等边三角形，推出S △EBC =S △DBC =34×42=43，再证明△EMN ∽△EBC ，可得EMN EBC S S ∆∆=（MN BC ）2=14，推出S △EMN =3，由此即可解决问题. 【题目详解】 解：如图，连接BD ．∵四边形ABCD 是菱形， ∴AB=BC=CD=AD=4，∠A=∠BCD=60°，AD ∥BC ，∴△BCD 是等边三角形，∴S △EBC =S △DBC 3423 ∵EM=MB ，EN=NC ，∴MN ∥BC ，MN=12BC ， ∴△EMN ∽△EBC ， ∴EMN EBC S S ∆∆=（MN BC ）2=14， ∴S △EMN 3，∴S 阴333 故答案为3【题目点拨】本题考查相似三角形的判定和性质、三角形的中位线定理、菱形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．三、解答题（共8题，共72分）17、（1）①60；②CP BF =．理由见解析；（2）2tan BF BP DE α-=⋅，理由见解析.【解题分析】（1）①根据直角三角形斜边中线的性质，结合30A ∠=，只要证明CDB ∆是等边三角形即可；②根据全等三角形的判定推出DCP DBF ∆≅∆，根据全等的性质得出CP BF =，（2）如图2，求出DC DB AD ==，DE AC ，求出2FDB CDP PDB α∠=∠=+∠，DP DF =，根据全等三角形的判定得出DCP DBF ∆≅∆，求出CP BF =，推出BF BP BC -=，解直角三角形求出tan CE DE α=即可．【题目详解】解：（1）①∵30A ∠=，90ACB ∠=，∴60B ∠=，∵AD DB =，∴CD AD DB ==，∴CDB ∆是等边三角形，∴60DCB ∠=．故答案为60.②如图1，结论：CP BF =．理由如下：∵90ACB ∠=，D 是AB 的中点，DE BC ⊥，A α∠=，∴DC DB AD ==，DE AC ，∴A ACD α∠=∠=，EDB A α∠=∠=，2BC CE =，∴2BDC A ACD α∠=∠+∠=，∵2PDF α∠=，∴2FDB CDP PDB α∠=∠=-∠，∵线段DP 绕点D 逆时针旋转2α得到线段DF ，∴DP DF =，在DCP ∆和DBF ∆中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩，∴DCP DBF ∆≅∆，∴CP BF =．（2）结论：2tan BF BP DE α-=⋅．理由：∵90ACB ∠=，D 是AB 的中点，DE BC ⊥，A α∠=，∴DC DB AD ==，DE AC ，∴A ACD α∠=∠=，EDB A α∠=∠=，2BC CE =，∴2BDC A ACD α∠=∠+∠=，∵2PDF α∠=，∴2FDB CDP PDB α∠=∠=+∠，∵线段DP 绕点D 逆时针旋转2α得到线段DF ，∴DP DF =，在DCP ∆和DBF ∆中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩，∴DCP DBF ∆≅∆，∴CP BF =，而CP BC BP =+，∴BF BP BC -=，在Rt CDE ∆中，90DEC ∠=， ∴tan DE DCE CE∠=， ∴tan CE DE α=，∴22tan BC CE DE α==，即2tan BF BP DE α-=．【题目点拨】本题考查了三角形外角性质，全等三角形的性质和判定，直角三角形的性质，旋转的性质的应用，能推出DCP DBF ∆≅∆是解此题的关键，综合性比较强，证明过程类似．18、（1）是;（2）见解析;（3）150°．【解题分析】（1）由菱形的性质和等边三角形的判定与性质即可得出结论；（2）根据题意画出图形，由勾股定理即可得出答案；（3）由SAS 证明△AEC ≌△BED ，得出AC=BD ，由等距四边形的定义得出AD=AB=AC ，证出AD=AB=BD ，△ABD 是等边三角形，得出∠DAB=60°，由SSS 证明△AED ≌△AEC ，得出∠CAE=∠DAE=15°，求出∠DAC=∠CAE+∠DAE=30°，∠BAC=∠BAE ﹣∠CAE=30°，由等腰三角形的性质和三角形内角和定理求出∠ACB 和∠ACD 的度数，即可得出答案．【题目详解】解：（1）一个内角为120°的菱形是等距四边形；故答案为是；（2）如图2，图3所示：在图2中，由勾股定理得：CD ==在图3中，由勾股定理得：CD ==（3）解：连接BD ．如图1所示：∵△ABE 与△CDE 都是等腰直角三角形，∴DE=EC ，AE=EB ，∠DEC+∠BEC=∠AEB+∠BEC ，即∠AEC=∠DEB ，在△AEC 和△BED 中，,DE CE AEC BED AE BE =⎧⎪∠=∠⎨⎪=⎩，∴△AEC ≌△BED （SAS ），∴AC=BD ，∵四边形ABCD 是以A 为等距点的等距四边形，∴AD=AB=AC ，∴AD=AB=BD ，∴△ABD 是等边三角形，∴∠DAB=60°，∴∠DAE=∠DAB ﹣∠EAB=60°﹣45°=15°，在△AED 和△AEC 中，,AD AC DE CE AE AE =⎧⎪=⎨⎪=⎩∴△AED ≌△AEC （SSS ），∴∠CAE=∠DAE=15°，∴∠DAC=∠CAE+∠DAE=30°，∠BAC=∠BAE ﹣∠CAE=30°，∵AB=AC ，AC=AD ， ∴180301803075,75,22ACB ACD --∠==∠== ∴∠BCD=∠ACB+∠ACD=75°+75°=150°．【题目点拨】本题是四边形综合题目，考查了等距四边形的判定与性质、菱形的性质、等边三角形的判定与性质、勾股定理、全等三角形的判定与性质、等腰三角形的性质、三角形内角和定理等知识；本题综合性强，有一定难度，证明三角形全等是解决问题的关键．19、（2）方程有两个不相等的实数根；（2）b=-2，a=2时，x 2=x 2=﹣2．【解题分析】分析：（2）求出根的判别式24b ac ∆=-，判断其范围，即可判断方程根的情况.（2）方程有两个相等的实数根，则240b ac ∆=-=，写出一组满足条件的a ，b 的值即可.详解：（2）解：由题意：0a ≠．∵()22242440b ac a a a ∆=-=+-=+>，∴原方程有两个不相等的实数根．（2）答案不唯一，满足240b ac -=（0a ≠）即可，例如：解：令1a =，2b =-，则原方程为2210x x -+=，解得：121x x ==．点睛：考查一元二次方程()200++=≠ax bx c a 根的判别式24b ac ∆=-， 当240b ac ∆=->时，方程有两个不相等的实数根.当240b ac ∆=-=时，方程有两个相等的实数根.当240b ac ∆=-<时，方程没有实数根.20、 (1)见解析;(2)见解析.【解题分析】（1）根据题意作图即可；（2）先根据BD 为AC 边上的中线，AD=DC ，再证明△ABD ≌△CED （AAS ）得AB=EC ，已知∠ABC=90°即可得四边形ABCE 是矩形．【题目详解】（1）解：如图所示：E 点即为所求；（2）证明：∵CE ⊥BC ，∴∠BCE=90°，∵∠ABC=90°，∴∠BCE+∠ABC=180°，∴AB ∥CE ，∴∠ABE=∠CEB ，∠BAC=∠ECA ，∵BD 为AC 边上的中线，∴AD=DC ，在△ABD 和△CED 中，∴△ABD ≌△CED （AAS ），∴AB=EC ，∴四边形ABCE 是平行四边形，∵∠ABC=90°，∴平行四边形ABCE 是矩形．【题目点拨】本题考查了全等三角形的判定与性质与矩形的性质，解题的关键是熟练的掌握全等三角形的判定与性质与矩形的性质.21、（1）y=6x ；（2）454；（3）32＜x ＜1． 【解题分析】（1）先利用矩形的性质确定C 点坐标（1，4），再确定A 点坐标为（3，2），根据反比例函数图象上点的坐标特征得到k 1=1，即反比例函数解析式为y=6x ；（2）利用反比例函数解析式确定F 点的坐标为（1，1），E 点坐标为（32，4），然后根据△OEF 的面积=S 矩形BCDO ﹣S △ODE ﹣S △OBF ﹣S △CEF 进行计算；（3）观察函数图象得到当32＜x ＜1时，一次函数图象都在反比例函数图象上方，即k 2x+b ＞1k x ． 【题目详解】（1）∵四边形DOBC 是矩形，且点C 的坐标为（1，4），∴OB=1，OD=4，∵点A 为线段OC 的中点，∴A 点坐标为（3，2），∴k 1=3×2=1，∴反比例函数解析式为y=6x ； （2）把x=1代入y=6x得y=1，则F 点的坐标为（1，1）； 把y=4代入y=6x 得x=32，则E 点坐标为（32，4）， △OEF 的面积=S 矩形BCDO ﹣S △ODE ﹣S △OBF ﹣S △CEF=4×1﹣12×4×32﹣12×1×1﹣12×（1﹣32）×（4﹣1） =454； （3）由图象得：不等式不等式k 2x+b ＞1k x 的解集为32＜x ＜1． 【题目点拨】本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解即可．22、（1）4133（2）63(3) 15. 【解题分析】（1）由勾股定理求出BP 的长， D 是边AB 的中点，P 为AC 的中点，所以点E 是△ABC 的重心,然后求得BE 的长. （2）过点B 作BF ∥CA 交CD 的延长线于点F ,所以BD FD BF DA DC CA ==，然后可求得EF =8，所以14CP CE BF EF ==，所以13CP PA =，因为PD ⊥AB ，D 是边AB 的中点，在△ABC 中可求得cosA 的值. （3）由22BP CD CD BD AB =⋅=⋅，∠PBD=∠ABP ，证得△PBD ∽△ABP ，再证明△DPE ∽△DCP 得到2PD DE DC =⋅，PD 可求.【题目详解】解：（1）∵P 为AC 的中点，AC =8，∴CP =4,∵∠ACB =90°，BC =6，∴BP =213,∵D 是边AB 的中点，P 为AC 的中点，∴点E 是△ABC 的重心,∴241333BE BP ==, （2）过点B 作BF ∥CA 交CD 的延长线于点F ,∴BD FD BF DA DC CA==, ∵BD=DA ，∴FD=DC ，BF=AC ,∵CE=2，ED=3，则CD =5，∴EF =8,∴2184CP CE BF EF ===, ∴14CP CA =， ∴13CP PA =，设CP=k ，则PA=3k ， ∵PD ⊥AB ，D 是边AB 的中点，∴PA=PB=3k,∴22BC k =，∴26AB k =，∵4AC k =，∴6cos 3A =, （3）∵∠ACB =90°，D 是边AB 的中点，∴12CD BD AB ==, ∵222BP CD =，∴22BP CD CD BD AB =⋅=⋅,∵∠PBD=∠ABP ，∴△PBD ∽△ABP ,∴∠BPD=∠A ,∵∠A=∠DCA ，∴∠DPE=∠DCP ，∵∠PDE=∠CDP ，△DPE ∽△DCP ，∴2PD DE DC =⋅,∵DE=3,DC=5，∴.【题目点拨】本题是一道三角形的综合性题目，熟练掌握三角形的重心，三角形相似的判定和性质以及三角函数是解题的关键.23、方程的根120=2x x =-或【解题分析】（1）根据方程的系数结合根的判别式，即可得出关于k 的一元一次不等式，解之即可得出k 的取值范围； （1）取k=0，再利用分解因式法解一元二次方程，即可求出方程的根．【题目详解】（1）∵关于x 的一元二次方程x 1﹣1（k ﹣a ）x+k （k+1）=0有两个不相等的实数根，∴△=[﹣1（k ﹣1）]1﹣4k （k ﹣1）=﹣16k+4＞0，解得：k ＜14． （1）当k=0时，原方程为x 1+1x=x （x+1）=0，解得：x 1=0，x 1=﹣1．∴当k=0时，方程的根为0和﹣1．【题目点拨】本题考查了根的判别式以及因式分解法解一元二次方程，解题的关键是：（1）牢记“当△＞0时，方程有两个不相等的实数根”；（1）取k=0，再利用分解因式法解方程．24、（1）y =10x +160；（2）5280元；（3）10000元.【解题分析】试题分析：（1）根据题意，由售价是80元/个时，每周可卖出160个，若销售单价每个降低2元，则每周可多卖出20个，可得销售量y 个与降价x 元之间的函数关系式；（2）根据题意结合每周获得的利润W =销量×每个的利润，进而利用二次函数增减性求出答案；（3）根据题意，由利润不低于5200元列出不等式，进一步得到销售量的取值范围，从而求出答案．试题解析：（1）依题意有：y =10x +160；（2）依题意有：W =（80﹣50﹣x ）（10x +160）=﹣10（x ﹣7）2+5290，∵-10＜0且x 为偶数，故当x =6或x =8时，即故当销售单价定为74或72元时，每周销售利润最大，最大利润是5280元；（3）依题意有：﹣10（x﹣7）2+5290≥5200，解得4≤x≤10，则200≤y≤260，200×50=10000（元）．答：他至少要准备10000元进货成本．点睛：此题主要考查了二次函数的应用以及一元二次方程的应用等知识，正确利用销量×每个的利润=W得出函数关系式是解题关键．。
2023年浙江省杭州市中考数学模拟卷五
2023年浙江杭州中考数学模拟卷五学校:___________姓名：___________班级：___________考号：___________一、选择题：本大题有10小题每小题3分共30分。
在每小题给出的四个选项中只有一项是符合题目要求的。
1．绝对值大于1且小于4的所有整数和是（）A．6B．﹣6C．0D．4 2．如图由4个大小相同的正方体组成的几何体的主视图是（）A．B．C．D．3.根据浙江省统计局发布的最新数据2021年前三季度杭州市GDP达到13151亿元是前三季度全国14座GDP达到1万亿元的城市之一.数13151用科学记数法可以表示为（）A．1.31514B．1.3151×104C．0.13151×105D．13151×1084.垃圾分类能有效减少占地、减少污染以及节约资源以下为垃圾分类的四种标志其中不是轴对称图形的是（）A． B．C． D．5. 如图△ABC中DE//BC将△ADE沿DE翻折使得点A落在平面内的A′处若∠B=40°则∠BDA′的度数是（）试卷第1页共6页试卷第2页 共6页A ．70°B ．80°C ．90°D ．100°6．化简24142m m +--的结果是（ ） A ．12m -+ B ．12m + C ．264m m +- D ．12m -+ 7 . 函数y ＝m x与y ＝mx ﹣m （m ≠0）在同一平面直角坐标系中的图象可能是（ ） A ．B ．C ．D ．8. 如图 在ABC 中 9030C B ∠=︒∠=︒， 以A 为圆心 任意长为半径画弧分别交AB 、AC 于点M 和N 再分别以M N 、为圆心 大于12MN 的长为半径画弧 两弧交于点P 连接AP 并延长交BC 于点D则下列说法中正确的个数是( )①AD 平分BAC ∠；②60ADC ∠=︒；③点D 在AB 的中垂线上；④13DAC ABD S S =：：．A ．4B ．3C ．2D ．19. 为30．某数学社团开展实践性研究 在大明湖南门A 测得历下亭C 在北偏东37°方向继续向北走105m 后到达游船码头B 测得历下亭C 在游船码头B 的北编东53°方向．试卷第3页 共6页 请计算一下南门A 与历下亭C 之间的距离约为（ ）（参考数据：3tan 374≈ 4tan 533≈）A ．225mB ．275mC ．300mD ．315m 10.已知 P 1(x 1，y 1) P 2(x 2，y 2) 为抛物线 y =−ax 2+4ax +c(a ≠0) 图象上的两点 且 x 1<x 2 则下列说法正确的是（ ）A ．若 x 1+x 2<4 则 y 1<y 2B ．若 x 1+x 2>4 则 y 1<y 2C ．若 a(x 1+x 2−4)<0 则 y 1>y 2D ．若 a(x 1+x 2−4)>0 则 y 1>y 2第Ⅱ卷（非选择题 共110分）二、填空题：（本大题共6个小题 每小题4分 共24分．）11．分解因式： 4a 2b ﹣3ba 2=12．在一个不透明的盒子里装有5个黑色棋子和若干白色棋子 每个棋子除颜色外都相同 任意摸出一个棋子 摸到白色棋子的概率是34则白色棋子的个数为_______ 13．如图 直线1l 、2l 的交点坐标可以看作方程组______的解．14．如图 有一所正方形的学校 北门（点A ）和西门（点B ）各开在北 西面围墙的正中间．在北门的正北门30米处（点C ）有一棵大榕树．如果一个学生从西门出来 朝正为O的直径_________．三、解答题：本大题共7个小题共66分。
[中考数学]-浙教版[原创]初中数学中考模拟卷试题卷(附答案和评分标准)
![[中考数学]-浙教版[原创]初中数学中考模拟卷试题卷(附答案和评分标准)](https://img.taocdn.com/s3/m/4bdfc9742af90242a995e52e.png)
初中数学中考模拟卷试题卷：一． 选择题（每题4分，共48分） １．8的绝对值是（▲）A 8B 8- C81 D 81- 2．不等式x 5>1的解是（▲）A x <5B x >5C x <51 D x >513．已知分式的取值是的值为零，则x x x12-（▲）A 1-B 1C 0D 1±4．图象上的是个点，在函数下列直角坐标系中的四x y 21=（▲） A ()12--，B ()21--，C ()21，D ()12，- 5．圆锥的侧面展开图是（▲）A 圆环B 扇形C 等腰三角形D 矩形 6．=⋅=-+21221022,x x x x x x 的两根，则是方程已知（▲） A 1 B 21-C 21D 1-7．的取值是只有一个实数根，则的高次方程若关于x ax x x x 04223=+-（▲） A a >1 B 1≤a C a >2 D 2≥a8．天员送上太空．按照成功，将我国第一名航“神州五号”飞船发射计划，公里，远地点高度地点高度飞船在变轨前运行在近200350公里的椭圆形 为高度用科学记数法表示轨道上，那么远地点的（▲）A 米41035⨯ B 米5105.3⨯ C 米4105.3-⨯ D 米5105.3-⨯9．1当<x <,2()的值是则化简213-+-x x （▲）A 42-xB 2-C x 24-D 210．五的各种费用．某投资卖一次需交千分之七点我国股市交易中每买、元时全部卖当该股票涨到股元的价格买入上某股票者以每股12,100010 该投资者实际盈利为（▲）A 元1835B 元1910C 元1925D 元200011．，，三人放出的风筝线长、乙、丙参加风筝比赛身高相等的三名同学甲 ），则三人所放的风筝（假设风筝线是拉直的线与地面的夹角如上表中（▲）A 甲的最高B 丙的最高C 乙的最低D 丙的最低12．个红个白球；右边抽屉有个红球，边抽屉有有左、右两个抽屉，左432 概率为取１个恰好都是白球的个白球．从两个抽屉各球，1（▲）A94 B 207 C 253 D 52 二． 填空题（每题5分，共30分） 13．==-+b a b a b a :,5322则已知：▲ ．14．已知如图,DE ∥BC,△ADE 2的面积是cm 2,梯形DBCE 6的面积为cm 2, 则DE:BC 的值是 ▲ ．A BCE DAB CDO PA B CDEP(第14题) (第16题) (第17题)15．的解是方程112=-x ▲ ．16．如图，⊙O 内AB 、CD 两弦相交于点P ，若PA ，4=PB ，3=PC ，2=则弦CD 的长度为 ▲ ．17．如图，菱形ABCD 中，AB ，2=∠BAD =60,E 是AB 的中点，P 是对角线AC上的一个动点，则PE+PB 的最小值为 ▲ ．18．，借助计算器可以求得，53422=+，55334422=+ ,55533344422=+计算结果，猜想仔细观察上面几道题的=+2200422004333444个个▲ ． 三． 解答题（本题有7小题，共72分．必须写出解答过程） 19．(本题8分)计算： 2sin 60+(-2cos45)0141132-⎪⎭⎫ ⎝⎛-+-20．(本题8分)解方程：2121222=-+-x xx x 21．(本题8分)是：应缴纳税，其计算方法章、出版著作所获稿费国家规定，个人发表文 ①元，不纳税；稿费不高于800②元，应缴纳元，但不高于稿费高于4000800 14800元的那一部分的超过%的税；③元，应缴纳全部稿费稿费高于4000的 11%．元的税，纳了作获得一笔稿费，他缴今知王教授出版一本著550问王教 授这笔稿费有多少元？22．(本题10分)已知正△ABC 内接于⊙O,D 是劣弧BC 上一点，连结AD,BD,CD ．求证：BD+CD=ADABCOD23．(本题10分)系内的梯形已知：如图，直角坐标AOBC,AC ∥OB,AC,OB 长分别是关于的x 5:1:04622==++-∆∆BOC AOC S S m mx x 的两根，并且方程① 求AC 、OB 的长；②当BC ⊥OC 时，求OC 的长及OC 所在直线的解析式；③在②的条件下，线段OC 上是否存在一点M,过M 点 作x 轴的平行线，交y 轴于F,交BC 于D,过D 点作y 轴的平行线，交x 轴于E,AOBC FOED S S 梯形矩形使21=． 若存在，请直接写出点M 的坐标（不必写过程）； 若不存在，说明理由． 24．(本题12分)元，为了扩大件，每件盈利，平均每天可售出光明商场销售一批衬衫4020 取适当的降价措施减少库存，商场决定采销售，增加利润，尽快．经市场 件：售元，商场平均每天可多衫每降价调查发现，如果每件衬21 ①少元？元，每件衬衫应降价多若商场平均每天要盈利1200 ②？是多少元？商场平均每天盈利最多每件衬衫降价多少元时25．(本题14分)标系中，以已知：如图，在直角坐y 轴上的点C 为为圆心，1半径的圆与x 轴 相切于原点O ,点P 在x 轴的负半轴上， PA 切⊙C 于点A ,AB 为⊙C 的直径，PC 交OA 于点D ．①求证：PC ⊥OA ；②若点P ()，求直线，的坐标为02-AB 的解析式；③若点P 在x 题的其它条件不变，设轴的负半轴上运动，原P ()，，的坐标为0x四边形POCA 与点求的面积为S S ,P 的横坐之间的函数关系式；标x④在③是否存在这样一点的情况下，分析并判断P, 使,AOB POCA S S ∆=四边形 若存在，直接写出点P 的坐标（不写过说明理由程）；若不存在，简要．Pxy C ADOB初三数学中考模拟卷答题卷:一． 选择题（每题4分，共48分）二． 填空题（每题5分，共30分）13． 14． 15． 16． 17． 18．三． 解答题（本题有7小题，共72分．必须写出解答过程）19．(本题8分)计算： 2sin 60+(-2cos 45)0141132-⎪⎭⎫ ⎝⎛-+-20．(本题8分)解方程：2121222=-+-x xx x21．(本题8分)22．(本题10分)ABCOD23．(本题10分) 24．(本题12分)25．(本题14分)Pxy C ADOB初三数学中考模拟卷参考答案及评分标准：一．选择题（每题4分，共48分）二．填空题（每题5分，共30分） 13． 13：1 14． 1：2 15．2±16． 8 17．3 18．个2004555 三． 解答题（本题有7小题，共72分．必须写出解答过程） 19．(本题8分) 解：原式=()4131232---+⨯分6=2- 分220．(本题8分) 解：设则原方程化为：,122x x y -=21=+yy 0122=+-y y 即： ∴121==y y 分2∴1122=-xx ∴0122=--x x 分2 ∴21,121-==x x 分2经检验：21,121-==x x 都是原方程的根． 分221．(本题8分) 解：()148004000⨯-%448=元<元550设王教授这笔稿费有x 元 分1 根据题意得：11%550=x 分4 解得 5000=x 分2答：王教授这笔稿费有5000元． 分1 22．(本题10分) 证明：延长CD 到M,使DM=DB,连结BM ． ∵∠ADB=∠ACB=60 ∠ADC=∠ABC=60 ∴∠BDM=60 分2 ∴△BDM 是正三角形． ∴∠BMC=∠BDA=60∵∠BAD=∠BCM AB=BC 分2 ∴△BAD ≌△BCM 分1∴CM=AD 分2 ∵CM=CD+DM=CD+DB 分1 ∴BD+CD=AD ． 分223．(本题10分)解：①∵5:1:=∆∆BOC AOC S S∴AC:OB=1:5不妨设AC=k OB=5k 由⎩⎨⎧+=⋅=+45652m k k mk k 分1 解得⎩⎨⎧==11k m 或⎩⎨⎧-=-=11k m ()不合题意，舍去 分1 ∴AC=1 OB=5 分2 ②∵∠OAC=∠BCO=90 ∠ACO=∠BOC∴△OBC ∽△COA 分1 ∴AC OB OC OAOCOC OB ⋅==2, ∴OC 5=或 OC ()舍去5-= 分1∵AC=1 ∴AO=2 ∴C (1,2) 分1 ∴直线OC 的解析式是：y = 2x 分1 ③存在．)1,21(1M ⎪⎭⎫⎝⎛23,432M ． 分2 24．(本题12分)解：①设每件衬衫应降价x 元，由题意得： 分1 ()()12004020=-⋅+x x 分2 整理得：0200302=+-x x∴ 101=x ，202=x 分2 ∵要尽快减少库存，故 20=x 分1 ②设每件衬衫应降价x 元，商场平均每天盈利是y 元 分1 则可知：()()x x y -⋅+=4020 分2 即：8006022++-=x x y∴当 15=x 时，1250=最大值y 元． 分2 答：略． 分125．(本题14分)解：① ∵AB 是⊙C 的直径，PA 是切线∴PA ⊥AB ∵∠POC=90∴∠PAC= ∠POC=90 ∵PA,PO 是⊙C 的切线 ∴PA=PO ∵PC=PC∴△PAC ≌△POC 分2 ∴∠APC= ∠OPC 分1 ∴PC ⊥OA ②过点A 作AM ⊥PO,垂足为M∵PO=2,OC=1, ∠POC=90∴PC=5 分1 ∵PC ⊥OA∴OC PO OD PC ⋅=⋅ ∴552=OD 分1 ∴5542==OD AO ∵ PO 是⊙C 的切线 ∴∠AOM= ∠ABO ∵∠AMO= ∠AOB=90 ∴△AMO ∽△AOB ∴AM ：AO=AO ：AB ∴AM=58分1 在Rt △AMO 中：MO=545855422=⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛ ∴点A 的坐标为：⎪⎭⎫⎝⎛-58,54 分1 ∵直线AB 过点C(0,1)∴可设直线AB 的解析式为：1+=kx y 把A ⎪⎭⎫⎝⎛-58,54代入得：43-=k 分1∴直线AB 的解析式为： 143+-=x y 分1 ③∵△PAC ≌△POC ∴POC POCA S S ∆=2四边形∵()x x S POC 21121-=⨯-⨯=∆ 分1 ∴x S -= 分2 ④存在．()0,1-P ． 分2试卷说明：一、考试采用闭卷笔答形式，试卷满分为150分，考试时间为100分钟；二、在结构上，容易题占70%，中等题占20%，稍难题占10%，难度系数在0.7到0.75之间。
2023年浙江省杭州市中考数学全真模拟试卷附解析
2023年浙江省杭州市中考数学全真模拟试卷 学校：__________ 姓名：__________ 班级：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1．如图，几何体的主视图是（ ）A ．B ．C ．D ．2．如图所示,从山顶A 望地面C 、D 两点，俯角分别为 45°、30°，如果CD= 100 m ，那么山高AB 为（ ）A ．lOOmB ． 50(31)+mC ．502D ．5033．对于反比例函数6y x =，当6x -≤时，y 的取值范围是（ ） A ．y ≥1- B ．y ≤1- C ．1-≤y ＜0 D ．y ≥14．如图，P 是Rt △ABC 的斜边BC 上异于B ，C 的一点，过P 点作直线截△ABC ，使截得的三角形与△ABC 相似，满足这样条件的直线共有（ ）A ．1条B ．2条C ．3条D ．4条5．正方形的面积 y （cm 2）与它的周长 x （cm ）之间的函数关系式是（ ）A ．214y x =B ．2116y x =C ． 2164y x =D ．24y x = 6．下列不能判定一个四边形是平行四边形的条件是（ ）A ．两组对边分别平行B ．两组对边分别相等C ．一组对边平行且相等D ．一组对边平行，另一组对边相等7．下列推理正确的是（ ）A ．∵a>0，b>0，∴a>bB ．∵a>0，b>a ，∴b>0C ．∵a>0，a>6，∴b>0D ．∵a>0，a>b ，∴ab>O8．如图，已知 AB ∥CD ，∠A = 70°，则∠1 的度数为（ ） A ． 70° B ． 100° C ．110° D ． 130°9． 如图，1l ∥2l ，将 AB 沿2l 向右平移 1.5 cm 后至 CD 位置，若AB=2，则 CD 等于（ ）A ．1.5cmB ．2 cmC ．3.5 cmD ．1.5 cm 或2 cm10．若∠1和∠3是同旁内角，∠1=78°，则下列说法正确的是（ ）A ．∠3=78°B ．∠3=12°C ．∠1+∠3=180°D ．∠3的度数无法确定 11．已知a 2+b 2=3，a －b ＝2，那么ab 的值是（ ）A ．－0.5B ．0.5C ．－2D ．2 12．某市出租车的收费标准是：起步价7元（即行驶距离不超过3 km 都需付7元车费），超过3 km 以后，每增加l km ，加收2．4元（不足l km 按1 km 计）．某人乘这种出租车从甲地到乙地共付车费19元，设此人从甲地到乙地的路程是x （km ），那么x 的最大值是 （ ）A ．11B ．8C ．7D ．5二、填空题13．如图，某处位于北纬 36°4′，通过计算可以求得：在冬至日正午时分的太阳入射角为 30°30′'，因此，在规划建设楼高为20m 的小区时，两楼间的距离最小为 m ，才能保证不挡光. (结果保留四个有效数字)14．在⊙O 中，弦 AB ∥CD ，AB=24，CD=10，弦 AB 的弦心距为 5，则 AB 和 CD 之间的距离是 ． 15．如图所示，把一个面积为1的正方形等分成两个面积为12的矩形，接着把一个面积为12的矩形等分成两个面积为14的矩形，再把一个面积为14的矩形等分成两个面积为18的矩形，如此进行下去．试利用图形揭示的规律计算：11111111248163264128256+++++++= ．解答题(共40分)16．如图，为测量一个池塘的宽AB ，在池塘一侧的平地上选一点C ，再分别找出线段AC ，BC 的中点D ，E.现量得DE ＝18m ，则池塘的宽AB ＝ m ． 17．若方程x 2-4x+m=0有两个相等的实数根，则m 的值是____ ___.18．学校篮球队五名队员的年龄分别为l7，15，17，l6，15，其方差为0．8，则四年后这五名队员年龄的方差为 ．19．在△ABC 中，∠A+∠B=∠C ，且AC=12AB ，则∠B ．20．如图，如果_____，那么a ∥b ．21．如图，AF 、AD 分别是△ABC 的高和角平分线，且∠B=36°，∠C=76°，则∠DAF = .22．已知正方形的面积是2269y xy x ++ （x>0，y>0）,利用分解因式，写出表示该正方形的边长的代数式 ． 三、解答题23．已知：开口向下的抛物线y ＝ax 2+bx+c 与x 轴交于A(x l ，0)、B(x 2，0)两点(x 1<x 2)，与y 轴交于点C(0，5)，且a+b ＋c ＝0，S △ABC ＝15．求这条抛物线的解析式．24．点 C 是线段 AB 的黄金分割点，且AC>BC ．若 AB=2．求：（1）AC 与 BC 的长度的积；（2）AC 与 BC 的长度的比．25．如图，有一直径是lm的圆形铁皮，要从中剪出一个最大的圆心角是 90°的扇形 ABC，求：(1)被剪掉的阴影部分面积；(2)用所留的扇形铁皮围成一个圆锥，该圆锥的底面半径是多少？(结果可用根号表示)26．四边形ABCD中，M是BC的中点，AM，BD互相平分于点O．求证：AM=DC．27．如图，△ABC中D，E分别是AC，AB上的点，BD与CE交于点0，给出下列四个条件：①∠EB0=∠DCO；②∠BE0=∠CDO；③BE=CD；④OB=OC．(1)上述四个条件中，哪两个条件可判定AB=AC(用序号写出所有情形)?(2)选择第(1)小题的一种情形．证明AB=AC．28．桌上放着两个物体，它的三视图如图，你知道这两个物体是什么吗?29．在数轴上画出表示实数2.30．滴水成河，若20滴水流在一起为1cm3，现有一条河流总体积为l万m3．试求该河流相当于多少滴具有相同体积的水滴?【参考答案】学校：__________ 姓名：__________ 班级：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1．C2．B3．C4．C5．答案:B6．D7．B8．C9．B10．D11．AB二、填空题13．33.9514．7 或 1715．25525616． 36m17．418．0．819．30°20．∠1=∠2(∠1=∠3或∠2+∠4=180)21．20022．3x+y三、解答题23．y ＝－x 2－4x ＋5．24．∵点 C 是线段 AB 的黄金分割点，且 AC>BC ．∴1AB =，21)3BC AB AC =-=-=(1）1)(38AC BC ⋅==(2）AC BC ==(1)∵ABC 为扇形，∴AB=AC,∴△ABC 为等腰直角三角形， ∵∠BAC=90°,∴BC 为直径，∵BC=1，∴22AB =， ∴22112()()2428S S S πππ=-=⋅-⨯⨯=阴影大圆扇形m 2.(2)由题意得⌒BC =1222424π⨯⋅⨯=，又∵⌒BC 等于所围圆锥的底面周长. ∴⌒BC =22r π⨯=，2r = m ． 26．提示：连结DM 即可27．(1)①③，①④，②③，②④；(2)略28．一个长方体，一个圆柱体(答案不唯一)29．略30．2×1O 11滴。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
北京四中2011年中考数学全真模拟试题（5）考生注意：１、数学试卷共8页，共24题．请您仔细核对每页试卷下方页码和题数，核实无误后再答题．２、请您仔细思考、认真答题，不要过于紧张，祝考试顺利！一、选择题：（本大题共10小题，每小题4分，共40分）在每小题给出的四个选项中，只．有一项是符合题意的，请把你认为正确的选项前的字母填写在本答案表中． 题号 1 2 3 4 5 6 7 8 9 10 答 案蕴藏量就达56000万m 3，用科学记数法记作 （ ）Ａ．95.610⨯m 3Ｂ．85610⨯m 3Ｃ．85.610⨯m 3Ｄ．45600010⨯m 3２．请阅读一小段约翰斯特劳斯作品，根据乐谱中的信息，确定最后一个音符的时值长应 为 （ ）Ａ．18Ｂ．12Ｃ．14Ｄ．34３．在“手拉手，献爱心”捐款活动中，九年级七个班级的捐款数分别为：260、300、240、220、240、280、290(单位：元)，则捐款数的中位数为 （ ）Ａ．280 Ｂ．260 Ｃ．250 Ｄ．270 ４．已知1O 和2O 的半径分别是5和4，1O 23O =，则1O 和2O 的位置关系是（ ）Ａ．外离Ｂ．外切Ｃ．相交Ｄ．内切 ５．在平面直角坐标系中，点(43)-，所在象限是（ ）Ａ．第一象限Ｂ．第二象限Ｃ．第三象限Ｄ．第四象限６．如图，已知一坡面的坡度1:3i =，则坡角α为 （ ）Ａ．15Ｂ．20Ｃ．30Ｄ．45７．下列图形中，是轴对称而不是中心对称图形的是 （ ）Ａ．平行四边形 Ｂ．菱形 Ｃ．等腰梯形Ｄ．直角梯形８．若使分式22231x x x +--的值为0，则x 的取值为（ ）Ａ．1或1- Ｂ．3-或１ Ｃ．3- Ｄ．3-或1- ９．若一个多边形的内角和为外角和的3倍，则这个多边形为 （ ）Ａ．八边形 Ｂ．九边形 Ｃ．十边形 Ｄ．十二边形第6题图 ＣＢＡ 1:3i =α10．估算50232+的值 （ ）Ａ．在4和5之间 Ｂ．在5和6之间 Ｃ．在6和7之间Ｄ．在7和8之间二、填空题：（本大题共6小题，每小题5分，共30分） 11．函数6y x =-中，自变量x 的取值范围是 ．12．已知等腰三角形两边长为7和3，则它的周长为 ． 13．若反比例函数my x=-的图象经过点(32)--，，则m = ． 14．计算：332(3)a a = ．15．在珠穆朗玛峰周围2千米的范围内，还有较著名的洛子峰（海拔8516米）、卓穷峰（海拔7589米）、马卡鲁峰（海拔8463米）、章子峰（海拔7543米）、努子峰（海拔7855 米）、和普莫里峰（海拔7145米）六座山峰，则这六座山峰海 拔高度的极差为 米．16．已知三个边长分别为2、3、5的正方形如图排列，则图中 阴影部分面积为 ．三、解答题：本大题共8小题，共80分，解答应写明文字说明和运算步骤． 17．（本题共两小题，每小题6分，满分12分）（1）解不等式组：235321x x -<⎧⎨+-⎩≥（2）因式分解：324y x y - 解：（1）解：（2）18．（本小题满分8分） 如图，已知在半圆AOB 中，30AD DC CAB =∠=，，23AC =，求AD 的长度． 解：ＯＢＣＤ Ａ30第18题图2 3 ５ 第16题图下图是由权威机构发布的，在1993年4月～2005年4月期间由中国经济状况指标之一中国经济预警指数绘制的图表．（1）请你仔细阅读图表，可从图表 中得出：我国经济发展过热的最高点出现在 年；我国经济发展过冷的最低 点出现在 年．（2）根据该图表提供的信息，请你 简单描述我国从1993年4月到2005年4 月经济发展状况，并预测2005年度中国 经济发展的总体趋势将会怎样？ 答：第19题图 20．（本小题满分8分）如图，PA 为O 的切线，A 为切点，PO 交O 于点36B OA OP ==，，，求BAP ∠的度数． 解：21．（本小题满分10分）如图（1）所示为一上面无盖的正方体纸盒，现将其剪开展成平面图，如图（2）所示． 已知展开图中每个正方形的边长为1．（1）求在该展开图中可画出最长线段的长度？这样的线段可画几条？ （2）试比较立体图中BAC ∠与平面展开图中B A C '''∠的大小关系？ 解：ACB 第21题图(1)A 'C ' B '第20题图 ＰＯ Ａ Ｂ已知二次函数图象经过(23)-，，对称轴1x =，抛物线与x 轴两交点距离为4，求这个二次函数的解析式？ 解： 23．（本小题满分12分）小胖和小瘦去公园玩标准的．．．跷跷板游戏，两同学越玩越开心，小胖对小瘦说：“真可惜！ 我只能将你最高翘到1米高，如果我俩各边的跷跷板都再伸长相同的一段长度，那么我就能翘到1米25，甚至更高！”（1）你认为小胖的话对吗？请你作图分析说明；（2）你能否找出将小瘦翘到1米25高的方法？试说明． 解：24．（本小题满分12分）在科技馆里，小亮看见一台名为帕斯卡三角的仪器，如图所示，当一实心小球从入口落下，它在依次碰到每层菱形挡块时，会等可能地向左或向右落下．（1）试问小球通过第二层A 位置的概率是多少？（2）请用学过的数学方法模拟试验，并具体说明小球下落到第三层B 位置和第四层C位置处的概率各是多少？ 解：第23题图第24题图中考数学模拟试题（5）参考答案及评分标准11．6x ≤ 12．1713．6-14．654a15．137116．3.75三、解答题：本大题共8小题，共80分，解答应写明文字说明和运算步骤． 17．（本小题满分12分）（1）23532x x -<⎧⎨+⎩，①≥-1.②解：由①得 4x <． ························· 2分由②得 x ≥-1． ························· 4分 ∴不等式组解集为14x -<≤． ··················· 6分 （2）解：324y x y -22(4)y y x =- ························· 2分 (2)(2)y y xy x =+-． ····················· 6分 18．（本小题满分8分） 解：AB 为直径，90ACB ∴∠=， ················· 1分13060..2CAB ABC BC AC ∠=∴∠=∴=， ···· 2分 1.2AD DC AD DC AC BC AD =∴==∴=，．BC AD ∴=． ···························· 4分 在ABC Rt △中30CAB AC ∠==，且tan BC AC CAB =∠． ··········· 5分 tan 302BC ∴==． ······················ 6分2AD ∴=． ····························· 8分19．（本小题满分8分） 答：（1）1993，1998． ························· 4分 （2）从1993年经济过热逐渐降温，到1998年经济过冷，之后经济逐步回升并趋于稳 定． ································· 6分 由图表预测2005年经济虽然有所降温，但总体保持稳定． ·········· 8分 20．（本小题满分8分）解：PA 为O 的切线，A 为切点90OA PA OAP ∴∠=⊥，∴． ····················· 2分ＯＢＡ 第18题图在OAP Rt △中 31sin 3062OA OPA OPA OP ∠===∴∠= ········ 4分 90903060AOP OPA ∴∠=-∠=-=．在OAB △中6060AOP OA OB OAB ∠==∴∠=，，． ········ 6分906030BAP OAP OAB ∴∠=∠-∠=-=． ·············· 8分21．（本小题满分10分）解：（1······················ 1分如图（1）中的A C ''，在A C D '''Rt △中 13C D A D ''''==，，由勾股定理得：A C ''∴== ··· 3分 答：这样的线段可画4条（另三条用虚线标出）． · 4分 （2）立体图中BAC ∠为平面等腰直角三角形的一锐角，45BAC ∴∠=． ·············· 5分在平面展开图中，连接线段B C ''，由勾股定理可得：A B B C ''''== ··········· 7分又222A B B C A C ''''''+=，由勾股定理的逆定理可得A B C '''△为直角三角形． 又A B B C ''''=， A B C '''∴△为等腰直角三角形． ········ 8分45B A C '''∴∠=． ············· 9分 所以BAC ∠与B A C '''∠相等． ········ 10分 22．（本小题满分10分）解：∵抛物线与x 轴两交点距离为4，且以1x =为对称轴．∴抛物线与x 轴两交点的坐标为(10)(30)-，，，． ··············· 4分 设抛物线的解析式(1)(3)y a x x =+-． ·················· 6分 又抛物线过(23)-，点， 3(21)(23)a ∴-=+-． ························ 8分解得1a =． ······························ 9分∴二次函数的解析式为223y x x =--． ················· 10分第21题图(1)A 'C 'B '第21题图(2)A 'C 'B 'D 'D '23．（本小题满分12分） 解：（1）小胖的话不对． ········· 2分 小胖说“真可惜！我现在只能将你最高翘到1 米高”，情形如图（1）所示，OP 是标准跷跷 板支架的高度，AC 是跷跷板一端能翘到的最 高高度1米，BC 是地面．.OP BC AC BC OBP ABC OBP ABC ∠=∠∴⊥，⊥，，△∽△.BO OPBA AC∴=····························· 4分 又此跷跷板是标准跷跷板，BO OA =， 12BO BA ∴=，而1AC =米，得0.5OP =米． ................ 5分 若将两端同时都再伸长相同的长度，假设为a 米(0)a >． 如图（2）所示，BD a =米，AE a =米 . (6)BO OA BO a OA a =∴+=+，，即DO OE =．12DO DE ∴=，同理可得DOP DEF △∽△． DO OPDE EF ∴=，由0.5OP =米，得1EF =米． ······················ 7分 综上所述，跷跷板两边同时都再伸长相同的一段长度， 跷跷板能翘到的最高高度始终为支架OP 高度的两倍， 所以不可能翘得更高．（2）方案一：如图（3）所示，保持BO 长度不变．将 OA 延长一半至E ，即只将小瘦一边伸长一半． · 8分使12AE OA =，则25BO BE =． ········· 9分 由BOP BEF △∽△，得.BO OPBE EF= ······11分 1.25EF ∴=米． ··············12分 方案二：如图（4）所示，只将支架升高0.125米．······················ 8分12B O B O P B AC B A ''''''''=''，△∽△， 又0.50.1250.625O P ''=+=米． ······· 9分B O O P B A A C''''∴=''''． ··························· 11分1.25A C ''∴=米．··························· 12分 （注：其它方案正确，可参照上述方案评分！）24．（本小题满分12分） 方法1：①实心小球在碰到菱形挡块时向左或向右下落是等可能性的∴经过一个菱形Ｃ（１）Ｃ （3）F'（4） CP ' B 'Ｃ挡块后向左或向右下落的概率各是原概率的一半．············· 1分画树状图可知，落到A点位置的概率为111442+=．············ 4分②同理可画树状图得，落到B点位置的概率为113488+=．········· 8分③同理可画树状图得，落到C点位置的概率为13116164+=．········12分（注：①中画图1分，算出概率2分．②、③中画图2分，算出概率2分．）方法2：（1）实心小球碰到每个菱形挡块时向左或向右是等可能性的，因此小球下落到A的可能性会有以下的途径｛左右，右左｝两种情况，·········· 1分而下落到第二层，共｛左左，左右，右左，右右｝四种情况········· 2分由概率定义得21()42P A==······················· 4分（2）同理，到达第三层B位置会有以下途径｛左右右，右左右，右右左｝三种情况··································· 5分而下落到第三层共有｛左左左，左左右，左右左，左右右，右左左，右左右，右右左，右右右｝八种情况··························· 6分由概率定义得3()8P B=························· 8分（3）同理，到达第四层C位置会有｛左左左右，左左右左，左右左左，右左左左｝四种情况································ 9分而下落到第四层共有｛左左左左，左左左右，左左右左，左右左左，右左左左，左右左右，左右右左，左左右右，右左左右，右左右左，右右左左，右右右左，右右左右，右左右右，左右右右，右右右右｝共16情况·················10分由概率定义得41()164P C==······················12分方法3：本题也可用贾宪三角方法，先算出小球下落路径条数，如下图．由题意知：小球经过每条路径的可能性相同．A B C由概率定义易得221()12142P A ===++，（其中画图2分，算出概率2分） ·· 4分 33()13318P B ==+++，（其中画图2分，算出概率2分） ········· 8分 441()14641164P C ===++++．（其中画图2分，算出概率2分） ····· 12分（注：其它方案正确，可参照上述方案评分！）A B C。