八年级数学线段的和差问题专题
中考复习线段和差的最大值与最小值(拔高)

中考二轮复习之线段和(差)的最值问题一、两条线段和的最小值。
填空题:1.如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是.2.如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则P A+PC的最小值是.3.如图,在锐角△ABC中,AB=42,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是.4.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________.5.已知A(-2,3),B(3,1),P点在x轴上,若P A+PB长度最小,则最小值为.若P A—PB长度最大,则最大值为.6.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为.7、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为8、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD 和AE上的动点,则DQ+PQ的最小值为.综合题:1.如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.第1题第2题第3题第4题2.如图,已知平面直角坐标系,A ,B 两点的坐标分别为A (2,-3),B (4,-1)设M ,N 分别为x 轴和y 轴上的动点,请问:是否存在这样的点M (m ,0),N (0,n ),使四边形ABMN 的周长最短?若存在,请求出m =______,n = ______(不必写解答过程);若不存在,请说明理由.中考赏析:1.著名的恩施大峡谷(A )和世界级自然保护区星斗山(B )位于笔直的沪渝高速公路X 同侧,AB =50km 、B 到直线X 的距离分别为10km 和40km ,要在沪渝高速公路旁修建一服务区P ,向A 、B 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(AP 与直线X 垂直,垂足为P ),P 到A 、B 的距离之和S 1=P A +PB ,图(2)是方案二的示意图(点A 关于直线X 的对称点是A',连接BA'交直线X 于点P ),P 到A 、B 的距离之和S 2=P A +PB . (1)求S 1、S 2,并比较它们的大小; (2)请你说明S 2=P A +PB 的值为最小;(3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B 到直线Y 的距离为30km ,请你在X 旁和Y 旁各修建一服务区P 、Q ,使P 、A 、B 、Q 组成的四边形的周长最小.并求出这个最小值.2.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.3、在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC 绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F.(1)求经过A、B、C三点的抛物线的解析式;(2)当BE经过(1)中抛物线的顶点时,求CF的长;(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ 的周长最小,求出P、Q两点的坐标.4.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.5、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题 (运用三角形两边之差小于第三边)1.直线2x-y-4=0上有一点P ,它与两定点A (4,-1)、B (3,4)的距离之差最大,则P 点的坐标是 .2.已知A 、B 两个村庄的坐标分别为(2,2),(7,4),一辆汽车(看成点P )在x 轴上行驶.试确定下列情况下汽车(点P )的位置:(1)求直线AB 的解析式,且确定汽车行驶到什么点时到A 、B 两村距离之差最大? (2)汽车行驶到什么点时,到A 、B 两村距离相等?3. 如图,抛物线y =-14x 2-x +2的顶点为A ,与y 轴交于点B .(1)求点A 、点B 的坐标;(2)若点P 是x 轴上任意一点,求证:P A -PB ≤AB ; (3)当P A -PB 最大时,求点P 的坐标.4. 如图,已知直线y =21x +1与y 轴交于点A ,与x 轴交于点D ,抛物线y =21x 2+bx +c 与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B (1)求该抛物线的解析式;(3)在抛物线的对称轴上找一点M ,使|AM -MC |大,求出点M 的坐标.5. 如图,直线y =-3x +2与x 轴交于点C ,与y 轴交于点B ,点A 为y 轴正半轴上的一点,⊙A 经过点B 和点O ,直线BC 交⊙A 于点D . (1)求点D 的坐标;(2)过O ,C ,D 三点作抛物线,在抛物线的对称轴上是否存在一点P ,使线段PO 与PD 之差的值最大?若存在,请求出这个最大值和点P 的坐标.若不存在,请说明理由.好题赏析:原型:已知:P 是边长为1的正方形ABCD 内的一点,求P A +PB +PC 的最小值.例题:如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM . (1)求证:△AMB ≌△ENB ;(2)①当M 点在何处时,AM +CM 的值最小;②当M 点在何处时,AM +BM +CM 的值最小,并说明理由; (3)当AM +BM +CM 的最小值为3+1时,求正方形的边长.变式:如图四边形ABCD 是菱形,且∠ABC =60,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM ,则下列五个结论中正确的是( )①若菱形ABCD 的边长为1,则AM +CM 的最小值1; ②△AMB ≌△ENB ;③S 四边形AMBE =S 四边形ADCM ;④连接AN ,则AN ⊥BE ;⑤当AM +BM +CM 的最小值为23时,菱形ABCD 的边长为2. A .①②③ B .②④⑤ C .①②⑤三、其它非基本图形类线段和差最值问题1、求线段的最大值与最小值需要将该条线段转化到一个三角形中,在该三角形中,其他两边是已知的,则所求线段的最大值为其他两线段之和,最小值为其他两线段之差。
八年级数学专题 全等三角形之线段的和差

八年级数学培优第2课时全等三角形线段的和差问题一、截长补短例1.已知四边形ABCD 中,AB ⊥AD,BC ⊥CD,AB=BC, 0120,60ABC MBN ∠=∠=,MBN ∠绕B 点旋转,它的两边分别交AD 、CD(或它们的延长线)与E 、F 。
(1)如图1,求证:AE CF EF +=。
(2)当MBN ∠绕B 点旋转至如图2所示的位置,求证:AE —CF=EF 。
例2.在正方形ABCD 中,045MAN ∠=,MAN ∠绕点A 顺时针旋转,它的两边分别交CB 、DC (或它们的延长线)于M 、N 。
(1)如图1,求证:BM+DN=MN.(2)当MAN ∠绕点A 顺时针旋转至如图2所示的位置时,求证:MN+BM=DN.NMF E DCBAN M F E D C B A N MD CBA M DC BA巩固练习:1.已知如图1,在△ABC 中,2ABC ACB ∠=∠,AD 为BAC ∠的平分线。
(1)求证:AC=AB+BD ;(2)如图2,若AD 为BAC ∠的外角的平分线,其它条件不变,探索AC 、AB 、BD 三者之间的关系,并证明你的结论。
2.已知:如图,在△ABC 中,2ABC ACB ∠=∠,且AD ⊥BC 于D , (1)求证:CD=AB+BD 。
(2)若2ABC ACB ∠=∠>90º,其它条件不变,探索(1)中线段CD 、AB 、BD 三者之间的关系,画图并证明你的结论。
D C BAD C B A CB AD B C A3.已知:AD ⊥CD ,BC ⊥CD, 12,34∠=∠∠=∠,直线DC 过点E 交AD 于D ,交BC 于C 。
求证:AD+BC=AB.4.如图:在在△ABC 中,AB=AC, ∠A=90°,BD 平分∠ABC 。
求证:AB+AD=BC.5. 如图:在△ABC 中,AB=AC, ∠A=108°,BD 平分∠ABC. 求证:AB+CD=BC.6.已知:如图,在△ABC 中,O 是,ABC ACB ∠∠的角平分线的交点,BD+CE=BC. 求A ∠的度数。
《线段的和与差》PPT课件

AE B
C
F
D
解:设AB=3x,BC=2x,CD=5x,
因为E、F分别是AB、CD的中点,
所以 BE 1 AB 3 x,
2
2
CF 1 CD 5 x,
2
2
所以EF=BE+BC+CF=
3 2
x
2x
5 2
x
6 x.
因为EF=24,所以6x=24,解得x=4.
所以AB=3x=12,BC=2x=8,CD=5x=20.
∴ MN=CM+CN=4+2=6(cm).
(2)猜测MN
=
1 2
a
cm.
∵ M,N分别是AC,BC的中点,∴ CM=
1AC,CN= 1BC,
2
2
∴
MN=CM+CN=
12(AC+BC)=
1 2
a
cm.
随堂训练
1. A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么
A,C两点的距离是(C)
B
几何语言:∵ M 是线段 AB 的中点,
∴ AM = MB = 1 AB , ( 或 AB = 2 AM = 2 MB ).
2
反之也成立:∵
AM
=
MB
=
1 2
AB(
或
AB
=
2
AM
=
2
AB
),
∴ M 是线段 AB 的中点.
点 M , N 是线段 AB 的三等分点: A
M
N
B
1
AM = MN = NB = _3__ AB (或 AB = _3__AM = __3_ MN = __3_NB)
初中几何中线段和差的最大值与最小值练习题(最全)

初中几何中线段和差的最大值与最小值练习题(最全)初中几何中线段和(差)的最值问题一、两条线段和的最小值基本图形解析:一)已知两个定点:1、在一条直线m上,求一点P,使PA+PB最小。
1)点A、B在直线m两侧:在直线m上找到点P使得PA=PB,则PA+PB最小。
2)点A、B在直线同侧:在直线m上找到点A',使得A'是关于直线m的对称点,再找到点P使得PA'+PB最小,则PA+PB最小。
2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。
1)两个点都在直线外侧:在直线m上找到点A',使得A'是关于直线m的对称点,在直线n上找到点B',使得B'是关于直线n的对称点,再找到点P和Q,使得PA'+PQ+QB'最小,则PA+PQ+QB最小。
2)一个点在内侧,一个点在外侧:在直线m上找到点P,使其与A点连线垂直直线m,再在直线n上找到点Q,使其与B点连线垂直直线n,使PA+PQ+QB最小。
3)两个点都在内侧:在直线m上找到点A',使得A'是关于直线m的对称点,在直线n上找到点B',使得B'是关于直线n的对称点,再找到点P和Q,使得PA'+PQ+QB'最小,则PA+PQ+QB最小。
4)、台球两次碰壁模型变式一:已知点A、B位于直线m,n的内侧,在直线n、m分别上求点D、E点,使得围成的四边形ADEB周长最短。
在直线m上找到点A',使得A'是关于直线m的对称点,在直线n上找到点B',使得B'是关于直线n的对称点,连接A'和B',交直线m和n于D和E,使ADEB为矩形,则ADEB周长最短。
变式二:已知点A位于直线m,n的内侧,在直线m、n分别上求点P、Q点PA+PQ+QA周长最短。
在直线m上找到点A',使得A'是关于直线m的对称点,连接AA',在直线n上找到点Q,使得A'Q垂直直线n,连接AQ,使得PA+PQ+QA最小。
中考数学之 线段和(差)的最值问题
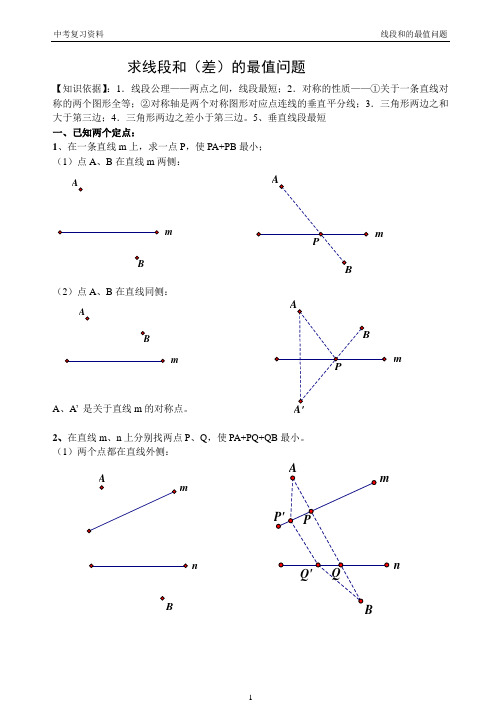
求线段和(差)的最值问题【知识依据】:1.线段公理——两点之间,线段最短;2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三角形两边之和大于第三边;4.三角形两边之差小于第三边。
5、垂直线段最短 一、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:mm ABm ABm n mn(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.nm Annnm二、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:m nm nm nmmmmm三、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左移动PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:四、求两线段差的最大值问题(运用三角形两边之差小于第三边) 1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:(2)点A 、B 在直线m 异侧:过B 作关于直线m 的对称点B ’,连接AB ’交点直线m 于P,此时PB=PB ’,PA-PB 最大值为AB ’Bmmmmm Q。
初中数学线段和差最值问题(史上最全版)

初中数学线段和差最值问题(史上最全版)⼀、知识依据1.线段公理:两点之间,线段最短;2.对称的性质:①关于⼀条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三⾓形的三边关系:①三⾓形两边之和⼤于第三边;②三⾓形两边之差⼩于第三边。
4.垂直线段最短。
⼆、从“将军饮马”说起话说在古罗马时代,在亚历⼭⼤城有⼀位精通数学和物理的学者,名叫海伦。
⼀天,⼀位罗马将军专程去拜访他,向他请教⼀个百思不得其解的问题:将军每天从军营A出发,先到河边饮马,然后再去河岸同侧B地开会,应该怎样⾛才能使路程最近?从此,这个被称为“将军饮马”的问题⼴泛流传。
这个问题的解决并不难,据说海伦略作思考就解决了它。
为了解决“将军饮马”问题,我们先看下⾯的问题。
(⼀)点A、B在直线m的异侧,在直线m上,求⼀点P,使PA+PB最⼩由两点之间线段最短知,由A到B⾛直线距离最短,所以连接AB与直线m交于点P,此时PA+PB最⼩。
我们选取除P之外的任意⼀点P’,由三⾓形的三边关系可以证明。
综上,我们可知点A、B在直线m异侧时,连接AB与直线m交于点P,即为所求。
搞清楚上⾯这个问题后,我们再来研究“将军饮马”问题就简单了。
(⼆)点A、B在直线m的同侧,在直线m上,求⼀点P,使PA+PB最⼩作图步骤:①作点A关于直线m的对称点A,②连接BA,,与直线L相交于点P③此时PA+PB最⼩。
看到这个问题后,我们会怎么思考呢?结合上⾯的问题及解答思路,我们会想到将直线m同侧的两个点转化到直线m异侧,那么问题就迎刃⽽解了。
所以,我们作A关于直线m的对称点A’(做B的对称点也⼀样),则将同侧的两点A、B转化到了异侧两点A’、B。
此时,连接A’B与直线m交于点P,即为所求。
综上,我们可知“将军饮马”问题转化为对称点,则问题就轻松解决了。
三、“将军饮马”的拓展延伸总结“将军饮马”问题,我们发现是两个顶点及定直线上的⼀个动点问题,那么接下来我们将刚才的问题进⾏升级。
线段的和差问题

线 段 的 和 差 问 题薛志军(湖南长沙中南大学附属实验中学 410083)线段的和差问题是几何证明中常见的题型,它与证明线段相等紧密相联.一般来说,通过作辅助线可转化为线段相等问题.解决线段的和差问题,需要综合应用三角形全等,直角三角形斜边上的中线等于斜边的一半,含有30º角的直角三角形的性质,线段中垂线的性质,角平分线性质,三角形,梯形中位线性质等知识.因此,通过此问题的讨论,一方面,帮助学生对与之相关的知识、定理进行梳理,系统化,进而建构有效的知识系统;另一方面,使他们在学习具体的几何知识的同时,掌握“化归”的数学思想方法.一、 利用图形中已有的线段和差关系进行证明例1 已知:如图1,在△ABC 中,∠ABC 的平分线与∠ACB 相邻外角∠ACG 的平分线相交于D ,DE∥BC 交AB 于E ,交AC 于F .求证:EF=BE-CF . 分析 要证EF=BE-CF ,而图中有EF=ED-FD ,若能证出BE=ED ,CF=FD ,则此题可证出.说明 本题利用了等腰三角形的判定来证明线段的差的问题. (图1) 例2 已知:如图2,△ABC 中,∠BAC=90o ,AB=AC ,AE 是过点A 的一条直线且B ,C 在AE 的异侧,BD⊥AE 于D ,CE⊥AE 于E . 求证:BD=DE+CE .E 分析 本题主要利用△BAD≌△ACE,得BD=AE ,AD=CE ,从而得BD=AE=DE+AD=DE+CE .说明 本题主要利用三角形全等的方法直接证明线段的和的问题.二、截长法(在第三条线段上截取一段等于第一条线段,然后证明余下的线段等于第二条线段)例3 已知:如图3,四边形ABCD 中,AC 平分∠BAD,CE⊥AB 于E ,且∠B+∠D=180°,求证:AE=AD+BE .分析 要证AE=AD+BE ,则可转化为证AE-BE=AD ,则需找到一条线段使它等于AE-BE ,再证其与AD 相等,在EA 上截取EF=BE ,连结CF ,问题转化为证AF=AD ,即要证出△AFC≌△ADC .证明 在EA 上截取EF=BE ,连结CF . ∵CE⊥AB 于E, ∴CF=CB . ∴∠1=∠B .∵∠1+∠2=180°,∠B+∠D=180°, (图3) ∴∠2=∠D .∵∠FAC =∠D AC ,AC=AC,∴△AFC≌△ADC .∴AF=AD.∵AE=AF+EF, ∴AE=AD+BE.三、补短法(延长一条线段,作出两条线段的和,然后证明这条线段等于第三条线段)例4 已知: 如图4,在△ABC 中,∠BAC =2∠B,CD 是∠ACB 的平分线.求征: BC=AC+AD .证明 延长CA 至E ,使AE=AD ,连结DE .∴∠E=∠EDA . (图4) ∴∠BAC=∠E+∠EDA=2∠E . ∵∠BAC=2∠B , ∴∠B =∠E .在△CDE 和△CDB 中 . ∠1=∠2,CD=CD ,∠E=∠B , ∴△CDE≌△CDB .E'∴CE=CB ,∴BC=CE=EA+AC=AD+AC .四、旋转法例5 已知:如图5,已知F 为正方形ABCD 的边BC 上一点,AE 平分∠DAF.求证:DE=AF-BF.分析 将△ADE 绕A 点顺时针旋转90º,则AE ⊥AE ´ 可证E ´,B ,F 共线,∠E ´= ∠E ´ (图5)则有AF= E ´F.∴DE=BE ´=E ´F-BF=AF-BF. 五、等积变换法例6 已知:如图6,已知在△ABC 中,AB=AC ,BD 为AC 边上的高,如果在BC 上取一点F ,过F 作FG ⊥AB 于G ,作FH ⊥AC 于H.求证:FG+FH=BD. 分析 连接AF.S SSAFCABFABC∆∆∆+=AC FH GF AC AC FH GF AB BD AC ⋅+⋅=⋅+⋅=⋅∴2121212121(图6)得BD=GF+FH . 例7 已知:如图7,在△ABC 中,∠A=90º,D 是AC 上一点,BD=CD ,P 是BC 上任一点,PE ⊥BD 于E ,PF ⊥AC 于F.求证:分析 连接PD .由S S SPDB PCD BCD∆∆∆+= , (图7)得得AB=PE+PF.六、归一法(将处于不同位置的线段转化到同一条线段中来) 例8 已知:如图8,已知平行四边形ABCD 的对角线交于O ,点P 是BD 上任一点(异于B ,O ,D 三点),过P 点作平行于AC 的直线交直线AD 于E ,交BA 的延长线于F.求证:AC=PE+PF.分析 ∵OD PD AO PE = ,OBPBAO PF =, 且OB=OD=BD 21, (图8) ∴OBPBOD PD AO PF AO PE +=+. 即22121==+=+BD BDBD PB PD AOPF PE . )(212121212121PE PF CD PE CD PF CD PE BD PF CD BA DC +=⋅+⋅=⋅+⋅=⋅∴1=+ACPFPE ,即AC=PE+PF.七、特殊定理法证明线段的和差时,可适当添加辅助线,以便于运用某些特殊的定理.这些 特殊的定理包括:三角形,梯形的中位线定理,直角三角形斜边上的中线等于斜边的一半等.例9 已知:如图9,AB 是O Θ的直径,直线MN 与 O Θ相切于C ,AE ⊥MN 于E ,BF ⊥MN 于F.求证:分析 连接OC ,则有OC ⊥MN.∵AE ⊥MN ,BF ⊥MN,∴AE ∥OC ∥BF . (图9) ∵OA=OB, ∴EC=CF.∴AE+BF=2OC=AB.。
线段和差问题与截长补短法(含答案)

线段和差问题的截长补短方案(一题多解)系列文章之一线段和差问题与截长补短法(含答案)四川崇州 平生曜曜数学好玩,因为定题型、树模型,招式路数皆可寻。
几何中的线段和差问题,截长补短法在实施过程中都有四种截长方案,八种补短方案,可谓十二重关。
本文即将推出一道线段和差问题,希望同学们努力破之。
作者曾闲着没事碰巧把这十二种方案都尝试成功了,所以对于同学而言这十二关障的破解就不再是渺茫的探求,而是一个已经有了答案的考题。
同学们尽管去尝试,要深信这十二种方案皆能破题,但也仅限于本文所推题目而已,至于其它的线段和差问题十二关障能否一一告破就不好说了。
比如本人正在攻克一道线段和差问题,被弄得昏天地转,仍未冲破牛角,现在只得将之当作休闲佐料耳。
作者打心底告诉各位同学,把一道“典型题”做透了,会领悟n 多,积淀一抹多。
但说得再多也是空谈,当你正真去把它做实,你才能感受到其中的丰富与藕联,而后你再通过提炼啊,总结啊,什么,什么的,定能铸就非凡的解题技艺。
数学可玩,因为按需补、应需造,综合分析可当道。
好了,大家来凑凑热闹,去感受那应需而生的几何构造是如何美妙? 如图,等边⊿ABC 中M 、N 分别为线段AB 、BC 上的两点,且BM=CN ,AN 、CM 相交于点E ,将⊿ABC 绕点C 旋转,使CB 与CA 重合得到⊿ACD ,连结DE.(1)、求证:⊿BCM ≌⊿CAN ; (2)、求∠AED 的度数; (3)、求证:AE + CE = DE ;第一篇章:探讨第(1)、(2)问的解答第(1)问的解答(1)、∵⊿ABC 是等边三角形 , ∴ BC = AC ,∠B =∠ACN又∵BM = CN ,∴⊿BCM ≌⊿CAN .第(2)问的解答〈分析一〉:通过量角器测量,可大胆猜想ο∠AED,怎样求证?60= Array由(1)题,容易证获CAN=∠,BCM∠再由外角性质易证ο∠AEM,从而∠=60得ο∠AEC,那么关键环节来了!120=在四边形AECD中,欲证边AD所对“帆尖角”ο60∠ACD,所以=60=∠AED,考虑到边AD所对另一“帆尖角”ο只需去求证“A、E、C、D”四点共圆即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
练习题
1.如图 已知四边形 如图,已知四边形 如图 已知四边形ABCD中,AC平分∠BAD, 中 平分 且∠D+ ∠ B=1800 求证: 求证:则AE=AD+BE
A D
D
F E B
C
练习题
1.如图 已知四边形 如图,已知四边形 如图 已知四边形ABCD中,AC平分∠BAD, 中 平分 且∠D+ ∠ B=1800 求证: 求证:则AE=AD+BE
F
C E
要证明两条线段的和与一条线段 要证明两条线段的和与一条线段 时常用的两种方法: 相等时常用的两种方法 相等时常用的两种方法: 长线段上截取与 、可在长线段上截取 D1、可在长线段上截取与两条线段 中一条相等的一段, 中一条相等的一段,然后证明剩 余的线段与另一条线段相等。 余的线段与另一条线段相等。 (割) B 2、把一个三角形移到另一位置, 、把一个三角形移到另一位置, 移到另一位置 两线段补成一条线段, 使两线段补成一条线段,再证明 它与长线段相等。(补) 它与长线段相等。(补 长线段相等。(
M DBC来自拓展题3.如图 已知 ∥BD,EA、EB分别平分∠CAB和∠DBA, 如图,已知 如图 已知AC , 、 分别平分 和 , CD过点 ,则AB与AC+BD相等吗?请说明理由。 过点E, 相等吗? 过点 与 相等吗 请说明理由。
C E D
A
F
B
拓展题
3.如图 已知 ∥BD,EA、EB分别平分∠CAB和∠DBA, 如图,已知 如图 已知AC , 、 分别平分 和 , CD过点 ,则AB与AC+BD相等吗?请说明理由。 过点E, 相等吗? 过点 与 相等吗 请说明理由。
1.如图,AC=AB, ∠ACB=900,AD平分∠CAB, 如图, 平分∠ 如图 平分 求证: 求证:AC+CD=AB
A D F
E B
C
要证明两条线段的和与一条线段相等时常用的两种方法: 要证明两条线段的和与一条线段相等时常用的两种方法: 两条线段的和与一条线段相等时常用的两种方法 1、可在长线段上截取与两条线段中一条相等的一段,然 、可在长线段上截取与两条线段中一条相等的一段, 长线段上截取 后证明剩余的线段与另一条线段相等。( 。(割 后证明剩余的线段与另一条线段相等。(割) 2、把一个三角形移到另一位置,使两线段补成一条线 、把一个三角形移到另一位置, 移到另一位置 再证明它与长线段相等。(补 长线段相等。( 段,再证明它与长线段相等。(补) 注意辅助线的作法及语言的表达, 3、注意辅助线的作法及语言的表达,辅助线只能 实现一种功能。 实现一种功能。
A
3.如图 已知 ∥BD,EA、EB分别平分∠CAB和∠DBA, 如图,已知 如图 已知AC , 、 分别平分 和 , CD过点 ,则AB与AC+BD相等吗?请说明理由。 过点E, 相等吗? 过点 与 相等吗 F请说明理由。
C E D C E D A
F
B
B 要证明两条线段的和与一条线段相等时常用的两种方法: 两条线段的和与一条线段相等时常用的两种方法 要证明两条线段的和与一条线段相等时常用的两种方法: 1、可在长线段上截取与两条线段中一条相等的一段,然后证明 、可在长线段上截取与两条线段中一条相等的一段, 长线段上截取 剩余的线段与另一条线段相等。( 。(割 剩余的线段与另一条线段相等。(割) 2、把一个三角形移到另一位置,使两线段补成一条线段,再证 、把一个三角形移到另一位置, 两线段补成一条线段, 移到另一位置 明它与长线段相等。(补 长线段相等。( 明它与长线段相等。(补)
类型题回放: 类型题回放: 1.已知 在等腰Rt ABC中 已知: Rt△ 1.已知:在等腰Rt△ABC中,AC = BC ∠C=90° AD平分 平分∠ BAC,DE⊥AB于点 于点E ∠C=90°,AD平分∠ BAC,DE⊥AB于点E。 求证:BD+ 求证:BD+DE =AC A
E
C
D
B
类型题回放: 类型题回放: 2.已知 已知: ABC中 AC,直线MN经过点A, MN经过点 2.已知:△ABC中,AB = AC,直线MN经过点A, ∠BAC=90° BD⊥MN于点 于点D, CE⊥MN于点 于点E ∠BAC=90°,BD⊥MN于点D, CE⊥MN于点E 。 求证: 求证:DE =BD+CE N E A
