附录A 平面图形的几何性质 - 合肥工业大学精品课程
材料力学 平面图形的几何性质 安徽理工大学精品课程要点

本章重点1、静矩与形心2、惯性矩、极惯性矩和惯性积3、平行移轴公式、转轴公式关键概念静矩、惯性矩、极惯性矩、惯性积、主惯性轴、形心主惯性轴目录§I-1 静矩和形心§I-2极惯性矩·惯性矩·惯性积§I-3 平行移轴公式§I-4 惯性矩和惯性积的转轴公式.截面的§I-1 静矩和形心一、基本概念1. 静矩(或一次矩)x⋅dAy⋅dA——微面积对y轴的静矩——微面积对x轴的静矩Sy=⎰AxdA——整个平面图形对y轴的静矩Sx=⎰AydA——整个平面图形对x轴的静矩常用单位:m3或mm3。
数值:可为正、负或0 。
2.形心坐标公式x=xdA =SyAAy=ydAASx=A3.静矩与形心坐标的关系Sy=A xSx=A y推论:截面对形心轴的静矩恒为0,反之,亦然。
二、讨论:1.组合截面的静矩根据静矩的定义:整个平面图形对某轴的静矩应等于它的各组成部分对同一轴的静矩的代数和,即:Sy=∑Ai xii=1nSx=∑Aiyii=1n2.组合截面的形心坐标公式组合截面静矩Sy=∑Ai xii=1nSx=∑Aiyii=1nn组合截面面积A=∑Aii=1组合截面的形心坐标公式为:例I—1:计算由抛物线、y轴和z轴所围成的平面图形对y轴和z轴的静矩,并确定图形的形心坐标。
2z=h⎛⎝1-y⎫b2⎪⎭22y⎫4bh22⎪dyb⎭=15Sz=⎰ydA=A⎰yh22 ⎫bh0⎝1-b2⎪⎭dy=4b2A=⎰dA=A⎰h⎛ 1-y20⎝b形心坐标为:⎧2⎪bh⎪ySz⎪C=A=2bh=⎪⎨3⎪4bh2⎪⎪zC=Sy==2h⎪A2bh5⎩3 例I—2:确定图示图形形心C的位置。
解:ySC=zA=10⨯120⨯5+70⨯10⨯451200+700=19.7mmzC==目录(即截面对一点的极惯性矩,等于截面对以该点为原点的任意两正交坐标轴的惯性矩之和。
)3.惯性积Ixy=⎰AxydA(其值可为正、为负或为零)结论:截面对于包含对称轴在内的一对正交轴的惯性积为0。
(建筑力学二版)第4章平面图形的几何性质

惯性矩
定义
惯性矩是描述平面图形抵抗弯 曲变形能力的量,也称为抗弯
矩。
计算方法
通过积分或求和的方法计算平 面图形的质量分布,然后根据 质量分布和几何形状确定惯性 矩。
特性
惯性矩与平面图形的形状和质 量分布有关,不同形状的图形 可能有不同的惯性矩。
应用
在建筑结构中,惯性矩是结构 设计的重要参数,用于计算结 构的弯曲变形、应力分布和稳
定性等。
重心与惯性矩的应用
结构设计
在建筑结构设计中,需要 计算结构的重心位置和惯 性矩,以评估结构的稳定 性和承载能力。
施工安装
在施工安装过程中,需要 确定结构的重心位置,以 防止结构发生倾覆或侧翻。
抗震设计
在抗震设计中,需要计算 结构的惯性矩,以评估结 构在不同地震作用下的响 应和稳定性。
04
三角形
01
02
03
04
三角形是最简单的多边 形,具有稳定性、灵活 性和实用性。
三角形的三个内角之和 等于180度,而三条边 的长度之和等于其周长。
三角形的面积可以通过 底和高来计算,公式为: 面积=(底×高)/2。
三角形的重心位于其三 条中线的交点,同时也 是三条高线的交点。
感谢您的观看
THANKS
分类
根据形状和结构特点,平面图形可分为简单图形和组合图形。简单图形包括直 线、圆、圆弧、椭圆等;组合图形则是由两个或多个简单图形组合而成。
平面图形的几何特性
01
02
03
封闭性
平面图形是封闭的,即其 边界是完整的,没有缺口 或断裂。
大小和形状
平面图形的大小和形状是 固定的,不会因为观察角 度或位置的变化而改变。
刚度分类
材料力学(理工科课件)附录A_平面图形的几何性质()[25P][9.63MB]
![材料力学(理工科课件)附录A_平面图形的几何性质()[25P][9.63MB]](https://img.taocdn.com/s3/m/d59f3f242af90242a895e59e.png)
z
y
所以
A.3 平行移轴公式
(Parallel-axis theorem)
一、平行移轴公式(Parallel-Axis theorem for moment of inertia)
y,z ― 任意一对坐标轴 C ―截面形心 (a , b ) ―形心C在 yOz坐标系下的坐标
a O C(a,b) y
yC
积,求截面对与形心轴平行的 y,z轴惯性矩和
惯性积,则平行移轴公式
b
二、组合截面的惯性矩 、惯性积( Moment of inertia &
product of inertia for composite areas )
组合截面的惯性矩,惯性积
 ̄第
i个简单截面对 y, z 轴的惯性矩,惯性积.
z1
z
y1
O
y
显然
二、截面的主惯性轴和主惯性矩(principal axes &
principal moment of inertia)
主惯性轴(Principal axes ):总可以找到一个特定的角0 , 使截面 对新坐标轴y0 , z0的惯性积等于0 , 则称 y0 , z0 为主惯性轴. 主惯性矩(Principal moment of inertia) :截面对主惯性轴y0 , z0 的惯性矩. 形心主惯性轴(Centroidal principal axes) :当一对主惯性轴的交 点与截面的形心重合时,则称为形心主惯性轴. 形心主惯性矩( Centroidal principal moment of inertia) :截面对 形心主惯性轴的惯性矩.
(1)主惯性轴的位置 设 为主惯性轴与原坐标轴之间的夹角
合工大机械原理课件

第一章平面机构的结构分析一. 基本概念1. 机械: 机器与机构的总称。
机器: 具有三个共性。
机构: 只具有机器的前两个共性。
2. 构件与零件零件——制造单元构件——运动单元构件可以由一个零件或多个零件刚接而成3. 运动副: 两构件通过表面直接接触而形成的可动联接。
运动副元素: 两构件表面直接接触的点、线、面。
4. 运动副的分类:平面运动副:两构件在同一平面内作相对运动平面低副—两构件以面接触构成的可动联接平面高副—两构件以点或线接触构成的可动联接平面低副:转动副—联接的两构件只能作相对转动移动副—联接的两构件只能作相对移动空间运动副:两构件在不同平面内作相对运动5. 运动链: 多个构件以运动副联接而成的系统分类:空间运动链、平面运动链闭式运动链、开式运动链6. 机构:有机架并有确定运动的运动链分类:平面机构、空间机构二. 基本知识和技能1. 机构运动简图的绘制与识别图在机构运动简图中:运动副—按国家标准所规定的代表符号画出构件—用线段、小方块等简单图形画出尺寸—按选定的比例画出2.平面机构的自由度的计算及机构运动确定性的判别F = 3n - 2P L- P Hn —活动构件数P L —低副数P H —高副数自由度计算时须注意:(1) K个构件在同一处构成的复合铰链中有( K - 1 )个转动副(2) 局部自由度应去除(通常每个滚子有一局部自由度)(3) 虚约束应去除。
(注意虚约束出现的场合)机构具有确定运动的条件F > 0 能动原动件数< F 机构运动不确定原动件数= F 机构运动确定原动件数> F 机构运动相互干涉F ≤0 不能动,为刚性构架3. 机构的结构分析(1)高副低代:用一个构件,两个低副代替一个高副须满足:代替前后机构的自由度不变代替前后机构的瞬时运动不变高副低代必须遵循一定的方法:曲线对曲线的高副低代点对曲线的高副低代曲线对直线的高副低代点对直线的高副低代2. 机构的结构分析(1)基本杆组及杆组的级别自由度为零的,不能再拆分的构件组Ⅱ级杆组:二杆三低副组Ⅲ级杆组:四杆六低副组含有一个带三低副的中心构件(2)机构的拆组及机构的级别从远离原动件的构件开始拆分杆组机构的级别由机构中杆组的最高级别所决定(3)机构的组成原理把杆组依次与机架和原动件相联得到机构第二章平面机构的运动分析一. 基本概念:(一)瞬心1. 瞬心的定义瞬心是两构件的瞬时等速重合点2. 机构中的瞬心数目机构中,每两个构件有一个瞬心。
第五章平面图形几何性质(讲稿)材料力学教案(顾志荣)
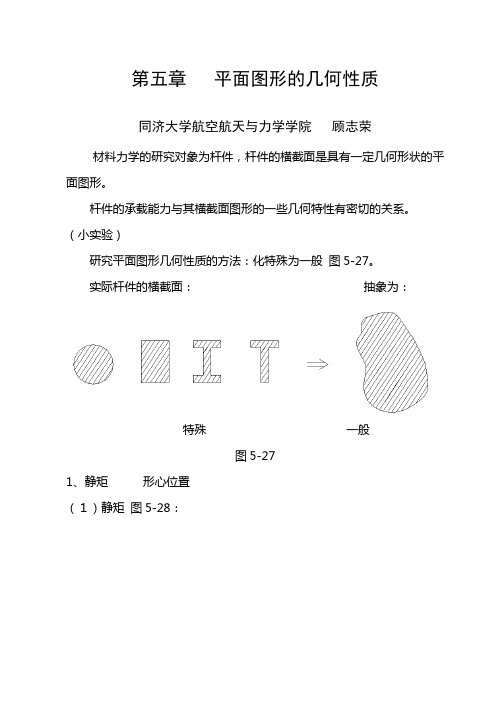
第五章平面图形的几何性质同济大学航空航天与力学学院顾志荣材料力学的研究对象为杆件,杆件的横截面是具有一定几何形状的平面图形。
杆件的承载能力与其横截面图形的一些几何特性有密切的关系。
(小实验)研究平面图形几何性质的方法:化特殊为一般图5-27。
实际杆件的横截面:抽象为:特殊一般图5-271、静矩形心位置(1)静矩图5-28:图5-28微面积dA 与Z 轴、Y 轴间距离的乘积ydA,zdA 分别称为微面积dA 对Z 轴、Y 轴的静矩。
整个截面对Z 轴、Y 轴的静矩可用下式来定义:(若把A 看作力)定义:截面A 对Z 轴:⎪⎭⎪⎬⎫==⎰⎰Ay A ZSZdA S ydA (4-1) 截面A 对Y 轴:计算:①对(4-1)式直接积分:②若已知截面的形心位置C ,则y Z S S ,可以写成:⎭⎬⎫==c Z c Y AY S AZ S (4-2)(2)形心的位置:⎪⎪⎭⎪⎪⎬⎫==A S Z A S Y y C Z C (4-3)性质:①截面对某一轴的静矩等于零,则该轴必通过形心。
②截面对通过形心的轴的静矩恒等于零,即: ;0=ZC S 0=YC S决定因素:静矩与截面尺寸、形状、轴的位置有关。
数值范围:可以为正、或负、或等于零。
单位:333,,m cm mm (3)组合截面的静矩:⎪⎪⎭⎪⎪⎬⎫==∑∑==n i i i y n i i i Z A S Y A z S 11(4-4) 即组合截面的整个图形对于某一轴的静矩,等于各组部分对于同一轴静矩代数和。
(4)组合截面的形心位置:⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫====∑∑∑∑====n i i ni i i y ni i ni i i z A Z A AS A Y A AS c c z y 1111(4-5) 例题5-7 求图5-29所示截面图形的形心。
图5-29解:把T 形看成为由矩形Ⅰ和Ⅱ组成 ∵y 轴是对称轴 ∴形心必在y 轴上① 求?'=Z S216002080mm A I =⨯= A Ⅱ=2240020120mm =⨯ mm y c 10=I (到Z ′轴) y c Ⅱ=60+20=80mm则:3120800802400101600'mm Y A ni ii z s =⨯+⨯==∑=②求c y=?c y=As z =∑∑==ni ini i i A Y A 11=201202080208000⨯+⨯=52mm 2、惯性矩(形心主惯性矩) 惯性半径 极惯性矩图5-30定义:(1)惯性矩⎪⎭⎪⎬⎫==⎰⎰A yA Z dA Z I dA y I 22(4-6) 定义为截面对z 轴,y 轴的惯性矩。
08 建筑力学 第八章 平面图形的几何性质 课件
dI x1 0 d
dI y1 d
0
同样可以得到式(8-10)或(8-11)的结论。这表 明:当α改变时, I x 、I y 的数值也发生变化,而当 α=α0时,二者分别为极大值和极小值。 定义 过一点存在这样一对坐标轴,图形对于其 惯性积等于零,这一对坐标轴便称为过这一点 的主轴。图形对主轴的惯性矩称为主轴惯性 矩,简称主惯性矩。显然,主惯性矩具有极大 或极小的特征。
i i
第二节 静矩
一、定义 任意平面几何图形如图A-1所示。在其上取面 积微元dA,该微元在Oxy坐标系中的坐标为x、 y。定义下列积分:
S x ydA
A
S y zdA
A
(8-4)
分别称为图形对于x轴和y轴的截面一次矩或静 矩,其单位为 。
如果将dA视为垂直于图形平面的力,则ydA 和zdA分别为dA对于z轴和y轴的力矩; 和 则分 别为dA对z轴和y轴之矩。图8-6图形的静矩与形 心图形几何形状的中心称为形心,若将面积视为 垂直于图形平面的力,则形心即为合力的作用 点。 设z、y为形心坐标,则根据合力之矩定理
二、一般物体重心的坐标公式 1、一般物体重心的坐标公式 如图8—1所示,为确定物体重心的位置, 将它分割成n个微小块,各微小块重力分别为 Gl 、 G2 、 ……Gn ,其作用点的坐标分别为 (X1、Y1,、z1)、(X2、Y2、z2)…(Xn,Yn、 Zn) ,各微小块所受重力的合力W即为整个物 体所受的重力 G =ΣGi ,其作用点的坐标为 C(xc,yc、zc)。对y轴应用合力矩定理,有:
第八章
平面图形的几何性质
在建筑力学以及建筑结构的计算中,经常 要用到与截面有关的一些几何量。例如轴向拉 压的横截面面积A、圆轴扭转时的抗扭截面系数 WP 和极惯性矩 IP 。等都与构件的强度和刚度有 关。以后在弯曲等其他问题的计算中,还将遇 到平面图形的另外一些如形心、静矩、惯性矩、 抗弯截面系数等几何量。这些与平面图形形状 及尺寸有关的几何量统称为平面图形的几何性 质。
合肥工业大学课程设计

合肥工业大学课程设计一、课程目标知识目标:1. 让学生掌握合肥工业大学五年级数学课程中关于复数的概念、运算及其应用,理解复数在解决实际问题中的作用。
2. 使学生掌握复平面内复数的几何表示,并能够运用复数解决几何问题。
3. 培养学生运用数学软件进行复数运算和分析的能力。
技能目标:1. 培养学生运用复数知识解决实际问题的能力,包括数学建模、计算和数据分析。
2. 提高学生在复数学习过程中的逻辑思维和批判性思维能力,能够独立完成复数相关的证明和推导。
3. 培养学生运用数学软件进行复数计算、作图等操作,提高数学实践能力。
情感态度价值观目标:1. 培养学生对数学学科的兴趣和热情,特别是对复数这一抽象概念的理解和欣赏。
2. 培养学生面对复杂数学问题时的耐心、细心和合作精神,树立正确的学习态度。
3. 通过复数知识的学习,引导学生认识到数学在自然科学、工程技术等领域的广泛应用,增强学生的社会责任感和使命感。
课程性质分析:本课程为合肥工业大学五年级数学专业课程,旨在帮助学生建立扎实的复数理论基础,培养实际应用能力。
学生特点分析:五年级学生已具备一定的数学基础,具有较强的逻辑思维和自主学习能力,但可能对复数这一抽象概念的理解存在困难。
教学要求:1. 教师应注重理论与实践相结合,引导学生从具体实例中认识复数的概念。
2. 教师应充分运用多媒体、数学软件等教学资源,提高学生的学习兴趣和实践能力。
3. 教师应关注学生的个体差异,因材施教,使每位学生都能在课程中取得实际进步。
二、教学内容本章节教学内容依据课程目标,结合合肥工业大学五年级数学课程教材,主要包括以下几部分:1. 复数的基本概念- 复数的定义与表示方法- 复数的分类(实数、虚数、纯虚数)- 复数的相等与共轭复数2. 复数的运算- 复数的加减乘除运算- 复数的乘方与开方- 复数的模与辐角主值3. 复数的几何意义- 复数在复平面上的几何表示- 复数的模与辐角的几何意义- 复数运算的几何解释4. 复数的应用- 复数在电路分析中的应用- 复数在信号处理中的应用- 复数在其他领域中的应用实例5. 数学软件在复数学习中的应用- 使用数学软件进行复数运算- 使用数学软件绘制复数图形- 利用数学软件解决复数相关问题教学内容安排和进度:第1-2周:复数的基本概念与分类第3-4周:复数的运算第5-6周:复数的几何意义第7-8周:复数的应用第9-10周:数学软件在复数学习中的应用教材章节:第1章 复数的基本概念与运算第2章 复数的几何意义第3章 复数的应用第4章 数学软件在复数学习中的应用教学内容确保科学性和系统性,注重理论与实践相结合,以帮助学生更好地理解和应用复数知识。
高一数学必修课件平面基本性质

汇报人:XX 2024-01-20
目录
• 平面及其基本性质 • 直线与直线的位置关系 • 平面与平面的位置关系 • 直线与平面的位置关系 • 空间几何体的基本性质
01
平面及其基本性质
平面的概念与表示
平面的概念
平面是无限延展的,没有厚度,可以看作是由无数个点组成 的集合。
判定
如果一个平面内的任意直线与另一个平面都相交 ,那么这两个平面相交。
垂直平面
定义
如果两个平面相交,且它们的交线与第三个平面垂直,则称这两 个平面与第三个平面垂直。
性质
垂直平面内的任意直线与第三个平面垂直;垂直平面间的距离为零 。
判定
如果一个平面内有一条直线与另一个平面垂直,那么这两个平面垂 直。
判定
两条直线被第三条直线所截,如果同位角相等,那么这两 条直线平行;如果内错角相等,那么这两条直线平行;如 果同旁内角互补,那么这两条直线平行。
异面直线
定义
不在同一平面内的两条直线叫做 异面直线。
性质
异面直线没有公共点;异面直线的 公垂线段是唯一的。
判定
过空间一点与两条异面直线都平行 的直线有且仅有一条;过空间一点 与两条异面直线都相交的直线有无 数条。
性质
直线与平面相交,则它们有且仅有一个公共点,称为交点。
判定方法
如果直线上的某一点在平面内,而另一点不在该平面内,则这条 直线与该平面相交。
直线与平面平行
定义
一条直线与一个平面没有公共点,则称这条直线与这个平面平行 。
性质
直线与平面平行,则它们之间没有交点,且保持一定的距离。
判定方法
如果直线上的任意两点连成的线段都与该平面平行,则这条直线与 该平面平行。
