【最新】华东师大版八年级数学上册:第12章整式的乘除 第16课时 导学案(无答案)
华东师大版八年级上册第12章整式的乘除复习导学案设计(无答案)
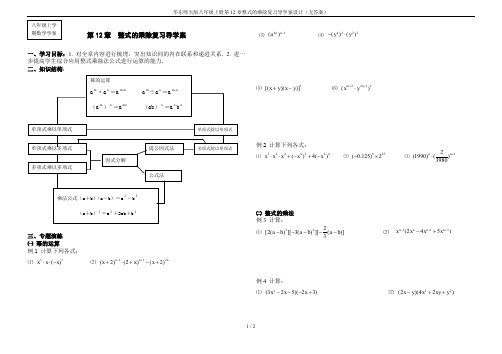
第12章 整式的乘除复习导学案一、学习目标:1. 对全章内容进行梳理,突出知识间的内在联系和递进关系. 2. 进一步提高学生综合应用整式乘除法公式进行运算的能力. 二、知识结构:三、专题演练 ㈠ 幂的运算例1 计算下列各式:⑴ 53()x x x ⋅⋅- ⑵ 112(2)(2)(2)n n n x x x -++⋅+-+⑶ 41()n n a - ⑷ 4223()()y y -⋅⑸ 5[()()]x y x y +- ⑹ 2212()m n x y +-⋅例2 计算下列各式:⑴ 3244224()4()x x x x x ⋅⋅+-+- ⑵ 825(0.125)2-⨯ ⑶ 12(1990)()3980nn +⋅㈡ 整式的乘法 例3 计算:⑴ 322[2()][3()][()]3a b a b a b ----- ⑵ 113(245)n n n n x x x x -++-+例4 计算:⑴ 2(325)(23)x x x ---+ ⑵ 22(2)(42)x y x xy y -++㈢ 乘法公式 例5 计算:⑴ (3)(3)a ab ab a ---+ ⑵ 98102⨯⑶ 24(12)(12)(14)(116)x x x x -+++ ⑷ ()()a b c a b c +--+例6 计算:⑴ 298 ⑵ 2(1)(1)(1)y y y --+-- ⑶ 2(23)x y z +-㈣ 整式的除法例7 先化简,再求值:42622322[5(4)(3)()](2)a a a a a a ---÷÷-,其中5a =-㈤ 因式分解 例8 分解因式:⑴ 324(1)2(1)q p p -+- ⑵ 221()()()m m m ab x y a b x y ab x y +-+---⑶2a ab ac bc -+- ⑷ 22412925x xy y -+-五、能力提升 1.已知212448x x ++=,求x 的值.2.已知4,6x y x y +=-=,求代数式22()(2)3xy y y y xy x xy +-+-的值.3.已知一个多项式除以多项式243a a +-,所得商式是21a +,余式为28a +,求这个多项式.4. 已知2(8)a pa ++与2(3)a a q -+的乘积中不含有3a 和2a 项,求p 、q 的值.。
八年级数学上册第12章整式的乘除复习教案华东师大版(2021-2022学年)

整式的乘除ﻬﻬ ﻬ 整式的乘除复习 1. 对全章内容进行梳理,突出知识间的内在联系和递进关系。
2. 进一步提高学生综合应用整式乘除法公式进行运算的能力. 难点目标 目标三导 学做思一:知识结构 学做思二: ㈠ 幂的运算 例1 计算下列各式: ⑴ ⑵ ⑶⑷ ⑸ ⑹ 例2 计算下列各式: ⑴ ⑵ ⑶㈡ 整式的乘法 例3 计算: ⑴ ⑵例4 计算: ⑴ ⑵ ㈢ 乘法公式 例5 计算: ⑴ ⑵ ⑶⑷ 例6 计算:⑵ ⑶㈣ 整式的除法 例7 先化简,再求值:,其中㈤ 因式分解例8 分解因式: ⑴ ⑵ ⑶ ⑷反思总结 1.知识建构 2。
能力提高3。
课堂体验 课后练习 1。
已知,求的值。
2。
已知,求代数式的值.3。
已知一个多项式除以多项式,所得商式是 ,余式为,求这个多项式. 4. 已知与的乘积中不含有和项,求、的值. 53()x x x ⋅⋅-112(2)(2)(2)n n n x x x -++⋅+-+41()n n a -4223()()y y -⋅5[()()]x yx y +-2212()m n x y +-⋅3244224()4()x x x x x ⋅⋅+-+-825(0.125)2-⨯12(1990)()3980n n +⋅322[2()][3()][()]3a b a b a b -----113(245)n n n n x x x x -++-+2(325)(23)x x x ---+22(2)(42)x yx x y y -++(3)(3)aa b a b a ---+98102⨯24(12)(12)(14)(116)x x x x -+++()()a b c a b c +--+2982(1)(1)(1)y y y --+--2(23)x y z +-42622322[5(4)(3)()](2)a a aa a a ---÷÷-5a =-324(1)2(1)q p p -+-221()()()m m m ab x y a b x ya b x y +-+---2a a ba cbc -+-22412925x x y y -+-212448x x ++=x 4,6xy xy +=-=22()(2)3x y yy y x yxx y +-+-243a a +-21a +28a +2(8)a p a ++2(3)a a q -+3a 2a p q。
华东师大版八年级上册 第12章 整式的乘除 复习学案

八年级数学上册导学案22命题人:刘英明 审题人:曹金满 课型:复习课课题:第12章 整式的乘除(复习Ⅱ)强化训练类型一:单项式与多项式的次数1.已知m y x 27-是7次单项式,求m 的值.22128b a b a a m +++2.已知单项式3421y x -的次数与多项式22128b a b a a m +++的次数相同,求m 的值. 3.若单项式n y x n --12)2(是关于y x ,的三次单项式,求n 的值.4.已知c b a 、、满足:(1)022)3(52=-++b a ;(2)c b a y x ++-1231是7次单项式; 求多项式()22222234⎡⎤------⎣⎦a b a b abc a c a b a c abc 的值. 类型二:同类项1.已知35y x m -与n y x 34能合并,求n m 的值.2.若2222b a m +与3343-+-n m b a 是同类项,求n m +的值. 3.如果b a m 3--与n ab 431是同类项且m 与n 互为倒数,求1141)44(3-----m m mn n 的值. 类型三:整式的加减1.已知三角形的第一边长是b a 2+,第二边比第一边长)2(-b ,第三边比第二边小5. 求三角形的周长。
2.已知222c b a A -+=,222324c b a B ++-=,且A +B +C =0.求:(1)多项式C (2)若311=-==c b a ,,,求A +B 的值.3.已知xyz x A -=32,xyz z y B +-=23,xyz y x C -+-=222,且01)1(2=+-++z y x ; 求:A -(2B -3C)的值.01)1(2=+-++z y x4.下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.⎪⎭⎫ ⎝⎛-+-22213y xy x 2222123421y x y xy x +⎪⎭⎫ ⎝⎛-+--222123421y x xy x -= ⎝⎛-+--,阴影部分即为被墨迹弄污的部分. 求:被墨汁遮住的一项.类型四:缺项与无关1.多项式83322-+--xy y kxy x 化简后不含xy 项,求k 值.2.若多项式222)25(23mx x y x +-+-的值与x 的值无关,求m 的值.3.若)192()72(22-+--+-+y x bx y ax x 的值与字母x 的取值无关,求b a 、的值.4.试说明:不论x 取何值代数式7)13()345(223x x x x x x --+----++67425(32323x x x x x +---++)6()132()345(323223x x x x x x x x ++--+---++的值是不会改变的. 类型五:整体代入法1.当2=+b a 时,求代数式2()2()3a b a b +-++的值.2.已知532++x x 的值为3,求1932-+x x 的值.3.已知41=+-b a b a ,求代数式)(3)(2b a b a b a b a -+-+-的值. 4.已知3=+y x xy ,求代数式y xy x y xy x -+-+-3353的值. 类型六:化简绝对值1.若0<+b a ,化简b a b a ----+312.已知有理数c b a 、、在数轴上的位置如图所示且b a =.化简dc d c b a a -+--+- 3.当00<>y x ,时;化简 (1) x y y 21125++-+-;(2)182356-----y y x y . 类型七:自定义计算1.“*”是新规定的这样一种运算法则:ab a b a 22+=*比如3)2(323)2(32-=-⨯⨯+=-*.(1)试求)1(2-*的值;(2)若22=*x ,求x 的值;(3)若9)1()2(+=**-x x ,求x 的值.2.对正整数b a ,,b a ∆等于由a 开始的的连续b 个正整数之和,如:43232++=∆, 又如:26876545=+++=∆.若151=∆x ,求x 的值.。
新维度华东师大版八年级数学上册第12章整式的乘除 《整式的除法》学案设计(无答案)

新维度八年级数学上册《整式的除法》【学习目标】1. 会用同底数幂的除法性质进行计算.2. 会进行单项式除以单项式的计算.3. 会进行多项式除以单项式的计算.【要点梳理】要点一、同底数幂的除法法则同底数幂相除,底数不变,指数相减,即______________要点二、零指数幂任何不等于0的数的0次幂都等于1.即01a =(a ≠0)要点三、单项式除以单项式法则单项式相除,把系数与同底数幂分别相除作为商的因式,对于只有被除式里含有的字母,则连同它的指数作为商的一个因式.要点四、多项式除以单项式法则多项式除以单项式:先把多项式的每一项除以这个单项式,再把所得的商相加.即________________________________________类型一、同底数幂的除法1、计算:(1)83x x ÷; (2)3()a a -÷; (3)52(2)(2)xy xy ÷; (4)531133⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭.类型二、单项式除以单项式2、计算:(1)342222(4)(2)x y x y ÷; (2)2137323m n m m n x y z x y x y z +⎛⎫÷÷- ⎪⎝⎭;(3)22[()()]()()x y x y x y x y +-÷+÷-; (4)2[12()()][4()()]a b b c a b b c ++÷++.举一反三:【变式】计算:(1)3153a b ab ÷; (2)532253x y z x y -÷;(3)2221126a b c ab ⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭; (4)63(1010)(210)⨯÷⨯.3、夏天是多雷雨的季节,大家都知道,雷雨时往往是先看到闪电,后听到雷声,这是因为光的传播速度比声音的传播速度快的缘故.已知光在空气中的传播速度约为8310⨯米/秒,而声音在空气中的传播速度约为23.410⨯米/秒.(1)光的速度大约是声音速度的多少倍?(结果保留两个有效数字)(2)如果你看到闪电8秒后,才听到了雷声,那么你能算出闪电离你大约有多远吗?(注:光传播到地球的时间忽略不计)类型三、多项式除以单项式4、计算:(1)324(67)x y x y xy -÷; (2)42(342)(2)x x x x -+-÷-;(3)22222(1284)(4)x y xy y y -+÷-;(4)232432110.3(0.5)36a b a b a b a b ⎛⎫--÷- ⎪⎝⎭.举一反三:【变式】计算:(1)23233421(3)2(3)92xy x x xy y x y ⎡⎤--÷⎢⎥⎣⎦; (2)2[(2)(2)4()]6x y x y x y x +-+-÷.。
华师版 数学八年级上册第12章 整式乘除导学案

第十二章“整式的乘除”导学计划一、课标要求1、了解整数指数幂的意义和基本性质2、会进行简单的整式乘法运算(其中的多项式相乘仅指一次式相乘)。
3、会推导乘法公式:(a+b)(a-b)=a2-b2;(a+b)2=a2+2ab+b2,了解公式的几何背景,并能进行简单计算。
4、会用提公因式法、公式法(直接用公式不超过二次)进行因式分解(指数是正整数)。
二、导学目标1。
使学生掌握正整数幂的乘、除运算性质,能用代数式和文字语言正确地表述这些性质,并能运用它们熟练地进行运算.使学生掌握单项式乘(或除以)单项式、多项式乘(或除以)单项式以及多项式乘多项式的法则,并运用它们进行运算.2. 使学生会推导乘法公式(平方差公式和完全平方公式),了解公式的几何意义,能利用公式进行乘法运算. 3。
使学生掌握整式的加、减、乘、除、乘方的较简单的混合运算,并能灵活地运用运算律与乘法公式简化运算。
4.使学生理解因式分解的意义,并感受分解因式与整式乘法是相反方向的运算,掌握提公因式法和公式法(直接运用公式不超过两次)这两种分解因式的基本方法,了解因式分解的一般步骤;能够熟练地运用这些方法进行多项式的因式分解。
三、本章编写特点1、强调重要数学思想方法的渗透2、充分体现从具体到抽象再到具体的认知过程3、根据数学知识的逻辑关系循序渐进安排教学内容四、导学核心点1、导学重点(1)幂的运算性质(2)整式的乘除2、导学难点(1)乘法公式的运用(2)多项式的因式分解五、本章总课时安排:本章共安排了4个小节,导学时间约需13课时(供参考):12.1幂的运算4课时12。
2整式的乘法4课时12。
3乘法公式4课时12.4整式的除法3课时12.5 因式分解3课时复习2课时六本章知识结构框图12。
1 幂的运算第一课时同底数幂的乘法导学目标:1 、知识与技能:①、理解同底数幂的乘法法则.②、运用同底数幂的乘法法则解决一些实际的问题。
2、过程与方法:在推导同底数幂的乘法性质的过程中,培养学生初步运用“转化”思想能力,培养学生观察概括与抽象的能力.3、情感态度与价值观:体会科学的思想方法,接受数学文化的熏陶,激发学生探索创新的精神. 导学核心点:1。
华东师大版(新版)八年级数学上册:第12章整式的乘除小结与复习课件

8.因式分解的步骤 如果多项式的各项有公因式,那么先 提取公因式; 在各项提出公因式后或各项没有公因式的情况下,视察多项 式的次数:二项式可以尝试运用 平方差公式分解因式;三项 式可以尝试运用 两数和(差)公的式分解因式; 分解因式必须分解到每一个因式在指定的范围内都不能
再分解 为止.
9.图形面积与代数恒等式
整体思想
例6 若2a+5b-3=0,则4a·32b= 8 . 【解析】已知条件是2a+5b-3=0,无法求出a,b的值因此可以 逆用积的乘方先把4a·32b.化简为含有与已知条件相关的部分, 即4a·32b=22a·25b=22a+5b.把2a+5b看做一个整体,因为2a+5b3=0,所以2a+5b=3,所以4a·32b=23=8.
[注意] 其中的a、b代表的不仅可以是单独的数、单独的字
母,还可以是一个任意的代数式;这几个法则容易混淆,计算 时必须先搞清楚该不该用法则、该用哪个法则.
2.整式的乘法 单项式与单项式相乘,把它们的 系数 、 相同字母的幂 分别 相乘,对于只在一个单项式中出现的字母,则连同它的指数一 起作为积的一个 因式 . 单项式与多项式相乘,用 单项式 和 多项式 的每一项分别相 乘,再把所得的积 相加 . 多项式与多项式相乘,先用一个多项式的 每一项 与另一个 多项式的 每一项 相乘,再把所得的积 相加 .
5.因式分解的意义 把一个多项式化成几个整式的 积 的情势,叫做多项式的 因式分解.
因式分解的过程和 整式乘法 的过程正好相反.
6.用提公因式法分解因式 公因式的确定:公因式的系数应取多项式各项整数系数的 最大公约数 ;字母取多项式各项 相同 的字母;各字母 指数取次数最 低 的. 一般地,如果多项式的各项都含有公因式,可以把这个公 因式提到 括号 外面,将多项式写成 因式乘积 的情势,这 种分解因式的方法叫做提公因式法. [注意] 提公因式法是因式分解的首选方法,在因式分解时 先要考虑多项式的各项有无公因式.
华东师大数学八上《第12章《整式的乘除》教案 (新版)华东师大版

课前
预习
【导学提纲】
知识结构与知识归纳:
(一)知识结构见教材P43
(二)知识归纳:
1、整式乘除相关法则及公式有哪些?
2、因式分解:
(1)因式分解的步骤是什么?
(2)因式分解的常用方法有哪些?
(3)分解因式要注意哪些问题?
典例
讲解
1、幂的运算性质
例1已知 (m、n为正整数),求 的值.(思路点拨:注意公式的逆用)
整式的乘除
课 题
单元复习
课 型
复习课
教师复备
教学
目标
1、牢固掌握幂的运算性质和整式乘除的运算法则,理解、掌握乘法公式;
2、分解因式的方法及运用;
3、培养自己的运算能力,以及分析问题、解决问题的能力.
教学重点、难点
重点:有关乘除法的各种运算法则和公式的理解与运用.
难点:有关乘除法的各项运算法则的理解与应用.
2、整式的乘除
例2先化简,再求值: ,其中 .(思路点拨:注意运算顺序及准确性)
(变式训练):若 ,
求 的值.
3、乘法公式的灵活运用
例3已知 ,求 ; 的值.
(思路点拨:注意公式的变形及相互关系)
4、因式分解的运用
例4求 的值
(思路点拨:注意观察数字特征,灵活运用因式分解进行有关计算)
(变式训练)计算:
八年级数学上册 第12章 整式的乘除 12.2 整式的乘法 1

12.2.3 多项式与多项式相乘 【学习目标】 1、探索并理解多项式与多项式相乘的法则,并会熟练运用它们进行运算. 2、主动参与到探索过程中去,逐步形成独立思考、主动探索的习惯【学习重难点】理解多项式与多项式相乘的法则,并会熟练运用它们进行运算【学习过程】一、课前准备1、回忆单项式乘以单项式和单项式乘以多项式的运算法则;2、利用法则进行计算:①263x xy g = ; ②22(3)ab ab -g =③2(4)(2)a b b --g = ; ④212()2x x -= ;⑤5(20.2)ab a b -+g =二、学习新知自主学习:1、问题:为了扩大绿地面积,要把街心花园的一块长a 米,宽m 米的长方形绿地增长b 米,加宽n 米,求扩地以后的面积是多少?思考:可以用几种方法表示扩大后绿地的面积?不同的表示方法之间有什么关系?方法一:这块花园扩地后长 米,宽 米,因而面积为 米2. 方法二:这块花园现在是由 小块组成,它们的面积分别为: 米2、 米2、 米2、 米2,故这块绿地的面积为 米2.由此可得: 和 表示的是同一块绿地面积。
所以有: = ;2、由上题可得,多项式乘多项式的公式:(a+b)(m+n)= + + + 多项式与多项式相乘: 理解升华1.运用多项式的乘法法则时,必须做到不重不漏.2.多项式与多项式相乘,结果仍是 .3.注意确定积中的每一项的符号,多项式中每一项都包含它前面的 ,“同号 ,异号 ”.4.多项式与多项式相乘的展开式中,有同类项要 .实例分析:例1、计算:(1)(x+2)(x-3) (2)(2x+5y)(3x-2y)例2、计算:(1))3)(2(22n mn m n m -+- (2))12)(223(2++-x x x【随堂练习】1.计算(5b+2)(2b -1)=______ _.2.计算:(3-2x )(2x -2)=___ ___.3.计算:(x+1)(x 2-x+1)=____ _ ____.4.若(x -8)(x+5)=x 2+bx+c ,则b=____ __,c=____ ___.5.当a=-1时,代数式)3)(2()2)(1(+---+a a a a 的值等于 .【中考连线】已知m ,n 满足│m+1│+(n -3)2=0,化简(x -m )(x -n )=_________.【参考答案】随堂练习1.2102--b b ;2. 61042-+-x x ;3. 13+x ;4. b=-3,c =-40;5.6.中考连线322--x x。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:运用完全平方公式分解因式
学习目标
1.会用完全平方公式分解因式;
2.会选择适当方法分解因式。
学习方法
勾画圈点法、旁批法、识记法等。
预习
一、自学
1.阅读教材44页
2.我们已经学过的因式分解的方法有什么?尝试分解因式: =
3.根据乘法公式进行计算:
二、互学
1.探究一:
观察上面3、4中各式的左、右两边有什么共同特点?
左边的特点:______________________________________,
右边的特点:______________________________________.
试用公式表示:_______________________________________
这个公式你能用语言来描述吗?
公式中的a、b代表什么?
我们把形如a2+2ab+b2和 的式子叫完全平方式
2.探究二:下列各式是否是完全平方式?如果不是,请说明理由。
(1)a2-4a+4;(2)x2+4x+4y2 ;(3)4a2+2ab+ b2;
(4)a2-ab+b2;(5)x2-6x-9;(6)a2+a+0. 25.
(1) = ______________(2) =______ __________
(3) = _________ (4) =__________
4.猜一猜:你能将下面的多项式分解因式吗?
(1) =_____________ (2) =___________
(3)a2+2ab+b2=(4)a2-2ab+b2=_________
(4)多项式首项带有“-”号时,则需先提出“-”号候在进行分解
(5)另一项为底数积的2倍;若底数积的2倍与平方项(同号还是异号),则选择和的完全平方
(6)如果多项式各项有公因式,一定要先,然后在考虑用哪个公式。其方法、步骤及结果检查可总结成以下口诀:首先提取,然后考虑用,两种方法反复试,提净、分完连乘式。
二、当堂检测
1.下列多项式是不是完全 平方式?为什么?
(1) a2-4a+ 4 (2) 1 +4a2(3) 4b2+ 4b–1 (4) a2+ ab + b2
2.若x2—6x +k是一个 完全平方式,那么k=
3.把下列各式分解因式:
(1)3ax2+6axy+3ay2;(2)-x2-4y2+4xy.
4.将各式因式分解:
4.将下面各式分解因式:
(1) (2) (3)
展示
一、质疑
将下面各式分解因式:(1) (2) 4(2a+b)2-12(2a+b)+9
二、点拨(由小组提出有价值的问题,其他小组 发表意见,帮助解决问题;展示过程中,教师适时引导、点拨、调控和激励。)
反馈
一、小结
1.本节课学了什么?
2.如果多项式各项有公因式,一定要先,然后在考虑用哪个公式。其方法、步骤及结果检查可总结成以下口诀:首先提取,然后考虑用,两种方法反复试,提净、分完连乘式。
(1)x2+14xy+4 9y2; (2 )
(3)-4xy-4x2-y2(4) 2x3y2-16x2y+32x
(5) x2+2xy+2y2(6)(x+y)2-14(x+y)+49
反思 :判断一个式子是否是完全平方式应从几个方面思考?
3.归纳概括:
(1)用完全平方公式分解因式时,各公式中的字母既可以表示数,也可以表示式或式。
(2)在运用完全平方公式进行多项式的分解因式时,要根据其特点进行公式的选择,若多项式为三项式,才考虑用公式。
(3)完 全平方公式特征:左边是三项式,其中两项为平方式且同号,另一项为底数积的2倍。
