会面问题 利用概率论及MATLAB来求解
matlab在概率统计中的计算

4.1 计算组合数、验证概率的频率定义,计算古典概率
4.1.1 计算nk.
P
P
使用语句n^k
4
第4章 概率统计
例如计算 511
N=5^11 N=
48828125
如计算 5−2.8
N=5^(-2.8) N=
0.0110
4.1.2 计算组合数 Cnk
计算组合数 Cnk 时,使用语句nchoosek(n,k).
1
MATLAB6.0数学手册
光驱:8倍速以上; 内存:至少64MB,但推荐128MB以上; 硬盘:视安装方式不同要求不统一,但至少留1GB用于安装(安装后未必有1GB); 显卡:8位; MATLAB 6对软件的要求 Windows95 、Window98、Windows NT或Windows2000; Word97或word2000等,用于使用MATLAB Notebook; Adobe Acrobat Reader 用于阅读MATLAB的PDF的帮助信息。 MATLAB 6的安装和其它应用软件类似,可按照安装向导进行安装,这里不再赘述。 MATLAB的启动和退出 与常规的应用软件相同,MATLAB的启动也有多种方式,首先常用的方法就是双击桌面的 MATLAB图标,也可以在开始菜单的程序选项中选择MATLAB组件中的快捷方式,当然也可 以在MATLAB的安装路径的子目录中选择可执行文件“MATLAB.exe”。 启动MATLAB后,将打开一个MATLAB的欢迎界面,随后打开MATLAB的桌面系统(Desktop) 如图2-1所示。
在MATLAB命令行操作中,有一些键盘按键可以提供特殊而方便的编辑操作。比如:“↑” 可用于调出前一个命令行,“↓”可调出后一个命令行,避免了重新输入的麻烦。当然下 面即将讲到的历史窗口也具有此功能。 历史窗口(Command History) 历史命令窗口是MATLAB6新增添的一个用户界面窗口,默认设置下历史命令窗口会保留自 安装时起所有命令的历史记录,并标明使用时间,以方便使用者的查询。而且双击某一 行命令,即在命令窗口中执行该命令。 当前目录窗口(Current Directory )
Matlab在《概率论与数理统计》教学中的应用

Matlab在《概率论与数理统计》教学中的应用
Matlab提供了丰富的概率分布函数,可以帮助学生更好地理解不同的概率分布。
学生可以使用Matlab生成正态分布、二项分布、泊松分布等不同的概率分布,并画出相应的概率密度函数、累积分布函数等图形。
通过实际的计算和绘图,学生可以更直观地看到不同概率分布的特点,加深对概率分布的理解。
Matlab提供了各种统计函数,可以方便地进行数据的描述性统计和推断性统计。
学生可以使用Matlab计算样本的平均值、方差等描述性统计量,还可以使用Matlab进行假设检验、置信区间估计等推断性统计。
通过实际的计算和分析,学生可以更好地掌握统计学中的概念和方法。
Matlab还可以进行模拟实验,帮助学生理解概率和统计的原理。
学生可以使用Matlab 模拟抛硬币的实验,验证概率的定义和性质。
学生还可以使用Matlab模拟中心极限定理,观察样本均值的分布趋于正态分布的情况。
通过实际的模拟实验,学生可以更深入地理解抽样分布和极限定理等重要概念。
Matlab还可以用于数据的可视化。
学生可以使用Matlab绘制直方图、散点图、箱线图等图形,展示数据的分布和变化。
通过可视化的方式,学生可以更好地理解数据的特点和规律,并能够更直观地展示和解释统计分析的结果。
Matlab在《概率论与数理统计》教学中具有广泛的应用价值。
通过利用Matlab进行计算、模拟和可视化等任务,可以帮助学生更好地理解概率和统计的概念和方法,提高学习效果。
在教学中合理地使用Matlab可以有效地促进学生对概率论与数理统计的学习和理解。
概率论问题MATLAB仿真求解程序

clc; clear; close all; a=10; b=3; p=0.55; S=0; N=10000; m=6; %甲的赌本 %乙的赌本 %甲赢的概率 % 计数设置为0 % 模拟次数 %设定随机数状态值(1 2 3 4 5 6 ),改变这个值可以进行不同的实验
rand('state',m); %设置随机数状态 for k=1:N; at=a;%初始化甲的赌本 bt=b;%初始化乙的赌本 while at>0.5&bt>0.5;%模拟整个赌博过程 r=[(rand<p)-0.5]*2; % 算输赢 at=at+r;%交换赌本 bt=bt-r;%交换赌本 end S=S+(at<0.5); %如甲输,累加甲输的次娄 end P=S/N %计算甲输的概率值 g=p/[1-p]; Po=[1-g^b]/[1-g^(a+b)] %返回甲输光的概率理论值
%n 次中与平行线相交的次数的频率比,即相交的概率,vpa() 以任意精度(4 位小数点,默认值为 32 位)显示出来 pi_m=vpa((2*L*n)/(m*d),15) %利用投针频率估计圆周率 pi,vpa()以任意精度(15 位小数点,默认值为 32 位)显示出来
运行结果
p =.3207 pi_m =3.11817898347365
(A)
(B)
在图(A)中,当小球从顶部向下降落时,遇到第一层竖隔板,此时小球分别向左 右下落的概率各占一半(0.5);当小球继续下落遇到第二层竖隔板时,小球仍以 左右相同的概率往下落,以后每层均如此(如图(B)所示)。最后到了第 8 层底 部,小球将落入底部 9 个槽中的一个。但是小球落入每个槽内的概率是不一样的。 如查将这个 9 个槽编号为:1、2、3、45、6、7、8、9,计算小球落入第 9 个槽中 的概率。 理论分析:这是一个经典的二项分布概率模型。考虑在第 K 层小球运动方向有两种 可能,用 X k 表示,则 X k 服从两点分布。这里用 X k = 1 表示向右侧竖隔板方向运 动,用 X k = 0 表示向左侧竖隔板方向运动,它们发生的概率均为 0.5。最终位置 X 由 X = ∑ X k 决定,即二项分布决定,上述第 8 层即有 X ~ Binomial (8, 0.5) ,上述该
第8章 matlab 概率论与数理统计问题的求解

8.1.3 概率问题的求解
图4-9
• 例:
>> b=1; p1=raylcdf(0.2,b); p2=raylcdf(2,b); P1=p2-p1 P1 = 0.8449
>> p1=raylcdf(1,b); P2=1-p1 P2 = 0.6065
• 例:
>> syms x y; f=x^2+x*y/3; >> P=int(int(f,x,0,1/2),y,0,1/2) P= 5/192 >> syms x y; f=x^2+x*y/3; P=int(int(f,x,0,1),y,0,2) P= 1
8.1.2.3
பைடு நூலகம்
分布
• 例:
>> x=[-0.5:.02:5]‘; %x=[-eps:-0.02:-0.5,0:0.02:5]; x=sort(x’);替代 >> y1=[]; y2=[]; a1=[1,1,2,1,3]; lam1=[1,0.5,1,2,1]; >> for i=1:length(a1) y1=[y1,gampdf(x,a1(i),lam1(i))]; y2=[y2,gamcdf(x,a1(i),lam1(i))]; end >> plot(x,y1), figure; plot(x,y2)
8.1.2.2 正态分布
正态分布的概率密度函数为:
• 例:
>> x=[-5:.02:5]'; y1=[]; y2=[]; >> mu1=[-1,0,0,0,1]; sig1=[1,0.1,1,10,1]; sig1=sqrt(sig1); >> for i=1:length(mu1) y1=[y1,normpdf(x,mu1(i),sig1(i))]; y2=[y2,normcdf(x,mu1(i),sig1(i))]; end >> plot(x,y1), figure; plot(x,y2)
利用matlab辅助《概率论与数理统计》教学时需要注意的一个问题

助 其克服学 习和生活 中的 困难,极大 的带动和鼓舞 了苗 圃幼 高 自身的领导能力和组织能力, 实现 了预备党 员与入党积极分 苗 。例如 , 丁中有一个 叫别传杰 的学生 , 园 他在 2 1 0 0年“ 友 子 的 共 同 成 长 。 用 杯’ , 第六届全 国大学 生创 业设计暨沙盘模拟经营大赛总决赛 一 等奖, 作为会 计 5 8 班 的一名 园丁 , 03 在他 的鼓舞和带动下 , 班
先 争优 活 动 开 展 以来 , 丁 多 次 组 织 各 苗 圃理 论 学 习或 时事 讨 分 子 的 共 同 成长 。班 级联 系 人 在 实 施 《 色 苗 圃》 园 红 的过 程 中 需要
论 活动 , 学习 内容包 括朝核 问题 , 日关 系 , 中 社会主义新 农村 ,
自学入党 的基本知识、入党材 料的书写规范和政治学习 内容 ,
懂、 方法难以掌握 。 a 1 b是一种高性能的、 M 乞a 用于工程计 算的编 这篇论文抛砖 弓 玉, l 引起大家的共鸣 。 程 软件 , 它把科学 计算 、 结果 的可视化 和编程都集 中在一个 使 二、 数组地址和坐标系地址的微妙差异
圃活动使园丁从政 治 、 思想 、 习、 作、 学 工 生活纪律 、 考勤 、 动 会继续将这份“ 活 优秀 ’ 爱心 , , 和“ , 传承下去。例如 , 为苗 圃的会 作 参 与情况 、奖 惩情况等 8个方面 对入党积 极分子进 行综合考 计 5 8 0 1班 , 因学习 的校 区变 更、 导员老师 的调整 , 个班级 辅 整 察 。支部按照“ 成熟一个 , 发展一个 ” 的原则, 认真做好党 员发展 在很长一段 时间里凝聚力明显 下降。该班 的园丁王雯了解情况 工作。在‘ ‘ 创先争优 ” 动开展 以来 , 活 共发展党 员 1 0 , 2 人 预备党 后针对班 级同学 的情况 , 同学们进行 交流谈心 , 与 开展一些班 员转 正 3 人 , 中包括“ 0 2 ” 雄集 体成 员龚想 涛 和孟 亮 级活动 以增加班级凝聚力。通过相互的交流和学习下, 7 其 1・4英 班级凝 雨 支部党员在创 先争优活动开展 以来 , 在各类竞 赛活动 中, 获 聚 力 增 强 了 , 习 氛 围 也浓 厚 了 , 计 5 8 班 成 为全 院 英语 四 学 会 01 得国家级奖项 4人次 ,省级奖项 5 次,院级奖项 2 1人次 。 级一次性过级率最高 的班级,全班 4 人 4 9人 ,通过四级人数 达 4 6 () 2 党员教育得到 了加 强, 弥补 了“ 重发展 , 培养 ” 轻 的不足 。创 名 , 通过 六级人数达 2 7人。 () 4 促进 了班级联系人 与入党积极
matlab在概率论与数理统计课程教学过程中的应用

matlab在概率论与数理统计课程教学过程中的应用
Matlab在概率论与数理统计课程教学过程中的应用包括:
1. 使用Matlab处理、显示和分析概率分布。
可以使用Matlab 绘制直方图、折线图和其他可视化工具,表示不同类型的概率分布;
2. 使用Matlab进行统计模拟分析,包括随机变量的生成,抽样方法的分析,以及统计量的估计;
3. 使用Matlab进行统计推断,如检验统计假设、拟合概率分布并测试其相关性、以及定量比较等;
4. 利用Matlab进行多元统计分析,包括协方差和相关分析,多元回归分析等;
5. 利用Matlab进行数据处理测试,包括卡方检验、t检验、ANOVA等;
6. 使用Matlab进行非参数统计模型拟合,如Kolmogorov-Smirnov检验等;
7. 使用Matlab应用概率论方法,如随机事件分析、随机过程分析、以及马尔可夫链等;
8. 使用Matlab来计算和估计两个随机变量之间的各种统计函数,如相关系数、协方差等。
会面问题 利用概率论及MATLAB来求解
会面问题甲乙两人相约某天9:00-10:00在某地会面商谈生意,双方约定先到者必须等候另一人20分钟,过时如果另一人仍未到则可离去,试求两人能够会面的概率。
1用所学概率论知识建模并求解;2用Matlab 软件编程模拟实现这个过程,并与理论结果相比较。
解:用所学概率论知识建模并求解将9点到10点看成是0到60分钟,则甲乙两人到达的时间概率分布可看做是分布,此时不妨设甲到达的时间为t1,乙到达的时间为t2,(0<=t1,t2<=60) 当t1,t2满足|t1-t2|<=20时,两人则可碰面。
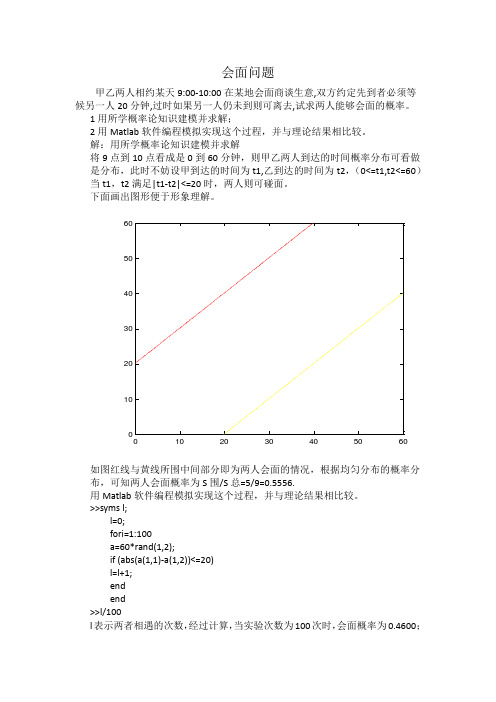
下面画出图形便于形象理解。
如图红线与黄线所围中间部分即为两人会面的情况,根据均匀分布的概率分布,可知两人会面概率为S 围/S 总=5/9=0.5556.用Matlab 软件编程模拟实现这个过程,并与理论结果相比较。
>>syms l;l=0;fori=1:100a=60*rand(1,2);if (abs(a(1,1)-a(1,2))<=20)l=l+1;endend>>l/100l 表示两者相遇的次数,经过计算,当实验次数为100次时,会面概率为0.4600; 01020304050600102030405060下面我们增大实验次数,实验次数为1000时,会面概率为0.5590;实验次数为10000时,会面概率为0.5525;实验次数为100000时,会面概率为0.5546;实验次数为1000000时,会面概率为0.5552;…从随机实验可以发现,当实验次数越来越大时,随机事件发生的概率就越来越稳定于一个值,而这个值与我们理论计算出来的值是一致的,因此从实验角度证明了概率论概率计算理论的正确性。
培养解决实际问题的能力,概率论与数理统计问题matlab实战

培养解决实际问题的能力,概率论与数理统计问题matlab实战
培养解决实际问题的能力,需要注重以下几点:
1. 提供真实的实际问题:了解实际问题,并且确保这些问题是切实存在的,而不仅仅是假设或者理论上的问题。
2. 培养综合运用知识的能力:让学生了解和掌握广泛的理论知识,并能够将这些知识应用到解决实际问题中。
这包括数学、统计学、编程等多个领域的知识。
3. 强调实践与动手能力:通过实际的操作和实践,学生能够掌握具体的解决问题的方法和技巧,培养他们的动手能力。
4. 提供合适的工具和资源:对于解决实际问题,合适的工具和资源是非常重要的,比如MATLAB等软件工具可以用来进行概率论和数理统计的实战练习。
5. 激发学生的兴趣和探索精神:鼓励学生主动探索和思考,培养他们对实际问题的兴趣,让他们通过解决实际问题来提升自己的能力。
至于概率论与数理统计问题的MATLAB实战,您可以通过以下几个步骤进行:
1. 确定问题和目标:选择一个与概率论和数理统计相关的实际问题,明确解决问题的目标和方法。
2. 收集数据:根据问题的要求,收集相应的数据,可以是实际观测数据或模拟生成的数据。
3. 数据预处理:对数据进行清洗、整理和转换,确保数据的质量和可用性。
4. 数据分析与建模:根据问题的要求,运用概率论和数理统计的相关方法,对数据进行分析和建模。
5. 结果可视化与解释:利用MATLAB等软件工具,将分析结果进行可视化展示,并对结果进行解释和讨论。
6. 结论总结与讨论:根据分析结果,总结结论,并进行讨论和推测,提出可能的解决方案或建议。
请注意,以上回答仅供参考,具体操作中需根据具体情况和问题的要求进行调整和完善。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
会面问题
甲乙两人相约某天9:00-10:00在某地会面商谈生意,双方约定先到者必须等候另一人20分钟,过时如果另一人仍未到则可离去,试求两人能够会面的概率。
1用所学概率论知识建模并求解;
2用Matlab 软件编程模拟实现这个过程,并与理论结果相比较。
解:用所学概率论知识建模并求解
将9点到10点看成是0到60分钟,则甲乙两人到达的时间概率分布可看做是分布,此时不妨设甲到达的时间为t1,乙到达的时间为t2,(0<=t1,t2<=60) 当t1,t2满足|t1-t2|<=20时,两人则可碰面。
下面画出图形便于形象理解。
如图红线与黄线所围中间部分即为两人会面的情况,根据均匀分布的概率分布,可知两人会面概率为S 围/S 总=5/9=0.5556.
用Matlab 软件编程模拟实现这个过程,并与理论结果相比较。
>>syms l;
l=0;
fori=1:100
a=60*rand(1,2);
if (abs(a(1,1)-a(1,2))<=20)
l=l+1;
end
end
>>l/100
l 表示两者相遇的次数,经过计算,当实验次数为100次时,会面概率为0.4600; 0102030405060
010
20
30
40
50
60
下面我们增大实验次数,
实验次数为1000时,会面概率为0.5590;
实验次数为10000时,会面概率为0.5525;
实验次数为100000时,会面概率为0.5546;
实验次数为1000000时,会面概率为0.5552;
…
从随机实验可以发现,当实验次数越来越大时,随机事件发生的概率就越来越稳定于一个值,而这个值与我们理论计算出来的值是一致的,因此从实验角度证明了概率论概率计算理论的正确性。
