2016-2017学年高中数学 第一章 三角函数 8 函数y=Asin(ωx+φ)的图像课时作业 北师大版必修4
高中 函数y=Asin(ωx+φ)的图象及性质 知识点+例题 全面
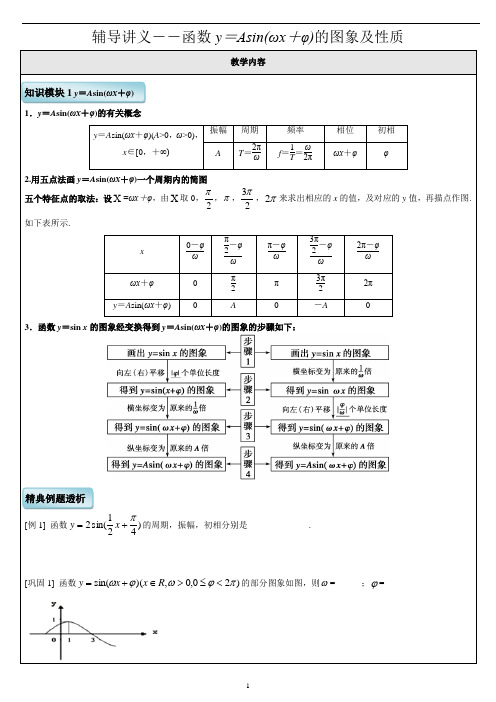
辅导讲义――函数y =Asin(ωx +φ)的图象及性质教学内容1.y =A sin(ωx +φ)的有关概念y =A sin(ωx +φ)(A >0,ω>0),x ∈[0,+∞)振幅 周期 频率 相位 初相 AT =2πωf =1T =ω2πωx +φφ2.用五点法画y =A sin(ωx +φ)一个周期内的简图 五个特征点的取法:设X =ωx +φ,由X 取0,2π,π,23π,π2来求出相应的x 的值,及对应的y 值,再描点作图.如下表所示.x0-φω π2-φω π-φω 3π2-φω 2π-φω ωx +φ 0 π2 π 3π2 2π y =A sin(ωx +φ)A-A3.函数y =sin x 的图象经变换得到y =A sin(ωx +φ)的图象的步骤如下:[例1] 函数)421sin(2π+=x y 的周期,振幅,初相分别是______________.[巩固1] 函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图,则ω=______;ϕ=______知识模块1 y =A sin(ωx +φ)精典例题透析[巩固] 若关于x 的方程01sin sin 2=+-+m x x 有解,则实数m 的取值范围为_____________.[例5] 要得到)21sin(x y -=的图象,只需将)621sin(π--=x y 的图象_______________.[巩固1] 为得到函数)3cos(π+=x y 的图象,只需将函数x y sin =的图象_____________________.[巩固2] 为得到函数)62sin(π-=x y 的图象,只需将函数x y 2cos =的图象_____________________.[例6] 已知函数x x f πsin )(=的图象的一部分如左图,则右图的函数图象所对的函数解析式为_____________.[巩固1] 函数)0,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的部分图象如图所示,则)(x f 的解析式为____________.[巩固2] 已知函数),0,)(sin()(πϕπωϕω<<->∈+=R x x A x f 的部分图象如图所示,则函数)(x f 的解析式 是_______________.[例7] 设函数f (x )=3sin(ωx +φ)(ω>0,-π2<φ<π2)的图象关于直线x =2π3对称,它的周期是π,则下列说法正确的是________.(填序号)[例](1)已知函数f (x )=2sin(ωx +φ)(其中ω>0,|φ|<π2)的最小正周期是π,且f (0)=3,则ω=_____,φ=_______.(2)已知函数f (x )=A sin(ωx +φ) (A >0,|φ|<π2,ω>0)的图象的一部分如图所示,则该函数的解析式为____________.[巩固] 如图为y =A sin(ωx +φ)的图象的一段.(1)求其解析式;(2)若将y =A sin(ωx +φ)的图象向左平移π6个单位长度后得y =f (x ),求f (x )的对称轴方程.题型三:函数y =A sin(ωx +φ)的性质[例] (2014·重庆改编)已知函数f (x )=3sin(ωx +φ)(ω>0,-π2≤φ<π2)的图象关于直线x =π3对称,且图象上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)当x ∈[0,π2]时,求函数y =f (x )的最大值和最小值.[巩固] 已知函数f (x )=A sin(ωx +φ)(x ∈R ,ω,A >0,0<φ<π2)的最大值为2,最小正周期为π,直线x =π6是其图象的一条对称轴.(1)求函数f (x )的解析式;(2)求函数g (x )=f (x -π12)-f (x +π12)的单调递增区间.1.(2013·山东)将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( )A .3π4B .π4C .0D .-π42.(2013·浙江)函数f (x )=sin x cos x +32cos 2x 的最小正周期和振幅分别是__________.3.已知函数f (x )=2sin(ωx +φ)(ω>0,且|φ|<π2)的部分图象如图所示,则函数f (x )的一个单调递增区间是______________.4.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图象如右图所示,则当t =1100秒时,电流强度是_____________.5.已知函数f (x )=2sin ωx 在区间[-π3,π4]上的最小值为-2,则ω的取值范围是_________________.6.设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图象如图所示,△KLM 为等腰直角三角形,∠KML =90°, KL =1,则f (16)的值为________.,7.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎡⎦⎤π6(x -6) (x =1,2,3,…,12,A >0)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值 为________℃.夯实基础训练。
高中 函数y=Asin(ωx+φ)的图象及性质 知识点+例题 全面

辅导讲义――函数y =Asin(ωx +φ)的图象及性质教学内容1.y =A sin(ωx +φ)的有关概念y =A sin(ωx +φ)(A >0,ω>0),x ∈[0,+∞)振幅 周期 频率 相位 初相 AT =2πωf =1T =ω2πωx +φφ2.用五点法画y =A sin(ωx +φ)一个周期内的简图 五个特征点的取法:设X =ωx +φ,由X 取0,2π,π,23π,π2来求出相应的x 的值,及对应的y 值,再描点作图.如下表所示.x0-φω π2-φω π-φω 3π2-φω 2π-φω ωx +φ 0 π2 π 3π2 2π y =A sin(ωx +φ)A-A3.函数y =sin x 的图象经变换得到y =A sin(ωx +φ)的图象的步骤如下:[例1] 函数)421sin(2π+=x y 的周期,振幅,初相分别是______________.[巩固1] 函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图,则ω=______;ϕ=______知识模块1 y =A sin(ωx +φ)精典例题透析[巩固] 若关于x 的方程01sin sin 2=+-+m x x 有解,则实数m 的取值范围为_____________.[例5] 要得到)21sin(x y -=的图象,只需将)621sin(π--=x y 的图象_______________.[巩固1] 为得到函数)3cos(π+=x y 的图象,只需将函数x y sin =的图象_____________________.[巩固2] 为得到函数)62sin(π-=x y 的图象,只需将函数x y 2cos =的图象_____________________.[例6] 已知函数x x f πsin )(=的图象的一部分如左图,则右图的函数图象所对的函数解析式为_____________.[巩固1] 函数)0,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的部分图象如图所示,则)(x f 的解析式为____________.[巩固2] 已知函数),0,)(sin()(πϕπωϕω<<->∈+=R x x A x f 的部分图象如图所示,则函数)(x f 的解析式 是_______________.[例7] 设函数f (x )=3sin(ωx +φ)(ω>0,-π2<φ<π2)的图象关于直线x =2π3对称,它的周期是π,则下列说法正确的是________.(填序号)[例](1)已知函数f (x )=2sin(ωx +φ)(其中ω>0,|φ|<π2)的最小正周期是π,且f (0)=3,则ω=_____,φ=_______.(2)已知函数f (x )=A sin(ωx +φ) (A >0,|φ|<π2,ω>0)的图象的一部分如图所示,则该函数的解析式为____________.[巩固] 如图为y =A sin(ωx +φ)的图象的一段.(1)求其解析式;(2)若将y =A sin(ωx +φ)的图象向左平移π6个单位长度后得y =f (x ),求f (x )的对称轴方程.题型三:函数y =A sin(ωx +φ)的性质[例] (2014·重庆改编)已知函数f (x )=3sin(ωx +φ)(ω>0,-π2≤φ<π2)的图象关于直线x =π3对称,且图象上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)当x ∈[0,π2]时,求函数y =f (x )的最大值和最小值.[巩固] 已知函数f (x )=A sin(ωx +φ)(x ∈R ,ω,A >0,0<φ<π2)的最大值为2,最小正周期为π,直线x =π6是其图象的一条对称轴.(1)求函数f (x )的解析式;(2)求函数g (x )=f (x -π12)-f (x +π12)的单调递增区间.1.(2013·山东)将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( )A .3π4B .π4C .0D .-π42.(2013·浙江)函数f (x )=sin x cos x +32cos 2x 的最小正周期和振幅分别是__________.3.已知函数f (x )=2sin(ωx +φ)(ω>0,且|φ|<π2)的部分图象如图所示,则函数f (x )的一个单调递增区间是______________.4.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图象如右图所示,则当t =1100秒时,电流强度是_____________.5.已知函数f (x )=2sin ωx 在区间[-π3,π4]上的最小值为-2,则ω的取值范围是_________________.6.设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图象如图所示,△KLM 为等腰直角三角形,∠KML =90°, KL =1,则f (16)的值为________.,7.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎡⎦⎤π6(x -6) (x =1,2,3,…,12,A >0)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值 为________℃.夯实基础训练。
高中数学第一章三角函数1.3三角函数的图象和性质1.3.3函数y=Asin(ωx+φ)的图象课件苏教

中的第三点和第五点),有
π3ω+φ=π,
ω=2.
56πω+φ=2π,解得φ=π3.
∴y=3sin(2x+π3).
法三:(图象变换法)
由 T=π,点(-π6,0),A=3 可知图象由 y=3sin 2x 向左
平移π6个单位长度而得,所以有 y=3sin 2(x+π6),
即 y=3sin(2x+π3),且 ω=2,φ=π3.
2
第八页,共42页。
2.(2014·高考江苏卷)已知函数 y=cos x 与 y=sin(2x+ φ)(0≤φ<π),它们的图象有一个横坐标为π3的交点,则 φ 的
π 值是____6____. 解析:利用函数 y=cos x 与 y=sin(2x+φ)(0≤φ<π)的交点横 坐标,列方程求解.
由题意,得 sin2×π3+φ=cos π3,因为 0≤φ<π,所以 φ=π6.
2.已知函数 y=Asin(ωx+φ),ω>0,且|φ|<π2的图象的一段 如图所示,求此函数的解析式.
第二十七页,共42页。
解:由图易知 A= 2,T2=|10-2|=8,所以 T=16. 又因为 T=|2ωπ|,ω>0,所以 ω=π8. 因为点(2, 2)在图象上,所以 y= 2sin(π8×2+φ)= 2, 所以 sin(π4+φ)=1,所以π4+φ=2kπ+π2(k∈Z), 又|φ|<π2,所以 φ=π4,所以 y= 2sin(π8x+π4).
第十五页,共42页。
法二:①把 y=sin x 的图象上所有点的横坐标伸长到原来 的 2 倍(纵坐标不变),得到 y=sin12x 的图象; ②把 y=sin12x 图象上所有的点向右平移π2个单位长度,得到 y=sin12(x-π2)=sin(12x-π4)的图象; ③把 y=sin(12x-π4)的图象上所有点的纵坐标伸长到原来的 3 倍(横坐标不变),就得到 y=3sin(12x-π4)的图象.
高中数学 第1章 三角函数 8 函数y=Asin(ωx+φ)的图像与性质(2)练习 北师大版必修4-

8 函数y =A sin(ωx +φ)的图像与性质(2)课时跟踪检测一、选择题1.函数y =sin(2x +π)是( ) A .周期为π的奇函数 B .周期为π的偶函数 C .周期为2π的奇函数D .周期为2π的偶函数解析:y =sin(2x +π)=-sin2x ,周期为2π2=π.∵f (-x )=-sin2(-x )=sin2x =-f (x ), ∴y =sin(2x +π)为奇函数. 答案:A2.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π4,若存在α∈(0,π),使得f (x +α)=f (x +3α)恒成立,则α的值是( )A .π6B .π3C .π4D .π2解析:函数f (x )的周期T =2π2=π. ∵f (x +α)=f (x +3α),∴T =2α=π,即α=π2.答案:D3.已知函数y =sin ⎝⎛⎭⎪⎫π4-2x ,则其图像的下列结论中,正确的是( )A .向左平移π8后得到奇函数B .向左平移π8后得到偶函数C .关于点⎝ ⎛⎭⎪⎫-π8,1中心对称 D .关于直线x =π8轴对称答案:A4.若将函数y =2sin2x 的图像向左平移π12个单位长度,则平移后图像的对称轴为( )A .x =k π2-π6(k ∈Z )B .x =k π2+π6(k ∈Z ) C .x =k π2-π12(k ∈Z ) D .x =k π2+π12(k ∈Z ) 解析:由题意,将函数y =2sin2x 的图像向左平移π12个单位得y =2sin2⎝ ⎛⎭⎪⎫x +π12=2sin ⎝ ⎛⎭⎪⎫2x +π6,则平移后函数的对称轴为2x +π6=π2+k π,k ∈Z ,即x =π6+k π2,k ∈Z ,故选B .答案:B5.已知函数f (x )=2sin(ωx +φ)(ω>0)的图像关于直线x =π3对称,且f ⎝ ⎛⎭⎪⎫π12=0,则ω的最小值为( )A .2B .4C .6D .8解析:由题意得π3ω+φ=k 1π+π2(k 1∈Z ),π12ω+φ=k 2π(k 2∈Z ),∴π4ω=(k 1-k 2)π+π2(k 1,k 2∈Z ).∴ω=4(k 1-k 2)+2(k 1,k 2∈Z ).∵ω>0,∴ω的最小值为2.答案:A6.设函数f (x )=cos ωx (ω>0),将y =f (x )的图像向右平移π3个单位长度后,所得的图像与原图像重合,则ω的最小值等于( )A .13B .3C .6D .9解析:依题意得f ⎝ ⎛⎭⎪⎫x -π3=cos ⎣⎢⎡⎦⎥⎤ω⎝ ⎛⎭⎪⎫x -π3=cos ⎝ ⎛⎭⎪⎫ωx -π3ω=cos ωx ,∴-π3ω=2k π(k ∈Z ),∴ω=-6k .又ω>0,∴当k =-1时,ω有最小值6. 答案:C 二、填空题7.函数y =sin ⎝ ⎛⎭⎪⎫12x +π3,x ∈⎣⎢⎡⎦⎥⎤-π,π2的单调递增区间为________.解析:由-π2+2k π≤12x +π3≤π2+2k π,k ∈Z 得函数的单调递增区间为⎣⎢⎡⎦⎥⎤4k π-5π3,π3+4k π,k ∈Z .又x ∈⎣⎢⎡⎦⎥⎤-π,π2,∴单调递增区间为⎣⎢⎡⎦⎥⎤-π,π3.答案:⎣⎢⎡⎦⎥⎤-π,π3 8.(2018·某某卷)已知函数y =sin(2x +φ)⎝ ⎛⎭⎪⎫-π2<φ<π2的图像关于直线x =π3对称,则φ的值是________.解析:由题意可得sin ⎝ ⎛⎭⎪⎫23π+φ=±1,所以23π+φ=π2+k π,φ=-π6+k π(k ∈Z ),因为-π2<φ<π2,所以当k =0时,φ=-π6.答案:-π69.设函数y =sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,φ∈⎝ ⎛⎭⎪⎫-π2,π2的最小正周期为π,且图像关于直线x =π12对称,则在下面四个结论中:①图像关于点⎝ ⎛⎭⎪⎫π4,0对称; ②图像关于点⎝ ⎛⎭⎪⎫π3,0对称; ③在⎣⎢⎡⎦⎥⎤0,π6上是增函数; ④在⎣⎢⎡⎦⎥⎤-π6,0上是增函数. 那么所有正确结论的编号为________. 解析:∵2πω=π,∴ω=2.∴f (x )=sin(2x +φ), 又∵f (x )关于x =π12对称,∴sin ⎝ ⎛⎭⎪⎫2·π12+φ=±1, ∴π6+φ=k π+π2, ∴φ=k π+π3,k ∈Z ,又∵φ∈⎝ ⎛⎭⎪⎫-π2,π2, ∴令k =0得φ=π3,∴f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3. 令f (x )=0得2x +π3=k π,∴x =k π2-π6,k ∈Z , 令k =1得一个对称中心⎝ ⎛⎭⎪⎫π3,0, 令-π2≤2x +π3≤π2,-512π≤x ≤π12, ∴f (x )的一个增区间为⎣⎢⎡⎦⎥⎤-512π,π12,又∵⎣⎢⎡⎦⎥⎤-π6,0⊆⎣⎢⎡⎦⎥⎤-512π,π12,∴②④正确. 答案:②④ 三、解答题10.已知函数f (x )=12sin ⎝ ⎛⎭⎪⎫2x +π6+54.(1)求f (x )的最大值、最小值,及相应x 的值; (2)求f (x )的最小正周期、对称轴和对称中心;(3)函数f (x )的图像至少向左平移多少个单位长度时才为偶函数?解:(1)当2x +π6=2k π+π2(k ∈Z )时,f (x )有最大值74,即当x =π6+k π(k ∈Z )时,f (x )max =74,当2x +π6=-π2+2k π(k ∈Z )时,f (x )有最小值34,即当x =k π-π3(k ∈Z )时,f (x )min =34.(2)由T =2π|ω|知函数f (x )的最小正周期为T =π.令2x +π6=k π+π2(k ∈Z ),则x =k π2+π6(k ∈Z ),∴对称轴为直线x =k π2+π6(k ∈Z ), 令2x +π6=k π(k ∈Z ),则x =k π2-π12(k ∈Z ),∴对称中心为⎝⎛⎭⎪⎫k π2-π12,54(k ∈Z ).(3)由函数性质知若函数y =A sin(ωx +φ)+b 为偶函数,φ>0,则φ至少为π2,即y =12sin ⎝⎛⎭⎪⎫2x +π2+54=12cos2x +54为偶函数.∴应将函数y =12sin ⎝ ⎛⎭⎪⎫2x +π6+54的图像平移至函数y =12sin ⎝ ⎛⎭⎪⎫2x +π2+54的图像处.由函数图像平移方法知:y =12sin ⎝ ⎛⎭⎪⎫2x +π6+54的图像――→向左平移π6个单位长度y =12sin ⎝ ⎛⎭⎪⎫2x +π2+54的图像,∴函数f (x )的图像至少向左平移π6个单位长度才为偶函数.11.已知函数f (x )=A sin(ωx +φ),x ∈R ⎝ ⎛⎭⎪⎫其中A >0,ω>0,0<φ<π2的图像与x 轴的交点中,相邻两个交点之间的距离为π2,且图像上一个最低点为M ⎝ ⎛⎭⎪⎫2π3,-2.(1)求f (x )的解析式; (2)当x ∈⎣⎢⎡⎦⎥⎤π12,π2,求f (x )的值域.解:(1)由最低点为M ⎝⎛⎭⎪⎫2π3,-2得A =2.由x 轴上相邻的两个交点之间的距离为π2得T 2=π2,即T =π,ω=2πT =2ππ=2.由点M ⎝ ⎛⎭⎪⎫2π3,-2在图像上知,2sin ⎝ ⎛⎭⎪⎫2×2π3+φ=-2, 即sin ⎝ ⎛⎭⎪⎫4π3+φ=-1. 故4π3+φ=2k π-π2(k ∈Z ),∴φ=2k π-11π6(k ∈Z ). 又∵φ∈⎝ ⎛⎭⎪⎫0,π2,∴φ=π6.故f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π6.(2)∵x ∈⎣⎢⎡⎦⎥⎤π12,π2,∴2x +π6∈⎣⎢⎡⎦⎥⎤π3,7π6.当2x +π6=π2,即x =π6时,f (x )取得最大值2;当2x +π6=7π6,即x =π2时,f (x )取得最小值-1,故f (x )的值域为[-1,2].12.已知函数f (x )=sin(ωx +φ)-b (ω>0,0<φ<π)的图像两相邻对称轴之间的距离是π2,若将f (x )的图像先向右平移π6个单位,再向上平移3个单位,所得函数g (x )为奇函数.(1)求f (x )的解析式;(2)求f (x )的对称轴及单调区间.解:(1)∵2πω=2×π2,∴ω=2,∴f (x )=sin(2x +φ)-b .又∵g (x )=sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x -π6+φ-b +3为奇函数,且0<φ<π,则φ=π3,b =3,故f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3- 3. (2)由(1)知f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3-3,其对称轴由2x +π3=k π+π2(k ∈Z ),得x =k π2+π12(k ∈Z ).由2k π-π2≤2x +π3≤2k π+π2(k ∈Z ),得k π-5π12≤x ≤k π+π12(k ∈Z ),由2k π+π2≤2x +π3≤2k π+3π2(k ∈Z ),得k π+π12≤x ≤k π+7π12(k ∈Z ).∴函数f (x )的对称轴为x =k π2+π12(k ∈Z ),增区间为⎣⎢⎡⎦⎥⎤k π-5π12,k π+π12(k ∈Z ), 减区间为⎣⎢⎡⎦⎥⎤k π+π12,k π+7π12(k ∈Z ).13.已知函数f (x )=A sin(ωx +φ)与对数函数y =g (x )在同一坐标系中的图像如图所示.(1)分别写出两个函数的解析式; (2)方程f (x )=g (x )共有多少个解? 解:(1)由图像知A =2,φ=0,T =2, 故ω=π,f (x )=2sinπx .设g (x )=log a x ,由图像知log a 4=-1, 故a =14,g (x )=log 14x .(2)因g (x )为减函数,f (x )最小值为-2.故当g (x )≥-2时,可能有交点,由log 14x ≥-2,得0<x ≤16.当2≤x ≤16时,f (x )与g (x )在f (x )的每一个周期上的图像均有两个交点,共14个交点;当0<x <2时,由图像知有3个交点;当x>16时,图像无交点.综上可知f(x)=g(x)共有17个解.。
函数y=Asin(ωx+φ)的性质-三角函数

数 学 BS 自 主 通 道
探究通道
巩固通道
高效课时作业
自主通道
填一填
函数 y=Asin(ωx+φ)(A>0,ω>0)的性质
定义域
R
值域
1 __[_-___A__,___A__]_____
周期
T=2ωπ
第3 页
数 学 BS 自 主 通 道
探究通道
巩固通道
高效课时作业
第4 页
奇偶性 φ= 2 kπ,k∈Z 时,y=Asin(ωx+φ)是奇函数;φ= 3 kπ+π2,k∈Z
数 学 BS 自 主 通 道
ห้องสมุดไป่ตู้
探究通道
巩固通道
高效课时作业
第 12 页
类型 二 函数 y=Asin(ωx+φ)的性质及应用(自主探究) 1.若函数 y=sin(x+φ)(0≤φ≤π)是 R 上的偶函数,则 φ=( C )
A.0
π B.4
π C.2
D.π
解析 因为函数 y=sin(ωx+φ)在 φ=kπ±2π(k∈Z)时为偶函数,且 0≤φ≤π,所以
数 学 BS 自 主 通 道
探究通道
巩固通道
高效课时作业
第 20 页
类型 三 函数 y=Asin(ωx+φ)的图象与性质的综合应用 【例】 函数 h(x)=Asin(ωx+φ)A>0,ω>0,|φ|<π2的部分图象如图所示.若把函 数 h(x)的图象上所有点的纵坐标不变,横坐标伸长到原来的 2 倍,得到函数 f(x)的图 象. (1)求函数 f(x)的解析式; (2)若函数 y=f(x+φ′)0<φ′<2π是奇函数,求函数 g(x)=cos(2x-φ′)在[0,2π]上的单调递减区间.
高中数学第1章三角函数8函数y=Asin(ωx+φ)的图像与性质第1课时函数y=Asin(ωx+φ)的图像课件北师大版

判断(正确的打“√”,错误的打“×”) (1)A 的大小决定了函数的振幅.( ) (2)ω 的大小与函数的周期有关.( ) (3)φ 的大小决定了函数与 y=sin x 的相对位置.( ) (4)b 的大小决定了函数图像偏离平衡位置的幅度.( ) 【解析】 由 A,ω,φ,b 的几何意义知全对. 【答案】 (1)√ (2)√ (3)√ (4)√
y
0
A
0
-A
0
第二步:在同一坐标系中描出各点.
第三步:用光滑的曲线把它们连接起来.
三角函数的图像变换
写出由 y=sin x 的图像变化到 y=3sin12x-π4的图像的不同方法步骤. 【导学号:66470026】
【精彩点拨】 变换过程可以先伸缩后平移,也可以先平移后伸缩.
由 y=sin x 的图像,通过变换得到 y=Asin(ωx+φ)的图像时,可以先相位变换, 后周期变换,也可以先周期变换,后相位变换.两种变换的顺序不同,变换的量 也有所不同,前者平移|φ|个单位,而后者则平移|ωφ|个单位.不论哪一种变换,都是 对字母 x 而言的,即看“变量”变化多少,而不是“角”变化多少.
0
π 2
π
3π 2
2π
y 0 2 0 -2 0
描点作图,如图.
1.利用“五点法”作图像时,确定 x 的值是本题的关键.
2.用“五点法”作函数 y=Asin(ωx+φ)的图像的一般步骤:
第一步:列表. ωx+φ 0
π 2
π
3π 2
2π
x -ωφ 2πω-ωφ ωπ-ωφ 23ωπ -ωφ 2ωπ-ωφ
人教版(新教材)高中数学第一册 匀速圆周运动的数学模型 函数y=Asin(ωx+φ)的图象

解析 ω=4>1,因此只需把正弦曲线上所有点的横坐标缩短到原来的14,纵坐标 不变.
答案 B
2.把函数y=2sin 3x的图象上所有点的横坐标变为原来的2倍,纵坐标变为原来的 3倍,得到________的图象. 答案 y=6sin32x
3.将函数 y=cos 2x 的图象向右平移π3个单位长度,所得图象对应的解析式为 ________.
5.6 函数y=Asin(ωx+φ) 5.6.1 匀速圆周运动的数学模型 5.6.2 函数y=Asin(ωx+φ)的图象 第一课时 函数y=Asin(ωx+φ)的图象
课标要求
素养要求
1.会用“五点法”画出y=Asin(ωx+φ)的
图象.
通过整体代换和图象的变换提
2.理解参数A,ω,φ对函数y=Asin(ωx+ 升学生的直观想象、逻辑推理
【训练 1】 请用“五点法”画出函数 y=12sin(2x-π6)的图象. 解 函数 y=12sin2x-π6的周期 T=22π=π,先用“五点法”作它在长度为一个周
期上的图象,令 X=2x-π6,则 x 变化时,y 的值如下表:
X
0
π 2
π
3π 2
2π
x
π 12
π 3
7π 12
5π 6
13π 12
解析 答案
由题意得所得图象对应的解析式为 y=cos 2(x-π3)=cos(2x-23π). y=cos(2x-23π)
[微思考] 1.由y=sin ωx(ω>0)的图象得到y=sin(ωx+φ)的图象是如何平移的呢?
提示 ∵y=sin(ωx+φ)=sin ωx+ωφ, ∴由 y=sin ωx 的图象向左(右)平移ωφ个单位.
y
2017-2018版高中数学 第一章 三角函数 8 函数y=Asin(ωx+φ)的图像与性质(二) 北师大版必修4

φ的值.
(1)一般可由图像上的最大值、最小值来确定|A|. (的2)交因点为从T=而2ω确π,定所T,以即往相往邻通的过最求高得点周与期最T来低确点定之ω间,的可距通离过为已T2知;曲相线邻与的x轴两 个最高点(或最低点)之间的距离为T.
答案
梳理
用“五点法”作y=Asin(ωx+φ) 的图像的步骤:
第一步:列表:
ωx+φ 0
π 2
πห้องสมุดไป่ตู้
3π 2
2π
x
-ωφ 2πω-ωφ ωπ -ωφ 23ωπ-ωφ 2ωπ-ωφ
y
0
A
0
-A
0
第二步:在同一坐标系中描出各点. 第三步:用光滑曲线连接这些点,形成图像.
知识点二 函数y=Asin(ωx+φ),A>0,ω>0的性质
4.已知函数f(x)=sinωx+π3 (ω>0)的最小正周期为π,则该函数的图像
√A.关于点π3,0对称
B.关于直线 x=π4对称
C.关于点π4,0对称
D.关于直线 x=π3对称
解析 ω=2ππ=2,所以 f(x)=sin(2x+π3). 将 x=π3代入 f(x)=sin2x+π3,
解答
(2)求函数y=f(x)的单调区间及最值.
解答
当堂训练
1.函数y=Asin(ωx+φ)(A>0,0<φ<π)的图像的一段如图所示,它的解析式 可以是
√A.y=23sin(2x+23π)
B.y=23sin(2x+π3) C.y=23sin(2x-π3) D.y=23sin(2x+π4)
12345
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解析:由3x- = ,x= 知,应填( ,-2).
8.函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图像如下,此函数的解析式为__________________________.
答案:y=2sin(2x+ )
解析:A=2,T=2( -(- ))=π,∴ω=2.由最高点的坐标可知,2×(- )+φ= +2kπ(k∈Z),所以y=2sin(2x+ π).
11.已知函数y= sin(2x+ ),借助“五点作图法”画出函数f(x)在[0, ]上的简图,并且依图写出函数f(x)在[0, ]上的递增区间.
解:可先画出区间[- , ]的图像,再截取所需.
列表
μ=2x+
0
π
2π
x
-
y
0
0
-
0
图像略,注意f(0)=1,由图像可知函数在区间[0, ]上的单调递增区间是[0, ],[ , ].
(2)由-1<f(x)-m<1⇔-1+f(x)<m<1+f(x)对x∈[ , ]恒成立.
即-1<f(x)-m<1⇔-1+f(x)max<m<1+f(x)min(x∈[ , ]).
当x∈[ , ]时, ≤2x- ≤ .
故当2x- = 时,即x= 时,f(x)取得最大值0;
当2x- = 时,即x= 时,f(x)取得最小值- .
解析:振幅为3,周期为 =4π,初相为- .
2.把函数y=sinx的图像上所有点向左平移 个单位长度,再把所得图像上所有点的横坐标缩短到原来的 (纵坐标不变),得到的图像所对应的函数是()
A.y=sin B.y=sin
C.y=sin D.y=sin
答案:C
解析:把函数y=sinx的图像上所有点向左平行移动 个单位长度后得到函数y=sin 的图像,再把所得图像上所有点的横坐标缩短到原来的 ,得到函数y=sin 的图像.
12.已知函数f(x)=sin(2x- )-1.
(1)写出函数f(x)的单调递增区间;
(2)若不等式-1<f(x)-m<1在x∈[ , ]恒成立,求实数m的取值范围.
解:(1)因为f(x)=sin(2x- )-1
由- +2kπ≤2x- ≤ +2kπ(k∈Z)得:- +kπ≤x≤ +kπ(k∈Z).
所以f(x)的单调递增区间是[- +kπ, +kπ](k∈Z).
3.函数y=2sin(x+ )的一条对称轴为()
A.x=- B.x=0
C. D.-
答案:C
解析:因为y=2sin(x+ ),其对称轴可由x+ =kπ+ ,(k∈Z)求得,解得x=kπ+ ,k∈Z,选项中只有C符合.
4.函数y=1-2cos x(x∈[0, ])的最小值、最大值分别是()
A.-1,3 B.-1,2
三、解答题:(共35分,11+12+12)
10.把函数y=f(x)的图像上各点向右平移 个单位,再把横坐标伸长到原来的2倍,再把纵坐标缩短到原来的 倍,所得到图像的解析式是y=2sin( x+ ),求f(x)的解析式.
解:y=2sin( x+ )的图像纵坐标伸长到原来的 倍,得y=3sin( x+ )的图像,横坐标缩短到原来的 倍得到y=3sin(x+ )的图像,再向左平移 个单位得到y=3sin[(x+ )+ ]=3cosx的图像.故f(x)=3cosx.
9.将函数y=2sinx的图像向左平移 个单位,再将得到的图像上各点的横坐标变为原来的 倍(纵坐标不变),得到函数y=f(x)的图像,若x∈[0, ],则函数y=f(x)的值域为________.
答案:[-1,2]
解析:由y=sinx→y=2sin(x- )→y=2sin(2x- )知,f(x)=2sin(2x- ).由x∈[0, ]得2x- ∈[- , ],所以函数y=f(x)的值域为[-1,2].
故m的取值范围为(-1, ).
8函数y=Asin(ωx+φ)的图像
时间:45分钟 满分:80分
班级________姓名________分数________
一、选择题:(每小题5分,共5×6=30分)
1.函数y=3sin( x- )的振幅、周期、初相分别为()
A.-3,4π, B.3,4π,-
C.3,π,- D.-3,π,
答案:B
C.0,3 D.0,2
答案:B
解析:因为0≤ x≤ ,所以- ≤cos x≤1,所以得函数y=1-2cos x的最小值、最大值分别是-间是()
A.(- , ) B.(- , )
C.[- ,0) D.(- , )
答案:B
解析:由2kπ- ≤2x+ ≤2kπ+ (k∈Z),解得kπ- ≤x≤kπ+ (k∈Z),选项中只有B符合.
6.如果函数y=sin(2x+φ)的图像关于点( ,0)中心对称,那么φ的值可以是()
A.- B.-
C. D.
答案:D
解析:由题意得sin(2× +φ)=0,φ的值可以是 .
二、填空题:(每小题5分,共5×3=15分)
7.用五点法画函数y=2sin(3x- )的图像,这五个点可以分别是( ,0)( ,2),( ,0),__________,( ,0).
