福建省厦门市第五中学2014届九年级数学上学期周末自测卷(概率、解直角三角形)
九年级数学解直角三角形与图形的相似综合过关测试
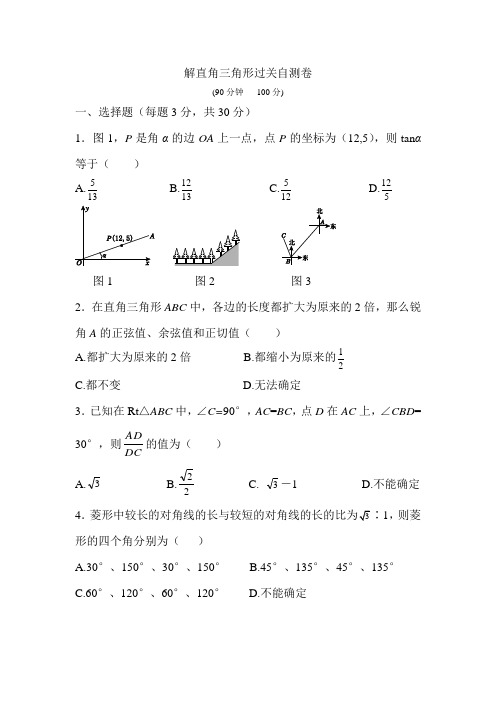
解直角三角形过关自测卷(90分钟 100分)一、选择题(每题3分,共30分)1.图1,P 是角α的边OA 上一点,点P 的坐标为(12,5),则tan α等于( ) A.135 B.1312 C.125 D.512图1 图2 图32.在直角三角形ABC 中,各边的长度都扩大为原来的2倍,那么锐角A 的正弦值、余弦值和正切值( )A.都扩大为原来的2倍B.都缩小为原来的21 C.都不变 D.无法确定3.已知在Rt △ABC 中,∠C=90°,AC =BC ,点D 在AC 上,∠CBD =30°,则DCAD 的值为( )A.3B.22C. 3-1D.不能确定 4.1,则菱形的四个角分别为( )A.30°、150°、30°、150°B.45°、135°、45°、135°C.60°、120°、60°、120°D.不能确定5.如图2,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4 m.如果在坡度为0.75的山坡上种树,也要求株距为4 m,那么相邻两树间的坡面距离为()A.5 mB.6 mC.7 mD.8 m6.已知∠A,∠B是Rt△ABC的两个锐角,则方程tan A·x²-2x+tan B=0( )A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.根的情况无法确定7.如图3,一艘轮船由海平面上A地出发向南偏西40°的方向行驶40 n mile到达B地,再由B地向北偏西20°的方向行驶20 n mile到达C地,则A,C两地相距()A.30 n mileB.40 n mileC.203n mileD.103n mile 8.(2012,四川广安,有改动)如图4,某水库堤坝横断面迎水坡AB 的坡度i=1BC=50 m,则迎水坡面AB的长度是()A.100 mB.1003mC.150 mD.503m图4 图5 图69.如图5所示,学校的保管室里,有一架5 m长的梯子OC斜靠在墙上,此时梯子OC与地面所成的角为45°,如果梯子底端O固定不动,顶端C靠到对面墙上的C′点,此时梯子OC′与地面所成的角为60°,则此保管室的宽度AB为()A.25(2+1)mB.25(3+2)mC.32mD.25(3+1)m10.(2013,广州)如图6所示,四边形ABCD 是梯形,AD ∥BC ,CA 是∠BCD 的平分线,且AB ⊥AC ,AB =4,AD =6,则tan B 等于( )A .23 B.22 C.411D.55二、填空题(每题3分,共24分)11.(2012,湖北孝感)计算:cos 245°+tan30°·sin60°=________. 12.在△ABC 中,∠A ,∠B 都是锐角,且(cos A -21)²+|1-tan B |=0,则∠C =__________. 13.若tan α=5,则ααααcos 3sin 2cos -sin +=__________.14.如图7,孔明同学背着一桶水,从山脚A 出发,沿与地面成30°角的山坡向上走,送水到山上因春季受旱缺水的王奶奶家(B 处),AB =80 m ,则孔明从A 到B 上升的高度BC 是________m.图7 图8 图9 图10 15.(2014,厦门莲花中学模拟)如图8,△ABC 中,∠B =30°, ∠A =15°,若BC 边上的高为2,则BC =__________.16.在△ABC 中,∠A ,∠B 都是锐角,且sin A =21,tan B =3,AB =10,则△ABC 的面积为___________.17.全市动员修海堤抗台风,某海堤的横断面是梯形,如图9所示,迎水坡BC的坡角为30°,背水坡AD的坡度i=1∶1.2,堤顶宽DC 为3 m,堤高DF为10 m,则堤底宽AB约为________m.(精确到0.1 m)18.(2013,荆门)如图10,在Rt△ABC中,∠ACB=90°,D是AB 的中点,过D点作AB的垂线交AC于点E,BC=6,sin A=53,则DE=________.三、解答题(19题4分,20题6分,24题8分,其余每题7分,共46分)19.(1)计算:121-⎪⎭⎫⎝⎛+8+|1-2|0-2sin60°·tan60°;(2)计算:sin²30°+cos²45°+2sin60°·tan45°.20.(2013,昭通)小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图11所示).小船从P 处出发,沿北偏东60°方向划行200 m到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1 m)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,2≈1.41,3≈1.73)图1121.小明将一副三角尺如图12所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长,若已知CD=2,求AC的长.图1222.(2013,贵阳)在一次综合实践活动中,小明要测某地一座古塔AE 的高度,如图13,已知塔基AB的高为4 m,他在C处测得塔基顶端B的仰角为30°,然后沿AC方向走5 m到达D点,又测得塔顶E 的仰角为50°.(人的身高忽略不计)(1)求AC的距离;(结果保留根号)图13(2)求塔高AE.(参考数据:tan50°≈1.2,sin50°≈0.77,cos50°≈0.64,3≈1.73,2≈1.41,结果保留整数)23.如图14,一艘小船从码头A出发,沿北偏东53°方向航行,航行一段时间到达小岛B处后,又沿着北偏西22°方向航行了10 n mile到达C处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离.(2≈1.4, 3≈1.7,结果保留整数)图1424.某过街天桥的截面图为梯形,如图15所示,其中天桥斜面CD 的坡度i=1∶3,CD的长为10 m,天桥另一斜面AB的坡角∠ABG=45.(1)求过街天桥斜面AB的坡度;(2)求DE的长;(3)若决定对该过街天桥进行改建,使AB斜面的坡度变缓,将其45°坡角改为30°,方便过路群众,改建后斜面为AF,试计算此改建需占路面的宽度FB.(结果精确到0.01 m)图1525.阅读下列材料,并解决后面的问题.如图16所示,在锐角三角形ABC 中,设∠BAC ,∠B ,∠C 的对边分别是a ,b ,c .过点A 作AD ⊥BC 于点D ,则sin B =c AD ,sin C =b AD,即AD =c ·sin B ,AD =b ·sin C .于是c ·sin B =b ·sin C ,即CcB b sin sin =,同理有,sin sin sin sin B b BAC a BAC a C c =∠∠=,所以CcB b BAC a sin sin sin ==∠. 即:在一个锐角三角形中,各边和它所对角的正弦的比相等.图16(1)在锐角三角形中,∠A ,∠B ,∠C 的对边分别是a ,b ,c ,若已知三个元素,a ,b ,∠A ,运用上述结论和有关定理就可以求出其余三个未知元素c ,∠B ,∠C .请你按照下列步骤填空,完成求解过程.第一步:由a ,b ,∠A −−−→−用关系式__________求出∠B ; 第二步:由∠A ,∠B −−−→−用关系式__________求出∠C ; 第三步:由__________−−−→−用关系式__________求出c ;(2)一货轮在C 处测得灯塔A 在货轮北偏西30°方向上,随后货轮以28.4 n mile/h 的速度按北偏东45°的方向航行,0.5 h 后到达B 处,此时又测得灯塔A在货轮的北偏西70°方向上(如图17所示),利用上面的结论求此时货轮到灯塔A的距离AB.(结果精确到0.1 n mile,参考数据:sin40°≈0.643,sin65°≈0.906,sin70°≈0.940,sin75°≈0.966)图17参考答案及点拨一、1.C 2.C 3.C4.C 点拨:设较大内角为α,则tan2α =3,所以2α=60°,所以α=120°.5.A 6.B 点拨:因为b 2-4ac =(-2)2-4·tan A ·tan B =4-4×1=0,故方程有两个相等的实数根.7.C 8.A 9.A10.B 点拨:过点D 作AB 的平行线交AC 于点E ,交BC 于点F ,如答图1,易知四边形ABFD 是平行四边形,∴BF =AD =6,DF =AB =4,∵AB ⊥AC ,DF ∥AB ,∴DF ⊥AC ,又∵CA 是∠BCD 的平分线,∴CD =CF ,∠DCA =∠ACB ,又∵AD ∥BC ,∴∠DAC =∠ACB ,∴∠DAC =∠DCA .∴DC =DA =6,∴CF =6,∴BC =BF +CF =12.易求得AC =82,∴tan B =AB AC =428=22. 答图1二、11.1 点拨:cos 245°+tan30°·sin60°=222⎪⎪⎭⎫⎝⎛+33×23=21+21=1. 12.75°13.83 点拨:原式=3cos sin 2cos sin +-αααα=3tan 2tan +-αα=3525+-=83.14.4015.32-2 点拨:设BC 边上的高为AD ,由题意知,AD =2,∠ACD =∠B +∠BAC =45°,∴tan 45°=CD AD =CD 2=1,∴CD =2, ∴tan B =BD AD =22-BC =33,解得BC =23-2. 16.2325 点拨:在该题中,并没有直接指明△ABC 是直角三角形,所以需先判断其为直角三角形,然后才能利用解直角三角形的知识解题.17.32.318.415 点拨:由题易证△AED ∽△ABC ,在△ABC 中,BC =6,sin A =53,可求得AB =10,AC =8.利用相似三角形的性质可求得DE 的长. 三、19.解:(1)原式=2+22+1-2×23×3=2+22+1-3=22. (2)原式=221⎪⎭⎫ ⎝⎛+222⎪⎪⎭⎫ ⎝⎛+2×23×1=41+21+26=43+26. 20.解:过P 作PC ⊥AB 于C ,如答图2,在Rt △APC 中,AP =200 m ,∠ACP =︒90,∠P AC =60°.∴PC =200×sin60°=200×23=1003(m ).∵在Rt △PBC 中,sin ︒37=PB PC ,∴PB =︒37sin PC ≈6.073.1100⨯≈288(m ). 答:这时小亮与妈妈相距约288 m.答图221.解:在Rt △BCD 中,∠BCD =45°,CD =2,cos ∠BCD =BC CD ,∴BC =BCD CD ∠cos =︒45cos 2=22.在Rt △ABC 中,∠BAC =60°,sin ∠BAC =AC BC ,∴AC =BAC BC ∠sin =︒60sin 22=2322=364.∴AC 的长为364. 点拨:△ABC 和△BCD 都是有特殊锐角的直角三角形,所以利用特殊角的三角函数值便可求得AC 的长.22.解:(1)在Rt △ABC 中,AB =4 m ,∠BCA =30°,由tan ∠BCA =ACAB ,得AC =BCA AB ∠tan =︒30tan 4=334=43(m ). ∴AC 的距离为43 m.(2)设AE=x m ,在Rt △AED 中,由tan50°=ADx ,得AD =︒tan50x ≈1.2x (m ), ∵CD =AD -AC =5,∴1.2x -43≈5,解得x ≈14, ∴塔高AE 约为14m.23.解:由题意知:∠BAC =53°-23°=30°,∠C =23°+22°=45°.过点B 作BD ⊥AC ,垂足为D ,则CD =BD .∵BC =10 n mile ,∴CD =BD =BC ·cos45°=10×22=52 (n mile),∴AD =325332530tan ⨯==︒BD ≈5×1.4×1.7=11.9(n mile).∴AC =AD +CD ≈11.9+25≈11.9+7.0=18.9≈19(n mile ).答:此时小船与码头之间的距离约为19 n mile.24.解:(1)在Rt △AGB 中,∠ABG =45°,所以AG =BG .所以AB 的坡度为AG ∶BG =1∶1.(2)在Rt △DEC 中,tan C =33=EC DE ,所以∠C =30°.又因为CD =10 m, 所以DE =CD ·sin30°=5 m.(3)由(1)(2)知,AG =BG =DE =5 m,在Rt △AFG 中,∠AFG =30°,tan ∠AFG =FGAG ,即5533-=FB .所以FB =35-5≈3.66 (m ). 答:此改建需占路面的宽度FB 约为3.66 m.25.解:(1)Bb A a sin sin =;∠A +∠B +∠C =180°;a ,∠A ,∠C ;Cc A a sin sin = (2)根据题意,得∠ABC =180°-45°-70°=65°,∠A =180°-(30°+45°+65°)=40°,BC =0.5×28.4=14.2(n mile ).因为︒=︒40sin 2.1475sin AB ,所以AB ≈643.0966.02.14⨯≈21.3(n mile ),所以此时货轮到灯塔A 的距离AB 约为21.3 n mile.图形的相似过关自测卷(90分钟100分)一、选择题(每题3分,共24分)1.已知:a=0.2,b=1.6,c=4,d=1,则下列各式中正确的是()2A.a∶b=c∶dB.a∶c=d∶bC.a∶b=d∶cD.a∶d=c∶b 2.下列命题中:①所有的等腰三角形都相似;②有一对锐角相等的两个直角三角形相似;③四个角对应相等的两个梯形相似;④所有的正方形都相似,正确命题的个数为()A.1B.2C.3D.43.如图1,位似图形由三角尺与其灯光照射下的中心投影组成,位似比为2∶5,且三角尺的一边长为8 cm,则投影三角形的对应边长为()A.8 cmB.20 cmC.3.2 cmD.10 cm 4.如图2,已知△ABC的BC边上有两点D、E,且△ADE是正三角形,则下列条件不一定能使△ABD与△AEC相似的是()A.∠BAC=120°B.AC²=EC·EBC.DE²=BD·ECD.∠EAC+∠B=60°图1 图2 图35.如图3,AD是△ABC的高,EF⊥BC,F为垂足,E是AB边的中点,DC=1BF,若BC=10,则DC的长是()2A.310B.25C.2D. 45 6.如图4,在平行四边形ABCD 中,过点B 的直线BF 与对角线AC 、边AD 分别交于点E 和F .过点E 作EG ∥BC ,交AB 于G ,则图中相似三角形有( )A.4对B.5对C.6对D.7对图4 图5 图67.如图5,小东用长为3.2 m 的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8 m ,与旗杆相距22 m ,则旗杆的高为( )A.12 mB.10 mC.8 mD.7 m8.(2013,新疆)如图6,在Rt △ABC 中,∠ACB =90°,∠ABC = 60°,BC =2cm ,D 为BC 的中点,若动点E 以1cm/s 的速度从A 点出发,沿着A →B →A 的方向运动,设E 点的运动时间为t 秒(0≤t <6),连接DE ,当△BDE 是直角三角形时,t 的值为( )A.2B.2.5或3.5C.3.5或4.5D.2或3.5或4.5二、填空题(每题3分,共24分)9.一个多边形的边长依次为1,2,3,4,5,6,与它相似的另一个多边形的最大边长为8,那么另一个多边形的周长是__________.10.如图7,D ,E 分别是△ABC 的边AB ,AC 上的点,DE ∥BC ,BDAD =2,则ADE S △︰ABC S △=_________.图7 图8 图9 图1011.如图8,△ABC 中,点D 在AB 上,请填上一个你认为适合的条件_______________,使得△ACD ∽△ABC .12.(2013,淄博)在△ABC 中,P 是AB 上的动点(P 异于A ,B ),过点P 的一条直线截△ABC ,使截得的三角形与△ABC 相似,我们不妨称这种直线为过点P 的△ABC 的相似线.如图9,∠A =36°,AB =AC ,当点P 在AC 的垂直平分线上时,过点P 的△ABC 的相似线最多有___________条.13.如图10,光源P 在横杆AB 的上方,AB 在灯光下的影子为CD ,AB ∥CD ,已知AB =2 m ,CD =6 m ,点P 到CD 的距离是2.7 m ,那么AB 与CD 间的距离是__________.14.如图11,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时,PB 的长为____________.图11 图12 图1315.(2013,南通)如图12,在□ABCD中,AB=6 cm,AD=9 cm,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂cm,则EF+CF的长为_________cm.足为G,BG16.(2013,苏州)如图13,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上.点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P.则点P的坐标为___________.三、解答题(23题10分,其余每题7分,共52分)17.如图14,在△ABC中,AB=AC,∠BAC=120°,求AB∶BC的值.图1418.(2013,怀化)如图15,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°.求证:△ABC∽△DEF.图1519.如图16,已知△ADE∽△ABC,∠A=70°,∠B=45°,AE=3cm,EB=4cm,AD=4cm,求∠AED的度数及AC的长.图1620.(2013,滨州)某高中学校为高一新生设计的学生板凳的正视图如图17所示,其中BA=CD,BC=20 cm,BC、EF平行于地面AD且到地面AD的距离分别为40 cm、8 cm,过B点作BH⊥AD,分别交EF,AD于M,H,过C点作CG⊥AD,分别交EF,AD于N,G.为使板凳两腿底端A、D之间的距离为50 cm,那么横梁EF应为多长?(材质及其厚度等暂忽略不计).图1721.如图18,在正方形ABCD中,E是BC上的一点,连接AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.求证:(1)BH=CG;图18(2)FC ²=BF ·GF ;(3)22AB FC =GB GF .22.如图19,在边长均为1的小正方形网格纸中,△OAB 的顶点O 、A 、B 均在格点上,且O 是直角坐标系的原点,点A 在x 轴上. (1)以O 为位似中心,将△OAB 放大,使得放大后的△11B OA 与 △OAB 对应线段的比为2∶1,画出△11B OA (所画△11B OA 与△OAB 在原点两侧);图19(2)求出线段11B A 所在直线对应的函数关系式.23.(2013,遵义)如图20,在Rt△ABC中,∠C=90°,AC=4 cm,BC=3 cm.动点M,N从点C同时出发,均以每秒1 cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2 cm 的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?.图20(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由参考答案及点拨一、1.C 点拨:∵a =0.2,b =1.6,c =4,d =21,且0.2×4=1.6×21,∴ac=bd ,∴a ∶b =d ∶c ,故选C .2.B 点拨:①所有的等腰三角形形状不一定相同,故不一定都相似,故此选项错误;②有一对锐角相等的两个直角三角形相似,根据已知可得出三角形两对对应角相等,故此选项正确;③在梯形内,做一腰的平行线,得一小梯形,显然小梯形与原梯形不相似,故此选项错误;④所有的正方形的四个角都是直角,对应边成比例,所以所有的正方形都相似,此选项正确,故正确的有2个,故选B . 3.B 点拨:∵位似图形由三角尺与其灯光照射下的中心投影组成,位似比为2∶5,三角尺的一边长为8 cm ,∴投影三角形的对应边长为:8÷52=20(cm ),故选B .4.B 点拨:本题在根据各选项中条件判定△ABD 与△AEC 相似时,易不理解判定定理2中“两边成比例且夹角相等”这一条件而出错. 5.C 点拨:∵AD 是△ABC 的高,EF ⊥BC ,F 为垂足,E 是AB 边的中点,∴EF ∥AD ,∴BF=DF ,∵DC =21BF ,BC =10,∴25BF =10,∴BF =4,∴DC =2.故选C .6.B 点拨:题图中相似三角形有△ABC ∽△CDA ,△AGE ∽△ABC ,△AFE ∽△CB E ,△BGE ∽△BAF ,△AGE ∽△CDA 共5对,理由是:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB ∥CD ,AD=BC ,AB=CD ,∠D =∠ABC ,∴△ABC ≌△CDA ,即△ABC ∽△CDA ,∵GE ∥BC ,∴△AGE ∽△ABC ∽△CDA ,∵GE ∥BC ,AD ∥BC ,∴GE ∥AD ,∴△BGE ∽△BAF ,∵AD ∥BC ,∴△AFE ∽△CBE ,故选B . 7.A 点拨:如答图1,∵ED ⊥AD ,BC ⊥AC ,∴ED ∥BC ,∴△AED∽△ABC ,∴BCED =AC AD,而AD =8 m ,AC=AD+CD =8+22=30(m ),ED =3.2 m ,∴BC=AD AC ED ∙ =8302.3⨯=12(m ),∴旗杆的高为12 m ,故选A .答图18.D 点拨:∵在Rt △ABC 中,∠ACB =90°,∠ABC =60°,BC =2 cm ,∴AB =2BC =4 cm ,∵BC =2 cm ,D 为BC 的中点,动点E 以1 cm/s 的速度从A 点出发,∴BD =21BC =1 cm ,BE=AB -AE ,若∠BED =90°,当A →B 时,∵∠ABC =60°,∴∠BDE =30°,∴BE =21BD =12cm ,∴t =3.5,当B →A 时,t =4+0.5=4.5.若∠BDE =90°,当A →B 时,∵∠ABC=60°,∴∠BED =30°,∴BE=2BD =2 cm ,∴t =4-2=2,当B →A 时,t =4+2=6(舍去).综上可得:t 的值为2或3.5或4.5,故选D .二、9.28 点拨:设另一个多边形的周长是x ,依题意,有x ∶(1+2+3+4+5+6)=8∶6,解得x =28,故另一个多边形的周长是28. 10.4∶9 点拨:∵DE ∥BC ,∴△ADE ∽△ABC ,又∵AD ∶DB =2∶1,∴AD ∶AB =2∶3,∴S △ADE ∶S △ABC =4∶9.11.∠2=∠ACB 点拨:要使△ACD ∽△ABC ,已知有一对公共角,则可添加∠2=∠ACB 或∠1=∠B ,从而利用有两组角对应相等的两个三角形相似来判定,答案不唯一.12.3 点拨:如答图2,过P 点作PD ∥BC 交AC 于D ,过P 点作PE ∥AC ,交BC 于E ,当PD ∥BC 时,△APD ∽△ABC ;当PE ∥AC 时,△BPE ∽△BAC ;连接PC ,∵∠A =36°,AB=AC ,点P 在AC 的垂直平分线上,∴AP=PC ,∠ABC=∠ACB =72°,∴∠ACP =∠P AC =36°,∴∠PCB =36°,∴∠B =∠B ,∠PCB =∠A ,∴△CPB ∽△ACB ,故过点P 的△ABC 的相似线最多有3条,故答案为3.答图213.1.8 m 点拨:∵AB ∥CD ,∴△P AB ∽△PCD ,设CD 到AB 距离为x m ,则7.27.2x -=CD AB ,又∵AB =2 m ,CD =6 m ,∴7.27.2x -=31,∴x =1.8,故答案为1.8 m .14.3 点拨:延长CB 到E ,使EB =CB ,连接DE 交AB 于P .则DE 就是PC+PD 的和的最小值,如答图3.∵AD ∥BE ,∴∠A =∠PBE ,∠ADP =∠E ,∴△ADP ∽△BEP ,∴AP ∶BP =AD ∶BE =4∶6=2∶3,∴PB =23P A ,又∵P A+PB=AB =5,∴PB =53AB =3.答图315.5 点拨:∵AE 平分∠BAD ,∴∠DAE =∠BAE ;又∵AD ∥BC ,∴∠BEA =∠DAE =∠BAE ,∴AB=BE=6 cm ,∴EC =9-6=3(cm ),∵BG ⊥AE ,垂足为G ,∴AE =2AG .在Rt △ABG 中,∵∠AGB =90°,AB =6 cm ,BG =42 cm ,∴AG =2BG AB—2 =2 cm ,∴AE =2AG =4 cm ;∵EC ∥AD ,∴EF AE EF + =AD EC =CD FC FC + =93=31,∴4+EF EF =31,6+FC FC =31,解得:EF =2 cm ,FC =3 cm ,∴EF+CF 的长为5 cm ,故答案为5.16.(2,4-22) 点拨:∵四边形OABC 是边长为2的正方形,∴OA=OC =2,OB =22,∵QO=OC ,∴BQ=OB -OQ =22-2,∵AB ∥OC ,∴△BPQ ∽△OCQ ,∴OC BP =OQBQ,即2BP =2222—,解得BP =22-2,∴AP=AB -BP =2-(22-2)=4-22,∴点P 的坐标为(2,4-22),故答案为(2,4-22).三、17.解:如答图4,过点A 作AD ⊥BC 于D ,∵AB=AC ,∠BA C=120°,∴∠B =∠C =30°,BC =2BD ,设AD=x ,则AB =2AD =2x ,根据勾股定理,BD =22AD AB — =()222x x — =3x ,∴BC =23x ,∴AB ∶BC =2x ∶23x =1∶3.答图418.证明:在△DEF 中,∠D =180°-∠E -∠F =180°-79°-54°=47°,∵∠C =∠F =54°,∠A =∠D =47°,∴△ABC ∽△DEF . 19.解:∵∠A =70°,∠B =45°,∴∠C =180°-∠A -∠B =180°-70°-45°=65°,∵△ADE ∽△ABC ,∴∠AED =∠C =65°;AE ∶AC=AD ∶AB ,而AE =3 cm ,EB =4 cm ,AD =4 cm ,∴AB=AE+EB =4+3=7(cm ),∴AC =473 =421(cm ).∴∠AED 的度数为65°,AC 的长为421cm . 20.解:由题意得,MH =8 cm ,BH =40 cm ,则BM =32 cm ,易知四边形ABCD 是等腰梯形,AD =50 cm ,BC =20 cm ,∴AH =21(AD -BC )=15 cm .∵EF ∥AD ,∴△BEM ∽△BAH ,∴AH EM =BHBM ,即15EM =4032,解得:EM =12 cm ,∵四边形ABCD 是等腰梯形,且EF ∥AD ,∴EF=EM+NF+BC =2EM+BC =44 cm . 答:横梁EF 应为44 cm .21.证明:(1)∵BF ⊥AE ,CG ∥AE ,∴CG ⊥BF ,∵在正方形ABCD 中,∠ABH +∠CBG =90°,∠CBG +∠BCG =90°,∠BAH +∠ABH =90°,∴∠BAH =∠CBG ,∠ABH =∠BCG ,AB=BC ,∴△ABH ≌△BCG ,∴BH=CG .(2)∵∠BFC =∠CFG ,∠BCF =∠CGF=90°,∴△CFG ∽△BFC ,∴BF FC =FCGF,即FC 2=BF ·GF ; (3)∵BF ⊥AE ,CG ∥AE ,∴CG ⊥BF ,∴∠CBG+∠BCG =90°,∵四边形ABCD 为正方形,∴∠BCD =90°,∴∠CBG +∠BFC =90°,∴∠BCG =∠BFC ,∵∠CBG =∠FBC ,∴△BCG ∽△BFC ,∴BFBC=BCBG,BC 2=BG ·BF ,∵AB =BC ,∴AB 2=BG ·BF ,∴22AB FC =BF BG BF FG ⋅⋅,即22ABFC =GB GF.22.解:(1)如答图5,△OA 1B 1为所求作的三角形.答图5(2)由(1)可得点A 1、B 1的坐标分别为A 1(4,0)、B 1(2,-4),故设线段A 1 B 1所在直线对应的函数关系式为y=kx+b (k ≠0), ∴⎩⎨⎧+=+=,24,40b k b k - 解得⎩⎨⎧==.82-,b k故线段A 1 B 1所在直线对应的函数关系式为:y =2x -8. 23.解:∵如答图6,答图6在Rt △ABC 中,∠C =90°,AC =4 cm ,BC =3 cm .∴根据勾股定理,得AB =22BC AC — =5 cm .(1)以A ,P ,M 为顶点的三角形与△ABC 相似,分两种情况:①当△AMP ∽△ABC 时,AB AM =AC AP ,即54t —=425t —,解得t =23;②当△APM ∽△ABC 时,AC AM =AB AP ,即44t —=525t—,解得t =0(不合题意,舍去),综上所述,当t =23时,以A ,P ,M 为顶点的三角形与△ABC 相似.(2)存在某一时刻t ,使四边形APNC 的面积S 有最小值.假设存在某一时刻t ,使四边形APNC 的面积S 有最小值.如答图6,过点P作PH ⊥BC 于点H .则PH ∥AC ,∴△BPH ∽△BAC ,∴AC PH =BABP,即4PH =52t ,∴PH =58t cm ,∴S =S △ABC -S △BPN =21×3×4-21×(3-t )·58t =54(t -23)2+521(0<t <2.5).∵54>0,∴S 有最小值.当t =23时,S 最小值=521.答:当t =23时,四边形APNC 的面积S 有最小值,其最小值是521cm 2.。
福建省厦门市第五中学九年级数学上学期周末自测卷3(圆

CAB OED CABOE D图1A BCOABCOD 图2图3 ABO CDABCO 图4ABCDO图5九年级上数学周末自测卷—圆3班级 姓名 座号 一、选择题1.半径为cm 2的正六边形的边心距等于 ( )A .cm 1B .cm 3C .cm 5D .cm 22.已知⊙O 的半径为cm 6,弦AB 所对的圆周角等于︒30,则弦AB 的长为 ( )A .cm 3B .cm 4C .cm 5D .cm 6 3.如图,⊙O 的两条弦AE 、BC 相交于点D ,连结AC 、BE .若∠ACB =60°,则下列结论正确的是 ( ) A .∠AOB =︒60 B .∠AEB =︒60 C .∠ADB =︒60 D .∠AEB =︒304.如图,AB 是⊙O 直径,CD 是弦,AB 与CD 相交于点E ,连结AC 、AD 、OD 则下列结论不能成立....的是 ( ) A .∠ACB =︒90 B .∠ADC =∠ABC C .∠ACD =21∠AOD D .∠D EB =21∠BOD 5.Rt△ABC 的两条直角边长分别为6、8,以直角顶点C 为圆心,5为半径的⊙C 与直线AB ( )A .相交B .相切C .相离D .相交或相切6.以半径为1的正三角形、正方形、正六边形的边心距为三边作三角形,则 ( )A . 不能构成三角形B .这个三角形是等腰三角形C .这个三角形是直角三角形D .这个三角形是钝角三角形7.如图2,在△ABC 中,AB=AC=2,BC=2。
以A 为圆心作圆弧切BC 于点D ,且分别交边AB 、AC 于点E 、F ,则扇形AEF 的面程是 ( ) A .8π B .4π C .2πD .π 二、填空8.正三角形的中心角等于= °.9.(1)已知圆弧的半径为12,圆心角为60○,则此弧的弧长为 .(2)一个扇形所在圆的半径为10,圆心角为108○,则扇形的面积为 .(3)一个扇形所在圆的半径为6,扇形的面积为π12,则扇形的圆心角为 °. (4)已知扇形圆心角为150○,它所对弧长为20π,则扇形半径是 ,扇形面积是 .10.如图1,在⊙O 中,△ABC 的三个顶点都在圆周上,且∠OBC =︒40,则∠A = 度. 11.如图2,在⊙O 中,AB 是直径,∠AOC =︒130,则∠BDC = .12.如图3,在⊙O 中,AB 是直径,AC 、CD 是弦,AB =cm 6,∠CDB =︒30,则∠ABC = ,BC = ,AC = . 13.如图4,在⊙O 中,弦AB 等于它的半径,点C 在优弧AB 上,则∠ACB = . 14.如图5,在⊙O 中,AB 是直径,点C .D 在⊙O 上,AC =BD , ∠COD =40°,则∠COB = °,∠A = °.ABC DOD OPCBABOCA二、解答题15.如图,已知A 、B 、C 是⊙O 上的三点,∠ACB=900,BC=3,AC=4,求⊙O 直径的长度.16.如图,AB 、AC 、B C 都是⊙O 的弦,OC 与AB 交于点D ,∠CAB =∠CBA (1)写出图中除半径之外的五个等量关系;(不再自己标字母) (2)试证明:OC ⊥AB .17.如图,AB 为⊙O 的直径,CD 为⊙O 的弦, (1)若∠ACD=42°,求∠BAD 的度数; (2)连结BD ,若AD=6,BD=8,求⊙O 的半径.18.如图,直线AB 经过⊙O 上的点C ,并且OA =OB ,CA =CB ,求证:直线AB 是⊙O 的切线.19.如图,AB 是⊙O 的直径,点D 在AB 的延长线上,直线CD 与⊙O 相切,点C 为切点,且CA =CD .(1)求∠CDA 的度数;(2)若⊙O 的半径为4,求点A 到CD 所在直线的距离.20.如图,AB 是⊙O 的直径,C 是AD ︵的中点,∠AOD=120°,延长BA 至P ,连接PC .(1)求证:四边形AODC 是菱形; (2)若PA=OA ,PC=33① 判断直线PC 与⊙O 的位置关系,并说明理由; ② 求劣弧BC ︵的长.OCOAB COAB CDE DAO21.如图,点A 、B 、C 分别是⊙O 上的点,∠B=600,AC=3,CD 是⊙O 的直径,P 是CD 延长线上的一点,且AP=AC .(1)求证:AP 是⊙O 的切线; (2)求PD 的长.22.如图,O 为正方形ABCD 对角线AC 上一点,以O 为圆心,OA 长为半径的⊙O 与边BC 相切于点M .(1)求证:CD 与⊙O 相切;(2)若⊙O 的半径为1,求正方形ABCD 的面积.23.如图,AB 是⊙O 的切线,B 为切点,BC 是⊙O 的弦,直线AC 与⊙O 交于D ,∠C =45°, DE⊥AB,垂足为E .(1)判断直线DE 与⊙O 的位置关系,并说明理由; (2)若∠A =30°,AB=232 ,求⊙O 的半径.。
福建省厦门市2014年九年级上学期期末质量检测数学试题

福建省厦门市2014年九年级上学期期末质量检测数学试题(试卷满分:150分 考试时间:120分钟)准考证号 姓名 座位号 考生注意:本学科考试有两张试卷,分别是本试题(共4页26题)和答题卡.试题答案要填在答题卡相应的答题栏内,否则不能得分.一、选择题(本大题有7小题,每小题3分,共21分.每小题有四个选项,其中有且只有一个选项正确)1.下列计算正确的是( )A .333=⨯B .933=⨯C .333=+D .633=+2.方程022=+x x 的根是( )A .0B .-2C .0或-2D .0或2 3.下列事件中,属于随机事件的是( )A .掷一枚质地均匀的正方体骰子,向上的一面点数小于7B .某射击运动员射击一次,命中靶心C .在只装了红球的袋子中摸到白球D .在三张分别标又数字2,4,6的卡片中摸两张,数字和是偶数 4.已知⊙O 的半径是3,OP =3,那么点P 和⊙O 的位置关系是( )A .点P 在⊙O 内B .点P 在⊙O 上C .点P 在⊙O 外D .无法确定5.下列图行中,属于中心对称图形的是( )A .等边三角形B .直角三角形C .矩形D .等腰梯形 6.反比例函数xm y 2-=的图像在第二、四象限内,则m 的取值范围( ) A .0>m B .2>m C .0<m D .2<m 7.如图1,在⊙O 中,弦AC 和BD 相交于点E,⌒AB =⌒BC =⌒CD , 若∠BEC =110°,则∠BDC ( )A .35°B .45°C .55°D .70°DCABE二、填空题(本大题有10小题,每小题4分,共40分) 8.化简:3-= .9. 一个圆形转盘平均分成红、黄、蓝、白4个扇形区域,向其投掷一枚飞镖, 飞镖落在红色区域的概率是 .10.已知点)2,1(--A 与点)2,(m B 关于原点对称,则m 的值是 . 11.已知△ABC 的三边长分别是6,8,10,则△ABC 外接圆的直径是__________. 12.九年级有一个诗歌朗诵小组,其中男生5人,女生12人,先从中随机抽取一名同学参加表演,抽到男生的概率是 .13.若直线12)2(-+-=k x k y 与y 轴交于点(0,1),则k 的值等于 . 14.如图,A 、B 、C 、D 是⊙O 上的三个点,若∠AOC =110°,则∠ABC = .15.电流通过导线时会产生热量,设电流是I(安培),导线电阻为R(欧姆),t 秒产生的热量为Q(焦),根据物理公式Q=I²Rt ,如果导线的电阻为5欧姆,2秒时间导线产生60焦热量, 则电流I 的值是 安培.16.如图,以正方形ABCD 的顶点D 为圆心画圆,分别交AD 、CD 两边于点E 、F ,若∠ABD =15°,BE =2,则扇形DEF 的面积是________.17.求代数式12411)2411(2++-+--+c a aca ac a 的值是 . 三、解答题(本大题有9小题,共89分) 18.(本题满分21分) (1)计算32762-+⨯; (2)在平面直角坐标系中,已知点A (2,1),B (2,0),C (1,-1),请在图上画出△ABC ,并画出与△ABC 关于原点O 对称的图形;C F AB DE(3)如图,AB 是⊙O 的直径,直线AC ,BD 是⊙O 的 切线,A ,B 是切点.求证:AC ∥BD .19.(本题满分21分)(1)第一盒乒乓球中有2个白球1个黄球,第二盒子乒乓球中有1个白球1个黄球,分别从每个盒中随机地取出1个球,求这两个球中欧一个是白球一个是黄球的概率;(2)解方程:0232=-+x x ; (3)如图,在⊙O 中,⌒AB =⌒AC ,∠A=30°,求∠B 的度数20.(本题满分6分)判断关于x 的方程0)2(2=-++p px x 的根的情况.A COB D21.(本题满分6分)2,已知O是平面直角坐标系的原点,点A(1,n),B(-1,-n)(n>0),AB的长是5若点C在x轴上,且OC=AC,求点C的坐标.22.(本题满分6分)如图,利用一面长度为7米的墙,用20米长的篱笆能否围出一个面积为48平方米的矩形菜园?若能,求出该菜园与墙平行一边的长度;若不能,说明理由.23.(本题满分6分)如图,平行四边ABCD中,O为AB上的一点,连接OD、OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P、Q.若OB=4,OD=6,∠ADO=∠A,=2π,判断直线DCD C与⊙O的位置关系,并说明理由.A O B24.(本题满分6分)已知点))(,(),,(212211m m n m B n m A <在直线b kx y +=上,若b m m 321=+,,2421>+=+b kb n n , 试比较1n 和2n 的大小,并说明理由.25.(本题满分6分)如图,⊙O 是△ABC 的外接圆,D 是弧ACB 的中点,DE ∥BC 交AC 的延长线于点E ,若AE =10,∠ACB =60°,求BC 的长.CA BED26.(本题满分11分)已知关于的方程)0(02≠=++b b ax x 与02=++d cx x 都有实数根,若这两个方程有且只有一个公共根,且cd ab =,则称它们互为“同根轮换方程”. 如062=--x x 与0322=--x x 互为“同根轮换方程”.(1)若关于x 的方程042=++m x x 与062=+-n x x 互为“同根轮换方程”,求m 的值;(2)若p 是关于x 的方程)0(02≠=++b b ax x 的实数根,q 是关于x 的方程02122=++b ax x 的实数根,当p 、q 分别取何值时,方程)0(02≠=++b b ax x 与02122=++b ax x互为“同根轮换方程”,请说明理由.2013—2014学年(上) 厦门市九年级质量检测数学参考答案及评分标准一、选择题(本大题共7小题,每小题3分,共21分)题号 1 2 3 4 5 6 7 选项ACBBCDA二、填空题(本大题共10小题,每题4分,共40分)8. 3; 9. 14; 10.1; 11. 10; 12. 517; 13. 1; 14. 125; 15. 6; 16. π2; 17. 1.18.(本题满分21分) (1)(本题满分7分)计算:2×6+27- 3解:原式=23+33- 3 ……………………………4分 =43. ……………………………7分 (2)(本题满分7分)解: 正确画出△ABC . ……………………………3分正确画出△A ,B ,C .,……………………………7分(3) (本题满分7分)证明:∵直线AC ,BD 是⊙O 的切线,又∵AB 是⊙O 的直径, ……………………………3分 ∴OA ⊥AC .OB ⊥BD . ……………………………5分 ∴AC ∥BD . ……………………………7分19.(本题满分21分) (1)(本题满分7分)P (一个白球一个黄球) ……………………………1分=12. ……………………………7分(2)(本题满分7分)解:∵a =1,b =3,c =-2,∴ △=b 2-4ac=17. ……………………………2分 ∴ x =-b ±b 2-4ac2a=-3±172. ……………………………5分∴x 1=-3+172,x 2=-3-172. ……………………………7分 (3)(本题满分7分) 解:在⊙O 中,∵︵AB =︵AC ,∴∠B =∠C .……………………………3分∵∠A =30°,∠A +∠B +∠C =180°,∴∠B =75°. ……………………………7 20.(本题满分6分)解: ∵ △=b 2-4ac=p 2-4×1×(p -2)=p 2-4p +8 ……………………………2分=(p -2)2+4. ……………………………4分∵(p -2)2≥0,∴(p -2)2+4﹥0. ……………………………5分即△﹥0.∴方程x 2+px +(p -2)=0有两个不相等的实数根.…………………6分21.(本题满分6分)解: 过点A 作AD ⊥x 轴于点D ,∵A (1,n ),B (-1,-n ), ∴点A 与点B 关于原点O 对称.∴点A 、B 、O 三点共线. ……………1分∴AO =BO =5. …………………2分在Rt △AOD 中, n 2+1=5, ∴ n =±2. ∵ n >0,∴ n =2. ……………………………3分 若点C 在x 轴正半轴,设点C (a ,0),则CD =a -1. 在Rt △ACD 中,AC 2=AD 2+CD 2=4+(a -1)2. ……………………………4分OC B A又∵OC =AC∴ a 2=4+(a -1)2.∴ a =52. ……………………………5分 若点C 在x 轴负半轴,∵AC >CD >CO ,不合题意.∴点C (52,0). ……………………………6分22.(本题满分6分)答:不能. ……………………………1分设该菜园与墙平行的一边的长为x 米, 则该菜园与墙垂直的一边的长为12(20-x )米,若 12(20-x ) x =48.即 x 2-20x +96=0. ……………………………4分解得x 1=12,x 2=8. ……………………………5分∵墙长为7米,12﹥7且8﹥7, ……………………………6分 ∴ 用20米长的篱笆不能围出一个面积为48平方米的矩形菜园. 23.(本题满分6分)解:如图, 在⊙O 中,半径OB =4, 设∠POQ 为n °,则有 2π=8πn 360.n =90°.……………………………1分∴∠POQ =90°. ∵∠ADO =∠A ,∴AO =DO =6. ……………………………2分 ∴AB =10.∵四边形ABCD 是平行四边形,∴DC =AB =10. ……………………………3分 ∴ CO =8. ……………………………4分 过点O 作OE ⊥CD 于点E , 则OD ×OC =OE ×CD .∴OE =4.8. ……………………………5分 ∵4.8>4,∴直线DC 与⊙O 相离. ……………………………6分24.(本题满分6分) 解:∵A (m 1,n 1),B (m 2,n 2)在直线y =kx +b 上,∴ n 1=k m 1+b ,n 2=km 2+b . ……………………………1分 ∴ n 1+n 2=k (m 1+m 2) +2b . ∴ kb +4=3kb +2b .∴k +1=2b . ……………………………3分 ∵ b >2,∴ 0<2b <1. ……………………………4分 ∴ 0<k +1<1.∴ -1<k <0. ……………………………5分 ∵ m 1<m 2,∴ n 2<n 1. ……………………………6分 25.(本题满分6分)解:连结DA 、DB .∵D 是︵ACB 的中点,∴ DA =DB .∵∠ACB=60°,∴∠ADB=60°……………1分∴△ADB 是等边三角形. ∴∠DAB=∠DBA=60°. 连结DC .则∠DCB=∠DAB=60°. ∵ DE ∥BC ,∴∠E=∠ACB=60°.∴∠DCB=∠E . ……………………………2分 ∵ ∠ECD=∠DBA=60°, ∴ △ECD 是等边三角形.∴ ED=CD . ……………………………3分 ∵ ︵CD=︵CD ,∴∠EAD=∠DBC . ……………………………4分 ∴△EAD ≌△CBD . ……………………………5分 ∴ BC=EA=10. ……………………………6分 26.(本题满分11分) (1)(本小题满分4分)解:∵方程x 2+4x +m =0与x 2-6x +n =0互为“同根轮换方程”,∴ 4m =-6n . ……………………………1分设t 是公共根,则有t 2+4t +m =0,t 2-6t +n =0.解得,t =n -m10. ……………………………2分∵ 4m =-6n . ∴ t =-m6. ……………………………3分 ∴(-m 6)2+4(-m6)+m =0.∴ m =-12. ……………………………4分(2)(本小题满分7分)解1:∵ x 2-x -6=0与x 2-2x -3=0互为“同根轮换方程”,它们的公共根是3. ……………………………1分 而 3=(-3)×(-1)=-3×(-1).又∵ x 2+x -6=0与x 2+2x -3=0互为“同根轮换方程” .它们的公共根是-3.而-3=-3×1.∴当p =q =-3a 时, ……………………………3分 有9a 2-3a 2+b =0.解得,b =-6a 2.∴ x 2+ax -6a 2=0,x 2+2ax -3a 2=0.解得,p =-3a ,x 1=2a ;q =-3a ,x 2=a .……………………………4分 ∵b ≠0,∴-6a 2≠0,∴a ≠0.∴ 2a ≠a .即x 1≠x 2. ……………………………5分又∵ 2a ×12b =ab , ……………………………6分∴方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0互为“同根轮换方程” .……………………………7分解2:∵ x 2-x -6=0与x 2-2x -3=0互为“同根轮换方程”;它们的非公共根是-2,-1. ……………………………1分 而-2=2×(-1),-1=1×(-1).又∵ x 2+x -6=0与x 2+2x -3=0互为“同根轮换方程” .它们的非公共根是2,1.而2=2×1,1=1×1.∴当p =2a ,q =a 时, ……………………………3分 有4a 2+2a 2+b =0.解得,b =-6a 2.∴有 x 2+ax -6a 2=0,x 2+2ax -3a 2=0.解得,x 1=-3a ,p =2a ;x 3=-3a ,q =a .……………………………4分 ∵b ≠0,∴-6a 2≠0,∴a ≠0.∴2a ≠a .即p ≠q . ……………………………5分 且x 1=x 3=-3a .∵ 2a ×12b =ab , ……………………………6分∴方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0互为“同根轮换方程” .……………………………7分解3:若方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0有公共根.则由x 2+ax +b =0,x 2+2ax +12b =0解得x =b 2a . ……………………………1分∴ b 24a 2+b 2+b =0.∴b =-6a 2. ……………………………3分 当b =-6a 2时,有 x 2+ax -6a 2=0,x 2+2ax -3a 2=0.解得,x 1=-3a ,x 2=2a ;x 3=-3a ,x 4=a .…………………………4分 若 p =q =-3a ,∵b ≠0,∴-6a 2≠0,∴a ≠0.∴2a ≠a .即x 2≠x 4. …………………………5分∵ 2a ×12b =ab , …………………………6分∴方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0互为“同根轮换方程” .…………………………7分。
福建省厦门市第五中学九年级数学上学期周末自测卷(相似)

遇见我是你我今生的缘分,祝你考试顺利,学习进步,金榜题名!798765123465432145cmDB ACBAOyx图3 图2 图1AE D图4BCDEAEDCBA九年级上数学周末自测卷一、选择题1.下列各组图形中,不一定相似的是....... ( ) A .两个等腰直角三角形 B .两个等边三角形 C .两个菱形 D .两个正方形 2.如图,∠AD E=∠C,AD=EC=3,AE=4, 则DE:BC 等于 ( )A .4:3B .7:4C .2:1D .7:33.如图,在△ABC 中,DE ∥BC ,AD=2, DB=3,则DE:BC 等于 ( )A .32 B .52C .31D .534.如图,∠ADE=∠C ,则下列能成立的等式是 ( )A .AC AE AB AD = B .BC DE AB AD = C .DB AE EC AD = D .BCDE AC AD = 5.如图,铁道口的栏杆短臂OA 长1m ,长臂OB 长8m .当短臂外端A 下降0.5m 时, 长臂外端B 升高 ( ) A .2m B .4mC .4.5mD .8m二、填空:6.如图1,在△ABC 中,DE∥BC,32=DB AD ,则=BC DE.7.若线段a ,b ,c ,d 满足cbb a =,且4=ac ,则=b . 8.相似三角形的面积比为1:3,则相似比是 .9.如图2,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上, 则球拍击球的高度h = m .10.如图5是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB 的高度为36cm ,那么它在暗盒中所成的像 CD 的高度应为 cm .11.如图4,平行四边形ABCD 中,E 是边BC 的中点,AE 交BD 于点F ,则AFD BEF :∆∆S S = . 三、解答题12.已知:如图,AB ∥CD ,AC 与BD 相交于E ,CE=2,AE=3. (1)求AB CD 的值;(2)若∠AEB =90°,BD =320,求sinA 的值.13.已知:如图,等边△ABC 中,D 、E 分别是BC 、AC 上的点,且∠ADE=60°, 若BD=4,EC=3,求AB 的长.E DCBA E DCB A遇见我是你我今生的缘分,祝你考试顺利,学习进步,金榜题名!14.如图所示,E 是边长为4正方形ABCD 的边AB 上的一点, EF⊥DE 交BC 于点F . (1)若BF=43,求AE 的长; (2)BF 的长能否等于23?说明理由.。
福建省厦门市第五中学九年级数学上学期周末自测卷(无答案) 新人教版

资料1第3题第6题第8题第9题DNMA 九年级上数学周末自测卷班级 姓名 座号1.计算:(1) =⨯73 ;(2)=-+)13)(13( . 2.方程3)2(2=-x 的解为 . 3.如图,在⊙O 中,AB ︵=AC ︵,∠B =︒07,则∠A= 度. 4.掷两枚硬币,正面都朝上的概率为 .5.若关于x 的方程c x =2有解,则c 的取值范围是 . 6.如图,四边形ABCD 内接于⊙O,若∠BOD=130°, 则它的一个外角∠DCE 等于 °.7.写出一个两根互为相反数的一元二次方程: . 8.如图,点D 是等边△ABC 内一点,如果△ABD 绕点A 逆时针旋转后能与△A CE重合,那么旋转了 度.9.如图,已知∠A BC =90°,AB =πr ,BC =πr2,半径为r 的⊙O 从点A 出发,沿A →B →C 方向滚动到点C 时停止.请你根据题意,在图上画出圆心..O 运动路径的示意图;圆心O 运动的路程是 .10.一次抽奖活动设置了如下的翻奖牌,如果你只能在9个数字中选中一个翻牌, (1)写出得到一架显微镜的概率;(2)请你根据题意写出一个事件,使这个事件发生的概率是2. 翻奖牌正面11.如图,AB 为⊙O 的弦,C 为劣弧AB 的中点,(1)若⊙O 的半径为5,AB=8,求圆心O 到AB 的距离; (2)若∠D AC=∠BAC ,且点D 在⊙O 的外部,判断AD 与⊙O的位置关系,并说明理由. 212.如图,在△ABC 中,AB=AC ,以BC 为直径的⊙O 分别交AB,AC , AO于M ,N ,D .资料1(1)求证:BM=CN ;(2)若AB =10,BC =12,求BM 的长.13.已知关于x 的一元二次方程02)1(222=-+--m m x m x 的两个实数根分别为1x ,2x . (1)若方程有一个根是1,求m 的值;(2)若012>>x x ,421<+x x ,且123x x y -=,求y 的取值范围.14.如图,△ABC 是等腰直角三角形,AB=22,D 为斜边BC 上的一点(D 与B 、C 均不重合),连结AD ,把△ABD 绕点A 按逆时针旋转后得到△ACE,连结DE ,设BD=x . (1)判断△ADE 的形状,并说明理由; (2)当△DCE 的面积为1.5时,求x 的值;(3)试问:△DCE 的面积是否存在最大值,若存在,请求出这个最大值,并指出此时x 的取值,若不存在;请说明理由.15.在平面直角坐标系xOy 中,直线1l 过点A (1,0)且与y 轴平行,直线2l 过点B (0,2)且与x 轴平行,直线1l 与2l 相交于P ,点E 为直线2l 一点,反比例函数xky =(0>k )的图象过点E ,且与直线1l 相交于点F (点E 与F 不重合),连接OE ,OF ,EF . AB DE资料1(1)线段OE 与OF 能否相等?若相等,求出k 的值;若不能,说明理由; (2)若2 k ,且△OEF 是直角三角形,求点E 的坐标.。
厦门市2014-2015学年初三质检考试模拟试卷

厦门市2014-2015学年初三数学质量检测模拟试卷(二)(试卷满分:150分考试时间:120分钟)一、选择题(本大题有10小题,每小题4分,共40分.每小题有四个选项,其中有且只有一个选项正确)1. 下列图案中不是中心对称图形的是()A.B.C.D.2. 下列事件中,属于确定事件的个数是()(1)打开电视,正在播广告;(2)投掷一枚普通的骰子,掷得的点数小于10;(2)射击运动员射击一次,命中10环;(4)在一个只装有红球的球袋中摸出白球A.0B.1C.2D.33. 配方:x²-3x+ =(x- )²A. 9,3B. 3,3C.3322,D.9342,4.如图,⊙O中,若∠AOC=150°,那么∠ABC=()A.150°B.125°C.105°D.100°A第4题第5题5. 如图,正方形OABC的边长为2,则该正方形绕点O逆时针旋转45°后,B点的坐标为()。
A.2,2()B.()C.(D.0,2()6.已知二次函数22(3)1y x =-+下列判断正确的是( )A 其图像的开口向下B 其图像的对称轴为直线=-3C 其最小值为1D 当x<3是,y 随着x 的增大而增大 7. 边长为a 的正六边形的面积等于( )A2a B 、2a C、2 D28. 根据下列表格对应值:判断关于x 的方程ax 2+bx +c =0(a ≠0)的一个解x 的范围是( )A .x <3.24B .3.24<x <3.25C .3.25<x <3.26D .3.25<x <3.28 9. 已知一个半径为6的扇形面积是4π,则这个扇形的圆心角是( ) A .30° B .40°C .45°D .60°10. 如图,已知抛物线y 1=-2x 2+2,直线y 2=2x +2,当x 任取一值时,x 对应的函数值分别为y 1、y 2.若y 1≠y 2,取y 1、y 2中的较小值记为M ;若y 1=y 2,记M = y 1=y 2.例如:当x =1时,y 1=0,y2=4,y 1<y 2,此时M =0. 下列判断:①当x >0时,y 1>y 2; ②当x <0时,x 值越大,M 值越小;③使得M 大于2的x 值不存在; ④使得M =1的x 值是12-或其中正确的是 ( )A . ①②B .①④C .②③D .③④二、填空题(本大题有6小题,每小题4分,共24分)11. “任意打开一本200页的数学书,正好是第50页”,这是_______事件(选填“随机”,“必然”或“不可能”). 12. 在平面直角坐标系中,将线段OA 绕原点旋转90°,已知OA =2且与x 轴正半轴的夹角是30°,记点A 的对应点为A 1,则A 1的坐标为 。
福建省厦门市第五中学九年级数学上学期周末自测卷2(圆)(无答案) 新人教版

ODB C第7题第8题第2题第5题第6题第10题 A BCO第11题第12题九年级上数学周末自测卷—(圆2)班级 姓名 座号 一、选择题1.已知在半径为cm 10的⊙O 中,圆心O 到弦AB 的距离为cm 6,则弦AB 的长 ( )A .cm 8B .cm 10C .cm 12D .cm 162.如图,AB 、BC 、CA 是⊙O 的三条弦,∠OBC =50º,则∠A 等于 ( )A .25ºB .40ºC .80ºD .100º3.已知⊙O 的半径r ,圆心O 到直线l 的距离为d ,当d =r 时,直线l 与⊙O 的位置关系是( )A .相交B .相切C .相离D .以上都不对4.Rt △ABC 的两条直角边长分别为6、8,以直角顶点C 为圆心,r 为半径的⊙C 与斜边AB 相切,则⊙C 的半径r 取值为 ( )A .6=rB .4=rC .8.4=rD .5=r 5.如图,⊙O 的两条弦AE 、BC 相交于点D ,连结AC 、BE .若∠ACB =70°,则下列结论正确的是 ( )A .∠AOB =130° B .∠AEB =70°C .∠ADB =70°D .∠AEB =80°6.如图,∠AOB =110°,点C 在⊙O 上,且点C 不与A 、B 重合,则∠ACB 的度数为 ( ) A .55° B .55°或70° C .125° D .55° 或125° 二、填空7.如图,OB 是⊙O 的半径,点C 、D 在⊙O 上,∠DCB=27°, 则∠OBD= 度.8.如图,AB 是⊙O 的直径,点C 在圆周上,∠A=65°,则∠B = °.9.如图,四边形ABCD 内接于⊙O,若它的一个外角∠DCE =70°,则∠BOD 等于10.圆内接菱形一定是 形. 11.如图,∠MAB=30°,P 为AB 上的点,且AP =6,圆P 与AM 相切,则圆P 的半径为 . 12. 如图,AB 是⊙O 的直径,点D 在AB 的延长线上,DC 切⊙O 于C ,若∠A=25°,则∠D= °.13.如图,⊙O 过点B 、C ,圆心O 在等腰Rt△ABC 的内部,∠BAC=90°,OA=1,BC=6,则⊙O 的半径为 . 二、解答题14.如图,在⊙O 中,∠ACB=∠BDC=60°,AC =cm 32, (1)求证:△AB C 是等边三角形; (2)求⊙O 的周长.CA15.如图,OA =OB=10,AB =16,⊙O 的直径为12,求证:直线AB 是⊙O 的切线.16.如图,等腰△OAB 中,OA=OB ,以点O 为圆心作圆与底边AB 相切于点C .求证:AC=BC .17.如图,AB ,AC ,BC 都是⊙O 的三条弦,AC =BC ,OC 与AB 交于点D . (1)若∠CAB =28°,求∠OAB 的度数;(2)过点C 作直线PQ ∥AB ,求证:直线PQ 是⊙O 的切线.18.如图,AB 为⊙O 的直径,弦BD 的延长线与直线AC 交点C ,连结AD ,且∠B=∠CAD .(1)求证:AC 是⊙O 的切线;(2)若AC:AB=2:3,B C=132,求⊙O 的半径及AD 的长.19.如图,⊙O 的直径AB =4,C 为圆周上一点,AC =2,过点C 作⊙O 的切线l ,过点B 作直线l 的垂线BD ,垂足为D ,BD 与⊙O 交于点 E .(1)求∠AEC 的度数;(2)求证:四边形OBEC 是菱形.20.如图,⊙O 为△ABC 的外接圆,BC 为⊙O 的直径,BA 平分∠CBE,AD⊥BE,垂足为D .(1)求证:AD 为⊙O 的切线; (2)若AD=2,BD=1,求⊙O 的半径.22.已知:如图8,⊙O 是△ABC 的外接圆,AB 为⊙O 的直径,弦CD 交AB 于E ,∠BCD =∠BAC .(1)求证:AC =AD ;(2)过点C 作直线CF ,交AB 的延长线于点F ,若∠BCF =30°,则结论“CF 一定是⊙O 的切线” 是否正确?若正确,请证明;若不正确,请举反例.图8A。
人教版九年级数学上册厦门五中第一学期期中考试.docx

第10题第4题ABC OD OAE 第13题第7题初中数学试卷桑水出品厦门五中2013—2014学年度第一学期期中考试初三数学试卷(全卷满分:150分; 考试时间:120分钟)班级 座号 姓名注意事项:1.全卷三大题,26小题,试卷共4页,另有答题卡; 2.答案一律写在答题卡上,否则不予得分; 3.可直接用2B 铅笔画图.一、选择题(本大题有7小题,每小题3分,共21分.每小题的四个选项中,只有一个选项正确)1.计算23)(的值是 A .3 B .3± C .3± D .9 2.方程022=-x x 的根是A .2B .2和0C .0D .2和-2 3.下列等式能成立的是A .2222=-B .2222=⨯C .2222=+D .022=÷4.如图,AB 、BC 、CA 是⊙O 的三条弦,∠OBC =50º,则∠A 等于A .80ºB .60ºC .50ºD .40º5.点P (3,-2)关于原点的对称点的坐标是A .(-3,-2)B .(3, 2)C .(-3, 2)D .(-2,3)6.要组织一次篮球赛,参赛的形式是单循环赛(即每两个队之间都要比赛一次).根据时间和场地条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x 支球队参赛,则由题意可列方程 A .28)1(=+x x B .28)1(=-x x C .28)2(=-x x D .282)1(=-x x 7.如图,直线AB 是⊙O 的切线,点C 是切点,OA ,OB 分别与⊙O 交于点D 和点E , OA =OB=6,∠AOB =120°.则扇形ODE 的面积是A .π6B .π3C .π4D .π2 二、填空题(本大题有10小题,每小题4分,共40分)8.二次根式3-x 中有意义,则x 的取值范围是 .9.若2是方程022=+-c x x 的根,则=c .10.如图,点D 是等边△ABC 内一点,如果△ABD 绕点A 逆时针旋转后能与△ACE 重合,那么旋转了 度.11.一元二次方程042=+-k x x 有两个相等的实数根,则k = . 12.半径为1的正六边形的周长等于 .13.如图,在⊙O 中,AB ︵=AC ︵,∠B =75°,则∠A = °. 14.一个正多边形绕着它的中心旋转90°后仍与原图形重合,则这个多边形的边数是 .15.四边形ABCD 的四个顶点都在⊙O 上,且∠A :∠C=1:2,则∠C = °. 16.如图,圆的两条弦AB ,CD 相交于点P ,若∠APC=125°,第16题CB AE ∠B =85°,则∠A = °.17.已知101<<-m ,且72+m 为整数,则m = .三、解答题(本大题有9小题,共89分) 18.(本题满分18分)(1)计算:6283223⨯--+; (2)如图,画出△ABC 关于点C 对称的图形;(3)如图,在Rt △ABC 中,∠ACB=900,⊙O 是△ABC 的外接圆,BC=6,AC=8,求⊙O 半径的长.19.(本题满分7分)解方程:0242=+-x x .20.(本题满分7分)如图,E 是正方形ABCD 中AB 边上一点,以D 为旋转中心,把△ADE 逆时针旋转90°后,点E 的对应点为点F . (1)画出旋转后的图形; (2)若DE=22,求E F 的长. 21.(本题满分8分)若12+=a x ,12-=a y .(1)当=a 1时,求xy 的值; (2)若=-22xy y x 10,求a 的值22.(本题满分8分)学校原有一块周长为140米的矩形场地,宽为x 米,且3520<≤x . (1)若矩形场地的面积为1200平方米,求x 的值;(2)现因整治环境需要,将场地改成了长增加10米,宽减少10米的矩形,结果场地的面积减少了y 平方米,求出y 的取值范围;23.(本题满分10分)已知:如图,在⊙O 中,AB 是直径,AC ,AD 是弦,CE ∥AD 交AB 的延长线于E ,AC ︵=AD ︵,连接DE . (1)求证:AC =CE ;(2)若CE 与⊙O 相切,且⊙O 半径为2,求四边形ACED 的面积.24.(本题满分10分)如图,在边长为21+的正方形ABCD 中,P 是BC P 顺时针旋转得到线段PQ .(1)如图1,若点Q 恰好落在边CD 上,且∠APQ=60°,求∠BAP (2)如图2,若点Q 落在正方形的外部,且∠APQ=90°,△CPQ 25.(本题满分10分)如果一元二次方程02=++c bx ax 的两根1x ,2x 满足21,那么称这个方程有“近似根”.(1)判断方程03522=+-x x 是否有“近似根”,并说明理由;(2)已知关于x 的一元二次方程01)12(2=+++-m x m mx 有“近似根”,求m 的取值范围. 26.(本题满分11分)如图,已知四边形ABCD 是矩形,以BC 为直径的⊙O 交OA 于点E ,点P 是CD 边上一点,设PC=a ,AB=b ,BC=m (0>>>a b m ). (1)若点E 是OA 的中点,且6=m ,求劣弧CE ︵的长; (2)若ab m 2=,求证:直线AP 与与圆O 相切.EDCBA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图 3
九年级上数学周末自测卷
班级 姓名 座号 一、选择题
1.Sin60°的值等于 ( )
A .
21 B .23 C .3 D .3
3 2.已知tanA =1,且∠A 为锐角,则cosA 等于 ( ) A .
23 B .2
2
C .21
D .33
3.如图,在直角△ABC 中,∠C=90°,若AB =5,BC =3,则cosA 的值是 ( ) A . 35 B . 45 C .34 D .4
3
4.Rt△ABC 中,∠C=90°,AC 35=,BC=15,则∠A 的度数为 ( )
A .30°
B .45° C.60° D.无法确定
5.下列事件中,是必然事件的是 ( )
A .抛掷一枚硬币,掷得的结果是正面
B .度量三角形内角和,结果等于181 º
C .任意翻开数学书的某页,页码不是奇数就是偶数
D .购买一张彩票会中奖
6.下列事件中,是随机事件的是 ( ) A .抛掷一枚硬币,掷得的结果不是正面就是反面 B .三角形内角和等于181 º C .在标准大气压下把水加热到100℃,水沸腾 D .经过一个路口遇到红灯
7.掷一个均匀正方体骰子,当骰子停止后,朝上一面的点数为2的概率是 ( ) A .1 B .21 C .31 D .6
1
三、填空题
8.Rt△ABC 中,∠C=90°,BC 、AC 、AB 所对的边分别为a 、b 、c ,6=a , 8=c ,
则sinA= ,cosA= , tanA= ,tanB= .
9.如图2,飞机A 在目标B 的正上方3000米处,飞行员测得地面目标C 的俯角∠DAC =30°,则地面目标BC 的长是 米.
10.如图3,已知在直角三角形ABC 中,∠C =90°,AC =53,
AB =10,则∠B = 度.
11.甲袋中放有10只红球和2只黑球,乙袋中则放有30只红球、20只黑球和10只白球,这三种球除了颜色以外没有其他区别。
从口袋中随机取出1只球,如果你想取出的是黑球,应选 袋成功机会更大. 12.等边三角形的边长为2,则它的面积为 . 13
.在坡度为1α是 度.
14.在分别写有整数1到10的10张卡片中,随机抽取1张卡片,则该卡片上的数字恰好是奇数的 概率是 .
15.从一副除去大小王的52张扑克牌洗匀后正面向下放在桌子上,从中任意抽取一张,则: (1)抽出的牌的点数是6的概率是 ; (2)抽出的牌的是红心10的概率是 ; 16.△ABC 中,AB=AC=10,tanB=
4
3
,则△ABC 的面积为 . 17.在平面直角坐标系中,已知点O(0,0),A(1,n ),B(2,0),其中n >0,△OAB 是等边三角形.
图2
D C
B
A
B
C
A
点P 是线段OB 的中点,将△OAB 绕点O 逆时针旋转30°,记点P 的对应点为点Q . 则n = ,点Q 的坐标是 . 三、解答题
18.(1)如图,在Rt△ABC 中,∠C=90°,sinA=53
,求 cosA 及tan A 的值.
(2)一个批发商从某服装制造公司购进了50包型号为L 的衬衫,由于包装工人的疏忽,
一位零售商从50包中任意选取了一包,求下列事件的概率:
(1)包中没有混入的M 号衬衫; (2)包中混入的M 号衬衫数不超过7;
19.四张大小、质地均相同的卡片上分别标有1,2,3,4.现将标有数字的一面朝下扣在桌子上,然后由小明从中随机抽取一张(不放回),再从剩下的3张中随机取第二张,两张卡片上的数字相加. (1)求取得的两张卡片上的数字之和为6的概率;
(2)在所有的随机事件中,你认为最有可能出现的点数之和是多少?请说明理由.
20.如图,某飞机于空中A 处探测到目标C ,此时飞行高度AC =1200米,从飞机上看地面控制点B
的俯角 =18.6°,求飞机A 到控制点B 的距离.(精确到1米)
(参考数值:sin18.6°=0.32,cos18.6°=0.95,tan18.6°=0.34 )
21.一艘船向正东方向匀速般行,到O 处时,看到一灯塔在它的北偏东600
且距离为363海里
的A 处;经过2小时到达B 处,看到该灯塔恰好在它的正北方向. (1)根据题意,画出示意图; (2)求这艘船的速度.
22.第一盒乒乓球中有1个白球和2个黄球,第二盒乒乓球中有2个白球和1个黄球.
(1)从第一盒乒乓球中取出1个球,求这个球恰好是黄球的概率; (2)分别从每盒乒乓球中取出1个球,求取出的2个球都是黄球的概率.
23.如图,△ABC中,AB=AC,BD⊥BC,连接AD交BC于E,∠BDE=∠DCB,BE:CE=1:3.
(1)求tan∠DCB;
(2)若CD=5
2,求AC的长.
24.我们知道,在直角三角形中,一个锐角的对边与斜边的比叫做这个角的正弦.类似地,我们定义:在等腰三角形中,等腰三角形中底边与腰的比叫做顶角的正对(sad).
如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=BC
AB
.解下列问题:
(1)在△ABC中,AB=AC=5,sinB=0.6,求sadA的值;
(2)在△ABC中,AB=AC ,若sadA=
55
2
,且∠A为锐角,试求sinA的值.。
