全等三角形作辅助线专题一(重点:截长补短法)-可打印版
全等三角形辅助线之截长补短法

B
D
C
三角形全等之截长补短法
已知:如图,在△ABC中,∠1=∠2,∠B=2∠C.求证:AC=AB+BD.
方法一:截长法
A
在AC上取一点E,使AE=AB
12
E
由1=2,AD=AD,AE=AB 可证ADB ADE(ASA), 得DB=DC,AED=B,而B=2C,
故AED=2C而AED=C+EDC,
解:(1)过A作AF BC,可求得AB= 10
(2)由ABD : AEB可得ADgAE=AB2 =10
(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.
补短法1:延长CD至G,过A作AG CD 1.证ADG ADH(ADG=ABC (圆内接四边形的外角等于内对角)) 2.证AGC AHB,可证得结论
E
三角形全等之截长补短法
已知:如图,在△ABC中,∠1=∠2,∠B=2∠C.求证:AC=AB+BD.
A
延长DB至E使BA=BE,
12
E=BAE,ABD=E+BAE=2E
ABD 2C,故E=C
可证BAC=ADE
可证EAD CBA,故AC=AB+BD
E
B
D
C
已知:如图,在正方形ABCD中,AD=AB,∠B=∠D=∠BAD=90°,E,F 分别为CD,BC边上的点,且∠EAF=45°,连接EF. 求证:EF=BF+DE.
今天我们学习截长补短法,见线段和差倍分关系,考虑截长补短法.
其实截长补短法包含两种方法,一种是截长法,即在较长的线段长截 取与较短线段相等的线段;另一种是补短法,将较短线段延长.截长 补短的目的在于将问题合理的转化,进而达到简化结论,并证明结论 或者求解.
全等三角形证明题辅助线专题--截长补短和倍长中线
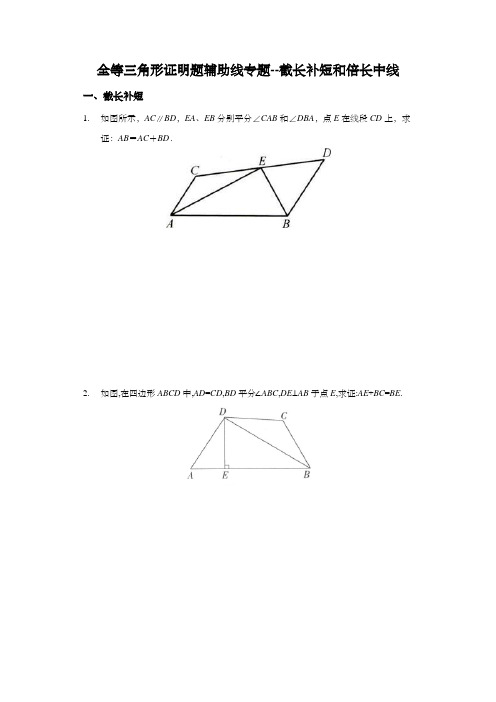
全等三角形证明题辅助线专题--截长补短和倍长中线一、截长补短1.如图所示,AC∥BD,EA、EB分别平分∠CAB和∠DBA,点E在线段CD上,求证:AB=AC+BD.2.如图,在四边形ABCD中,AD=CD,BD平分∠ABC,DE⊥AB于点E,求证:AE+BC=BE.3.如图,△ABC中,∠CAB=∠CBA=45∘,点E为BC的中点,CN⊥AE交AB于点N,连接EN.求证AE=CN+EN.4.如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,(1)求∠BFC的度数.(2)求证:BC=BE+CD.5.如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD.求证:第2页,共28页BC=AB+CE.6.(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=1∠BAD,求证:EF=BE+DF;2(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=1∠BAD,(1)中的结论是否仍然成立?2(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF=1∠BAD,(1)中的结论是否仍然成立?若成立,请证明;2若不成立,请写出它们之间的数量关系,并证明.7.如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF = 60°.探究图中线段BE,EF,FD之间的数量关系.8.如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,(1)求∠AOC的度数;(2)求证:OE=OD;(3)猜测AE,CD,AC三者的数量关系,并证明.第4页,共28页9.如图在△ABC中,∠ABC=60°,AC=2AB,AD平分∠BAC交BC于点D,延长DB点F,使BF=BD,连接AF.(1)求证:AF=CD;(2)若CE平分∠ACB交AB于点E,试猜想AC、AF、AE三条线段之间的数量关系,并证明你猜想的结论.二、倍长中线10.如图,在△ABC和△DEF中,AB=DE,AC=DF,AM和DN分别是中线,且AM=DN.求证:△ABC≌△DEF.11.(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图①,△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:Ⅰ.由已知和作图能得到△ADC≌△EDB,依据是______.A.SSS B.SAS C.AAS D.HLⅡ.由“三角形的三边关系”可求得AD的取值范围是______.解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.(2)【初步运用】如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.12.已知:在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BC交AC于F,求证:AF=EF.第6页,共28页13.如图,在△ABC中,AD是中线,∠BAC=∠BCA,点E在BC的延长线上,CE=AB,连接AE.求证:AE=2AD.14.如图,Rt△ABC中,∠ABC=90°(1)如图1,若BD为高线,AB=4,BC=3,AC=5,求BD的长(2)如图2,若BD为中线,求证:BD=1AC215.如图,在五边形ABCDE中,∠E=90O,BC=DE,,连接AC,AD,且AB=AD,AC⊥BC.(1)求证:AC=AE(2)如图,若∠ABC=∠CAD,AF为BE边上的中线,求证:AF⊥CD;(3)如图,在(2)的条件下,AE=8,DE=5,则五边形ABCDE的面积为_______。
全等三角形作辅助线专题一重点截长补短法可

D CBAED F CBA全等三角形作辅助线经典例题常见辅助线的作法有以下几种:1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”.3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”;(遇垂线及角平分线时延长垂线段,构造等腰三角形)5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.一、倍长中线(线段)造全等1:已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是_________.2:如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小.3:如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.ED CBA中考应用:以ABC∆的两边AB、AC为腰分别向外作等腰Rt ABD∆和等腰Rt ACE∆,90,BAD CAE∠=∠=︒连接DE,M、N分别是BC、DE的中点.探究:AM与DE的位置关系及数量关系.(1)如图①当ABC∆为直角三角形时,AM与DE的位置关系是,线段AM与DE的数量关系是;(2)将图①中的等腰Rt ABD∆绕点A沿逆时针方向旋转︒θ(0<θ<90)后,如图②所示,(1)F E D C BA 21D CB A PQC BA 问中得到的两个结论是否发生改变?并说明理由.二、截长补短1.如图,ABC ∆中,AB=2AC ,AD 平分BAC ∠,且AD=BD ,求证:CD ⊥AC2:如图,AD ∥BC ,EA,EB 分别平分∠DAB,∠CBA ,CD 过点E ,求证:AB =AD+BC3:如图,已知在ABC 内,060BAC ∠=,040C ∠=,P ,Q 分别在BC ,CA 上,并且AP ,BQ 分别是BAC ∠,ABC ∠的角平分线。
全等三角形~截长补短

1 2截长补短截长补短”是几何证明题中十分重要的方法, 通常用来证明几条线段的数量关系, 即若 题目条件或结论中含有 a b c ”的条件,需要添加辅助线时可以考虑截长补短”的方法。
另外的较短线段。
补短法: ①延长较短线段中的一条,使延长出来的线段等于另外的较短线段,然后证明两线段之和等 于较长线段。
即延长a ,得到b ,证:a b①延长较短线段中的一条, 使延长后的线段等于较长线段, 一条较短线段。
即延长a ,得到c ,证:b c-a 。
例1.已知:如图,在 △ ABC 中,△仁△Z, △ B=2AC .求证:1.补短法:证明:如图,延长 AB 到E ,使BE=BD ,连接DE .△ △ABD 是 △BDE 的一个外角△ △ABDME + △BDEABE=BD △ △EMBDE△ △ABD=2 △E△ △ABD=2 △C△ △EMC在 AADE 和 AADC 中△ △ADE △△ADC (AAS )截长法:在较长的线段上截取一条线段等于较短线段,再设法证明较长线段的剩余线段等于 然后证明延长出来的部分等于另AC=AB+BD.ADAD1 2证明:如图,在 CD 上截取CF=CB .△CE 平分△CBD在△CFE 和 △CBE 中△AE=AC△AC=AB + BE=AB + BD2.截长法:证明:如图,在 AC 上截取AF=AB ,连接DF .在△ABD 和△AFD 中AB AFAD AD△ △ABD △△AFD ( SAS )△ ABMAFD , BD=FD△ △B=2 △C△ △AFD =2 △C△ △AFD 是^DFC 的一个外角△ △AFD me + 舉DC△ AFDCmCADF=FCABD=FC△AC=AF+FC=AB+BD例2.如图,在四边形 ABCD 中,△ A=AB=90,点E 为AB 边上一点,且 DE 平分△ ADC ,CE 平分△ BCD .求证:CD=AD+BC.CF CBCE CE△ △CFE △△CBE (SAS)△ △CFEMB△ △B=90△ △CFEMDFE =90△ △A=90 °△ △DFE=AA△DE 平分△ADC在△DEF和△DEA中DFE ADE DE△ △DEF △△DEA (AAS )ADF=AD△CD = DF + CF =AD + BC例3.已知:如图,在正方形ABCD中,AD =AB ,/ B= / D= / BAD =90° E, F 分别为CD , BC 边上的点,且/ EAF=45°,连接EF.求证:EF=BF+DE .证明:如图,延长FB到G,使BG=DE,连接AG . △ △D=^ABC=90△ △ABG = ^D=90在AABG和AADE中AB=ADABG= DBG=DE△ △ABG△△ADE ( SAS)△AG=AE, △ 1 = △△ △BAD=90 △EAF =45△ △ 2+ △ 3=45△ △ 1 = △+△2△ △ 1 = △+△2DB DE△ △ABD △△AED ( SAS )△ △B=2 △C△ △ 1=20△ △1是AAEC 的一个外角△AE=CE△CD=CE+ED=AE+BD=AB+BD△ △ 1 + △ 3=45即△GAF =45°△ △GAFMEAF在△AGF 和 AAEF 中AG AEGAF EAFAF AF△ △AGF △△AEF (SAS )△GF=EF△GF=BF+BGAEF=BF+DE例4.在△ABC 中,AD △BC 于 D , △B=2AC .求证:CD=AB+BD.证明:如图,在线段 DC 上截取DE=BD ,连接AE .△AD △BC△ △ADB = AADE=90在 AABD 和 AAED 中 AD ADADB ADE例5.如图,在△ABC 中,AB>AC , △ 1=A2, P 为AD 上任意一点,连接 BP , CP .求证:AB-AC > PB-PC .1.截长法:证明:如图,在 CF 上截取CM=BA ,连接DM .证明:如图,在线段 AB 上截取AE=AC ,连接PE .贝U AB-AC=AB-AE=EB在MEP 和MCP 中AE ACAP AP△ △\EP^mCP (SAS)APE=PC在APEB 中, PB PE<EBAPB-P C<EB△AB-AC > PB-PC例6.如图,在梯形ABCD 中,ADABC , CEAAB 于E , ABDC 为等腰直角三角形, ABDC=90° BD=CD ,CE 与 BD 交于 F ,连接 AF .求证:CF=AB+AF.△ △BDC 为等腰直角三角形,BD=CD△ △仁△CB=45°△CEAAB, ABDC=90°△ △CEB=^BDC=90°△ △ 2=A3△ △ 4=^5在△ABD 和△MCD 中△ △ABD ^^MCD (SAS )ADA=DM ,△ 6=^7 △AD^BC△ △ ?=△ 1=45°△ △ 6=45°△ △ 8=45°△ △ 7=^8在△ADF 和△MDF 中△ △ADF △△MDF ( SAS )△AF=MF△CF=CM+MF =AB+AF补短法:证明:如图,延长BA 交CD 的延长线于点G . △ △BDC 为等腰直角三角形△ △GDBMBDCrgO 。
全等三角形问题中常见的辅助线截长补短法

全等三角形问题中常见的辅助线——截长补短法
例 1、如图, ABC 中,AB=2AC AD 平分 BAC ,且 AD=BD
求证:CD 丄AC
BQ+AQ=AB+BP
例4、如图,在四边形 ABCD 中, BC> BA,AD = CD ,BD 平分
ABC ,
180
求证: A C 例 2、如图,AD// BC, AE, BE 分别平分/ DAB,/CBA 0 例3、如图,已知在 VABC 内, BAC 60 , C 400, P , Q 分别在
BC, CA 上,并且AP ,BQ 分别是 BAC , ABC 的角 平分线。
求证: 过点E ,求证;AB = AD+BC
顶角为1200的等腰三角形,以D为顶点作一个60°的MDN,点M、N分别在AB、AC上,求
AMN的周长.
变式练习
如图所示,ABC是边长为4的正三角形,BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的MDN,点M、N分别在AB、AC上,求AMN的周长.
例11、五边形ABCDE中, AB=AE BC+DE=CD / ABC+Z AED=180,求
证:DA平分Z CDE
例12、如图,在四边形ABCD中, AD// BC,点E是AB上一个动点,若Z
BC的关系并证明你的结论。
全等三角形辅助线的做法-截长补短

全等三角形辅助线的做法一:截长补短月日姓名【知识要点】1.遇到求证一条线段等于另两条线段之和时,一般方法是截长补短法.(1)截长:在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;(2)补短:将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段.2.角平分线问题的作法角平分线具有两条性质:(1)对称性,作法是在一侧的长边上截取短边;(2)角平分线上的点到角两边的距离相等,作法是从角平分线上的点向角两边作垂线段.【典型例题】例1. 如图,AC平分∠BAD,CE⊥AB,且∠B+∠D=180°,求证:AE=AD+BE.例2. 已知:如图,等腰三角形ABC中,AB=AC,∠A=108°,BD平分∠ABC.求证:BC=AB+DC.例3. 如图,AB>AC, ∠1=∠2,求证:AB-AC>BD-CD. DCBADAE CB12ACD例4.△ABC 中,AC=BC ,∠ACB=90°,D 是AC 上一点,AE ⊥BD 交BD 的延长线于E ,且AE=21BD ,求证:BD 平分∠ABC.例5.已知:△ABC 为等边三角形,AE=BD.求证:EC=DE.【考点突破】1. 如图,AB ∥CD ,AE 、DE 分别平分∠BAD 和∠ADE ,求证:AD=AB+CD.EEEDC2. 已知:CE、AD是△ABC的角平分线,∠B=60°,求证:AC=AE+CD.3. 已知,如图,∠C=2∠A,AC=2BC.求证:△ABC是直角三角形. 4.已知:如图,AB=2AC,∠1=∠2,DA=DB,求证:DC⊥AC. AEB D CCABAB D C1 2CBA5.已知:如图在△ABC 中,∠A=90°,AB=AC ,BD 是∠ABC 的平分线,求证:BC=AB+AD.6.已知:四边形ABCD 中,AB=AD ,∠BAD=60°,∠BCD=120°.求证:AC=BC +CD.课后作业月 日 姓 名 成 绩1. 如图,已知在ABC 内,060BAC ∠=,040C ∠=,P ,Q 分别在BC ,CA 上,并且AP ,BQ 分别是BAC ∠,ABC ∠的角平分线。
(完整版)全等三角形经典题型——辅助线问题

全等三角形问题中常见的辅助线的作法(含答案) 总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一”法:遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”:遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”法构造全等三角形.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,D C BAED F CB A利用的思维模式是全等变换中的“旋转”法构造全等三角形.3)遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
三角形全等之辅助线——截长补短类经典习题讲解(精编文档).doc

【最新整理,下载后即可编辑】三角形全等之截长补短一、知识点睛 截长补短:题目中出现线段间的和差倍分时,考虑截长补短;截长补短的目的是把几条线段间的数量关系转为两条线段的等量关系.二、精讲精练(可以尝试用多种方法)1.已知:如图,在△ABC 中,∠1=∠2,∠B =2∠C .求证:AC =AB +BD .21A 21DCA 21CA2.已知:如图,在正方形ABCD 中,AD =AB ,∠D =∠ABC =∠BAD =90°,E ,F 分别为DC ,BC 边上的点,且∠EAF =45°,连接EF .求证:EF =BF +DE .3.已知:如图,在△ABC 中,∠ABC =60º,△ABC 的角平分线AD ,CE 交于点O .求证:AC =AE +CD .F EA B DCF EA B DCAEBD COA EBD CO4.已知:如图,在△ABC 中,∠A =90º,AB =AC ,BD 平分∠ABC ,CE ⊥BD 交BD 的延长线于点E .求证:CE =21BD .5.如图,在梯形ABCD 中,AD ∥BC ,CE ⊥AB 于E ,△BDC 为等腰直角三角形,∠BDC =90°,BD CD ,CE 与BD 交于F ,连接AF .求证:CF =AB +AF .AB CDEABCDEBFCEDA BFCEDA【参考答案】1.证明略提示:方法一:在AC上截取AE=AB,连接DE,证明△ABD≌△AED,然后再证明CE=BD;方法二:延长AB到E,使BE=BD,证明△ADE≌△ADC 2.证明略提示:延长FB到G,使BG=DE,连接AG,证明△ABG≌△ADE,再证明△AFG≌△AFE)3.证明略提示:在AC上截取AF=AE,连接OF,证明△AEO≌△AFO,∠AOC=120°,再证明△COF≌△COD)4.证明略提示:延长CE交BA的延长线于点F,证明△BEF≌△BEC,得EC=EF,再证明△ACF≌△ABD,得CF=BD)5.证明略提示:方法一:延长BA交CD的延长线交于点H,证明△BDH≌△CDF,得DH=DF,BH=CF,再证明△ADH≌△ADF,得AH=AF;方法二:在CF上截取CH=AB,连接DH,证明△DHC≌△DAB,得DH=DA,CH=BA,∠HDF=∠ADF=45°,再证明△ADF≌△HDF,得AF=HF)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D C
B
A
E
D F C
B
A
全等三角形作辅助线经典例题
常见辅助线的作法有以下几种:
1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”.
2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全
等变换中的“旋转”.
3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中
的“对折”,所考知识点常常是角平分线的性质定理或逆定理.
4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻
转折叠”;(遇垂线及角平分线时延长垂线段,构造等腰三角形)
5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是
之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.
特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.
一、倍长中线(线段)造全等
1:已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是_________.
2:如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小.
3:如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
E
D C
B
A
中考应用:
以ABC
∆的两边AB、AC为腰分别向外作等腰Rt ABD
∆和等腰Rt ACE
∆,90,
BAD CAE
∠=∠=︒
连接DE,M、N分别是BC、DE的中点.探究:AM与DE的位置关系及数量关系.(1)如图①当ABC
∆为直角三角形时,AM与DE的位置关系
E
D
C
B
A
D
C
B
A
P
2
1
D
C
B
A
P
Q
C
B
A
是 ,线段AM 与DE 的数量关系是 ;
(2)将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转︒
θ(0<θ<90)后,如图②所示,(1)问中得到的两个结论是否发生改变?并说明理由.
二、截长补短
1.如图,ABC ∆中,AB=2AC ,AD 平分BAC ∠,且AD=BD ,求证:CD ⊥AC
2:如图,AD ∥BC ,EA,EB 分别平分∠DAB,∠CBA ,CD 过点E ,求证:AB =AD+BC
3:如图,已知在ABC 内,0
60BAC ∠=,0
40C ∠=,P ,Q 分别在BC ,CA 上,并且AP ,
BQ 分别是BAC ∠,ABC ∠的角平分线。
求证:BQ+AQ=AB+BP
4:如图,在四边形ABCD 中,BC >BA,AD =CD ,BD 平分ABC ∠,求证:
180=∠+∠C A
5:如图在△ABC 中,AB >AC ,∠1=∠2,P 为AD 上任意一点,求证;AB-AC >PB-PC
C
D
B
A
F E
D C B A 2
1A F
H D
C
G B E
6.如图,在△ABC 中,AD 平分∠BAC ,AB+BD=AC ,求∠B ∶∠C 的值.
中考应用:如图,在四边形ABCD 中,AD//BC ,点E 是AB 上一个动点,若∠B=60°,AB=BC ,且∠DEC=60°,判断AD+AE 与BC 的关系并证明你的结论。
三、找全等
1. 已知:如图,在Rt △ABC 中,∠ACB=90º,
AC=BC ,D 为BC 的中点,CE ⊥AD 于E ,交AB 于F ,连接DF . 求证:∠ADC=∠BDF .
2.如图,△ABC 中,AB=AC ,过点A 作GE ∥BC ,角平分线BD 、CF 相交于点H ,它们的延长线分别交GE 于点E 、G .试在图10中找出3对全等三角形,并对其中一对全等三角
形给出证明.
四.借助角平分线造全等
说明:①遇到有关角平分线的问题时,可引角的两边的垂线,先证明三角形全等,然后根
据全等三角形的性质得出垂线段相等,再利用角的平分线性质得出两角相等. 练习:
1. 已知:△ABC 中,BD=CD ,∠1=∠2.求证:AD 平分∠BAC .
2.如图22,AB ∥CD ,E 为AD 上一点,且BE 、CE 分 别平分∠ABC 、∠BCD .求证:AE=ED .
A D C
B E
A F
D C B
E C E B A D ②以角的平分线为对称轴构造对称图形
例: 如图,在△ABC 中,AD 平分∠BAC ,∠C=2∠B .求证:AB=AC+CD .
分析:由于角平分线所在的直线是这个角的对称轴,因此在AB 上截取AE=AC ,连接DE ,我们就能构造出一对全等三角形,从而将线段AB 分成AE 和BE 两段,只需证明BE=CD 就可以了.
③延长角平分线的垂线段,使角平分线成为垂直平分线
例: 如图,在△ABC 中,AD 平分∠BAC ,CE ⊥AD 于E . 求证:∠ACE=∠B+∠ECD .
分析:注意到AD 平分∠BAC ,CE ⊥AD ,于是可延长CE 交AB 于点F ,即可构造全等三角形.
④利用角的平分线构造等腰三角形
如图,在△ABC 中,AD 平分∠BAC ,过点D 作DE ∥AB ,DE 交AC 于点E .易证△AED 是等腰三角形.因此,我们可以过角平分线上一点作角的一边的平行线,构造等腰三角形.
例: 如图,在△ABC 中,AB=AC ,BD 平分∠ABC ,DE ⊥BD 于D ,交BC 于点E .
求证:CD=2
1
BE .
全等三角形作辅助线·课后练习
1.在△ABC 中,∠BAC=60º,∠C=40º,
AP 平分∠BAC 交BC 于P ,BQ 平分∠ABC 交AC 于Q .
求证:AB+BP=BQ+AQ .
C
B A
D C
B
A D
43
21
C
E
B
A D C
E
B
A
D C
B A D
A
C
B D A
F M
2.如图,在△ABC 中,AD 平分∠BAC ,AB=AC+CD .
求证:∠C=2∠B .
3.已知,E 为△ABC 的∠A 的平分线 AD 上一点,AB >AC .
求证:AB -AC >EB -EC . 4.如图,在四边形ABCD 中,BC >BA ,
AD=CD ,BD 平分∠ABC . 求证:∠A+∠C=180º.
5.如图所示,已知AD ∥BC ,∠1=∠2, ∠3=∠4,直线DC 过点E 作交AD 于点D ,交
BC 于点C .
求证:AD+BC=AB .
6.已知,如图,△ABC 中,∠ABC=90º,
AB=BC ,AE 是∠A 的平分线,CD ⊥AE 于D .求证:CD=2
1
AE .
7.△ABC 中,AB=AC ,∠A=100º,
BD 是∠B 的平分线.求证:AD+BD=BC .
8.如图,△ABC 中,AD 平分∠BAC ,AD 交BC 于点D ,且D 是BC 的中点.
求证:AB=AC .
9.已知:如图,△ABC 中,AD 是∠BAC
的平分线,E 是BC 的中点,EF ∥AD ,交AB 于M ,
交CA 的延长线于F .求证:BM=CF .
10.如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线AD,CE 相交 于点O ,求证:OE=OD
11.如图,△ABC 中,AD 平分∠BAC ,DG ⊥BC 且平分BC ,DE ⊥AB 于E ,DF ⊥AC 于F. (1)说明BE=CF 的理由;(2)如果AB=a ,AC=b ,求AE 、BE 的长.
中考应用:
如图①,OP 是∠MON 的平分线,请你利用该图形画一对以OP 所在直线为对称轴的全等三角形。
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC 中,∠ACB 是直角,∠B =60°,AD 、CE 分别是∠BAC 、∠BCA 的平分线,AD 、CE 相交于点F 。
请你判断并写出FE 与FD 之间的数量关系;
(2)如图③,在△ABC 中,如果∠ACB 不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
E
D
G
F C
B
A
O
P A
M
N
E
B C
D F
A
C
E
F
B
D
图①
图② 图③。
