2020届山东省烟台市高三新高考数学模拟试题解析
2020年山东省新高考数学第三次模拟检测试卷 含解析

2020年新高考数学第三次模拟试卷一、选择题1.设集合M={x|0≤x<2},N={x|x2﹣x﹣6<0},则集合M∩N等于()A.{x|0≤x<2}B.{x|﹣2≤x<3}C.{x|0<x≤3}D.{x|﹣2≤x<0} 2.若复数z1,z2,在复平面内的对应点关于虚轴对称,z1=1+i,则=()A.i B.﹣i C.1D.﹣13.设a∈R,b>0,则“3a>2b”是“a>log3b”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占50%,三星销量约占30%,苹果销量约占20%),根据该图判断,以下结论中一定正确的是()A.四个季度中,每季度三星和苹果总销量之和均不低于华为的销量B.苹果第二季度的销量小于第三季度的销量C.第一季度销量最大的为三星,销量最小的为苹果D.华为的全年销量最大5.如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC上的高,则的值等于()A.2B.4C.6D.86.函数f(x)=的图象大致为()A.B.C.D.7.已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1、F2,实轴长为4,渐近线方程为y=,|MF1|﹣|MF2|=4,点N在圆x2+y2﹣4y=0上,则|MN|+|MF1|的最小值为()A.2B.5C.6D.78.已知函数f(x)=lnx+ln(a﹣x)的图象关于直线x=1对称,则函数f(x)的值域为()A.(0,2)B.[0,+∞)C.(﹣∞,2]D.(﹣∞,0]二、多项选择题(共4小题)9.在△ABC中,内角A,B,C所对的边分别为a,b,c,∠ABC=60°,∠ABC的平分线交AC于点D,且BD=,则下列说法正确的是()A.ac的最小值是4B.ac的最大值是4C.a+2c的最小值是2+2D.a+2c的最小值是3+210.若非零实数a,b满足a<b,则下列不等式不一定成立的是()A.<1B.+≥2C.D.a2+a<b2+b11.已知半径为10的球的两个平行截面圆的周长分别是12π和16π,则这两个截面圆间的距离为()A.2B.4C.12D.1412.若三条直线l1:ax+y+1=0,l2:x+ay+1=0,l3:x+y+a=0不能围成三角形,则a的取值为()A.a=1B.a=﹣1C.a=﹣2D.a=2三、填空题(共4小题)13.现有5人要排成一排照相,其中甲与乙两人不相邻,且甲不站在两端,则不同的排法有种.(用数字作答)14.意大利数学家列昂那多•斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55,…,即F(1)=F(2)=1,F(n)=F(n﹣1)+F(n﹣2)(n≥3,n∈N*),此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用.若此数列被2整除后的余数构成一个新数列{a n},则a2019=,数列{a n}的前2019项的和为.15.若函数f(x)=mx2﹣e x+1(e为自然对数的底数)在x=x1和x=x2两处取得极值,且x2≥2x1,则实数m的取值范围是.16.若F(c,0)是双曲线=1(a>0,b>0)的右焦点,过点F作该双曲线一条渐近线的垂线并与两条渐近线分别相交于A,B两点,O为坐标原点,△OAB的面积为,则该双曲线的离心率为.四、解答题(本题共6小题)17.在△ABC中,内角A,B,C的对边分别为a,b,c,且4b cos2=2b+a sin B.(1)求cos A;(2)若a=2,c=5,求b.18.已知正项数列{a n}的前n项和为.(1)求数列{a n}的通项公式;(2)设{a n}是递增数列,,T n为数列{b n}的前n项和,若恒成立,求实数m的取值范围.19.随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)经常网购偶尔或不用网购合计男性50100女性70100合计(Ⅰ)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?(Ⅱ)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为X,求随机变量X的数学期望和方差.参考公式:P(K2≥k0)0.150.100.050.0250.0100.0050.001 k0 2.072 2.706 3.841 5.024 6.6357.87910.828 20.四边形ABCD是菱形,ACEF是矩形,平面ACEF⊥平面ABCD,AB=2AF=2,∠BAD =60°,G是BE的中点.(Ⅰ)证明:CG∥平面BDF(Ⅱ)求二面角E﹣BF﹣D的余弦值.21.已知椭圆E:的左、右焦点分别为F1,F2,离心率为,动点P在椭圆E上,△PF1F2的周长为6.(1)求椭圆E的方程;(2)设直线PF2与椭圆E的另一个交点为Q,过P,Q分别作直线l:x=t(t>2)的垂线,垂足为M,N,l与x轴的交点为T.若四边形PMNQ的面积是△PQT面积的3倍,求直线PQ斜率的取值范围.22.已知函数f(x)=xe x﹣1﹣alnx(无理数e=2.718…).(1)若f(x)在(1,+∞)单调递增,求实数a的取值范围:(2)当a=0时,设g(x)=•f(x)﹣x2﹣x,证明:当x>0时,g(x)>1﹣﹣()2.参考答案一、单项选择题(共8小题)1.设集合M={x|0≤x<2},N={x|x2﹣x﹣6<0},则集合M∩N等于()A.{x|0≤x<2}B.{x|﹣2≤x<3}C.{x|0<x≤3}D.{x|﹣2≤x<0}【分析】可求出集合N,然后进行交集的运算即可.解:N={x|﹣2<x<3};∴M∩N={x|0≤x<2}.故选:A.2.若复数z1,z2,在复平面内的对应点关于虚轴对称,z1=1+i,则=()A.i B.﹣i C.1D.﹣1【分析】由已知求得z2,把z1,z2代入,再由复数代数形式的乘除运算化简得答案.解:∵z1,z2在复平面内的对应点关于虚轴对称,且z1=1+i,∴z2=﹣1+i,∴==.故选:B.3.设a∈R,b>0,则“3a>2b”是“a>log3b”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【分析】根据充分条件和必要条件的定义;指数函数和对数函数的图象和性质分别进行判断.解:若3a>2b,b>0,则a>log32b,可得a>log3b;若a>log3b,可得3a>b,无法得到3a>2b,所以“3a>2b”是“a>log3b”的充分而不必要条件.故选:A.4.如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占50%,三星销量约占30%,苹果销量约占20%),根据该图判断,以下结论中一定正确的是()A.四个季度中,每季度三星和苹果总销量之和均不低于华为的销量B.苹果第二季度的销量小于第三季度的销量C.第一季度销量最大的为三星,销量最小的为苹果D.华为的全年销量最大【分析】根据图象,逐一分析选项,得出答案.解:根据图象,分析如下:A,错误,第四季度三星和苹果总销量之和低于华为的销量;B,错误,苹果第二季度的销量大于第三季度的销量;C,错误,第一季度销量最大的为华为;D,华为在每个季度的销量都最大,所以华为的全年销量最大,故D正确,故选:D.5.如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC上的高,则的值等于()A.2B.4C.6D.8【分析】由题意,=•(+)=•+•;⊥;•=||•||cos∠BAD=||•sin30°•||•cos60°;从而求得.解:=•(+)=•+•=•=||•||cos∠BAD=||•sin30°•||•cos60°=4×4×=4;故选:B.6.函数f(x)=的图象大致为()A.B.C.D.【分析】判断函数的奇偶性与图象对称性之间的关系,利用特殊值的对应性是否一致利用排除法进行求解即可.解:f(﹣x)====﹣=﹣f(x),即函数f(x)是奇函数,图象关于原点对称,排除C,D,f(1)=<0,排除B,故选:A.7.已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1、F2,实轴长为4,渐近线方程为y=,|MF1|﹣|MF2|=4,点N在圆x2+y2﹣4y=0上,则|MN|+|MF1|的最小值为()A.2B.5C.6D.7【分析】求得双曲线的a,b,可得双曲线方程,求得焦点坐标,运用双曲线的定义和三点共线取得最小值,连接CF2,交双曲线于M,圆于N,计算可得所求最小值.解:由题意可得2a=4,即a=2,渐近线方程为y=±x,即有=,即b=1,可得双曲线方程为﹣y2=1,焦点为F1(﹣,0),F2,(,0),由双曲线的定义可得|MF1|=2a+|MF2|=4+|MF2|,由圆x2+y2﹣4y=0可得圆心C(0,2),半径r=2,|MN|+|MF1|=4+|MN|+|MF2|,连接CF2,交双曲线于M,圆于N,可得|MN|+|MF2|取得最小值,且为|CF2|==3,则则|MN|+|MF1|的最小值为4+3﹣2=5.故选:B.8.已知函数f(x)=lnx+ln(a﹣x)的图象关于直线x=1对称,则函数f(x)的值域为()A.(0,2)B.[0,+∞)C.(﹣∞,2]D.(﹣∞,0]【分析】根据题意,分析可得f(a﹣x)=f(x),即可得函数f(x)的图象关于直线x =对称,据此可得a的值,进而可得f(x)=lnx+ln(2﹣x)=ln(2x﹣x2),设t=2x﹣x2,则y=lnt,由换元法分析可得答案.解:根据题意,对于函数f(x)=lnx+ln(a﹣x),有f(a﹣x)=ln(a﹣x)+ln[a﹣(a﹣x)]=lnx+ln(a﹣x)=f(x),则函数f(x)的图象关于直线x=对称,若函数f(x)=lnx+ln(a﹣x)的图象关于直线x=1对称,则有=1,则a=2,则f(x)=lnx+ln(2﹣x)=ln(2x﹣x2),其定义域为(0,2),设t=2x﹣x2,则y=lnt,又由t=﹣(x﹣1)2+1,0<x<2,则有0<t≤1,则y=lnt≤0,即函数f(x)的值域为(﹣∞,0];故选:D.二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)9.在△ABC中,内角A,B,C所对的边分别为a,b,c,∠ABC=60°,∠ABC的平分线交AC于点D,且BD=,则下列说法正确的是()A.ac的最小值是4B.ac的最大值是4C.a+2c的最小值是2+2D.a+2c的最小值是3+2【分析】现根据三角形面积公式得条件,再利用基本不等式求最值.解:有题意知S△ABC=S△ABD+S△BDC,由角平分线性质以及面积公式可得:,化简得ac=a+c,∴,当且仅当a=c时成立,解之得ac≥4,选项A对;∵ac=a+c,∴1=,∴≥3+2,当且仅当a=,选项D对;故选:AD.10.若非零实数a,b满足a<b,则下列不等式不一定成立的是()A.<1B.+≥2C.D.a2+a<b2+b【分析】当a<b<0时,<1不成立可判断A;当时,不成立可判断B;利用作差可判断C,D.解:当a<b<0时,<1不成立,当时,不成立,因为=<0,则一定成立,因为a2﹣b2+a﹣b=(a﹣b)(a+b+1)符号不定,故a2a<b2+b不一定成立.故选:ABD.11.已知半径为10的球的两个平行截面圆的周长分别是12π和16π,则这两个截面圆间的距离为()A.2B.4C.12D.14【分析】由平行截面的周长求出两个半径,再由截面圆的半径,球的半径和球心到截面的距离构成直角三角形求出球心到截面的距离,分平行平面在球心的同一侧和两边求出平行平面的距离.解:两个平行截面圆的周长分别是12π和16π,可得两个半径分别为6,8,如果这两个平行平面在球心同一侧时,取球的中截面可得球心到截面的距离OB===8,OA===6,所以平行线间的距离d=OB﹣OA=8﹣6=2,如果这两个平行平面在球心两侧时,所以平行线间的距离d'=OB+OA=8+6=14,故选:AD.12.若三条直线l1:ax+y+1=0,l2:x+ay+1=0,l3:x+y+a=0不能围成三角形,则a的取值为()A.a=1B.a=﹣1C.a=﹣2D.a=2【分析】l1和l3平行,或l2和l3平行,l1和l2平行,分类讨论,利用两条直线平行的条件分别求得m的值,综合可得结论.解:由于l1的斜率﹣a,l3的斜率为﹣1,则由题意可得l1和l3平行,或l2和l3平行,l1和l2平行.若l1和l3平行,则=,求得a=1;若l2和l3平行,则=,求得a=1.若l1和l2平行,则=,求得a=±1.综上可得,实数a所有可能的值为﹣1,1,故选:AB.三、填空题(本题共4小题,每小题5分,共20分)13.现有5人要排成一排照相,其中甲与乙两人不相邻,且甲不站在两端,则不同的排法有36种.(用数字作答)【分析】根据题意,分2步进行分析:①,将除甲乙的三人全排列,排好后有4个空位,②,分析甲乙的安排方法数目,由分步计数原理计算可得答案.解:根据题意,分2步进行分析:①,将除甲乙的三人全排列,有A33=6种情况,排好后有4个空位,②,由于甲不站在两端,则甲有2个空位可选,乙在剩下的3个空位中任选1个,有3种选法,则甲乙的选法有2×3=6种,故不同的排法有6×6=36种;故答案为:36.14.意大利数学家列昂那多•斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55,…,即F(1)=F(2)=1,F(n)=F(n﹣1)+F(n﹣2)(n≥3,n∈N*),此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用.若此数列被2整除后的余数构成一个新数列{a n},则a2019=0,数列{a n}的前2019项的和为1346.【分析】根据题意写出数列{a n}的前若干项,观察发现此数列是以3为周期的周期数列,继而可求解.解:∵“兔子数列”的各项为:1,1,2,3,5,8,13,21,34,55,…,∴此数列被2整除后的余数依次为:1,1,0,1,1,0,1,1,0,……,即a1=1,a2=1,a3=0,a4=1,a5=1,a6=0,……,∴数列{a n}是以3为周期的周期数列,∴a2019=a3=0,∴数列{a n}的前2019项的和为:a1+a2+a3+……+a2019=673(a1+a2+a3)=673×2=1346,故答案为:0,1346.15.若函数f(x)=mx2﹣e x+1(e为自然对数的底数)在x=x1和x=x2两处取得极值,且x2≥2x1,则实数m的取值范围是.【分析】方法1:f'(x)=2mx﹣e x,x=x1和x=x2两处取得极值,且x2≥2x1,设A(2x1,4mx1),B(2x1,),构造,,在(0,1)递减,转化求解即可.方法2:f'(x)=2mx﹣e x,有两个不等的实数根x1,x2且x2≥2x1,令,则,利用函数的单调性转化求解即可.解:方法1:f'(x)=2mx﹣e x,,,直线y=2mx,曲线y=e x,x2≥2x1,A(2x1,4mx1),B(2x1,),,x1≤ln2,构造,,在(0,1)递减,.方法2:f'(x)=2mx﹣e x由题知有两个不等的实数根x1,x2且x2≥2x1,令,则,易知h(x)在(﹣∞,0),(0,1)上为减函数;在(1,+∞)上为增函数.当x2=2x1时,由,得x1=ln2,此时;当x2>2x1时,综上.故答案为:.16.若F(c,0)是双曲线=1(a>0,b>0)的右焦点,过点F作该双曲线一条渐近线的垂线并与两条渐近线分别相交于A,B两点,O为坐标原点,△OAB的面积为,则该双曲线的离心率为.【分析】求出双曲线的渐近线方程,设两条渐近线的夹角为θ,由两直线的夹角公式,可得tanθ=tan∠AOB,求出F到渐近线y=x的距离为b,即有|OB|=a,△OAB的面积可以表示为•a•a tanθ,结合条件可得a,b的关系,再由离心率公式即可计算得到.解:双曲线﹣=1的渐近线方程为y=±x,设两条渐近线的夹角为θ,则tanθ=tan∠AOB==,设FB⊥OB,则F到渐近线y=x的距离为d==b,即有|OB|=a,则△OAB的面积可以表示为•a•a tanθ==,解得=,则e===.故答案为:.四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.在△ABC中,内角A,B,C的对边分别为a,b,c,且4b cos2=2b+a sin B.(1)求cos A;(2)若a=2,c=5,求b.【分析】(1)由已知结合正弦定理及同角平方关系即可求解cos A,(2)由已知结合余弦定理可求b.解:(1)因为4b cos2=2b+a sin B,所以2b(1+cos A)=2c+a sin B,即4b cos A=3a sin B,由正弦定理可得,4sin B cos A=3sin A sin B,因为sin B≠0,所以4cos A=3sin A,又sin2A+cos2A=1且sin A>0,cos A>0,所以cos A=;(2)由余弦定理可得,cos A==,整理可得,b2﹣6b+5=0,解可得,b=1或b=5.18.已知正项数列{a n}的前n项和为.(1)求数列{a n}的通项公式;(2)设{a n}是递增数列,,T n为数列{b n}的前n项和,若恒成立,求实数m的取值范围.【分析】(1)n≥2时,4a n=4S n﹣4S n﹣1,化为:=,a n>0.化简进而得出.(2){a n}是递增数列,取a n=2n﹣1.可得==,利用裂项求和方法、数列的单调性即可得出.解:(1)n≥2时,4a n=4S n﹣4S n﹣1=+4n﹣1﹣[+4(n﹣1)﹣1],化为:=,a n>0.∴a n﹣a n﹣1=2,或a n+a n﹣1=2,a n﹣a n﹣1=2时,数列{a n}是等差数列,a n=1+2(n﹣1)=2n﹣1.a n+a n﹣1=2,∵a1=1,可得a n=1.(2){a n}是递增数列,∴a n=2n﹣1.==,数列{b n}的前n项和T n==,∵恒成立,∴,解得m≥3.∴实数m的取值范围是[3,+∞).19.随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)经常网购偶尔或不用网购合计男性50100女性70100合计(Ⅰ)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?(Ⅱ)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为X,求随机变量X的数学期望和方差.参考公式:P(K2≥k0)0.150.100.050.0250.0100.0050.001 k0 2.072 2.706 3.841 5.024 6.6357.87910.828【分析】(1)完成列联表,由列联表,得k2=,由此能在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关.(2)①由题意所抽取的10名女市民中,经常网购的有10×=7人,偶尔或不用网购的有10×=3人,由此能选取的3人中至少有2人经常网购的概率.②由2×2列联表可知,抽到经常网购的市民的频率为:,由题意X~B(10,0.6),由此能求出随机变量X的数学期望E(X)和方差D(X).解:(1)完成列联表(单位:人):经常网购偶尔或不用网购合计男性5050100女性7030100合计12080200由列联表,得:k2==,∴能在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关.(2)①由题意所抽取的10名女市民中,经常网购的有10×=7人,偶尔或不用网购的有10×=3人,∴选取的3人中至少有2人经常网购的概率为:P==.②由2×2列联表可知,抽到经常网购的市民的频率为:,将频率视为概率,∴从我市市民中任意抽取一人,恰好抽到经常网购市民的概率为0.6,由题意X~B(10,0.6),∴随机变量X的数学期望E(X)=10×0.6=6,方差D(X)=10×0.6×0.4=2.4.20.四边形ABCD是菱形,ACEF是矩形,平面ACEF⊥平面ABCD,AB=2AF=2,∠BAD =60°,G是BE的中点.(Ⅰ)证明:CG∥平面BDF(Ⅱ)求二面角E﹣BF﹣D的余弦值.【分析】(Ⅰ)根据线面平行的判定定理或者面面平行的性质定理即可证明:CG∥平面BDF(Ⅱ)建立空间坐标系,求出平面的法向量,利用向量法即可求二面角E﹣BF﹣D的余弦值.【解答】(I)证法一:设AC∩BD=O,BF的中点为H,因为G是BE的中点,,∴OCGH是平行四边形∴CG∥OH,CG⊄平面BDF,OH⊂平面BDF,∴CG∥平面BDF证法二:因为G是BE的中点,,∴CG∥DF,∵CG⊄平面BDF,DF⊂平面BDF,∴CG∥平面BDF(II)设EF的中点为N,ACEF是矩形,ON⊥AC,平面ACEF⊥平面ABCD,∴ON⊥面ABCD∴ON⊥AC,ON⊥BD四边形ABCD是菱形,∴AC⊥BD,以O为原点,OB所在直线为x轴,OC所在直线为Y轴,ON所在直线为Z轴建立空间直角坐标系,AB=2,AF=1,∠BAD=60°,则平面BEF的法向量为,平面BDF的法向量为,令z1=1,则,由设二面角E﹣BF﹣D的大小为θ则,则二面角E﹣BF﹣D的余弦值是.21.已知椭圆E:的左、右焦点分别为F1,F2,离心率为,动点P在椭圆E上,△PF1F2的周长为6.(1)求椭圆E的方程;(2)设直线PF2与椭圆E的另一个交点为Q,过P,Q分别作直线l:x=t(t>2)的垂线,垂足为M,N,l与x轴的交点为T.若四边形PMNQ的面积是△PQT面积的3倍,求直线PQ斜率的取值范围.【分析】(1)根据椭圆的离心率和焦点三角形的周长建立方程求出a,c的值即可;(2)先设出直线PQ的方程为x=my+1,联立方程组得出根与系数关系,利用四边形PMNQ的面积是△PQT面积的3倍,得出t关于m的表达式,由t>2建立不等式,解出m的取值范围,进而根据得出k的取值范围.解:(1)因为P是E上的点,且F1,F2为E的左、右焦点,所以|PF1|+|PF2|=2a,又因为|F1F2|=2c,△PF1F2的周长为6,所以2a+2c=6,又因为椭圆的离心率为,所以,解得a=2,c=1.所以,E的方程为.……………(2)依题意,直线PQ与x轴不重合,故可设直线PQ的方程为x=my+1,由,消去x得:(3m2+4)y2+6my﹣9=0,设P(x1,y1),Q(x2,y2)则有△>0且.…设四边形PMNQ的面积和△PQT面积的分别为S1,S2,则S1=3S2,又因为,S2=.所以,即3(t﹣1)=2t﹣(x1+x2),得t=3﹣(x1+x2),又x1=my1+1,x2=my2+1,于是t=3﹣(my1+my2+2)=1﹣m(y1+y2),所以,由t>2得,解得,设直线PQ的斜率为k,则,所以,解得,所以直线PQ斜率的取值范围是.……………22.已知函数f(x)=xe x﹣1﹣alnx(无理数e=2.718…).(1)若f(x)在(1,+∞)单调递增,求实数a的取值范围:(2)当a=0时,设g(x)=•f(x)﹣x2﹣x,证明:当x>0时,g(x)>1﹣﹣()2.【分析】(1)由题意可得f′(x)=(1+x)e x﹣1﹣=≥0在(1,+∞)上恒成立.可得a≤(x+x2)e x﹣1=h(x),利用导数研究其单调性可得实数a的取值范围.(2)当a=0时,g(x)=•f(x)﹣x2﹣x=e x﹣x2﹣x.g′(x)=e x﹣2x﹣1=u(x).利用导数研究其单调性极值,进而证明结论.【解答】(1)解:由题意可得f′(x)=(1+x)e x﹣1﹣=≥0在(1,+∞)上恒成立.∴a≤(x+x2)e x﹣1=h(x),h′(x)=(1+3x+x2)e x﹣1>0,∴函数h(x)在(1,+∞)上单调递增.∴a≤h(1)=2.∴实数a的取值范围是(﹣∞,2].(2)证明:当a=0时,g(x)=•f(x)﹣x2﹣x=e x﹣x2﹣x.g′(x)=e x﹣2x﹣1=u(x).u′(x)=e x﹣2,可得x=ln2时,函数u(x)取得极小值,g′(ln2)=u(ln2)=1﹣2ln2<0.∵g′(0)=0,又=﹣2(1+ln2)﹣1=e﹣3﹣ln2>0.∴存在x0∈(ln2,1+ln2),使得g′(x0)=﹣2x0﹣1=0,=2x0+1.由单调性可得:x=x0时,函数g(x)取得极小值即最小值,∴g(x)≥g(x0)=﹣﹣x0=2x0+1﹣﹣x0=﹣+x0+1=﹣+.由x0∈(ln2,1+ln2),可得函数y=g(x0)单调递减,故g(x))≥g(x0)>﹣+>1﹣﹣()2.∴当x>0时,g(x)>1﹣﹣()2.。
2020届山东省、海南省新高考数学4月模拟试题和答案详细解析及家长必读

2020届山东省、海南省新高考数学4月模拟试题一、单项选择题:1.(3分)设集合A={x||3x+1|≤4},B={x|log2x≤3},则A∪B=()A.[0,1] B.(0,1] C.[﹣,8] D.[﹣,8)2.(3分)已知(2﹣i)=i2019,则复平面内与z对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限3.(3分)已知A(1,﹣2),B(4,﹣1),C(3,2),则cos∠BAC=()A.﹣B.C.﹣D.4.(3分)我省高考实行3+3模式,即语文数学英语必选,物理、化学、生物、历史、政治、地理六选三,今年高一的小明与小芳进行选科,假若他们对六科没有偏好,则他们选课至少两科相同的概率为()A.B.C.D.5.(3分)已知双曲线C:﹣=1(a>0,b>0)的一条渐近线与直线x=0的夹角为60°,若以双曲线C的实轴和虚轴为对角线的四边形周长为8,则双曲线C的标准方程为()A.﹣y2=1 B.﹣=1C.﹣=1 D.x2﹣=16.(3分)函数f(x)=cos x•sin(3x﹣)的图象大致为()A.B.C.D.7.(3分)已知在锐角三角形ABC中,角A,B,C的对边分别为a,b,c,若sin2A﹣sin B sin C=0,则的取值范围为()A.(﹣)B.[0,)C.[0,)D.(﹣1,1)8.(3分)已知函数f(x)=﹣x2+a,g(x)=x2e x,若对任意的x2∈[﹣1,1],存在唯一的x1∈[﹣,2],使得f(x1)=g(x2),则实数a的取值范围是()A.(e,4] B.(e+,4] C.(e+,4)D.(,4]二、多项选择题:9.(3分)对于实数a,b,c,下列命题是真命题的为()A.若a>b,则<B.若a>b,则ac2≥bc2C.若a>0>b,则a2<﹣abD.若c>a>b>0,则>10.(3分)将函数f(x)=2sin x(sin x﹣cos x)﹣1图象向右平移个单位得函数g (x)的图象,则下列命题中正确的是()A.f(x)在(,)上单调递增B.函数f(x)的图象关于直线x=对称C.g(x)=2cos2xD.函数g(x)的图象关于点(﹣,0)对称11.(3分)如图,正方体ABCD﹣A1B1C1D1的棱长为a,线段B1D1上有两个动点E,F,且EF=a,以下结论正确的有()A.AC⊥BEB.点A到△BEF的距离为定值C.三棱锥A﹣BEF的体积是正方体ABCD﹣A1B1C1D1体积的D.异面直线AE,BF所成的角为定值12.(3分)已知函数f(x)=,若方程f(x)=m有四个不同的实根x1,x2,x3,x4满足x1<x2<x3<x4,则下列说法正确的是()A.x1x2=1 B.+=1C.x3+x4=12 D.x3x4∈(27,29)三、填空题:13.(3分)函数f(x)=在点P(1,f(1))处的切线与直线2x+y﹣3=0垂直,则a=.14.(3分)如果(3x+)n的展开式中各项系数之和为4096,则n的值为,展开式中x的系数为.15.(3分)各项均为正数且公比q>1的等比数列{a n}的前n项和为S n,若a1a5=4,a2+a4=5,则的最小值为.16.(3分)如图所示,三棱锥A﹣BCD的顶点A,B,C,D都在半径为同一球面上,△ABD 与△BCD为直角三角形,△ABC是边长为2的等边三角形,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P﹣QCO体积的最大值为.四、解答题:17.(10分)(开放题)在锐角△ABC中,a=2,_______,求△ABC的周长l的范围.在①=(﹣cos,sin),=(cos,sin),且•=﹣,②cos A(2b﹣c)=a cos C,③f(x)=cos x cos(x﹣)﹣,f(A)=注:这三个条件中任选一个,补充在上面问题中并对其进行求解.18.(12分)已知数列{a n}满足a1+a2+a3+…+a n=2n(n∈N*).(1)求数列{a n}的通项公式;(2)若b n=(n+1)•log2a n,求数列{}(n∈N*)的前n项和S n.19.(12分)如图,在多面体ABCDE中,DE∥AB,AC⊥BC,BC=2AC=2,AB=2DE,且D点在平面ABC内的正投影为AC的中点H且DH=1.(1)证明:面BCE⊥面ABC(2)求BD与面CDE夹角的余弦值.20.(12分)已知椭圆C:+=1(a>b>0),椭圆上的点到焦点的最小距离为2﹣且过点P(,1).(1)求椭圆C的方程;(2)若过点M(3,0)的直线l与椭圆C有两个不同的交点P和Q,若点P关于x轴的对称点为P',判断直线P'Q是否经过定点,如果经过,求出该定点坐标;如果不经过,说明理由.21.(12分)《中国制造2025》是经国务院总理李克强签批,由国务院于2015年5月印发的部署全面推进实施制造强国的战略文件,是中国实施制造强国战略第一个十年的行动纲领.制造业是国民经济的主体,是立国之本、兴国之器、强国之基.发展制造业的基本方针为质量为先,坚持把质量作为建设制造强国的生命线.某制造企业根据长期检测结果,发现生产的产品质量与生产标准的质量差都服从正态分布N(μ,σ2),并把质量差在(μ﹣σ,μ+σ)内的产品为优等品,质量差在(μ+σ,μ+2σ)内的产品为一等品,其余范围内的产品作为废品处理.优等品与一等品统称为正品.现分别从该企业生产的正品中随机抽取1000件,测得产品质量差的样本数据统计如下:(1)根据频率分布直方图,求样本平均数(2)根据大量的产品检测数据,检查样本数据的方差的近似值为100,用样本平均数作为μ的近似值,用样本标准差s作为σ的估计值,求该厂生产的产品为正品的概率.(同一组中的数据用该组区间的中点值代表)[参考数据:若随机变量ξ服从正态分布N(μ,σ2),则:P(μ﹣σ<ξ≤μ+σ)≈0.6827,P(μ﹣2σ<ξ≤μ+2σ)≈0.9545,P(μ﹣3σ<ξ≤μ+3σ)≈0.9973.(3)假如企业包装时要求把3件优等品球和5件一等品装在同一个箱子中,质检员每次从箱子中摸出三件产品进行检验,记摸出三件产品中优等品球的件数为X,求X的分布列以及期望值.22.(12分)已知f(x)=e x﹣ax2﹣x(a>0).(1)讨论f'(x)得单调性;(2)已知函数f(x)有两个极值点x1,x2,求证:x1+x2<2ln2a.2020届山东省、海南省新高考数学4月模拟试题答案一、单项选择题:1.C; 2.A; 3.D; 4.D; 5.A; 6.C; 7.A; 8.B;二、多项选择题:9.BD; 10.AC; 11.ABC; 12.BCD;三、填空题:13.; 14.6;1215; 15.8; 16.;四、解答题:17.; 18.; 19.; 20.; 21.; 22.;陪孩子高考的10点建议1.了解本省现行的高考制度和高考改革情况,掌握每年本省的招生基本情况(含当年报考人数、文、理科的报考比例和主要院校的招生人数);2.了解当今主要高校文、理科的一般专业和新专业的设置走向以及近几年的就业形势;了解平行志愿填报的基本原则和某些误区;3.了解高三学生学习的基本情况(高考科目、学校课程开设情况、高三学生学习要求、生活要求、考试要求等);4.简要摘录今年全国主要高等院校的招生情况,主要专业的招生计划数以及专业的最低投档线和录取平均分;5.了解自己小孩的学习现状(在文科或理科的全级排名位置、主要优势和弱势、目前的主要存在问题和成因,以及今后的努力方向等);6.在沟通交流方面父母要学会借力,主动、持续地和小孩的班主任以及其他科任老师保持联系,随时把握小孩的学习和生活情况,并以此作为和小孩沟通的基础。
2020届山东省新高考高三优质数学试卷分项解析-专题03-函数及其应用(解析版)

专题3 函数及其应用1.关于函数图象的考查: (1)函数图象的辨识与变换;(2)函数图象的应用问题,运用函数图象理解和研究函数的性质,数形结合思想分析与解决问题的能力; 2.关于函数性质的考查:以考查能力为主,往往以常见函数(二次函数、指数函数、对数函数)为基本考察对象,以绝对值或分段函数的呈现方式,与不等式相结合,考查函数的基本性质,如奇偶性、单调性与最值、函数与方程(零点)、不等式的解法等,考查数学式子变形的能力、运算求解能力、等价转化思想和数形结合思想.其中函数与方程考查频率较高.涉及函数性质的考查;3.常见题型,除将函数与导数相结合考查外,对函数独立考查的题目,不少于两道,近几年趋向于稳定在选择题、填空题,易、中、难的题目均有可能出现.,预测2020年将保持对数形结合思想的考查,主要体现在对函数图象、函数性质及其应用的考查,客观题应特别关注分段函数相关问题,以及与数列、平面解析几何、平面向量、立体几何的结合问题.主观题依然注意与导数的结合.一、单选题1.(2019·山东师范大学附中高三月考)函数()312xf x x ⎛⎫=- ⎪⎝⎭的零点所在区间为( )A .()1,0-B .10,2⎛⎫ ⎪⎝⎭C .1,12⎛⎫ ⎪⎝⎭D .()1,2【答案】C 【解析】311(1)(1)()302f --=--=-<,301(0)0(102f =-=-<,@13211112()()()02228f =-=-<,31111(1)1()10222f =-=-=>,321115(2)2()80222f =-=-=>,由()1102f f ⎛⎫⋅< ⎪⎝⎭. 故选:C2.(2020届山东省泰安市高三上期末)函数()3ln xf x x=的部分图象是( ) A . B .C .D .【答案】A 【解析】:()()()33ln ln ,x xf x f x f x x x=-==--, ()f x 为奇函数,排除B 当1x >时,()3ln 0xf x x=>恒成立,排除CD 故答案选A3.(2020·河南高三月考(理))已知(2)f x +是偶函数,()f x 在(]2-∞,上单调递减,(0)0f =,则(23)0f x ->的解集是( )A .2()(2)3-∞+∞,,B .2(2)3, C .22()33-,D .22()()33-∞-+∞,, 【答案】D 【解析】》因为(2)f x +是偶函数,所以()f x 关于直线2x =对称; 因此,由(0)0f =得(4)0f =;又()f x 在(]2-∞,上单调递减,则()f x 在[)2,+∞上单调递增;所以,当232x -≥即0x ≤时,由(23)0f x ->得(23)(4)f x f ->,所以234x ->, 解得23x <-; 当232x -<即0x >时,由(23)0f x ->得(23)(0)f x f ->,所以230x -<, 解得23x >; 因此,(23)0f x ->的解集是22()()33-∞-+∞,,. 》4.(2020·全国高三专题练习(文))函数()()22log ,1,1,1,x x f x f x x ≥⎧=⎨+<⎩,若方程()2f x x m =-+有且只有两个不相等的实数根,则实数m 的取值范围是 ( ) A .(),4-∞ B .(],4-∞C .()2,4-D .(]2,4-【答案】A 【解析】令()2g x x m =-+,画出()f x 与()g x 的图象,平移直线,当直线经过()1,2时只有一个交点,此时4m =,向右平移,不再符合条件,故4m < 故选:A$5.(2020届山东省烟台市高三上期末)设0.5log 3a =,30.5b =,0.513c -⎛⎫= ⎪⎝⎭,则,,a b c 的大小关系为( )A .a b c <<B .a c b <<C .b a c <<D .b c a <<【答案】A 【解析】由题,因为0.5log y x =单调递减,则0.50.5log 3log 10a =<=;因为0.5xy =单调递减,则3000.50.51b <=<=;因为3xy =单调递增,则0.50.5013313c -⎛⎫==>= ⎪⎝⎭,所以01a b c <<<<,—故选:A6.(2020届山东省潍坊市高三上期中)函数ln ()xf x x x=-的大致图象为( )A .B .C .D .【答案】A 【解析】函数的定义域为(,0)(0,)-∞+∞,||||()()()ln x ln x f x x x f x x x--=--=--=--,则函数()f x 是奇函数,图象关于原点对称,排除B ,D ,"当0x >且0x →,()f x →+∞,排除C . 故选:A.7.(2020届山东省潍坊市高三上期中)已知3log 2a =,143b =,2ln 3c =,则a ,b ,c 的大小关系为( ) A .a b c >> B .b a c >> C .c b a >>D .c a b >>【答案】B 【解析】因为3log 2(0,1)a =∈,1431b =>,203c ln =<,则a ,b ,c 的大小关系:b a c >>.|故选:B.8.(2020届山东省泰安市高三上期末)若()33log 21log a b ab +=+2+a b 的最小值为( )A .6B .83C .3D .163【答案】C 【解析】∵()3log 21a b +=+∴()33log 21log a b ab +=+()3log 3ab =, ∴23a b ab +=,且0a >,0b >,《∴123a b+=, ∴()112223a b a b a b ⎛⎫+=++ ⎪⎝⎭122143b a a b ⎛⎫=+++ ⎪⎝⎭5233b a a b ⎛⎫=++ ⎪⎝⎭5233≥+⋅3=, 当且仅当b aa b =且123a b+=即1a b ==时,等号成立; 故选:C .9.(2020届山东省日照市高三上期末联考)三个数0.87,70.8,0.8log 7的大小顺序是( )A .70.80.8log 70.87<< B .0.870.8log 770.8<<C .70.80.80.87log 7<<D .0.870.870.8log 7<<,【答案】A 【解析】0.871>,700.81<<,0.8log 70<,故70.80.8log 70.87<<.故选A.10.(2020届山东省济宁市高三上期末)若0.1212,ln 2,log 5a b c ===,则( ) A .b c a >> B .b a c >> C .c a b >> D .a b c >>【答案】D 【解析】,0.10221a =>=;0ln1ln 2ln 1b e =<=<=;221log log 105c =<=,即a b c >> 故选:D11.(2020·山东省淄博实验中学高三上期末)“0x <”是“ln(1)0x +<”的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】B 【解析】由题意得,ln(1)001110x x x +<⇔<+<⇔-<<,故是必要不充分条件,故选B .)12.(2020届山东省滨州市三校高三上学期联考)若a ,b ,c ,满足2log 3a =,25b =,3log 2c =,则( )A .b c a <<B .c a b <<C .a b c <<D .c b a <<【答案】B 【解析】2221log log 3log 242=<<=,故12a <<;又22542b =>=,故2b >; 33log 2log 31c =<=,c a b ∴<<,)故选:B.13.(2020届山东省九校高三上学期联考)若函数()y f x =的大致图像如图所示,则()f x 的解析式可以为( )A .()22x xxf x -=+B .()22x xxf x -=-C .()22x xf x x-+=D .()22x xf x x--=【答案】C 【解析】对四个选项解析式分析发现B ,D 两个均为偶函数,图象关于y 轴对称,与题不符,故排除;(极限思想分析,0,222,022xxx x xx +--→+→→+,A 错误;220,222,x xx xx x-+-+→+→→+∞,C 符合题意.故选:C14.(2020届山东省枣庄、滕州市高三上期末)函数()y f x =是R 上的奇函数,当0x <时,()2xf x =,则当0x >时,()f x =( ) A .2x - B .2x - C .2x -- D .2x【答案】C 【解析】`0x <时,()2xf x =.当0x >时,0x -<,()2xf x --=,由于函数()y f x =是奇函数,()()2xf x f x -∴=--=-,因此,当0x >时,()2xf x -=-,故选C.15.(2020届山东省德州市高三上期末)已知1232a b -=⋅,()212log 23c b x x -=++,则实数a ,b ,c 的大小关系是( ) A .a b c >> B .b a c >> C .c b a >> D .a c b >>【答案】A 【解析】…1232a b -=⋅,1232a b -+∴=>,11a b ∴-+>,则a b >.()2223122x x x ++=++≥,()21122log 23log 21c b x x ∴-=++≤=-,b c ∴>.因此,a b c >>. 故选:A.16.(2020·山东省淄博实验中学高三上期末)已知定义在[]5,12m m --上的奇函数()f x ,满足0x >时,()21x f x =-,则()f m 的值为( )A .-15B .-7C .3D .15【答案】A 【解析】?因为奇函数的定义域关于原点中心对称 则5120m m -+-=,解得4m =-因为奇函数()f x 当0x >时,()21xf x =-则()()()4442115f f -=-=--=-故选:A17.(2020届山东省临沂市高三上期末)函数()22xf x =-(0x <)的值域是( )A .1,2B .(),2-∞C .()0,2D .1,【答案】A$【解析】0x <,021x ∴<<, 120x ∴-<-<1222x ∴<-<. 即()()2221,xf x =-∈故选:A18.(2020届山东实验中学高三上期中)若,a b 是任意实数,且a b >,则( ))A .22a b >B .1b a<C .()10g a b ->D .1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭【答案】D 【解析】a 、b 是任意实数,且a b >,如果0a =,2b =-,显然A 不正确;如果0a =,2b =-,显然B 无意义,不正确; 如果0a =,12b =-,显然C ,102lg <,不正确;因为指数函数12xy ⎛⎫= ⎪⎝⎭在定义域上单调递减,且a b >,1122ab⎛⎫⎛⎫∴< ⎪ ⎪⎝⎭⎝⎭满足条件,正确.故选:D .~19.(2020届山东省滨州市高三上期末)已知x ∈R ,则“121x⎛⎫ ⎪⎭>⎝”是“21x -<<-”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】B 【解析】由121x⎛⎫ ⎪⎭>⎝解得0x <,所以由“21x -<<-”能推出“0x <”,反之,不能推出; 因此“121x⎛⎫ ⎪⎭>⎝”是“21x -<<-”的必要不充分条件. 故选:B.~20.(2020届山东省济宁市高三上期末)已知奇函数()f x 在R 上单调,若正实数,a b 满足()()490f a f b +-=,则11a b+的最小值是( ) A .1B .92C .9D .18【答案】A 【解析】奇函数()f x 在R 上单调,()()490f a f b +-=,则()()()499f a f b f b =--=- 故49a b =-即49a b +=()()11111141452451999b a a b a b a b a b ⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪⎝⎭⎝⎭当4b a a b =即3,32a b ==时等号成立 ~故选:A21.(2020届山东省枣庄、滕州市高三上期末)已知ln ,1()(2),1x x f x f x k x ≥⎧=⎨-+<⎩若函数()1y f x =-恰有一个零点,则实数k 的取值范围是( ) A .(1,)+∞ B .[1,)+∞C .(,1)-∞D .(,1]-∞【答案】B 【解析】1x ≥时,()ln 1f x x ==,x e =,所以函数()1y f x =-在1x ≥时有一个零点,从而在1x <时无零点,即()1f x =无解.而当1x <时,21x ->,()(2)f x f x k =-+ln(2)x k =-+,它是减函数,值域为(,)k +∞, 要使()1f x =无解.则1k.|故选:B.22.(2020届山东省潍坊市高三上期末)函数()y f x =与()y g x =的图象如图所示,则()()y f x g x =⋅的部分图象可能是( )A .B .C .D .【答案】A 【解析】由图象可知()y f x =的图象关于y 轴对称,是偶函数,()y g x =的图象关于原点对称,是奇函数,并且定义域{}0x x ≠,$()()y f x g x ∴=⋅的定义域是{}0x x ≠,并且是奇函数,排除B ,又0,2x π⎛⎫∈ ⎪⎝⎭时,()0f x >,()0g x <,()()0f x g x ∴⋅<,排除C,D.满足条件的只有A. 故选:A23.(2020届山东省滨州市高三上期末)已知31log 3aa ⎛⎫= ⎪⎝⎭,133log bb =,131log 3cc ⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系是( ) A .c b a << B .a b c << C .b c a << D .b a c <<【答案】C 【解析】/在同一直角坐标系内,作出函数13x y⎛⎫= ⎪⎝⎭,3logy x=,3xy=,13logy x=的图像如下:因为31log3aa⎛⎫=⎪⎝⎭,133logb b=,131log3cc⎛⎫=⎪⎝⎭,所以a是13xy⎛⎫= ⎪⎝⎭与3logy x=交点的横坐标;b是3xy=与13logy x=交点的横坐标;c是13xy⎛⎫= ⎪⎝⎭与13logy x=交点的横坐标;由图像可得:b c a<<.故选:C.24.(2020届山东师范大学附中高三月考)函数()312xf x x⎛⎫=- ⎪⎝⎭的零点所在区间为()A.()1,0-B.10,2⎛⎫⎪⎝⎭C.1,12⎛⎫⎪⎝⎭D.()1,2(【答案】C【解析】311(1)(1)()302f--=--=-<,301(0)0()102f=-=-<,13211112()()()022282f=-=-<,31111(1)1()10222f=-=-=>,321115(2)2()80222f =-=-=>,由()1102f f ⎛⎫⋅< ⎪⎝⎭. 故选:C25.(2020届山东省德州市高三上期末)已知()f x 为定义在R 上的奇函数,当0x ≥时,有()()1f x f x +=-,且当[)0,1x ∈时,()()2log 1f x x =+,下列命题正确的是( )A .()()201920200f f +-=B .函数()f x 在定义域上是周期为2的函数{C .直线y x =与函数()f x 的图象有2个交点D .函数()f x 的值域为[]1,1-【答案】A 【解析】函数()y f x =是R 上的奇函数,()00f ∴=,由题意可得()()100f f =-=, 当0x ≥时,()()()21f x f x f x +=-+=,()()()()()()2019202020192020100f f f f f f ∴+-=-=-=,A 选项正确;当0x ≥时,()()1f x f x +=-,则2616log 555f f ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,2449log 555f f ⎛⎫⎛⎫-=-=- ⎪ ⎪⎝⎭⎝⎭,4462555f f f ⎛⎫⎛⎫⎛⎫∴-≠-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则函数()y f x =不是R 上周期为2的函数,B 选项错误; 若x 为奇数时,()()10f x f ==,%若x 为偶数,则()()00f x f ==,即当x ∈Z 时,()0f x =,当0x ≥时,()()2f x f x +=,若n N ∈,且当()2,21x n n ∈+时,()20,1x n -∈,()()()20,1f x f x n =-∈,当()1,2x ∈时,则()10,1x -∈,()()()11,0f x f x ∴=--∈-,当()21,22x n n ∈++时,()21,2x n -∈,则()()()21,0f x f x n =-∈-, 所以,函数()y f x =在[)0,+∞上的值域为()1,1-,由奇函数的性质可知,函数()y f x =在(),0-∞上的值域为()1,1-, 由此可知,函数()y f x =在R 上的值域为()1,1-,D 选项错误;|如下图所示:由图象可知,当11x -<<时,函数y x =与函数()y f x =的图象只有一个交点, 当1x ≤-或1x ≥时,()()1,1f x ∈-,此时,函数y x =与函数()y f x =没有交点, 则函数y x =与函数()y f x =有且只有一个交点,C 选项错误. 故选:A.26.(2020届山东实验中学高三上期中)已知函数()()221,0log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若方程()f x a =有四个不同的解12341234,,,,x x x x x x x x <<<且,则()3122341x x x x x ⋅++⋅的取值范围是( ) A .(]1,1-B .[]1,1-C .[)1,1- D .()1,1-'【答案】A 【解析】先作()f x 图象,由图象可得12343121,1.2x x x x x ⎡⎫+=-=∈⎪⎢⎣⎭,,因此()31232343112x x x x x x x ⋅++=-+⋅为1,12⎡⎫⎪⎢⎣⎭单调递减函数,从而()(] 31223411,1x x xx x⋅++∈-⋅,选A.二、多选题27.(2020届山东省临沂市高三上期末)若104a=,1025b=,则()…A.2a b+=B.1b a-=C.281g2ab>D.lg6b a->【答案】ACD【解析】由104a=,1025b=,得lg4a=,lg25b=,则lg4lg25lg1002a b∴+=+==,25lg25lg4lg4b a∴-=-=,25lg101lg lg64=>>lg6b a∴->)24lg2lg54lg2lg48lg2ab∴=>=,故正确的有:ACD故选:ACD.28.(2020届山东省日照市高三上期末联考)已知定义在R上的函数()y f x=满足条件()()2f x f x+=-,且函数()1y f x=-为奇函数,则()A.函数()y f x=是周期函数B.函数()y f x=的图象关于点()1,0-对称C .函数()y f x =为R 上的偶函数D .函数()y f x =为R 上的单调函数【答案】ABC 【解析】、因为()()2f x f x +=-,所以()()()42f x f x f x +=-+=,即4T=,故A 正确;因为函数()1y f x =-为奇函数,所以函数()1y f x =-图像关于原点成中心对称,所以B 正确; 又函数()1y f x =-为奇函数,所以()()11f x f x --=--,根据()()2f x f x +=-,令1x -代x 有()()11f x f x +=--,所以()()11f x f x +=--,令1x -代x 有()()f x f x -=,即函数()f x 为R 上的偶函数,C 正确;因为函数()1y f x =-为奇函数,所以()10f -=,又函数()f x 为R 上的偶函数,()10f =,所以函数不单调,D 不正确. 故选:ABC.29.(2020届山东省潍坊市高三上期中)已知函数22,0()(2),0x x x f x f x x ⎧--<=⎨-≥⎩,以下结论正确的是( )A .(3)(2019)3f f -+=-B .()f x 在区间[]4,5上是增函数》C .若方程() 1f x k x =+恰有3个实根,则11,24k ⎛⎫∈-- ⎪⎝⎭D .若函数()y f x b =-在(,4)-∞上有6个零点(1,2,3,4,5,6)i x i =,则()61iii x f x =∑的取值范围是()0,6【答案】BCD 【解析】函数()f x 的图象如图所示:对A ,(3)963f -=-+=-,(2019)(1)(1)1f f f ==-=,所以(3)(2019)2f f -+=-,故A 错误; 对B ,由图象可知()f x 在区间[]4,5上是增函数,故B 正确;对C ,由图象可知11,24k ⎛⎫∈-- ⎪⎝⎭,直线() 1f x k x =+与函数图象恰有3个交点,故C 正确; ]对D ,由图象可得,当函数()y f x b =-在(,4)-∞上有6个零点(1,2,3,4,5,6)i x i =,则01b <<,所以当0b →时,()610i i i x f x =→∑;当1b →时,()616i i i x f x =→∑,所以()61i i i x f x =∑的取值范围是()0,6,故D 正确. 故选:BCD.30.(2020届山东省枣庄、滕州市高三上期末)如图所示,一座小岛距离海岸线上最近的P 点的距离是2km ,从P 点沿海岸正东12km 处有一个城镇.假设一个人驾驶的小船的平均速度为3/km h ,步行的速度为5/km h ,时间t (单位:h )表示他从小岛到城镇的时间,x (单位:km )表示此人将船停在海岸处距P 点的距离.设24,u x x =++24v x x =+-,则( )A .函数()v f u =为减函数B .15432t u v --=C .当 1.5x =时,此人从小岛到城镇花费的时间最少D .当4x =时,此人从小岛到城镇花费的时间不超过3h?【答案】AC 【解析】A.∵,u x =v x =,22u v u vx +-==, 由题意4uv =,4v u=在(0,)+∞上是减函数,A 正确.B.125x t -=+126510u v u v+-=+-,整理得15436t u v =++,B 错误;C.由A 、B 得1615363644t u u =++≥=,16u u =即4u =时取等号,4x =,解得31.52x ==,C 正确;D.4x =时,85t =+,7305t -===>,3t >,D 错. :故选:AC.31.(2020届山东省枣庄市高三上学期统考)下列函数既是偶函数,又在(),0-∞上单调递减的是( ) A .2xy = B .23y x-=C .1y x x=- D .()2ln 1y x =+【答案】AD 【解析】对于A 选项,2xy =为偶函数,且当0x <时,122xx y -==为减函数,符合题意. 对于B 选项,23y x -=为偶函数,根据幂函数单调性可知23y x -=在(),0-∞上递增,不符合题意. 对于C 选项,1y x x=-为奇函数,不符合题意. {对于D 选项,()2ln 1y x =+为偶函数,根据复合函数单调性同增异减可知,()2ln 1y x =+在区间(),0-∞上单调递减,符合题意. 故选:AD.32.(2020届山东省潍坊市高三上期末)把方程1169x x y y+=-表示的曲线作为函数()y f x =的图象,则下列结论正确的有( )A .()y f x =的图象不经过第一象限B .()f x 在R 上单调递增C .()y f x =的图象上的点到坐标原点的距离的最小值为3D .函数()()43g x f x x =+不存在零点 【答案】ACD;【解析】当0,0x y >>,方程是221169x y +=-不表示任何曲线,故A 正确;当0,0x y ≥≤ ,方程是221169x y -=-,即221916y x -= ,当0,0x y ≤≥ ,方程是221169x y -+=- ,即221169x y -=,当0,0x y ≤≤ ,方程是221169x y --=-,即221169x y+= ,如图画出图象由图判断函数在R 上单调递减,故B 不正确;、由图判断()y f x =图象上的点到原点距离的最小值点应在0,0x y ≤≤的图象上,即满足221169x y += ,设图象上的点(),P x y2222279191616x PO x y x x ⎛⎫=+=+-=+ ⎪⎝⎭当0x =时取得最小值3,故C 正确; 当()430f x x += ,即()34f x x =-, 函数()()43g x f x x =+的零点,就是函数()y f x = 和34y x =-的交点, 而34y x =-是曲线221916y x -=,0,0x y ≥≤和221169x y -=0,0x y ≤≥的渐近线,所以没有交点,由图象可知34y x =-和221169x y +=,0,0x y ≤≤没有交点,所以函数()()43g x f x x =+不存在零点,故D 正确.<故选:ACD33.(2020届山东省滨州市高三上期末)在平面直角坐标系xOy 中,如图放置的边长为2的正方形ABCD 沿x 轴滚动(无滑动滚动),点D 恰好经过坐标原点,设顶点(),B x y 的轨迹方程是()y f x =,则对函数()y f x =的判断正确的是( )A .函数()y f x =是奇函数B .对任意的x ∈R ,都有()()44f x f x +=-C .函数()y f x =的值域为0,22⎡⎣D .函数()y f x =在区间[]6,8上单调递增【答案】BCD 【解析】由题意,当42x -≤<-时,顶点(),B x y 的轨迹是以点(2,0)A -为圆心,以2为半径的14圆; ,当22x -≤<时,顶点(),B x y 的轨迹是以点(0,0)D 为圆心,以214圆;当24x ≤<时,顶点(),B x y 的轨迹是以点(2,0)C 为圆心,以2为半径的14圆; 当46x ≤<,顶点(),B x y 的轨迹是以点(4,0)A 为圆心,以2为半径的14圆,与42x -≤<-的形状相同,因此函数()y f x =在[]4,4-恰好为一个周期的图像; 所以函数()y f x =的周期是8; 其图像如下:A 选项,由图像及题意可得,该函数为偶函数,故A 错;B 选项,因为函数的周期为8,所以(8)()f x f x +=,因此(4)(4)f x f x +=-;故B 正确;·C 选项,由图像可得,该函数的值域为0,22⎡⎣;故C 正确;D 选项,因为该函数是以8为周期的函数,因此函数()y f x =在区间[]6,8的图像与在区间[]2,0-图像形状相同,因此,单调递增;故D 正确; 故选:BCD.34.(2020届山东师范大学附中高三月考)下列函数中,既是偶函数,又在(0,)+∞上单调递增的是( ) A .3y x = B .2yxC .xy e =D .2lg y x =【答案】CD 【解析】本题主要考查函数的单调性和函数的奇偶性.|A 项,对于函数3y x =,因为()33()()f x x x f x -=-=-≠,所以函数3y x =不是偶函数.故A 项不符合题意.B 项,对于函数2yx ,因为当1x =时,1y =,当2x =,14y =,所以函数2y x 在区间(0,)+∞上不是单调递增的.故B 项不符合题意.C 项,对于函数x y e =,因为定义域为R ,()()x x g x g x e e --===,所以函数xy e =为偶函数,因为函数xy e =,当0x >时,xx y e e ==,而1e >,函数x y e =在R 上单调递增,所以函数xy e =在区间(0,)+∞上为增函数.故C 项符合题意.D 项,对于函数2lg y x =,因为函数()22lg )(l ()g h x x x h x -=-==,所以函数2lg y x =是偶函数.而2yx 在(0,)+∞上单调递增,lg y x =在(0,)+∞上单调递增,所以函数2lg y x =在(0,)+∞上单调递增.故D 项符合题意. 故选:CD.35.(2020届山东实验中学高三上期中)设定义在R 上的函数()f x 满足()()2f x f x x -+=,且当0x ≤时,()f x x '<.己知存在()()()220111122x x f x x f x x ⎧⎫∈-≥---⎨⎬⎩⎭,且0x 为函数()x g x e a =-(,a R e ∈为自然对数的底数)的一个零点,则实数a 的取值可能是( )A .12B .2C .2e D【答案】BCD—【解析】令函数21()()2T x f x x =-,因为2()()f x f x x -+=,22211()()()()()()()022T x T x f x x f x x f x f x x ∴+-=-+---=+--=,()T x ∴为奇函数,当0x 时,()()0T x f x x '='-<, ()T x ∴在(],0-∞上单调递减, ()T x ∴在R 上单调递减.存在0{|()(1)}x x T x T x ∈-,/∴得00()(1)T x T x -,001x x -,即012x ,()x g x e a =-;1()2x, 0x 为函数()y g x =的一个零点;当12x时,()0x g x e '=-, ∴函数()g x 在12x 时单调递减,由选项知0a >,取12x =<,又0g ee ⎛-=> ⎝,∴要使()g x 在12x时有一个零点,.只需使102g a ⎛⎫= ⎪⎝⎭, 解得e a, a ∴的取值范围为⎡⎫+∞⎪⎢⎪⎣⎭, 故选:BCD . 三、填空题36.(2020届山东省枣庄市高三上学期统考)若()3,0{1,0x x f x x x≤=>,则()()2f f -=__________. 【答案】9 【解析】《因为21(2)309f --==>,所以1((2))()99f f f -==,应填答案9. 37.(2020届山东省潍坊市高三上期中)已知函数()f x 是定义在R 上的偶函数,且在[)0,+∞上是减函数,10,3f ⎛⎫-= ⎪⎝⎭则不等式18log 0f x ⎛⎫> ⎪⎝⎭的解集为__________.【答案】1,22⎛⎫ ⎪⎝⎭【解析】()f x 是定义在R 上的偶函数,且在[0,)+∞上是减函数,1()03f -=,11()()033f f ∴=-=,则不等式18(log )0f x >等价为不等式181(|log |)()3f x f >,即181|log |3x <⇒1811log 33x -<<⇒122x <<,{即不等式的解集为1(,2)2, 故答案为:1(,2)2.38.(2020届山东省九校高三上学期联考)已知[]x 表示不超过x 的最大整数,如[]33=,[]1.51=,[]1.72-=-.令()2x f x x =⋅,[]()()g x f x x =-,则下列说法正确的是__________.①()g x 是偶函数 ②()g x 是周期函数③方程()0g x -=有4个根④()g x 的值域为[]0,2 【答案】②③|【解析】1111()([])()33333g f f =-==,1112()([])()33333g f f -=---== 显然11()()33g g -≠,所以()g x 不是偶函数,所以①错误;[][](1)(11)()()g x f x x f x x g x +=+-+=-=,所以()g x 是周期为1的周期函数,所以②正确; 作出函数y x =的图象和()g x 的图象:根据已推导()g x 是周期为1的周期函数,只需作出()g x 在[0,1)x ∈的图象即可,当[0,1)x ∈时[]()()()2x g x f x x f x x =-==⋅,根据周期性即可得到其余区间函数图象,如图所示:》可得()g x 值域为[0,2),函数y x =()g x 的图象一共4个交点,即方程()0g x x =有4个根, 所以③正确,④错误; 故答案为:②③39.(2020届山东省滨州市三校高三上学期联考)已知定义在R 上的函数满足(3)(3)f x f x -=-+,且()f x 图像关于1x =对称,当(1,2]x ∈时,2()log (21)f x x =+,则8252f ⎛⎫= ⎪⎝⎭________. 【答案】-2 【解析】因为()f x 图像关于1x =对称,则()(2)f x f x =-,()(2)(31)(31)(4)(8)f x f x f x f x f x f x =-=--=-++=-+=+,)故()f x 是以8为周期的周期函数,82511113851443131222222f f f f ff⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫∴=⨯++=+=++=---=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭23log (21)22=-⨯+=-故答案为:2-.40.(2020届山东师范大学附中高三月考)已知函数()f x 是定义在R 上的奇函数,当12x x ≠时,有1212[()()]()0f x f x x x --<恒成立,若(31)(2)0f x f ++>,则x 的取值范围是________.【答案】(,1)-∞- 【解析】根据已知条件:当12x x ≠时,有1212[()()]()0f x f x x x --<恒成立,得函数()f x 是定义在R 上的减函数,…又因为函数()f x 是定义在R 上的奇函数,所以(2)(2)f f -=-,故(31)(2)0f x f ++>等价于(31)(2)(2)f x f f +>-=-,所以312x +<-,即1x <-. 故答案为:(),1-∞-.41.(2020届山东省济宁市高三上期末)2019年7月,中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳14的质量N 随时间t (单位:年)的衰变规律满足573002tN N -=⋅(0N 表示碳14原有的质量),则经过5730年后,碳14的质量变为原来的________;经过测定,良渚古城遗址文物样本中碳14的质量是原来的12至35,据此推测良渚古城存在的时期距今约在________年到5730年之间.(参考数据:22log 3 1.6,log 5 2.3≈≈) 【答案】124011 【解析】当5730t =时,100122N N N -=⋅=∴经过5730年后,碳14的质量变为原来的12令035N N =,则5730325t-= 2223log log 3log 50.757305t ∴-==-≈- 。
【4月烟台市一模数学】山东省烟台市2020届高三4月诊断性模拟考试(一模)数学试卷及答案解析评分标准

A.当 a 1时, f ( x) 在 (0, f (0)) 处的切线方程为 2 x y 1 0
B.当 a 1时, f ( x) 存在唯一极小值点 x0 且 1 f (x0 ) 0 C.对任意 a 0 , f ( x) 在 ( , ) 上均存在零点
D.存在 a 0 , f ( x) 在 ( , ) 上有且只有一个零点
合题目要求。
1.已知集合 M x y ln(x 1) , N y y ex ,则 M I N
A. (1, 0)
B. (1, +)
C. (0, +)
D. R
2.已知复数 z 满足 (1 i) z 2i ( i 为虚数单位),则 z
A.1 i
ቤተ መጻሕፍቲ ባይዱ
B.1 i
C.1 2i
3.设 xR ,则“| x 2 | 1”是“ x2 2 x 3 0 ”的
切点,则四边形 APBC 面积的最小值为
A. 3
B. 2 3
C. 5
D. 2 5
8.已知函数
f
(x)
ex ex
ex ex
,实数 m, n 满足不等式
f
(2m n)
f
(2 n)
0 ,则下列不等关系成立
的是
A. m n 1
B. m n 1
C. m n 1
D. m n 1
二、多项选择题:本题共 4 小题,每小题 5 分,共 20 分。在每小题给出的选项中,有多项符合要求。
10.已知 P 是双曲线 C : x2 y2 1上任一点, A, B 是双曲线上关于坐标原点对称的两点,设直线 3m
PA,
PB
的斜率分别为
k1, k2(k1k2
0),若 |
2020年山东省新高考数学模拟试卷(二)
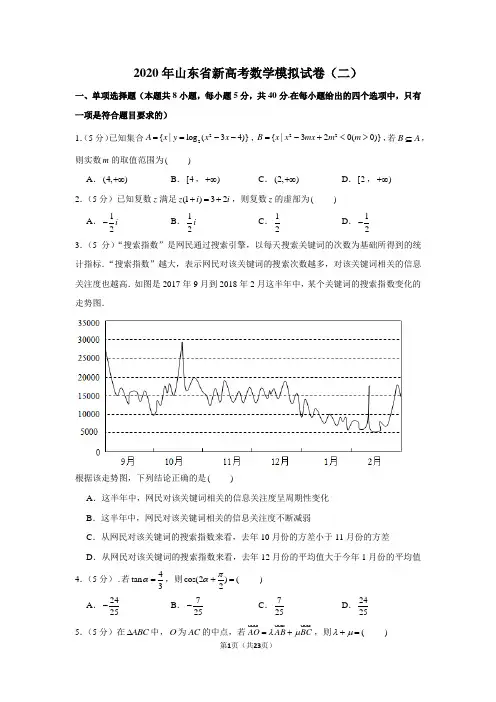
2020年山东省新高考数学模拟试卷(二)一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合22{|log (34)}A x y x x ==--,22{|320(0)}B x x mx m m =-+<>,若B A ⊆,则实数m 的取值范围为( ) A .(4,)+∞B .[4,)+∞C .(2,)+∞D .[2,)+∞2.(5分)已知复数z 满足(1)32z i i +=+,则复数z 的虚部为( ) A .12i -B .12iC .12 D .12-3.(5分)“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.如图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.根据该走势图,下列结论正确的是( )A .这半年中,网民对该关键词相关的信息关注度呈周期性变化B .这半年中,网民对该关键词相关的信息关注度不断减弱C .从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差D .从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值 4.(5分).若4tan 3α=,则cos(2)(2πα+= )A .2425-B .725-C .725 D .24255.(5分)在ABC ∆中,O 为AC 的中点,若AO AB BC λμ=+u u u r u u u r u u u r,则(λμ+= )A .1B .12C .23D .436.(5分)优题速享如图是函数()sin()(0,0,||)2f x A x A πωϕωϕ=+>><的部分图象,将函数()f x 的图象向右平移6π个单位长度得到()g x 的图象,给出下列四个命题: ①函数()f x 的表达式为()2sin(2)3f x x π=+;②()g x 的一条对称轴的方程可以为4x π=-;③对于实数m ,恒有()()33f m f m ππ+=-;④()()f x g x +的最大值为2.其中正确的个数有( )A .1个B .2个C .3个D .4个7.(5分)一个各面均为直角三角形的四面体容器,有三条棱长为2,若四面体容器内完全放进一个球,则该球的半径最大值为( ) A 21B .22C .1D .28.(5分)定义在R 上的函数()f x 满足:()1()f x f x '>-,(0)0f =,()f x '是()f x 的导函数,则不等式()1x x e f x e >-(其中e 为自然对数的底数)的解集为( ) A .(0,)+∞B .(-∞,1)(0-⋃,)+∞C .(-∞,0)(1⋃,)+∞D .(1,)-+∞二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分) 9.(5分)已知两圆221x y +=和22(4)()25x y a ++-=相切,则实数(a = ) A .213±B .25±C .0D .以上均有可能10.(5分)在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c .若ABC ∆为锐角三角形,且满足sin (12cos )2sin cos cos sin B C A C A C +=+,则下列等式成立的是( )A .2a b =B .2b a =C .A B >D .B A >11.(5分)已知2()(0)f x ax bx c a =++≠,且关于x 的方程()f x x =无实数根,现有下列说法,其中说法正确的是( )A .若0a >,则不等式(()f f x )x >对一切x R ∈恒成立B .若0a <,则必然存在实数0x 使不等式00(())f f x x >成立C .关于x 的方程(())f f x x =一定没有实数根D .若0a b c ++=,则不等式(()f f x )x <对一切x R ∈恒成立12.(5分)已知圆锥曲线22:1(0)C mx ny n m +=>>与222:1(0,0)C px qy p q -=>>的公共焦点为1F ,2F .点M 为1C ,2C 的一个公共点,且满足1290F MF ∠=︒,若圆锥曲线1C 的离心率为34,则下列说法正确的是( )A .2C 的离心率为92B .2CC .2C 的渐近线方程为2y x = D .2C 的渐近线方程为2y x =±三、填空题(本题共4小题,每小题5分,共20分) 13.(5分)已知函数81()(1)1x f x ln x x -=--+,则函数()f x 的图象在(2,5)-处的切线方程为 .14.(5分)若正数x ,y 满足53x y xy +=,则5x y +的最小值是 .15.(5分)已知直线:10l mx ny +-=与圆22:1O x y +=相交的弦长||AB =,则22m n += .16.(5分)如图,四边形ABCD 是边长为1的正方形,其中边DA 在x 轴上,点D 与坐标原点重合,若正方形沿x 轴正向滚动,先以A 为中心顺时针旋转,当B 落在x 轴上时,再以B 为中心顺时针旋转,如此继续,即当正方形ABCD 的某个顶点落在x 轴上时,则以该顶点为中心顺时针旋转.设顶点(,)C x y 滚动时形成的曲线为()y f x =,则(2019)f = ,20191()i f i ==∑.四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)在①1(0)2f=,②()(0)fx f…恒成立,③()f x的图象关于点(3πω,0)中心对称这三个条件中任选一个,补充在下面问题中.若问题中的ω存在,求出ω的范围;若ω不存在,说明理由.设函数()sin()(0f x xωϕω=+>,)22ππϕ-剟,是否存在ω,使得函数()f x在[0,]2π上是单调的?18.(12分)已知等差数列{}na满足3221a a=-,47a=,等比数列{}nb满足35242()b b b b+=+,且2*22()n nb b n N=∈.(1)求数列{}na,{}nb的通项公式;(2)记数列{}na的前n项和为nS,若数列{}nc满足*1212()nnncc cS n Nb b b++⋯+=∈,求{}nc的前n项和为nT.19.(12分)如图,在多面体ABCDEF中,四边形ABCD是边长为43的菱形,60BCD∠=︒,AC与BD交于点O,平面FBC⊥平面ABCD,//EF AB,FB FC=,23EF=.(1)求证:OE⊥平面ABCD;(2)若FBC∆为等边三角形,点Q为AE的中点,求二面角Q BC A--的余弦值.20.(12分)某高校为增加应届毕业生就业机会,每年根据应届毕业生的综合素质和学业成绩对学生进行综合评估,已知某年度参与评估的毕业生共有2000名.其评估成绩Z近似的服从正态分布2(,)Nμσ.现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了如下频率分布直方图:(1)求样本平均数x 和样本方差2s (同一组中的数据用该组区间的中点值作代表); (2)若学校规定评估成绩超过82.7分的毕业生可参加A 、B 、C 三家公司的面试.()i 用样本平均数x 作为的估计值ˆμ,用样本标准差s 作为σ的估计值ˆσ.请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;()ii 若三家公司每家都提供甲、乙、丙三个岗位,岗位工资表如下:公司甲岗位 乙岗位 丙岗位 A 9600 6400 5200 B9800 7200 5400 C1000060005000李华同学取得了三个公司的面试机会,经过评估,李华在三个公司甲、乙、丙三个岗位的面试成功的概率均为0.3,0.3,0.4.李华准备依次从A 、B 、C 三家公司进行面试选岗,公司规定:面试成功必须当场选岗,且只有一次机会,李华在某公司选岗时,若以该岗位与未进行面试公司的工资期望作为抉择依据,问李华可以选择A 、B 、C 公司的哪些岗位?并说明理由. 附:16112.7≈若随机变量2~(,)Z N μσ,则()0.6826P Z μσμσ-<<+=,(22)0.9544P Z μσμσ-<<+=.21.(12分)已知函数()1alnx bf x x x=++,曲线()y f x =在点(1,f (1))处的切线方程为230x y +-=.(Ⅰ)求a 、b 的值;(Ⅱ)如果当0x >,且1x ≠时,()1lnx kf x x x>+-,求k 的取值范围. 22.(12分)已知圆22:4O x y +=,抛物线2:2(0)C x py p =>.(1)若抛物线C 的焦点F 在圆O 上,且A 为抛物线C 和圆O 的一个交点,求||AF ; (2)若直线l 与抛物线C 和圆O 分别相切于M ,N 两点,设0(M x ,0)y ,当0[3y ,4]时,求||MN 的最大值.2020年山东省新高考数学模拟试卷(二)参考答案与试题解析一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合22{|log (34)}A x y x x ==--,22{|320(0)}B x x mx m m =-+<>,若B A ⊆,则实数m 的取值范围为( ) A .(4,)+∞B .[4,)+∞C .(2,)+∞D .[2,)+∞【解答】解:解一元二次不等式2340x x -->得:1x <-或4x >,即(A =-∞,1)(4-⋃,)+∞,解一元二次不等式22320(0)x mx m m -+<>得2m x m <<,即(,2)B m m =, 又B A ⊆,所以210m m -⎧⎨>⎩„或40m m ⎧⎨>⎩…,解得4m …, 故选:B .2.(5分)已知复数z 满足(1)32z i i +=+,则复数z 的虚部为( ) A .12i -B .12iC .12 D .12-【解答】解:由(1)32z i i +=+, 得32(32)(1)511(1)(1)22i i i z i i i i ++-===-++-, ∴复数z 的虚部为12-. 故选:D .3.(5分)“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.如图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.根据该走势图,下列结论正确的是( )A .这半年中,网民对该关键词相关的信息关注度呈周期性变化B .这半年中,网民对该关键词相关的信息关注度不断减弱C .从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差D .从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值 【解答】解:在A 中,这半年中,网民对该关键词相关的信息关注度没有规律,故A 错误; 在B 中,这半年中,网民对该关键词相关的信息关注度呈现出一定的波动性,没有减弱,故B 错误;在C 中,从网民对该关键词的搜索指数来看,去年10月份的方差大于11月份的方差,故C 错误;在D 中,从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值,故D 正确. 故选:D . 4.(5分).若4tan 3α=,则cos(2)(2πα+= )A .2425-B .725-C .725D .2425【解答】解:22242sin cos 2tan 243cos(2)sin 2216212519sin cos tan παααααααα+=-=-=-=-⨯=-+++, 故选:A .5.(5分)在ABC ∆中,O 为AC 的中点,若AO AB BC λμ=+u u u r u u u r u u u r,则(λμ+= )A .1B .12C .23D .43【解答】解:如图, O 为AC 的中点;∴1111()2222AO AC BC BA AB BC ==-=+u u u r u u u r u u u r u u u r u u ur u u u r ;又AO AB BC λμ=+u u u r u u u r u u u r ;根据平面向量基本定理得,12λμ==; 1λμ∴+=.故选:A .6.(5分)优题速享如图是函数()sin()(0,0,||)2f x A x A πωϕωϕ=+>><的部分图象,将函数()f x 的图象向右平移6π个单位长度得到()g x 的图象,给出下列四个命题: ①函数()f x 的表达式为()2sin(2)3f x x π=+;②()g x 的一条对称轴的方程可以为4x π=-;③对于实数m ,恒有()()33f m f m ππ+=-;④()()f x g x +的最大值为2.其中正确的个数有( )A .1个B .2个C .3个D .4个【解答】解:由图象知,2A =,5746124T πππ=-=,即T π=,则2ππω=,得2ω=, 由五点对应法得5226πϕπ⨯+=,得3πϕ=, 则()2sin(2)3f x x π=+,故①正确, 当3x π=时,()2sin 03f ππ==,则函数关于3x π=不对称,故③错误, 将函数()f x 的图象向右平移6π个单位长度得到()g x 的图象,即()2sin[2()]2sin 263g x x x ππ=-+=,当4x π=-时,()2sin()242g ππ-=-=-为最小值,则4x π=-是函数()g x 的一条对称轴,故②正确,()()2sin(2)2sin 22sin cos 2cos2sin 2sin 23sin 2)3336f xg x x x x x x x x x ππππ+=++=++==+,则()()f x g x +的最大值为④错误, 故正确的是①②, 故选:B .7.(5分)一个各面均为直角三角形的四面体容器,有三条棱长为2,若四面体容器内完全放进一个球,则该球的半径最大值为( )A 1B .2C .1D .2【解答】解:满足条件的四面体的容器如图, 四面体ABCD 中,AD ⊥平面BCD ,BD BC ⊥, 满足各面均为直角三角形,此时,2AD BD BC ===,则AB CD ==AC =要满足题意,则当球与四面体各面均相切时半径最大, 此时设球心为O ,则原四面体可看成是以O 为顶点,其余各面为底面的四个四面体组合而成,且这4个四面体的高均为内切球半径, 由等体积法有:111222(22323r ⨯⨯⨯⨯=⨯⨯++,解得21r =-. 故选:A .8.(5分)定义在R 上的函数()f x 满足:()1()f x f x '>-,(0)0f =,()f x '是()f x 的导函数,则不等式()1x x e f x e >-(其中e 为自然对数的底数)的解集为( ) A .(0,)+∞B .(-∞,1)(0-⋃,)+∞C .(-∞,0)(1⋃,)+∞D .(1,)-+∞【解答】解:设()()x x g x e f x e =-,()x R ∈, 则()()()[()()1]x x x x g x e f x e f x e e f x f x '=+'-=+'-,()1()f x f x '>-Q , ()()10f x f x ∴+'->, ()0g x ∴'>,()y g x ∴=在定义域上单调递增,()1x x e f x e >-Q ,()1g x ∴>-,又00(0)(0)1g e f e =-=-Q ,()(0)g x g ∴>,0x ∴>,∴不等式的解集为(0,)+∞;故选:A .二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分) 9.(5分)已知两圆221x y +=和22(4)()25x y a ++-=相切,则实数(a = )A .±B .±C .0D .以上均有可能【解答】解:圆221x y +=的圆心为(0,0),半径为1,圆22(4)()25x y a ++-=的圆心为(4,)a -,半径为5,若两圆相切,分两种情况讨论:当两圆外切时,有222(4)(15)a -+=+,解得a =± 当两圆内切时,有222(4)(15)a -+=-,解得0a =,综合可得:实数a 的值为0或± 故选:BC .10.(5分)在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c .若ABC ∆为锐角三角形,且满足sin (12cos )2sin cos cos sin B C A C A C +=+,则下列等式成立的是( ) A .2a b =B .2b a =C .A B >D .B A >【解答】解:因为sin (12cos )2sin cos cos sin B C A C A C +=+, 所以sin 2sin cos 2sin cos cos sin B B C A C A C +=+,所以sin cos sin cos 2sin cos 2sin cos cos sin A C C A B C A C A C ++=+, 整理可得,2sin cos sin cos B C A C =, 因为C 为锐角,cos 0C ≠, 所以2sin sin B A =, 由正弦定理可得,2a b =,由三角形的大边对大角可得,A B >, 故选:AC .11.(5分)已知2()(0)f x ax bx c a =++≠,且关于x 的方程()f x x =无实数根,现有下列说法,其中说法正确的是( )A .若0a >,则不等式(()f f x )x >对一切x R ∈恒成立B .若0a <,则必然存在实数0x 使不等式00(())f f x x >成立C .关于x 的方程(())f f x x =一定没有实数根D .若0a b c ++=,则不等式(()f f x )x <对一切x R ∈恒成立【解答】解:函数[()]f f x 为一个复合函数,可以把方括号里的()f x 看作为一个未知数t ,t的范围就是()f x 的值域;对于A ,[()]f f x 可以看作()f t ,而题中()f x x =无实根,方括号里的()f x 看作为一个未知数t ,则外层为一个开口向上的2次函数,且()f x x =无实根,且0a >, 所以不等式[()]f f x x >对一切x R ∈都成立,A 正确;对于B ,0a <时,由()f x x =无实根知二次函数()y f x x =-开口向下,且与x 轴没有交点, 同理,令()t f x =,则二次函数()y f t t =-也开口向下,且与横轴没有交点, 所以不等式[()]f f x x <对一切x R ∈都成立,B 错误;对于C ,[()]f f x 看为()f t ,而题中()f x x =无实根,所以方程[()]f f x x =无实根,所以C 正确;对于D ,由0a b c ++=知f (1)01=<,又()f x x =无实根,所以0a <, 由选项B 知不等式(()f f x )x <对一切x R ∈恒成立,D 正确. 故选:ACD .12.(5分)已知圆锥曲线22:1(0)C mx ny n m +=>>与222:1(0,0)C px qy p q -=>>的公共焦点为1F ,2F .点M 为1C ,2C 的一个公共点,且满足1290F MF ∠=︒,若圆锥曲线1C 的离心率为34,则下列说法正确的是( )A .2C 的离心率为92B .2CC .2C 的渐近线方程为y =D .2C 的渐近线方程为y x = 【解答】解:由题意,不妨取M 为两曲线在第一象限的交点, 令21a m=,21b n =,211a p =,211b q =,则曲线1C 的方程为22221(0)x y a b a b+=>>,曲线2C 的方程为22122111(0x y a a b -=>,10)b >,又由两曲线有公共焦点,则2222211a b a b c -=+=,由圆锥曲线定义可得:12||||2MF MF a +=,121||||2MF MF a -=, 解得11||MF a a =+,21||MF a a =-.又1290F MF ∠=︒,∴2221212||||||MF MF F F +=, 可得22212a a c +=,整理得2212112e e +=, Q 134e =,∴232e =;由1322c a =,可得22211221192a b c a a +==,得11142b a =,2C ∴的渐近线方程为14y x =±. 故选:BC .三、填空题(本题共4小题,每小题5分,共20分) 13.(5分)已知函数81()(1)1x f x ln x x -=--+,则函数()f x 的图象在(2,5)-处的切线方程为 50y += .【解答】解:因为81()(1)1x f x ln x x -=--+,点坐标为(2,5)-, 可知点在曲线上, 则219()1(1)f x x x '=--+, 则f '(2)110=-=,即切线的斜率为0, 又因为过点(2,5)-, 所以切线方程为50y +=, 故答案为:50y +=.14.(5分)若正数x ,y 满足53x y xy +=,则5x y +的最小值是 12 . 【解答】解:正数x ,y 满足53x y xy +=,则153y x+=, 1151551555(5)()(251)(262)12333x y x yx y x y y x y x y x∴+=++=++++=g …,当且仅当2x y ==时取等号, 故5x y +的最小值是12, 故答案为:1215.(5分)已知直线:10l mx ny +-=与圆22:1O x y +=相交的弦长2||AB =,则22m n += .【解答】解:2222|1|2||21()2AB m n -=-=+Q , 化简得:2287m n +=. 故答案为:87. 16.(5分)如图,四边形ABCD 是边长为1的正方形,其中边DA 在x 轴上,点D 与坐标原点重合,若正方形沿x 轴正向滚动,先以A 为中心顺时针旋转,当B 落在x 轴上时,再以B 为中心顺时针旋转,如此继续,即当正方形ABCD 的某个顶点落在x 轴上时,则以该顶点为中心顺时针旋转.设顶点(,)C x y 滚动时形成的曲线为()y f x =,则(2019)f = 0 ,20191()i f i ==∑.【解答】解:Q 正方形的边长为1,∴正方形的对角线2AC =, 则由正方形的滚动轨迹得到0x =时,C 位于(0,1)点,即(0)1f =, 当1x =时,C 位于(1,2)点,即f (1)2=, 当2x =时,C 位于(2,1)点,即f (2)1=, 当3x =时,C 位于(3,0)点,即f (3)0=, 当4x =时,C 位于(4,1)点,即f (4)1=, 则(4)()f x f x +=,即()f x 具备周期性,周期为4, 则(2019)(50443)f f f =⨯+=(3)0=,20191()504(2101)21050521009i f i ==⨯++++++=+∑,故答案为:0;50521009+.四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)在①1(0)2f =,②()(0)f x f „恒成立,③()f x 的图象关于点(3πω,0)中心对称这三个条件中任选一个,补充在下面问题中.若问题中的ω存在,求出ω的范围;若ω不存在,说明理由.设函数()sin()(0f x x ωϕω=+>,)22ππϕ-剟,①203ω<„.②02ω<„.③503ω<„. 是否存在ω,使得函数()f x 在[0,]2π上是单调的?【解答】解:①1(0)sin(0)sin 2f ϕϕ=+==Q ,52266k k ππϕππ∴=++或, 22ππϕ-Q 剟,6πϕ∴=.此时()sin()6f x x πω=+. 当[0,],[,]26626x x πππωππω∈+∈+,要使得函数()f x 在[0,]2π上是单调的,262ωπππ+„,∴23ω„.0ω>Q ,∴203ω<„. ②()(0)f x f Q „恒成立,()(0)sin 1max f x f ϕ∴===. 22ππϕ-Q 剟,2πϕ∴=.此时()sin()cos 2f x x x πωω=+=. [0x ∈Q ,]2π,[0,]2x ωπω∈,要使得函数()f x 在[0,]2π上是单调的,2ωππ„,2ω∴„.0ω>Q ,02ω∴<„.③()f x 的图象关于点(3πω,0)中心对称, 3k πωϕπω+=g ,3k πϕπ=-+,22ππϕ-Q 剟,3πϕ∴=-.此时()sin()3f x x πω=-. [0x ∈Q ,]2π,[,]3323x ππωππω-∈--.要使得函数()f x 在[0,]2π上是单调的,232ωπππ-„,∴53ω„.0ω>Q ,503ω∴<„.. 故答案为:①203ω<„.②02ω<„.③503ω<„. 18.(12分)已知等差数列{}n a 满足3221a a =-,47a =,等比数列{}n b 满足35242()b b b b +=+,且2*22()n nb b n N =∈.(1)求数列{}n a ,{}n b 的通项公式;(2)记数列{}n a 的前n 项和为n S ,若数列{}n c 满足*1212()n n nc c c S n N b b b ++⋯+=∈,求{}n c 的前n 项和为n T .【解答】解:(1)等差数列{}n a 满足3221a a =-,47a =, 可得1141222137a d a d a a d +=+-⎧⎨=+=⎩,解得11a =,2d =, 12(1)21n a n n ∴=+-=-,Q 等比数列{}n b 满足35242()b b b b +=+,3222222()b q b q b b q ∴+=+, 即322(1)q q q +=+,2q ∴=,Q 2*22()n nb b n N =∈. 22112b b b q ∴==, 11b ∴=12n n b -∴=,(2)由(1)可得2(121)2n n n S n +-==, ∴1212n n n c c c S b b b ++⋯+=, ∴1121121n n n c c c S b b b ---++⋯+=, 两式相减可得1nn n n nc S S a b -=-=, 1(21)2n n n n c a b n -∴==-,0121123252(21)2n n T n -∴=⨯+⨯+⨯+⋯+-, 1232123252(21)2n n T n ∴=⨯+⨯+⨯+⋯+-,两式相减可得1123112(12)12(2222)(21)212(21)2142(21)23(32)212n n n n n n nn T n n n n --+--=++++⋯+--=+⨯--=-+--=-+--,3(23)2n n T n ∴=+-.19.(12分)如图,在多面体ABCDEF 中,四边形ABCD 是边长为43的菱形,60BCD ∠=︒,AC 与BD 交于点O ,平面FBC ⊥平面ABCD ,//EF AB ,FB FC =,23EF =. (1)求证:OE ⊥平面ABCD ;(2)若FBC ∆为等边三角形,点Q 为AE 的中点,求二面角Q BC A --的余弦值.【解答】证明:(1)如图,取BC 中点G ,连接FG ,OG , 因为FB FC =, 所以FG BC ⊥,又因为平面FBC ⊥平面ABCD ,平面FBC ⋂平面ABCD BC =,FG ⊂平面FBC , 所以FG ⊥平面ABCD , O ,G 分别为BD ,BC 中点,所以//OG AB ,12OG AB = 因为2312EF AB =,//EF AB , 所以四边形EFGO 为平行四边形, 所以//OE FG , 所以OE ⊥平面ABCD .(2)如图,以AC 所在直线为x 轴,BD 所在直线为y 轴,OE 所在直线为z 轴建立空间坐标系,显然二面角Q BC A --为锐二面角,设该二面角为θ,向量(0n =r ,0,1)是平面ABC 的法向量,设平面QBC 的法向量(v x =r,y ,1),由题意可知sin602FG OE BF ==︒=,所以(2C -,0,0),(0B ,23,0),(0E ,0,2),(1Q ,0,1) 所以(1BQ =u u u r ,23-,1),(3CQ =u u u r ,0,1),则00v BQ v CQ ⎧=⎪⎨=⎪⎩u u u r r g u u u r r g ,即2310310x y x ⎧-+=⎪⎨⎪+=⎩, 所以1(3v =-r,3,1),所以||313cos ||||131n v n v θ===⨯r r g r r .20.(12分)某高校为增加应届毕业生就业机会,每年根据应届毕业生的综合素质和学业成绩对学生进行综合评估,已知某年度参与评估的毕业生共有2000名.其评估成绩Z 近似的服从正态分布2(,)N μσ.现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了如下频率分布直方图:(1)求样本平均数x 和样本方差2s (同一组中的数据用该组区间的中点值作代表); (2)若学校规定评估成绩超过82.7分的毕业生可参加A 、B 、C 三家公司的面试.()i 用样本平均数x 作为的估计值ˆμ,用样本标准差s 作为σ的估计值ˆσ.请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;()ii 若三家公司每家都提供甲、乙、丙三个岗位,岗位工资表如下:公司甲岗位 乙岗位 丙岗位 A960064005200B9800 7200 5400 C1000060005000李华同学取得了三个公司的面试机会,经过评估,李华在三个公司甲、乙、丙三个岗位的面试成功的概率均为0.3,0.3,0.4.李华准备依次从A 、B 、C 三家公司进行面试选岗,公司规定:面试成功必须当场选岗,且只有一次机会,李华在某公司选岗时,若以该岗位与未进行面试公司的工资期望作为抉择依据,问李华可以选择A 、B 、C 公司的哪些岗位?并说明理由. 附:16112.7≈若随机变量2~(,)Z N μσ,则()0.6826P Z μσμσ-<<+=,(22)0.9544P Z μσμσ-<<+=.【解答】解:(1)由所得数据绘制的频率直方图,得:样本平均数450.05550.18650.28750.26850.17950.0670x =⨯+⨯+⨯+⨯+⨯+⨯=; 样本方差2222222(4570)0.05(5570)0.18(6570)0.28(7570)0.26(8570)0.17(9570)0.06161s =-⨯+-⨯+-⨯+-⨯+-⨯+-⨯=;( i )由(1)可知,ˆ70μ=,2ˆ161σ=,故评估成绩Z 服从正态分布(70,161)N , 所以1ˆˆ(82.7)()(10.6826)0.15872P Z P Z μσ>=>+=-=. 在这2000名毕业生中.能多加三家公司面试的估计有20000.1587317⨯≈人. ()ii 李华可以选择A 公司的甲岗位,B 公司的甲,乙岗位,C 公司的三个岗位, 理由如下:设B .C 公司提供的工资为B X ,C X ,则B X ,C X 都为随机变量,其分布列为公司 甲岗位 乙岗位 丙岗位 B X980072005400则B 公司的工资期望()98000.372000.354000.47260B E X =⨯+⨯+⨯=(元), C 公司的工资期望:()100000.360000.350000.46800C E X =⨯+⨯+⨯=(元),因为A 公司的甲岗位工资9600元大于B ,C 公司的工资期望,乙岗位工资6400元小于B ,C 公司的工资期望,故李华先去A 公司面试,若A 公司给予甲岗位就接受,否则去B 公司;B 公司甲,乙岗位工资都高于C 公司的工资期望,故B 公司提供甲,乙岗位就接受,否则去C 公司;在C 公司可以依次接受甲,乙,丙三种岗位中的一种岗位. 21.(12分)已知函数()1alnx bf x x x=++,曲线()y f x =在点(1,f (1))处的切线方程为230x y +-=.(Ⅰ)求a 、b 的值;(Ⅱ)如果当0x >,且1x ≠时,()1lnx kf x x x>+-,求k 的取值范围. 【解答】解:由题意f (1)1=,即切点坐标是(1,1)(Ⅰ)221()()(1)x a lnx b x f x x x +-'=-+由于直线230x y +-=的斜率为12-,且过点(1,1),故(1)11(1)2f f =⎧⎪⎨'=-⎪⎩即1122b a b =⎧⎪⎨-=-⎪⎩解得1a =,1b =.(Ⅱ)由(Ⅰ)知1()1lnx f x x x=++,所以 221(1)(1)()()(2)11lnx k k x f x lnx x x x x---+=+--.考虑函数2(1)(1)()2(0)k x h x lnx x x--=+>,则22(1)(1)2()k x xh x x -++'=. ()i 设0k …,由222(1)(1)()k x x h x x +--'=知,当1x ≠时,()0h x '<.而h (1)0=,故当(0,1)x ∈时,()0h x '<,可得21()01h x x>-; 当(1,)x ∈+∞时,()0h x '<,可得21()01h x x >- 从而当0x >,且1x ≠时,()()01lnx k f x x x -+>-,即()1lnx kf x x x>+-. ()ii 设01k <<.由于当1(1,)1x k∈-时,2(1)(1)20k x x -++>,故()0h x '>, 而h (1)0=,故当1(1,)1x k∈-时,()0h x >,可得21()01h x x <-,与题设矛盾. ()iii 设1k ….此时()0h x '>,而h (1)0=,故当(1,)x ∈+∞时,()0h x >,可得21()01h x x <-,与题设矛盾. 综合得,k 的取值范围为(-∞,0].22.(12分)已知圆22:4O x y +=,抛物线2:2(0)C x py p =>.(1)若抛物线C 的焦点F 在圆O 上,且A 为抛物线C 和圆O 的一个交点,求||AF ; (2)若直线l 与抛物线C 和圆O 分别相切于M ,N 两点,设0(M x ,0)y ,当0[3y ∈,4]时,求||MN 的最大值.【解答】解:(1)依题意(0,)2p F 在圆224x y +=上,2044p ∴+=,解得4p =,∴抛物线C的方程为:28x y =,联立22248x y x y⎧+=⎨=⎩消去x 得2840y y +-=,解得4y =-+,||()4222pAF y ∴=--=-+=.(2)y 依题意设切线l 的方程为000()xy y x x p-=-,整理得000x x py py --=,由||2ON =,得:0||py == 所以02084y p y =-且24y >, 所以222222200002016||||442444y MN OM x y py y y y =-=+-=+-=+-- 2020644164y y =-++-,设204[5t y=-∈,12],则64||16MN tt=++,求导可知:函数在{5,12]上是递减函数,5t∴=,即03y=时,||MN.。
2020届山东省烟台市高三3月高考诊断性测试(一模)数学(理)试题Word版含答案

2020届山东省烟台市高三3月高考诊断性测试(一模)数学(理)试题注意事项:1.本试题满分150分,考试时间为120分钟.2.使用答题纸时,必须使用0.5毫米的黑色签字笔书写,要字迹工整,笔迹清晰.超出答题区书写的答案无效;在草稿纸、试题卷上答题无效.3.答卷前将密封线内的项目填写清楚.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个选项符合题目要求.1.若集合A={}1,0,1,2,3-,B={}21,y y x x A =-∈,集合C=A ∩B ,则C 的真子集个数为A .3B .4C .7D .8 2.若复数1a i i+-(i 为虚数单位,a 为实数)为纯虚数,则不等式3x a x ++>的解集为 A .{}1x x > B .{}2x x <- C .{}1x x x <->2或 D .{}2x x x <->1或3.“1m =”是“函数()()()22log 1log 1f x mx mx =+--为奇函数”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.用0,1,2,…,299给300名高三学生编号,并用系统抽样的方法从中抽取15名学生的数学成绩进行质量分析,若第一组抽取的学生的编号为8,则第三组抽取的学生编号为A .20B .28C .40D .485.若,αβ是两个不同平面,,m n 是两条不同直线,则下列结论错误的是A .如果//m n ,//αβ,那么m 与α所成的角和n 与β所成的角相等B .如果m n ⊥,m α⊥,//n β,那么αβ⊥C .如果//αβ,m α∈,那么//m βD .如果m α⊥,//n α,那么m n ⊥6.一个几何体的三视图如右图所示,其中俯视图是一个正三角形及其内切圆,则该几何体的体积为A .161633π-B .163163π-C .8833π- D .8383π- 7.若变量x ,y 满足220,20,10,x y x y x y +-≥⎧⎪+-≤⎨⎪--≤⎩则211x y ++的最小值为A .13B .16C .23D .328.已知函数()()()sin 0,0,0f x A x A ωϕωϕπ=+>><<,其导函数的图象()f x '如右图所示,则2f π⎛⎫ ⎪⎝⎭的值为 A .23 B .2 C .22 D .49.执行右图所示的程序框图,输出的n 值为A .4B .6C .8D .1210.已知()2,0,0ax x x f x x x ⎧+>=⎨-≤⎩,若不等式()()1f x f x -≥对一切x R ∈恒成立,则实a 数的最大值为A .916- B .-1 C .12- D .1 二、填空题:本大题共有5个小题,每小题5分,共25分. 11.若12e dx a x =⎰,则6a x x ⎛⎫- ⎪⎝⎭展开式中的常数项为 12.已知x ,y 均为正实数,若()(),1,2,1a x yb =-=,且a b ⊥,则12x y+的最小值是 l3.过双曲线2218y x -=的右支上一点P 分别向圆C 1:()2234x y ++=和圆C 2:()2231x y -+=作切线,切点分别为A ,B ,则22PA PB -的最小值为14.从曲线22x y x y +=+所围成的封闭图形内任取一点,则该点在单位圆中的概率为15.已知()f x 是定义在R 上的函数,()f x '是()f x 的导函数。
2020届山东省新高考高三优质数学试卷分项解析 专题09 立体几何与空间向量(解析版)
专题9 立体几何与空间向量从近几年的高考试题来看,所考的主要内容是:(1)有关线面位置关系的组合判断,试题通常以选择题的形式出现,主要是考查空间线线、线面、面面位置关系的判定与性质;(2)有关线线、线面和面面的平行与垂直的证明,试题以解答题中的第一问为主,常以多面体为载体,突出考查学生的空间想象能力及推理论证能力;(3)线线角、线面角和二面角是高考的热点,选择题、填空题皆有,解答题中第二问必考,一般为中档题,在全卷的位置相对稳定,主要考查空间想象能力、逻辑思维能力和转化与化归的应用能力.预测2020年将保持稳定,一大二小.其中客观题考查面积体积问题、点线面位置关系(各种角的关系或计算)等;主观题以常见几何体为载体,考查平行或垂直关系的证明、线面角或二面角三角函数值的计算等.一、单选题1.(2020届山东省潍坊市高三上期中)m 、n 是平面α外的两条直线,在m ∥α的前提下,m ∥n 是n ∥α的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A 【解析】//m α,则存在l α⊂有//m l .而由//m n 可得//n l ,从而有//n α.反之则不一定成立,,m n 可能相交,平行或异面.所以//m n 是//n α的充分不必要条件,故选A2.(2020届山东省潍坊市高三上期末)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“盖”的术:置如其周,令相承也.又以高乘之,三十六成一.该术相当于给出了有圆锥的底面周长L 与高h ,计算其体积V 的近似公式21.36v L h ≈它实际上是将圆锥体积公式中的圆周率π近似取为3.那么近似公式2275v L h ≈相当于将圆锥体积公式中的π近似取为( )A .227 B .258C .15750D .355113【答案】B 【解析】设圆锥底面圆的半径为r ,高为h ,依题意,r L π2=,h r h r 22)2(75231ππ=, 所以275831ππ=,即π的近似值为258,故选B.3.(2020届山东省滨州市三校高三上学期联考)设α,β为两个平面,则αβ∥的充要条件是( ) A .α内有无数条直线与β平行B .α,β平行与同一个平面C .α内有两条相交直线与β内两条相交直线平行D .α,β垂直与同一个平面【答案】C 【解析】对于A ,α内有无数条直线与β平行,可得α与β相交或α或β平行; 对于B ,α,β平行于同一条直线,可得α与β相交或α或β平行; 对于C ,α内有两条相交直线与β内两条相交直线平行,可得α∥β; 对于D ,α,β垂直与同一个平面,可得α与β相交或α或β平行. 故选:C .4.(2020·河南高三期末(文))张衡是中国东汉时期伟大的天文学家、数学家,他曾经得出圆周率的平方除以十六等于八分之五.已知三棱锥A BCD -的每个顶点都在球O 的球面上,AB ⊥底面BCD ,BC CD ⊥,且AB CD ==2BC =,利用张衡的结论可得球O 的表面积为( )A .30B .C .33D .【答案】B 【解析】因为BC CD ⊥,所以BD =AB ⊥底面BCD ,所以球O 的球心为侧棱AD 的中点,从而球O .利用张衡的结论可得25168π=,则π=所以球O 的表面积为24102ππ⎛== ⎝⎭故选:B5.(2020届山东省潍坊市高三上学期统考)已知边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕进行折叠,使折后的2BDC π∠=,则过A ,B ,C ,D 四点的球的表面积为( )A .3πB .4πC .5πD .6π【答案】C 【解析】边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕进行折叠,使折后的2BDC π∠=,构成以D 为顶点的三棱锥,且三条侧棱互相垂直,可构造以其为长宽高的长方体,其对角线即为球的直径,三条棱长分别为1,12R ==245S ππ==,故选C.6.(2020届山东省日照市高三上期末联考)已知四棱锥P ABCD -的体积是底面ABCD 是正方形,PAB ∆是等边三角形,平面PAB ⊥平面ABCD ,则四棱锥P ABCD -外接球体积为( )A .BCD .【答案】A 【解析】设AB 的中点为Q ,因为PAB ∆是等边三角形,所以PQ AB ⊥,而平面PAB ⊥平面ABCD , 平面PAB ⋂平面ABCD AB =,所以PQ ⊥平面ABCD ,四棱锥P ABCD -的体积是13AB AB PQ =⨯⨯⨯13AB AB AB =⨯⨯,所以边长6AB =,PQ =OH x =,OM x =,()(222222R OA OM AM x==+=+,2222223R OP OH PH x ==+=+,x =2212321R =+=3428213V R ππ==球.故选:A.7.(2020届山东省泰安市高三上期末)已知正三棱锥S ABC -的侧棱长为43,底面边长为6,则该正三棱锥外接球的表面积是( ) A .16π B .20πC .32πD .64π【答案】D 【解析】如图所示,因为正三棱锥S ABC -的侧棱长为43,底面边长为6,则236233AE =⋅⋅=,所以三棱锥的高2222(43)(23)6SE SA AE =-=-=, 又由球心O 到四个顶点的距离相等,在直角三角形AOE 中,,6AO R OE SE SO R ==-=-,又由222OA AE OE =+,即222(23)(6)R R =+-,解得4R =, 所以球的表面积为2464S R ππ==, 故选D.二、多选题8.(2020届山东省潍坊市高三上期末)等腰直角三角形直角边长为1 ,现将该三角形绕其某一边旋转一周 ,则所形成的几何体的表面积可以为( ) A .2π B .()12π+C .22πD .()22π+【答案】AB 【解析】如果是绕直角边旋转,形成圆锥,圆锥底面半径为1,高为1,母线就是直角三角形的斜边2, 所以所形成的几何体的表面积是()2212121S rl r πππππ=+=⨯⨯+⨯=+.如果绕斜边旋转,形成的是上下两个圆锥,圆锥的半径是直角三角形斜边的高22,两个圆锥的母线都是直角三角形的直角边,母线长是1,所以写成的几何体的表面积222122S rl πππ=⨯=⨯⨯⨯=. 综上可知形成几何体的表面积是()21π+或2π.故选:AB9.(2020届山东省泰安市高三上期末)已知,αβ是两个不重合的平面,,m n 是两条不重合的直线,则下列命题正确的是( ) A .若//m n m α⊥,,则n α⊥ B .若//,m n ααβ⋂=,则//m n C .若m α⊥,m β⊥,则//αβ D .若,//,m m n n αβ⊥⊥,则//αβ 【答案】ACD 【解析】若m α⊥,则,a b α∃⊂且a b P =I 使得m a ⊥,m b ⊥,又//m n ,则n a ⊥,n b ⊥,由线面垂直的判定定理得n α⊥,故A 对;若//m α,n αβ=I ,如图,设m AB =,平面1111D C B A 为平面α,//m α,设平面11ADD A 为平面β,11A D n αβ⋂==,则m n ⊥,故B 错;垂直于同一条直线的两个平面平行,故C 对;若,//m m n α⊥,则n α⊥,又n β⊥,则//αβ,故D 对; 故选:ACD .10.(2020届山东省滨州市高三上期末)已知菱形ABCD 中,60BAD ∠=︒,AC 与BD 相交于点O ,将ABD △沿BD 折起,使顶点A 至点M ,在折起的过程中,下列结论正确的是( )A .BD CM ⊥B .存在一个位置,使CDM V 为等边三角形C .DM 与BC 不可能垂直D .直线DM 与平面BCD 所成的角的最大值为60︒【答案】ABD 【解析】A 选项,因为菱形ABCD 中,AC 与BD 相交于点O ,所以AO BD ⊥,CO BD ⊥;将ABD △沿BD 折起,使顶点A 至点M ,折起过程中,AO 始终与BD 垂直,因此MO BD ⊥, 又MO CO I ,由线面垂直的判定定理,可得:BD ⊥平面CMO ,因此BD CM ⊥,故A 正确;B 选项,因为折起的过程中,AD 边长度不变,因此MD CD =;若CDM V 为等边三角形,则CM CD =;设菱形ABCD 的边长为2,因为60BAD ∠=︒,则sin 60AO AB =⋅=o AO MO =2CM CD ==,所以3341cos 233MOC +-∠==⨯,即二面角M BD C --的余弦值为13时,CDM V 为等边三角形;故B 正确;C 选项,DM OM OD =-u u u u r u u u u r u u u r ,BC OC OB =-u u ur u u u r u u u r ,由A 选项知,MO BD ⊥,CO BD ⊥,所以0OM OB OD OC ⋅=⋅=u u u u r u u u r u u u r u u u r,因此()()DM BC OM OD OC OB OM OC OD OB ⋅=-⋅-=⋅-⋅u u u u r u u u r u u u u r u u u r u u u r u u u r u u u u r u u u r u u u r u u u r ,同B 选项,设菱形ABCD 的边长为2,易得OC OM =1OB OD ==,所以3cos 1DM BC MOC ⋅=∠+u u u u r u u u r ,显然当1cos 3MOC ∠=-时,0DM BC ⋅=u u u u r u u u r ,即DM BC ⊥;故C 错误;D 选项,同BC 选项,设菱形ABCD 的边长为2,则OM =1OD =,2MD =,由几何体直观图可知,当OM ⊥平面BCD ,直线DM 与平面BCD 所成的角最大,为MDO ∠,易知60MDO ∠=︒. 故选:ABD.11.(2020届山东省济宁市高三上期末)己知mn 、为两条不重合的直线,αβ、为两个不重合的平面,则下列说法正确的是( )A .若//,//m n αβ且//,αβ则//m nB .若//,,,m n m n αβ⊥⊥则//αβC .若//,,//,m n n m ααββ⊂⊄,则//m βD .若//,,m n n ααβ⊥⊥,则//m β 【答案】BC 【解析】A. 若//,//m n αβ且//,αβ则可以//m n ,,m n 异面,或,m n 相交,故A 错误;B. 若//,,m n m α⊥则n α⊥,又,n β⊥故//αβ,B 正确;C. 若//,,m n n α⊂则m αP 或m α⊆,又//,m αββ⊄,故//m β,C 正确;D. 若//,,m n n α⊥则m α⊥,αβ⊥,则//m β或m β⊆,D 错误; 故选:BC12.(2020届山东省枣庄、滕州市高三上期末)在正方体1111ABCD A B C D -中,N 为底面ABCD 的中心,P 为线段11A D 上的动点(不包括两个端点),M 为线段AP 的中点,则( )A .CM 与PN 是异面直线B .CM PN >C .平面PAN ⊥平面11BDD B D .过P ,A ,C 三点的正方体的截面一定是等腰梯形【答案】BCD 【解析】,,C N A 共线,即,CN PM 交于点A ,共面,因此,CM PN 共面,A 错误;记PAC θ∠=,则2222212cos cos 4PN AP AN AP AN AP AC AP AC θθ=+-⋅=+-⋅, 2222212cos cos 4CM AC AM AC AM AC AP AP AC θθ=+-⋅=+-⋅,又AP AC <, 22223()04CM PN AC AP -=->,22CM PN >,即CM PN >.B 正确;由于正方体中,AN BD ⊥,1BB ⊥平面ABCD ,则1BB AN ⊥,1BB BD B ⋂=,可得AN ⊥平面11BB D D ,AN ⊂平面PAN ,从而可得平面PAN ⊥平面11BDD B ,C 正确;取11C D 中点K ,连接11,,KP KC AC ,易知11//PK A C ,又正方体中,11//A C AC ,∴//PK AC ,,PK AC 共面,PKCA 就是过P ,A ,C 三点的正方体的截面,它是等腰梯形.D 正确. 故选:BCD.13.(2020·蒙阴县实验中学高三期末)已知四棱锥P ABCD -,底面ABCD 为矩形,侧面PCD ⊥平面ABCD ,23BC =26CD PC PD ===.若点M 为PC 的中点,则下列说法正确的为( )A .BM ⊥平面PCDB .//PA 面MBDC .四棱锥M ABCD -外接球的表面积为36π D .四棱锥M ABCD -的体积为6 【答案】BC【解析】作图在四棱锥P ABCD -中:由题:侧面PCD ⊥平面ABCD ,交线为CD ,底面ABCD 为矩形,BC CD ⊥,则 BC ⊥平面PCD ,过点B 只能作一条直线与已知平面垂直,所以选项A 错误;连接AC 交BD 于O ,连接MO ,PAC ∆中,OM ∥PA ,MO ⊆面MBD ,PA ⊄面MBD ,所以//PA 面MBD ,所以选项B 正确;四棱锥M ABCD -的体积是四棱锥P ABCD -的体积的一半,取CD 中点N ,连接PN ,PN CD ⊥,则PN ^平面ABCD ,32PN =M ABCD -的体积112326321223M ABCD V -=⨯⨯=所以选项D 错误.矩形ABCD 中,易得6,3,3AC OC ON ===PCD V 中求得:16,2NM PC ==在Rt MNO V 中223MO ON MN =+= 即: OM OA OB OC OD ====,所以O 为四棱锥M ABCD -外接球的球心,半径为3, 所以其体积为36π,所以选项C 正确 故选:BC14.(2020届山东省潍坊市高三上期中)正方体1111ABCD A B C D -的棱长为2,已知平面1AC α⊥,则关于α截此正方体所得截面的判断正确的是( ) A .截面形状可能为正三角形 B .截面形状可能为正方形 C .截面形状可能为正六访形 D .截面面积最大值为33【答案】ACD 【解析】如图,显然A,C 成立,下面说明D 成立,如图设截面为多边形GMEFNH ,设1AG x =,则01x ≤≤, 则2,2(2),22,GH ME NF x MG HN EF x MN ======-=所以多边形GMEFNH 的面积为两个等腰梯形的面积和, 所以1211()()22S GH MN h MN EF h =⋅+⋅+⋅+⋅ 因为22221222133[2(2)]()(22)(2)(2)2222x h x x x x -=--=+⋅-=-, 22222(2)223(2)[]22x x h x --=-=,所以221313(222)(2)[222(2)]2222S x x x x =+⋅-++-⋅ 232323x x =-++当1x =时,max 33S =,故D 成立. 故选:ACD .15.(2020届山东省烟台市高三上期末)如图,在正方体1111ABCD A B C D -中,点P 在线段1B C 上运动,则 ( )A .直线1BD ⊥平面11AC DB .三棱锥11P ACD -的体积为定值C .异面直线AP 与1AD 所成角的取值范围是[]45,90︒︒ D .直线1C P 与平面11AC D 所成角的正弦值的最大值为63【答案】ABD 【解析】对于选项A,连接11B D ,由正方体可得1111AC B D ⊥,且1BB ⊥平面1111D C B A ,则111BB AC ⊥,所以11A C ⊥平面11BD B ,故111AC BD ⊥;同理,连接1AD ,易证得11A D BD ⊥,则1BD ⊥平面11ACD ,故A 正确; 对于选项B,1111P A C D C A PD V V --=,因为点P 在线段1B C 上运动,所以1112A DP S A D AB =⋅,面积为定值,且1C 到平面11A PD 的距离即为1C 到平面11A B CD 的距离,也为定值,故体积为定值,故B 正确;对于选项C,当点P 与线段1B C 的端点重合时,AP 与1A D 所成角取得最小值为60︒,故C 错误;对于选项D,因为直线1BD ⊥平面11AC D ,所以若直线1C P 与平面11AC D 所成角的正弦值最大,则直线1C P 与直线1BD 所成角的余弦值最大,则P 运动到1B C 中点处,即所成角为11C BD ∠,设棱长为1,在11Rt D C B V 中,111126cos 33C B C BD BD ∠===,故D 正确 故选:ABD 三、填空题16.(2020届山东省潍坊市高三上学期统考)如图,已知六棱锥P -ABCDEF 的底面是正六边形,PA ⊥平面ABC ,PA =2AB ,则下列结论中:①PB ⊥AE ;②平面ABC ⊥平面PBC ;③直线BC ∥平面PAE ;④∠PDA =45°. 其中正确的有________(把所有正确的序号都填上) 【答案】①④ 【解析】对于①,因为PA ⊥平面ABC ,所以PA ⊥AE ,又,EA AB PA AB A ⊥⋂=,所以EA ⊥平面PAB ,从而可得EA PB ⊥,故①正确.对于②,由于PA ⊥平面ABC ,所以平面ABC 与平面PBC 不可能垂直,故②不正确.对于③,由于在正六边形中BC AD ∥,所以BC 与EA 必有公共点,从而BC 与平面PAE 有公共点,所以直线BC 与平面PAE 不平行,故③不正确.对于④,由条件得PAD ∆为直角三角形,且PA ⊥AD ,又2PA AB AD ==,所以∠PDA=45°.故④正确. 综上①④正确. 答案:①④17.(2020届山东省潍坊市高三上期中)如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的表面积为__________;若该六面体内有一小球,则小球的最大体积为___________.【答案】332 86729【解析】(1)因为13336(12S =⨯⨯=33. (2)由图形的对称性得,小球的体积要达到最大,即球与六个面都相切时, 32倍,所以六面体体积是26. 由于图像的对称性,内部的小球要是体积最大,就是球要和六个面相切,连接球心和五个顶点,把六面体分成了六个三棱锥,设球的半径为R , 所以21366()6349R R =⨯⨯⨯⇒=,所以球的体积33446()3863V R πππ===. 故答案为:332;86729π. 18.(2020届山东省滨州市三校高三上学期联考)已知三棱锥S ABC -,SA ⊥平面ABC ,6ABC π∠=,3SA =,1BC =,直线SB 和平面ABC 所成的角大小为3π.若三棱锥S ABC -的四个顶点都在同一球面上,则该球的表面积为________. 【答案】13π 【解析】 如图:SA ⊥Q 平面ABC ,则SBA ∠为直线SB 和平面ABC 所成的角,即3SBA π∠=在Rt SAB ∆中:33tan3SA AB π=== 如图,设O 为三棱锥S ABC -外接球的球心,G 为ABC ∆外接圆圆心, 连结,,,,OA OB GA GB OG ,则必有OG ⊥面ABC 在ABC ∆,22232cos 312316AC AB BC AB BC π=+-⋅⋅=+-=, 则1AC = 其外接圆半径122,1sin sin 6AC r r ABC π====∠, 又1322OG SA ==,所以三棱锥S ABC -外接球半径为22913142R OG r =+=+=该球的表面积为21344134S R πππ==⨯=, 故答案为:13π.19.(2020届山东省枣庄、滕州市高三上期末)如图,在三棱锥P-ABC 中,,PA AB ⊥PC BC ⊥,,AB BC ⊥22,AB BC ==5PC =,则P A 与平面ABC 所成角的大小为________;三棱锥P-ABC 外接球的表面积是________.【答案】45︒ 6π 【解析】如图,作平行四边形ABCD ,连接PD ,由AB BC ⊥,则平行四边形ABCD 是矩形.由BC CD ⊥,BC PC ⊥,PC CD C =I ,∴BC ⊥平面PCD ,而PD ⊂平面PCD ,∴BC PD ⊥,同理可得AB PD ⊥,又AB BC B ⋂=,∴PD ⊥平面ABCD .,PD CD PD AD ⊥⊥,PAD ∠是P A 与平面ABC 所成角. 由2,5CD AB PC ===1PD =,又1AD BC ==,∴45PAD ∠=︒.∴P A 与平面ABC 所成角是45︒.由,PA AB ⊥PC BC ⊥知PB 的中点到,,,A B C P 的距离相等,PB 是三棱锥P-ABC 外接球的直径. 由BC ⊥平面PCD 得BC PC ⊥,2222(5)16PB PC BC =+=+=24()62PB S ππ==. 故答案为:45︒;6π.20.(2020届山东省烟台市高三上期末)已知三棱锥P ABC -的四个顶点都在球O 的表面上,PA ⊥平面ABC ,6PA =,23AB =2AC =,4BC =,则:(1)球O 的表面积为__________;(2)若D 是BC 的中点,过点D 作球O 的截面,则截面面积的最小值是__________. 【答案】52π 4π 【解析】(1)由题,根据勾股定理可得AC AB ⊥,则可将三棱锥P ABC -可放入以,,AP AC AB 为长方体的长,宽,高的长方体中,则体对角线为外接球直径,即()22222623213r +=+=,则13r =,所以球的表面积为22441352r πππ=⨯=;(2)由题,因为Rt ABC V ,所以D 为底面ABC 的外接圆圆心,当DO ⊥截面时,截面面积最小,即截面为平面ABC ,则外接圆半径为2,故截面面积为224ππ⨯=故答案为:(1)52π;(2)4π21.(2020届山东省滨州市高三上期末)在四面体S ABC -中,2SA SB ==,且SA SB ⊥,5BC =,3AC =________,该四面体外接球的表面积为________.【答案】3068π 【解析】因为2SA SB ==,且SA SB ⊥,5BC =,3AC =222AB SA ==,因此222BC AC AB +=,则AC BC ⊥;取AB 中点为O ,连接OS ,OC ,则2OA OB OC OS ====,所以该四面体的外接球的球心为O ,半径为2OC=所以该四面体外接球的表面积为24(2)8 Sππ=⋅=;又因为SA SB=,所以SO AB⊥;因为底面三角形ABC的面积为定值11522AC BC⋅=,SO的长也为确定的值2,因此,当SO⊥平面ABC时,四面体的体积最大,为13036ABCV S SO=⋅=V.故答案为:(1).306(2). 8π22.(2020届山东省潍坊市高三上期末)正方体1111ABCD A B C D-的棱长为1,点K在棱11A B上运动,过,,A C K三点作正方体的截面,若K为棱11A B的中点,则截面面积为_________,若截面把正方体分成体积之比为2:1的两部分,则11A KKB=_______【答案】9851-【解析】(1)取11B C的中点M,连接KM,MC,11//KM AC Q ,而11A C //AC ,//KM AC ∴,,,A C M K ∴四点共面,且AK MC = ∴四边形ACMK 是等腰梯形,如图,2KM =2AC =2215122AK ⎛⎫=+= ⎪⎝⎭, 222224AH ==, 22225232244KH AK AH ⎛⎫⎛⎫∴=-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 12329228ACKM S ∴=⨯=⎝; (2)设1B K x =,取11B C 上的点M ,11B K B M x ==,连接,KM MC , 由(1)知,,,A C M K 四点共面, 由图象可知11111133B MK BCA A B CD ABCD V V --==1221111111322223B MK BCAV x x -⎛∴=⨯++⨯⨯= ⎝, 即210x x +-= ,解得:15x -+=即115B K-+ =,115351A K-+-=-=,此时1135512215A KKB--==-+.故答案为:98;51-23.(2020届山东省临沂市高三上期末)在正方体1111ABCD A B C D-中,E为棱CD上一点,且2CE DE=,F为棱1AA的中点,且平面BEF与1DD交于点G,与1AC交于点H,则1DGDD=______,1AHHC=______. 【答案】1638【解析】1111ABCD A B C D-Q是正方体∴面11//A B BA面11C D DCBF⊂Q面11A B BA//BF∴平面11CDD C,Q面BFGE I面11C D DC GE=则//BF GE,则AF DGAB DE=,即12DGDE=,又2CE DE=,则116DGDD=.连接AC交BE于M,过M作1//MN CC,MN与1AC交于N,连接FM,则H为FM与1AC的交点.因为//AB CE,所以32AM ABMC CE==,则132AN ACMMCN==.所以135MNCC=,所以65MN HNFA AH==,故138AHHC=.故答案为:16;3824.(2020届山东省济宁市高三上期末)下图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A BD C--,则三棱锥A BCD-的外接球的体积为__________3cm.【答案】5003π【解析】由题设可将该三棱锥拓展成如图所示的正方体,则该正方体的外接球就是三棱锥的外接球,由于正方体的对角线长为2103l R==即球的半径3R=该球的体积3450033V Rππ==,应填答案3π.25.(2020届山东实验中学高三上期中)现有橡皮泥制作的底面半径为5,高为93高为8的圆柱各一个.若将它们重新制作成总体积与各自的高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为_________;若新圆锥的内接正三棱柱表面积取到最大值,则此正三棱柱的底面边长为_________.【答案】335【解析】由题意可知,底面半径为5,高为9的圆锥和底面半径为3,高为8的圆柱的总体积为22159(3)8993πππ⨯⨯⨯+⨯⨯=,设新的圆锥和圆柱的底面半径为r ,则:22198993r r πππ⨯⨯⨯+⨯⨯=,解得:3r =,设新圆锥的内接正三棱柱的底面边长为a ,高为h ,底面正三角形的外接圆的半径为r ',∴993h r '-=,93h r '∴=-, 又3233r a a '∴=⨯⨯=, 93h a ∴=-,∴正三棱柱的表面积2135332()272S a h a a a a =⨯⨯+⨯⨯⨯=-+,∴当93532()a =-=⨯-故答案为:3,935. 26.(2020届山东省德州市高三上期末)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知PA ⊥平面ABCE ,四边形ABCD 为正方形,5AD =,3ED =,若鳖臑P ADE -的外接球的体积为92π,则阳马P ABCD -的外接球的表面积等于______.【答案】20π 【解析】Q 四边形ABCD 是正方形,AD CD ∴⊥,即AD CE ⊥,且5AD =3ED =,所以,ADE ∆的外接圆半径为221222AE AD ED r +===设鳖臑P ADE -的外接球的半径1R ,则314923R ππ=,解得132R =. PA ⊥Q 平面ADE ,22112PA R r ⎛⎫∴=+ ⎪⎝⎭,可得22111022PA R r =-=,10PA ∴=. 正方形ABCD 的外接圆直径为22210r AC AD ===,210r ∴=, PA ⊥Q 平面ABCD ,所以,阳马P ABCD -的外接球半径222252PA R r ⎛⎫=+= ⎪⎝⎭,因此,阳马P ABCD -的外接球的表面积为22420R ππ=.故答案为:20π.四、解答题27.(2020届山东省烟台市高三上期末)如图,在四棱锥S ABCD -中,ABCD 为直角梯形,//AD BC ,BC CD ⊥,平面SCD ⊥平面ABCD ,SCD ∆是以CD 为斜边的等腰直角三角形,224BC AD CD ===,E 为BS 上一点,且2BE ES =.(1)证明:直线//SD 平面ACE ;(2)求二面角S AC E --的余弦值.【答案】(1)证明见解析 (2)13【解析】(1)连接BD 交AC 于点F ,连接EF ,因为//AD BC ,所以AFD ∆与BCF ∆相似, 所以2BF BC FD AD==, 又=2BE BF ES FD =,所以//EF SD , 因为EF ⊂平面ACE ,SD ⊄平面ACE ,所以直线//SD 平面ACE(2)由题,因为平面SCD ⊥平面ABCD ,平面SCD I 平面ABCD CD =,BC ⊂平面ABCD ,BC CD ⊥,所以BC ⊥平面SCD ,以C 为坐标原点,,CD CB u u u r u u u r 所在的方向分别为y 轴、z 轴的正方向,与,CD CB u u u r u u u r 均垂直的方向作为x 轴的正方向,建立如图所示的空间直角坐标系C xyz -,因为224BC AD CD ===,2BE ES =,则(0,0,0)C ,(1,1,0)S ,(0,2,2)A ,224(,,)333E ,所以(0,2,2)CA =u u u r ,(1,1,0)CS =u u u r ,224(,,)333CE =,设平面SAC 的一个法向量为(,,)m x y z =u r ,则00m CA m CS ⎧⋅=⎨⋅=⎩u u u v vu u u vv ,即00y z x y +=⎧⎨+=⎩,令1z =,得1x =,1y =-,于是(1,1,1)m =-u r ,设平面EAC 的一个法向量为(,,)n x y z =r ,则0n CA n CE ⎧⋅=⎨⋅=⎩u u u v v u u u v v ,即020y z x y z +=⎧⎨++=⎩,令1z =,得1x =-,1y =-,于是(1,1,1)m =--u r ,设二面角S AC E --的平面角的大小为θ,则1cos 3m n m n θ⋅==ur ru r r ,所以二面角S AC E --的余弦值为1328.(2020届山东省泰安市高三上期末)如图,在三棱锥P —ABC 中,△P AC 为等腰直角三角形,90,APC ABC ∠=∆o 为正三角形,D 为A 的中点,AC =2.(1)证明:PB ⊥AC ;(2)若三棱锥P ABC -的体积为33,求二面角A —PC —B 的余弦值【答案】(1)证明见解析 (27【解析】(1)证:PAC ∆Q 为等腰直角三角形,D 为中点,PD AC ∴⊥,又ABC ∆为正三角形,D 为中点,BD AC ∴⊥,又PD BD D ⋂=,,PD BD ⊂平面PBD ,AC ∴⊥平面PBD ,又PB ⊂平面PBD ,PB AC ∴⊥(2)解:设三棱锥P ABC -的高为h ,sin 603BD BC ==o1132P ABC V AC BD h -∴=⨯⨯⨯⨯3=31h ∴=,又11,2PD AC ==PD ∴⊥平面ABC ,如图,以D 为坐标原点,建立空间直角坐标系D xyz -,则()1,0,0A ,()0,3,0B ,()1,0,0C-,()0,0,1P , ()0,3,0DB ∴=u u u r ,()1,0,1CP =u u u r ,()1,3,0CB =u u u r , 设(),,n x y z =r 为平面PBC 的一个法向量,则00CP n CB n ⎧⋅=⎨⋅=⎩u u u v v u u u v v ,即030x z x y +=⎧⎪⎨+=⎪⎩, 令1x =,得31y z ⎧=-⎪⎨⎪=-⎩,∴31,,13n ⎛⎫=-- ⎪ ⎪⎝⎭r , 又DB uuu r 是平面PAC 的一个法向量,∴7cos ,DB n DB DB n n⋅<>==-⋅u u u r u u u r r r u u u r r , 由图可知二面角A PC B --的平面角为锐角,∴二面角A PC B --的余弦值为7. 29.(2020届山东省潍坊市高三上期中)如图,在棱长均为2的三棱柱111ABC A B C -中,平面1ACB ⊥平面11A ABB ,11AB A B =,O 为1AB 与1A B 的交点.(1)求证:1AB CO ⊥;(2)求平面11ACC A 与平面ABC 所成锐二面角的余弦值.【答案】(1)详见解析;(2)1 3 .【解析】(1)因为四边形11A ABB为菱形,所以11A B AB⊥,又平面1ACB⊥平面11A ABB,平面1A CB I平面111A ABB A B=,所以1AB⊥平面1A CB,因为CO⊂平面1A CB,所以1AB CO⊥.(2)因为11A B AB=,所以菱形11A ABB为正方形,在Rt COA∆中,222CO AC OA=-=,在COB∆中,2CO OB==,2CB=,222CO OB CB+=,所以,CO OB⊥,又1CO AB⊥,11A B AB O⋂=,所以,CO⊥平面11A ABB;以O为坐标原点,以OA,OB,OC所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系O xyz-.()2,0,0A,()10,2,0A,(2C,()2,0B,设平面11ACC A的一个法向量为()1111,,n x y z=u r平面ABC的一个法向量为()2222,,n x y z=u u r,则1111220,220,xx z⎧-=⎪⎨-+=⎪⎩令11x=,得()11,1,1=-u u rn,2222220,220,x y x z ⎧-+=⎪⎨-+=⎪⎩ 令21x =,得()21,1,1=u u r n ,设平面11ACC A 与平面ABC 所成锐二面角为α, 则21121cos 333α⋅===⨯u u r u u r u u r u u r n n n n , 所以平面11ACC A 与平面ABC 所成锐二面角的余弦值为13. 30.(2020届山东省九校高三上学期联考)已知四棱柱1111ABCD A B C D -的底面为菱形,12AB AA ==,3BAD π∠=,AC BD O =I ,AO ⊥平面1A BD ,11A B A D =.(1)证明:1//B C 平面1A BD ;(2)求钝二面角1B AA D --的余弦值.【答案】(1)证明见解析;(2) 17-【解析】(1)证明:连接1AB 交1A B 于点Q ,易知Q 为1AB 中点,∵O 为AC 中点,∴在1AB C ∆中,11//2OQ B C , ∵OQ ⊂平面1A BD ,1B C ⊄平面1A BD ,∴1//B C 平面1A BD .(2)∵AO ⊥平面1A BD ,∴1AO A O ⊥,∵11A B A D =且O 为BD 的中点,∴1AO BD ⊥,∵AO BD ⊂、平面ABCD 且AO BD O =I ,∴1A O ⊥平面ABCD ,如图,建立空间直角坐标系O xyz -. 易得:()3,0,0A ,()0,1,0B ,()0,1,0D -,()10,0,1A ,∴()13,0,1AA =-u u ur ,()3,1,0AB =-uu u r,设平面1A AB 的一个法向量为(),,n x y z =r,则1n AA n AB ⎧⊥⎨⊥⎩u u u vv u u u v v ,∴3030x z xy ⎧-+=⎪⎨-+=⎪⎩,令1x =,得3y z ==,∴()1,3,3n =r .同理可得平面1A AD 的一个法向量为()1,3,3m =-u r ,∴1cos ,7m n m n m n ⋅<>==u r ru r r u r r ,∴钝二面角1B AA D --的余弦值为17-.31.(2020届山东省潍坊市高三上期末)在底面为正方形的四棱锥P ABCD -中,平面PAD ⊥平面,,,ABCD PA PD E F =分别为棱PC 和AB 的中点.(1)求证://EF 平面PAD ;(2)若直线PC 与AB 所成角的正切值为5,求平面PAD 与平面PBC 所成锐二面角的大小.【答案】(1)见解析(2)4π【解析】(1)证明:取CD 的中点M ,连接,EM FM ,因为,E F 分别为PC 和AB 的中点,四边形ABCD 为正方形,所以//, //EM PD FM AD ,因为,EM FM ⊂平面,,EFM PD AD ⊂平面PAD ,所以平面//EFM 平面PAD ,因为EF ⊂平面EFM ,所以//EF 平面PAD .(2)因为平面PAD ⊥平面ABCD ,平面PAD I 平面,ABCD AD CD AD =⊥ CD ⊂平面ABCD 所以CD ⊥平面PAD ,所以CD PD ⊥,因为//AB CD ,所以PCD ∠就是直线PC 与AB 所成的角,所以52PD tan PCD DC ∠==,设5,2PD CD ==,分别取AD 和BC 的中点,O N ,连,PO ON ,因为PA PD =,所以PO AD ⊥,因为平面PAD ⊥平面ABCD ,平面PAD I 平面,ABCD AD PO =⊂平面PAD ,所以PO ⊥平面ABCD如图,建立空间直角坐标系O xyz -,则()()()0,0,2,1,2,0,1,2,0P C B -,所以()()2,0,0,1,2,2CB CP ==-u u u r u u u r ,设(),,m x y z =u r 是平面BPC 的一个法向量,则2200x y z x -+=⎧⎨=⎩取1y =,则1z =,所以()0,1,1m =u r()0,1,0n =r 是平面PAD 的一个法向量, 所以2,221m n cos m n m n⋅<>===⨯u r r u r r u r r ,,4m n π<>=u r r 所以所求二面角的大小为4π 32.(2020届山东省日照市高三上期末联考)如图,扇形AOB 的半径为2,圆心角120AOB ∠=o ,点C 为弧AB 上一点,PO ⊥平面AOB 且5PO =,点M PB ∈且2BM MP =,PA ∥平面MOC .(1)求证:平面MOC ⊥平面POB ;(2)求平面POA 和平面MOC 所成二面角的正弦值的大小.【答案】(1)见证明;(2)64【解析】(1)如图,连接AB 交OC 于点N ,连接MN ,Q PA ∥平面MOC ,∴PA ∥MN ,Q 2BM MP =,2BN NA ∴=,2OA OB ==Q ,120AOB ∠=o ,23AB∴=,43BN ∴=, 又30OBA ∠=o Q ,∴在BON △中,根据余弦定理得23ON =, 222ON OB BN ∴+=,90BON ∴∠=o ,ON OB ∴⊥,又Q PO ⊥平面AOB ,ON OP ∴⊥,ON ∴⊥平面POB ,又ON ⊂Q 平面MOC ,∴平面MOC ⊥平面POB(2)由(1)得,,OC OB OP OC OP OB ⊥⊥⊥,如图建立空间直角坐标系O xyz -,5OP =Q ,2OA OB OC ===,∴5)OP =u u u r ,3,1,0)OA =-u u u r ,(2,0,0)OC =u u u r ,(0,2,0)OB =u u u r ,Q 点M PB ∈且2BM MP =,225(0,3OM ∴=u u u u r , 设平面POA 的法向量为1111(,,)x y z =n ,则1100n OP n OA u u u v u u u v ⎧⋅=⎪⎨⋅=⎪⎩,即1115030z x y =-=, 令11x =,得13y 10z =,∴1(13,0)=n ,设平面MOC 的法向量为2222(,,)x y z =n ,则2200n OC n OM ⎧⋅=⎪⎨⋅=⎪⎩u u u v u u u u v ,即2222022503x y z =⎧⎪⎨=⎪⎩,即222050x y z =⎧⎪⎨+=⎪⎩,令21z =,得25y =-,20x =,∴2(0,5,1)=-n ,设平面POA 和平面MOC 所成二面角的大小为θ,则1510 |cos|426θ==,6sin4θ∴=,∴平面POA和平面MOC所成二面角的正弦值的大小为6433.(2020届山东省德州市高三上期末)如图(1),边长为2的正方形ABEF中,D,C分别为EF、AF 上的点,且ED CF=,现沿DC把CDF∆剪切、拼接成如图(2)的图形,再将BEC∆,CDF∆,ABD∆沿BC,CD,BD折起,使E、F、A三点重合于点A',如图(3).(1)求证:'⊥BA CD;(2)求二面角'--B CD A最小时的余弦值.【答案】(1)证明见解析;(2)13.【解析】(1)折叠前BE EC⊥,BA AD⊥,折叠后''⊥BA A C,''⊥BA A D,又'''⋂=A C A D A,所以'⊥BA平面ACD',因此'⊥BA CD;(2)由(1)及题意知A C A D''⊥,因此以A'为原点,A C'、A D'、A B'分别为x、y、z轴建立空间直角坐标系如图:令'=A C a,'=A D b,2a b+=,所以(),0,0C a,()0,,0D b,()0,0,2B设平面BCD法向量为(),,m x y z=u r则m BCm BD⎧⋅=⎨⋅=⎩u u u vvu u u vv所以2020ax zbx z-=⎧⎨-=⎩,令1z=,则22,,1ma b⎛⎫= ⎪⎝⎭u r又平面ACD '法向量为()0,0,1m =u r,设二面角'--B CD A 的大小为θ,所以22cos 1411m nm na bθ⋅==⨯++u r r u r r , 又22224412119b a b a b a a b a b a b a b ⎛⎫⎛⎫⎛⎫++=++++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎭≥⎝, 当且仅当1a b ==取等号,所以1cos 3θ≤. 所以二面角'--B CD A 最小时的余弦值为13.34.(2020届山东省滨州市三校高三上学期联考)如图,在直三棱柱111ABC A B C -中,1AB AC ==,且AB AC ⊥,点M 在棱1CC 上,点N 是BC 的中点,且满足1AM B N ⊥.(1)证明:AM ⊥平面11A B N ;(2)若M 为1CC 的中点,求二面角111A B N C --的正弦值.【答案】(1)详见解析;(215. 【解析】(1)∵三棱柱111ABC A B C -为直三棱柱,∴1AA AB ⊥∵AB AC ⊥,1AA ⊂平面11AAC C ,AC ⊂平面11AAC C ,且1AA AC A =I , ∴AB ⊥平面11AAC C ,(或者由面面垂直的性质证明) 又∵AM ⊂平面11AAC C ,∴AB AM ⊥ ∵11A B AB ∥,∴11A B AM ⊥,∵1AM B N ⊥,11A B ⊂平面11A B N ,1B N ⊂平面11A B N ,且1111A B B N B ⋂=, ∴AM ⊥平面11A B N(2)以A 为原点,分别以AB 、AC 、1AA 为x 轴、y 轴、z 轴建立空间直角坐标系A xyz -﹐设1AA a =,则(0,0,0)A ,(1,0,0)B ,(0,1,0)C ,1(1,0,)B a ,1(0,1,1)C ,11,,022N ⎛⎫ ⎪⎝⎭,0,1,2a M ⎛⎫ ⎪⎝⎭,∵1AM B N ⊥,∴211110,1,,,022222a aAM B N a ⎛⎫⎛⎫⋅=⋅--=-= ⎪ ⎪⎝⎭⎝⎭u u u u r u u u u r ,∴1a = ∴1(1,0,1)B ,10,1,2M ⎛⎫ ⎪⎝⎭, 设平面11A B N 法向量为{,,}m x y z =r11(1,0,0)A B =u u u u r ,111,,122B N ⎛⎫=-- ⎪⎝⎭u u u u r∴11101122m A B x m B N x y z ⎧⋅==⎪⎨⋅=-+-=⎪⎩u u u uv r u u u u v r ,∴可取(0,2,1)m =r 设平面1B NC 法向量为{,,}n x y z =r1(1,1,0)BC =-u u u r ,111,,122B N ⎛⎫=-- ⎪⎝⎭u u u u r ∴1101122n B C x y n B N x y z ⎧⋅=-+=⎪⎨⋅=-+-=⎪⎩u u u vr u u u u v r ,∴可取(1,1,0)n =r ∴10cos ,||||5m n m n m n ⋅〈〉==⋅r r r rr r所以二面角111A B N C --的正弦值为155. 35.(2020届山东省枣庄、滕州市高三上期末)如图,在四棱锥P-ABCD 中,23,AD =3,AB =3,AP =//AD BC ,AD ⊥平面P AB ,90APB ︒∠=,点E 满足2133PE PA PB =+u u u r u u u r u u u r .(1)证明:PE DC ⊥; (2)求二面角A-PD-E 的余弦值. 【答案】(1)证明见解析 (2)226【解析】(1)证明:在Rt PAB ∆中,由勾股定理,得22PB AB AP =-223(3)=-6=.因为21,33PE PA PB =+u u u r u u u r r AB PB PA =-u u u r u u u r u u u r,所以21()33PE AB PA PB PB PA ⎛⎫⋅=+⋅- ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r22211333PA PB PA PB =-++⋅u uu r u u u r u u u r u u u r22211(3)(6)0333=-⨯+⨯+⨯0=.所以PE AB ⊥u u u r u u u r,所以PE AB ⊥.因为AD ⊥平面P AB ,PE ⊂平面P AB , 所以PE AD ⊥.又因为,PE AB ⊥AB AD A ⋂=, 所以PE ⊥平面ABCD. 又因为DC ⊂平面ABCD , 所以PE DC ⊥.(2)由21,33PE PA PB =+u u u r u u u r u u u r 得2EB AE =u u u r u u u r.所以点E 是靠近点A 的线段AB 的三等分点.所以113AE AB ==. 分别以,AB uuu r AD u u u r所在方向为y 轴,z 轴的正方向,建立如图所示的空间直角坐标系A xyz -.则(0,0,0),A (0,0,23),D (0,1,0),E )2,1,0P .设平面PDE 的法向量为()111,,m x y z =u r, 由00m EP m ED ⎧⋅=⎨⋅=⎩u u u v v u u u v v ,得11120230x y z ⎧=⎪⎨-+=⎪⎩. 令11z =,则(0,23,1)m =-u r;设平面APD 的法向量为()222,,,n x y z =r (2,1,0),AP =u u u r (0,0,23)AD =u u u r, 由00n AP n AD ⎧⋅=⎨⋅=⎩u u u v v u u u v v ,得22220230x y z ⎧+=⎪⎨=⎪⎩,令21x =,则()1,2,0n =-r.设向量m u r 与n r的夹角为θ,则cos ||||m n m n θ⋅=⋅u r ru r r 222226(23)11(2)-=+⨯+-22613=-. 所以二面角A PD E --的余弦值为226. 36.(2020·山东省淄博实验中学高三上期末)如图,点C 在以AB 为直径的圆O 上,PA 垂直与圆O 所在平面,G 为 AOC ∆的垂心(1)求证:平面OPG ⊥平面 PAC ;(2)若22PA AB AC ===,求二面角A OP G --的余弦值.【答案】(1)见解析(2)25117. 【解析】(1)如图,延长OG 交AC 于点M .因为G 为AOC ∆的重心,所以M 为AC 的中点.因为O 为AB 的中点,所以//OM BC .因为AB 是圆O 的直径,所以BC AC ⊥,所以OM AC ⊥. 因为PA ⊥平面ABC ,OM ⊂平面ABC ,所以PA OM ⊥.又PA ⊂平面PAC ,AC ⊂平面,PAC PA AC ⋂=A ,所以OM ⊥ 平面PAC .即OG ⊥平面PAC ,又OG ⊂平面OPG ,所以平面OPG⊥平面PAC.(2)以点C 为原点,CB u u u r ,CA u u u r ,AP u u u r方向分别为x ,y ,z 轴正方向建立空间直角坐标系C xyz -,则()0,0,0C ,()0,1,0A ,)3,0,0B,31,02O ⎫⎪⎪⎝⎭,()0,1,2P ,10,,02M ⎛⎫⎪⎝⎭,则3OM ⎛⎫= ⎪ ⎪⎝⎭u u u u r ,31,22OP ⎛⎫= ⎪ ⎪⎝⎭u u u r .平面OPG 即为平面OPM ,设平面OPM 的一个法向量为(),,n x y z =r,则30,2{3120,2n OM x n OP x y z ⋅=-=⋅=++=u u u u r r u u u r r 令1z =,得()0,4,1n =-r .过点C 作CH AB ⊥于点H ,由PA ⊥平面ABC ,易得CH PA ⊥,又PA AB A ⋂=,所以CH ⊥平面PAB ,即CH u u u r为平面PAO 的一个法向量.在Rt ABC ∆中,由2AB AC =,得30ABC ∠=︒,则60HCB ∠=︒,1322CH CB ==. 所以3cos H x CH HCB =∠=3sin 4H y CH HCB =∠=.所以33,044CH ⎛⎫= ⎪ ⎪⎝⎭u u u r . 设二面角A OP G --的大小为θ,则cos CH n CH n θ⋅==⋅u u u r r u u u r r 2233041044511739411616⨯-⨯+⨯=+⨯+. 37.(2020届山东省潍坊市高三上学期统考)如图,四棱锥P ABCD -中,底面ABCD 为梯形,PD ⊥底面ABCD ,//AB CD ,AD CD ⊥,1AD AB ==,2BC =.(1)求证:平面PBD ⊥平面PBC ;(2)设H 为CD 上一点,满足2CH HD =u u u r u u u r,若直线PC 与平面PBD 6,求二面角H PB C --的余弦值.【答案】(1)证明见解析;(227【解析】(I )由,//,1AD CD AB CD AD AB ⊥==,可得2BD =,又2,,.4BC BC BD π=∠=∴⊥从而2CD =,PD ⊥Q 底面ABCD ,BC PD ∴⊥PD BD D ⋂=Q ,BC ∴⊥平面,PBD 所以平面PBD ⊥平面PBC .(II )由(I )可知BPC ∠为PC 与底面PBD 所成角. 所以6tan BPC ∠=,所以3,1PB PD == 又23CH HD =u u u v u u u v及2CD =,可得64,55CH DH ==, 以D 点为坐标原点,,,DA DC DP 分别,,x y z 轴建立空间直角坐标系,则()()()41,1,0,0,0,1,0,2,0,0,,05B P C H ⎛⎫⎪⎝⎭. 设平面HPB 的法向量(),,n x y z =r.则由00n PB n PB ⎧⋅=⎨⋅=⎩u u u v r u u u v r 得4050y z x y z ⎧-+=⎪⎨⎪+-=⎩取()1,5,4n =--r。
山东省2020年高考模拟考试数学试题 Word版含答案
山东省2020年普通高等院校统一招生模拟考试高三教学质量检测数学试题2020.02本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,将第I 卷选择题的正确答案选项填涂在答题卡相应位置上,考试结束,将答题卡交回.考试时间120分钟,满分150分. 注意事项:1.答卷前,考生务必将姓名、座号、准考证号填写在答题卡规定的位置上. 2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案标号.答案不能答在试题卷上.3.第Ⅱ卷答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第I 卷(选择题 共60分)一、选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知复数2,i z z 在复平面内对应的点分别为()()11221,1,0,1z Z Z z =,则 A .1i +B .1i -+C .1i --D .1i -2.设a R ∈,则“sin cos αα=”是“sin 21α=”的 A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件3.向量a b r r ,满足()()1,2a b a b a b ==+⊥-u u r u u r r r r r,则向量a b r r 与的夹角为 A .45oB .60oC .90oD .120o4.已知数列{}n a 中,372,1a a ==.若1n a ⎧⎫⎨⎬⎩⎭为等差数列,则5a = A .23B .32C .43D .345.已知点()2,4M 在抛物线()2:20C y px p =>上,点M 到抛物线C 的焦点的距离是A .4B .3C .2D .16.在ABC ∆中,2,20AB AC AD AE DE EB x AB y AC +=+==+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r,若,则 A .2y x =B .2y x =-C .2x y =D .2x y =-7.已知双曲线()2222:1,0,0x y C a b a b-=>>的左、右焦点分别为12,F F O ,为坐标原点,P是双曲线在第一象限上的点,()21212=2=2,0,PF PF m m PF PF m >⋅=u u u u r u u u u r u u u r u u u u r ,则双曲线C 的渐近线方程为 A .12y x =±B .22y x =±C .y x =±D .2y x =±8.已知奇函数()f x 是R 上增函数,()()g x xf x =则A. 233231log 224g g g --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B .233231log 224g g g --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C. 23323122log 4g g g --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D. 23323122log 4g g g --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭二、多项选择题:本题共4小题,每小题5分,共20分。
山东省烟台市2020届高三4月模拟考试(一模)数学试题+Word版含答案
2021年高考诊断性测试数学考前须知:1 。
本试题总分值150分,考试时间为120分钟。
2 。
答卷前,务必将姓名和准考证号填涂在答题卡上。
3 。
使用答题纸时,必须使用 0。
5毫米的黑色签字笔书写,要字迹工整,笔迹清晰。
超出答 题区书写的答案无效;在草稿纸、试题卷上答题无效。
一、单项选择题:此题共 8小题,每题5分,共40分。
在每题给出的四个选项中, 只有一项符合题目要求。
顺序构成新的数列 a 1 ,那么数列a n 的前50项和为绝密★启用前1。
集合M x y ln(x 1) , N,那么 M I NA. ( 1,0)B. ( 1,+ )C 。
(0,+ )D 。
R2。
复数z 满足〔1 i)z 2i 〔i 为虚数单位〕,那么A. 1 iB. 1 iC. 1 2iD. 1 2i2| 1〞是 2x 2x3 0〞的A 。
充分不必要条件B 。
必要不充分条件C 。
充要条件D 。
既不充分也不必要条件4。
数列 F n : F IF 2 1, F n在1202年所著的?算盘全书? F n1 F n2。
假设将数n 2 ,最初记载于意大利数学家斐波那契 F n 的每一项除以2所得的余数按原来项的A 。
33B 。
34C 。
49D 。
50uur uuu5 。
设ABCD 为平行四边形,|AB| 4, |AD| 6, BAD — 。
假设点M ,N 满足3uuir uum uuu uuu uuuruuirBM MC , AN 2ND ,那么 NMgAMA 。
23B 。
17C 。
15D 。
96 。
右图是一块高尔顿板示意图:在一块木板上钉着假设干排互相平行但相互错开的圆柱形小22。
7 。
设P 为直线3x 4y 4 0上的动点,PA ,PB 为圆C:(x 2)2 y 2 1的两条切线,A ,B 为切点,那么四边形 APBC 面积的最小值为A 。
。
3B 。
2。
3C 。
。
5D 。
2 5x x. __ e e 8 。
2024年山东省烟台市高三一模卷数学试题及答案
2024年高考诊断性测试数学注意事项:1.本试题满分150分,考试时间为120分钟.2.答卷前,务必将姓名和准考证号填涂在答题纸上.3.使用答题纸时,必须使用0.5毫米的黑色签字笔书写,要字迹工整,笔迹清晰;超出答题区书写的答案无效;在草稿纸、试题卷上答题无效.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.1.已知集合R U =,集合{}{}2230,02A xx x B x x =+−<=≤≤∣∣,则图中阴影部分表示的集合为( )A.()3,0−B.()1,0−C.()0,1D.()2,32.若5250125(12)x a a x a x a x −=++++L ,则24a a +=( )A.100B.110C.120D.1303.若点()1,2A 在抛物线22y px =上,F 为抛物线的焦点,则AF =( ) A.1 B.2 C.3 D.44.若π1cos 43α⎛⎫−= ⎪⎝⎭,则sin2α=( ) A.59−B.59C.79− D.795.将8个大小形状完全相同的小球放入3个不同的盒子中,要求每个盒子中至少放2个小球,则不同放法的种数为( )A.3B.6C.10D.156.设,a b 为两条不同的直线,,αβ为两个不同的平面,下列说法正确的是( ) A.若a ∥,b α∥α,则a ∥b B.若,a b 与α所成的角相等,则a ∥bC.若,a αβ⊥∥,b α∥β,则a b ⊥D.若,,a b αβαβ⊥⊥⊥,则a b ⊥7.已知定义在R 上的奇函数()f x 满足()()2f x f x −=,当01x ≤≤时,()21xf x =−,则()2log 12f =( ) A.13−B.14− C.13 D.128.在平面直角坐标系xOy 中,点()()1,0,2,3A B −,向量OC mOA nOB =+u u u r u u u r u u u r,且40m n −−=.若P 为椭圆2217y x +=上一点,则PC u u u r 的最小值为( )D. 二、多选题:本题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知12,z z 为复数,下列结论正确的有( ) A.1212z z z z +=+ B.1212z z z z ⋅=⋅C.若12z z ⋅∈R ,则12z z =D.若120z z ⋅=,则10z =或20z =10.先后抛掷一枚质地均匀的骰子两次,记向上的点数分别为,x y ,设事件A =“(1)log x y +为整数”,B =“x y +为偶数”,C =“2x y +为奇数”,则( ) A.()16P A =B.()112P AB = C.事件B 与事件C 相互独立 D.()718P AC =∣ 11.给定数列{}n a ,定义差分运算:2*11Δ,ΔΔΔ,n n n n n n a a a a a a n N ++=−=−∈.若数列{}n a 满足2n a n n =+,数列{}n b 的首项为1,且()1*Δ22,n n b n n N −=+⋅∈,则( )A.存在0M >,使得Δn a M <恒成立B.存在0M >,使得2Δn a M <恒成立C.对任意0M >,总存在*n ∈N ,使得n b M >D.对任意0M >,总存在*n ∈N ,使得2Δnnb M b > 三、填空题:本题共3小题,每小题5分,共15分.12.若圆22()(1)1x m y −+−=关于直线y x =对称的圆恰好过点()0,4,则实数m 的值为__________. 13.在三棱锥P ABC −中,2PB PC ===,且,,APB BPC CPA E F ∠∠∠==分别是,PC AC 的中点,90BEF ∠=o ,则三棱锥P ABC −外接球的表面积为__________,该三棱锥外接球与内切球的半径之比为__________.(本小题第一空2分,第二空3分.)14.若函数()sin 1f x x x ωω=+−在[]0,2π上佮有5个零点,且在ππ,415⎡⎤−⎢⎥⎣⎦上单调递增,则正实数ω的取值范围为__________.四、解答题:本题共5小题,共77分,解答应写出文字说明、证明过程或演算步骤.15.(13分)已如曲线()()22ln ,f x ax x x b a b =+−+∈R 在2x =处的切线与直线210x y ++=垂直.(1)求a 的值:(2)若()0f x ≥恒成立,求b 的取值范围.16.(15分)如图,在三棱柱111ABC A B C −中,,3,2AB AC AB AD DB ⊥===,O 为BC 的中点,1A O ⊥平面ABC .(1)求证:1AA OD ⊥;(2)若1AA =1B AA O −−的余弦值.17.(15分)联合国新闻部将我国农历二十四节气中的“谷雨”定为联合国中文日,以纪念“中华文字始祖”仓颉的贡献.某大学拟在2024年的联合国中文日举行中文知识竞赛决赛决赛分为必答、抢答两个环节依次进行.必答环节,共2道题,答对分别记30分、40分,否则记0分:抢答环节,包括多道题,设定比赛中每道题必须进行抢答,抢到并答对者得15分,抢到后未答对,对方得15分:两个环节总分先达到或超过100分者获胜,比赛结束.已知甲、乙两人参加决赛,且在必答环节,甲答对两道题的概率分别41,53,乙答对两道题的概率分别为21,32,在抢答环节,任意一题甲、乙两人抢到的概率都为12,甲答对任意一题的概率为512,乙答对任意一题的概率为34,假定甲、乙两人在各环节、各道题中答题相互独立(1)在必答环节中,求甲、乙两人得分之和大于100分的概率: (2)在抢答环节中,求任意一题甲获得15分的概率:(3)若在必答环节甲得分为70分,乙得分为40分,设抢答环节经过X 道题抢答后比赛结束,求随机变量X 的分布列及数学期望.18.(17分)已知双曲线2222:1(0,0)x y C a b a b−=>>经过点()2,0A −l 过点()3,0D 且与双曲线C 交于两点,P Q (异于点A ).(1)求证:直线AP 与直线AQ 的斜率之积为定值.并求出该定值:(2)过点D 分别作直线,AP AQ 的垂线.垂足分别为,M N ,记,ADM ADN V V 的面积分别为12,S S ,求12S S ⋅的最大值.19.(17分)如图,在平面直角坐标系xOy 中,半径为1的圆A 沿着x 轴正向无滑动地滚动,点M 为圆A 上一个定点,其初始位置为原点,O t 为AM 绕点A 转过的角度(单位:弧度,0t ≥).(1)用t 表示点M 的横坐标x 和纵坐标y :(2)设点M 的轨迹在点()()0000,0M x y y ≠处的切线存在,且倾斜角为θ,求证:1cos2y θ+为定值: (3)若平面内一条光滑曲线C 上每个点的坐标均可表示为()()()[],,,x t y t t αβ∈,则该光滑曲线长度为()()F F βα−,其中函数()F t 满足()F t ='.当点M 自点O 滚动到点E时,其轨迹»OE为一条光滑曲线,求»OE 的长度.2024年高考诊断性测试数学参考答案及评分标准一、选择题A CBC BD A A 二、选择题9.ABD 10.BCD 11.BC 三、填空题12.4 13.10π214.95[,]42四、解答题15.解:(1)x ax x f 212)('−+=, ··································· 2分 直线210x y ++=的斜率21−=k ,由题意知2)2('=f , ··································· 4分 即2114=−+a ,所以21=a . ···································· 5分 (2))(x f 的定义域为)0(∞+,. ··································· 6分 因为()0f x ≥,所以x x x b ln 2212+−−≥.设),0(,ln 221)(2+∞∈+−−=x x x x x g ,则max ()b g x ≥.························ 8分 xx x x x x x x x g )2)(1(221)('2++−=+−−=+−−= ··················· 9分 当)1,0(∈x 时,0)('>x g ,所以)(x g 在)1,0(单调递增,当),1(+∞∈x 时,0)('<x g ,所以)(x g 在),1(+∞单调递减, ··············· 11分 所以max 3()(1)2g x g ==−. 所以23−≥b . ······························· 13分16.解:(1)因为AB AC ⊥,3AB ==,所以60ACB ∠=,12OA BC == ············································ 1分因为3AB =,2AD DB =,所以1DB =.在DBO 中,30DBO ∠=,1DB =,OB =,由余弦定理222121cos301OD ︒=+−⨯=,所以1OD =. ········· 3分在ADO 中,1OD =,2AD =,AO =AO OD ⊥. ····· 4分因为1AO ⊥平面ABC ,OD ⊂平面ABC , 所以1A O OD ⊥. ····················································· 5分因为1AOAO O =,所以OD ⊥平面1AOA . ······································ 6分 因为1AA ⊂平面1AOA ,所以1AA OD ⊥; ····································· 7分 (2)由(1)可知,1,,OA OD OA 两两垂直,以O 为坐标原点,1,,OA OD OA 方向分别为,,x y z 轴正方向,建立如图所示的空间直角坐标系O xyz −. ······ 8分因为1AA =AO =13AO =. ············· 9分则A , 1(0,0,3)A,3(,,0)22B −. ··········· 10分可得133(,,3)22BA =−,333(,,0)22BA =−, 设(,,)x y z =m 为平面1ABA 的一个法向量,则33023022x y z x y −+=⎨⎪−=⎪⎩,取x =,则3y =,1z =, 故=m , ····························· 12分 由题意可知,(0,1,0)=n 为平面 ······················· 13分因为3cos ,||||13<>===m n m n m n ,所以二面角1B AA O −−的余弦值为13. ······························· 15分17.解:(1)两人得分之和大于100分可分为甲得40分、乙得70分,甲得70分、乙得40分,甲得70分、乙得70分三种情况,所以得分大于100分的概率112141114121753325332533245p =⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=. ·························· 4分(2)抢答环节任意一题甲得15分的概率15111212243p =⨯+⨯=. ············ 7分 (3)X 的可能取值为2,3,4,5.因为甲任意一题得15分的概率为13,所以任意一题乙得15分的概率为23. ····· 8分 211(2)()39P X ===, 121214(3)33327P X C ==⨯⨯⨯=, 1243121228(4)()()333381P X C ==⨯⨯⨯+=, 13334412121232(5)()()33333381P X C C ==⨯⨯⨯+⨯⨯⨯=. ··················· 12分所以的分布列为·································· 13分所以142832326()2345927818181E X =⨯+⨯+⨯+⨯=. ····················· 15分 18.解:(1)由题意知,2a =,c a= 又因为222=+c a b , ··················· 2分解得4=b .所以,双曲线C 的方程为221416x y −=. ············································· 3分 设直线l 的方程为3x my =+,联立2214163x y x my ⎧−=⎪⎨⎪=+⎩,消x 可得,22(41)24200m y my −++=. ··············· 4分不妨设1122(,),(,)P x y Q x y , 则12m ≠±,且1222441m y y m −+=−,1222041y y m =−. ························· 5分 所以12122121212225()25AP AQ y y y y k k x x m y y m y y =⋅=+++++ ····················· 7分 45=−. ····························· 9分 (2)设直线AP 的方程为(2)y k x =+,则直线1:(3)DM y x k=−−,联立(2)1(3)y k x y x k =+⎧⎪⎨=−−⎪⎩,解得251M k y k =+, ····································· 11分 用45k −替换上式中的k 可得21002516N ky k −=+. ······························· 13分 故21222253125||4(1)(2516)M N k S S y y k k ⋅==++ ································· 15分 223125162541k k=++.因为22162540k k +≥=,当且仅当5k =±时,“=”成立,所以12312581S S ⋅≤, 故12S S ⋅的最大值为312581. ························· 17分 19.解:(1)由题意可得1cos y t =−,||OB BM t ==,所以||sin sin x OB t t t =−=−, ································ 2分所以sin x t t =−,1cos y t =−. ································ 4分(2)证明:由复合函数求导公式t x t y y x '''=⋅,所以sin 1cos x tt x t t y x y t y x x t '''⋅'===''−. ·········································· 7分 所以sin tan 1cos ttθ=−,因为222222cos 21cos 22cos sin cos tan 1θθθθθθ+===++ 20222(1cos )1cos sin 22cos ()11cos t t y t t t −===−=−+−,所以01+cos2y θ为定值1. ········································· 10分(3)由题意,()2|sin |2t F t '===. ·········· 13分因为02t ≤≤π,sin 02≥所以()2sin 2tF t '=,所以()4cos 2tF t c =−+(c 为常数), ······································ 15分(2)(0)(4cos )(4cos0)8F F c c π−=−π+−−+=,所以OE 的长度为8. ································· 17分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密★启用前2020届山东省烟台市高三新高考数学模拟试题学校:___________姓名:___________班级:___________考号:___________注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上 一、单选题1.已知集合1|244xA x ⎧⎫=≤≤⎨⎬⎩⎭,1|lg 10B y y x x ⎧⎫==>⎨⎬⎩⎭,,则A B =I ( )A .[]22-,B .(1,)+∞C .(]1,2-D .(](1)2-∞-⋃+∞,,解:由题,不等式1244x ≤≤,解得22x -≤≤,即{}|22A x x =-≤≤; 因为函数lg y x =单调递增,且110x >,所以1y >-,即{}|1B y y =>-, 则(]1,2A B ⋂=-, 故选:C2.设i 是虚数单位,若复数5i2i()a a +∈+R 是纯虚数,则a 的值为( ) A .3- B .3C .1D .1-解:由题,()()()()5252112222i i ia a a i a i i i i -+=+=++=++++-, 因为纯虚数,所以10a +=,则1a =-, 故选:D3.“2a <”是“10,x a x x∀>≤+”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件解:若10,x a x x ∀>≤+,则min 1a x x ⎛⎫≤+ ⎪⎝⎭, 因为12x x +≥,当且仅当1x x=时等号成立, 所以2a ≤,因为{}{}|2|2a a a a <⊆≤, 所以“2a <”是“10,x a x x∀>≤+”的充分不必要条件, 故选:A4.甲、乙两名学生的六次数学测验成绩(百分制)的茎叶图如图所示.①甲同学成绩的中位数大于乙同学成绩的中位数; ②甲同学的平均分比乙同学的平均分高; ③甲同学的平均分比乙同学的平均分低; ④甲同学成绩的方差小于乙同学成绩的方差. 以上说法正确的是( ) A .③④B .①②C .②④D .①③④解:由茎叶图可得甲同学成绩的中位数为8082812+=,乙同学成绩的中位数为878887.52+=,故①错误; ()1=72+76+80+82+86+90=816x ⨯甲,()1=69+78+87+88+92+96=856x ⨯乙,则x x <甲乙,故②错误,③正确;显然甲同学的成绩更集中,即波动性更小,所以方差更小,故④正确, 故选:A5.刘徽(约公元225年-295年),魏晋期间伟大的数学家,中国古典数学理论的奠基人之一他在割圆术中提出的,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的佳作,割圆术的核心思想是将一个圆的内接正n 边形等分成n 个等腰三角形(如图所示),当n 变得很大时,这n 个等腰三角形的面积之和近似等于圆的面积,运用割圆术的思想,得到sin 2o 的近似值为( )A .π90B .π180C .π270D .π360答案:A设圆的半径为r ,每个等腰三角形的顶角为360n︒,则每个等腰三角形的面积为21360sin2r n ︒,由割圆术可得圆的面积为221360sin 2r n r n π︒=⋅,整理可得3602sin n nπ︒=,当180n =时即可为所求. 解:由割圆术可知当n 变得很大时,这n 个等腰三角形的面积之和近似等于圆的面积, 设圆的半径为r ,每个等腰三角形的顶角为360n︒, 所以每个等腰三角形的面积为21360sin2r n ︒, 所以圆的面积为221360sin2r n r n π︒=⋅,即3602sin n n π︒=, 所以当180n =时,可得3602sin sin 218018090ππ︒=︒==, 故选:A6.函数()22xf x a x=--的一个零点在区间()1,2内,则实数a 的取值范围是( )A .()1,3B .()1,2C .()0,3D .()0,2解:由题,显然函数()22xf x a x=--在区间()1,2内连续,因为()f x 的一个零点在区间()1,2内,所以()()120f f <,即()()22410a a ----<,解得0<<3a , 故选:C 7.已知圆截直线所得线段的长度是,则圆与圆的位置关系是( )A .内切B .相交C .外切D .相离答案:B 化简圆到直线的距离,又两圆相交. 选B8.《九章算术》中记载,堑堵是底面为直角三角形的直三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵111ABC A B C -中,AC BC ⊥,12AA =,当阳马11B ACC A -体积的最大值为43时,堑堵111ABC A B C -的外接球的体积为( )A .4π3B 82π C .32π3D 642解:由题意易得BC ⊥平面11ACC A , 所以()11222112113333B ACC A V BC AC AA BC AC BC AC AB -=⋅⋅=⋅≤+=, 当且仅当AC BC =时等号成立, 又阳马11B ACC A -体积的最大值为43, 所以2AB =,所以堑堵111ABC A B C -的外接球的半径221222AA AB R ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭所以外接球的体积34823V r π==, 二、多选题9.下列函数中,既是偶函数,又在(0,)+∞上单调递增的是( ) A .2ln(193)y x x =+ B .e e x x y -=+ C .21y x =+D .cos 3y x =+解:由题,易知A,B,C,D 四个选项中的函数的定义域均为R , 对于选项A,()()))22ln193ln1930f x f x x x x x -+=+++=,则()2ln(193)f x x x =+为奇函数,故A 不符合题意;对于选项B,()()xx f x ee f x --=+=,即()e e x x f x -=+为偶函数,当(0,)x ∈+∞时,设()1xt et =>,则1y t t=+,由对勾函数性质可得,当()1,t ∈+∞时是增函数,又x t e =单调递增,所以()e e xxf x -=+在(0,)+∞上单调递增,故B 符合题意; 对于选项C,()()()2211f x x x f x -=-+=+=,即()21f x x =+为偶函数,由二次函数性质可知对称轴为0x =,则()21f x x =+在(0,)+∞上单调递增,故C 符合题意;对于选项D,由余弦函数的性质可知cos 3y x =+是偶函数,但在(0,)+∞不恒增,故D 不符合题意; 故选:BC10.已知2((0)n ax a>的展开式中第5项与第7项的二项数系数相等,且展开式的各项系数之和为1024,则下列说法正确的是( ) A .展开式中奇数项的二项式系数和为256 B .展开式中第6项的系数最大 C .展开式中存在常数项 D .展开式中含15x 项的系数为45解:由二项式的展开式中第5项与第7项的二项数系数相等可知10n =, 又展开式的各项系数之和为1024,即当1x =时,()1011024a +=,所以1a =,所以二项式为10101222x x x-⎛⎫⎛+=+ ⎪ ⎝⎝⎭,则二项式系数和为1021024=,则奇数项的二项式系数和为110245122⨯=,故A 错误; 由10n =可知展开式共有11项,中间项的二项式系数最大,即第6项的二项式系数最大, 因为2x 与12x -的系数均为1,则该二项式展开式的二项式系数与系数相同,所以第6项的系数最大,故B 正确;若展开式中存在常数项,由通项()12102110r r r r T C xx--+=可得()121002r r --=,解得8r =,故C 正确; 由通项()12102110r r r r TC xx--+=可得()1210152r r --=,解得2r =,所以系数为21045C =,故D 正确, 故选: BCD11.在ABC V 中,D 在线段AB 上,且5,3AD BD ==若2,cos CB CD CDB =∠=,则( ) A .3sin 10CDB ∠=B .ABC V 的面积为8C .ABC V 的周长为8+D .ABC V 为钝角三角形解:因为5cos CDB ∠=-,所以225sin 1cos 5CDB CDB ∠=-∠=,故A 错误; 设CD a =,则2BC a =,在BCD V 中,2222cos BC CD BD BC CD CDB =+-⋅⋅∠,解得5a =,所以1125sin 353225DBC S BD CD CDB =⋅⋅∠=⨯⨯⨯=V , 所以3583ABC DBC S S +==V V ,故B 正确; 因为ADC CDB π∠=-∠,所以()5cos cos cos 5ADC CDB CDB π∠=-∠=-∠=, 在ADC V 中,2222cos AC AD CD AD DC ADC =+-⋅⋅∠,解得25AC =, 所以()352525845ABC C AB AC BC =++=+++=+V ,故C 正确;因为8AB =为最大边,所以2223cos 025BC AC AB C BC AC +-==-<⋅,即C ∠为钝角,所以ABC V 为钝角三角形,故D 正确.故选:BCD12.如图,在四棱锥P ABCD -中,PC ⊥底面ABCD ,四边形ABCD 是直角梯形,//,,222AB CD AB AD AB AD CD ⊥===,F 是AB 的中点,E 是PB 上的一点,则下列说法正确的是( )A .若2PB PE =,则//EF 平面PACB .若2PB PE =,则四棱锥P ABCD -的体积是三棱锥E ACB -体积的6倍C .三棱锥P ADC -中有且只有三个面是直角三角形D .平面BCP ⊥平面ACE解:对于选项A,因为2PB PE =,所以E 是PB 的中点, 因为F 是AB 的中点,所以//EF PA ,因为PA ⊂平面PAC ,EF ⊄平面PAC ,所以//EF 平面PAC ,故A 正确; 对于选项B,因为2PB PE =,所以2P ABCD E ABCD V V --=,因为//,,222AB CD AB AD AB AD CD ⊥===, 所以梯形ABCD 的面积为()()113121222CD AB AD +⋅=⨯+⨯=,1121122ABC S AB AD =⋅=⨯⨯=V ,所以32E ABCD E ABC V V --=,所以3P ABCD E ABC V V --=,故B 错误;对于选项C,因为PC ⊥底面ABCD ,所以PC AC ⊥,PC CD ⊥,所以PAC V ,PCD V 为直角三角形,又//,AB CD AB AD ⊥,所以AD CD ⊥,则ACD V 为直角三角形, 所以222222PA PC AC PC AD CD =+=++,222PD CD PC =+, 则222PA PD AD =+,所以PAD △是直角三角形, 故三棱锥P ADC -的四个面都是直角三角形,故C 错误; 对于选项D,因为PC ⊥底面ABCD ,所以PC AC ⊥,在Rt ACD V 中,AC ==在直角梯形ABCD 中,BC ==,所以222AC BC AB +=,则AC BC ⊥, 因为BC PC C ⋂=,所以AC ⊥平面BCP , 所以平面BCP ⊥平面ACE ,故D 正确, 故选:AD三、填空题13.已知向量(2,)a m =v,(1,2)b =-v ,且a b ⊥v v ,则实数m 的值是________.解:解:∵a b ⊥rr; ∴220a b m ⋅=-=rr ; ∴m =1. 故答案为:1.14.已知数列{}n a 的前n 项和公式为221n S n n =-+,则数列{}n a 的通项公式为___.解:由题意,可知当1n =时,112a S ==;当2n ≥时,()221221143n n n a S S n n n n n -=-=---+-=-.又因为11a =不满足43n a n =-,所以2,143,2n n a n n =⎧=⎨-≥⎩. 15.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点和点()2,P a b 为某个等腰三角形的三个顶点,则双曲线C 的离心率为________.解:由题设双曲线的左、右焦点分别为()1,0F c -,()2,0F c , 因为左、右焦点和点()2,P a b 为某个等腰三角形的三个顶点,当122F F PF =时,2c =,由222b c a =-可得222430c ac a +-=,等式两边同除2a 可得22430e e +-=,解得1e =<(舍);当121F F PF =时,2c =由222b c a =-可得222430c ac a --=,等式两边同除2a 可得22430e e --=,解得e =故答案为 16.设定义域为R 的函数()f x 满足()()f x f x '>,则不等式()()121x e f x f x -<-的解集为__________. 解:设F (x )()xf x e=,则F ′(x )()()'xf x f x e-=,∵()()f x f x '>,∴F ′(x )>0,即函数F (x )在定义域上单调递增. ∵()()121x ef x f x -<-∴()()2121xx f x f x ee--<,即F (x )<F (2x 1-)∴x 2x 1-<,即x >1 ∴不等式()()121x ef x f x -<-的解为()1,+∞故答案为:()1,+∞。
