大学物理光栅衍射完整ppt课件
合集下载
《光栅的衍射》课件
《光栅的衍射》PPT课件
欢迎大家来到《光栅的衍射》PPT课件。本课件将带领你们探索光栅的神奇世 界，了解衍射现象以及光栅在各个领域中的应用。
背景介绍
光栅是一种由许多等距且平行的刻槽组成的光学元件，可以用来分离和分析 光的不同波长。 在本节中，我们将深入研究光栅的定义、原理和结构。
光栅的衍射现象
衍射图案
实验步骤和操作
1. 准备实验装置
搭建光栅实验装置，确保光源、光栅和探测器正确设置。
2. 进行实验测量
用光栅照射光源，并使用探测器记录衍射图案和干涉条纹。
3. 测试不同波长
改变光源的波长，记录不同波长下的衍射和干涉现象。
实验结果和数据分析
衍射图案
光栅衍射图案清晰可见，条纹间距随波长变化。 1. 研究不同光源的衍射图案。 2. 计算出不同波长的衍射角度。
光栅通过衍射现象产生独特的图案，展示了光的波动性 和干涉效应。
干涉条纹
不同波长的光在光栅上产生干涉，形成明暗相间的条纹， 帮助我们研究光的特性。
光栅的应用
1
光谱学
光栅广泛应用于光谱学领域，用于分析光的成分和波长。
2
激光技术
光栅在激光技术中起到关键作用，用于光束展宽和光谱仪、光栅显微镜等，提供高分辨率的图像。
干涉条纹
干涉条纹清晰可见，条纹间距随波长变化。 1. 测量不同波长下的条纹间距。 2. 分析条纹的亮度和对比度。
结论和展望
通过本实验，我们深入了解了光栅的衍射现象和应用。光栅技术在科学研究和工程领域中的应用前景广阔。 未来，我们可以进一步探索光栅的优化方法，研究更复杂的衍射现象，并将其应用于更多实际问题的解决。
欢迎大家来到《光栅的衍射》PPT课件。本课件将带领你们探索光栅的神奇世 界，了解衍射现象以及光栅在各个领域中的应用。
背景介绍
光栅是一种由许多等距且平行的刻槽组成的光学元件，可以用来分离和分析 光的不同波长。 在本节中，我们将深入研究光栅的定义、原理和结构。
光栅的衍射现象
衍射图案
实验步骤和操作
1. 准备实验装置
搭建光栅实验装置，确保光源、光栅和探测器正确设置。
2. 进行实验测量
用光栅照射光源，并使用探测器记录衍射图案和干涉条纹。
3. 测试不同波长
改变光源的波长，记录不同波长下的衍射和干涉现象。
实验结果和数据分析
衍射图案
光栅衍射图案清晰可见，条纹间距随波长变化。 1. 研究不同光源的衍射图案。 2. 计算出不同波长的衍射角度。
光栅通过衍射现象产生独特的图案，展示了光的波动性 和干涉效应。
干涉条纹
不同波长的光在光栅上产生干涉，形成明暗相间的条纹， 帮助我们研究光的特性。
光栅的应用
1
光谱学
光栅广泛应用于光谱学领域，用于分析光的成分和波长。
2
激光技术
光栅在激光技术中起到关键作用，用于光束展宽和光谱仪、光栅显微镜等，提供高分辨率的图像。
干涉条纹
干涉条纹清晰可见，条纹间距随波长变化。 1. 测量不同波长下的条纹间距。 2. 分析条纹的亮度和对比度。
结论和展望
通过本实验，我们深入了解了光栅的衍射现象和应用。光栅技术在科学研究和工程领域中的应用前景广阔。 未来，我们可以进一步探索光栅的优化方法，研究更复杂的衍射现象，并将其应用于更多实际问题的解决。
大学物理PPT课件12-9衍射光栅
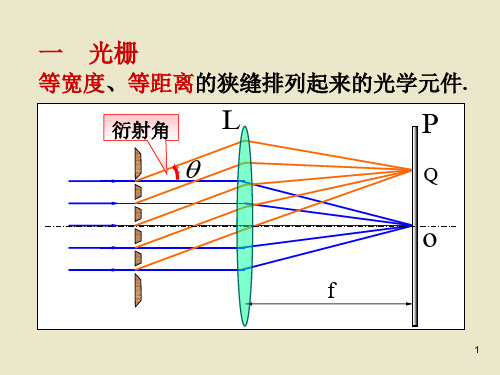
4级为第一个缺级。求(1)光栅上相邻两缝的距 离是多少？ (2)狭缝可能的最小宽度是多少？ (3)按上述选定的b 、b'值，实际上能观察到的 全部明纹数是多少？
解: (1) (b b)sin k k 2 sin 0.2
(b b) k 6m sin
(2) k (b b) k k 4,取k 1
k=4
k=6
k=-5 k=-3
k=-1 k=1
k=3
k=5
若
b
b b
k k
3 1
6 2
9 3
缺级：k
= 3,6,9,...
9
三 衍射光谱
入射光为白光时，形成彩色光谱.
I
sin
0 一级光谱
三级光谱
b b'
二级光谱
10
例如 二级光谱重叠部分光谱范围
(b b') sin 3紫
19
sin1 k11 2k1 sin2 k22 3k2
两谱线重合， 1 2，
所以 k1 3 6 k2 2 4
第二次重合k1=6, k2=4
d sin 600 61 d 3.05 10 3 mm
20
三 X 射线的衍射
1885年伦琴发现，受高速电子撞击的金属 会发射一种穿透性很强的射线称Ｘ射线.
13
例1 用白光垂直照射在每厘米有6500条刻 痕的平面光栅上，求第三级光谱的张角.
解 400 ~ 760nm b b'1cm / 6500
紫光
sin 1
k1
b b'
3 4 105 cm 1cm 6500
解: (1) (b b)sin k k 2 sin 0.2
(b b) k 6m sin
(2) k (b b) k k 4,取k 1
k=4
k=6
k=-5 k=-3
k=-1 k=1
k=3
k=5
若
b
b b
k k
3 1
6 2
9 3
缺级：k
= 3,6,9,...
9
三 衍射光谱
入射光为白光时，形成彩色光谱.
I
sin
0 一级光谱
三级光谱
b b'
二级光谱
10
例如 二级光谱重叠部分光谱范围
(b b') sin 3紫
19
sin1 k11 2k1 sin2 k22 3k2
两谱线重合， 1 2，
所以 k1 3 6 k2 2 4
第二次重合k1=6, k2=4
d sin 600 61 d 3.05 10 3 mm
20
三 X 射线的衍射
1885年伦琴发现，受高速电子撞击的金属 会发射一种穿透性很强的射线称Ｘ射线.
13
例1 用白光垂直照射在每厘米有6500条刻 痕的平面光栅上，求第三级光谱的张角.
解 400 ~ 760nm b b'1cm / 6500
紫光
sin 1
k1
b b'
3 4 105 cm 1cm 6500
光栅衍射PPT
光栅光谱
解 （1）根据光栅方程 (ab)s得in k
kabsin
按题意知，光栅常数为
a b 5 1m 00 2 m 1 6 m 0
可见 k的可能最大值相应于 sin1
代入数值得
k 2106 58.39109
3.4
k只能取整数 ，故取k=3,即垂直入射时能看到第 三级条纹。
光栅光谱
（2）如平行光以 角入射时，光程差的计算公式应
k (ab)(s i9n0()si3n0)
2
(a5b8).3 ( 91 1 0 09.5)5.0取 9k25
所以斜入射时，总共有 k1k2 条1明纹7。
（3）对光栅公式两边取微分
( a b ) ck o d k sk d
光栅光谱
波长为 及 第kd 级的两条纹分开的角距离
为
d d k k (ab)co ks
同样，k的可能最大值相应于 sin 1
在O点上方观察到的最大级次为 k1，取 9得0
k 1 . 7 取 k 0 1 ( a b )9 ( s 0 3 i )n 0 2 1 6 ( 1 0 0 . 5 )
1
5 . 3 1 8 90 9
1
光栅光谱
而在O点下方观察到的最大级次为 k2，取 得90
N=4
-2(/d)
-(/d)
0
n
2/d
光栅衍射
光栅衍射的谱线特点：
（1）主级大明纹的位置与缝数N无关，它们对称 地分布在中央明纹的两侧，中央明纹光强最大； （2）在相邻的两个主级大之间，有 N1个极小 （暗纹）和N2=2个光强很小的次极大，当N 很大 时，实际上在相邻的主极大之间形成一片暗区，即 能获得又细又亮暗区很宽的光栅衍射条纹。
《光栅衍射讲》课件
前景
在光电子学、信息技术和 生物医学等领域具有广阔 的应用前景。
《光栅衍射讲》PPT课件
# 光栅衍射讲 PPT课件
光栅衍射是一种重要的光学现象，本课件将介绍光栅衍射的定义、应用和原 理，以及光栅的构造、实验、性能指标和应用，最后总结其优缺点、未来发 展和应用前景。
概述
1 光栅衍射的定义
光线通过光栅时产生的衍射现象。
2 光栅衍射的应用
用于光学、物理和化学等领域的实验和技术。
包括选择光源、调整光栅和观察衍射图
样等。
3
光栅衍射实验的注意事项
确保实验环境暗无光线干扰，准确记录 实验结果。
光栅的性能指标
1 光栅的分辨率
能够区分最小特征的能力。
3 光栅的精度
与实际测量值的接近程度。
2 光栅的灵敏度
对入射光强的响应程度。
光栅衍射的应用
光栅衍射在光学中的应用
用于光谱分析、光学显微镜和激光技术等。
3 光栅衍射的原理
光波在光栅上的相位差导致光栅衍射。
光栅构造
光栅的结构
由一系列平行的凸起或凹陷的平行线组成。
光栅的类型
包括均匀光栅、非均匀光栅和衍射光栅等。
光栅参数的影响
包括光栅常数、光栅间距和光栅材料等。
光栅衍射的实验
1
光栅衍射实验的原理
通过光线通过光栅时产生的衍射现象来
光栅衍射实验步骤
2Leabharlann 验证光栅的特性。光栅衍射在物理中的应用
用于材料研究、波动力学和量子力学等。
光栅衍射在化学中的应用
用于表征化学物质的结构和分子间相互作用。
总结
1 光栅衍射的优缺点
提高光栅衍射的分辨率和 灵敏度，但需要精确控制 光栅参数。
在光电子学、信息技术和 生物医学等领域具有广阔 的应用前景。
《光栅衍射讲》PPT课件
# 光栅衍射讲 PPT课件
光栅衍射是一种重要的光学现象，本课件将介绍光栅衍射的定义、应用和原 理，以及光栅的构造、实验、性能指标和应用，最后总结其优缺点、未来发 展和应用前景。
概述
1 光栅衍射的定义
光线通过光栅时产生的衍射现象。
2 光栅衍射的应用
用于光学、物理和化学等领域的实验和技术。
包括选择光源、调整光栅和观察衍射图
样等。
3
光栅衍射实验的注意事项
确保实验环境暗无光线干扰，准确记录 实验结果。
光栅的性能指标
1 光栅的分辨率
能够区分最小特征的能力。
3 光栅的精度
与实际测量值的接近程度。
2 光栅的灵敏度
对入射光强的响应程度。
光栅衍射的应用
光栅衍射在光学中的应用
用于光谱分析、光学显微镜和激光技术等。
3 光栅衍射的原理
光波在光栅上的相位差导致光栅衍射。
光栅构造
光栅的结构
由一系列平行的凸起或凹陷的平行线组成。
光栅的类型
包括均匀光栅、非均匀光栅和衍射光栅等。
光栅参数的影响
包括光栅常数、光栅间距和光栅材料等。
光栅衍射的实验
1
光栅衍射实验的原理
通过光线通过光栅时产生的衍射现象来
光栅衍射实验步骤
2Leabharlann 验证光栅的特性。光栅衍射在物理中的应用
用于材料研究、波动力学和量子力学等。
光栅衍射在化学中的应用
用于表征化学物质的结构和分子间相互作用。
总结
1 光栅衍射的优缺点
提高光栅衍射的分辨率和 灵敏度，但需要精确控制 光栅参数。
《光栅衍射实验》PPT课件
A）千万注意： 只测定汞灯第二级（k=2）各谱线衍射角k
k2
k 1
k 1
k2
图 光栅衍射光谱示意图
-
14
B）注意：测量时“一口气” 测完，中途不走 开，
不讲话，望远镜一个方向偏转，不回头。
k2
k 1
k 1
-
图 光栅衍射光谱示意图
k2
15
第四步：按实验讲义要求好好处理数据
-
16
以光栅平面作为反射面，仅调节
载物台来的绿色 “+” 字像 与分划板上方叉丝重合。然后
光栅放置
旋紧游标制动螺丝，锁定游标盘。
-
12
2) 光栅刻线与分光计主轴平行
转动望远镜，如观察 到左右衍射光线不在 同一高度可调节载物 台螺钉 C 使各级谱线 等高.
-
13
第三步：如何测量角度
入
射
d: 光栅常数 ：谱线的衍射角
f
复色 光衍 射条 纹
-
5
b a d
f
当入射光垂直入射时，光谱线位置满足 光的加强条件，即光栅方程为
dsin kk (k 0 , 1 , 2 ,.....)
k=0、±1、±2、±3、……，k为衍射级次
k为第k级谱线的衍射角- 。
6
入射光为一束 复色光垂直入射后产生的谱线
kk2 -
2
10
四：怎么测量
实质是测量角度
第一步：首先是分光计本身调整（略）
-
11
第二步：透射光栅调整
透射光栅调整时望远镜、平行光管的倾斜度调节螺
钉已调好，不能再动！
1）调光栅平面与平行光管的光轴垂直。
将光栅如图所示放置在载物台上，
光栅平面垂直于a、b 连线，使望
k2
k 1
k 1
k2
图 光栅衍射光谱示意图
-
14
B）注意：测量时“一口气” 测完，中途不走 开，
不讲话，望远镜一个方向偏转，不回头。
k2
k 1
k 1
-
图 光栅衍射光谱示意图
k2
15
第四步：按实验讲义要求好好处理数据
-
16
以光栅平面作为反射面，仅调节
载物台来的绿色 “+” 字像 与分划板上方叉丝重合。然后
光栅放置
旋紧游标制动螺丝，锁定游标盘。
-
12
2) 光栅刻线与分光计主轴平行
转动望远镜，如观察 到左右衍射光线不在 同一高度可调节载物 台螺钉 C 使各级谱线 等高.
-
13
第三步：如何测量角度
入
射
d: 光栅常数 ：谱线的衍射角
f
复色 光衍 射条 纹
-
5
b a d
f
当入射光垂直入射时，光谱线位置满足 光的加强条件，即光栅方程为
dsin kk (k 0 , 1 , 2 ,.....)
k=0、±1、±2、±3、……，k为衍射级次
k为第k级谱线的衍射角- 。
6
入射光为一束 复色光垂直入射后产生的谱线
kk2 -
2
10
四：怎么测量
实质是测量角度
第一步：首先是分光计本身调整（略）
-
11
第二步：透射光栅调整
透射光栅调整时望远镜、平行光管的倾斜度调节螺
钉已调好，不能再动！
1）调光栅平面与平行光管的光轴垂直。
将光栅如图所示放置在载物台上，
光栅平面垂直于a、b 连线，使望
衍射光栅 PPT课件
求 (1) 光栅狭缝可能的宽度； (2) 第二级主极大的半角宽度。
解 (1) 光栅常数 a b 1 1102 mm
100
第四级主极大缺级，故有 4 k a b
1 k 4
a
k 1 时 a a b 1102 2.5103 mm
4
4
k 2 时，第二级主极大也发生缺级，不符题意，舍去。
1 51.190
sin 2
37 1.54
10 7 10 6
1.36
1
900
对于k=3红光级不存在。那么，对于白光k=3能看到的光谱的
波长为：
sin 1
900
ab
1.54 10 6
5.133 107 m
5133
0
A
在绿光附近
k
3
(2).对于 4300 A0 光入射,能看到衍射条纹的级数
第四节 衍射光栅
一. 衍射光栅
1. 光栅 — 大量等宽等间距的平行狭缝(或反射面)构成的光学元件
透射光栅
反射光栅
2 . 光栅常数d
d ab
光栅宽度为 l ，每毫米缝数
为 m ，则总缝数
N ml
a 透光宽度 b 不透光宽度
3. 光栅衍射的基本特点
1 I I0
以二缝光栅为例 x
s2
d s1 a
d 3a
缺级
单缝衍射
光栅光谱
单缝衍射 缝间干涉
暗 明纹 明 加强
暗 暗纹
暗 减弱
4. 暗纹条件 光栅衍射中，两主极大条纹之间分布着一些暗纹，这是缝
间干涉相消而成。
设光栅总缝数为 N，各缝在观察屏上某点 P 引起的光振动
矢量为
rr
《衍射光栅》PPT课件
b)( a )一b 定，
大，大 k 小，小
P
白光入射,中央白色， 两侧位彩色条纹
f
xk
xk
o
f
2021/4/26 太原理工大学物理系 14
2)各级明纹在屏幕上的线位置
xk
f
tank f
很小
sin k
f
k
ab
P
xk
o
f
2021/4/26 太原理工大学物理系 15
3）单色平行光斜入射，光栅公式修正为
缝衍射的调制。
I
I
单缝衍射
N=4
轮廓线
2021/4/26 太原理工大学物理系 9
综上所述：
单色光垂直照射光栅，出现明纹条件
P127,14.29
(a b)sin k (k 0,1,2.....) 光栅方程
且 a sin k (k 1, 2,3.....)
k=0称为中央明纹，k=1,2,…对应各级明纹， 称为k级主极大。主极大为细而亮的明条纹—— 为一条亮线。各级主极大之间充满了大量暗纹 (N-1个暗纹，N-2个次极大，N为总缝数）。
P127,14.29下面段
2021/4/26 太原理工大学物理系 10
光栅中狭缝条数越多，明纹越细，分得越开.
1条缝
5条缝
3条缝
20 条 缝
条纹特点：漆黑背景上一条条细而亮的线。
2021/4/26 太原理工大学物理系 11
4.条纹特点：漆黑背景上一条条细而亮的线。 1)主极大
(a b)sin k (k 0,1,2.....) 光栅方程
叠时，它们有相同的衍射角
即1＝2=
由光栅公式 (a b)sin k
可得，(a b) sin k11 k22
光栅衍射PPTPPT
光栅衍射
1.4 缺级
a b
为整数比时，明纹会出现缺级
I0单 I单
-2
-1
光栅衍射 光强曲线
0
1
2 sin ( /a)
I N2I0单
N=4
单缝衍射 d = 4a
轮廓线
-8
-4
此图为N = 4，
d a
0
=
4
4
8 sin ( /d )
的单缝衍射和光栅衍射的
光强分布曲线，这里主极大缺±4,±8…级。
光栅衍射
sin
2/d
光栅衍射
光栅衍射的谱线特点：
（1）主级大明纹的位置与缝数N无关，它们对称 地分布在中央明纹的两侧，中央明纹光强最大； （2）在相邻的两个主级大之间，有 N1个极小 （暗纹）和N2=2个光强很小的次极大，当N 很大 时，实际上在相邻的主极大之间形成一片暗区，即 能获得又细又亮暗区很宽的光栅衍射条纹。
光栅衍射
1.2 光栅的衍射图样
光栅衍射演示
光栅衍射
1.2 光栅的衍射图样
不考虑衍射时, 多缝干涉的光强分布图：
多光束干涉光强曲线
sin2N/sin2
N2
-8
-4
0
4
8 sin (/d)
设光栅的每个缝宽均为a，在夫琅禾费衍射下，每 个缝的衍射图样位置是相重叠的。
光栅衍射
透镜
θ
λ
a d
θ
θ
f
衍射光相干叠加
光栅光谱
解 （1）根据光栅方程 (a b) si得n k
k
ab
sin
按题意知，光栅常数为
a
b
1 500
mm
2ห้องสมุดไป่ตู้
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2）主要公式
光栅方程： (ab)sink k01.2.3..
缺级公式：
ab d
k k'
k'
a.
a
k'1.2.103...
3）几点注意：
A）一定时，光栅常数越小，条纹越稀疏， B）d一定时，波长越大，衍射角越大。
C）当白色光入射光栅时，将产生彩色的衍射光谱。
-2级光谱 -1级光谱
非连续光谱
中央明纹
1级光谱
由明纹公式（光栅方程）：
(ab )sinkL(1 ) k01.2.3...
由单缝衍射的暗纹公式：
asink'L(2) k'1.2.3...
在同一衍射方向同时满足，
得：
ab k a k'
缺级公式：
k k'ab k 'd
a
a
. k'1.2.3...8
缺级公式：
k k' ab k' d aa
k'1.2.3...
0
f
两线谱重合 4 3
由①、 ② 1 =32/4 = 450nm
tg4=x/f ==0.1 4=5.7
sin4 tg4=0.1
代入①得：
d
= si4n14
==1.8103cm
.
15
例3．在垂直入射光栅的平行光中，有1和2两种波长。已知1的 第四级光谱与2的第三级光谱恰好重合在离中央明纹5cm处。若 2=600nm，并发现2的第5级光谱线缺级，透镜的焦距f=0.5m。 试问： (2) 最小缝宽? (3) 能观察到2的多少条光谱线？
2级光谱
-2级光谱
-1级光谱 中央明. 纹
1级光谱
2级1光1 谱
(光栅光谱仪)
光栅
构造：
光源 准直
1）准直部分--产生平行光
望远镜
2）分光器件--光栅
3）观察部分--可改变角度观察不同衍射角出
射光的望远镜
原理： (ab)sink
.
12
例10-13 以波长589.3 nm的钠黄光垂直入射到光栅
上，测得第二级谱线的偏角为2808’，用另一未知波长
'
第3级缺级 14
例3．在垂直入射光栅的平行光中，有1和2两种波长。已知1 的第四级光谱与2的第三级光谱恰好重合在离中央明纹5cm处。 若2=600nm，并发现2的第5级光谱线缺级，透镜的焦距 f=0.5m。试问：
(1) 1=?，d=?
(2) 光栅的最小缝宽?
x
(3) 能观察到2的多少条光谱线？
解：(1) 1 dsin4= 41 ① 2 dsin 3=32 ②
的级次。
解：(1) dsin = k
① k=2
= 30°
d=2.4104 cm
(2) 第三级缺级 k k' d k 3
a
a k d k
屏幕上出现全部谱
am in0.8104cm线为：0、±1、±2
d
级，共5条主明纹。
(3) 先定最高级kmax kmax
kmax =3
再看缺级
k
k
'
d a.
3k
的单色光入射时，它的第一级谱线的偏角13030’.
求：(1)试求未知波长；
(2)未知波长的谱线最多能观测到第几级？
解 (1)设λ0＝589.3 nm，φ0＝28°8′，k0＝2，λ为未知波长，
φ＝13°30′，k＝1，根据光栅方程可得：
d s in0 20 d s in
20ssiinn0 584.9(nm)
光栅方程
任意相邻两狭缝间的光程差为 (a+b)sin
d
a b BC
(a+b)sin = ± k k=0, 1, 2, 3 ···
则它们相干加强，形成明条纹。
狭缝越多，条纹就越明亮。 多缝干涉明条纹也称为主极大明条纹
光栅常数(a+b)越小，各明纹对应的衍射角越大，
相邻条纹间距越大，有利于分辨和测量。
(2) 已知2的k2=5缺级
k k 'd a
a3.6104cm
(3)
kmax
d
2
kmax 29
谱线数229+1－25=49条
.
16
E
L1
S
L2
A
f
条纹特点：亮、细、疏
.
4
二、光栅的衍射规律
衍射条纹的形成:
1）各单缝分别同时产生单缝衍射
注意：每一个单缝衍射的图
I
样和位置都是一样的。
2）各单缝衍射的平行
sin
光产生多光束干涉。
显然干涉条纹要受到
衍射光的影响。
sin
3）光栅衍射条纹是单缝衍射
与多缝干涉的综合效果。
sin
.
5
定量分析： 1、明纹公式
§10-5 光栅衍射
主讲教师：刘秀英 预习：§10.7 作业：P132，10-22，10-24
.
1
单缝衍射明暗纹公式
0
bsin (2k 1)
2
2k 2
中央明纹
k1.2.3... 明纹 k1.2.3... 暗纹
中央明纹的半角宽度 其他明纹的角宽度
0பைடு நூலகம்
b
b
.
2
一、光栅衍射现象
一）基本概念
光栅—大量等宽等间距的平行狭缝(或反射面) 构成的光学元件。
（分光装置）
种类：
透射光栅
反射光栅
d d
光栅常数 a是透光（或反光）部分的宽度
b是不透光(或不反光)部分的宽度
a
d=a+b 光栅常数 b d
（10-5——10-6 m）
（即一厘米内刻有1000---10000条狭缝或反射面）
.
3
二）装置和现象
.
6
2. 衍射的影响、缺级 A）明纹的光强受到衍射光强的影响
如果只有衍射：
I
-2
-1
1
2
如果只有干涉：
I
干涉、衍射均有之：
I
缺
-2
级
-5 -4 -2 -1 . 1
缺 级
24
2
5
7
B）出现缺级现象 在某些特定方向，满足光栅方程的明纹条件，又满足衍射 的暗纹条件时，这一方向的明纹将不出现，称为“缺级”。
例：一光栅，b=2a，则缺级的明纹：
k k ' a b 3k' a
故 k 3 k ' 3 . 6 . 9 .I..
k'1.2.3..
缺
-2
级
缺
级
2
-5 -4
-2 -1
12
.
45
9
综述：
1）光栅衍射条纹具有亮、细、疏的特点。 亮--每一单缝出射的光强虽小，但N条单缝 的光强叠加起来，光强很大。 细--光栅的单缝数量很大，在两级明纹之间 存在N-1个暗纹，占着很大的角宽度。 疏--光栅常数可作得很小，能使衍射角较大。
(2) 光栅方程 dsink
k d sin | sin |1
最多能观测到
kmax
d
20 .
sin
4.3
第四级谱线.
13
例2．波长为 =600nm的单色光垂直入射一光栅上，测得第二级
主明纹的衍射角为，且第三级缺级。求：
(1) 光栅常数d等于多少？(2) 透光缝可能的最小宽度是多少？
(3) 在选定了上述d和b之后，求在屏幕上可能出现的全部主明纹
光栅方程： (ab)sink k01.2.3..
缺级公式：
ab d
k k'
k'
a.
a
k'1.2.103...
3）几点注意：
A）一定时，光栅常数越小，条纹越稀疏， B）d一定时，波长越大，衍射角越大。
C）当白色光入射光栅时，将产生彩色的衍射光谱。
-2级光谱 -1级光谱
非连续光谱
中央明纹
1级光谱
由明纹公式（光栅方程）：
(ab )sinkL(1 ) k01.2.3...
由单缝衍射的暗纹公式：
asink'L(2) k'1.2.3...
在同一衍射方向同时满足，
得：
ab k a k'
缺级公式：
k k'ab k 'd
a
a
. k'1.2.3...8
缺级公式：
k k' ab k' d aa
k'1.2.3...
0
f
两线谱重合 4 3
由①、 ② 1 =32/4 = 450nm
tg4=x/f ==0.1 4=5.7
sin4 tg4=0.1
代入①得：
d
= si4n14
==1.8103cm
.
15
例3．在垂直入射光栅的平行光中，有1和2两种波长。已知1的 第四级光谱与2的第三级光谱恰好重合在离中央明纹5cm处。若 2=600nm，并发现2的第5级光谱线缺级，透镜的焦距f=0.5m。 试问： (2) 最小缝宽? (3) 能观察到2的多少条光谱线？
2级光谱
-2级光谱
-1级光谱 中央明. 纹
1级光谱
2级1光1 谱
(光栅光谱仪)
光栅
构造：
光源 准直
1）准直部分--产生平行光
望远镜
2）分光器件--光栅
3）观察部分--可改变角度观察不同衍射角出
射光的望远镜
原理： (ab)sink
.
12
例10-13 以波长589.3 nm的钠黄光垂直入射到光栅
上，测得第二级谱线的偏角为2808’，用另一未知波长
'
第3级缺级 14
例3．在垂直入射光栅的平行光中，有1和2两种波长。已知1 的第四级光谱与2的第三级光谱恰好重合在离中央明纹5cm处。 若2=600nm，并发现2的第5级光谱线缺级，透镜的焦距 f=0.5m。试问：
(1) 1=?，d=?
(2) 光栅的最小缝宽?
x
(3) 能观察到2的多少条光谱线？
解：(1) 1 dsin4= 41 ① 2 dsin 3=32 ②
的级次。
解：(1) dsin = k
① k=2
= 30°
d=2.4104 cm
(2) 第三级缺级 k k' d k 3
a
a k d k
屏幕上出现全部谱
am in0.8104cm线为：0、±1、±2
d
级，共5条主明纹。
(3) 先定最高级kmax kmax
kmax =3
再看缺级
k
k
'
d a.
3k
的单色光入射时，它的第一级谱线的偏角13030’.
求：(1)试求未知波长；
(2)未知波长的谱线最多能观测到第几级？
解 (1)设λ0＝589.3 nm，φ0＝28°8′，k0＝2，λ为未知波长，
φ＝13°30′，k＝1，根据光栅方程可得：
d s in0 20 d s in
20ssiinn0 584.9(nm)
光栅方程
任意相邻两狭缝间的光程差为 (a+b)sin
d
a b BC
(a+b)sin = ± k k=0, 1, 2, 3 ···
则它们相干加强，形成明条纹。
狭缝越多，条纹就越明亮。 多缝干涉明条纹也称为主极大明条纹
光栅常数(a+b)越小，各明纹对应的衍射角越大，
相邻条纹间距越大，有利于分辨和测量。
(2) 已知2的k2=5缺级
k k 'd a
a3.6104cm
(3)
kmax
d
2
kmax 29
谱线数229+1－25=49条
.
16
E
L1
S
L2
A
f
条纹特点：亮、细、疏
.
4
二、光栅的衍射规律
衍射条纹的形成:
1）各单缝分别同时产生单缝衍射
注意：每一个单缝衍射的图
I
样和位置都是一样的。
2）各单缝衍射的平行
sin
光产生多光束干涉。
显然干涉条纹要受到
衍射光的影响。
sin
3）光栅衍射条纹是单缝衍射
与多缝干涉的综合效果。
sin
.
5
定量分析： 1、明纹公式
§10-5 光栅衍射
主讲教师：刘秀英 预习：§10.7 作业：P132，10-22，10-24
.
1
单缝衍射明暗纹公式
0
bsin (2k 1)
2
2k 2
中央明纹
k1.2.3... 明纹 k1.2.3... 暗纹
中央明纹的半角宽度 其他明纹的角宽度
0பைடு நூலகம்
b
b
.
2
一、光栅衍射现象
一）基本概念
光栅—大量等宽等间距的平行狭缝(或反射面) 构成的光学元件。
（分光装置）
种类：
透射光栅
反射光栅
d d
光栅常数 a是透光（或反光）部分的宽度
b是不透光(或不反光)部分的宽度
a
d=a+b 光栅常数 b d
（10-5——10-6 m）
（即一厘米内刻有1000---10000条狭缝或反射面）
.
3
二）装置和现象
.
6
2. 衍射的影响、缺级 A）明纹的光强受到衍射光强的影响
如果只有衍射：
I
-2
-1
1
2
如果只有干涉：
I
干涉、衍射均有之：
I
缺
-2
级
-5 -4 -2 -1 . 1
缺 级
24
2
5
7
B）出现缺级现象 在某些特定方向，满足光栅方程的明纹条件，又满足衍射 的暗纹条件时，这一方向的明纹将不出现，称为“缺级”。
例：一光栅，b=2a，则缺级的明纹：
k k ' a b 3k' a
故 k 3 k ' 3 . 6 . 9 .I..
k'1.2.3..
缺
-2
级
缺
级
2
-5 -4
-2 -1
12
.
45
9
综述：
1）光栅衍射条纹具有亮、细、疏的特点。 亮--每一单缝出射的光强虽小，但N条单缝 的光强叠加起来，光强很大。 细--光栅的单缝数量很大，在两级明纹之间 存在N-1个暗纹，占着很大的角宽度。 疏--光栅常数可作得很小，能使衍射角较大。
(2) 光栅方程 dsink
k d sin | sin |1
最多能观测到
kmax
d
20 .
sin
4.3
第四级谱线.
13
例2．波长为 =600nm的单色光垂直入射一光栅上，测得第二级
主明纹的衍射角为，且第三级缺级。求：
(1) 光栅常数d等于多少？(2) 透光缝可能的最小宽度是多少？
(3) 在选定了上述d和b之后，求在屏幕上可能出现的全部主明纹