最新大学物理-光栅衍射整理
合集下载
大学物理12光衍射汇总
b sin 5 (2k 1) (k=2)
2
2
A
b
5
C B
2
半波带 半波带
半波带
半波带
半波带
P5
二级明纹
二级暗纹
一级明纹
一级暗纹
一级暗纹
一级明纹
二级暗纹
P5
二级明纹
单缝被分为五个半波带，在P5点有四个波带的光强被抵消，产生第二级明纹， 但是，透光面积（半波带面积）减少，条纹亮度比第一级明纹暗。
bsin 0 0
各光线等光程,会聚在中央(透镜主光轴)叫中央明纹
A
A b a
BC B
P
P0
中央
明纹
BC=aSin
b sin 2k (k 1, 2,) 暗纹
2
b sin (2k 1) (k 1, 2,) 明纹
2
b sin 0
中央明纹
k:条纹级次,与半波带个数m的关系,
k级暗纹 m 2k个半波带
x
2级明纹 1级明纹
明纹位置
k
1得 :
x1
3 f
2b
两条，
1 2
其它各级明纹也两条，对称分布中央明纹两侧。 3
I
1级明纹
2级明纹
x k f (k 1, 2,) 暗纹中心
b
x (2k 1) f (k 1, 2,) 明纹中心
2b x 0 中央明纹
中央明纹宽度：两个一级暗纹间距。
l0
2x1
多缝干涉
k=3 光栅衍射
k=2
讨 论 光栅方程：d sin k (k 0,1, 2,L ) k:主极大级次 若λ给定,则k正比于sin, 观察屏上能看到的最高级次为:
大学物理光栅衍射
数与波长、 狭缝间距和狭缝数量的关系。
结论总结
根据分析结果，总结光栅衍射的规律和特点，并得出结论。
04
光栅衍射的应用实例
光学仪器制造
光学仪器制造中，光栅衍射技术被广泛应用于透镜、反射镜、棱镜等光学元件的 检测和校正。通过光栅衍射，可以测量光学元件的表面形貌、角度、折射率等参 数，确保其光学性能的准确性和稳定性。
VS
在光学计量领域，光栅衍射可以用于 测量各种光学元件的尺寸、角度和光 学性能参数，如透镜的焦距、棱镜的 角度等。此外，在光谱分析、光学干 涉等领域，光栅衍射也具有广泛的应 用。
光学信息处理
光栅衍射在光学信息处理中具有重要的应用。例如，在全息成像中，光栅衍射可以用于记录和再现全息图，从而实现三维图 像的记录和再现。
光子晶体和负折射材料
光子晶体和负折射材料在光栅衍射领域的应用研究，有望 为新型光学器件和光子调控技术提供新的思路和方法。
非线性光学效应
利用光栅衍射研究非线性光学效应，如倍频、和频等，有 助于深入理解光与物质相互作用机制，开拓新的光学应用 领域。
THANKS FOR WATCHING
感谢您的观看
光栅衍射的实验方法
实验设备与器材
01
02
03
04
单色光源
用于提供单一波长的光束，如 激光。
光栅
具有多个平行等间距狭缝的透 明板，用于产生衍射现象。
屏幕
用于观察衍射图样。
测量工具
用于测量光栅的参数，如狭缝 间距和狭缝数量。
实验步骤与操作
安装光栅
将光栅放置在合适的位置，确 保单色光源的光束能够照射在 光栅上。
在光学计算中，光栅衍射可以通过对光的衍射进行编程和控制，实现各种复杂的光学计算和信息处理任务。此外，在光学加 密、光学图像处理等领域，光栅衍射也具有广泛的应用。
结论总结
根据分析结果，总结光栅衍射的规律和特点，并得出结论。
04
光栅衍射的应用实例
光学仪器制造
光学仪器制造中，光栅衍射技术被广泛应用于透镜、反射镜、棱镜等光学元件的 检测和校正。通过光栅衍射，可以测量光学元件的表面形貌、角度、折射率等参 数，确保其光学性能的准确性和稳定性。
VS
在光学计量领域，光栅衍射可以用于 测量各种光学元件的尺寸、角度和光 学性能参数，如透镜的焦距、棱镜的 角度等。此外，在光谱分析、光学干 涉等领域，光栅衍射也具有广泛的应 用。
光学信息处理
光栅衍射在光学信息处理中具有重要的应用。例如，在全息成像中，光栅衍射可以用于记录和再现全息图，从而实现三维图 像的记录和再现。
光子晶体和负折射材料
光子晶体和负折射材料在光栅衍射领域的应用研究，有望 为新型光学器件和光子调控技术提供新的思路和方法。
非线性光学效应
利用光栅衍射研究非线性光学效应，如倍频、和频等，有 助于深入理解光与物质相互作用机制，开拓新的光学应用 领域。
THANKS FOR WATCHING
感谢您的观看
光栅衍射的实验方法
实验设备与器材
01
02
03
04
单色光源
用于提供单一波长的光束，如 激光。
光栅
具有多个平行等间距狭缝的透 明板，用于产生衍射现象。
屏幕
用于观察衍射图样。
测量工具
用于测量光栅的参数，如狭缝 间距和狭缝数量。
实验步骤与操作
安装光栅
将光栅放置在合适的位置，确 保单色光源的光束能够照射在 光栅上。
在光学计算中，光栅衍射可以通过对光的衍射进行编程和控制，实现各种复杂的光学计算和信息处理任务。此外，在光学加 密、光学图像处理等领域，光栅衍射也具有广泛的应用。
大学物理(11.8.2)--光栅衍射
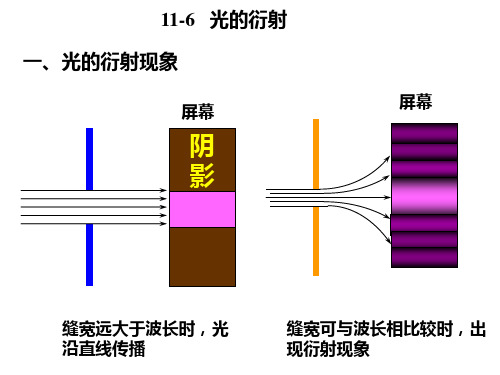
第八讲 光栅 光栅衍射第八讲 光栅 光栅衍射一、光栅衍射现象二、光栅方程三、屏上明条纹的位置四、缺级现象五、光栅光谱一、光栅衍射现象1、光栅：d反射光栅d透射光栅大量等宽等间距的平行狭缝(或反射面)构成的光学元件。
它能等宽、等距地分割入射光的波阵面d = a + b2、光栅衍射光栅衍射是多光束干涉与夫琅禾费单缝衍射的综合结果：来自不同缝的相干光的叠加是多光束干涉，而同一条缝的波阵面上各点发出的衍射光的叠加是单缝衍射。
一系列又窄又亮的明纹也叫主极大多光束干涉单缝衍射光栅衍射：受单缝衍射调制的多光束干涉。
光栅衍射sin θ0I 单I 0单-2-112(λ/a )单缝衍射光强曲线I N 2I 0单48-4-8sin θ(λ/d )单缝衍射 轮廓线光栅衍射光强曲线sin θN 24-8-48(λ/d )多光束干涉光强曲线4 4N d a ,==主极大次极大相邻主极大之间有3个暗纹，2个次级大7光栅狭缝条数越多，明纹越细亮(a)1条缝(f)20条缝(e)6条缝(c)3条缝(b)2条缝(d)5条缝二、光栅方程 0屏fxab()a b +sin θθ()sin a b θ+相邻两缝光线的光程差：= 0123()sin ,,,a b k k θλ+=ﾱﾱﾱK ，光栅方程 明纹、主极大、谱线012sin d k k ,,,θλ==ﾱﾱKoP fScreenLendλθd sin θdθ三、屏上明条纹的位置xtan x f θ=θθθtg sin ≠≠,2,1,0sin ±±==k k d ，λθ单缝衍射光强为零的位置：,3,2,1 sin ±±±=''='k k a ，λθ光栅衍射主极大（明纹）所缺级次：k ad k '=多光束干涉主极大位置：四、缺级现象,3,2,1 ,±±±='k −− k 只能取整数如果某一θ 角同时满足这两个方程，则光栅衍射中k 级主极大消失−− 缺级现象3=da λλaλ2dλ2d λ缺级缺级缺级缺级,2,1,0sin ±±==k k d ，λθ a sin k k ,,,θλﾱﾱ==ﾱﾱﾱ123，例题：用波长为λ=600nm 的单色光垂直照射光栅，观察到第二级明纹出现在sin θ =0.20处，第四级缺级。
大学物理 衍射2(光栅衍射)
222?0sinsinsinsinsinsinsin????????????????????????bbaabanii18222?0sinsinsin2sinsin????????????????????babai222?0sinsinsincossinsin2sin????????????????????????bababaisin?cossin?4222?0??di?22?20sin2cos4????i19式中
(a +b)sin θ1 = λ
θ1 = arcsin( ±λ / d) = arcsin( ±0.12) ≈ 0.12
(2)可见k的最大可能值对应 (2)可见k的最大可能值对应sinθ=1. 可见 的最大可能值对应sinθ=1.
kmax = ±
d sin π / 2
λ
= ±8.3
K只能取整数，故取 =8，总共可有 只能取整数，故取k ，总共可有2k+1=17条明纹 条明纹. 只能取整数 条明纹 是指中央明纹） （加1是指中央明纹）再考虑缺级 是指中央明纹 再考虑缺级,d=3a,故±3,±6将 故 3,± 缺级.实际将观察到17 4=13条光谱线 17条光谱线. 缺级.实际将观察到17-4=13条光谱线.
1
广义地,任何具有空间周期性的结构,都可作为光栅. 广义地,任何具有空间周期性的结构,都可作为光栅. 分类:透射光栅、反射光栅、阶跃光栅、全息光栅… 分类 透射光栅、反射光栅、阶跃光栅、全息光栅 透射光栅 作用:色散 分光 光谱分析研究. 作用 色散(分光 光谱分析研究 色散 分光),光谱分析研究 2.光栅衍射图样的形成 光栅衍射图样的形成 光栅衍射图样是由来自每一个单缝上许多子波 以及来自各单缝对应的子波相干叠加而形成。因此， 以及来自各单缝对应的子波相干叠加而形成。因此， 它是单缝衍射和多缝干涉的总效果。 它是单缝衍射和多缝干涉的总效果。
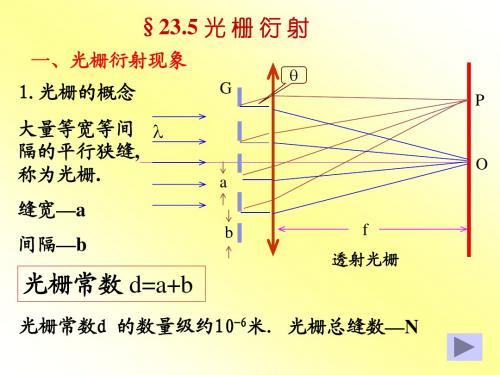
(a +b)sin θ1 = λ
θ1 = arcsin( ±λ / d) = arcsin( ±0.12) ≈ 0.12
(2)可见k的最大可能值对应 (2)可见k的最大可能值对应sinθ=1. 可见 的最大可能值对应sinθ=1.
kmax = ±
d sin π / 2
λ
= ±8.3
K只能取整数，故取 =8，总共可有 只能取整数，故取k ，总共可有2k+1=17条明纹 条明纹. 只能取整数 条明纹 是指中央明纹） （加1是指中央明纹）再考虑缺级 是指中央明纹 再考虑缺级,d=3a,故±3,±6将 故 3,± 缺级.实际将观察到17 4=13条光谱线 17条光谱线. 缺级.实际将观察到17-4=13条光谱线.
1
广义地,任何具有空间周期性的结构,都可作为光栅. 广义地,任何具有空间周期性的结构,都可作为光栅. 分类:透射光栅、反射光栅、阶跃光栅、全息光栅… 分类 透射光栅、反射光栅、阶跃光栅、全息光栅 透射光栅 作用:色散 分光 光谱分析研究. 作用 色散(分光 光谱分析研究 色散 分光),光谱分析研究 2.光栅衍射图样的形成 光栅衍射图样的形成 光栅衍射图样是由来自每一个单缝上许多子波 以及来自各单缝对应的子波相干叠加而形成。因此， 以及来自各单缝对应的子波相干叠加而形成。因此， 它是单缝衍射和多缝干涉的总效果。 它是单缝衍射和多缝干涉的总效果。
大学物理：12-10 光栅衍射
红 760nm 7.6 107 m
根据光栅方程 (a b)sin k
对第k级光谱，角位置从 到k紫
光谱，即要求 的第(k+紫1)级纹在
，亦即：
k紫 k红
，要k红产生完整的 的第k级红条纹之后
由
(a b)sink红 k红
(a b)sink 1 （k 1）紫
得
k红 (k 1)
ab
ab
5.09取
k2
5
所以斜入射时，总共有 k1 k2 条1明纹7 。
（3）对光栅公式两边取微分
(a b) coskdk kd
波长为 及 第k级d的两条纹分开的角距
离为
d d k k (a b) cos k
光线正入射时，最大级次为第3级，相应的
角位置3 为
3 sin
1
(
) k
ab
sin
( ) 1 3589.3109 2106
§12.10 光栅衍射 一、光栅（grating）
光栅是现代科技中常用的重要光学元件。光通 过光栅衍射可以产生明亮尖锐的亮纹，复色光入射 可产生光谱，用以进行光谱分析。
1、光栅的概念
光栅是由大量的等宽等间距的平行狭缝 （或反射面）构成的光学元件。
从广义上理解，任何具有空间周期性的衍射屏， 都可叫作光栅。
（ 58n9m.3），问
（1）平行光线垂直入射时； （2）平行光线以入射角30入射时，最多能看见第几级条
纹？总共有多少条条纹？
（3）由于钠光谱线实际上是1 589.及0nm 589.6nm
两条谱线的平均波长，求在正入射时最高级条纹此 双线分开的角距离及在屏上分开的线距离。设光栅 后透镜的焦距为2m.
k (a b)(sin sin )
11-9衍射光栅(大学物理)
第五版
1111-9
衍射光栅
例如 二级光谱重叠部分光谱范围
(b + b ' ) sin θ = 3λ紫
(b + b' ) sin θ = 2λ
3 λ = λ紫 = 600 nm 2
λ = 400 ~ 760 nm
二级光谱重叠部分: 二级光谱重叠部分:
600 ~ 760 nm
第十一章 光学
9
物理学
第五版
物理学
第五版
1111-9
衍射光栅
一
光栅
衍射角
等宽度,等距离的狭缝排列起来的光学元件. 等宽度,等距离的狭缝排列起来的光学元件 的狭缝排列起来的光学元件
L
P
QθBiblioteka of第十一章 光学
1
物理学
第五版
1111-9
衍射光栅
二 光栅衍射条纹的形成
衍射角
θ
b b' b +b '
光栅常数
(b+ b' ) sin θ
( k = 0,1, 2, )
第十一章 光学
3
物理学
第五版
1111-9
衍射光栅
讨 论
(b + b' ) sin θ = ± kλ
( k = 0,1,2, )
光强分布
I
3λ 2λ λ
0
λ 2λ 3λ
(b + b' ) sin θ
第十一章 光学
4
物理学
第五版
1111-9
衍射光栅
条纹最高级数
kλ sin θ k = ± b + b'
θ1 = 51.26
1111-9
衍射光栅
例如 二级光谱重叠部分光谱范围
(b + b ' ) sin θ = 3λ紫
(b + b' ) sin θ = 2λ
3 λ = λ紫 = 600 nm 2
λ = 400 ~ 760 nm
二级光谱重叠部分: 二级光谱重叠部分:
600 ~ 760 nm
第十一章 光学
9
物理学
第五版
物理学
第五版
1111-9
衍射光栅
一
光栅
衍射角
等宽度,等距离的狭缝排列起来的光学元件. 等宽度,等距离的狭缝排列起来的光学元件 的狭缝排列起来的光学元件
L
P
QθBiblioteka of第十一章 光学
1
物理学
第五版
1111-9
衍射光栅
二 光栅衍射条纹的形成
衍射角
θ
b b' b +b '
光栅常数
(b+ b' ) sin θ
( k = 0,1, 2, )
第十一章 光学
3
物理学
第五版
1111-9
衍射光栅
讨 论
(b + b' ) sin θ = ± kλ
( k = 0,1,2, )
光强分布
I
3λ 2λ λ
0
λ 2λ 3λ
(b + b' ) sin θ
第十一章 光学
4
物理学
第五版
1111-9
衍射光栅
条纹最高级数
kλ sin θ k = ± b + b'
θ1 = 51.26
大学物理-第五节 光栅衍射
四 主极大的缺级 如果某主极大的位置 同时又是单缝衍射极小位置 则该衍射角同时满足两个光程差公式
d sin m 和 asin k
结果:
由于单缝衍射满足极小
A( ) 0
所以使得这一级主极大无法出现
这一现象叫主极大缺级
从 d sin m 和 asin k
得
d m
ak
缺级满足关系
m d k (k 1,2,) a
a
5000
2 104
0
A
0 25
（3）由光栅公式
I
d sin k
k 4 sin 0 25 0
d
4 5000
8 104
0
A
0 25
或由缺级条件： d 4 a
0
d 4a 8104 A
sin 0.25
0、1、 3
0
例3 入射光 5000A ，由图中衍射光强分布确定
(1) 缝数 N = ?
I
(2) 缝宽 a = ?
(3) 光栅常数 d = a+b = ? 0
sin 0.25
解： （1）由相邻主极大之间有N-1条暗纹，N-2条 次极大可知：N＝5。
（2）由单缝衍射暗纹公式 a sin k k 1 sin 0 25
d sin 3紫
d sin 2
400 ~ 760nm
3 2
紫
600nm
二级光谱重叠部分:
600 ~ 760nm
用途——光谱分析
如果光源发出的是白光，则光栅光谱中除零级 近似为一条白色亮线外，其它各级亮线都排列成连 续的光谱带。由于电磁波与物质相互作用时，物质 的状态会发生变化，伴随有发射和吸收能量的现象， 因此关于对物质发射光谱和吸收光谱的研究已成为 研究物质结构的重要手段之一。
大学物理 光栅衍射
K
P
E2
铅板 单晶片的衍射 1912年劳厄 1912年劳厄 悚
<
E1
劳厄斑点
照 像 底 片 单晶片
1913年英国布拉格父子提出了一种解释Ｘ射线 年英国布拉格父子提出了一种解释Ｘ 年英国布拉格父子提出了一种解释 衍射的方法，给出了定量结果，并于1915年荣获物 衍射的方法，给出了定量结果，并于 年荣获物 理学诺贝尔奖． 理学诺贝尔奖． 布拉格反射 入射波 散射波 晶格常数d 晶格常数 掠射角θ
I1 = 0 I = N 2 I1 = 0
该主明纹不出现——缺级 缺级 该主明纹不出现
光栅衍射图样的特点
1、主极大条件
r r A A 1 2
A= NA 1
r A N r A
δ = 2kπ，β＝kπ
A = NA 1
I = N 2 I1
亮度高
(k = 0， 1， 2 L) ± ±
π d sin ϕ β = = kπ λ
o
d = a + b = 10 −5 m
d sin ϕ = kλ
sin ϕ1 =
k = 1:
λ1 = 4 ×10 m
−7
λ1
d
= 0 ⋅ 04
= 0 ⋅ 07
λ2 = 7 ×10 −7 m
sin ϕ 2 =
λ2
d
∆x = f ( tgϕ 2 − tgϕ1 ) ≈ f (sin ϕ 2 − sin ϕ1 ) = 3(cm )
O
sinϕ
O
sinϕ
例： 一平行衍射光栅，每厘米刻 一平行衍射光栅，每厘米刻1000条，用可见光 条 垂直入射，缝后透镜焦距f 垂直入射，缝后透镜焦距 = 100cm 1、光栅衍射第一级完整可见光谱所占宽度 、 2、证明第二、三级光谱重叠 、证明第二、 3、 入射， 用红光λ = 7000 A 入射，b = 3a, 最多看到主明纹条数 解： 1.