计量经济学第八章
计量经济学八章06.5(XS)

违反经典假设的线性回 时间序列分析:介绍了 归模型:探讨了当经典 时间序列数据的特性、 假设不满足时,如何对 平稳性检验、ARIMA模 线性回归模型进行修正, 型等内容,是计量经济 包括异方差性、自相关 学中处理时间序列数据 性、多重共线性等问题 的重要方法。 的处理方法。
面板数据分析:阐述了 面板数据的结构、特点 以及固定效应模型、随 机效应模型等面板数据 分析方法,为处理多维 数据提供了有效工具。
ARIMA模型法
自回归移动平均模型,是一种时间序列预测方法 ,可以消除自相关的影响并进行预测。
05
多重共线性问题探讨
多重共线性概念及产生原因
多重共线性概念
经济变量相关的共同趋势
多重共线性是指在多元线性回归模型中, 解释变量之间存在高度线性相关关系,导 致模型估计失真或难以准确估计的现象。
时间序列数据中,不同经济变量可能受共 同因素影响,表现出高度相关性。
数据具有趋势性,即数据可能呈现出长期上升或下降 的趋势。
时间序列数据特点与处理方法
01
数据具有季节性,即数据可能呈现出周期性变化,如季度、 月度等。
02
时间序列数据处理方法
03
缺失值处理:对于时间序列数据中的缺失值,可以采用插值 法、平均值法等方法进行处理。
时间序列数据特点与处理方法
异常值处理
对于时间序列数据中的异常值,可以采用标准差法、箱线图法等方法进行识别和处理。
02
计量经济学与经济 学的关系
计量经济学是经济学的一个分支, 旨在为经济学提供定量分析和实 证研究的工具和方法。
03
计量经济学的研究 对象
主要研究经济变量之间的关系, 以及经济政策对经济变量的影响。
章节概述与学习目标
第八章计量经济学

第八章异方差 (1)第一部分背景资料 (1)一、学习目的和要求 (1)二、本章要点........................................ 错误!未定义书签。
第二部分练习题 (2)一、名词解释 (2)二、简答题 (2)三、计算题 (2)第三部分参考答案 (5)一、名词解释 (5)二、简答题 (7)三、计算题 (9)第八章异方差第一部分学习目的和要求经典线性回归模型的一个重要假设是干扰项具有相同的方差。
如果该假设不满足,就可能出现异方差问题。
本章主要讲述了异方差的基本理论、检验方法和校正问题。
主要需要掌握并理解以下几个问题:1.异方差的概念;2.出现异方差的原因;3.存在异方差情况下用OLS估计的后果;4.异方差的检验,主要是图形检验、戈德费尔德—匡特检验、帕克检验、White检验、Glejser检验和布鲁尔什—培甘检验;5.广义最小二乘法的概念和步骤;6.用GLS对一般形式的异方差模型估计的校正。
σ。
如果此假定不7.经典线性回归模型的一个关键性的假定是干扰项都有相同的方差2成立,则说明有异方差。
8.异方差并不破坏OLS估计量的无偏性和一致性。
9.在异方差条件下的得到的估计量不再是最小方差或有效的,即不再是BLUE。
σ已知,那么加权最小二乘法可给出BLUE估计量。
10.如果相异的误差方差2i11.当异方差出现时,OLS估计量的方差并不由常用的OLS公式给出。
如果我们一味地使用OLS公式,则以这些公式为依据的t检验和F检验可能严重误导,以致引出错误的结论。
12.检验异方差的方法有若干种,但在不同的情况下使用哪一种方法最有效,现在并没有结论。
13.即使异方差受到怀疑并已被检验出来,其校正也很困难,我们常用广义最小二乘法进行校正。
第二部分 练习题一、名词解释1.异方差 2.图形检验3.戈德费尔德—匡特检验 4.帕克检验 5.White 检验 6.Glejser 检验 7.广义最小二乘法二、简答题1.异方差的存在对下面各项有何影响? (1)OLS 估计量及其方差; (2)置信区间;(3)显著性t 检验和F 检验的使用。
计量经济学第八章 联立方程模型

第一节 联立方程模型的概念
迄今为止,我们的介绍都是围绕单方程模型进行的 ,可是,很多经济理论是建立在一组经济关系上的, 其数学模型是一个方程组,称为多方程模型或联立方 程模型(simultaneous equations model)。
熟悉的例子有市场均衡模型、商品需求方程组和宏 观经济模型等。联立方程模型用于描述整个经济系统 或其子系统。
如果光是需求函数和供给函数,情况还简单一点, 问题在于,如果
Qt = α + β Pt + ut Qt = + Pt + vt
两式成立,则对于任意常数λ 和μ (λ +μ ≠0),上 述两式的线性组合
( ) Q t ( ) ( ) P t (u t v t )
(8)
Yt 3 4It v2t
(9)
其中诸π 为结构参数的函数,v1t 和 v2t 是简化式方程的扰动项,是结构
式方程扰动项的函数。
对第二个例子,我们也不难写出其简化式如下:
Wt 10 11UN t 12Rt 13M t v1t Pt 20 21UN t 22Rt 23M t v2t
上述两例都是按结构式的形式给出的。
2. 简化式(reduced form)
我们的第一个例子,收入决定模型:
Ct= Yt u t
Yt Ct It
若将模型中的内生变量C t 和Yt 用外生变量和扰动项来表示,则得到该
模型的简化式如下:
Ct
1
1
I
t
ut 1
一般来说,如果我们能够用经济理论或额外信息 为联立方程组施加约束条件,则可以消除识别问题 。这些约束条件可以采取各种形式,但最常用的是 所谓的“零约束”,即规定某些结构参数为0,也就 是说,某些内生变量和外生变量不出现在某些方程 之中。
计量经济学课件第8章

( x 2 i )( x 3 i ) ( x 2 i x 3 i )
2 2
2
5
如果X3与X2存在完全共线性,即 X 3 i X 2 i
X
3i
则:
X (
2
2i
, x3i x 2 i y i x 2 i )( x 2 i ) ( y i x 2 i )( x 2 i )
2
( y i x 2 i )( x 3 i ) ( y i x 3 i )( x 2 i x 3 i )
2
( x 2 i )( x 3 i ) ( x 2 i x 3 i )
2 2
2
3
( y i x 3 i )( x 2 i ) ( y i x 2 i )( x 2 i x 3 i )
其中, r 为 X 和 X 的样本相关系数。
12
20
8.4
多重共线性的补救措施
8.4.1 什么也不做
理由一、如果t统计量仍然显著,参数的符号也和预期 的一致,则不用补救;
理由二、剔除变量有可能导致设定偏误,后果可能更 严重; 理由三、出于理论上的考虑,重新回归会导致设定误 差。多重共线性本质上由样本引起。 所以,什么也不做,除非是极其严重的多重共线性
性的变量的参数估计几乎不受影响。
如果目的是预测,则多重共线性不是问题,R2 值越高,预测越准。
15
8.2.2 关于多重共线性的后果的两 个例子P142-144
16
8.3 多重共线性的诊断
克曼塔(Kmenta)的忠告: 1、多重共线性是一个程度问题而不是有无的问题 2、多重共线性是一种样本现象也是一种理论现象。 给定方程的多重共线性的严重程度随样本的不同 而不同;对于给定的样本,依赖数据导向技术来判断 多重共线性的严重程度. 而解决多重共线性的策略则依赖于方程的理论基础, 即找到一组理论上相关并且统计上不存在多重共线 性的变量.
计量经济学第八章

计量经济学夏凡第八章动态计量模型基础第一节分布滞后模型第二节单位根检验第三节协整与误差修正模型计量经济学夏凡引言⏹传统的时序模型●一般先从已知相关理论出发设定模型形式,再由样本数据估计模型中的参数⏹这种方法使建模过程对相关理论有很强的依赖性⏹动态计量经济学模型●20世纪70年代末,以英国计量经济学家Hendry为代表,将理论和数据信息有效结合,提出了动态计量经济学模型的理论与方法●为时序模型带来了重要的发展量经济学夏凡第一节分布滞后模型⏹几何分布滞后模型⏹多项式分布滞后模型⏹自回归分布滞后模型量经济学夏凡基本概念⏹分布滞后模型●⏹如果p是有限数,称为有限分布滞后模型⏹如果p是无限数,称为无限分布滞后模型npptxxxytptpttt,,2,111++=+++++=--εβββα计量经济学夏凡基本概念(续)⏹分布滞后模型的两个问题●由于存在滞后值,则要损失若干个自由度⏹如果滞后时期长,而样本较小,自由度损失就较大,有时甚至无法进行估计●通常一个变量的滞后变量之间共线性问题严重,影响估计量的精度⏹解决方法●对系数施加约束条件,减少待估参数的数目计量经济学夏凡几何分布滞后模型⏹几何分布滞后模型●又称Koyck滞后模型●反映变量的影响程度随滞后期的延长而按几何级数递减⏹经济变量间的因果关系,往往随着时间间隔的延伸而逐渐减弱●模型⏹●()1221ti ititttttxxxxyελβαεβλλββα++=+++++=∑∞=---1<λ计量经济学夏凡几何分布滞后模型(续1)⏹模型的第二种表达形式●⏹对(1)式取一期滞后,并两边同乘λ得●⏹(1)式减去(2)式得●⏹令,即可得到模型的第二种表达式●用y t-1代替了x的滞后变量⏹减小了多重共线性的程度()ttttuyxy+++-=-11λβλα()212211----++++=ttttxxyλεβλλβλαλ()111---++-=-tttttxyyλεεβλαλ1--=tttuλεε计量经济学夏凡几何分布滞后模型(续2)⏹模型的估计●模型中的随机扰动项通常存在一阶负相关关系⏹参数估计变得较复杂●可采用工具变量法和广义差分法相结合的估计方法计量经济学夏凡多项式分布滞后模型⏹多项式分布滞后模型●为解决几何分布滞后模型存在的问题,Almon提出了多项式分布滞后(PDL:Polynomial Distributed Lag)模型⏹用多项式表示滞后变量系数βi和滞后长度i的关系⏹一般,多项式阶数不超过3次计量经济学夏凡多项式分布滞后模型(续1)⏹对于模型●其解释变量之间存在多重共线性,不能采用OLS估计●将βi分解为⏹●其中,且●即将每个参数用一个多项式表示()()()()pqpipipi qqi<-++-+-+=ααααβ221pi,,2,1,0=()()Nkkpkpppp∈⎩⎨⎧-==-=1222/12/()30tpi ititxyεβα++=∑=-计量经济学夏凡多项式分布滞后模型(续2)⏹模型的估计●(3)式可改写为⏹●其中●则(4)式实际上比(3)式少了p-q个参数●可对模型施加约束条件⏹近端(near end)约束和远端(far end)约束⏹应用时,可同时指定上述两种约束,或其中之一,也可不含约束条件()4110tqtqtttzzzyμαααα+++++=()()qjxpizitjpijt,,1,0=-=-=∑计量经济学夏凡多项式分布滞后模型(续3)⏹PDL模型的确定因素●滞后期p、多项式次数q和约束条件⏹PDL模型的特点●优点⏹减少了待估参数,因此减小了多重共线性的程度⏹方程的变换并没有改变干扰项的形式,没有引入自相关问题,可用OLS直接估计变换后的方程●缺点⏹样本损失没有减少●只有(n-q)个观测值可用于估计计量经济学夏凡多项式分布滞后模型(续4)⏹操作命令●ls y x1 x2pdl(series_name,lags,order,options)⏹lags:代表滞后期p⏹order:表示多项式阶数q⏹options:指定约束类型,没有约束条件时缺省●1:近端约束●2:远端约束●3:同时采用近端和远端两种约束计量经济学夏凡多项式分布滞后模型(续5)⏹[例8-1]某水库1998年至2000年各旬的流量、降水量数据如下所示。
计量经济第八章

线性预测子
线性预测子是广义线性模型中自 变量与参数的线性组合,用于预 测响应变量的数学期望。
广义线性模型的参数估计
1 2 3
最大似然估计
最大似然估计是广义线性模型参数估计的常用方 法,通过最大化似然函数得到参数的估计值。
迭代加权最小二乘法
迭代加权最小二乘法是一种迭代算法,用于求解 广义线性模型的参数估计值,通过不断迭代更新 参数估计值直到收敛。
利用核函数对数据进行局部加权,得 到概率密度的估计,适用于任意形状 的数据分布。
局部加权回归
在回归分析中,通过给不同数据点赋 予不同的权重,使得模型更加关注于 局部数据的拟合效果,从而提高模型 的预测精度。
半参数方法的基本思想
结合参数和非参数方法的特点,既考 虑数据的总体分布,又充分利用数据 的局部信息。
因果推断的方法
因果推断的方法包括回归分析、倾向得分匹配、工具变量法等。
工具变量法和断点回归法
工具变量法
工具变量法是一种用于处理内生性问题的计量经济学方法。 它通过寻找一个与内生解释变量相关、但与误差项不相关的 工具变量,用工具变量替代内生解释变量进行回归分析,从 而得到一致的估计量。
断点回归法
断点回归法是一种非参数回归方法,适用于处理具有断点特 征的数据。它通过比较断点两侧的数据差异来推断因果关系 ,可以有效避免参数回归中可能存在的模型误设问题。
因果分析法
因果分析法是通过研究时间序列 与其他相关因素之间的因果关系, 建立相应的数学模型进行预测的 方法。常用的因果分析法包括回 归分析、计量经济模型等。
05 面板数据分析
CHAPTER
面板数据的基本概念
面板数据的定义
面板数据是指在时间序列上取多个截面,在这些截面上同时选取样 本观测值所构成的样本数据。
计量经济学第八章完整课件

对于矩阵形式: Y=X+
采用工具变量法(假设X2与随机项相关,用工具 变量Z替代)得到的正规方程组为:
ZY ZXβ
参数估计量为:
β~ (ZX)1 ZY
其中
1 1
X
11
X 12
Z
Z1
Z2
X k1 X k 2
1
X
1n
Zn
X kn
称为工具变量矩阵
3、工具变量法估计量是一致估计量
工具变量法是GMM的一个特例。 6、要找到与随机扰动项不相关而又与随机解释 变量相关的工具变量并不是一件很容易的事
可以用Xt-1作为原解释变量Xt的工具变量。
五、案例——中国居民人均消费函数
例4.4.1 在例2.5.1的中国居民人均消费函数的估 计中,采用OLS估计了下面的模型:
CONSP 0 1GDPP
通常把这种过去时期的,具有滞后作用的变量 叫做滞后变量(Lagged Variable),含有滞后变量 的模型称为滞后变量模型。
滞后变量模型考虑了时间因素的作用,使静态 分析的问题有可能成为动态分析。含有滞后解释变 量的模型,又称动态模型(Dynamical Model)。
1、滞后效应与与产生滞后效应的原因
Cov( X 2i, i ) E(x2i i ) 0 Cov( X 2i, is ) E(x2i is ) 0
s0
3. 随机解释变量与随机误差项同期相关 (contemporaneously correlated)。
Cov( X 2i, i ) E(x2i i ) 0
二、实际经济问题中的随机解释变量问题
第一步,用OLS法进行X关于工具变量Z的回归:
Xˆ i ˆ0 ˆ1Zi
《计量经济学》第8章数据
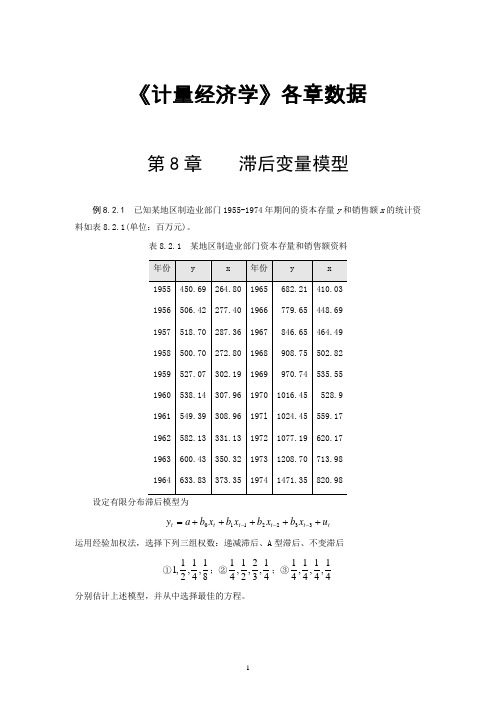
《计量经济学》各章数据第8章 滞后变量模型例8.2.1 已知某地区制造业部门1955-1974年期间的资本存量y 和销售额x 的统计资料如表8.2.1(单位:百万元)。
表8.2.1 某地区制造业部门资本存量和销售额资料设定有限分布滞后模型为t t t t t t u x b x b x b x b a y +++++=---3322110运用经验加权法,选择下列三组权数:递减滞后、A 型滞后、不变滞后①81,41,21,1;②41,32,21,41;③41,41,41,41 分别估计上述模型,并从中选择最佳的方程。
例8.2.2 表8.2.3给出了某企业产品1988-2007年的产量y 和销售量x 的资料。
试利用分布滞后模型建立产量关于销售量的回归模型。
表8.2.3 某企业产品1988-2007年产量和销售量资料例8.3.1 表8.3.1给出了1994-2005年某地区居民消费y 与可支配收入x 的调查数据。
假定本期消费不仅与本期收入有关,而且与以前各期收入有关,此时消费函数模型有如下形式t t t t t u x b x b x b a y +++++=-- 22110其中,t y 与t x 分别代表第t 期的消费和收入。
假定随机项t u 满足全部经典假定,试用库伊克模型估计这一消费模型。
表8.3.1 某地区居民消费与收入调查数据8.5 案例分析表8.5.1给出了某地区消费总额y(亿元)和货币收入总额x(亿元)的年度资料,试分析消费同收入的关系。
表8.5.1 某地区消费总额和货币收入总额年度资料思考与练习14.表1给出了某行业1975-1994年的库存额y 和销售额x 的资料。
试利用分布滞后模型:t t t t t t u x b x b x b x b a y +++++=---3322110建立库存函数(用2次有限多项式变换估计这个模型)。
表1 某行业1975-1994年库存额和销售额资料15.表2给出了美国1970-1987年间个人消费支出(C )与个人可支配收入(I )的数据(单位:10亿美元,1982年为基期)表2 美国1970-1987年个人消费支出与个人可支配收入数据t t t u I a a C ++=21 t t t t u C b I b b C +++=-1321请回答以下问题:(1)估计以上两模型;(2)估计边际消费倾向(MPC )17.表3给出了1970-1991年美国制造业固定厂房设备投资y 与销售额x 的相关数据(单位:亿元)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多元回归:
TSS y ' y nY 2
ˆ ESS ' X ' y nY 2 ˆ ˆ ˆ RSS u ' u y ' y ' X ' y
ˆ ( ' X ' y nY 2 ) /(k 1) F ˆ ( y ' y ' X ' y) /(n k )
回归方程:yt = 1 + 2x2t + 3x3t + 4x4t + ut 我们希望检验: 3+4 = 1: 约束回归 • yt = 1 + 2x2t + 3x3t + 4x4t + ut • s.t. 3+4 = 1
3+4 = 1 4 = 1- 3 yt = 1 + 2x2t + 3x3t + (1-3)x4t + ut 整理,得 (yt - x4t) = 1 + 2x2t + 3(x3t - x4t) + ut
( RUR RR ) / m F 2 (1 RUR ) /(n k )
16
在F-检验中确定约束个数
例 : H0: hypothesis 1 + 2 = 2 2 = 1 and 3 = -1 2 = 0, 3 = 0 and 4 = 0
约束个数m 1 2 3
不能用F-检验来检验非线性的假设, 如:H0: 2 3 = 2 or H0: 2 2 = 1
计量经济学
主讲人:薛明皋
2013年7月19日
1
第8章 多元回归分析:推断问题
§8-1 偏回归系数的假设检验 §8-2 总显著性检验 §8-3 回归系数相等的检验 §8-4 约束回归 §8-5 结构稳定性检验:邹至庄检验
§8-6 预测
2
§8-1 偏回归系数的假设检验:t 检验
Yi 1 2 X i 2 K X iK ui
( R新 2 R老 2 ) 自由度 F (1 R新 2 ) 自由度 ( R新 2 R老 2 ) 新回归元个数 (1 R新 2 ) 自由度( n 新模型中的参数个数)
10
其它判据:
F检验可以决定是否在回归方程中增加一个变量。 调整的R2也可以作为选择的标准,目的是使得调 整的R2最大化。 何时引入一个新变量
19
Wald Test: Equation: Untitled Test Statistic F-statistic Chi-square Value 3.779440 3.779440 df (1, 17) 1 Probability 0.0686 0.0519
2、增加变量FLR:
8
从r2->R2,模型的拟合能力增强了。 如何度量这种增量贡献:
问题: FLR的增量贡献在统计上显著吗?
9
1、增量的贡献计算:
( ESS新 ESS老 ) 新回归元个数 RSS新 自由度( n 新模型中的参数个数)
Q2 自由度 F Q4 自由度
2、F比的另一计算式:
(i 1, 2,, n)
检验假设步骤: 1.假设: H0:i=0; H1:i0 (i=1,2…k) 2.给出检验统计量: ˆ 2 t t (n k ) ˆ se( 2 ) 3.给定显著性水平,可得到临界值t/2(n-k),由 样本求出统计量t的数值,通过 |t| t/2(n-k) 或 |t|t/2(n-k) 来拒绝或接受原假设H0,从而判定对应的解释变 3 量是否应包括在模型中。
ˆ ˆ 由 ~ N ( , 2 ( X ) 1 )知 i ~ N ( i , 2 ( X ) ii1 ) X X ˆ i i ~ N (0,1) 1 ( X X )ii ˆ 但是 未知,所以用其估计量 代替,此时有 ˆ ˆ ) i i t ( i ~ t (n k ) 1 ˆ ( X X )ii 检验统计量 H 0 : i 0 ˆ t ( i ) ˆ i 0 ˆ ( X X )
令 Pt = yt - x4t , Qt = x3t - x4t Pt = 1 + 2x2t + 3Qt + ut 就是要估计的约束回归14
在同一样本下,记无约束样本回归模型为: Y X u 受约束样本回归模型为: Y X u r r 于是: ur Y X r X u X r X ( r ) u 受约束样本回归模型的残差平方和RSSR ur ' ur u ' u (r )' X ' X (r ) u ' u u’u为无约束样本回归模型的残差平方和RSSUR 受约束与无约束模型都有相同的TSS 这意味着,通常情况下,对模型施加约束条件会 降低模型的解释能力。但是,如果约束条件为真, 则受约束回归模型与无约束回归模型具有相同的 15 解释能力,RSSR 与 RSSUR的差异将会很小。
H1 : 3 4 或 (3 4 0)
3.构造统计量
ˆ ˆ ( 3 4 ) ( 3 4 ) t ˆ ˆ se( )
3 4
可证明t服从自由度为(n-4)的t分布,其中
ˆ ˆ ˆ ˆ ˆ ˆ se( 3 4 ) var( 3 ) var( 4 ) 2cov( 3 , 4 )
1 ii
ˆ i ˆ ( X X )
1 ii
~ t (n k )
4
§8-2 总显著性检验:F检验
方差分析
方差分析回顾:
Yi i2 ui2 ˆ ˆ 22 xi2 ui2
TSS ESS RSS
F与R2同向变化:R2越大,F值也越大。 当R2=0时,F=0;当R2=1时,F为无穷大; 因此,F检验是回归方程总的显著性的一个度量, 也是R2的一个显著性度量。
检验H0:2= =k=0等价于检验R2=0
7
引进变量是否显著增加ESS
儿童的死亡率(CM)可能同人均GNP(PGNP) 和妇女识字率(FLR)有关。 1、仅对PGNP回归
F ( n k ) ESS n k ESS ( k 1) RSS k 1 TSS ESS nk ESS TSS n k R2 k 1 1 ( ESS TSS ) k 1 1 R 2 R 2 ( k 1) (1 R 2 ) /( n k )
构造 F-检验统计量
可用RSSR - RSSUR的大小来检验约束的真实性 ( RSS R RSSUR ) / m 统计量 F
ˆ ˆ ( uR 2 uUR 2 ) / m uUR 2 /(n k ) ˆ RSSUR /(n k )
m =约束数目,n = 观测数 k =非约束回归中的解释变量数目(含常数项). 上式还可表示为: 2 2
若引入的新变量的系数的t值在绝对值上大于1,调整
的R2就会增加。 或者,当引入新变量的F值大于1时,才会使调整的R2 增加。
何时加入一组变量
当引入的一组新变量的F值大于1时,才会使调整的R2
增加。
11
§8-3 回归系数相等的检验 1.回归模型: Yi 1 2 X 2i 3 X 3i 4 X 4i ui 或 ( 3 4 ) 0 2.检验假设: H 0 : 3 4
2 3 i
( 2 3 ) ( 2 3 ) t t (n k ) ˆ ) ˆ se( 2 3 ˆ ˆ ( 2 3 ) 1 ˆ ˆ ˆ ˆ var( 2 ) var( 3 ) 2cov( 2 , 3 )
13
2、F-检验:非约束回归和约束回归
任何一个可以用t-检验的假设都可以用F-检 验来检验, 反之,则不行。 17 因为t-分布是F-分布的一个特例。
例:柯布-道格拉斯生产函数
用F-检验考参是否存在规模报酬不变效应。 数据见表8.8
18
Dependent Variable: LOG(GDP) Method: Least Squares Date: 12/05/06 Time: 21:18 Sample: 1955 1974 Included observations: 20 LOG(GDP)=C(1)+C(2)*LOG(EMPLOYMENT)+C(3)*LOG(CAPITAL) Coefficient C(1) -1.652419 C(2) 0.339732 C(3) 0.845997 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Std. Error 0.606198 0.185692 0.093352 0.995080 0.994501 0.028289 0.013604 44.55221 t-Statistic -2.725873 1.829548 9.062488 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion Durbin-Watson stat Prob. 0.0144 0.0849 0.0000 12.22605 0.381497 -4.155221 -4.005861 0.425667
一般的F检验方法
1.回归模型: Yi 1 2 X 2i k X ki ui 2.检验假设: H0假设可根据实际情况确定。 如:H0: β2 = β3 H0 : β3 + β4 + β5 = 3 H0 : β3 = β4 = β5 = β6 = 0 3.决策规则: 若计算的F超过Fα(m, n− k),则拒绝原假设; 否则就接受它。
