七年级数学展开与折叠练习 (1)
七年级数学北师大版上册课时练第1章《展开与折叠》 练习测试卷 含答案解析
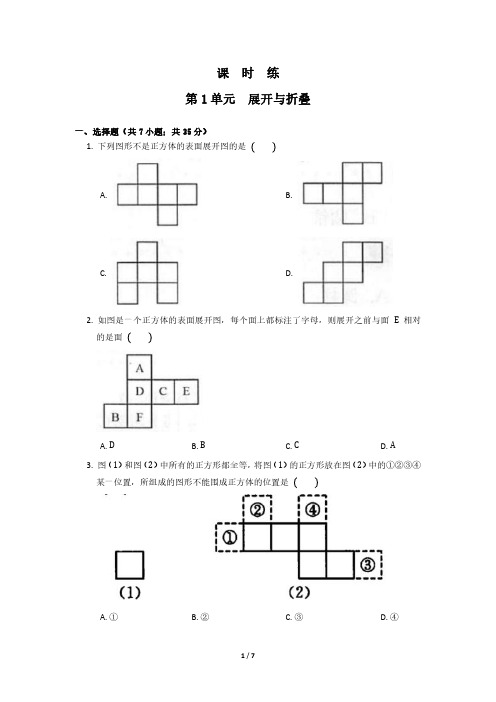
课时练第1单元展开与折叠一、选择题（共7小题；共35分）1.下列图形不是正方体的表面展开图的是 A. B.C. D.2.如图是一个正方体的表面展开图，每个面上都标注了字母，则展开之前与面E相对的是面 A.DB.BC.CD.A3.图（1）和图（2）中所有的正方形都全等，将图（1）的正方形放在图（2）中的①②③④某一位置，所组成的图形不能围成正方体的位置是 A.①B.②C.③D.④4.下图中的平面图形可以看做是正方体的表面展开图的是 A. B.C. D.5.图中的硬纸片经过折叠，能围成一个正方体，这个正方体的2号面的对面是 A.3号面B.4号面C.5号面D.6号面6.下图给定的是纸盒的外表面，下面能由它折叠而成的是 A. B.C. D.7.如图，下面哪一个平面图形是下边正方体的表面展开图 A. B.C. D.二、填空题（共5小题；共25分）8.正方体的表面展开图有种形式．9.如图是正方体的表面展开图，如果a在下面，d在右面，f在前面，那么e在，c在，b在．10.将一个正方体的表面沿某些棱剪开，展开成一个平面图形，至少需要剪开条棱，至多可以剪开条棱．11.将一个正方体的表面沿某些棱剪开，展开成一个平面图形，下列可能的图形有：．12.如图是正方体的展开图，则原正方体相对两个面上的数字之和的最小值是．三、解答题（共4小题；共40分）13.下图是正方体的表面展开图的一部分，请你在这个图形的基础上，添加两个小正方形，使它成为一个完整的正方体的表面展开图．14.我们知道如图不能看做正方体的表面展开图，请你移动其中一个小正方形，使其变为正方体的表面展开图（至少画出三种示意图）．15.如图是一个各面涂了不同颜色的正方体，根据所画的四种情况，回答问题：“红”“绿”“蓝”的对面各是什么颜色?16.图是一些几何体的平面展开图，写出这些几何体的名称．参考答案1.C2.A3.A4.D5.C6.B7.D8.119.上面，后面，左面10.7，711.②③④⑤⑥⑦12.613.答案不唯一，如图所示．14.移动正方形E，放在正方形D下面，如图（1）；移动正方形D，放在正方形E右边，如图（2）；移动正方形F，放在正方形D下面，如图（3）．（其他方法符合题意亦可）15.“红”的对面是“黄”，“绿”的对面是“棕”，“蓝”的对面是“紫”．16.①四棱锥；②三棱锥；③三棱柱；④圆锥．。
展开与折叠 同步练习北师大版七年级数学上册
北师大版七上 1.2 展开与折叠一、选择题（共15小题）1. 如图是一个正方体的表面展开图，若折叠成正方体后相对面上的两个数互为相反数，则x，y，z的值分别为( )A. 2，−3，−10B. −10，2，−3C. −10，−3，2D. −2，3，−102. 如图所示的立体图形，它的展开图是( )A. B.C. D.3. 下列图形中，是圆锥的侧面展开图的为( )A. B.C. D.4. 下列四个图形中是三棱柱的表面展开图的是( )A. B.C. D.5. 如图，如果把一个圆锥的侧面沿图示中的线剪开，则得到的图形是( )A. 三角形B. 圆C. 圆弧D. 扇形6. 如图所示的图形，是下面哪个正方体的展开图( )A. B.C. D.7. 如图中的圆柱体，表面展开后得到的平面图形是( )A. B.C. D.8. 下图所示是一个三棱柱纸盒，在下面四个图中，只有一个是这个纸盒的展开图，那么这个展开图是( )A. B.C. D.9. 如图为一直棱柱，其底面是三边长分别为5，12，13的直角三角形．若下列选项中的图形均由三个长方形与两个直角三角形组合而成，且其中一个为如图所示的直棱柱的展开图，则根据图形中标示的边长与直角符号判断，此展开图为( )A. B.C. D.10. 如图所示的正方体的展开图是( )A. B.C. D.11. 如图，一个几何体上半部为正四棱锥，下半部为立方体，且有一个面涂有颜色，该几何体的表面展开图是( )A. B.C. D.12. 某个几何体的展开图如图所示，该几何体是( )A.长方体B.圆柱体C.球体D.圆锥体13. 一个正方体的六个面上分别写有六个字“建”、“设”、“生”、“态”、“密”、“云”．将这个正方体展开后如图所示，则该正方体在展开前，与“建”字所在面相对的面上的字是( )A. 生B. 态C. 密D. 云14. 如图是某种几何体的表面展开图，这个几何体是( )A. 圆锥B. 球C. 圆柱D. 棱柱15. 如图中，不可能围成正方体的是()A. B.C. D.二、填空题（共10小题）16. 若要使图中平面展开图折叠成正方体后，相对面上两个数之和为6，则x+y=．17. 小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上，下列给出的四个图案中，符合图示胶滚涂出的图案是．（填写序号）18. 一个几何体的表面展开图如图所示，则这个几何体是．19. 长方体的表面沿某些棱剪开，展开成平面图形，共有个形，其中剪的过程中，需要剪条棱．20. 如图是一个没有完全剪开的正方体，若再剪开一条棱，则得到的平面展开图可能是下列六种图中的．（填写字母）21. 下列各图是几何体的表面展开图，请写出对应的几何体的名称．①②③22. 如图是正方体的展开图，则原正方体相对两个面上的数字和的最大值是．23. 如图所示的两个平面图形分别是两种包装盒的展开图，这两个包装盒的形状分别是，．24. 圆柱的侧面展开图是形．25. 一个正方体的展开图已有一部分（如图），还有一个正方形未画，现有10个位置可供选择，请问：放在哪些位置能围成正方体，放在哪些位置不能围成正方体?仔细观察下图，或许你还要动手做做呢！放在可围成正方体，放在不可以围成正方体．三、解答题（共5小题）26. 如图，在一个正方体的上面、前面、右面分别标有数字1，2，3．1的对面标有数字4，2的对面标有数字5，3的对面标有数字6．（1）求与数字3所在平面垂直的面的数字之积．（2）如果与一个面垂直的面上的数字之和是14，那么这个面上的数字是多少?27. 给出一张正方形纸片（见图），要求将其剪拼成一个上、下底面均为正方形的直四棱柱模型，使它的表面积与原正方形的面积相等．请设计一种剪拼方法，在图中用虚线标示，并作简要说明．28. 四棱柱按如图所示粗线剪开一些棱，展成平面图形，请画出平面图．29. 将一个正方体的表面沿某些棱剪开，展成以下平面图形，先想一想，再动手剪．30. 下图是一个几何体的侧面展开图．（1）请写出这个几何体的名称；（2）根据图中所标的尺寸，计算这个几何体的侧面积．答案1. B 【解析】x与10为对面，y与−2为对面，z与3为对面，∴x=−10，y=2，z=−3．2. C3. A【解析】圆锥的侧面展开图是光滑的曲面，没有棱，只是扇形．4. A5. D6. D【解析】根据正方体的展开图可得选D．7. B8. C【解析】把三棱柱纸盒往上打开为上底面，同时展开侧面，上面阴影正好与下面空白在最左边，且三角形垂直于矩形，利用空间想象能力，可以确定，C选项符合该展开图．9. D【解析】A选项中，展开图下方的直角三角形的斜边长为12，不合题意；B选项中，展开图上下两个直角三角形的直角边不能与对应的棱完全重合，不合题意；C选项中，展开图下方的直角三角形的直角边不能与对应的棱完全重合，不合题意；D选项中，展开图能折叠成一个如题图所示的直棱柱，符合题意．10. C【解析】有图案的三个面是相邻的，可以排除B、D．对于A，如果三角形和圆正确的，那么棋盘格的方向反了．11. B【解析】选项A和C中涂有颜色的一个面是底面，不能折叠成题图中的几何体；选项B能折叠成题图中的几何体；D选项中有5个三角形，故不是这个几何体的表面展开图．12. B13. D14. A【解析】圆锥的展开图为一个扇形和一个圆，故这个几何体是圆锥．故选A．15. D【解析】【分析】此题需利用正方体及其表面展开图的特点解答即可得出答案．【解析】解：选项A，B，C折叠后都可以围成一个正方体，只有D折叠后有两个面重合，不能折成正方体．故选：D．【点评】本题考查了平面图形的折叠及正方体的展开图，解决此题的关键是记住正方体展开图的基本类型1−4−1型，2−3−1型，2−2−2型，3−3型．16. 817. （1）18. 四棱锥19. 6，长方，720. A、B、E【解析】将原图沿右底面棱剪开，可得到图A所示形状；将原图沿右侧面开，可得如图B示形状；将原图沿后方底面棱剪开，可得如图E所示形状.21. 圆锥，三棱锥，圆柱22. 8【解析】根据所给出的图形可得：2和6是相对的两个面；3和4是相对两个面；1和5是相对的两个面，则原正方体相对两个面上的数字和最大值是8．23. 长方体，正方体24. 长方25. ①⑦⑧⑨，②③④⑤⑥⑩26. （1）40（2）2或5的正方形，再沿虚线折叠，即可构成一个缺少上27. 在正方形的四个角上剪出四个边长为原正方形边长的14底，而下底为正方形的直四棱柱，而剪下的四个正方形恰好能拼成这个四棱柱的上底，如图所示．28.展成平面图如图所示.29. 分别沿虚线剪开即可．30. （1） 这个几何体是六棱柱．（2） 侧面积 =(2+4)ab =6ab ．。
1.2 展开与折叠 优化训练(第一课时) 2021—2022学年北师大版数学七年级上册
第一章丰富的图形世界第2节展开与折叠（第一课时）一．选择题1．图1是一个小正方体的展开图，小正方体从图2的所示位置依次翻到第1格，第2格，第3格，这时小正方体朝上一面的字是（）A．常B．州C．越D．来2．如图，有一个无盖的正方体纸盒，它的下底面标有字母“M”，若沿图中的粗线将其剪开展成平面图形，这个平面图形是（）A．B．C．D．3．有一个正六面体骰子放在桌面上，将骰子如图所示顺时针方向滚动，每滚动90°算一次，则滚动第2021次后，骰子朝下一面的数字是（）A．5B．4C．3D．24．如图，点A，B是正方体上的两个顶点，将正方体按图中所示方式展开，则在展开图中B 点的位置为（）A．B1B．B2C．B3D．B45．图①是由白色纸板拼成的立体图形，将它的两个面的外表面涂上颜色，如图②．则下列图形中，是图②的表面展开图的是（）A．B．C．D．二．填空题6．如图是一个正方体骰子的表面展开图，若1点在上面，3点在左面，则点在正面．【答案】2．7．把一个边长为1cm的正方体纸盒沿棱剪开，剪成一个连在一起的平面图形，这个平面图形的周长是cm．8．如图是一正方体的平面展开图，若AB＝5，则该正方体上A、B两点间的距离为．三．解答题9．如图，正方体（图1）的展开图如图2所示，在图1中M、N分别是FG、GH的中点，CM、CN、MN是三条线段；请在图2中画出CM、CN、MN这三条线段．10．如图，是一个没有完全剪开的正方体，若再剪开一条棱，得到的平面展开图可能是下列六种图中的哪一些？（写字母）11．如图1，一个边长为2cm的立方体按某种方式展开后，恰好能放在一个长方形内．（1）计算图1长方形的面积；（2）小明认为把该立方体按某种方式展开后可以放在如图2的长方形内，请你在图2中划出这个立方体的表面展开图；（图2每个小正方形边长为2cm）；（3）如图3，在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图（各个面都用数字“1”表示），请你在剩下部分再画出2个该立方体的表面展开图，把一个立方体的每一个面标记为“2”，另一个立方体的每一个面标记为“3”．第2节展开与折叠（第一课时）答案解析一．选择题1．B【解析】解：由正方体的表面展开图的“相间、Z端是对面”可知，“常”与“来”是对面，“州”与“好”是对面，“越”与“越”是对面，翻动第1次，第2次时，“好”在前面，“州”在后面，翻动第3次时，“好”在下面，“州”在上面，故选：B．2．A【解析】解：∵正方体纸盒无盖，∴底面M没有对面，∵沿图中的粗线将其剪开展成平面图形，∴底面与侧面的从左边数第2个正方形相连，根据正方体的表面展开图，相对的面之间一定相隔一个正方形可知，只有A选项图形符合．故选：A．3．D【解析】解：根据翻转规律，从第1次开始朝下的面的数字依次2、3、5、4、2、3、5、4……，又因为2021÷4＝505……1，所以第2021次后朝下的面的数字为2，故选：D．4．B【解析】解：由正方体可知，点A与点B不在该正方体的同一个面上，故排除选项A；将右边的展开图复原，则只有点B2处于体对角线的两端．与左边正方体中点A与点B的位置相同．故选：B．5．B【解析】解：由图中阴影部分的位置，首先可以排除C、D，又阴影部分正方形在左，三角形在右，而且相邻，故只有选项B符合题意．故选：B．二．填空题6．2．【解析】解：这是一个正方体的平面展开图，共有六个面，其中面“3点”和面“4点”相对，面“5点”和面“2点”相对，面“6点”和面“1点”相对，如果1点在上面，3点在左面，2点在正面，可知5点在后面．故答案为：2．7．14【解析】解：∵正方体有6个表面，12条棱，要展成一个平面图形必须5条棱连接，∴要剪12﹣5＝7条棱，1×（7×2）＝1×14＝14（cm）．答：这个平面图形的周长是14cm．故答案为：14．8．2.5【解析】解：由题意可得出：正方体上A、B两点间的距离为正方形对角线长，则A、B两点间的距离为2.5．故答案为：2.5．三．解答题9．【解析】如图所示：10．【解析】解：沿后面下面剪开可得E，沿后面右面剪开可得A，沿下面右面剪开可得B．故答案为：A、B、E．11．【解析】解：（1）∵立方体的棱长为2cm，∴长方形的面积为4×2×3×2＝48平方厘米；（2）如图所示：（3）如图所示：。
1.2 展开与折叠(1)练习
1.2 展开与折叠(1)练习一、基础过关1.在棱柱中，叫做棱，相邻两个侧面的叫做侧棱.2.人们通常根据将棱柱分为三棱柱、四棱柱等……长方体和正方体都是 .3.矩形绕其一边旋转一周形成的几何体叫__________，直角三角形绕其中一个直角边旋转一周形成的几何体叫__________.4.将一个无底无盖的长方体沿一条棱剪开得到的平面图形为_____________________.5.将一个无底无盖的圆柱剪开得到一个矩形，其中圆柱的_____________________等于矩形的一个边长，矩形的另一边长等于 .6.长方体共有_____________个顶点____________个面，其中有__________对平面相互平行.7.球面上任一点到球心的距离 .8.如下图，由6个边长相等的正方形组成的长方形ABCD中，包含*在内的正方形与长方形共________个.9.如果长方体从一点出发的三条棱长分别为2，3，4，则该长方体的表面积为______，体积为__________.10.用一个宽2cm，长3cm的矩形卷成一个圆柱，则此圆柱的侧面积为_______________.11.现实生活中的油桶、水杯等都给人以__________的形象.二、能力提升12.侧面展开图是一个长方形的几何体是( )A.圆锥B.圆柱C.四棱锥D.球13.侧面展开图是一个扇形的几何体是( )A.球B.圆柱C.棱柱D.圆锥14.在图中，( )是四棱柱的侧面展开图15.下面两个图中所示的平面图形是什么图形的表面展开图.16.下列图形不能够折叠成正方体的是( )17.在下列各平面图形中，是圆锥的表面展开图的是( )18.如图，把左边的图形折叠起来，它会变为 ( )19.用一个边长为10cm的正方形围成一个圆柱的侧面(接缝略去不计)，求该圆柱的体积.20.用如图所示的长31.4cm，宽5cm的长方形，围成一个圆柱体，求需加上的两个底面圆的面积分别是多少平方厘米？(取3.14)三、聚沙成塔朋友，上次的小问题解决了吗？好，快看看这次的“数学魔术”，面积怎么就少“一块”？。
七年级数学上册展开与折叠(同步练习)人教版
展开与折叠(同步练习) 课时1（3）从右面看是面C，面D在后面，面在上面。
7．如图所示图是长方体的表面展开图，折叠成一个长方体，那么与字母 J重合的点是哪几个？拓展应用8．用一X8K的白纸自做一个墨水盒。
课时2基础演练1 ．下列图形中不可以折叠成正方体的是（）A B C D2．一个同学画出了正方体的展开图的一个部分，还缺一个正方形（如下图所示），请在图中添上这个正方形。
3．一个无上盖的正方体纸盒，底面标有字母A，沿图中的粗线剪开，在右图中补上四个正方形，使其成为它的展开图。
【能力升级】4．一个正方体的平面展开图的如图所示，则正方形4的对面是正方形。
（第4题） （第5题）5．如图所示是一个正方体纸盒的展开图，请把8，－3，15分别填入余下的四个正方形中，使得按虚线折成正方体后，相对面上的两个数互为相反数。
6．如图所示的立方体，如果把它展开，可以是下列图形中的 （ ）A B C D7．在右图所示的正方体的平面展开图中，确定正方体上的点M 、N 的位置。
8．下列图形是正方体的展开图，还原成正方体后，其中完全一样的是（ ）（1） （2） （3） （4）A ．（1）和（2）B ．（1）和（3）C ．（2）和（3）D ．（3）和（4）【拓展应用】9．一个正方体的骰子，1和6，2和5，3和4是分别相对的面上的点。
现在有12个正方形格子的纸上画好了点状的图案，如图所示，若要经过折叠能做成一个骰子，你认为应剪掉哪6个正方形格子？（请用笔在要剪掉的正方形格子上1234563-815D C BA123456123456123456123456打“×”，不必写理由）。
北师大版七年级数学上册第一章第2节《 展开与折叠》同步练习题
北师大版七年级数学上册第一章第2节《展开与折叠》同步练习题一、选择题(本大题共12小题，共36.0分)1.下列各图不是正方体表面展开图的是（）A. B. C. D.2.哪个图形经过折叠可以围成一个棱柱（）A. B. C. D.3.一个几何体的展开图如图所示，这个几何体是（）A.圆锥B.圆柱C.四棱柱D.四棱锥第3题第4题第5题4.如图是下列几何体（）的平面展开图．A. B. C. D.5.如图，有一个正方体纸巾盒，它的平面展开图是（）A. B. C. D.6.如图，将四棱锥沿某些棱剪开，展成一个平面图形，至少需要剪开（）A.4条棱B.5条棱C.6条棱D.7条棱7.把图1所示的正方体的展开图围成正方体（文字露在外面），再将这个正方体按照图2，依次翻滚到第1格，第2格，第3格，第4格，此时正方体朝上一面的文字为（）A.富B.强C.文D.民8.如图是一个正方体纸盒的外表面展开图，则这个正方体是（）A. B. C. D.9.如图，在正方体的平面展开图中A、B两点间的距离为6，折成正方体后A、B两点是正方体的顶点，则这两个顶点的距离是（）A.3B.C.6D.310.下面四个图形都是由相同的六个小正方形纸片组成，小正方形上分别贴有北京2008年奥运会吉祥物五个福娃（贝贝、晶晶、欢欢、迎迎、妮妮）的卡通画和奥运五环标志，如果分别用“贝、晶、欢、迎、妮”五个字来表示五个福娃，那么折叠后能围成如图所示正方体的图形是（）A. B. C. D.第10题第11题第12题11.如图所示为一个无盖长方体盒子的展开图（重叠部分不计），根据图中数据，可知该无盖长方体的容积为（）A.4B.6C.8D.1212.如过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图所示的几何体，其正确的展开图为（）A. B. C. D.二、填空题(本大题共4小题，共6.0分)13.如图所示的平面纸能围成正方体盒子，请把与面A垂直的面用图中字母表示出来是______ ．14.如图是某几何体的平面展开图，则这个几何体是______ ．第13题第14题第15题15.将如图中的图形剪去一个正方形，使剩余的部分恰好能折成一个正方体，问应剪去哪个小正方形？______ （说出两种即可）16.以下三组图形都是由四个等边三角形组成．能折成多面体的选项序号是______ ．三、解答题(本大题共7小题，共56.0分)17.下面是两种立体图形的展开图．请分别写出这两个立体图形的名称：18.马小虎准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如图所示的拼接图形（实线部分），经折叠后发现还少一个面，请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子．（注：①只需添加一个符合要求的正方形；②添加的正方形用阴影表示）19.工人把一个长方形的纸盒展开时不小心多剪了一刀，结果展开后变成了两部分，如图，现在他想把这两部分粘贴成一个整体，使之能折成原来的长方体，请你帮他设计一下，应怎样粘贴？20.由6个大小相同的小正方形连成的一块硬纸板，可折叠成一个正方体纸盒，若把6个小正方形每种不同位置的排列作为一种纸样，你能做出几种这样的纸样（用图表示）？21.如图是一个正方体表面展开图，如果把它重新折成正方体，那么与点G重合的是哪两点？并用字母指出三对相对的面．22.用如图所示的长31.4cm，宽6.28cm的长方形，围成一个圆柱体，求底面圆的面积是多少平方厘米？（π取3.14）23.小明在学习了《展开与折叠》这一课后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的①和②．根据你所学的知识，回答下列问题：（1）小明总共剪开了______ 条棱．（2）现在小明想将剪断的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪断的纸条粘贴到①中的什么位置？请你帮助小明在①上补全．（3）小明说：他所剪的所有棱中，最长的一条棱是最短的一条棱的5倍．现在已知这个长方体纸盒的底面是一个正方形，并且这个长方体纸盒所有棱长的和是880cm，求这个长方体纸盒的体积．《展开与折叠》练习参考答案一、选择题：1. C解：根据分析可得：A、B、D是正方体表面展开图，能够折成一个正方体，而C不是正方体表面展开图，故选C．2. D解：三棱柱展开后，侧面是三个长方形，上下底各是一个三角形由此可得：只有D是三棱柱的展开图．故选：D．3. A解：因为圆锥的展开图为一个扇形和一个圆形，故这个几何体是圆锥．故选A．4.B解：由题意，可知如图是四棱台的平面展开图．故选B．5. B解：观察图形可知，一个正方体纸巾盒，它的平面展开图是．故选：B．6. A解：将四棱锥沿某些棱剪开，展成一个平面图形，至少需要剪开4条棱．故选：A．7. A解：由图1可得，“富”和“文”相对；“强”和“主”相对；“民”和“明”相对；由图2可得，小正方体从图2的位置依次翻到第4格时，“文”在下面，则这时小正方体朝上面的字是“富”，故选：A．8. C解：∵由图可知，实心圆点与空心圆点一定在紧相邻的三个侧面上，∴C符合题意．故选C．9.D解：∵AB=6，∴把正方形组合起来之后会发现A、B在同一平面的对角线上，∴该正方体A、B两点间的距离为3，故选：D．10. C解：由原正方体可知，“妮”、“迎”、“欢”三个字所在的面是相交的，而选项A、B中，“妮”和“欢”所在的面是相对的，故A，B错；D中“妮”、“迎”、“欢”三个字所在的面的位置与原正方体不符，故D错．故选C．11.B解：观察图形可知长方体盒子的长=5-（3-1）=3、宽=3-1=2、高=1，则盒子的容积=3×2×1=6．故选：B．12. B解：选项A、C、D折叠后都不符合题意，只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点，•与正方体三个剪去三角形交于一个顶点符合．故选：B．二、填空题：13. 解：因为正方体的表面展开图，相对的面之间一定相隔一个正方形，面“A”与“D”是相对面，它们互相平行，剩下的面都与A面垂直；所以：围成正方体盒子，与面A垂直的面用图中字母表示出来是：B、C、E、F；故答案为：B、C、E、F．14. 解：由几何体展开图可知，该几何体是三棱柱，故答案为：三棱柱．15. 解：根据有“田”字格的展开图都不是正方体的表面展开图可知，故应剪去我或喜或学，故答案为：我，喜．16. 解：只有图（1）、图（3）能够折叠围成一个三棱锥．故答案为：（1）（3）．三、简答题：17.解：（1）是长方体，（2）是三棱柱．18.解：答案不惟一，如图．19.解：．20.解：如图所示：共计11种．21.解：结合图形可知，围成立方体后A与点A和点C重合；四边形ABMN与四边形FEJI，四边形LMJK与四边形CBED，四边形MJEB与四边形HIFG 相对面．22.解：31.4÷2÷3.14=5（cm），5×5×3.14=78.5（cm2）．故底面圆的面积是78.5平方厘米．23. 解（1）小明共剪了8条棱，故答案为：8．（2）如图，四种情况．（3）∵长方体纸盒的底面是一个正方形，∴设最短的棱长高为acm，则长与宽相等为5acm，∵长方体纸盒所有棱长的和是880cm，∴4（a+5a+5a）=880，解得a=20cm，∴这个长方体纸盒的体积为：20×100×100=200000立方厘米．。
展开与折叠同步练习含试卷分析详解北师大版数学七年级上
北师大版数学七年级上册第一章第2节展开与折叠课时练习一、单选题（共15小题）1、如图是一个长方体包装盒，则它的平面展开图是（）A、B、C、D、2、下列四个图形中是正方体的平面展开图的是（）A、B、C、D、3、如图的正方体盒子的外表面上画有3条粗黑线，将这个正方体盒子的表面展开（外表面朝上），展开图可能是（）A、B、C、D、4、下列图形中可以作为一个三棱柱的展开图的是（）A、B、C、D、5、一个几何体的表面展开图如图所示，则这个几何体是（）A、四棱锥B、四棱柱C、三棱锥D、三棱柱6、下列图形中，能通过折叠围成一个三棱柱的是（）A、B、C、D、7、下面图形经过折叠不能围成棱柱的是（）A、B、C、D、8、如图是一个正方体纸巾盒，它的平面展开图是（）A、B、C、D、9、骰子可以看做是一个小立方体（如图），它相对两面之和的点数之和是7，下面展开图中符合规则的是（）A、B、C、10、如图，把左边的图形折叠起来，它会变为右面的哪幅立体图形（）A、B、C、D、11、下列图形经过折叠不能围成棱柱的是（）A、B、C、D、12、下面四个图形中，经过折叠能围成如图所示的几何图形的是（）B、C、D、13、如图是一个立方体图形的展开图，则这个立体图形是（）A、四棱柱B、四棱锥C、三棱柱D、三棱锥14、一个正方体的每个面都有一个汉字，其展开图如图所示，那么在该正方体中和“值”字相对的字是（）A、记B、观C、心D、间15、如图是一个正方体展开图，把展开图折叠成正方体后，“我”字一面的相对面上的字是（）A、的B、中C、国D、梦二、填空题（共5小题）16、如图是正方体的一种展开图，其中每个面上都标有一个数字，那么在原正方体中，与数字“2”相对的面上的数字是________．17、“仁义礼智信孝”是我们中华民族的传统美德，小明同学将这六个字分别写在一个正方体六个表面上，这个正方体的表面展开图如图所示，那么与“孝”所在面相对的面上的字是________．18、有一个正六面体骰子，放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动90°算一次，则滚动第次后，骰子朝下一面的点数是________．19、如图，是一个正方体的表面展开图，则原正方体中“梦”字所在的面相对的面上标的字是________．20、有一个正方体的六个面上分别标有数字1、2、3、4、5、6，从三个不同的角度观察这个正方体所得到的结果如图所示，如果标有数字6的面所对面上的数字记为a ，2的面所对面上数字记为b ，那么a+b的值为________．三、解答题（共5小题）21、一个正方体6个面分别写着1、2、3、4、5、6，根据下列摆放的三种情况，那么每个数对面上的数是几？22、如图是一个正方体的展开图，标注了字母a的面是正方体的正面，如果正方体相对两个面上的整式的值相等，求整式（x+y）a的值．23、如图是一个正方体骰子的表面展开图，请根据要求回答问题：(1)如果1点在上面，3点在左面，几点在前面？(2)如果5点在下面，几点在上面？24、解答题(1)如图：是有一些相同小正方体搭建而成的几何体的俯视图，其中小正方形中的数字表示在这个位置小立方体的个数，请画出该几何体的主视图与左视图．(2)已知、b互为相反数，c、d互为倒数，m的绝对值等于2，p是数轴上到原点的距离为1的数，求：p ﹣cd+ 的值．25、回答下列问题：(1)如图所示的甲、乙两个平面图形能折什么几何体？(2)由多个平面围成的几何体叫做多面体．若一个多面体的面数为f ，顶点个数为v ，棱数为e ，分别计算第（1）题中两个多面体的f+v﹣e的值？你发现什么规律？(3)应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数．答案解析部分一、单选题（共15小题）1、【答案】A【考点】几何体的展开图【解析】【解答】由四棱柱四个侧面和上下两个底面的特征可知，A．可以拼成一个长方体；B．C．D．不符合长方体的展开图的特征，故不是长方体的展开图．【分析】考查了几何体的展开图，牢记长方体展开图的各种情形是解题关键．2、【答案】B【考点】几何体的展开图【解析】【解答】A．不是正方体的平面展开图；B．是正方体的平面展开图；C．不是正方体的平面展开图；D．不是正方体的平面展开图．【分析】考查了正方体展开图，熟练掌握正方体的表面展开图是解题的关键．3、【答案】D【考点】几何体的展开图【解析】【解答】根据正方体的表面展开图，两条黑线在一列，故A错误，且两条相邻成直角，故B错误，中间相隔一个正方形，故C错误，只有D选项符合条件．【分析】考查了几何体的展开图，注意从相对面入手．4、【答案】A【考点】几何体的展开图【解析】【解答】三棱柱展开后，侧面是三个长方形，上下底各是一个三角形由此可得：只有A是三棱柱的展开图．【分析】查了三棱柱表面展开图，注意上、下两底面应在侧面展开图长方形的两侧．5、【答案】A【考点】几何体的展开图【解析】【解答】如图所示：这个几何体是四棱锥．【分析】考查了几何体的展开图，熟记常见立体图形的平面展开图的特征是解决问题的关键．6、【答案】C【考点】几何体的展开图【解析】【解答】A．折叠后少一面，故错误；B．折叠后两侧面重叠，不能围成三棱柱，故错误；C．折叠后能围成三棱柱，故正确；D．折叠后两侧面重叠，不能围成三棱柱，故错误．【分析】三棱柱表面展开图，上、下两底面应在侧面展开图长方形的两侧，且是全等的三角形，．7、【答案】D【考点】几何体的展开图【解析】【解答】A．能围成四棱柱；B．能围成五棱柱；C．能围成三棱柱；D．经过折叠不能围成棱柱．【分析】常见立体图形的平面展开图的特征，是解决此题的关键．8、【答案】B【考点】几何体的展开图【解析】【解答】根据正方体的展开图可得【分析】根据正方体的展开图，训练了学生空间想象能力．9、【答案】C【考点】几何体的展开图【解析】【解答】根据正方体的表面展开图，相对的面之间一定相隔一个正方形，A、1点与3点是相对面，4点与6点是相对面，2点与5点是相对面，所以不可以折成符合规则的骰子，故错误；B．3点与4点是相对面，1点与5点是相对面，2点与6点是相对面，所以不可以折成符合规则的骰子，故错误；C．4点与3点是相对面，5点与2点是相对面，1点与6点是相对面，所以可以折成符合规则的骰子，故正确；D．1点与5点是相对面，3点与4点是相对面，2点与6点是相对面，所以不可以折成符合规则的骰子，故错误．【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形用排除法求解．10、【答案】B【考点】几何体的展开图【解析】【解答】圆面的相邻面是长方形，长方形不指向圆，【分析】根据相邻面、对面的关系，可得答案．11、【答案】B【考点】几何体的展开图【解析】【解答】A可以围成四棱柱，C可以围成五棱柱，D可以围成三棱柱，B选项侧面上多出一个长方形，故不能围成一个三棱柱．【分析】由平面图形的折叠及棱柱的展开图解题，熟记常见立体图形的表面展开图的特征是解决此题的关键．12、【答案】B【考点】几何体的展开图【解析】【解答】根据立体图形可得，展开图中三角形图案的顶点应与圆形的图案相对，而选项A，D与此不符，所以错误；三角形图案所在的面应与圆形的图案所在的面相邻，而选项C与此也不符，正确的是B．【分析】根据图中三角形，圆，正方形所处的位置关系可选出答案，考查了空间想象力．13、【答案】C【考点】几何体的展开图【解析】【解答】∵三棱柱的展开图侧面是长方形，上下面是三角形，∴上图应是三棱柱的展开图．【分析】根据立体图形的展开图是平面图形以及三棱柱的侧面展开图是长方形，上下面是三角形，可解此题．14、【答案】A【考点】几何体的展开图【解析】【解答】对于正方体的平面展开图中相对的面一定相隔一个小正方形，由图形可知，与“值”字相对的字是“记”．【分析】由平面图形的折叠及立体图形的表面展开图的特点解题．15、【答案】D【考点】几何体的展开图【解析】【解答】正方体的表面展开图，相对的面之间一定相隔一个正方形，“们”与“中”是相对面，“我”与“梦”是相对面，“的”与“国”是相对面．【分析】考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手作答．二、填空题（共5小题）16、【答案】4【考点】几何体的展开图【解析】【解答】这是一个正方体的平面展开图，共有六个面，其中面“2”与面“4”相对，面“3”与面“5”相对，“1”与面“6”相对．【分析】利用正方体及其表面展开图的特点解题．17、【答案】义【考点】几何体的展开图【解析】【解答】结合展开图可知，与“孝”相对的字是“义”．【分析】根据正方体的平面展开图的特点，相对的两个面中间一定隔着一个小正方形，且没有公共的顶点，结合展开图很容易找到与“孝”相对的字．18、【答案】3【考点】几何体的展开图，探索图形规律【解析】【解答】观察图象知道点数三和点数四相对，点数二和点数五相对且四次一循环，∵÷4=503…2，∴滚动第次后与第二次相同，∴朝下的点数为3．【分析】观察图象知道点数三和点数四相对，点数二和点数五相对且四次一循环，解题的关键是发现规律．19、【答案】的【考点】几何体的展开图【解析】【解答】正方体的表面展开图，相对的面之间一定相隔一个正方形，“伟”与“国”是相对面，“大”与“中”是相对面，“的”与“梦”是相对面．【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形．20、【答案】7【考点】几何体的展开图【解析】【解答】由图可知，∵与1相邻的面的数字有2、3、4、6，∴1的对面数字是5，∵与4相邻的面的数字有1、3、5、6，∴4的对面数字是2，∴3的对面数字是6，∵标有数字6的面所对面上的数字记为a ，2的面所对面上数字记为b ，∴a=3，b=4，∴a+b=3+4=7．【分析】本题考查了正方体相对两个面上的文字，，由相邻面上的数字确定出相对面上的数字是解题的关键．三、解答题（共5小题）21、【答案】1对4，2对5，3对6．解答：根据正方体的特征知，相邻的面一定不是对面，所以面“1”与面“4”相对，面“2”与面“5”相对，“3”与面“6”相对．1对4，2对5，3对6．【考点】几何体的展开图【解析】【分析】根据正方体的特征知，相邻的面一定不是对面，所以面“1”与面“4”相对，面“2”与面“5”相对，“3”与面“6”相对22、【答案】81解答：根据题意得：y=3，x=6，a=2，故（x+y）a=（x+y）2=92=81．【考点】代数式求值，几何体的展开图，简单几何体的三视图【解析】【分析】由正方体的展开图的相对面和已知“相对两个面上的代数式的值相等”，可求得x、y、a 的值，再根据完全平方公式求解．23、【答案】（1）2点在前面，可知5点在后面解答：正方体的平面展开图，其中面“3点”和面“4点”相对，面“5点”和面“2点”相对，面“6点”和面“1点”相对，（1）如果1点在上面，3点在左面，2点在前面，可知5点在后面；（2）如果5点在下面，那么2点在上面【考点】几何体的展开图【解析】【分析】本题考查了正方体的表面展开图，注意正方体的空间图形，从相对面入手，分析及解答．24、【答案】（1）解答：根据俯视图上小正方形的个数，主视图、左视图，（2）答案：0或-2解答：a、b互=相反数，c、d互为倒数，m的绝对值等于2，p是数轴上到原点的距离为1的数，得a+b=0，cd=1，m=±2，p=±1，p=1时，p﹣cd+=1﹣1+0=0，当p=﹣1时，p﹣cd+=﹣1﹣1+0=﹣2，综上所述：p﹣cd+=0，或p﹣cd+=﹣2．【考点】几何体的展开图【解析】【分析】（1）根据俯视图上小正方形的个数，可的主视图、左视图；（2）根据相反数的和为零，根据倒数的积为1，根据绝对值的意义，可得答案．25、【答案】（1）长方体和五棱锥解答：图甲折叠后底面和侧面都是长方形，所以是长方体；图乙折叠后底面是五边形，侧面是三角形，实际上是五棱锥的展开图，所以是五棱锥．（2）甲：f=6，e=12，v=8，f+v﹣e=2；乙：f=6，e=10，v=6，f+v﹣e=2；规律：顶点数+面数﹣棱数=2．（3）设这个多面体的面数为x ，则x+x+8﹣50=2解得x=22．【考点】认识平面图形，几何体的展开图【解析】【分析】（1）由长方体与五棱锥的折叠及长方体与五棱锥的展开图解题．（2）列出几何体的面数，顶点数及棱数直接进行计算即可；（3）考查了欧拉公式，展开图折叠成几何体．。
七年级数学上册认识图形,展开与折叠练习题(附答案)
北师版七年级数学上册——同步题型第一章丰富的图形世界专题1.1生活中的立体图形第2课时点、线、面的认识一、题型过关知识点❶点、线、面、体的关系1．笔尖在纸上快速滑动写出一个又一个字，用数学知识解释为( )A．点动成线B．线动成面C．面动成体D．以上都不对2．下雨时汽车的雨刷把玻璃上的雨水刷干净属于下列哪个选项的实际应用( ) A．点动成线B．线动成面C．面动成体D．以上都不对3．把一张纸折叠，展开后得到一条折痕，这个现象用数学知识可解释为( ) A．面与面相交成线B．线动成面C．面动成体D．点动成线知识点❷立体图形的构成4．将下列各选项中的平面图形绕轴旋转一周，可得到如图所示的立体图形的是( )5．下列图形分别由几个面围成的，有几个平面和几个曲面．图①由______个面围成，分别有______个平面，_____个曲面；图②由_______个面围成，分别有______个平面，_____个曲面；图③由_____个面围成，分别有_____个平面，______个曲面．二、探索提升6．观察如图所示的棱柱，它的侧面和一个底面相交成( )A．3条线B．4条线C．5条线D．6条线7．一个几何体只有一个顶点，一个侧面，一个底面，则这个几何体可能是( ) A．棱柱B．棱锥C．圆锥D．圆柱8．下图中几何体没有曲面的是( )9．下列图形中，图(a)是正方体木块，把它切去一块，得到如图(b)，(c)，(d)，(e)的木块．(1)我们知道，图(a)的正方体木块有8个顶点，12条棱，6个面．请你将图(b)，(c)，(d)，(e)中木块的顶点数、棱数和面数填入下表：(2)根据上表中各种木块的顶点数、棱数、面数之间的数量关系可归纳出一个规律，请你试写出顶点数x、棱数y、面数z之间的数量关系．三、回顾与总结方法技能：1．图形是由点、线、面构成的；2．面与面相交得到线，线与线相交得到点；3．点动成线，线动成面，面动成体．易错提示：线分直线和曲线；面分平面和曲面．（参考答案）1. A2. B3. A4. A5.6，6,0,3，2,1,2,1,16. B7. C8. B9.解：(1)6 9 5 8 12 6 8 13 7 10 15 7(2)x＋z－y＝2北师版七年级数学上册——同步题型第一章丰富的图形世界专题1.2展开与折叠第1课时正方体的展开与折叠一、题型过关知识点❶正方体的展开与折叠1．(长春中考)下列图形中，可以是正方体表面展开图的是( )2．(达州期末)下列平面图形不能够围成正方体的是( )3．图1和图2中所有的正方形都相同，将图1的正方形放在图2中的①，②，③，④某一位置，所组成的图形不能围成正方体的位置是( )A．① B．② C．③ D．④4．(教材P9习题4改编)下面都是由五个相同的小正方形组成的图形，请你在各图中分别添加一个小正方形，使它们能折叠成小正方体．知识点❷利用正方体的展开图解答相关问题5．(达州期末)如图，是一个正方体的表面展开图，则原正方体中“梦”字所在的面相对的面上标的字是( )A．伟 B．大 C．的 D．国6．(达州月考)如图，有一个无盖的正方体纸盒，下底面标有字母“M”，沿图中粗线将其剪开展成平面图形，想一想，这个平面图形是( )7．正方体的六个面上分别标有1，2，3，4，5，6六个数字，如图是其三种不同的放置方式，与数字“6”相对的面上的数字是( )A．1 B．5 C．4 D．38．如图是一个正方体的展开图，如果正方体相对的面上标注的值相等，那么x＝_______，y＝_______.9．在如图的展开图中，分别填上数字1，2，3，4，5，6，使得折叠成正方体后，相对面上的数字之和相等，则a＝____，b＝_____，c＝______.二、探索提升10．将一正方体纸盒沿如图所示的裁剪线剪开，展开成平面图形，其展开图的形状为( )11．(淄博中考)将图①围成图②的正方体，则图②中的红心“♥”标志所在的正方形是正方体中的( )A．面CDHE B．面BCEF C．面ABFG D．面ADHG12．(无锡中考)如图的正方体盒子的外表面上画有3条粗黑线，将这个正方体盒子表面展开(外表面朝上)，展开图可能是( )13．将左图折叠起来围成一个正方体，应该得到( )14．图①是一个小正方体的表面展开图，小正方体从图②所示的位置依次翻到第1格、第2格、第3格、第4格，这时小正方体朝上一面的字是( )A．梦 B．水 C．城 D．美15．(达州期中)在图中剪去一个正方形，使剩余的部分恰好能折成一个正方体，问应剪去几号小正方形？所有可能的情况是__________________．16．如图所示是一张3×5的方格纸，现将其剪为三部分，使每部分都可以拆成一个无盖的小方盒，请问该如何剪？在图中画出裁剪线．17．把立方体的六个面分别涂上六种不同颜色，并画上朵数不等的花，各面上的颜色与花的朵数情况见表：现将上述大小相同，颜色、花朵分布也完全相同的四个立方体拼成一个水平放置的长方体，如图所示．问长方体的下底面共有多少朵花？三、回顾与总结方法技能：将正方体沿不同的棱展开，共有11种展开图，141型6种，231型3种，33型1种，222型1种．易错提示：注意在正方体展开图中，对面相隔不相邻．北师版七年级数学上册——同步题型第一章丰富的图形世界专题1.2展开与折叠第1课时正方体的展开与折叠（参考答案）10.D11.B12.A13.解：14.A15.B16.B17.x＝4，y＝10.18.a＝6，b＝2，c＝4.19.B20.A21.D22.D23.A24.剪去1号、2号或3号小正方形25.解：17.解：因为长方体是由大小相同，颜色、花朵分布也完全相同的四个立方体拼成，所以根据图中红色的面，可以确定出一个小立方体各个面的颜色为：红色面对绿色面，黄色面对紫色面，蓝色面对白色面，所以可知长方体下底面从左到右依次是紫色、黄色、绿色、白色，再由表格中花的朵数可知共有17朵.。
展开与折叠(一)
4.下列哪些是正方体的展开图？
A
B
C
D
E
F
（二）先猜想再实践，发展几何直觉
想一想，做一做
把一个正方体的表面沿某些棱剪开， 展成一个平面图形，你能得到下面 的些平面图形吗？
18
想一想，做一做
把一个正方体的表面沿某些棱剪开， 展成一个平面图形，你能得到下面 的这些平面图形吗？
×
×
×
×
23
相间、“Z”端是对面
A
B
A
B
A和B为相对的两个面
24
间二、拐角邻面知
C
D
C
D
C和D为相邻的两个面
25
如图1—6的图形都是正方体的展开图吗？
图1 是
图2 是
图3 是
图4 是
图5 不是
图6
不是Байду номын сангаас
26
下面图形都是正方体的展开图吗？
图（1）
不是
图（2）
不是
图（3）
是
图（4）
不是
图（5）
不是
同学们 同学们 大家好！ 下午好！
李兴林 李兴林
问题导入：
一个正方体木块的2个相 距最远的顶点处停了一只 壁虎和一只蚊子，那么壁 虎可以从哪条最短的路径 爬到蚊子处？说明理由？
北师大版 七年级数学上册
第一章
丰富的图形世界
（第一课时）
3
探究1:
把一个正方体的表面 沿某些棱剪开，展成一 个平面图形，能得到哪 些平面图形？请与同伴 进行交流。
A B C D E F
29
考考你
下面图形中，哪些是正方体的平面展开图？ 祝 1
2 3 4 5 6 前 你 似 程 锦
展开与折叠(一)
展开和折叠（一）
设计反思：
本课的设计中，有梯度的先安排了“做一做”，“想一想”、“议一议”、“试一试”，充分让学生动手操作、自主探索、合作交流，以积累有关图形的经验和数学活动经验，发展空间观念。
其中，动手操作是学习过程中的重要一环——在学习的开始阶段，它可以帮助学生认识图形、发展空间观念，以后，它可以用来验证学生对图形的空间想像。
因此，学习之初，先鼓励学生先动手、后思考，而后，则鼓励学生先想像，再动手。
本课的“想一想，折一折”以及课堂练习中很好的体现了这点，使学生的空间想象能力得到较大程度的提高。
最后的“想一想，试一试”这一开放性问题的设计让学生在编题中巩固知识，运用知识，并为学生提供了展示自我的机会，这样有意识地满足学生多样化的学习需求，发展学生的个性，不仅更好的激发学生的学习兴趣，更重要的是培养了学生的创新意识和创造力。
在本课的设计中两点还有待改进，其一是选择教具时和教学内容时应该更多的注意和现实生活相联系，“学习有价值的数学”的新课程精神有待更深刻的体现；其二是在拓展训练时在放手让学生发散上设计不够大胆。
最新北师大版七上数学展开与折叠(1)巩固练习及达标测试
A．6 C．2
B．3 D．1
4．如图，将硬纸片沿虚线折起来，便可做成一个 正方体，这个正方体的2号面的对面是 6 号
面．
5．如图是一个正方体纸盒的展开图，当折成纸盒 时，与数11重合的数是 1和7 ．
北师大版 七年级级上
1．（2018•长春模拟）下列图形不是正方体展开 图的是（ B ）
2．（2018•大庆）将正方体的表面沿某些棱剪开， 展成如图所示的平面图形，则原正方体中与“创”字所 在的面相对的面上标的字是（ A）
A．庆 B．力
C．大 D．魅
3．（2018•门头沟区二模）如图所示的图形，是 下面哪个正方体的展开图（ D ）
4．如图，有一个无盖的正方体纸盒，下底面标有 字母“M”，沿图中粗线将其剪开展成平面图形，想 一想，这个平面图形是（ B ）
5．（2018•山亭月考）图1是一个正方体的展开图，
该正方体从图2所示的位置依次翻到第1格、第2格、
第3格、第4格、第5格，此时这个正方体朝上一面的 字是 我 ．
6．如图，5个边长相等的小正方形拼成一个平面图形，
解：将4个数字和1个字母括起来的 不同的方法有： （1、2、3、4、A），（1、2、3、 4、B），（1、2、3、4、C），（1、 2、3、4、D），（1、2、3、4、 E）． 故一共有5种不同的方法．
1．（2018•内江中考）如图是正方体的表面展开图， 则与“前”字相对的字是（ B ）
A．认
B．真 C．复 D．习
2．（2018•巴中中考）毕业前夕，同学们准备了一 份礼物送给自己的母校．现用一个正方体盒子进行包 装，六个面上分别写上“祝、母、校、更、美、丽”， 其中“祝”与“更”，“母”与“美”在相对的面上．则此包 装盒的展开图（不考虑文字方向）不可能是（ D ）
北师大版七(上)数学1.2.1展开与折叠(1)课时同步检测(原创)
正方体的表面展开图，相对的面之间一定相隔一个正方形，
“M”与“x”是相对面，
“-2”与“-3”是相对面，
“4x”与“2x+3”是相对面，
（1）∵正方体的左面与右面标注的式子相等，
∴4x=2x+3，
解得x=1.5；
（2）∵标注了A字母的是正方体的正面，左面与右面标注的式子相等，
∴上面和底面上的两个数字-2和-3，
18．有一个正方体，在它的各个面上分别标有数字l、2、3、4、5、6．甲、乙、丙三位同学从三个不同角度去观察此正方体，观察结果如图l、2、3所示，那么这个正方体各个面上的数字对面各是什么数字?
甲 乙 丙
图1图2图3
19．马小虎准备制作一个封闭的正方体盒子，他先用4个大小一样的正方形制成如下图所示拼接图形（实线部分），经折叠后发现还少一个面，请你在下图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子．（添加所有符合要求的正方形，添加的正方形用阴影表示）
15．z=2，y=7，x=﹣5．
【解析】
【分析】
利用正方体及其表面展开图的特点，根据相对面上的两个数之和为5，列出方程求出x、y、z的值．
【详解】
这是一个正方体的平面展开图，共有六个面，
其中面“z”与面“3”相对，面“y”与面“﹣2”相对，“x”与面“10”相对．
则z+3=5，y+（﹣2）=5，x+10=5，
故答案为①或②或⑥．
【点睛】
本题考查了展开图折叠成几何体，解题时勿忘记四棱柱的特征及正方体展开图的各种情形．
11．4
【解析】
【分析】
结合正方体的平面展开图的特征，只要折叠后能围成正方体即可，
北师大版七年级数学上册《展开与折叠》专题训练(含答案)
1.2 展开与折叠专题一正方体的展开与折叠1．以下各图均有彼此连接的六个小正方形纸片组成，其中不能折叠成一个正方体的是（）A．B． C．D．2.如图是每个面上都有一个汉字的正方体的一种展开图，那么在原正方体“着”相对的面上的汉字是（）A．冷B．静C．应D．考3．将图1围成图2的正方体，则图1中的红心“”标志所在的正方形是正方体中的（）A．面CDHE B．面BCEF C．面ABFG D．面ADHG4.如图,有一正方体的房间,在房间内的一角A处有一只蚂蚁,它想到房间的另一角B处去吃食物,试问它采取怎样的行走路线是最近的?如果一只蜜蜂,要从A到B 怎样飞是最近呢?请同学们互相讨论一下.BA专题二三棱柱、圆柱与圆锥的展开与折叠5．左图是一个三棱柱，下列图形中，能通过折叠围成该三棱柱的是（）A．B．C．D．6．如下图所示的平面图形中，不可能围成圆锥的是（）A． B．C．D．状元笔记：【知识要点】1．掌握正方体的展开与折叠，能根据所给平面图形判断是否能折叠成正方体．2．根据简单立体图形的形状画出它的展开图，根据展开图判断立体图形的形状．【温馨提示】1．长方体有8个顶点，12条棱，6个面，且每个面都是长方形（正方形是特殊的长方形）．长方体是四棱柱，但四棱柱不一定是长方体，四棱柱的两个底面是四边形，不一定是长方形．2．一个平面展开图，折成立体图形的方式有两种：一种是向里折，一种是向外折，一般易忽略其中一种，造成漏解．3．棱柱的表面展开图是由两个相同的多边形和一些长方形连成的，沿棱柱表面不同的棱剪开，可能得到不同组合方式的平面展开图；圆柱的表面展开图是由两个相同的圆形和一个长方形连成的；圆锥的表面展开图是由一个圆形和一个扇形连成的．【方法技巧】确定正方体展开图的方法以口诀的方式总结出来：正方体经7刀剪，可得六面十四边；中间并排达四面，两旁各一随便站；三面并排在中间，单面任意双面偏；三层两面两层三，好似阶梯入云天；再问邻面何特点，“间二”“拐角”是关键；“隔1”、“Z端”是对面，识图巧排“七”“凹”“田”．参考答案：1．D 解析：选项A 、B 、C 都可以折叠成一个正方体；选项D ，有“田”字格，所以不能折叠成一个正方体．故选D ．考点：展开图折叠成几何体．分析：由平面图形的折叠及正方体的展开图解题．能组成正方体的“一，四，一”“三，三”“二，二，二”“一，三，二”的基本形态要记牢．2．B 解析：这是一个正方体的平面展开图，共有六个面，其中面“静”与面“着”相对，面“沉”与面“应”相对，“冷”与面“考”相对．3．A 解析：由图1中的红心“”标志，可知它与等边三角形相邻，折叠成正方体是正方体中的面CDHE ．考点：展开图折叠成几何体．分析：由平面图形的折叠及正方体的展开图解题，注意找准红心“”标志所在的相邻面．4．解：如图（1）所示，线段AB 是蚂蚁行走的最近路线；如图（2）所示，线段AB 是蜜蜂飞的最近路线．(1)(2)5．B 解析：A ．折叠后有二个侧面重合，不能得到三棱柱； B ．折叠后可得到三棱柱；C ．折叠后有二个底面重合，不能得到三棱柱； D ．多了一个底面，不能得到三棱柱．6．D 解析：根据圆锥的侧面展开图是扇形，可以直接得出答案，D 选项不符合要求．。
展开与折叠(提升训练)(原卷版) (1)
5.3 展开与折叠【提升训练】一、单选题1．有5个大小一样的正方形制成如图所示的拼接图形（阴影部分），请你在图中的拼接图形上再接一个正方形，使新拼接成的图形折叠后能成为一个封闭的正方体盒子，你不能选择图中A，B，C，D中的（）位置拼接正方形．A．A B．B C．C D．D2．下图是一个三棱柱纸盒的示意图，则这个纸盒的平面展开图是（）A．B．C．D．3．如图是一个长方体包装盒，则它的表面能展开成的平面图形是（）A．B．C．D．4．如图，是一个正方体的表面展开图，则原正方体中“伟”字所在的面相对的面上标的字是（）A．大B．梦C．国D．的5．下列图形中，不是正方体表面展开图的是（）A．B．C．D．6．下面的图形经过折叠可以围成一个棱柱的是（）A．B．C．D．++的值（）7．如图，若要使得图中平面展开图折叠成长方体后，相对面上的两个数之和为9，求x y zA．10B．11C．12D．138．如图1是一个小正方体的侧面展开图，小正方体从图2所示的位置依次翻到第1格→第2格→第3格→第4格，这时小正方体朝上的一面的字（）A．的B．梦C．我D．中9．防控疫情必须勤洗手、戴口罩，讲究个人卫生．如图是一个正方体展开图，现将其围成一个正方体后，则与“手”相对的是（）A．勤B．口C．戴D．罩10．正方体的平面展开图如图所示，则在原正方体中，“万”字的对面的字为（）A．溱B．州C．中D．学11．下列图形中可以作为一个正方体的展开图的是（）A．B．C．D．+-的值为（）12．如图，是一个正方体的表面展开图．若该正方体相对面上的两个数和为0，则a b cA．-6B．-2C．2D．413．经过折叠可以得到四棱柱的是（）A．B．C．D．14．图1是正方体的平面展开图，六个面的点数分别为1、2、3、4、5、6，将点数朝外折叠成一枚正方体骰子，并放置于水平桌面上，如图2所示，若骰子初始位置为图2所示的状态，将骰子向右翻滚90 ，则完成1次翻转，此时骰子朝下一面的点数是2，那么按上述规则连续完成2次翻折后，骰子朝下一面的点数是3；则连续完成2020次翻折后，骰子朝下一面的点数是（）A．2B．3C．4D．515．如图，是一个正方体纸盒的平面展开图，则写有“为”字的面所对的面上的是（）A．汉B．！C．武D．加16．如图，白纸上放有一个表面涂满染料的小正方体．在不脱离白纸的情况下，转动正方体，使其各面染料都能印在白纸上，且各面仅能接触白纸一次．．．．．．．．．．，则在白纸上可以形成的图形为（）A．①①①B．①①C．①①D．①①17．如图，是一个几何体的表面展开图，则该几何体中写“英”的面相对面上的字是( )A．战B．疫C．情D．颂18．下列图形中，不是立方体表面展开图的是（）A．B．C．D．19．下列展开图不能叠合成无盖正方体的是()A．B．C．D．20．长方体纸盒的长、宽、高分别是5cm、4cm、2cm ，若将它沿棱剪开，展成一个平面图形那么这个平面图形的周长的最小值是（）A．60B．56C．42D．40个点的骰子，将它抛掷三次得到不同的结果，看到的情形如图所示，则图中21．一枚六个面分别标有16写有“？”一面上的点数是（）A．6B．2C．3D．122．如图，有一个无盖的正方体纸盒，下底面标有字母“M”，沿图中粗线将其剪开展成平面图形，这个平面图形是（）A．B．C．D．23．有一个正六面体骰子放在桌面上，将骰子如图所示顺时针方向滚动，每滚动90°算一次，则滚动第70次后，骰子朝下一面的数字是（）A．2B．3C．4D．524．下列平面图中不能围成正方体的是（）A．B．C．D．25．如图，是正方体的展开图，2号面是前面，那么后面是（）号A．3号B．4号C．5号D．6号26．如图，正方体盒子的外表面上画有3条粗黑线，将这个正方体盒子的表面展开外表面朝上，展开图可能是（）A．B．C．D．27．下图为相同的小正方形组成，折叠后能围成正方形的是（）A．B．C．D．28．如图，一个正方体的平面展开图，若折成正方体后，每对相对面上标注的值的和均相等，则x+y等于（）A．10B．11C．12D．1329．如图，三个图形是由立体图形展开得到的，相应的立体图形顺序是( )A．圆柱、三棱柱、圆锥B．圆锥、三棱柱、圆柱C．圆柱、三棱锥、圆锥D．圆柱、三棱柱、半球30．2020年，两安市为创建全国文明城市，在街头制作了正方体宣传板进行宣传，它的展开图如图示，请你来找一找“创”字所在面的对面是哪个字（）A．明B．文C．北D．城第II卷（非选择题）请点击修改第II卷的文字说明二、填空题31．小强用5个大小一样的正方形制成如图所示的拼接图形（阴影部分），若在图中只添加一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子，这样的拼接方式有_____种．32．如图是某几何体的表面展开图，则该几何体的名称是______；侧面积＝______（用含π的代数式表示）．33．某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中“国”字所在面相对的面上的汉字是________．34．一张长50cm，宽40cm的长方形纸板，在其四个角上分别剪去一个小正方形（边长相等且为整厘米数）后，折成一个无盖的长方体形盒子，这个长方体形盒子的容积最大为_____cm3．+=______．35．若要使图中平面展开图折叠成正方体后，使得相对面上的数的和相等，则x y三、解答题36．在期末复习期间，悠悠碰到了这样一道习题：如图所示是一个正方体表面展开图，正方体的每个面上都写着一个整式，且相对两个面上的整式的和都相等．请根据展开图回答下列问题：（1）与A 相对的面是__________；与B 相对的面是____________；（填大写字母）（2）悠悠发现A 面上的整式为：3221x x y ++，B 面上的整式为：2312x y x -+，C 面上的整式为：2313x y x -，D 面上的整式为：()221x y -+，请你计算：F 面上的整式． 37．如图①，是一个边长为10cm 正方形，按要求解答下列问题：（1）如图①，若将该正方形沿粗黑实线剪下4个边长为 cm 的小正方形，拼成一个大正方形作为直四棱柱的一个底面，余下部分按虚线折叠成一个无盖直四棱柱，最后把两部分拼在一起，组成一个完整的直四棱柱，它的表面积等于原正方形的面积；（2）若该正方形是一个圆柱的侧面展开图，求该圆柱的体积．（结果保留π）38．一个正方体的六个面分别标有字母A 、B 、C 、D 、E 、F ，从三个不同方向看到的情形如图所示．（1）A 的对面是 ，B 的对面是 ，C 的对面是 ；（直接用字母表示）（2）若A ＝﹣2，B ＝|m ﹣3|，C ＝m ﹣3n ﹣112，E ＝（52+n ）2，且小正方体各对面上的两个数都互为相反数，请求出F 所表示的数．39．如图是一个正方体的平面展开图，标注了字母M 的是正方体的正面，标注了2-的是正方体的底面，正方体的左面与右面标注的式子相等．（1）求x 的值；（2）求正方体的上面和后面的数字和．40．如图所示，是一个长方体纸盒平面展开图，已知纸盒中相对两个面上的数互为相反数．求a ，b ，c 的值？41．如图是一个正方体纸盒的表面展开图，纸盒中相对两个面上的数互为倒数．（1）填空：a =______，b =_________； （2）先化简，再求值：()()2223252ab ab ab a ab ⎡⎤------⎣⎦．42．如图是一个长方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数． （1）填空：a =________，b =________，c =________．（2）先化简，再求值：()22253234a b a b abc a b abc ⎡⎤---+⎣⎦43．某班数学活动小组的同学用纸板制作长方体包装盒，其平面展开图和相关尺寸如图所示，其中阴影部分为内部粘贴角料．（单位：毫米）（1）此长方体包装盒的体积为 立方毫米；（用含x 、y 的式子表示）（2）此长方体的表面积（不含内部粘贴角料）为平方毫米；（用含x、y的式子表示）（3）若内部粘贴角料的面积占长方体表面纸板面积的16，求当x＝40毫米，y＝70毫米时，制作这样一个长方体共需要纸板多少平方米．44．下面是一个多面体的表面展开图每个面上都标注了字母，（所有字母都写在这一多面体的外表面）请根据要求回答问题：（1）如果面F在前面，从左边看是B，那么哪一面会在上面？（2）如果从右面看是面C面，面D在后边那么哪一面会在上面？（3）如果面A在多面体的底部，从右边看是B，那么哪一面会在前面．45．李明同学设计了某个产品的正方体包装盒如图所示，由于粗心少设计了其中一个顶盖，请你把它补上，使其成为一个两面均有盖的正方体盒子．（1）共有种弥补方法；（2）任意画出一种成功的设计图（在图中补充）；（3）在你帮忙设计成功的图中，要把-6，8，10，-10，-8，6这些数字分别填入六个小正方形，使得折成的正方体相对面上的两个数相加得0．（直接在图中填上）46．某班数学活动小组的同学用纸板制作长方体包装盒，其平面展开图和相关尺寸如图所示，其中阴影部分为内部粘贴角料．（单位：毫米）（1）此长方体包装盒的体积为立方毫米；（用含x、y的式子表示）（2）此长方体的表面积（不含内部粘贴角料）为平方毫米；（用含x、y的式子表示）（3）若内部粘贴角料的面积占长方体表面纸板面积的15，求当x＝40毫米，y＝70毫米时，制作这样一个长方体共需要纸板多少平方毫米．47．小明在学习了《展开与折叠》这一课后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的①和①．根据你所学的知识，回答下列问题：（1）小明总共剪开了条棱．（2）现在小明想将剪断的①重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪断的纸条粘贴到①中的什么位置？请你帮助小明在①上补全．（3）小明说：已知这个长方体纸盒高为20cm，底面是一个正方形，并且这个长方体纸盒所有棱长的和是880cm，求这个长方体纸盒的体积．48．已知：图①、图①、图①均为53的正方形网格，在网格中选择2个空白的正方形并涂上阴影，与图中的4个阴影正方形一起构成正方体表面展开图，且3种方法得到的展开图不完全重合．49．如图，上面的图形分别是下面哪个立体图形展开的形状，请你把有对应关系的平面图形与立体图形连接起来．50．如图所示，一个无盖的长方体纸盒，其长宽高分别为5cm，4cm，3cm．请你画出一种表面展开图（大概示意图），并计算其表面积．51．如图是一个长方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数．（1）填空：a＝，b＝，c＝．（2）求代数式的值：a2﹣|a﹣b|+|b+c|．52．如图是从三个方向看几何体得到的形状图．（1）说出这个几何体的名称； （2）画出它的一种表面展开图；（3）若从正面看到的形状图的宽为4 cm ，长为7 cm ，从左面看到的形状图的宽为3 cm ，从上面看到的形状图中斜边长为5 cm ，求这个几何体所有棱长的和，以及它的表面积和体积． 53．综合与实践某“综合与实践”小组开展了“长方体纸盒的制作”实践活动，他们利用边长为cm a 的正方形纸板制作出两种不同方案的长方体盒子（左图为无盖的长方体纸盒，右图为有盖的长方体纸盒）．（纸板厚度及接缝处忽略不计）华罗庚小组展示：根据左图方式制作一个无盖的长方体盒子，方法：先在纸板四角剪去四个同样大小边长为cm b 的小正方形，再沿虚线折合起来． 问题解决（1）该长方体纸盒的底面边长为______cm ；（请你用含a ，b 的代数式表示） （2）若12cm a =，3cm b =，则长方体纸盒的底面积为______2cm ； 陈省身小组展示：根据右图方式制作一个有盖的长方体纸盒．方法：先在纸板四角剪去两个同样大小边长为cm b 的小正方形和两个同样大小的小长方形，再沿虚线折合起来． 拓展延伸（3）该长方体盒子的A面长为______，宽为______（请你用含a，b的代数式表示）cm；（请你用含a，b的代数式表示）（4）该长方体纸盒的体积为______354．我们知道，将一个正方体或长方体的表面沿某些棱剪开，可以展成一个平面图形．（1）下列图形中，是正方体的表面展开图的是_______．（2）如图所示的长方体，长、宽、高分别为4、3、6，若将它的表面沿某些棱剪开，展成一个平面图形．则下列图形中，可能是该长方体表面展开图的有______（填序号）（3）下列图是题（2）中长方体的一种表面展开图，它的外围周长为52，事实上，题（2）中长方体的表面展开图还有不少，聪明的你能画出一个使外围周长最大的表面展开图吗？请画出这个表面展开图，并求出它的外围周长．55．在一次青少年模型大赛中，小高和小刘各制作了一个模型，小高制作的是棱长为acm的正方体模型，小刘制作的是棱长为acm的正方体右上角割去一个长为3cm，宽为2cm，高为1cm的长方体模型（如图2）（1）用含a的代数式表示，小高制作的模型的各棱长度之和是___________；（2）若小高的模型各棱长之和是小刘的模型各棱长之和的56，求a的值；（3）在（2）的条件下，①图3是小刘制作的模型中正方体六个面的展开图，图中缺失的有一部分已经很用阴影表示，请你用阴影表示出其余缺失部分，并标出边的长度．①如果把小刘的模型中正方体的六个面展开，则展开图的周长是________cm；请你在图方格中画出小刘的模型中正方体六个面的展开图周长最大时的图形．56．如图1所示，从大正方体中截去一个小正方体之后，可以得到图2的几何体．（1）设原大正方体的表面积为a，图2中几何体的表面积为b，那么a与b的大小关系是；A．a＞b；B．a＜b；C．a＝b；D．无法判断．（2）小明说“设图1中大正方体的棱长之和为m，图2中几何体的各棱长之和为n，那么n比m正好多出大正方体的3条棱的长度．”你认为小明的说法正确吗？为什么？（3）如果截去的小正方体的棱长为大正方体的棱长的一半，那么图3是图2几何体的表面展开图吗？如有错误，请予修正．57．如图所示，在一张正方形纸片的四个角上各剪去一个同样大小的正方形，然后把剩下的部分折成一个无盖的长方体盒子．请回答下列问题：（1）剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为；（2）如果设原来这张正方形纸片的边长为acm，所折成的无盖长方体盒子的高为hcm，那么，这个无盖cm；长方体盒子的容积可以表示为3（3）如果原正方形纸片的边长为20cm，剪去的小正方形的边长按整数值依次变化，即分别取cm cm cm cm cm cm cm cm cm cm时，计算折成的无盖长方体盒子的容积得到下表，由1,2,3,4,5,6,7,8,9,10此可以判断，当剪去的小正方形边长为cm时，折成的无盖长方体盒子的容积最大。
苏科版七年级上《展开与折叠》(1)练习及答案
5.3.1展开与折叠
【问题情境】
一只虫子从圆柱上A点处绕圆柱爬到B点处，你能画出它爬行的最短路线吗？
【自主探究】
1、做一做
⑴沿虚线剪开圆柱形纸筒的侧面，得到什么平面图形？小虫从A
点绕圆柱爬到B点的最短路线是什么？请画出圆柱的侧面展开示意图
和小虫爬行的最短路线。
⑵延虚线剪开圆锥形冰淇淋纸筒得到什么平面图形？请画出它的示
意图。
2、想一想
⑴下列图形中，哪些图形通过折叠可以围成一个棱柱？
⑵请把这些图形用纸复制下来，然后沿虚线折叠，验证你的想法。
⑶观察制成的棱柱，共有多少条棱，哪些棱的长度相等？共有多少个面，
它们分别是什么形状？哪些面的形状、大小完全相同？
⑷不能围成棱柱的，如何变化图形使得它能围成四棱柱?
3、练一练
下列图形是某些几何体的平面展开图，先尝试猜想
．．．．这些几何体的名称，然后用纸将这些
图形复制下来，折叠验证
．．．．你的想法。
【回顾反思】
拓展应用
8．用一张8K的白纸自做一个墨水盒。
答案：
自主探究1．做一做⑴长方形、长方形的对角线⑵扇形。
2．想一想⑷
3．练一练正方体、长方体、四棱锥、三棱柱；
回顾反思尝试猜想折叠验证
基础演练1．4、三角；2．圆、扇形；3．D。
能力升级4．图（2）能；5．（1）三棱锥，（2）三棱柱；6．（1）F，（2）E，（3）F；
7．H、N。
拓展应用8．略。
苏科版七年级数学上册展开与折叠
小壁虎的难题： 如图：一只无盖的圆桶下方有一只壁虎， 上方有一只蚊子，壁虎要想尽快吃到蚊子， 从侧面应该走哪条路径？
● 蚊子
壁虎 ●
壁虎 ●
● 蚊子
侧面展开
蚊子 ●
● 壁虎
圆柱体的侧面展开图： 长方形 .
圆锥体的侧面展开图： 扇形 .
想一想
图中纸筒纸盒沿红线或侧棱剪开，能展开 成平面图形吗？会是什么形状呢？
B A C
D
A
C
B D
.
.
B
B
.
A
.A
圆柱体的表面展开图：长方形+2个圆 .
A
A
圆锥体的表面展开图：扇形+1个圆 .
三 棱 锥
三 棱 柱
长 方 体
下列图形是哪些几何体的表面展开图?
正方体
长方体
四棱锥
三棱柱
长方体
五棱锥
三棱柱
正方体的展开
你能通过剪开某些棱，把你们手中的 正方体纸盒展开成一个平面图形吗？
体纸盒展开成一个平面图形。 7条
判断下列图形能不能折成正方体？
(1)
不能
(2)
不能
(3)
不能
(4)
能
二三一型
(5)
一四一型
能
(6)
不能
(7)
三三型
能
(8)
不能
(9)
不能
(10)
二三一型
能
(11)
不能
(12)
不能
探究学习
小壁虎在正方体的顶点A，在距它
最远的另一个顶点B处有一只蚊子，为
了尽快吃到这只蚊子，小壁虎走哪条路
2024年北师大版七年级上册数学复习专项突破练1 正方体的展开与折叠
图是一个正方体的平面展开图，把展开图折叠成正方体
后，“城”字对面的字是( B )
A. 文
B. 明
C. 典
D. 范
12345678
6. 【2024咸阳月考】如图，给正方体的各个侧面分别标上字 母 a ， b ， c ， d ， e ， f ，其中 a 在后面， b 在下面， c 在 左面，则下列结论错误的是( D )
12345678
题型2 找正方体展开图的相对面 4. 【新趋势·跨学科】诸葛亮的《诫子书》中有言“非学无
以广才”，将这六个字写在一个正方体的六个面上，如图
是该正方体的一种表面展开图，则原正方体中与“学”字
所在的面相对的面上的汉字是( B )
A. 非
B. 以
C. 广
D. 才
12345678
5. 【立德树人·创建文明城市】“争创全国文明典范城市， 让文明成为宜昌人民的内在气质和城市的亮丽名片”.如
北师陕西 七年级上册
第一章 丰富的图形世界 专项突破练1 正方体的展开与折叠
3星题 发展素养
题型1 判断正方体的展开图 1. 下列各图中，可以是一个正方体的平面展开图的是
(C)
A
B
C
D
12345678
2. 【2024咸阳实验中学月考】如图是一个没有完全剪开的正 方体，若再剪开一条棱，则得到的平面展开图不可能是 (B)
A
B
C
D
12345678
3. 【陕西人文信息·旅游】2024年3月2日，陕西“三秦 四 季 ·汉 中 有 约 ” 最 美 油 菜 花 海 汉 中 旅 游 文 化 节 推 介 发 布会在西安大唐不夜城举行.志愿者为会场设计了一些 正方体抽纸盒.如图所示，将写有“汉”字的正方形添 加到图中，使它们构成抽纸盒的展开图，则添加方式 共有 4 种.
七年级数学上册图形展开与折叠专项练习
图形展开与折叠专项练习一、基础演练 ：1、下列图形中（每个小正方形的大小相同），是一个正方体表面展开图的是（ ）DC BA2、下列各图形中能围成正方体的是（ ）D CBA 3．下列图形经过折叠不能围成棱柱的是 （ ）（A ） （B ） （C ） （D ）4、在下图中，能折叠成棱柱的有（ ）个。
（4）（3）（2）（1） BDA 、1B 、2C 、3D 、 45．用边长为1的正方形纸板，制成一副七巧板，如图所示，将它拼成“小天鹅”图案，其中阴影部分的面积为()A.12B.716C.38D.34二、强化训练：6．如图2是一个几何体的表面展成的平面图形，则这个几何体是7、根据正方体展开图5---3---6上的编号，写出向对面上的号码：3的对面 。
4的对面 。
5的对面 。
8、如图所示的硬纸片，沿虚线折起来便可成为一个正方体，与“我”相对的 是9、下图中的图形是某些立体图形的平面展开图，写出这些立体图形的名称：（1） (2)（2）10、下图中的几个图形能否折叠成为棱柱？先想一想，再折一折。
(4)(3)(2)（1)11、用如图所示，大小完全相同的两个直角三角形纸片，若将它们的某条边重合，能拼成几种不同形状的平面图形？请你画出拼成的图形．① ②12、今有一块正方形土地，要在其上修筑两条笔直的道路，使道路把这片土地分成形状相同且面积相等的4部分，若道路的宽度忽略不计，请你设计三种不同的修筑方案．（只需画简图）答案：1、C 2、B 3、D 4、B 5、C6．圆柱7、3的对面 6 4的对面 1 5的对面 28、名9、（1）五棱柱 (2)五棱锥10、（1）、(2)、（3）能(4)不能11答案：如图：12答案：。
七年级数学《展开与折叠》典型例题
七年级数学《展开与折叠》典型例题例1 填空（1）六棱柱有_____个顶点，有_______条侧棱．（2）是_________的表面展开的平面图．例2 如图是正方体纸盒的展开图，请把－10，8，10，－8，－2，2分别填入六个不同的正方形中，使得按虚线折成正方体后，相对面上的两个数都互为相反数．（填写出一种方案即可）例3 请画出一个长、宽、高分别是5cm、4cm、3cm的长方体的平面展开图，并标出各部分的长度．例4 下列图形是哪些多面体的平面展开图，说出这些多面体的名称．例5 已知一个正三棱锥，请画出它的展开图．例6 已知一个正三棱柱，请画出它的平面展开图．例7 如图（a）是正方体分割后的一部分，它的另一部分是图（b）中的（）参考答案例1 分析（1）通过观察六棱柱可知，六棱柱有12个顶点、有六条侧棱．（2）观察可以发现展开图有六个边长相等的长方形，并且有两个边长和长方形宽相等的六边形，所以是六棱柱的表面展开平面图．解（1）12，六．（2）六棱柱．说明（1）我们知道四棱柱有8个顶点，五棱柱有10个顶点，六棱柱有四个顶点……，以此类推n棱柱有2×n个顶点．（2）观察棱柱的展开图，首先作为底面的多边形必须是相同的多边形，另外多边形的边数必须等于展开图中长方形的个数．例2 分析为便于表述与思考，将每个小正方形写上字母，得下图．a、b、c、d四个小正方形呈“一”字形连在一起，可见它们是正方体的四个侧面，而e与f则是正方体的上、下底面．上、下底面是相对的．侧面中相对的面在展开图中隔着另一个侧面，所以写着a与c，b与d的面，分别是相对的面．在每两个相对的面中填入一组题目提供的相反数．解可如图所示．说明想象立体图形的展开图对于初一学生来说是件不太容易的事情．防止错误的最好的办法是在观察实物和自己动手操作的过程中，经历和体验图形的变化过程．就本题而言，把你画的图剪下来，折叠成模型，既简便易行，又能验证你填写的是否正确．例3 分析如图，这个长方体的上下两个面是长和宽分别是5cm和4cm的长方形，前后两个面是长和宽分别是5cm和3cm的长方形，左右两个面是长和宽分别是4cm和3cm的长方形，所以该长方体的展开平面图如下：解（如下图）说明（1）这个长方体的展开图不是惟一的，真正做长方体盒时其展开图还要因用料的尺寸而定．（2）真正做盒时还应考虑到接口部分的用料．例4 分析本题中的两图形的各边相互重合，没有哪个三角形或四边形与图形之间有较大的隔离，不好从想象中的空间上去比较、分析．那么我们还是从最容易确定的底面入手，观察（1）只有四个三角形，则它所在的多面体只可能有一个底，那么它就有三个侧面，显然，这是一个三棱锥；观察（2），发现刚好有两个三角形，三个长方形，那么两个三角形只可能作为底面，三个长方形作为侧面，它是三棱柱．答案（1）为三棱锥；（2）为三棱柱．说明：一个多面体在一般情况下，最多只有两个底面，而侧面却很多，根据这个特点，从判定多面体的底面入手，再判定多面体的侧面，则容易得出多面体的形状．例5 分析这又是一例文字性题目，在题目中没有具体的一个正三棱锥，因此，需要同学们自己先画出这个立体图形，再想象一下它的展开图的形状．解设已知的正三棱锥如图所示，展开图如图所示．说明我们给出两种不同的展开图，目的在于让同学们体会因展开方式不同会有不同的结果，但是它们都可以还原为原立体图形．例6 解设原正三棱柱如图．它的展开图如图．以上两种情况都符合条件．说明在此例中我们给出两种展开的方法，它还可以有不同的展开方式，让同学们自己动手试一试吧！例7 分析本题要求寻找出正方体分割成两部分后的对应图形，需要仔细观察分割后剩下的那部分图形的特征，发现图（a）呈“F”型，因此应在四个选项中寻找相应的“F”型．答案 B说明：本题涉及立体图形的分割与组合，要善于从局部到整体观察图形的轮廓特征（形状）．。
初一数学展开与折叠试题
初一数学展开与折叠试题1.右图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何题的主视图是 ( )【答案】A【解析】本题考查的是三视图俯视图中的每个数字是该位置小立方体的个数，分析其中的数字，得主视图有3列，从左到右分别是3，2，1个正方形．由俯视图中的数字可得：主视图有3列，从左到右分别是3，2，1个正方形．故选A．2.如图是正方体的平面展开图,每个面上标有一个汉字, 与“油”字相对的面上的字是( )A．北B．京C．奥D．运【答案】A【解析】本题考查了正方体的的表面展开图正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，据此作答即可．因为正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，所以与“油”字相对的字是“北”．故选A.3.圆锥侧面展开图可能是下列图中的( )【答案】D【解析】本题考查的是圆锥的侧面展开图根据圆锥的侧面展开图是一个扇形即可得到结果。
圆锥的侧面展开图是一个扇形，故选D。
4.观察下列图形,其中不是正方体的展开图的为( )【答案】D【解析】本题考查的是正方体的平面展开图根据正方体的表面展开图的常见形式即可判断．B、C经过折叠均能围成正方体，D折叠后第一行两个面无法折起来，而且缺少一个侧面，不能折成正方体．故选D．5.如图是一个正四面体,它的四个面都是正三角形,现沿它的三条棱AC、BC、CD剪开展成平面图形,则所得的展开图是( )【答案】B【解析】本题考查的是几何体的展开图亲自动手具体操作，或根据三棱锥的图形特点判断．根据三棱锥的图形特点，可得展开图为B．故选B．6.下列各图经过折叠不能围成一个正方体的是【答案】D【解析】本题考查的是正方体的平面展开图根据正方体的表面展开图的常见形式即可判断．A、B、C经过折叠均能围成正方体，D折叠后有两个面重合，不能折成正方体．故选D．7.下列展开图中,不能围成几何体的是( ).【答案】B【解析】本题考查的是几何体的平面展开图根据每个图形的特点即可判断可围成的几何体．A能围成三棱锥，C能围成三棱柱，D能围成四棱柱，只有B两个底面在侧面的同一侧，不能围成四棱柱．故选B．8.下列所示的平面图形中,是正方体的平面展开图的是 ( )【答案】C【解析】本题考查的是正方体的平面展开图根据正方体的表面展开图的常见形式即可判断．A、B、D折叠后均有两个面重合，C可以折叠成一个正方体．故选C．9.下列图形中,能够折叠成正方体的是( )【答案】C【解析】本题考查的是正方体的平面展开图根据正方体的表面展开图的常见形式即可判断．A、B、D折叠后均有两个面重合，C可以折叠成一个正方体．故选C．10.如图,该图形经过折叠可以围成一个正方体形,折好以后,与“静”字相对的字是___.【答案】着【解析】本题考查了正方体的的表面展开图正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，据此作答即可．因为正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，所以与“静”字相对的字是“着”．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
七年级数学展开与折叠练习（1）
1.圆柱的侧面展开图是形；圆锥的侧面展开图是形，棱柱的侧面展开图是形。
2.在如图所示的棱柱中，
（1）有条棱，有条侧棱，侧棱长都；
（2）有个面，有个侧面，上下底面是边形，
侧面个数与底面边数的关系是；
（3）这个棱柱共有个顶点。
3.下面每个图片由六个大小相同的正方形组成,其中不是正方体展开图的是( )
4.下列平面图形中，不是棱柱展开图的是（）
5.下面的4个图形中，棱柱的侧面展开图是（）
6.下列图形经过折叠后能围成一个三棱柱的图形是（）
A.2个
B.3个
C.4个
D.5个
7.下列图形都是几何体的平面展开图，在各图形下方的括号中写出相应几何体的名称。
（）（）（）（）
8.将三棱锥沿某些棱展开，可以得到如图所示的展开图。
（1）下面的两个图形能否折成三棱锥？
（）（）
（2）将原几何体改为四棱锥，请画出它的两种展开图。
9.如图是一个几何体的展开图，每个面内都标注了1－6中的一个数字，根据下列要求回答问题：
（1）若“1”面是几何体的左面，则“3”面是几何体
的面。
（2）若“2”面在前面，“4”在上面，则“1”面在
几何体的面。
（3）若“3”面在右面，从下面看到“5”面在下，
则“6”面在在几何体的面。
（4）若“4”面在左面，“1”面在前面，则“2”
面在在几何体的面。