2019年南京南师附中仙林学校(初中部)小升初登记表.doc
2018年南京南师附中仙林学校小升初登记表

编号(接待老师填写)本学区□是 □否
姓 名
性 别
出生
年月
民族
贴照片处
家庭住址
身份证号
毕业小学
户籍(注明市、区)
家庭
称谓
姓 名
工作单位、职务手 机主要父成员母学科
成绩
年级
语文
数学
外语
体育
担任学生
干部情况
校级荣誉(三好学生、优秀学干等)
四年级
上
下
五年级
上
下
六年级
上
区级及区级以上荣誉
学科竞赛情况(同一学科填写最高获奖)
时间
竞赛名称
获奖等第
科技、体育、艺术、文学特长
材料审核情况
审核人
注:学生简历装订次序:招生报名表、四五六年级成长脚印复印件、户口本复印件、房产证复印件及获奖证书复印件。有关材料复印件(原件自己带回)交学校存档,概不退还,谢谢您的配合!
南京29中初中部小升初报名登记表

姓名 称谓 父
家长姓名
母
<
家庭住址
户籍地址
成绩 学期
四
五
学科
上 下 上 下
[
语文
,
六上
性别 单位
#
毕业学校 职务
?
移动电话
数学
外语
是否三好/优少 (市、区、校)
担任职务
、 } 【 *
其他荣誉
时间
竞赛名称
获奖学科获奖情 况
(按获奖等级 从高到低依次 填写)
; :
, |
体艺特长 比赛考级
特长名称
比赛及考级情况
注:1)本表由学生本人本着诚实诚信的原则,如实填写;没有的项目或不知道的内容无须填写;
2)准备材料只附四、五、六年级素质报告书(我的学习、我的总结)和获奖证书复印件;
2023年初中新生入学报名登记表

2023年初中新生入学报名登记表(原创实用版)目录1.2023 年初中新生报名登记表概述2.报名登记表的具体内容3.报名流程及注意事项4.报名截止日期及提交方式正文【2023 年初中新生报名登记表概述】为了更好地安排 2023 年初中新生的入学工作,现将报名登记表的相关事宜进行公告。
本报名登记表主要用于收集新生的基本信息,以便于学校对新生进行统一管理。
请各位新生及家长务必认真填写,确保信息准确无误。
【报名登记表的具体内容】报名登记表主要包括以下内容:1.姓名、性别、出生日期和身份证号:请填写真实准确的姓名、性别、出生日期和身份证号,以便学校进行学籍注册。
2.民族、政治面貌和户籍所在地:请如实填写民族、政治面貌(如:群众、团员、党员等)以及户籍所在地。
3.毕业学校和班级:请填写学生当前所在学校及班级,以便学校了解学生的学术背景。
4.通讯地址和联系电话:请填写家长或监护人的详细通讯地址和联系电话,以便学校在必要时进行联系。
5.家庭主要成员:请填写父母或其他监护人的姓名、工作单位、职务、联系电话等信息。
6.学习经历和获奖情况:请简要填写学生在小学阶段的学习经历及获奖情况,以便学校了解学生的综合素质。
【报名流程及注意事项】1.报名流程:首先,请学生及家长认真阅读报名登记表上的各项内容,并如实填写。
填写完成后,将报名登记表及相关证件材料提交至学校指定的报名地点。
学校将对报名材料进行审核,审核通过后,学生方可参加入学考试。
2.注意事项: (1) 报名登记表上的信息务必真实、准确,如有虚假信息,学校有权取消其报名资格;(2) 报名材料一经提交,不予退还,请自行备份;(3) 报名截止日期为 2023 年某月某日,过期不予受理。
【报名截止日期及提交方式】1.报名截止日期:2023 年某月某日。
2.提交方式:请将填写好的报名登记表及相关证件材料提交至学校指定的报名地点。
2018-2019学年南京南师附中仙林校区初一第一学期英语学科期末测试卷(含答案)

2018-2019学年南京南师附中仙林校区初一第一学期英语学科期末测试卷一、听力(略)二、单项选择。
1.There is _________ “f” in the word “fix”.A. aB. anC. theD. 不填2.The Chinese people here always have a party_______ the Chinese New Year.A. celebrateB. to celebrateC. celebratingD. celebrates3.---_______ do we have for supper, dear?---Noodles with eggs.A. WhichB. WhereC. WhatD. How4. Dad, my shoes are old. I want to buy a new _______.A. shoesB. oneC. itD. pair5. The price of the TV is too _______, I don’t have enough money.A. muchB. highC. cheapD. expensive6.We are making a cake for my mother _______ a present for her birthday.A. forB. aboutC. asD. on7. The blue coat ________ cotton. It looks nice.A.is made inB. is made ofC. is made byD. is made from8. ---Millie, can you help me pick up the phone, please? I _______ the dishes.---I’m coming, Mom.A. washB. washingC. washesD. am washing9. ---Would you like _______ more cakes, David?---No, thanks. I’m full.A. muchB. manyC. someD. any10.Which of the underlined(画线)letter has a different sound from the other three?A. funB. studentC. clubD. but11. This is _______ car. It looks very beautiful.A. Kitty’s and SamB. Kitty and Sam’sC. Kitty’s and Sam’sD. Kitty and Sam12. Which word doesn’t have the sound /ɔi/A. boyB. toyC. buyD. toilet13.---Do you like TFBOYS?---Yes, their songs are _______ among the students.A. importantB. interestedC. specialD. popular14.---Let’s go to the zoo.---__________ I like animals very much.A. That’s a good idea!B. Sorry, I’m busy.C. No, I don’t like it.D. I’d love to, but I can’t.15. ---I am going to visit Nanjing Yangzi River Bridge with my family next month.---That sounds great! ________A. I’d like to.B. When will you go?C. Have a good time!D. How long will you stay there?三、完形填空。
小升初信息登记表
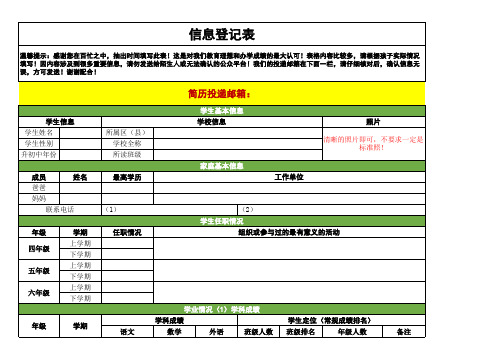
所学学科
(1) (2) (3)
【2】研学旅行:读万卷书,行万里路。 问题:最近两年你去过哪里旅游,用一句话概括你的收获!
【3】生涯规划:优秀的家长,成就优秀的孩子! 问题:亲爱的家长,请问您培养孩子最重要的理念是什么?对孩子未来学业规划是什么?
成员
姓名
爸爸
妈妈
联系电话
年级 四年级 五年级 六年级
学期 上学期 下学期 上学期 下学期 上学期 下学期
年级
学期
所属区(县) 学校全称 所读班级 最高学历
(1) 任职情况
学生基本信息 学校信息
家是
标准照!
工作单位
(2) 学生任职情况
组织或参与过的最有意义的活动
语文
学业情况(1)学科成绩
学科成绩
数学
外语
班级人数
学生定位(常规成绩排名)
班级排名
年级人数
备注
四年级 五年级 六年级 温馨提示
项目 奖项(1) 奖项(2) 奖项(3)
上学期 下学期 上学期 下学期 上学期 下学期
请根据家长手中所掌握情况,如实填写。 学业情况(2)获奖情况
◆仅登记四年级以后获得的奖项,每类最多只挑选最重要的三项奖项。 语文类
奖项(1) 奖项(2) 奖项(3)
项目
奖项(1) 奖项(2) 奖项(3) 温馨提示
综合类(三好学生,艺术类,体育类......)
奖项级别(国家级,市区 级,校级)
奖项名称
请如实填写。
获奖等级(特等、一 颁发机构
等、二等...)
学习时长 【1】 【2】
年级 四年级 五年级
调研
未来学习规划
学业情况【3】美术学习情况 美术类所获得最重要的奖项
七年级(6)班新生入学登记表

班号 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 姓名 胡雨洁 邓嘉豪 陈谦 罗婧 徐双双 何伟清 朱佳怡 朱凯鹏 尧佳伊 邱文浩 吴跃川 张梦婷 袁瑞翔 刘烨敏 辛思颖 王旭程 刘亚 齐曼 周国良 王纯 黄嘉怡 周震宇 何天宇 周雅婷 舒悦 万沐霖 欧阳琦根 艾弘昊 万雅琴 性别 女 男 男 女 女 男 女 男 女 男 男 女 男 女 女 男 女 女 男 女 女 男 男 女 女 男 男 男 女 出生年月 2004.5 2004.3 2004.1 2004.8 2003.8 2003.10 2004.6. 2003.6 2004.8 2004.8 2004.1 2003.11 2004.8 2004.1 2004.8 2004.12 2004.7 2004.8 2004.8 2004.4 2004.1 2003.9 2004.3 2004.3 2004.8 2003.7 2004.10 2004.9 2003.2 籍贯 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 临川 环城北西路8号 孝桥镇中洲村 赣东大道188号22栋2楼 滨湖世纪城21栋2栋 家庭地址 学府路338 学府路378 郭家桥10号 抚北东路15号 西湖村二组 唱凯镇灵山村 城西朱家村 城西朱家村 罗湖又林村委会 学府路338号附3号 西大街55号 二仙桥44号 羊城路51号 山水人家225/2707 抚州孝桥龙湾辛村 抚州二仙桥宏伟住宅 若士路四小对面 西大街57号 若士路44号 环城北路8号 抚州市临川区文昌街办西湖村 环城北路8号 二仙桥 利民嘉苑8栋 小学毕业学校 中学录取学校 家长姓名 工作单位 电话 学籍号
小学升初中报名信息登记表
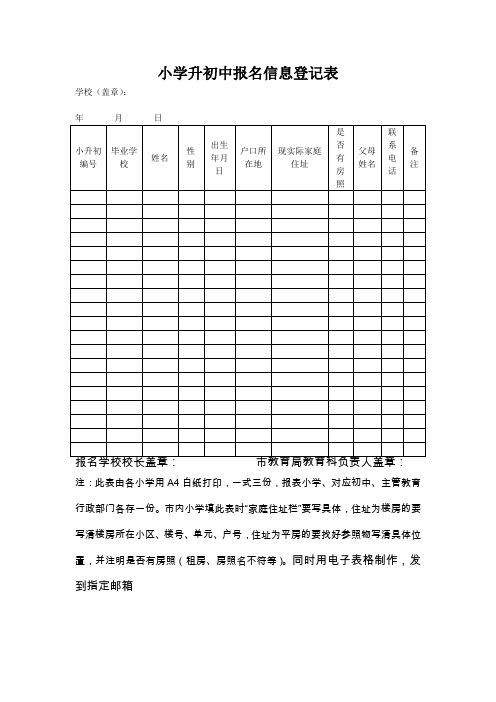
学校(盖章):
年月日
小升初编号
毕业学校
姓名
性别
出生年月日
户口所在地
现实际家庭住址
是否有房照
父母姓名
联系电话Βιβλιοθήκη 备注报名学校校长盖章: 市教育局教育科负责人盖章:
注:此表由各小学用A4白纸打印,一式三份,报表小学、对应初中、主管教育行政部门各存一份。市内小学填此表时“家庭住址栏”要写具体,住址为楼房的要写清楼房所在小区、楼号、单元、户号,住址为平房的要找好参照物写清具体位置,并注明是否有房照(租房、房照名不符等)。同时用电子表格制作,发到指定邮箱
江苏省南京师范大学附属中学仙林学校初中部2022-2023学年八年级下学期3月月考数学试题(含答案)

2022-2023学年南京师范大学附属中学仙林学校初中部初二下学期3月月考一.选择题(共4小题,每小题3分,共12分)1.下列汽车标志中既是轴对称图形,又是中心对称图形的是( )A.B.C.D.2.菱形具有而矩形不一定具有的性质是( )A.对角线相等B.对角线互相垂直C.对角相等D.对边平行3.如图,在▱ABCD中,对角线AC、BD相交于点O,下列条件中,不能判断这个平行四边形是菱形的是( )A.AB=AD B.∠BAC=∠DAC C.∠BAC=∠ABD D.AC⊥BD4.如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE 的中点,若BC=7,CE=1,则MN的长( )A.3B.5C.6D.8二.填空题(共10小题,每小题3分,共30分)5.当x 时,分式有意义.6.如图,矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,若AB=1,则BC = .7.如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于 .8.如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是 .9.如图,连接四边形ABCD各边中点,得到四边形EFGH,只要添加 条件,就能保证四边形EFGH是菱形.10.如图,△COD是△AOB绕点O顺时针方向旋转38°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠B的度数是 .11.如图,在平行四边形ABCD中,E为AD上一点,∠EBC=40°,且BE=BC,CE=CD,则∠A= .12.如图,已知菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC,垂足为点E,则AE的长是 cm.13.如图,▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为 .14.如图,矩形纸片ABCD中,已知AD=12,AB=9,E是BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .三.解答题(共7小题,共58分)15.(6分)解方程:(1);(2).16.(8分)先化简,再求值:,其中a是满足不等式3a﹣1>﹣4的最小整数解.17.(9分)如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).(1)画出△ABC关于原点成中心对称的△A'B'C';(2)将△ABC绕坐标原点O逆时针旋转90°,得△A″B″C″,画出△A″B″C″;(3)请直接写出,以A'、B'、C'为顶点的平行四边形的第四个顶点D'的坐标.18.(9分)如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.(1)求证:BE=DF;(2)求证:AF∥CE.19.(8分)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.(1)求证:∠ADB=∠CDB;(2)若∠ADC=90°,求证:四边形MPND是正方形.20.(9分)如图,点A在直线l外,点B在直线l上.(1)在l上求作一点C,在l外求作一点D,使得以A、B、C、D为顶点的四边形是菱形;(要求:用直尺和圆规作出所有大小不同的菱形)(2)连接AB,若AB=5,且点A到直线l的距离为4,通过计算,找出(1)中面积最小的菱形.21.(9分)如图1,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,M和N分别为OB、OC的中点,连接ED、EM、MN、ND.(1)求的值;(2)当△ABC满足什么条件时,四边形DEMN是矩形?给出你的结论并证明.(3)如图2,在△ABC中,BD、AF分别是边AC、BC上的中线,BD与AF相交于点O,若OA=4,OC=3,OB=5,则△ABC的面积为 (请直接写出结果).2022-2023学年南京师范大学附属中学仙林学校初中部初二下学期3月月考参考答案与试题解析一.选择题(共4小题)1.下列汽车标志中既是轴对称图形,又是中心对称图形的是( )A.B.C.D.【解答】解:A选项中的图形是轴对称图形,但不是中心对称图形,不符合题意;B选项中的图形既是轴对称图形,又是中心对称图形,符合题意;C选项选项中的图形是轴对称图形,但不是中心对称图形,不符合题意;D选项中的图形是中心对称图形但不是轴对称图形,不符合题意;故选:B.2.菱形具有而矩形不一定具有的性质是( )A.对角线相等B.对角线互相垂直C.对角相等D.对边平行【解答】解:∵菱形的性质有对角相等,对边平行,对角线互相垂直平分,矩形的性质有对角相等,对边平行,对角线互相平分且相等,故选:B.3.如图,在▱ABCD中,对角线AC、BD相交于点O,下列条件中,不能判断这个平行四边形是菱形的是( )A.AB=AD B.∠BAC=∠DAC C.∠BAC=∠ABD D.AC⊥BD【解答】解:A、邻边相等的平行四边形是菱形,故A选项不符合题意;B、对角线平分对角的平行四边形是菱形,故B选项不符合题意;C、由∠BAC=∠ABD不一定能够判断这个平行四边形是菱形,故C选项符合题意;D、对角线互相垂直平分的平行四边形是菱形,故D选项不符合题意.故选:C.4.如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE 的中点,若BC=7,CE=1,则MN的长( )A.3B.5C.6D.8【解答】解:连接AC、CF、AF,如图所示:∵矩形ABCD绕点C顺时针旋转90°得到矩形FFCE,∴∠ABC=90°,∴AC===5AC=BD=GE=CF,AC与BD互相平分,GE与CF互相平分,∵点M、N分别是BD、GE的中点,∴M是AC的中点,N是CF的中点,∴MN是△ACF的中位线,∴MN=AF,∵∠ACF=90°,∴△ACF是等腰直角三角形,∴AF=AC=5×=10,∴MN=5.故选:B.二.填空题(共10小题)5.当x ≠﹣3 时,分式有意义.【解答】解:由题意得:x+3≠0,解得:x≠﹣3,故答案为:≠﹣3.6.如图,矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,若AB=1,则BC= .【解答】解:∵四边形ABCD是矩形,∴∠ABC=90°,OA=AC,OB=BD,AC=BD,∴OA=OB,∵∠AOB=60°,∴△AOB是等边三角形,∴OA=AB=1,∴AC=2OA=2,∴BC===.故答案为:.7.如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于 3.5 .【解答】解:∵菱形ABCD的周长为28,∴AB=28÷4=7,OB=OD,∵E为AD边中点,∴OE是△ABD的中位线,∴OE=AB=×7=3.5.故答案为:3.5.8.如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是 22.5° .【解答】解:∵四边形ABCD是正方形,∴∠BAC=∠ACB=45°,∵AE=AC,∴∠ACE=∠E==67.5°,∴∠BCE=∠ACE﹣∠ACB=67.5°﹣45°=22.5°.故答案为:22.5°.9.如图,连接四边形ABCD各边中点,得到四边形EFGH,只要添加 AC=BD 条件,就能保证四边形EFGH是菱形.【解答】解:∵顺次连接四边形ABCD各边中点得到四边形EFGH即为平行四边形,∴根据菱形的性质,只要再有一组邻边相等就为菱形,只要添加的条件能使四边形EFGH 一组对边相等即可,例如AC=BD,故答案为:AC=BD.10.如图,△COD是△AOB绕点O顺时针方向旋转38°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠B的度数是 57° .【解答】解:根据旋转性质得△COD≌△AOB,∴CO=AO,由旋转角为38°,可得∠AOC=∠BOD=38°,∴∠OAC=(180°﹣∠AOC)÷2=71°,∴∠BOC=∠AOD﹣∠AOC﹣∠BOD=14°,∴∠AOB=∠AOC+∠BOC=52°,在△AOB中,由内角和定理得∠B=180°﹣∠OAC﹣∠AOB=180°﹣71°﹣52°=57°.答:∠B的度数为57°.11.如图,在平行四边形ABCD中,E为AD上一点,∠EBC=40°,且BE=BC,CE=CD,则∠A= 110° .【解答】解:如图所示:∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB,AB∥CD,∴∠2=∠3,∠A+∠D=180°,∵BE=BC,CE=CD,∴BE=BC=10,CE=CD=6,∠1=∠2,∠3=∠D,∴∠1=∠2=∠3=∠D,∵∠EBC=40°,∴∠D=∠1=∠3=70°,∴∠A=180°﹣70°=110°;故答案为:110°.12.如图,已知菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC,垂足为点E,则AE的长是 cm.【解答】解:如图,设AC与BD的交点为O,∵四边形ABCD是菱形,∴CO=AC=3cm,BO=BD=4cm,AC⊥BD,∴BC===5cm,∴S菱形ABCD=AC•BD=×6×8=24(cm2),∵S菱形ABCD=BC×AE,∴BC×AE=24,∴AE=(cm),故答案为:.13.如图,▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为 8 .【解答】解:连接EF,AE与BF交于点O,如图,∵AB=AF,AO平分∠BAD,∴AO⊥BF,BO=FO=BF=3,∵四边形ABCD为平行四边形,∴AF∥BE,∴∠1=∠3,∴∠2=∠3,∴AB=EB,而BO⊥AE,∴AO=OE,在Rt△AOB中,AO==4,∴AE=2AO=8.故答案为:8.14.如图,矩形纸片ABCD中,已知AD=12,AB=9,E是BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 或9 .【解答】解:有两种情形:①如图1中,当∠EFC=90°时,A,F,C共线,设BE=EF=x,在Rt△ABC中,∵∠B=90°,AB=9,BC=AD=12,∴AC==15,在Rt△EFC中,∵EC2=EF2+CF2,∴(12﹣x)2=x2+62,∴x=,②如图2中,当∠FEC=90°时,四边形ABEF是正方形,BE=AB=9,综上所述,BE的值为或9.三.解答题(共7小题)15.解方程:(1);(2).【解答】解:(1)两边都乘以x(x﹣6),得3(x﹣6)=2x,解得x=18,检验,当x=18时,x(x﹣6)=216≠0,∴x=18是方程的解;(2)两边都乘以x﹣2,得1﹣3(x﹣2)=x﹣1,去括号,得1﹣3x+6=x﹣1,移项,得﹣3x﹣x=﹣1﹣6﹣1,合并同类项,得﹣4x=﹣8系数化为1,得x=2,检验:当x=2时,x﹣2=0,x=2是方程的增根,∴原方程无解.16.先化简,再求值:,其中a是满足不等式3a﹣1>﹣4的最小整数解.【解答】解:A=•=,由3a﹣1>﹣4,解得:a>﹣1,即a=2(a=0与a=1原式没有意义),则原式=1.17.如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).(1)画出△ABC关于原点成中心对称的△A'B'C';(2)将△ABC绕坐标原点O逆时针旋转90°,得△A″B″C″,画出△A″B″C″;(3)请直接写出,以A'、B'、C'为顶点的平行四边形的第四个顶点D'的坐标.【解答】解:(1)如图,△A'B'C'即为所求作.(2)如图,△A″B″C″即为所求作.(3)D点的坐标(5,3)或(7,﹣3)或(﹣3,﹣3).18.如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.(1)求证:BE=DF;(2)求证:AF∥CE.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠5=∠3,∵∠1=∠2,∴∠AEB=∠4,在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴BE=DF;(2)由(1)得△ABE≌△CDF,∴AE=CF,∵∠1=∠2,∴AE∥CF,∴四边形AECF是平行四边形,∴AF∥CE.19.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P 作PM⊥AD,PN⊥CD,垂足分别为M、N.(1)求证:∠ADB=∠CDB;(2)若∠ADC=90°,求证:四边形MPND是正方形.【解答】证明:(1)∵对角线BD平分∠ABC,∴∠ABD=∠CBD,在△ABD和△CBD中,,∴△ABD≌△CBD(SAS),∴∠ADB=∠CDB;(2)∵PM⊥AD,PN⊥CD,∴∠PMD=∠PND=90°,∵∠ADC=90°,∴四边形MPND是矩形,∵∠ADB=∠CDB,PM⊥AD,PN⊥CD,∴PM=PN,∴四边形MPND是正方形.20.如图,点A在直线l外,点B在直线l上.(1)在l上求作一点C,在l外求作一点D,使得以A、B、C、D为顶点的四边形是菱形;(要求:用直尺和圆规作出所有大小不同的菱形)(2)连接AB,若AB=5,且点A到直线l的距离为4,通过计算,找出(1)中面积最小的菱形.【解答】解:(1)如图①②③;(2)图①中,菱形ABCD的面积=5×4=20,图②中,BC=6,AD=8,菱形ABDC的面积=×6×8=24,图③中,作AH⊥BC于H,设菱形的边长为x,在Rt△ABH中,AH=4,AB=5,则BH=3,所以CH=x﹣3,在Rt△ACH中,42+(x﹣3)2=x2,解得x=菱形ACBD的面积=×4=,所以面积最小的菱形为ACBD.21.如图1,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,M 和N分别为OB、OC的中点,连接ED、EM、MN、ND.(1)求的值;(2)当△ABC满足什么条件时,四边形DEMN是矩形?给出你的结论并证明.(3)如图2,在△ABC中,BD、AF分别是边AC、BC上的中线,BD与AF相交于点O,若OA=4,OC=3,OB=5,则△ABC的面积为 18 (请直接写出结果).【解答】解:(1)∵D、E、M、N分别为AC、AB、OB、OC的中点,∴DE∥BC,DE=BC,MN∥BC,MN=BC,∴DE∥MN,DE=MN,∴四边形EMND为平行四边形,∴OM=OD,∵OM=BM,∴OB=2OM=2OD,∴=2;(2)当AB=AC时,四边形DEMN为矩形,理由如下:∵D、E为AC、AB的中点,∴AD=AC,AE=AB,∴AD=AE,在△AEC和△ADB中,,∴△AEC≌△ADB(AAS),∴BD=CE,∵OD=OM=BM,∴MD=BD,同理EN=EC,∴MD=EN,∴四边形DEMN为矩形;(3)∵D,E,F分别为中点,设图中各小三角形的面积分别为a,b,c,由△ABF于△ACF等积,得a+2c=a+2b,∴b=c,同理可得a=b=c,∵OA=4,∴OF=2,延长OF到G,可得BG=OC=3,OG=2OF=4,∵OB=5,∴△OBG是直角三角形,且面积为6,∴a=3,∴△ABC的面积=6a=18.故答案为:18.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
编号(接待老师填写)__________本学区□是□否
姓名
性别
出生
年月
民族
贴照片处
家庭住址
身份证号
毕业小学
户籍(注明市、区)
家庭
称谓
姓名
工作单位、职务
手机
主要
父
ቤተ መጻሕፍቲ ባይዱ成员
母
学科
成绩
年级
语文
数学
外语
体育
担任学生
干部情况
校级荣誉(三好学生、优秀学干等)
四年级
上
下
五年级
上
下
六年级
上
区级及区级以上荣誉
学科竞赛情况(同一学科填写最高获奖)
时间
竞赛名称
获奖等第
科技、体育、艺术、文学特长
材料审核情况
审核人
注:学生简历装订次序:招生报名表、四五六年级成长脚印复印件、户口本复印件、房产证复印件及获奖证书复印件。有关材料复印件(原件自己带回)交学校存档,概不退还,谢谢您的配合!
