初三数学提高练习
初三数学提高班方程的整数根(练习)
初三数学提高班 方程的整数根(练习)1、设a 为整数,若存在整数b 和c,使(x+a)(x-15)-25=(x+b)x+c),则a 可取值为 。
2、设p 、q 为质数,则关于x 的方程x 2+px+q 4=0的整数解是 。
3、设k 为整数,关于x 方程(k 2－1)x 2－3(3k －1)x+18=0有两个不等正整数根,则k= 。
4、方程(a 2－1)x 2－2(5a+1)x+24=0有两个不等负整数根,则整数a 的值是 。
5、已知0122=-+ax x 能分解成两个整系数的一次因式的乘积,则符合条件的整数a 的个数为 。
6、若方程x 2+(4n+1)x+2n=0(n 为整数)有两个整数根,那么这两个根是( )(A)都是奇数 (B)都是偶数 (C)一奇一偶 (D) 无法判断7.若p 、q 都是自然数,方程px 2－qx+1985=0的两根都是质数,则12p 2+q 的值等于( )(A) 404 (B) 1998 (C)414 (D) 19968、已知方程a 2x 2－(3a 2－8a)x+2a 2－13a+15=0(其中是a 正整数)至少有一个整数根,求a 的值。
9、设m 为整数,且4＜m ＜40, 方程x 2+2(2m －3)x+4m 2－14m+8=0有两个整数根,求m的值10、求所有实数k,使方程kx 2+(k+1)x+(k －1)=0的根都是整数。
11、若k 为正整数,且一元二次方程(k －1)x 2－px+k=0的两根为正整数,求k kp (p p +k k )+(p+k)的值。
12、求所有的正整数a ，b ，c ，使得关于x 的方程0232=+-b ax x ，0232=+-c bx x ，0232=+-a cx x 的所有的根都是正整数。
13、试确定一切有理数r ，使得关于x 的方程rx 2+(r+2)x+r-1=0有且只有整数根14、周长为6面积为整数的直角三角形是否存在?若不存在,请给出证明,若存在,共有几个? .。
初三数学增长率练习题
初三数学增长率练习题增长率是数学中一个基本的概念，是计算一个数值相对于另一个数值增长的速度或程度。
对于初三学生来说，理解和运用增长率的概念是非常重要的。
本文将通过一些练习题来帮助初三学生提高他们的数学技巧和使用增长率的能力。
1. 小明的身高从去年的150厘米增长到今年的165厘米。
求小明的身高增长率。
解答：身高增长率是指身高的增长量与原身高的比值。
小明的身高增长量为165 - 150 = 15厘米。
原身高为150厘米。
所以小明的身高增长率为15 / 150 = 0.1，即10%。
2. 一个电子产品从去年的售价3000元涨到今年的售价3300元。
求该电子产品的价格增长率。
解答：价格增长率是指价格的增长量与原价格的比值。
该电子产品的价格增长量为3300 - 3000 = 300元。
原价格为3000元。
所以该电子产品的价格增长率为300 / 3000 = 0.1，即10%。
3. 一辆汽车在过去的1小时内行驶了50公里，而在接下来的2小时内行驶了120公里。
求该汽车的平均速度增长率。
解答：平均速度增长率是指平均速度的增长量与原平均速度的比值。
该汽车过去1小时的平均速度为50公里/小时，接下来2小时的平均速度为120公里/2小时 = 60公里/小时。
所以平均速度增长量为60 - 50 =10公里/小时。
原平均速度为50公里/小时。
所以该汽车的平均速度增长率为10 / 50 = 0.2，即20%。
通过以上例题，我们可以看出增长率是一个衡量变化速度的重要指标。
掌握增长率的计算方法可以帮助我们更好地理解数值之间的变化关系，并且在实际生活中能够更好地应用数学知识。
除了以上的练习题，我们还可以通过更多的实际例子来练习增长率的计算。
比如：4. 一个学生的数学成绩从上一次考试的80分提高到这一次考试的96分。
求该学生的数学成绩增长率。
解答：数学成绩增长量为96 - 80 = 16分。
原数学成绩为80分。
所以该学生的数学成绩增长率为16 / 80 = 0.2，即20%。
初三数学提高班练习题
初三数学提高班练习题一、填空题：1、抛物线2)1(2+-=x y 的顶点坐标是 ；当x______时，y 随x 增大而减小。
2、已知二次函数22y x x m =-++的部分图象如图所示，则关于x 的一元二次方程220x x m -++=的解为 ．3、如图，在△ABC 中，21=DBAD ，DE ∥BC ，若△ABC 的面积为9，则△ADE 的面积是__________.4、 若将二次函数223y x x =--配方为()2y x h k =-+的形式，则y = .5、如图，AB 为O 的直径，点C D ，在O 上，50BAC ∠=，则A D C ∠= ．二、选择题：6、已知二次函数2y ax bx c =++的图象如图所示，则下列结论正确的是（ ）． A ．ab ＞0，c ＞0 B ．ab ＞0，c ＜0C ．ab ＜0，c ＞0D ．ab ＜0，c ＜0 7、已知（m ，2）是抛物线2-2y x x =-上的一个点，则m m -2的值是( )A ． -2 B. 0 C. 2 D. 4 8、如图，如果从半径为9cm 的圆形纸片剪去13圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为 A ．6cmB ．35cmC ．8cmD ．53cm9、下列各组图形不一定相似的是（ ） （A ）两个等腰直角三角形；（B ）各有一个角是100°的两个等腰三角形；（C ）各有一个角是40°的两个直角三角形；（D ）两个菱形；DBAOyEDCBA 第3题yxO 13第2题 ACDOB第5题10、如图，AB 是斜靠在墙上的梯子，梯脚距墙2米，梯子上的D 点距墙1.8米，BD 长0.6米，则梯子的长为（ ）A 、5.60米B 、6.00米C 、6.10米D 、6.20米 11．元旦，6位朋友均匀地围坐在圆桌旁共度佳节．圆桌半径为60cm ，每人离圆桌的距离均为10cm ，现又来了两名客人，每人向后挪动了相同的距离，再左右调整位置，使8人都坐下，并且8人之间的距离与原来6人之间的距离（即在圆周上两人之间的圆弧的长）相等．设每人向后挪动的距离为x ，根据题意，可列方程（ ）A ．2π(6010)2π(6010)68x +++=B ．2π(60)2π6086x +⨯=C ．2π(6010)62π(60)8x +⨯=+⨯D ．2π(60)82π(60)6x x -⨯=+⨯12、在同一坐标系中一次函数y ax b =+和二次函数2y ax bx =+的图象可能为（ ）三、解答题13、（本题满分8分）请你设计一个关于x 、y 的函数关系，使得：当x=3时，y=8；当x=4时，y=6。
初三数学培优(提高班)
反比例函数练习姓名 班级 分数一、填空题：（分数2分×12=24分）1、u 与t 成反比，且当u ＝6时，81=t ，这个函数解析式为 ；2、函数2x y -=和函数xy 2=的图像有 个交点；3、反比例函数xky =的图像经过（－23，5）点、（a ，－3）及（10，b ）点，则k ＝ ，a ＝ ，b ＝ ；4、若函数()()414-+-=m x m y 是正比例函数，那么=m ，图象经过 象限；5、若反比列函数1232)12(---=k k xk y 的图像经过二、四象限，则k = _______6、已知y -2与x 成反比例，当x =3时，y =1，则y 与x 间的函数关系式为 ；7、已知正比例函数kx y =与反比例函数3y x=的图象都过A （m ，1），则m ＝ ，正比例函数与反比例函数的解析式分别是 、 ； 8、 设有反比例函数y k x=+1，(,)x y 11、(,)x y 22为其图象上的两点，若x x 120<<时，y y 12>，则k 的取值范围是___________9、右图3是反比例函数xk y =的图象，则k 与0的大小关系是k 0.10、函数xy 2-=的图像，在每一个象限内，y 随x 的增大而 ； 11、反比例函数()0>=k xk y 在第一象限内的图象如图，点M 是图像上一点，MP 垂直x 轴于点P ，如果△MOP 的面积为1，那么k 的值是 ；12、()7225---=m mx m y 是y 关于x 的反比例函数，且图象在第二、四象限，则m 的值为 ； 二、选择题： （分数2分×14=28分） 1、下列函数中，反比例函数是（ ） A 、1)1(=-y x B 、11+=x y C 、21xy = D 、x y 31=2、已知反比例函数的图像经过点（a ，b ），则它的图像一定也经过（ ） A 、(－a ,－b ) B 、(a ,－b ) C 、 (－a ，b ) D 、（0，0）3、如果反比例函数xky =的图像经过点（－3，－4），那么函数的图像应在（ ） A 、第一、三象限 B 、第一、二象限 C 、第二、四象限 D 、第三、四象限 4、若y 与－3x 成反比例，x 与z4成正比例，则y 是z 的（ ） yxO PMA 、正比例函数B 、反比例函数C 、一次函数D 、不能确定 5、若反比例函数22)12(--=mx m y 的图像在第二、四象限，则m 的值是（ ）A 、－1或1B 、小于21的任意实数 C 、－1 Ｄ、不能确定 6、函数x k y =的图象经过点（－4，6），则下列各点中在xky =图象上的是（ ）A 、（3，8）B 、（3，－8）C 、（－8，－3）D 、（－4，－6） 7、正比例函数kx y =和反比例函数xky =在同一坐标系内的图象为（ ）ABCD8、如上右图，A 为反比例函数xky =图象上一点，AB 垂直x 轴于B 点，若S △AOB ＝3，则k 的值为（ ） A 、6B 、3C 、23 D 、不能确定9、如果矩形的面积为6cm 2，那么它的长y cm 与宽x cm 之间的函数关系用图象表示大致（ ）ABCD10、在同一直角坐标平面内，如果直线x k y 1=与双曲线xk y 2=没有交点，那么1k 和2k 的关系一定是 A 、1k <0，2k >0B 、1k >0，2k <0C 、1k 、2k 同号D 、1k 、2k 异号11、已知变量y 与x 成反比例，当x =3时，y =―6；那么当y =3时，x 的值是（ ） A 、6 B 、―6 C 、9 D 、―9 12、当路程s 一定时，速度v 与时间t 之间的函数关系是（ ） A 、正比例函数 B 、反比例函数 C 、一次函数 D 、二次函数13、（2001北京西城）在同一坐标系中，函数x k y =和3+=kx y 的图像大致是 （ ）A B C D14、已知反比例函数)0(<=k xky 的图像上有两点A(1x ，1y )，B(2x ，2y )，且21x x <，则21y y -的y x o yxo y x o yxo A BOxyoy xy xoy xoy xo值是（ ）A 、正数B 、负数C 、非正数D 、不能确定 三、解答题：（共48分）1、如图，Rt △ABO 的顶点A 是双曲线xky =与直线)1(+--=k x y 在第二象限的交点， AB ⊥x 轴于B 且S △ABO =23 （1）求这两个函数的解析式（2）求直线与双曲线的两个交点A ，C 的坐标和△AOC的面积。
适合初三数学的练习题推荐
适合初三数学的练习题推荐初三是学生中学阶段的关键时期，数学是其中最为重要的学科之一。
通过做练习题可以帮助学生巩固所学知识，培养解决问题的能力。
本文将为初三学生推荐一些适合的数学练习题，以帮助他们提高数学水平。
一、代数与方程1. 基础练习：求解下列方程：a) 3x + 4 = 16b) 5(x - 2) = 15c) 2(3x + 1) = 4(5 - x)d) 7x + 3 = 8(x + 2) - 52. 整式化简：将下列各式化简，并写出最简形式：a) 3x + 2x + 5 - x + 4b) 4(x - 2) - 3(2x + 1)c) 2(x + 3) - 3(x - 2) + 2(4 + x)3. 基础应用题：某数的三倍加上4等于16，求这个数。
二、几何与图形1. 基础练习：根据已知条件，求以下图形的周长和面积：a) 一个正方形的边长为6cm。
b) 一个矩形的长和宽分别为8cm和5cm。
c) 一个圆的直径为10cm。
2. 图形运算：已知ABCD为一个平行四边形，E为AC的中点，连接BE，证明BE平分CD。
3. 基础应用题：一个正方形的边长是x cm，它的面积等于另一个正方形的面积的4倍，求另一个正方形的边长。
三、概率与统计1. 基础练习：某班级学生的身高数据如下（单位：cm）：155 158 160 162 165 170 172 174 176 178求出这组数据的众数、中位数和平均数。
2. 统计问题：某班级男生和女生人数的比例为2:3，如果班级增加了10名男生和15名女生，比例变为3:4，求原来班级的总人数。
3. 基础应用题：某次模拟考试中，某题正确率为80%，共有100人参加考试，求回答正确的人数。
四、函数与图像1. 基础练习：已知函数y = 2x + 3，求出以下各函数的值：a) y(1)b) y(-2)c) y(0)2. 图像问题：绘制函数y = 2x - 1的图像，并标出与坐标轴的交点。
最新人教版九年级初三数学上册《旋转作图》提升练习题
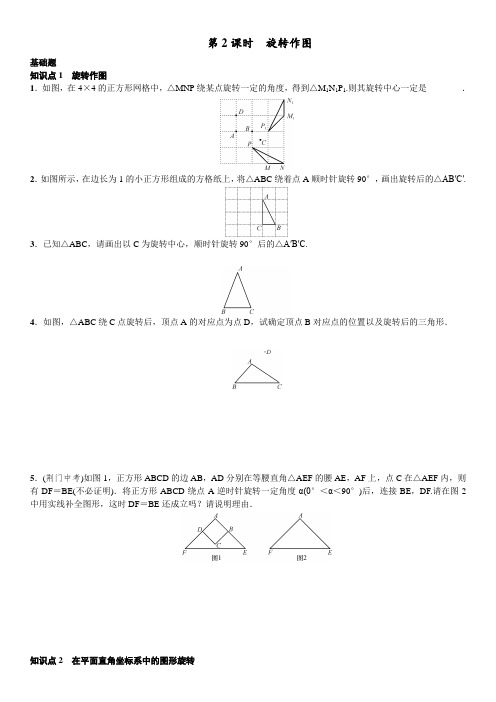
第2课时旋转作图基础题知识点1旋转作图1．如图，在4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1.则其旋转中心一定是________．2．如图所示，在边长为1的小正方形组成的方格纸上，将△ABC绕着点A顺时针旋转90°，画出旋转后的△AB′C′. 3．已知△ABC，请画出以C为旋转中心，顺时针旋转90°后的△A′B′C.4．如图，△ABC绕C点旋转后，顶点A的对应点为点D，试确定顶点B对应点的位置以及旋转后的三角形．5．(荆门中考)如图1，正方形ABCD的边AB，AD分别在等腰直角△AEF的腰AE，AF上，点C在△AEF内，则有DF＝BE(不必证明)．将正方形ABCD绕点A逆时针旋转一定角度α(0°＜α＜90°)后，连接BE，DF.请在图2中用实线补全图形，这时DF＝BE还成立吗？请说明理由．知识点2在平面直角坐标系中的图形旋转6．(烟台中考)如图，将△ABC绕点P顺时针旋转90°得到△A′B′C′，则点P的坐标是()A．(1，1) B．(1，2) C．(1，3) D．(1，4)7．(邵阳中考)如图，在平面直角坐标系xOy中，已知点A(3，4)，将OA绕坐标原点O逆时针旋转90°到OA′，则点A′的坐标是________．8．(青岛中考)如图，△ABC的顶点都在方格线的交点(格点)上，如果将△ABC绕C点按逆时针方向旋转90°，那么点B的对应点B′的坐标是________．中档题9．如图，该图形围绕点O按下列角度旋转后，不能与其自身重合的是()A．72°B．108°C．144°D．216°10．(巴中中考)如图，已知直线y＝－43x＋4与x轴、y轴分别交于A、B两点，把△AOB绕点A按顺时针方向旋转90°后得到△AO′B′，则点B′的坐标是________．11.(潜江、天门、仙桃中考)如图，在平面直角坐标系中，点A的坐标为(－1，2)点C的坐标为(－3，0)，将点C绕点A逆时针旋转90°，再向下平移3个单位，此时点C对应点的坐标为________．12．如图，四边形ABCD绕点O旋转后，顶点A的对应点为点E，试确定B，C，D的对应点的位置以及旋转后的四边形．13．(眉山中考)如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别是A(－3，2)，B(－1，4)，C(0，2)．(1)将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；(2)平移△ABC，若A的对应点A2的坐标为(－5，－2)，画出平移后的△A2B2C2；(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C，请直接写出旋转中心的坐标．综合题14．(永州中考)在同一平面内，△ABC和△ABD如图1放置，其中AB＝BD.小明做了如下操作：将△ABC绕着边AC的中点旋转180°得到△CEA，将△ABD绕着边AD的中点旋转180°得到△DFA，如图2.请完成下列问题：(1)试猜想四边形ABDF是什么特殊四边形，并说明理由；(2)连接EF，CD，如图3，求证：四边形CDFE是平行四边形．参考答案基础题1.点B2.图略所示，△AB′C′为所求三角形．3.如图所示．4.图略，顶点B对应点的位置在点E处，△DEC为△ABC绕点C旋转后得到的三角形．5.补全图形图略．DF＝BE成立．理由：∵四边形ABCD是正方形，△AEF是等腰直角三角形，∴AD＝AB，AF＝AE ，∠FAE ＝∠DAB ＝90°.∴∠FAD ＝∠EAB.在△ADF 和△ABE 中，⎩⎪⎨⎪⎧AD ＝AB ，∠FAD ＝∠EAB ，AF ＝AE.∴△ADF ≌△ABE(SAS)．∴DF ＝BE.6.B7.(－4，3)8.(1，0) 中档题9.B 10.(7，3) 11.(1，－3) 12.略．13．(1)图略．(2)图略．(3)旋转中心的坐标为(－1，0)． 综合题14．(1)四边形ABDF 是菱形．理由如下：∵△DFA 是由△ABD 绕AD 的中点旋转180°所得，∴AB ＝DF ，BD ＝FA.∴四边形ABDF 是平行四边形．又∵AB ＝BD ，∴四边形ABDF 是菱形．(2)证明：由(1)知四边形ABDF 是平行四边形，∴AB ∥DF 且AB ＝DF.由旋转易知四边形ABCE 是平行四边形，∴AB ∥CE 且AB ＝CE.∴DF ∥CE 且DF ＝CE ，∴四边形CDFE 是平行四边形．良好的学习态度能够更好的提高学习能力。
初三的学生适合做的练习题
初三的学生适合做的练习题初三是一个非常重要的学习阶段，学生们需要通过大量的练习来巩固所学知识，提高解题能力。
下面将介绍一些适合初三学生做的练习题，帮助他们更好地备考。
一、数学练习题1. 基础求解题：选择题或填空题，包括整数、分数、小数、百分数等概念的理解和运用。
2. 初步几何题：如平面图形的认识、计算周长和面积、求解角度等。
3. 代数与方程题：包括一元一次方程、二元一次方程、不等式等。
4. 应用题：生活中的实际问题，如时间、距离、速度等计算题。
二、语文练习题1. 阅读理解：文章阅读后回答问题，考查学生对文章的理解能力。
2. 词语运用：如读音、词义、词语搭配和造句等，帮助学生加深对语言知识的理解和掌握。
3. 作文练习：引导学生写作文，锻炼他们的写作能力和逻辑思维能力。
4. 古诗文默写：帮助学生记忆和理解古代文化，提高语言表达和写作水平。
三、英语练习题1. 语法练习：包括时态、语态、被动语态、疑问句等语法知识的强化训练。
2. 阅读理解：根据文章内容回答问题，培养学生的阅读理解能力。
3. 写作练习：引导学生写简单的英语作文，提高他们的写作表达能力。
4. 听力练习：通过听力材料测试学生对英语听力的理解和应对能力。
四、物理练习题1. 基本概念与定律：如物理基本量、物理单位、质量、速度等知识点的运用。
2. 基本公式的运用：如速度、加速度等的计算，培养学生运用公式解题的能力。
3. 实验练习：引导学生进行简单的实验，帮助他们理解物理现象和实验原理。
4. 应用题：如力的计算、功的计算等实际问题的解决。
五、化学练习题1. 基本元素与化合物：包括元素符号、化合物名称、化学方程式等基本知识的理解和记忆。
2. 化学计算题：如物质的质量、物质的量等计算题，培养学生运用公式解题的能力。
3. 反应方程式和化学平衡：通过练习题帮助学生理解和掌握反应方程式的写法和化学平衡概念。
4. 实验练习：引导学生进行一些简单的化学实验，加深对实验原理的理解和应用能力。
适合数学基础差的初三学生练习题
适合数学基础差的初三学生练习题数学是一门综合性的学科，对于很多初三学生来说，数学可能是他们的一块拦路石。
对于那些数学基础较差的学生来说，提供一些适合他们练习的题目，可以帮助他们加强对数学的理解和掌握。
下面是一些适合数学基础差的初三学生的练习题。
一、基础运算练习1. 计算下列各题：a) 9 + 5 =b) 16 - 7 =c) 3 × 4 =d) 21 ÷ 7 =2. 化简下列各式：a) 3x + 4x - 2x =b) 8y - 3y + 2y =3. 求解下列方程：a) 2x + 5 = 11b) 3y - 7 = 104. 按要求解下列算式：a) 12 × 3 - 5 =b) 20 ÷ 5 + 3 × 2 =c) 18 - (5 + 3) =二、分数运算练习1. 计算下列各题：a) 1/2 + 1/4 =b) 3/5 - 1/10 =c) 2/3 × 3/4 =d) 4/5 ÷ 2/3 =2. 化简下列各式：a) (3/4 + 1/8) × 2/3 =b) (5/6 - 1/2) ÷ 2/3 =3. 将下列百分数转化为分数：a) 60% =b) 25% =4. 求解下列问题：a) 小明吃了一块蛋糕的 3/5，还剩下 2/5，蛋糕原来有多少块？b) 公园里的花坛里有 48 朵花，其中的 2/3 是红色的，其他的是白色的，白色花有多少朵？三、几何问题练习1. 给出下列图形的名称：a) △ABCb) ○O2. 求解下列问题：a) 长方形的长是 6cm，宽是 4cm，求面积和周长。
b) 半径为 5cm 的圆的周长是多少？3. 计算下列各题：a) 两个角的度数分别是 30°和 60°，这两个角的和是多少度？b) 一个角的度数是 120°，那么这个角的补角是多少度？四、代数式与方程式练习1. 计算下列代数式：a) 2x + 3y，当 x = 4，y = 5 时的值是多少？b) 5a - 2b，当 a = 7，b = 3 时的值是多少？2. 解下列方程：a) 2x - 5 = 7b) 3y + 4 = 223. 求解下列问题：a) 某数的三倍减去 7 的结果等于 11，求这个数是多少？b) 一个数的 2/3 加上 4 等于 12，求这个数是多少？五、应用题练习1. 求解下列问题：a) 小明的年龄是小红的 2 倍，小红的年龄是 10 岁，求小明的年龄。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初三数学提高练习学校_____________班级_____________姓名_______________学号________ 一、选择题(共8小题，每小题5分，满分40分. 以下每小题均给出了代号为A 、B 、C 、D 的四个选项，其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填均得零分)1．如果226(21)x x m x ⎛⎫= ⎪-⎝⎭，那么代数式m 是（ ） （A ）3(21)x ±- （B ）2(21)x ±- （C ）3(21)x - （D ）2(21)x - 2．在平面直角坐标系中，点A （x -，1y -）在第四象限，那么点 B （1y -，x ）在（ ）（A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限 3．如图，以数轴的单位长线段为边作一个正方形，以数轴的原点为圆心 ，正 方形的对角线长为半径画弧，交数轴于点A 2的平方 根是（ ）（A ） 2± （B ）2- （C ）2 （D 4．如果,22,12=+=+cb b a ，那么ac 1+等于 ( )（A ）4 （B ）3 （C ）2 （D ）1 5．考虑下列4个命题：其中正确命题的序号是( ) ①有一个角是100°的两个等腰三角形相似； ②斜边和周长对应相等的两个直角三角形全等； ③对角线互相垂直且相等的四边形是正方形； ④对角线相等的梯形是等腰梯形．(A)①②③④ (B)①②④ (C)②③④ (D)①④6．已知如图，在矩形ABCD 中有两个一条边长为1的平行四边形.则它们的公共部分(即阴影部分)的面积是 ( )（A ）大于1 （B ）等于1 （C ）小于1（D ）小于或等于1AFBECD7．已知梯形的两条对角线分别为m 与n ，两对角线的夹角为60 0. 那么，该梯 形的面积为（ ）（A ）mn 23 （B ）mn 43 （C ）mn 83 （D ）mn 3 8．已知，正整数n ，k 满足不等式65119n k <<，那么当n 与k 取最小值时，n +k 的值为（ ）（A ）29 （B ）30 （C ）31 （D ）32二、填空题（共6小题，每小题5分，满分30分）9．已知⊙O 的直径AB=22cm ，过点A 有两条弦AC=2cm ，AD=6cm ，那 么劣弧CD 的度数为_________.10．已知，关于x 的一元二次方程260x kx --=与260x x k --=只有一个公共 的根，那么方程052||2=++-k x k x 所有的根的和是 .11．在写有整式 5，r ，a b -，2m ，π，5x ，2()x y +，3mn 的卡片中，任意 选取其中两张分别作为分子和分母，得到一个分式的概率是 . 12．如图，直线12125y x =-+与x 轴、 y 轴分别交于A 点和B 点，C 是OB 上的一 点，若将∆ABC 沿AC 翻折得到∆AB /C ，B / 落在x 轴上，则过A ，C 两点的直线的解析 式是 . 13．若251+=x ，则431xx x ++= . 14．如图，在∆ABC 中，∠C=90︒，D 、E 分别是 BC 上的两个三等分点，以D 为圆心的圆过点E ，且交AB 于点F ，此时CF 恰好与⊙D 相切于点F. 如果AC=245，那么⊙D 的半径= .三、解答题（共4题，分值依次为12分、12分、12分、14分，满分50分） 15．已知，一次函数11+-=k kxy （k 是不为0的自然数，且是常数）的图象与两坐标轴所围成的图形的面积为k S （即k=1时，得1S ，k=2时，得2S ，┅）.试求1S +2S +3S +2006S + 的值.16．一商店销售某种食品，每天从食品厂批发进货，当天销售. 已知进价为每千克5元，售价为每千克9元，当天售不出的食品可以按每千克3元的价格退还给食品厂. 根据以往销售统计，该商店平均一个月(按30天计算)中，有12天每天可以售出这种食品100千克，有18天每天只能售出60千克. 食品厂要求商店每天批进这种食品的数量相同，那么该商店每天从食品厂批进这种食品多少千克，才能使每月获得的利润最大?最大利润是多少?17．已知，∆ABC 和∆A 1B 1C 1均为正三角形，BC 和B 1C 1中点均为D ，如图1. (1)当∆A 1B 1C 1绕点D 旋转到∆A 2B 2C 2时，试判断AA 2与CC 2的位置关系，并证明你的结论.(2)如果当∆A 1B 1C 1绕点D 旋转一周，顶点A 1和AC 仅有一个交点，设该交点为A 3，如图3. 当AB=4时，求多边形ABDC 3C 的面积.18．给出一个三位数. 重排这个三位数三个数位上的数字，得到一个最大的数和一个最小的数，它们的差构成一个三位数（允许百位数字为零），再重排这个得到的三位数三个数位上的数字，又得到一个最大的数和一个最小的数，它们的差又构成另一个三位数（允许百位数字为零），重复以上过程. 问重复2007次后所得的数是多少？证明你的结论.CD 1 C 1CABD B 2C 2A 2ABCDB 3C 3A 3 图1图2图3《初三数学提高练习》参考答案和评分意见一、选择题(每小题5分，共40分) 1—8：ACAD BCBC二、填空题(每小题5分，共30分)9． 30︒或150︒ 10． 0 11．34 12． 21033y x =-+ 13．1 14 三、解答题（共4题，分值依次为12分、12分、12分、14分，满分50分）15．一次函数11+-=k kx y 的图象与两坐标轴的交点为（1k ，0）、（0，11k +），所围成的图形的面积为)1(12111121+⋅=+⋅=k k k k S k . …………4分 ∴1S +2S +3S +2006S +=20072006121431213212121121⨯⋅++⨯⋅+⨯⋅+⨯⋅ …………8分 =)200720061431321211(21⨯++⨯+⨯+⨯ =)200712006141313121211(21-++-+-+- =)200711(21- =20071003. …………12分 16．设该商店每天批进这种食品x 千克，每月获得的利润为y 元．（1）当60100x ≤≤时，由题意，30天中批进这种食品的成本为530x ⨯元，销售收入为元9(126018)x +⨯，退货所得为318(60)x ⨯-元，于是可得 9(126018)318(60)530y x x x =+⨯+⨯--⨯即126480y x =+ …………4分 ∵126480y x =+是一次函数，且y 随x 的增大而增大，∴当100x =时，即每天批进这种食品100千克时，可获得最大利润，最大利润为7680元． …………8分（2）当100x ≥时，由题意，CABDB 2C 2A 2FE ABCDB 33A 3 G 9(121006018)312(9100)318(60)530y x x x =⨯+⨯+⨯-+⨯--⨯化简得 6013680y x =-+∵6013680y x =-+是一次函数，且y 随x 的增大而减小，∴当100x =时，即每天批进这种食品100千克时，可获得最大利润，最大利润为7680元． …………12分17．AA 2⊥CC 2. …………2分 （1）在图2中，连接AD 、A 2D 、延长AA 2 交BC 于E ，交CC 2于F ，∵∠ADA 2=90︒-∠A 2DC=∠CDC 2，22AD DC=DA DC （等边三角形都相似，相似三角形对应高的比等于相似比） ∴∆AA 2D∽∆CC 2D ，于是得∠A 2AD=∠C 2CD …………5分 又因为∠AED=∠CEF ，∴∠ADE=∠CFE=90︒∴AA 2⊥CC 2. …………8分（2）在图3中，连接A 3D ，过C 3作C 3G ⊥BC 于G ，由（1）得AC ⊥CC 3， 由题意又得A 3D ⊥AC ， 四边形A 3CC 3D 是矩形.∴C 3C=A 3D=2sin 60︒=，C 360)︒-︒=∴多边形ABDC 3C 的面积=3ABC CC D S S ∆∆+21422+⨯. …………12分18．经过2007步后得到495或0. …………2分不妨设选定的三位数中的最大数字为x ，最小数字为z ，还有一个数字为y ，则(10010)(10010)99()P x y z z y x x z =++-++=-， …………4分现讨论如下：（1）0x z -=，0P =，第一步结果0.（2）1x z -=，99P =，第一步结果099,第二步结果891,第三步结果792 ,第四步结果693，第五步结果954,第六步结果495.（3）2x z -=，198P =，第一步结果198，第二步结果792，第三步结果692，第四步结果954，第五步结果495.（4）3x z -=，297P =，第一步结果297,第二步结果693,第三步结果954 ,第四步结果495.（5）4x z -=，396P =，第一步结果396,第二步结果594,第三步结果495. （6）5x z -=，495P =，第一步结果495.（7）6x z -=，594P =，第一步结果594,第二步结果495.（8）7x z -=，693P =，第一步结果693，第二步结果594，第三步结果495. （9）8x z -=，792P =，第一步结果792 ,第二步结果693,第三步结果954,第四步结果495.（10）9x z -=，891P =，第一步结果891,第二步结果792 ,第三步结果693,第四步结果954,第五步结果495.由以上讨论可知至多6步可将一个三位数变为495或0，然后就进入循环，所以经过2007步后将得到495或0.当x z =时，得到0；当x z >时，得到495. …………14分（讨论一种情况给1分）。