【恒心】【好卷速递】四川省成都七中2012届高三一诊模拟考试数学(文)试题
四川省成都市第七中学2023-2024学年高三上学期10月月考语文试题

成都七中2023-2024学年度2024届高三(上)10月阶段性考试语文试卷本试卷共23题,共8页,共150分。
考试时间150分钟。
一、现代文阅读(35分)(一)现代文阅读I(本题共5小题,19分)阅读下面的文字,完成下面小题。
对素食者和肠胃疾病患者来说,藜麦的发现是一个奇迹。
藜麦不含麸质,富含镁和铁,比其他种子含有更多的蛋白质,包括人体无法独自生成的必需的氨基酸。
美国宇航局宣布,藜麦是地球上营养最均衡的食物之一,是宇航员的理想之选。
产于安第斯山的藜麦有一个令西方消费者神往的传说:印加人非常重视藜麦,认为它是神圣的,并且称之为“万谷之母”。
不过,藜麦的爱好者却通过媒体发现了一个令人不安的事实。
从2006年到2013年,玻利维亚和秘鲁的藜麦价格上涨了两倍。
2011年,《独立报》称,玻利维亚的藜麦消费量“5年间下降了34%,当地家庭已经吃不起这种主食了,它已经变成了奢侈品”。
《纽约时报》援引研究报告称,藜麦种植区的儿童营养不良率正在上升。
2013年,《卫报》用煽动性标题提升了人们对这个问题的关注度:“素食者的肚子能装下藜麦令人反胃的事实吗?”该报称,贫穷的玻利维亚人和秘鲁人正在食用更加便宜的“进口垃圾食品”。
《独立报》2013年一篇报道的标题是“藜麦:对你有利--对玻利维亚人有害”。
这些消息传遍了全球,在健康饮食者之中引发了一场良心危机。
在社交媒体、素食博客和健康饮食论坛上,人们开始询问食用藜麦是否合适。
这种说法看似可信,被许多人认可,但是经济学家马克·贝勒马尔等人对此则持保留意见。
毕竟,藜麦贸易使大量外国资金涌入玻利维亚和秘鲁,其中许多资金进入了南美最贫穷的地区。
几位经济学家跟踪了秘鲁家庭支出的调查数据,将种植且食用藜麦的家庭、食用但不种植藜麦的家庭和从不接触藜麦的家庭划分为三个小组。
他们发现,从2004年到2013年,三个小组的生活水平都上升了,其中藜麦种植户家庭支出的增长速度是最快的。
四川省成都七中届高三数学一诊模拟考试试题 文 新人教A版

B (, 0)
)
的虚部为(
B -1
B
a2 a4
x
)
a1a4
|
0
C (1, )
个单位 (m 0) ,若所得图象对应的函数为偶函数,则 m 的最小值是()
A 2
3
B C
38
x
1 ,若
a2a3, 将函数
D 5
6
4.阅读下边的程序框图,若输出 S 的值为-14,则判断框内可填写( )
1
D
A
C0
f (x)
5
B
3 1
,则实数
D (0,1)
17
D
6
a
的取值范围是
cos x 的图象向左平移 m sinx
D1
1
BD 翻折成 A/ BD ,则在 A/ BD 折起至转到平面 BCD 内的过程中,直线 A/C 与平面
BCD 所成的最大角的正切值为( )
A1Biblioteka B123
C
3
9.已知 f (x) 、 g(x) 都是定义在 R 上的函数, g(x) 0 , f / ( x)g( x) f ( x)g/ ( x) 0 ,
A
x [0,1] 时, 2 f ( x ) f ( x), 且 f ( x) 图象关于点 ( 1 , 1 ) ,则 f ( 1 ) ( )
1
4
5
B
1
2
二、填空题(每小题 5 分,共 25 分,把答案填在题中的横线上。)
11. 已知一个几何体的三视图如图所示,则该几何体的体积为___________ cm3
A
8
3
B
11
2024届四川省成都市第七中学高三上学期一诊模拟考试试卷

2024届四川省成都市第七中学高三上学期一诊模拟考试试卷学校:___________姓名:___________班级:___________考号:___________一、阅读理解Community NoticeboardNew Forest Bike Project (NFBP)New Forest Bike Project is a not-for-profit community and social organization which takes in unwanted bicycles and then repairs, restores and relocates them. Aiming to help people from all walks of life get out on two wheels and enjoy some exercise as well as the beautiful New Forest! If you would like to donate any unwanted bikes, please drop them off at Walkers Garage, Burley Rd, Bransgore BH23 8DF.Ringwood's International Festival of Street Performance Art (RIFSPA)Held annually on March 15th from 10:30 a.m.-4:30 p.m.WANTED: street performers, musicians, choirs, bands etc. to entertain the crowds in the streets of Ringwood! If you or your group are interested in taking part in this event, please contact Roger Bettle 01425 489350 as soon as possible to ensure a place.Natural Wellbeing (NW)Weekly sessions using the natural environment to promote adult health and wellbeing. Participants can be involved in cooking and sharing an outdoor lunch, bird watching and outdoor craft activities.Date: Every FridayTime:11:00a.m.-2:30p.m.Booking:********************************************.ukLocation: Blashford Lakes Nature Reserve, Ellingham Drove, near Ringwood BH24 3PJ Event charge: £ 4 donationRingwood Health Walks (RHW)Guided by V olunteer Walk Leaders, Walks are FREE for anyone wishing to improve their fitness with one-hour walks.Start from the Medical Center on the lst and 3rd Tuesday in each month at 10:30 a.m. Meet outside the Medical Centre.Come along and join us: we are a friendly sociable group. For more information contact Craig Daters on 01590 646 671.NO NEED TO BOOK1.What can you do through NFBP?A.Give away old bikes.B.Purchase used bikes.C.Hike in the New Forest.D.Work at Walkers Garage.2.Which of the following is organized once a year?A.NFBP.B.RIFSPA.C.NW.D.RHW. 3.What do NW and RHW have in common?A.They each last a whole day.B.They are free of charge.C.Chances to exercise are provided.D.Advance reservations are required.For as long as I can remember, my body and I have shared a relationship of discontent. Growing up, I was skinnier than the other kids and at five I was told I wasn't attractive and that I must put on some weight. But no matter how much I ate, I stayed thin for years until adolescence. Then I started putting on weight almost immediately. I remember feeling happy as I began to fill out. However, my joy didn't last long.I was thirteen when I was first called fat. Friends and neighbours would make jokes on my big size. As I entered my late teens, I had completely lost confidence in my body and, subsequently, in myself. Having failed to live up to conventional beauty standards, I was convinced that if I wanted to be loved, I needed to offer more, doing anything to please everyone around.I entered adulthood thinking I wasn't “enough”—an idea that was seeded not only by the fact that “skinny” is celebrated, but also by the language associated with accounts of losing weight—selfimprovement, discipline—all virtues. Being fat quickly categorizes you as lazy and undisciplined. Consumed by thoughts of the way my body looked, I didn't notice the other ways my body needed attention. I failed to realize, for example, that my period was much heavier and more painful than ever before. Actually I developed a rare disease and later I had two surgeries.I was always made to feel that my weight was the root of a lot of problems in my life; I have learnt this is not true. After a lot of selfreflection and some professional help, I realized I never learnt to like myself. While two decades of selfhatred cannot be undone overnight, I have taken first steps to acceptance.I am now much lighter than before, in body and mind. There are days I find voices onsocial media saying I am too fat to be loved or to be worthy, but I am learning not to focus on that thought for long. As long as I like myself, just the way I am, opinions at the end of the day are just water off a duck's back.4.What can we learn about the author from the first two paragraphs?A.She could change her weight at will.B.She had different beauty standards from others.C.She tried to love others to build her confidence.D.She was greatly influenced by others' opinions.5.Why did the author think she wasn't “enough”?A.She was poorly disciplined.B.She failed to celebrate “skinny”.C.She was labelled as lazy for her weight.D.She put on more weight after entering adulthood.6.What caused the author to make a change?A.Her lighter body.B.A troublesome illness.C.Popular beauty standards.D.Others' critical comments.7.What is the best title for the text?A.Beauty matters.B.Opinions vary.C.Worth your weight.D.Beyond your limits.One day in 1995,a large,heavy middle-aged man robbed two Pittsburgh banks in broad daylight. He didn't wear a mask and he smiled at surveillance cameras before walking out of each bank. Later that night, police arrested a surprised McArthur Wheeler. When they showed him the surveillance tapes, Wheeler stared in disbelief. "But I wore the juice," he mumbled. Apparently, Wheeler thought that rubbing lemon juice on his skin would make him invisible to videotape cameras. After all, lemon juice is used as invisible ink, so, as long as he didn't come near a heat source, he should have been completely invisible.The case caught the eye of the psychologist David Dunning at Cornell University, who enlisted his graduate student, Justin Kruger, to see what was going on. They reasoned that, while almost everyone holds favourable views of their abilities in various social and intellectual fields, some people mistakenly assess their abilities as being much higher than they actually are. This "illusion of confidence" is now called" the Dunning-Kruger Effect",and describes the cognitive bias to inflate self-assessment.To investigate this phenomenon in the lab, Dunning and Kruger designed some clever experiments. In one study, they asked undergraduate students a series of questions about grammar, logic and jokes, and then asked each student to estimate his or her score overall, as well as their relative rankings compared to the other students. Interestingly, students who scored the lowest in these cognitive tasks always overestimated how well they did—by a lot. Students who scored in the bottom estimated that they had performed better than two-thirds of the other students!Sure, it's typical for people to overestimate their abilities. The problem is that when people are incompetent, not only do they reach wrong conclusions and make unfortunate choices, but also they are robbed of the ability to realize their mistakes. In a semester-long study of college students, good students could better predict their performance on future exams given feedback about their scores and rankings. However, the poorest performers showed no recognition, despite clear and repeated feedback that they were doing badly. Instead of being confused or thoughtful about their incorrect ways, incompetent people insist that their ways are correct. As Charles Darwin wrote in The Descent of Man(1871): "Ignorance more frequently begets confidence than does knowledge. "Interestingly, really smart people also fail to accurately self-assess their abilities. As much as D-and F-grade students overestimate their abilities, A-grade students underestimate theirs. The difference is that competent people can adjust their self-assessment if given appropriate feedback, while incompetent individuals cannot.8.Which of the following statements about the Dunning-Kruger Effect is true?A.The effect is true for everyone in daily life.B.It suggests that most people lack cognitive abilities.C.Some people are overconfident about their abilities.D.The conclusion is drawn based on a series of bank robberies.9.What does the college students' behaviour mentioned in the experiments prove?A.Feedback plays a significant role in estimating one's ability.B.Incompetent people have a rigid attitude towards their choice.C.Good students can predict their future performance accurately.D.People can't rely on their previous behaviour to make adjustments.10.The underlined word "begets" can be replaced by “________”.A.gives rise to B.takes advantage of C.makes up for D.breaks away from11.What can we infer from the passage?A.Real knowledge is knowing the extent of one's ignorance.B.It is difficult for people to evaluate their real competence.C.Illusion of confidence is the major source of people's failure.D.Those with great abilities often have a low opinion of themselves.Like infectious diseases, ideas in the academic world are epidemic (传染的). But why some travel far and wide while equally good ones has been a mystery? Now a team of computer scientists has used an epidemiological model to simulate (模仿) how ideas move from one academic institution to another. The model showed that ideas originating at famous institutions caused bigger “epidemics” than equally good ideas from less famous places, explains Allison Morgan, a computer scientist at the University of Colorado Boulder.“This implies that where an idea is born shapes how far it spreads,” says senior author Aaron Clauset.Not only is this unfair— “it reveals a big weakness in how we’re doing science,” says Simon DeDeo, a professor of social and decision sciences at Carnegie Mellon university, who was not involved in the study. “There are many highly trained people with good ideas who do not end up at top institutions. They are producing good ideas, and we know those ideas are getting lost,” DeDeo says. “Our science, our scholarships, is not as good because of this.”The Colorado researchers first looked at how five big ideas in computer science spread to new institutions. They found that hiring a new faculty member accounted for this movement a little more than a third of the time--and in 81 percent of those cases, transmissions took place from higher – to lower-prestige (声望) universities. Then the team simulated the spread of ideas using an infectious disease model and found that the size of an idea “epidemic” depended on the prestige of the originating institution.The researchers’ model suggests that there “may be a number of quite good ideas that originate in the middle of the pack, in terms of universities.” Clauset says. There is a lot of good work coming out of less famous places. he says: “You can learn a huge amount from it, and you can learn things that other people don’t know because they’re not even paying attention.”12.How did the scientists carry out their research?A.By making use of a model.B.By analyzing previous data.C.By comparing different results.D.By interviewing different people. 13.According to Simon DeDeo, What can we infer in Paragraph 3?A.All the people with higher education have good ideas.B.Some scholarships aren’t given to the right people.C.Most good ideas come from not-so-great institutions.D.People with higher education should work in top institutions.14.What is the fourth paragraph mainly about?A.The causes of the results.B.The importance of the research.C.The findings of the research.D.The characteristics of big ideas. 15.What may be the best title for the passage?A.Spread good ideas as far as possible.B.Best ideas come from top institutions.C.Save good ideas from less famous places.D.Ideas from top institutions travel farther.二、七选五阅读七选五。
四川省成都七中2012届高三一诊模拟考试理科综合试题.pdf

一、选择题(本题包括13小题,每小题只有一个选项符合题意)
1.甲状腺细胞可以将氨基酸和碘合成甲状腺球蛋白,并且将甲状腺球蛋白分泌到细胞外,其过程如下图所示。下
列叙述错误的是( )
A.若含18O的氨基酸在甲状腺细胞内的代谢过程中产生了H218O,那么水中的18O最可能来自于氨基酸的-COOH
相对分子质量为312,当该蛋白质与浓硝酸反应时显黄色。M中各元素的质量分数为C 54.8%,H 5.58%,N 7.11%,其
B.细胞内的碘浓度远远高于血浆中的碘浓度,这表明a是主动运输过程
C.与c过程有关的细胞器是内质网、高尔基体、线粒体
D.上图中结构是将氨基酸组装成蛋白质的主要场所
2.某同学看到如下表所示的血液检查结果后,产生以下想法。其中错误的是( )
项目测定值单位正常值谷丙转氨酶17IU?L—10~45尿素氮14.6mg?dL—16.0~23.0血糖223mg?dL—160~110甘油三
3.第卷共13题,共174分。
22.本题共两题(每空2分,共17分)
、打点计时器用频率50Hz交流电打出的匀加速运动的纸带,则根据此纸带的数据,纸带的加速度是
m/s2 和
打点计时器打第3个点的速度是
m/s(保留3位有效数字)
、为了测量一精密金属丝的电阻率:
(1)先用多用电表×1Ω挡初测其电阻为______Ω,然后用螺旋测微器测其直径为
成都七中2011-2012学年度高三年级一诊模拟考试
理科综合试卷
本试卷分第一部分(选择题)和第二部分(非选择题)两部分,第一部分1至5页,第二部分5至12页。考生作答时
,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。满分300分。考试时间150分钟。考试结束后,将本试题卷
四川成都第七中学届高三一诊模拟考试数学(文)试卷Word版含答案解析
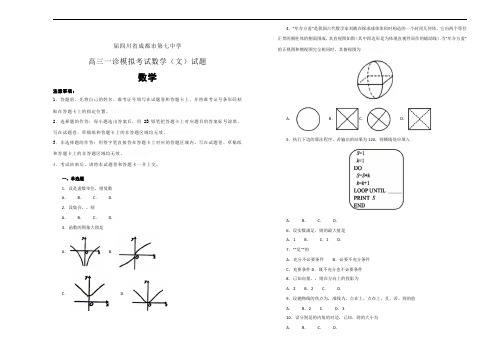
届四川省成都市第七中学高三一诊模拟考试数学(文)试题数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、单选题1.设是虚数单位,则复数A.B.C.D.2.设集合,,则A.B.C.D.3.函数的图象大致是A.B.C.D.4.“牟合方盖”是我国古代数学家刘徽在探求球体体积时构造的一个封闭几何体,它由两个等径正贯的圆柱体的侧面围成,其直视图如图(其中四边形是为体现直观性而作的辅助线).当“牟合方盖”的正视图和侧视图完全相同时,其俯视图为A.B.C.D.5.执行下边的算法程序,若输出的结果为120,则横线处应填入A.B.C.D.6.设实数满足,则的最大值是A.1 B.C.1 D.7.“”是“”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.已知向量,,则在方向上的投影为A.2 B.2 C.D.9.设抛物线的焦点为,准线为,点在上,点在上,且,若,则的值A.B.2 C.D.310.设分别是的内角的对边,已知,则的大小为A.B.C.D.11.已知正三棱锥的高为6,内切球(与四个面都相切)表面积为,则其底面边长为 A .18 B .12 C . D .12.已知函数(其中)的最小正周期为,函数,若对,都有,则的最小正值为 A . B . C . D .二、填空题13.某学校初中部共120名教师,高中部共180名教师,其性别比例如图所示,已知按分层抽样方法得到的工会代表中,高中部女教师有6人,则工会代表中男教师的总人数为.14.已知圆与轴相切,圆心在轴的正半轴上,并且截直线所得的弦长为2,则圆的标准方程是.15.已知均为锐角,且,则的最小值是.16.若函数有三个不同的零点,则实数的取值范围是.三、解答题17.正项等比数列中,已知,. 求的通项公式; 设为的前项和,,求.18.“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”……江南梅雨的点点滴滴都流润着浓烈的诗情.每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南镇2009~年梅雨季节的降雨量(单位:)的频率分布直方图,试用样本频率估计总体概率,解答下列问题:“梅实初黄暮雨深”.请用样本平均数估计镇明年梅雨季节的降雨量;“江南梅雨无限愁”.镇的杨梅种植户老李也在犯愁,他过去种植的甲品种杨梅,他过去种植的甲品种杨梅,亩产量受降雨量的影响较大(把握超过八成).而乙品种杨梅2009~年的亩产量(/亩)与降雨量的发生频数(年)如列联表所示(部分数据缺失).请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅受降雨量影响更小?(完善列联表,并说明理由).亩产量\降雨量合计 <600 2 1 合计100.50 0.40 0.25 0.15 0.100.4550.7081.3232.0722.703(参考公式:,其中)19.已知椭圆的离心率为,且经过点.求椭圆的标准方程;过点的动直线交椭圆于另一点,设,过椭圆中心作直线的垂线交于点,求证:为定值.。
成都七中高2012级高三三诊模拟考试试题(理数)

成都七中高2012级高三三诊模拟考试数学(理)试题时间:120分钟 满分:150分 命题人:张祥艳 审题人:廖学军一、选择题:每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求. 1.设全集为实数集R ,集合{}|2A x x =<,{}|3B x x =≥,则( )A.R A C B R ⋃= B. R R C A C B R ⋃= C. R A C B φ⋂= D. ()R C A B φ⋃= 2.函数13(10)x y x +=-<≤的反函数是 ( )A.31log (0)y x x =+> B.31log (0)y x x =-+>C.31log (13)y x x =+<≤D.31log (13)y x x =-+<≤3. 下列判断正确的是( )A. “正四棱锥的底面是正方形”的逆命题为真命题.B. 设,a b R ∈且0ab ≠,则a b >的一个充分条件是11a b<.C. 若“p 或q ”是真命题,则p ,q 中至少有一个真命题.D. 不等式111x ->的解集为{}x x |<2. 4.在数列}{n a 中,若2n a =1-n a +1+n a (*N n ∈,2≥n ),则下列不等式中成立的是( ) A .2342a a a ≤ B .2342a a a < C .2342a a a ≥ D .2342a a a >5. 以椭圆221169144x y +=的右焦点为圆心,且与双曲线221916x y -=的渐近线相切的圆的方程是( )A .221090x y x +-+= B . 221090x y x +--= C.221090x y x +++= D.221090x y x ++-=6.任意实数x ,有3230123(2)(2)(2)x a a x a x a x =+-+-+-,则2a 的值为( ) A .3 B .6 C .9 D .12C7.关于函数)125sin()12sin()(ππ+-=x x x f ,有下列命题:①此函数可以化为 15()sin(226f x x π=-+②函数)(x f 的最小正周期是π,其图像的一个对称中心是)0,12(π;③函数)(x f 的最小值是1,2-其图像的一条对称轴是;3x π=④函数)(x f 的图象按向量)1,6(-=π平移后所得的函数是偶函数;⑤函数)(x f 在区间)0,3(π-上是减函数.其中所有正确命题的序号个数是( )A. 2B. 3C. 4D. 58.如图是一个由三根细铁杆组成的支架,三根细铁杆的两夹角都是60︒,一个半径为1的球放在该支架上,则球心到P 的距离为( )ΑΒ.329. 三个实数a 、b 、c 成等比数列,若有1a b c ++=成立,则b 的取值范围是( )A. ⎥⎦⎤⎢⎣⎡31,0 B. ⎥⎦⎤⎢⎣⎡-31,1 C. 1(0,)3 D.[)⎥⎦⎤ ⎝⎛-31,00,110.将一骰子连续抛掷三次,它落地时向上的点数依次..成等差数列的概率为( ) A.19 B.112 C.115 D.11811.若()()()()()f x y f x f y f x f y +=⋅++且(1)1f =,则(1)(2)(2006)f f f ++⋅⋅⋅+=( )A. 2007B. 2008C. 200722006- D. 200822007- 12.平面α的斜线AB 交α于点B ,斜线AB 与平面α成30 角,过定点A 的动直线l 与斜线AB 成60 的角,且交α于点C ,则动点C 的轨迹是 ( ) A .圆 B .椭圆 C .抛物线 D .双曲线 二、填空题:本大题共4小题,每小题4分,共16分.答案填在答题卡上.13. 知直线0ax bx c ++=被圆M :⎩⎨⎧==θθsin 2cos 2y x 所截得的弦AB 的长为32,那么∙的值等于DPCABE14.已知函数,1)(,log )(21-==x x g x x f 设⎩⎨⎧<≥=)()(,)()()(,)()(x g x f x g x g x f x f x h ,则使2)(≥a h 成立的a的范围是 .15.设O 是ABC ∆内部的一点, 24,OA OB OC O ++=则::BOC AOC AOB S S S ∆∆∆=16. 关于函数2,0()21,0x e x f x ax x -⎧-⎪=⎨->⎪⎩≤(a 为常数,且a >0)对于下列命题:①函数f (x )的最小值为-1; ②函数f (x )在每一点处都连续; ③函数f (x )在R 上存在反函数;④函数f (x )在x =0处可导;⑤对任意的实数x 1<0, x 2<0且x 1<x 2,恒有1212()()()22x x f x f x f ++<. 其中正确命题的序号是_____________.三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. 17. (本小题满分12分)已知△ABC 中,角A ,B ,C 的对边分别为a ,b ,ccos 1B B -=,1=b .(Ⅰ)若125π=A ,求c ; (Ⅱ)若c a 2=,求△ABC 的面积.18. (本小题满分12分)已知8人组成的抢险小分队中有3名医务人员,将这8人分为A 、B 两组,每组4人. (Ⅰ)求A 、B 两组中有一组恰有一名医务人员的概率; (Ⅱ)求A 组中至少有两名医务人员的概率; (Ⅲ)求A 组中医务人员人数ξ的数学期望.19. (本小题满分12分) 如图,四棱锥P —ABCD 中,PB ⊥底面ABCD ,CD ⊥PD ,底面ABCD 为直角梯形,AD ∥BC ,AB ⊥BC ,AB=AD=PB =3,BC =6,点E 在棱P A 上且PE =2EA .(Ⅰ)求异面直线P A 与CD 所成角; (Ⅱ)求证PC ∥平面EBD ; (Ⅲ)求二面角A -BE -D 的大小.20. (本小题满分12分)已知双曲线22221(0,0)x y a b a b -=>>的离心率为e =过(0,)A b -和(,0)B a 的直线与原点的距离是23.(Ⅰ) 求双曲线方程;(Ⅱ) 直线(0)y kx m km =+≠与双曲线交于不同两点C 、D , 且C 、D 两点都在以A 为圆心的圆周上, 求m 的取值范围.21. (本小题满分12分)已知数列{}n a 中,11a =,且21231n n n na a n n --=+⋅-*(2,)n n N ≥∈. (Ⅰ) 求数列{}n a 的通项公式;(Ⅱ) 令13n n nb a -=*()n N ∈,数列{}n b 的前n 项和为n S ,试比较2n S 与n 的大小;(Ⅲ) 令11n n a c n +=+*()n N ∈,数列22{}(1)n n c c -的前n 项和为n T ,求证:对任意*n N ∈,都有 2n T <.22.(本小题满14分)设定义在R 上的函数4320123401234()(,,,,)f x a x a x a x a x aa a a a a R =++++∈,函数()g x x ,当1x =-时,()f x 取得极大值23,且函数(1)y f x =+的图象关于点(-1,0)对称.(Ⅰ)求函数()f x 的表达式;(Ⅱ)求证:当0x >时,()1[1](()g x e e g x +<为自然对数的底数); (Ⅲ)若1(1)()(),g n n b g n n N *+=∈数列{}n b 中是否存在()n m b b n m =≠?若存在,求出所有相等的两项;若不存在,请说明理由.成都七中高2012级高三三诊模拟考试数学(理)参考答案一、选择题:BDCAA BCCDB DD 二、填空题:13. -2 14. [)+∞,3]41,0( 15. 1:2:4 16. ①②⑤.三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. 17.解:(Ⅰ)由已知1cos sin 3=-B B ,整理得21)6sin(=π-B . ………………2分 因为π<<B 0,所以π<π-<π-6566B . 故66π=π-B ,解得3π=B . ……………4分由512A π=,且π=++C B A ,得4π=C . 由Bb Cc sin sin =,即3sin 14sin π=πc ,解得36=c . ………………6分 (Ⅱ)因为B ac c a b cos 2222-+=,又32π==B c a ,, 所以21442222⨯-+=c c c b ,解得c b 3=. ………………8分 由此得222c b a +=,故△ABC 为直角三角形,2π=A ,31=c . 其面积6321==bc S . ………………12分 18. 解:(Ⅰ)设“A 、B 两组中有一组恰有一名医务人员”为事件1A ,1()P A =.76482523482523=+C C C C C C …………………………………………………………4分 (Ⅱ)设“A 组中至少有两名医务人员”为事件2A ,2()P A =21481533482523=+C C C C C C .……………………………………………………8分(Ⅲ)ξ可取0、1、2、3.413535448822313535448813(0),(1),14731(2),(3),714C C C P P C C C C C C P P C C ξξξξ============ 133130123.1477142E ξ=⨯+⨯+⨯+⨯=……………………………………12分 19.解:(1) ∵PB ⊥平面ABCD ,CD ⊥PD ,∴CD ⊥BD ,又AD =AB =3,过D 作DF ⊥BC 于F , 则四边形ABFD 为正方形.BF =FC =3,∴∠CDF =45°,CF=FB =3,连结AF 则AF ∥CD ,∴异面直线P A 和CD 所成角就是P A 和AF 的夹角, E 在△P AF 中,AF=P A=PF =32,∴∠P AF =60°,即P A 和CD 所成角为60°.另法:如图(1)所示建立空间坐标系, 则P (0,0,3), A (3,0,0),C (0, -6 ,0),D (3,-3,0), 则 =(3,0,-3), =(3,3,0), ∴ cos 2123239||||=∙=∙>=<CD PA PA∴><CD PA ,=60°.(2)连AC 交BD 于G ,连结EG , ∵21,21===EP AE BC AD GC AG 又,∴EPAEGC AG =,∴PC ∥EG ,又EG ⊂平面EBD , PC ⊄平面EBD ,∴PC ∥平面EBD .(3)作AH ⊥BE 于H ,连结DH ,∵DA ⊥平面HBD ,∴DH ⊥BE , ∴∠AHD 即为二面角A-BE-D 的平面角, 在△ABE 中,BE =5,AH =55345sin =︒∙∙BE AE AB∴tan ∠AHD =5=AHAD,即二面角A-BE-D 为arctan 5. 20. 解: (Ⅰ).b 3a 34a b a 34a c 332a c e 22222=⇒=+⇒=⇒==l AB :0b 3y 3x a00x 0b b y =--⇒--=--+,…………2分 原点)0,0( 到直线l AB 的距离为23, 得: 3a ,1b 31|b 3|2322==⇒+= ,…………3分 ∴双曲线方程为: 1y 3x 22=-…………5分 (Ⅱ) 0m 33kmx 6x )k 31(1y 3x m kx y 22222=----⇒⎪⎩⎪⎨⎧=-+=. 0)1k 3m (1222>+-=∆………7分 ,k 31km 32x x 221-=+221k31m2y y -=+…………8分 CD 在以A 为圆心的圆上, ∴CD 为弦, 设CD 的中点为M, 则CD ⊥AM,∴中点M (,k 31km 32-2k31m-), A )b ,0(- 即A )1,0(- . ∴km 31m k 31k 3km 301k 3m1k 222AM ---=-+-+-=, 又直线m kx y +=(0km ≠)的斜率为k, , 则有:k1km 31m k 32-=---1m 4k 32+=⇒…………10分 代入0)1k 3m (1222>+-=∆中, 得: 0m 4m 0m 4m 2<>⇒>-或,又 41m 0k 31m 42->⇒>=+ ∴),4()0,41(m ∞+-∈ …………12分21. 解:(Ⅰ)由题21231n n n na a n n --=+⋅-知, 21231n n n a a n n --=+⋅-, 由累加法,当2n ≥时,22122323231n n a a n --=+⨯+⨯++⨯代入11a =得,2n ≥时,112(13)1313n n n a n ---=+=- 又11a =,故1*3()n n a n n N -=⋅∈. ................3分(II )*n N ∈时,131n n n b a n-==,则21111232n n S =++++记函数2111()(1)232n n f n S n n =-=++++- 所以1111(1)(1)(1)232n f n n ++=++++-+ .........5分则11112(1)()()1102122221nnn n n f n f n ++-=+++-<-<+++ 所以(1)()f n f n +<.由于121(1)1(1)102f S =-=+->,此时121S >;22111(2)2(1)20234f S =-=+++->,此时222S >;321111111(3)3(1)302345678f S =-=+++++++-<,此时323S <;由于,(1)()f n f n +<,故3n ≥时,()(3)0f n f ≤<,此时2n S n <.综上所述:当1,2n =时,2n S n >;当*3()n n N ≥∈时,2n S n <. ...........7分 (III )131n n n a c n +==+当2n ≥时,121123232311(31)(31)(33)(31)(31)3131n n n n n n n n n n---⨯⨯⨯≤==--------. 所以当2n ≥时,22222233232331111()()2(31)(31)22313131n n n T ⨯⨯=+++≤+-+------ +1111()22313131n n n -+-=-<--- .且1322T =<故对*n N ∈,2n T <得证. .................12分 22.解:(Ⅰ) 函数(1)y f x =+的图象关于点(-1,0)对称∴函数()y f x =的图象关于点(0,0)对称,即()y f x =是奇函数。
四川省成都七中2012届高三适应性考试数学(理)试题

UNM成都七中高2012级高考适应性考试数学(理科)试题时间:120分钟 满分:150分第Ⅰ卷(选择题,共60分)一、选择题:每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求. (1)已知全集U =R ,集合{}22M x x =-≤<和{}21,N y y k k Z ==-∈的关系的韦恩()Venn 图如图所示,则阴影部分所示的集合的元素共有 (A )3个 (B )2个(C )1个 (D )0个(2)圆22:(1)5M x y -+=上点到直线290x y -+=的最短距离为 (A )0(B )5(C)(D(3)已知数列{}n a 的满足:21()n na n a *+=-∈N ,若121,2a a ==,则36a a += (A )3(B ) 9 (C ) 1 (D )0(4)已知实数,x y 满足220,2,1,x y x y +-≥⎧⎪≤⎨⎪≤⎩,则342z x y =+-的最大值为 (A )8 (B )6 (C )5 (D )1(5)函数2()23f x x ax =-+在区间[]2,4-的值域为[](),(4)f a f ,则实数a 的取值范围为 (A )[]2,1- (B )(]2,1-(C )(],1-∞ (D )[]2,2-(6)把cos(2)13y x π=--的图象经过某种平移得到sin(2)2y x π=+的图象,则平移方式可为(A )按(,1)6=πa 平移(B )按(,1)()6=k k Z ππ-∈a 平移(C )先向右平移3π个单位再向上平移1个单位 (D )先向左平移6π个单位再向下平移1个单位(7)设,a b R ∈,()212ia b i -+-=(i 为虚数单位),则limn n nnn a b a b→+∞=-+(A )1 (B )1- (C )1-或1 (D )不存在 (8)若,2k k Z παβπ+≠+∈,则“sin sin(2)βαβ=+”是“sin 0α=”的(A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件(9)用边长为6分米的正方形铁皮做一个无盖的水箱,先在四角分别截去一个小正方形,然后把四边翻转90︒,再焊接而成(如图)。
四川省成都市成都七中2012年5月高三高考模拟考试试题(四,文数)

成都七中高2012级高考数学模拟(四)试题(文)一.选择题(每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求.)1.已知{}⎭⎬⎫⎩⎨⎧>==>==2,1,1,log 2x x y y P x x y y U ,则=P C U ( )A ⎪⎭⎫⎢⎣⎡+∞,21B ⎪⎭⎫ ⎝⎛21,0C ()+∞,0D (]⎪⎭⎫⎢⎣⎡+∞⋃∞-,210, 2.已知圆心为O 的扇形AOB 中,OA=OB=AB=2,则扇形AOB 的面积是( )一、3π B.32π C. 2 D.1 3.已知A (1,2),B (4,0),C (8,6),D (5,8)四点,则四边形ABCD 是( ) A 梯形 B 菱形 C 矩形 D 正方形 4.已知直线a y x =+与圆)(sin 2cos 2R y x ∈⎩⎨⎧==θθθ交于A 、B 两点,且-=+||||,其中O 为坐标原点,则实数a 的值等于( ) (A )2 (B )2±(C )2± (D )6±5.在平面直角坐标系中,若角α的顶点在坐标原点,始边在x 轴的非负半轴上,终边经过点P(3a,-4a)(其中a<0),则cos α的值为( )A.54-B.53-C.53D.546.若奇函数)(x f 满足)()1(x f x f -=+,当10≤≤x 时,222)(x x x f -=,则)25(-f =( )A21 B 41- C 41 D 21-7.设奇函数()f x 在[1,1]-上是增函数,且(1)1f -=-.若函数2()21f x t at ≤-+对所有的[1,1]x ∈-都成立,则当[1,1]a ∈-时,t 的取值范围是( ) A .22t -≤≤ B .2t ≤-或0t =或2t ≥ C .1122t -≤≤ D .12t ≤-或0t =或12t ≥8.将甲、乙、丙、丁四名学生分到三个不同的班,每个班至少分到一名学生,且甲、乙两名学生不能分到同一个班,则不同分法的种数为( ).18A .24B .30C .36D9.若'()()f x f x 是函数的导函数且二次函数'()f x 的图象开口向上,顶点坐标为(1,-3),那么曲线()y f x = 上任一点的切线的倾斜角α的取值范围是( ) A. (0,2π3] B. [0, π2)∪[2π3, π) C. [0, π2]∪[2π3, π) D. [π2,2π3] 10.已知函数32113y x x x =-++-的图象C 上存在一定点P .若过点P 的直线l 与曲线C 交于不同的两点1122(,),(,)M x y N x y ,且恒有12y y +为定值0y ,则0y 的值为 ( )A.23 B. 23- C. 43 D. 43-11.将边长为1的正方形ABCD 沿对角线BD 折成直二面角,若点P 满足2||,2121则+-=的值为( )A .23 B .2C .4210- D .49 12.若函数()f x 满足对于[],()x n m m n ∈>有km x f kn≤≤)(恒成立,则称函数()f x 在区间[],()n m m n >上是“被k 限制”的,若函数22)(a ax x x f +-=在区间)0(,1>⎥⎦⎤⎢⎣⎡a a a 上是“被2限制”的,则a 的范围是( ) A.(]2,1 B.⎥⎦⎤ ⎝⎛323,1 C. (]2,1 D. ⎥⎦⎤⎢⎣⎡2,323二、填空题:本大题共4小题,每题4分,共16分,把答案填在题中的横线上13.奇函数()()0f x x ≠在(0,+∞)上为增函数,且()10f =.那么不等式()10f x -< 的解集是 ;一、若一条直线与一个正四棱柱每条棱所成的角都相等,那么该角的正弦值为__________; 二、已知正项等比数列{}n a 满足7652a a a =+,若存在两项m n a a 、14a =,则14m n+的最小值是 ;16.已知函数()y f x =是R 上的偶函数,对于x R ∈都有(6)()(3)f x f x f +=+成立,且(4)2f -=-,当12,[0,3]x x ∈且12x x ≠时,都有1212()()0f x f x x x ->-,则给出下列命题:①(2010)2f =-; ② 函数()y f x =图象的一条对称轴为6x =-;③ 函数()y f x =在[9,6]--上为减函数;④ 方程()0f x = 在[9,9]-上有4个根 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成都七中高2012级高三一诊模拟考试数学(文)试题时间:120分钟 满分:150分 命题人:何毅章 审题人:税洪一、选择题:每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求. (1)已知集合2={1,},={2,1},{4},A a B a A B -= 若则实数a 等于(A )4 (B )0或4 (C )0或2 (D )2 (2)不等式210x->的解集为(A )()(,0)2-∞+∞ , (B )()02, (C )(),0-∞ (D )()2+∞, (3)已知向量、a b 不共线,()k k ∈c =a +b R ,2-d =a b ,如果c d ,那么 (A )12k =且c 与d 同向 (B )12k =且c 与d 反向 (C )12k =-且c 与d 同向 (D )12k =-且c 与d 反向(4)从总体中随机抽取一个容量为20的样本,其数据的分组及各组的频数如下表:其中x 、y *∈N ,依此估计总体中数据在[)2040,上个体的频率为 (A )107 (B )21 (C )41 (D )201 (5)函数)(x f 的反函数为12()1(0)f x x x -=+<,则3(log 9)f =(A )1 (B )-1 (C )1或-1 (D )-11(6)已知命题:0p a b >>,命题:q a b a b +=+,则命题p 是q 的(A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件(7)设函数2,0()(),0x x f x g x x ⎧≤=⎨>⎩,若()f x 为偶函数,则()f x 的值不可能是(A(B )1 (C )4 (D )14(8)已知n S 是公差不为0的等差数列{}n a 的前n 项和,若421,,S S S 成等比数列,则31a a = 分组 [)2010, [)3020, [)4030, [)5040, [)6050, [)7060,频数2xy3 1 4(A )7 (B )5 (C )3 (D )2(9)如图,单位正方体1111ABCD A BC D -中,下列说法错误的是(A )11BD B C ⊥(B )若113DP DD = ,13DE DC =,则PE 1A B(C )若点1BA D C 、、、在球心为O 的球面上, 则点A C 、13(D )若113DP DD = ,13DE DC =,则直线1A P 、BE 、AD 共点 (10)在ABC ∆中,若222sin sin 5sin A B C +=,则cos C 的最小值等于(A )45 (B )45- (C )25 (D )25- (11)将3只完全相同的二极管排到如图所示的六个位置中的某三个位置,但彼此不相邻,然后将它们都点亮,若每只二极管点亮时都会时而发红光,时而发绿光.根据这三只点亮的二极管不同位置和不同颜色的光来表示不同的信息,则产生的不同信息总数(A)8种 (B)32种 (C)80种 (D)96种(12)设函数)(x f 是定义在R 上的偶函数,且(2)()f x f x +=恒成立;当[]0,1x ∈时,3()43f x x x =-+.有下列命题:①315()<()42f f -;②当[]1,0x ∈-时3()43f x x x =++;③)(x f (0)x ≥的图象与x 轴的交点的横坐标由小到大构成一个无穷等差数列;④关于x 的方程()f x x =在[]3,4x ∈-上有7个不同的根.其中真命题的个数为(A )1个 (B )2个 (C )3个 (D )4个二、填空题:本大题共4小题,每小题4分,共16分.答案填在答题卡上.(13)5)1(xx -的二项展开式中第二项的系数是 (用数字作答). (14)已知tan()4αβ+=,tan 3β=,则tan α=(15)如图,90BAC ∠=︒的等腰直角三角形正三角形BCD 所在平面互相垂直,E 是线段BD 则AE 与CD 所成角的大小为 .1234561A CA C(16)已知数列{}n a 的前n 项和为n S ()n *∈N ,1a =1,48a =,n n S b q b =- (0,q ≠1,q ≠±0)b ≠,现把数列{}n a 的各项排成如图所示的三角形形状.记(,)A m n 为第m 行从左起第n 个数.有下列命题:①{}n a 为等比数列且其公比2q =±;②当2(3,)n m m m n *=>∈、N 时,(,)A m n③10028(6,9),(11,1)2a A A ==;④当3m >时,(1,1)4(,)m A m m A m m ++= . 其中你认为正确的所有命题的序号是___________.找家教,可以找柯南东升,可以关注824135830空间,更多精彩请加821435830 三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. (17)(本小题满分12分)已知函数2()4cos sin ()42xf x x π=+x 2cosx -. (Ⅰ)求()f x 的最小正周期;(Ⅱ)若0,2x π⎛⎫∈ ⎪⎝⎭,求()f x 的单调区间及值域.(18)(本小题满分12分)梯形ACPD 中,,,AD CP PD AD CB AD ⊥⊥ ,4DAC π∠=,PC =AC 2=,如图①;现将其沿BC 折成如图②的几何体,使得AD =.(Ⅰ)求直线BP 与平面PAC 所成角的大小;(Ⅱ)求二面角C PA B --的余弦值. (19)(本小题满分12分)为了拓展网络市场,腾讯公司为QQ 用户推出了多款QQ 应用, 如“QQ 农场”、“QQ 音乐”、“QQ 读书”等.某校研究性学习小组准备举行一次“QQ 使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下:(I)若从这10名学生中随机抽出2名,求这2名学生来自相同班级的概率;(Ⅱ)假设在某时段,三名学生代表甲、乙、丙准备分别从 “QQ 农场”、“QQ 音乐”、“QQ 读书”中任意选择一项,他们选择QQ 农场的概率都为16;选择QQ 音乐的概率都为13;选择QQ 读书的概率都为12;他们的选择相互独立.求在该时段这三名学生中“选择QQ 读书的总人数”大于“没有选择QQ 读书的总人数”的概率.(20)(本小题满分12分)已知函数2()(1)4f x x m x =-++.(Ⅰ)当(0,1]x ∈时,若0m >,求函数()()()1F x f x m x =--的最小值; (Ⅱ)若函数()()2f x G x =的图象与直线1y =恰有两个不同的交点12(,1),(,1)A x B x12(03)x x ≤<≤,求实数m 的取值范围.(21)(本小题满分12分)等差数列{}n a 的各项均为正数,11a =,前n 项和为n S ,{}n b 为等比数列, 11b =,且226,b S = 3324b S =,n *∈N .(Ⅰ)求数列{}n a 和{}n b 的通项公式; (Ⅱ)令21n n n n n C b a a +=+∙,123n n T C C C C =++++ ;求n T . ①求n T ;②记()2192()222k k k f k T k *-+=--∈N ,若21()110f k ≥恒成立,求k 的最大值.(22)(本小题满分14分)已知函数321()(32)632a f x x a x x =-++, 2()4g x ax x m =-+-,,a m ∈R .(I )当1a =,[]03x ,∈时,求()f x 的最大值和最小值;(Ⅱ)若2a <时关于x 的方程()()f x g x =总有三个不同的根,求m 的取值范围.成都七中高2012级高三一诊模拟考试 数学(文)参考答案及评分意见一、选择题:(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12)D A D B B A C B C A B B二、填空题: (13)5-;(14)111-;(15)4π;(16找家教,可以找柯南东升,可以关注824135830空间,更多精彩请加821435830三、解答题:(17)解:(Ⅰ)()4cos fx ==2cos (1x x =π.22T π==(Ⅱ) 0,2x π⎛⎫∈ ⎪⎝⎭,42333x πππ<+<, 由2033212x x ππππ<+≤⇒<≤,4223312x x πππππ≤+<⇒≤< ()f x 的单调递增区间为0,12x π⎛⎤∈ ⎥⎝⎦,单调递减区间为,122x ππ⎡∈⎢⎣⎭由2sin(2)23x π+≤,域值为(⎤⎦(18)解:(Ⅰ)由题意,PC=AC=2,AB ∴= =2BD ,在ABD ∆中,∵222AB DB AD +=,∴BD BA ⊥∴BD BA BC 、、两两垂直,分别以BC BA BD 、、所在直线为x 轴、y 轴、z 轴建立空间直角坐标系B xyz -(如图).(0,0,0),A B C P设平面PAC 的法向量为(,,)x y z =n ,(CA = ,(0,0,2)CP =,0000CA x y z CP ⎧=-=⎧⎪⇒⎨⎨==⎩⎪⎩n n ,取(1,1,0)=n 设直线BP 与平面PAC则sin BP BP θ===n n直线BP 与平面PAC AP BC ==(Ⅱ)设平面PAB 的法向量为(,,)x y z =m ,BA AP ==0,0,0,.0.20.y AB x AP z ⎧⎧=⎧⋅==⎪⎪⎪∴∴∴⎨⎨=⎪⋅=-+=⎪⎩⎩m m 令1,z =-∴=-m 由(Ⅰ)知平面PAC 的法向量为令(1,1,0)=n . cos ,⋅∴<>===m n m n m n 由图知二面角C PA B --为锐角, ∴二面角C PA B --(19)解:(I)记这两名学生都来自第i 班为事件(1,2,3,4)i A i =则()221210145C P A C ==;()232210345C P A C ==;()243210645C P A C ==;()40P A =∴()()()()1234102459P P A P A P A P A =+++== (Ⅱ) 记这三名学生选择QQ 读书的总人数是3人为事件E ,这三名学生选择QQ 读书的总人数是2人为事件F ,这三名学生中“选择QQ 读书的总人数”大于“没有选择QQ 读书的总人数” 为事件B ,则事件E 、F 互斥,()()()P B P E P F =+.311()28P E ⎛⎫== ⎪⎝⎭, 32313()28P F C ⎛⎫== ⎪⎝⎭,()()()PB P E P F=+=(20)解:(Ⅰ)()2()()124Fx f x m xx mx =--=-+,(0,1]x ∈对称轴x m =()0m >①当01m <≤时,2min ()()4F x F m m ==-②当1m >时,min ()(1)52F x F m ==-∴min 252(1)()4(01)m m F x m m ->⎧=⎨-<≤⎩(Ⅱ)2()(1)4()22f x xm x G x -++==与直线012y ==恰有两个不同的交点12(,1),(,1)A x B x12(03)x x ≤<≤⇔关于x 的方程2(1)40x m x -++=在[]0,3 2()(1)4f x x m x =-++则2(1)1601032(0)40(3)93(1)40m m f f m ⎧∆=+->⎪+⎪<<⎪⎨⎪=>⎪=-++≥⎪⎩, 解得1033m <≤, ∴103,3m ⎛⎤∈ ⎥⎝⎦.(21)解:(Ⅰ)设{}n a 的公差为(0),d d >{}n b 的公比为q ;11(1),n n n a n d b q -=+-=,依题意有233221(33)242(2)6d S b d q q S b d q =⎧=+=⎧⇒⎨⎨==+=⎩⎩或124d q ⎧=-⎪⎨⎪=⎩(解得1,2d q =⎧⎨=⎩故n a n =;12n n b -=()n *∈N(II )由(I )知11211111()2(2)222n n n n n n n n n C b a a n n n n --+=+=+=+-++ , ①111111()222nnn i i i i T i i -===+-+∑∑112ni i i -=∑是一个典型的错位相减法模型,1112422n i n i i n --=+=-∑1111()22ni ii =-+∑是一个典型的裂项求和法模型, 111111111111()(1)222324352ni i i n n =-=-+-+-++-++∑ 1111323(1)221242(1)(2)n n n n n +=+--=-++++ 112323192234242(1)(2)422(1)(2)n n n n n n n T n n n n --++++=-+-=--++++②记()2192()222k k k f k T k *-+=--∈N ,∵119223422(1)(2)n n n n T n n -++=--++, 21922311()222(1)(2)12k k k k f k T k k k k -++=--==+++++*112111*********k k +≥=+++,∴9k ≤,∴()max 9k =.(22)解:(I )'2()(32)6(2)(3)f x ax a x ax x =-++=--1=a ,'2()56(2)(3)f x x x x x =-+=--,[]0,3x ∈[]0,2x ∈,'()0f x ≥,()f x 单调递增; []2,3x ∈,'()0f x ≤,∴max 14()(2)3f x f ==min ()f x 为(0)0f =和9(3)2f =的最小者,min ()0f x = (Ⅱ)令()()()h x f x g x =-,则32()(1)232a a h x x x x m =-+++则'2()(2)2(2)(1)=-++=--h x ax a x ax x()()=f x g x 总有三个不同的根,即()y h x =的图象和x 轴总有三个不同的交点 ①当0a <时,21a<,()h x 的极大值为(1)16ah m =-+,()h x 的极小值为2264()3a h m a a -=+,要使()y h x =的图象和x 轴总有三个不同的交点,需满足(1)02()0h h a >⎧⎪⎨<⎪⎩在0a <时恒成立,即2(1)106264()03a h m a h m a a ⎧=-+>⎪⎪⎨-⎪=+<⎪⎩在0a <时恒有解max (1)6am ≥-,∴1m ≥- min264()3a m a -+≤,又10<,2233()0344a =-->,∴≤m ∴10-≤≤m . ②当0a =时,()h x ,显然不符合题意,舍去; ③当02<<a 时,'2()(2)2(2)(1)=-++=--h x ax a x ax x()h x 的极大值为(1)16a h m =-+,()h x 的极小值为2264()3a h m a a -=+ 即2(1)106264()03a h m a h m aa ⎧=-+>⎪⎪⎨-⎪=+<⎪⎩,即2334m m ⎧≥-⎪⎪⎨⎪≤-⎪⎩,舍去综上述,[]1,0m ∈-.注:对于解答题的其它解法,根据小题的小分值适度合理给分.。
