七年级数学上册平面直角坐标系习题 (新版)鲁教版

合集下载

初中数学鲁教版(五四制)七年级上册第五章位置与坐标本章综合与测试-章节测试习题(3)

章节测试题1.【答题】已知直角坐标平面内两点A（-3，1）和B（3，-1），则A、B两点间的距离等于______．【答案】2【分析】【解答】2.【题文】已知点A（a，3），B（-4，b），试根据下列条件求出a、b的值．（1）A、B两点关于y轴对称；（2）AB∥x轴；（3）A、B两点在第二、四象限两坐标轴夹角的平分线上．【答案】解：（1）∵点A（a，3），B（-4，b），A、B两点关于y轴对称，∴a＝4，b＝3；2分（2）∵点A（a，3），B（-4，b），AB∥x轴，∴b＝3，a为任意实数；3分（3）∵A、B两点在第二、四象限两坐标轴夹角的平分线上，∴a＝-3，b＝4．3分【分析】【解答】3.【题文】已知，点P（2m-6，m+2）．（1）若点P在y轴上，P点的坐标为______；（2）若点P的纵坐标比横坐标大6，求点P在第几象限？（3）若点P和点Q都在过A（2，3）点且与x轴平行的直线上，PQ＝3，求Q点的坐标．【答案】解：（1）∵点P在y轴上，∴2m-6＝0，解得m＝3，∴P点的坐标为（0，5）；故答案为（0，5）；2分（2）根据题意得2m-6+6＝m+2，解得m＝2，∴P点的坐标为（-2，4），∴点P在第二象限；2分（3）∵点P和点Q都在过A（2，3）点且与x轴平行的直线上，∴点P和点Q的纵坐标都为3，∴P（-4，3），而PQ＝3，∴Q点的横坐标为-1或-7，∴Q点的坐标为（-1，3）或（-7，3）．3分【分析】【解答】4.【题文】在平面直角坐标系中，△ABC的位置如图所示．（1）分别写出下列顶点的坐标：A______，B______；（2）顶点A关于y轴对称的点A′的坐标为：A′______；（3）△ABC的面积为______．【答案】解：（1）由题可得，A（-2，6），B（-4，3）；故答案为：（-2，6），（-4，3）；3分（2）点A关于y轴对称的点A′的坐标为（2，6）；故答案为：（2，6）；3分（3）△ABC的面积为×4×3+×4×3＝12，故答案为：12．4分【分析】【解答】5.【题文】如图，在平面直角坐标系中有一个轴对称图形，A（3，-2），B（3，-6）两点在此图形上且互为对称点，若此图形上有一个点C（-2，+1）．（1）求点C的对称点的坐标．（2）求△ABC的面积．【答案】解：∵A、B关于某条直线对称，且A、B的横坐标相同，∴对称轴平行于x轴，又∵A的纵坐标为-2，B的纵坐标为-6，∴故对称轴为y＝＝-4，∴y＝-4．则设C（-2，1）关于y＝-4的对称点为（-2，m），于是＝-4，解得m＝-9．则C的对称点坐标为（-2，-9）．5分（2）如图所示，S△ABC＝×（-2+6）×（3+2）＝10．5分【分析】【解答】6.【题文】附加题如图，已知平面直角坐标系中A（-1，3），B（2，0），C（-3，-1）（1）在图中作出△ABC关于y轴的对称图形△A1B1C1，并写出点A1，B1，C1的坐标．（2）在y轴上找一点P，使PA+PC最短，并求出P点的坐标．【答案】附加题．解：（1）A1（1，3），B1（-2，0），C1（3，-1）；5分（2）连接A1C，交y轴于P，这时PA+PC最短，15分设直线A1C解析式为y＝kx+b，∵直线经过A1（1，3）和C（-3，-1），∴，解得，∴直线A1C解析式为y＝x+2，当x＝0时，y＝2，∴P（0，2）．【分析】【解答】7.【答题】如果点P（m，1-2m）在第一象限，那么m的取值范围是（）A. 0＜m＜B. -＜m＜0C. m＜0D. m＞【答案】A【分析】【解答】8.【答题】点P（m，n）在平面直角坐标系中的位置如图所示，则坐标（m+1，n-1）对应的点可能是（）A. AB. BC. CD. D【答案】B【分析】【解答】9.【答题】如果P（m+3，2m+4）在y轴上，那么点P的坐标是（）A. （-2，0）B. （0，-2）C. （1，0）D. （0，1）【答案】B【分析】【解答】10.【答题】点M（-3，4）离原点的距离是多少单位长度（）A. 3B. 4C. 5D. 7【答案】C【分析】【解答】11.【答题】已知点A（1，2）与点A′（a，b）关于坐标原点对称，则实数a、b的值是（）A. a＝1，b＝2B. a＝-1，b＝2C. a＝1，b＝-2D. a＝-1，b＝-2【答案】D【分析】【解答】12.【答题】在平面直角坐标系中，点A的坐标为（-2，3），点B的坐标为（-2，-3），那么点A和点B的位置关系是（）A. 关于x轴对称B. 关于y轴对称C. 关于原点对称D. 关于坐标轴和原点都不对称【答案】A【分析】【解答】13.【答题】如图，已知棋子“车”的坐标为（-2，3），棋子“马”的坐标为（1，3），则棋子“炮”的坐标为（）A. （3，2）B. （3，1）C. （2，2）D. （-2，2）【答案】A【分析】【解答】14.【答题】已知点M（3，-4），在x轴上有一点与M的距离为5，则该点的坐标为（）A. （6，0）B. （0，1）C. （0，-8）D. （6，0）或（0，0）【答案】D【分析】【解答】15.【答题】已知点P（a，2a-1）在一、三象限的角平分线上，则a的值为（）A. -1B. 0C. 1D. 2【答案】C【分析】【解答】16.【答题】如图，右边坐标系中四边形的面积是（）A. 4B. 5.5C. 4.5D. 5【答案】C【分析】【解答】17.【答题】在平面直角坐标系中，已知点A（-2，-3），点B（1，3）．对A点作下列变换：①先把点A向右平移3个单位，再向上平移6个单位；②先把点A向上平移6个单位，再向右平移3个单位；③先作点A以y轴为对称轴的轴对称变换，再向左平移1个单位；④先作点A以x轴为对称轴的轴对称变换，再向右平移3个单位．其中能由点A得到点B的变换是______．【答案】①②④【分析】【解答】18.【答题】若点A（n，2）与点B（-3，m）关于原点对称，则n-m＝______．【答案】5【分析】【解答】19.【答题】如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动一个单位，依次得到点P1（0，1）；P2（1，1）；P3（1，0）；P4（1，-1）；P5（2，-1）；P6（2，0）……，则点P2019的坐标是______．【答案】（673，0）【分析】【解答】20.【答题】在平面直角坐标系中，若点M（2，4）与点N（x，4）之间的距离是3，则x的值是______．【答案】-1或5【分析】【解答】。

《平面直角坐标系》同步达标训练 2021-2022学年鲁教版七年级数学上册

2021-2022学年鲁教版七年级数学上册《5.2平面直角坐标系》同步达标训练（附答案）1．若点A（a+1，b﹣2）在第二象限，则点B（﹣a，b+1）在（）A．第一象限B．第二象限C．第三象限D．第四象限2．在平面直角坐标系中，点P（﹣2，x2+1）所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限3．如图，矩形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2021次相遇地点的坐标是（）A．（2，0）B．（﹣1，1）C．（﹣2，1）D．（﹣1，﹣1）4．如图，在5×4的方格纸中，每个小正方形边长为1，点O，A，B在方格纸的交点（格点）上，在第四象限内的格点上找点C，使△ABC的面积为3，则这样的点C共有（）A．2个B．3个C．4个D．5个5．在平面直角坐标系中，点M在第四象限，到x轴，y轴的距离分别为6，4，则点M的坐标为（）A．（4，﹣6）B．（﹣4，6）C．（﹣6，4）D．（﹣6，﹣4）6．已知点A（m，2m）和点B（3，m2﹣3），直线AB平行于x轴，则m等于（）A．﹣1B．1C．﹣1或3D．37．平面直角坐标系中，点A（﹣3，2），B（1，4），经过点A的直线l∥x轴，点C是直线l上的一个动点，则线段BC的长度最小时，点C的坐标为（）A．（﹣1，4）B．（1，0）C．（1，2）D．（4，2）8．已知点A（m，n），且有mn≤0，则点A一定不在（）A．第一象限B．第二象限C．第四象限D．坐标轴上9．已知点A（a﹣2，2a+7），点B的坐标为（1，5），直线AB∥y轴，则a的值是（）A．1B．3C．﹣1D．510．在直角坐标系中，坐标是整数的点称作格点，第一象限的格点P（x，y）满足2x+3y＝7，则满足条件的点有（）A．1个B．2个C．3个D．4个11．若点M（a+3，2a﹣4）到y轴的距离是到x轴距离的2倍，则a的值为（）A．或1B．C．D．或12．若+|b+2|＝0，则点M（a，b）在（）A．第一象限B．第二象限C．第三象限D．第四象限13．在平面直角坐标系中，点（﹣1，+1）一定在（）A．第一象限B．第二象限C．第三象限D．第四象限14．点A的坐标（x，y）满足（x+3）2+|y+2|＝0，则点A的位置在（）A．第一象限B．第二象限C．第三象限D．第四象限15．如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（1，1），（1，2），（2，2）…根据这个规律，第2021个点的横坐标为．16．如图，已知A1（1，0），A2（1，﹣1），A3（﹣1，﹣1），A4（﹣1，1），A5（2，1），…，则点A2022的坐标是．17．已知：A（0，1），B（2，0），C（4，3）（1）求△ABC的面积；（2）设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．18．在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位．其行走路线如图所示．（1）填写下列各点的坐标：A1（，），A3（，），A12（，）；（2）写出点A4n的坐标（n是正整数）；（3）指出蚂蚁从点A100到A101的移动方向．19．先阅读下列一段文字，在回答后面的问题．已知在平面内两点P1（x1，y1）、P2（x2，y2），其两点间的距离公式，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|．（1）已知A（2，4）、B（﹣3，﹣8），试求A、B两点间的距离；（2）已知A、B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为﹣1，试求A、B两点间的距离．（3）已知一个三角形各顶点坐标为A（0，6）、B（﹣3，2）、C（3，2），你能判定此三角形的形状吗？说明理由．20．问题情境：在平面直角坐标系xOy中有不重合的两点A（x1，y1）和点B（x2，y2），小明在学习中发现，若x1＝x2，则AB∥y轴，且线段AB的长度为|y1﹣y2|；若y1＝y2，则AB∥x轴，且线段AB的长度为|x1﹣x2|；【应用】：（1）若点A（﹣1，1）、B（2，1），则AB∥x轴，AB的长度为．（2）若点C（1，0），且CD∥y轴，且CD＝2，则点D的坐标为．【拓展】：我们规定：平面直角坐标系中任意不重合的两点M（x1，y1），N（x2，y2）之间的折线距离为d（M，N）＝|x1﹣x2|+|y1﹣y2|；例如：图1中，点M（﹣1，1）与点N（1，﹣2）之间的折线距离为d（M，N）＝|﹣1﹣1|+|1﹣（﹣2）|＝2+3＝5．解决下列问题：（1）如图2，已知E（2，0），若F（﹣1，﹣2），则d（E，F）；（2）如图2，已知E（2，0），H（1，t），若d（E，H）＝3，则t＝．（3）如图3，已知P（3，3），点Q在x轴上，且三角形OPQ的面积为3，则d（P，Q）＝．21．如图，已知A（﹣2，3）、B（4，3）、C（﹣1，﹣3）（1）求点C到x轴的距离；（2）求△ABC的面积；（3）点P在y轴上，当△ABP的面积为6时，请直接写出点P的坐标．22．已知点A（m+2，3）和点B（m﹣1，2m﹣4），且AB∥x轴．（1）求m的值；（2）求AB的长．23．已知：点P（2m+4，m﹣1）．试分别根据下列条件，求出P点的坐标．（1）点P在y轴上；（2）点P在x轴上；（3）点P的纵坐标比横坐标大3；（4）点P在过A（2，﹣3）点，且与x轴平行的直线上．24．如图，四边形OABC各个顶点的坐标分别是O（0，0），A（3，0），B（5，2），C（2，3）．求这个四边形的面积．25．如图，△ABC在正方形网格中，若A（0，3），按要求回答下列问题（1）在图中建立正确的平面直角坐标系；（2）根据所建立的坐标系，写出B和C的坐标；（3）计算△ABC的面积．26．已知点P（8﹣2m，m﹣1）．（1）若点P在x轴上，求m的值．（2）若点P到两坐标轴的距离相等，求P点的坐标．27．在平面直角坐标系中，已知点M（m﹣1，2m+3）（1）若点M在y轴上，求m的值．（2）若点M在第一、三象限的角平分线上，求m的值．28．在平面直角坐标系中，有A（﹣2，a+1），B（a﹣1，4），C（b﹣2，b）三点．（1）当AB∥x轴时，求A、B两点间的距离；（2）当CD⊥x轴于点D，且CD＝1时，求点C的坐标．29．已知点P（2a﹣2，a+5），解答下列各题．（1）点P在x轴上，求出点P的坐标．（2）点Q的坐标为（4，5），直线PQ∥y轴；求出点P的坐标．（3）若点P在第二象限，且它到x轴、y轴的距离相等，求a2020+2020的值．30．已知点M（3a﹣2，a+6）．（1）若点M在x轴上，求点M的坐标（2）变式一：已知点M（3a﹣2，a+6），点N（2，5），且直线MN∥x轴，求点M的坐标．（3）变式二：已知点M（3a﹣2，a+6），若点M到x轴、y轴的距离相等，求点M的坐标．参考答案1．解：由A（a+1，b﹣2）在第二象限，得a+1＜0，b﹣2＞0．解得a＜﹣1，b＞2．由不等式的性质，得﹣a＞1，b+1＞3，点B（﹣a，b+1）在第一象限，故选：A．2．解：∵x2≥0，∴x2+1≥1，∴点P（﹣2，x2+1）在第二象限．故选：B．3．解：方法一：矩形的长宽分别为4和2，因为物体乙是物体甲的速度的2倍，时间相同，物体甲与物体乙的路程比为1：2，由题意知：①第一次相遇物体甲与物体乙行的路程和为12×1，物体甲行的路程为12×＝4，物体乙行的路程为12×＝8，在BC边相遇；②第二次相遇物体甲与物体乙行的路程和为12×2，物体甲行的路程为12×2×＝8，物体乙行的路程为12×2×＝16，在DE边相遇；③第三次相遇物体甲与物体乙行的路程和为12×3，物体甲行的路程为12×3×＝12，物体乙行的路程为12×3×＝24，在A点相遇；…此时甲、乙回到原出发点，则每相遇三次，两点回到出发点，∵2021÷3＝673…2，故两个物体运动后的第2021次相遇地点的是：第二次相遇地点，即物体甲行的路程为12×2×＝8，物体乙行的路程为12×2×＝16，在DE边相遇；此时相遇点的坐标为：（﹣1，﹣1），方法二：设经过t秒甲、乙相遇，t+2t＝12，解得：t＝4，此时相遇点在（﹣1，1），事实上，无论从哪里起始，它们每隔4秒相遇一次，所以，再过4秒，第二次在（﹣1，﹣1）相遇，再过4秒，第三次在A（2，0）相遇，…此时甲、乙回到原出发点，则每相遇三次，两点回到出发点，∵2021÷3＝673…2，故两个物体运动后的第2021次相遇地点的是：第二次相遇地点，故选：D．4．解：由图可知，AB∥x轴，且AB＝3，设点C到AB的距离为h，则△ABC的面积＝×3h＝3，解得h＝2，∵点C在第四象限，∴点C的位置如图所示，共有3个．故选：B．5．解：因为点M在第四象限，所以其横、纵坐标分别为正数、负数，又因为点M到x轴的距离为6，到y轴的距离为4，所以点M的坐标为（4，﹣6）．故选：A．6．解：∵直线AB平行于x轴，∴点A的纵坐标与B的纵坐标相等，∴2m＝m2﹣3，即m2﹣2m﹣3＝0，∴（m﹣3）（m+1）＝0，∴m﹣3＝0或m+1＝0，∴m＝3或m＝﹣1．∵A、B是两个点，才能连线平行X轴，∴m≠3，∴m＝﹣1故选：A．7．解：如图，根据垂线段最短可知，BC⊥AC时BC最短．∵A（﹣3，2），B（1，4），AC∥x轴，∴BC＝2，∴C（1，2），故选：C．8．解：根据点A（m，n），且有mn≤0，所以m≥0，n≤0或m≤0，n≥0，所以点A一定不在第一象限，故选：A．9．解：∵点A（a﹣2，2a+7），点B的坐标为（1，5），直线AB∥y轴，∴a﹣2＝1，解得a＝3．故选：B．10．解：∵2x+3y＝7，∴x＝2，y＝1，满足条件的点有1个．故选：A．11．解：由题意得|a+3|＝2|2a﹣4|，∴a+3＝2（2a﹣4）或a+3＝2（4﹣2a），解得a＝或a＝1，故选：A．12．解：由题意得，a﹣3＝0，b+2＝0，解得a＝3，b＝﹣2，所以，点M的坐标为（3，﹣2），点M在第四象限．故选：D．13．解：因为点（﹣1，1），横坐标小于0，纵坐标1一定大于0，所以满足点在第二象限的条件．故选：B．14．解：∵（x+3）2+|y+2|＝0，∴x＝﹣3＜0，y＝﹣2＜0．则点A在第三象限．故选：C．15．解：根据图形，以最外边的矩形边长上的点为准，点的总个数等于x轴上右下角的点的横坐标的平方，例如：右下角的点的横坐标为1，共有1个，1＝12，右下角的点的横坐标为2时，共有4个，4＝22，右下角的点的横坐标为3时，共有9个，9＝32，右下角的点的横坐标为4时，共有16个，16＝42，…右下角的点的横坐标为n时，共有n2个，∵452＝2025，45是奇数，∴第2025个点是（45，0），第2021个点是（45，4），所以，第2021个点的横坐标为45．故答案为：45．16．解：易得4的整数倍的各点如A4，A8，A12等点在第二象限，∵2022÷4＝505…2；∴A2022的坐标在第四象限，横坐标为（2022﹣2）÷4+1＝506；纵坐标为﹣506，∴点A2022的坐标是（506，﹣506）．故答案为：（506，﹣506）．17．解：（1）S△ABC＝3×4﹣×2×3﹣×2×4﹣×1×2＝4；（2）如图所示：以BP1，BP2为底，符合题意的有P1（﹣6，0）、P2（10，0）、以AP3，AP4为底，符合题意的有：P3（0，5）、P4（0，﹣3）．18．解：（1）A1（0，1），A3（1，0），A12（6，0）；（2）当n＝1时，A4（2，0），当n＝2时，A8（4，0），当n＝3时，A12（6，0），所以A4n（2n，0）；（3）点A100中的n正好是4的倍数，所以点A100和A101的坐标分别是A100（50，0），A101的（50，1），所以蚂蚁从点A100到A101的移动方向是从下向上．19．解：（1）∵A（2，4）、B（﹣3，﹣8），∴|AB|＝＝13，即A、B两点间的距离是13；（2）∵A、B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为﹣1，∴|AB|＝|﹣1﹣5|＝6，即A、B两点间的距离是6；（3）△ABC是等腰三角形，理由如下：∵一个三角形各顶点坐标为A（0，6）、B（﹣3，2）、C（3，2），∴AB＝5，BC＝6，AC＝5，∴AB＝AC，∴△ABC是等腰三角形．20．解：【应用】：（1）AB的长度为|﹣1﹣2|＝3．故答案为：3．（2）由CD∥y轴，可设点D的坐标为（1，m），∵CD＝2，∴|0﹣m|＝2，解得：m＝±2，∴点D的坐标为（1，2）或（1，﹣2）．故答案为：（1，2）或（1，﹣2）．【拓展】：（1）d（E，F）＝|2﹣（﹣1）|+|0﹣（﹣2）|＝5．故答案为：＝5．（2）∵E（2，0），H（1，t），d（E，H）＝3，∴|2﹣1|+|0﹣t|＝3，解得：t＝±2．故答案为：2或﹣2．（3）由点Q在x轴上，可设点Q的坐标为（x，0），∵三角形OPQ的面积为3，∴|x|×3＝3，解得：x＝±2．当点Q的坐标为（2，0）时，d（P，Q）＝|3﹣2|+|3﹣0|＝4；当点Q的坐标为（﹣2，0）时，d（P，Q）＝|3﹣（﹣2）|+|3﹣0|＝8．故答案为：4或8．21．解：（1）∵C（﹣1，﹣3），∴|﹣3|＝3，∴点C到x轴的距离为3；（2）∵A（﹣2，3）、B（4，3）、C（﹣1，﹣3）∴AB＝4﹣（﹣2）＝6，点C到边AB的距离为：3﹣（﹣3）＝6，∴△ABC的面积为：6×6÷2＝18．（3）设点P的坐标为（0，y），∵△ABP的面积为6，A（﹣2，3）、B（4，3），∴6×|y﹣3|＝6，∴|y﹣3|＝2，∴y＝1或y＝5，∴P点的坐标为（0，1）或（0，5）．22．解：（1）∵A（m+2，3）和点B（m﹣1，2m﹣4），且AB∥x轴，∴2m﹣4＝3，∴m＝．（2）由（1）得：m＝，∴m+2＝，m﹣1＝，2m﹣4＝3，∴A（，3），B（，3），∵﹣＝3，∴AB的长为3．23．解：（1）令2m+4＝0，解得m＝﹣2，所以P点的坐标为（0，﹣3）；（2）令m﹣1＝0，解得m＝1，所以P点的坐标为（6，0）；（3）令m﹣1＝（2m+4）+3，解得m＝﹣8，所以P点的坐标为（﹣12，﹣9）；（4）令m﹣1＝﹣3，解得m＝﹣2．所以P点的坐标为（0，﹣3）．24．解：分别过C点和B点作x轴和y轴的平行线，如图，则E（5，3），所以S四边形ABCO＝S矩形OHEF﹣S△ABH﹣S△CBE﹣S△OCF＝5×3﹣×2×2﹣×1×3﹣×3×2＝．25．解：（1）如图所示：建立平面直角坐标系；（2）根据坐标系可得出：B（﹣3，﹣1）C（1，1）；（3）S△ABC＝4×4﹣4×2﹣×3×4﹣×1×2＝5．26．解：（1）∵点P（8﹣2m，m﹣1）在x轴上，∴m﹣1＝0，解得：m＝1；（2）∵点P到两坐标轴的距离相等，∴|8﹣2m|＝|m﹣1|，∴8﹣2m＝m﹣1或8﹣2m＝1﹣m，解得：m＝3或m＝7，∴P（2，2）或（﹣6，6）．27．解：（1）由题意得：m﹣1＝0，解得：m＝1；（2）由题意得：m﹣1＝2m+3，解得：m＝﹣4．28．解：（1）∵AB∥x轴，∴A、B两点的纵坐标相同．∴a+1＝4，解得a＝3．∴A、B两点间的距离是|（a﹣1）+2|＝|3﹣1+2|＝4．（2）∵CD⊥x轴，∴C、D两点的横坐标相同．∴D（b﹣2，0）．∵CD＝1，∴|b|＝1，解得b＝±1．当b＝1时，点C的坐标是（﹣1，1）．当b＝﹣1时，点C的坐标是（﹣3，﹣1）．29．解：（1）∵点P在x轴上，∴a+5＝0，∴a＝﹣5，∴2a﹣2＝2×（﹣5）﹣2＝﹣12，∴点P的坐标为（﹣12，0）．（2）点Q的坐标为（4，5），直线PQ∥y轴，∴2a﹣2＝4，∴a＝3，∴a+5＝8，∴点P的坐标为（4，8）．（3）∵点P在第二象限，且它到x轴、y轴的距离相等，∴2a﹣2＝﹣（a+5），∴2a﹣2+a+5＝0，∴a＝﹣1，∴a2020+2020＝（﹣1）2020+2020＝2021．∴a2020+2020的值为2021．30．解：（1）∵点M在x轴上，∴a+6＝0，∴a＝﹣6，3a﹣2＝﹣18﹣2＝﹣20，a+6＝0，∴点M的坐标是（﹣20，0）；（2）∵直线MN∥x轴，∴a+6＝5，解得a＝﹣1，3a﹣2＝3×（﹣1）﹣2＝﹣5，所以，点M的坐标为（﹣5，5）．（3）∵点M到x轴、y轴的距离相等，∴3a﹣2＝a+6，或3a﹣2+a+6＝0解得：a＝4，或a＝﹣1，所以点M的坐标为（10，10）或（﹣5，5）．。

七年级数学平面直角坐标系同步练习(三)鲁教版

§4.3平面直角坐标系(三) 同步练习一、选择题1. 已知点P(3,2)与Q(3,-2),则下列说法正确的是( )A.点P与Q关于y轴对称B. 点P与Q关于x轴对称C. 点P与Q关于直线x=1对称D. 点P与Q关于直线y=1对称2. 已知点P(2a-5,4)与Q(a+2,4)关于y轴对称,则a= ( )A. 7B. 1C. –7D. –13.已知a>0,b<0,则点P( a+1,b-1) 关于y轴对称的点一定在( )A.第一象限B. 第二象限C. 第三象限D. 第四象限4.已知点A(2x-4, -6)关于x轴对称的点在第二象限,则( )A. x>2B. x<2C. x>0D.x<05．一束光线从点Ａ（３，３）出发，经过ｙ轴上点Ｃ反射后经过点Ｂ（１，０）则光线从Ａ点到Ｂ点经过的路线长是（）Ａ．４Ｂ．５Ｃ．６Ｄ．７二、填空题6.点P(3,4)到原点的距离等于.7. 点A(-4, -3) 与B (4, -3) 关于轴对称.8.当m= 时, 点P(-4,3m-5)与Q(-4,2m-10)关于x轴对称.9.当m= 时, 点P(-3,3m-5)与Q(3,2m-10)关于原点对称.10.根据指令[s，A]( s≥0,00≤A<3600).机器人在平面上能完成如下动作：先在原地逆时针旋转角度A，再朝其面对的方向沿直线行走距离s ,现在机器人在平面直角坐标系的原点，且面对y轴的负方向: 为使其移动到点(—3，3),应下的指令是.三、简答题4,其中两个顶点在y轴上,第三个顶点在x轴上. (1)画出满足条件的图11.已知等边三角形的边长为3形;(2)写出三个顶点的坐标.12. 如图是一座“数学宝塔”的右半部分，试作出它的左半部分,并写出图中各点坐标.13.(1)在直角坐标系中,画出下列各点: A(-2,-4),B(0,-2), C(1,-2),D(3,0);(2)分别连结AB,CD,观察两线段的位置关系;(3)写出从AB到CD的变化过程.14.在平面直角坐标系中,已知点M(3,2),N(1,-1).(1)作出点N 关于y 轴的对称点P,并写出点P 坐标; (2)连结PM,利用网格的方法计算PM 的长度,则PM 与y 轴的交点A 一定满足条件: 在y 轴上使AM+AN 最短的点.15．如图所示的直角坐标系中,A 点坐标为 (-3,4) ,B(-1,-2), O 为原点,求△AOB 的面积.16．在平面直角坐标系内，已知点A （2，1），O 为原点，请你在坐标轴上确定点P ，使得△AOP 成为等腰三角形。

鲁教版-数学-七年级上册-《平面直角坐标系》习题

初中-数学-打印版 C 1A yO B A《平面直角坐标系》习题一、填空.1、在x 轴上与点(0，-2)距离是4个单位长度的点有_________.2、点A 在y 轴上，距离原点4个单位长度，则A 点的坐标是.3、在直角坐标系内，将点A (-2.3)向右平移3个单位到B 点，则点B 的坐标是________.4、某学校的平面示意图如图所示，如果实验楼所在位置的坐标为(-2，3)，教学楼所在位置的坐标为(-1，2)，那么图书馆所在位置的坐标为_________.5、在直角坐标系中，点P (3，5)在第________象限.6、点P (4，3-)到x 轴的距离是________，到y 轴的距离是________.7、点A 在y 轴上，距离原点4个单位长度，则A 点的坐标是.8、长方形ABCD 中，A 、B 、C 三点的坐标分别是(0，0)、(6，0)、(6，4)，则点D 的坐标是____________.二、选择题.1、点(2,1)A -在第( ) A ．第一象限 B ．第二象限 C ．第三象限 D2、课间操时，小华、小军、小刚的位置如图，小华对小刚说，如果我的位置用(0，0)表示，小军的位置用(2，1)表示，那么你的位置可以表示成( ).A (5，4)B (4，5)C (3，4)D (4，3) 小华小军小刚3、一个长方形在平面直角坐标系中三个顶点的坐标为(–1，–1)、(–1，2)、(3，–1)，则第四个顶点的坐标为( ).A (2，2)B (3，2)C (3，3)D (2，3)三、解答题1、在如图直角坐标系中，描出以下坐标点：(9，1)(11，6)(16，8)(11，10)(9，15)(7，10)(2，8)(7，6)(9，1)，并将各点用线段顺次连接起来.2、在图1的平面直角坐标系中，请完成下列各题：(1)写出图中A ，B ，C ，D 各点的坐标；(2)描出E (1，0)，F (1-，3)，G (3-，0)，H (1-，3-)；图11 O 1(3)顺次连接A，B，C，D各点，再顺次连接E，F，G，H，围成的两个封闭图形分别是什么图形？3、在直角坐标系中，矩形ABCD的顶点坐标为A(-4，0)，B(0，0)，C(0，2)，D(-4，2).将矩形的边AB和BC的长分别扩大一倍，所得矩形的四个顶点坐标是什么？初中-数学-打印版。

鲁教版七年级数学坐标轴,距离,平行对称专题练

专题1.点在坐标轴上：在x轴上纵坐标为0。

在y轴上横坐标为0。

在坐标轴上分横坐标为0或纵坐标为0或横纵坐标都为0三种情况1．若点P（m﹣2，2m+1）在x轴上，则m的值是．2．在平面直角坐标系中，若点P（﹣1，m﹣5）在x轴上，则m的值为．3．当m＝时，点A（2﹣m，3m﹣12）在x轴上．4．在平面直角坐标系中，点P（a2+2，﹣4）在第象限．5．已知P点坐标为（4﹣a，3a+9），且点P在x轴上，则点P的坐标是．6．在平面直角坐标系中，点（a2+1，﹣1）一定在第象限．7．若点P（a+1，2a+3）在平面直角坐标系的x轴上，则a的值为．8．平面直角坐标系中，若点A（2，m+3）在x轴上，则m的值是．9．若点M（a﹣2，a+3）在y轴上，则点N（a+2，a﹣3）在第象限．10．点p（m+2，m﹣1）在y轴上，则点P的坐标是．专题2.到x轴y轴的距离问题p（a,b）①到x轴的距离为纵坐标b的绝对值，②到y轴的距离为横坐标a的绝对值③到x轴y轴的距离相等的点在一三象限和二四象限角平分线上，a=b或a+b=0两种情况④一三象限角平分线上的点到坐标轴距离相等，横纵坐标相等a=b⑤二四象限角平分线上的点到坐标轴距离相等，横纵坐标互为相反数a+b=011．平面内点A（﹣5，4）到y轴的距离是．12．已知点A在第四象限，且到x轴，y轴的距离分别为4、5，则A点的坐标为．13．在平面直角坐标系中，点P（﹣3，2）在第象限；点P到x轴的距离是．14．点M在x轴下方，到x轴的距离是3，到y轴的距离是2，则点M的坐标是．15．若点P在第二象限，它到x轴，y轴的距离分别为3，1，则点P的坐标为．16．直角坐标系上第四象限的一点A到x轴的距离为4，到y轴的距离为3，则点A的坐标为．17．若A（a，b）位于第二象限，则B（﹣a，﹣b）位于第象限．18．当x时，点M（x﹣1，8﹣2x）在第四象限．19．若点M（2﹣a，3a+6）在坐标轴上，则点M的坐标是．20．已知点M（a，b）的坐标满足ab＞0，且a+b＜0，则点M在第象限．专题3，对称关于谁谁不变，关于原点都要变。

2019学年七年级数学上册坐标的应用习题 (新版)鲁教版

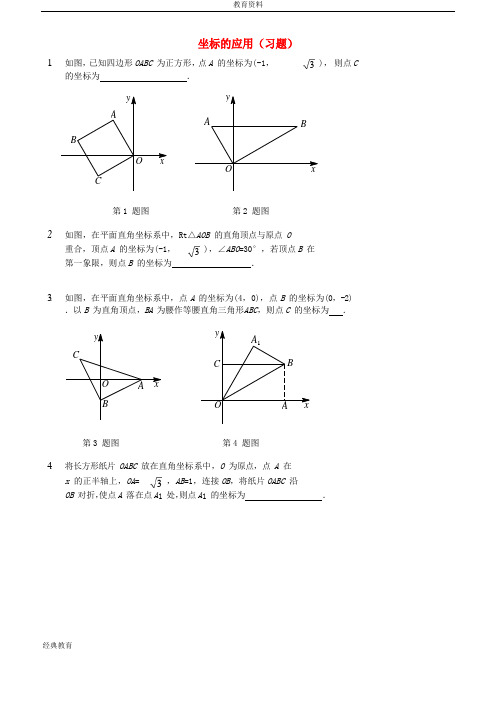
3 3 3 坐标的应用（习题）1.如图，已知四边形 OABC 为正方形，点 A 的坐标为(-1，)，则点 C 的坐标为．第 1 题图第 2 题图2. 如图，在平面直角坐标系中，Rt △AOB 的直角顶点与原点 O 重合，顶点 A 的坐标为(-1， )，∠ABO =30°，若顶点B 在第一象限，则点 B 的坐标为．3.如图，在平面直角坐标系中，点 A 的坐标为(4，0)，点 B 的坐标为(0，-2)．以 B 为直角顶点，BA 为腰作等腰直角三角形ABC ，则点 C 的坐标为．第 3 题图第 4 题图4. 将长方形纸片 OABC 放在直角坐标系中，O 为原点，点 A 在x 的正半轴上，OA = ，AB =1，连接 OB ，将纸片 OABC 沿 OB 对折，使点 A 落在点 A 1 处，则点 A 1 的坐标为．3 3 5. 如图，在 Rt △ABC 中，∠ABC =90°，AB 垂直 x 轴，点 D 为AC 的中点，连接 BD ，延长 BD 到点 E ，使 DE =BD ，连接 AE ．若点 A 的坐标为(-2，4)，点 C 的坐标为(3，-2)，则点 E 的坐标为．第 5 题图第 6 题图6. 如图，将△ABC 绕点 C (0，1)旋转 180°得到△A ′B ′C ，若点 A的坐标为(2，-2)，则点 A ′的坐标为．7. 如图，在平面直角坐标系 xOy 中，点 A 的坐标为(0，)，点 B 的坐标为(1，0)，将△AOB 沿直线 AB 折叠，点 O 落在点 C 处，则点 C的坐标为．第 7 题图第 8 题图8. 如图，在平面直角坐标系 xOy 中，Rt △OAB 的顶点 A 的坐标为( ，1)，直角顶点 B 在 x 轴上，若将△OAB 绕点 O 旋转 60°后，点 B 到达点 B ′处，则点 B ′的坐标为．9.如图，在平面直角坐标系中，O 为坐标原点，四边形OABC 是长方形，点A，C 分别在x 轴、y 轴的正半轴上，点B 的坐标为(5，4)．若P 为BC 边上的动点，则当△POA 是等腰三角形时，点P 的坐标为．10.如图，在平面直角坐标系中，已知点A 的坐标为(3，4)，过点A 作直线a//y轴，连接OA．点P 是直线a 上一动点，则当△AOP 是等腰三角形时，点P 的坐标为．3 3 【参考答案】巩固练习1. ( ，-1)2. (3， )3. (-2，2)4. (3 ， 3 ) 2 25. (3，4)6. (-2，4)7. ( 3 ， 3 )2 2 8. (3 ， 3 )或( 3 ， 3)2 2 2 29. (3，4)，(2，4)或( 5，4)210. (3，-4)，(3，9) ，(3，-1)或(3， 7)8。

部编版2020学年七年级数学上册坐标的应用习题 (新版)鲁教版

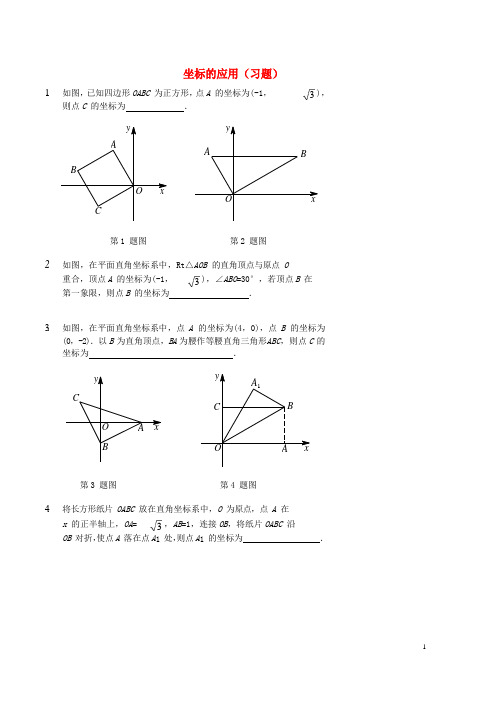
3 3 3 坐标的应用（习题）1. 如图，已知四边形 OABC 为正方形，点 A 的坐标为(-1， )，则点 C 的坐标为．第 1 题图第 2 题图2. 如图，在平面直角坐标系中，Rt △AOB 的直角顶点与原点 O 重合，顶点 A 的坐标为(-1， )，∠ABO =30°，若顶点 B 在第一象限，则点 B 的坐标为．3. 如图，在平面直角坐标系中，点 A 的坐标为(4，0)，点 B 的坐标为(0，-2)．以 B 为直角顶点，BA 为腰作等腰直角三角形ABC ，则点 C 的坐标为．第 3 题图第 4 题图4. 将长方形纸片 OABC 放在直角坐标系中，O 为原点，点 A 在 x 的正半轴上，OA = ，AB =1，连接 OB ，将纸片 OABC 沿 OB 对折，使点 A 落在点 A 1 处，则点 A 1 的坐标为． y A BO x CyA BO xy C O B A xy A 1C BO A x3 3 5. 如图，在 Rt △ABC 中，∠ABC =90°，AB 垂直 x 轴，点 D 为AC 的中点，连接 BD ，延长 BD 到点 E ，使 DE =BD ，连接 AE ．若点 A 的坐标为(-2，4)，点 C 的坐标为(3，-2)，则点 E 的坐标为．第 5 题图第 6 题图6. 如图，将△ABC 绕点 C (0，1)旋转 180°得到△A ′B ′C ，若点 A的坐标为(2，-2)，则点 A ′的坐标为．7. 如图，在平面直角坐标系 xOy 中，点 A 的坐标为(0， )，点 B 的坐标为(1，0)，将△AOB 沿直线 AB 折叠，点 O 落在点 C 处，则点 C 的坐标为．第 7 题图第 8 题图8. 如图，在平面直角坐标系 xOy 中，Rt △OAB 的顶点 A 的坐标为( ，1)，直角顶点 B 在 x 轴上，若将△OAB 绕点 O 旋转60°后，点 B 到达点 B ′处，则点 B ′的坐标为．y A E DO x B C yA'B'CO B x AyAC O B x yAO B x9.如图，在平面直角坐标系中，O 为坐标原点，四边形OABC 是长方形，点A，C 分别在x 轴、y 轴的正半轴上，点B 的坐标为(5，4)．若P 为BC 边上的动点，则当△POA 是等腰三角形时，点P 的坐标为．10.如图，在平面直角坐标系中，已知点A 的坐标为(3，4)，过点A 作直线a//y 轴，连接OA．点P 是直线a 上一动点，则当△AOP 是等腰三角形时，点P 的坐标为．3 3 【参考答案】巩固练习1. ( ，-1)2. (3， )3. (-2，2)4. ( 3 ， 3 )2 25. (3，4)6. (-2，4)7. ( 3 ， 3 )2 28. ( 3 ， 3 )或( 3 ， 3 )2 2 2 29. (3，4)，(2，4)或( 5 ，4)210. (3，-4)，(3，9) ，(3，-1)或(3，7 ) 8。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平面直角坐标系（习题）➢巩固练习
1.如图，小明用手盖住的点的坐标可能是（）
A．(2，3) B．(2，-3) C．(-2，3) D．(-2，-3)
2.平面直角坐标系中有一点P(a，b)，如果ab=0，那么点P 的位置在（
）
A．原点B．x 轴上C．y 轴上D．坐标轴上
3.在坐标平面内，有一点P(a，b)，若ab>0，那么点P 的位置在（）
A．第一象限B．第二象限 C．第一象限或第三象限D．第二象限或第四象限
4.若点A(a，b)在第三象限，则点C(-a+1，3b-5)在第象限．
5.在平面直角坐标系中，如果a<0，b>0，那么点(0，a)在
；点(b，0)在．
6.若点A(n-3，m-1)在x 轴上，点B(2n+1，m+4)在y 轴上，则点C(m，
n)在第象限．
7.若过A(4，m)，B(n，-3)两点的直线与y 轴平行，且AB=2，则m=
，n=_ ．
8.若点A(m，n)与点B(-3，-2)在同一条垂直于y 轴的直线上，点A 到y
轴的距离为4，则m= ，n= ．
9.如图，正方形ABCD 在平面直角坐标系中，其中三个顶点的坐标分别
为(2，3)，(-3，-1)，(2，-1)，则第四个顶点的坐标为．
10.已知点P(4，-3)，它到x 轴的距离为，到y 轴的距离为
，到原点的距离为．
11.点M 在y 轴的左侧，距离x 轴4 个单位长度，距离y 轴3 个单位
长度，则点M 的坐标为．
12.点P(3，-2)关于x 轴的对称点的坐标是，关于y 轴
的对称点的坐标是，关于原点的对称点的坐标是
．
13.点P(-2a-1，a-1)在y 轴上，则点P 关于x 轴的对称点的坐标为
．
14.若点P 先向左平移 2 个单位，再向上平移 1 个单位得到
P′(-1，3)，则点P 的坐标是．
15.如图，△ABC 内部任意一点P(a，b)平移后的对应点为
P′(a+4，b+1)，若将△ABC 作同样的平移得到△A′B′C′，则A′，B′，C′的坐标分别为、、．
16.作图：在平面直角坐标系中，将坐标是(2，0)，(2，2)，
(0，2)，(0，3)，(2，5)，(3，5)，(2，2)，(5，3)，(5，2)，
(3，0)，(2，0)的点用线段依次连接起来形成一个图案．
回答下列问题：
（1）每个点的纵坐标保持不变，横坐标分别乘以-1，顺次连接这些点，所得图案与原图案的位置关系是；
（2）每个点的横坐标保持不变，纵坐标分别乘以-1，顺次连接这些点，所得图案与原图案的位置关系是．
17.如图是小刚画的一张脸，如果用(0，2)表示左眼，用(2，2)表示右眼
，那么嘴的位置可以表示成．
18.如图，若OA=OC=4，则点A 的坐标是，点C
的坐标是．
y
A
B 45°
O
D
60°x
C
➢
思考小结
1. 坐标特征：
2. 若 a ，b 同号，则点 P (a
，b )在第
象限，若 a ，b 异号，则
点 P (a ，b )在第象限．
3. 点(x ，y )向左平移 a 个单位后的坐标为
；
点(x ，y )向下平移 b 个单位后的坐标为；点(x ，y )先向上平移 a 个单位，再向右平移 b 个单位后的坐标为． 4. 在如图所示的平面直角坐标系中，四边形 ABCD 各个顶点的坐标分别
是 A (-3，1)，B (3，3)，C (4，-3)，D (-2，-2)．
（1）这是一个不规则的四边形，所以要求面积准备采用（填“公式法”或“割补法”或“转化法”）；
（2）四边形 ABCD 的面积为．
2 2
3 【参考答案】
➢
巩固练习 1. B 2. D 3. C 4. 四
5. y 轴负半轴上；x 轴正半轴上
6.
四
7. -1 或-5，4
8. 4 或 -4，-2 9. (-3，3) 10. 3，4，5
11. (-3，4)或(-3，-4)
12. (3，2)，(-3，-2)，(-3，2)
13. (0， 3
)
2
14. (1，2)
15. (1，3)，(0，0)，(5，2)
16. 作图略（1）关于 y 轴对称；（2）关于 x 轴对称 17. (1，0)
18. ( 2 ， 2 )，(2， 2 ) ➢ 思考小结
1. 略
2. 一或三，二或四
3. (x -a ，y )；(x ，y -b )；(x +b ，y +a )
4. （1）割补法；（2）27.5
欢迎您的下载，资料仅供参考！。

七年级数学上册 平面直角坐标系习题 (新版)鲁教版

初中数学鲁教版(五四制)七年级上册第五章 位置与坐标本章综合与测试-章节测试习题(3)