二阶系统的过渡过程
过程控制技术-第三章 过程控制系统的分析

3 过程控制系统的分析
时曲线有极值点(n为正整数)。将上述两种t值代入式(3-18),就能求出过渡过程曲线的各个特殊点数值,其数值列入表3-2中。
3 过程控制系统的分析
根据表3-2中数据绘制出过渡过程曲线如图3-5中的曲线2所示
过程控制技术
第六讲 过程控制系统的过渡过程分析(二)
3 过程控制系统的分析
(2)衰减比n 是指过渡过程曲线同方向的前后相邻两个峰值之比,如图3-6中B/B′=n,或习惯表示为n∶1。可见n愈小,过渡过程的衰减程度越小,意味着控制系统的振荡程度越加剧烈,稳定性也就低,当n=1时,过渡过程为等幅振荡;反之,n愈大,过渡过程愈接近非振荡过程,相应的稳定性也越高。从对过程控制系统的基本性能要求综合考虑(稳定、迅速),
3 过程控制系统的分析
式中下标“0”表示系统在初始平衡状态下的数值,则
3 过程控制系统的分析
(4)控制器的控制规律 在过程控制系统中常使用的控制器,其控制规律有比例、比例积分和比例积分微分三种,它们的数学模型分别为:
3 过程控制系统的分析
在这个系统中若选用的是电动比例控制器,则p=Kce 在过程控制仪表中控制器的放大系数Kc是通过改变控制器的比例度δ来设置的,若采用测量范围(量程)为50~100℃,输出信号为4~20 mA DC的电动温度变送器,并选用电动控制器的比例度δ=20%,于是根据比例度的定义计算出控制器的放大系数是:
3 过程控制系统的分析
(5)余差C(残余偏差) 余差是过渡过程终了时设定值与被控变量的稳态值之差,用数学式表示为 余差是一个反映控制系统准确性的质量指标,也是一个精度指标。它由生产工艺给出,一般希望余差为零或不超过预定的范围。
3 过程控制系统的分析
自动控制_03b二阶系统计算举例.

解:直接利用二阶系统的阶跃响应特征值的计算公式
arctg
tr
1 2
n 1 2
1 0.62 3.14 arctg 3.14 0.93 0 . 6 0.55s 2 4 5 1 0.6
3.14 tp d n 1 2 = 4 0.785 s
p e
ts
1
2
100% = e
3.140.6 0.8
100% 9.5%
3
ts
n 4
1s
5%
n
1.33
2% 2%
注:N 1说明过渡过程只存在一次超调。振荡在一个 周期内可结束。
2 0 .8 0 .8 3.14 0.6 1 .5 1 2 1 .5 0 .8 N 0 .6 3.14 0.6
n 1
3
2
n 1.96(rad / s)
n
0.7809 ( N s 2 / cm)
f 2 n M 18( N s / cm)
五、单位速度函数作用下二阶系统的过渡过程
1 单位速度函数为 r (t ) t ,则有 R ( s ) 2 ,其对应的输出信号的 s 拉氏变换式为:
1 C ( s) 2 2 2 s 2 n s n s
2 n
1)
欠阻尼(
0 1 )时的过渡函数
2 2 ( s n ) (2 2 1)
1 n n 由 C (s) 2 2 s s s 2 2 n s n
t 0
2 n 1
2
e
( 2 1) n t
自动控制原理第三章二阶系统的数学模型及单位阶跃响应.ppt

定义: 由二阶微分方程描述的系统称为二阶 系统。
➢二阶系统数学模型
二阶系统的微分方程一般式为:
dd 2c t(2t)2 ndc d (tt)n 2c(t)n 2r(t)
(n 0)
阻尼比 n 无阻尼振荡频率
二阶系统的反馈结构图
R(s)
22 nn
ss((ss 22nn))
形式,而闭环零点的微分作用,将在保证响应特性 平稳的情况下,显著地提高系统的快速性。
2.输出量的速度反馈控制
将输出量的速度信号c(t)采用负反馈形式,反馈到输 入端并与误差信号e(t)比较,构成一个内回路,称为 速度反馈控制。如下图示。
闭环传函为:
(s)C R ( (s s) )s2(2 n n K 2tn 2)s n 2
等效阻尼比:
t
1 2
Ktn
等效阻尼比增大了,振荡倾向和超调量减小,改 善了系统的平稳性。
3.比例-微分控制和速度反馈控制比较
➢从实现角度看,比例-微分控制的线路结构比较简 单,成本低;而速度反馈控制部件则较昂贵。
➢从抗干扰来看,前者抗干扰能力较后者差。
➢从控制性能看,两者均能改善系统的平稳性,在相 同的阻尼比和自然频率下,采用速度反馈不足之处是 其会使系统的开环增益下降,但又能使内回路中被包 围部件的非线性特性、参数漂移等不利影响大大削弱。
3.发展 (1)原因: ①甲午战争以后列强激烈争夺在华铁路的 修。筑权 ②修路成为中国人 救的亡强图烈存愿望。 (2)成果:1909年 京建张成铁通路车;民国以后,各条商路修筑 权收归国有。 4.制约因素 政潮迭起,军阀混战,社会经济凋敝,铁路建设始终未入 正轨。
由此知道:
c(t)c1(t)c2(t)
实验九,离散系统的过渡过程概要

1、离散系统的零极点对系统过渡过程的影响( 注意,零, 极点可以自由修改,目的,通过零极点的变化找出对系统过渡过程的影响)(1)一阶系统:选取在单位圆内外实轴上不同位置的单极点对象做系统的单位阶跃响应曲线:{p=-2,-1,-0.5,0,0.5,1,2}设所控制的一阶系统模型为Gz=1,1+p编程实现此系统模型在不同实数零极点处的单位阶跃响应曲线。
程序代码如下所示:num=[0 1]a=[-2;-1;-0.5;0;0.5;1;2]k=length(a)for i=1:kden=[1 -a(i)]dstep(num,den)hold onend由上图可以看出,当闭环实数的极点位于右半Z平面,则输出动态响应形式为单向正脉冲序列。
实极点位于单位圆内,脉冲序列收敛,且实极点越接近原点,收敛越快;实极点位于单位圆上,脉冲序列等幅变化;实极点位于单位圆外,脉冲序列发散。
若闭环实数极点位于左半Z平面,则输出动态响应形式为双向交替脉冲序列。
实极点位于单位圆内,双向脉冲收敛;实极点位于单位圆上,双向脉冲序列等幅变化;实极点位于单位圆外,双向脉冲序列发散。
(2)二阶系统:选取在单位圆内外不同位置的一对共轭复数极点做系统的单位阶跃响应曲线:{ P1,2 =−1.4 ±2 j, −0.4 ±0.6 j,0.1 ±0.1j,0.1 ±0.9 j,0.5±0.7 j,1.4± 2 j } 设所控制的系统模型是Gz=1()()编程实现此系统模型在不同复数零极点处的单位阶跃响应曲线。
程序代码如下所示:num=1;p1=[-1.4+2j,-0.4+0.6j,0.1+0.1j,0.1+0.9j,0.5+0.7j,1.4+2j];p2=[-1.4-2j,-0.4-0.6j,0.1-0.1j,0.1-0.9j,0.5-0.7j,1.4-2j];for i=1:length(p1)figure(1);den=conv([1 -p1(i)],[1 -p2(i)]);sys_discrete_close=tf(num,den);subplot(3,2,i);[dnumc,ddenc]=tfdata(sys_discrete_close,'v');endgtext('p1=-1.4+2j p2=-1.4-2j');gtext('p1=-0.4+0.6j p2=-0.4-0.6j');gtext('p1=0.1+0.1j p2=0.1-0.1j');gtext('p1=0.1+0.9j p2=0.1-0.9j');gtext('p1=0.5+0.7j p2=0.5-0.7j');gtext('p1=1.4+2j p2=1.4-2j');可见:当闭环极点位于单位圆内时,其对应的暂态分量是衰减的,极点离原点越近衰减越快;当闭环极点位于正实轴之上时,暂态分量是按指数衰减的,一对共轭复数极点的暂态分量为振荡衰减,其角频率为θk/T;当闭环极点位于负实轴上时,暂态分量也出现衰减振荡,其振荡角频率为π/T。
3.3二阶系统
tp d 1 2 n
(6)最大超调量的计算:
p
c(t p ) c() c ( )
n t p
100%
1 2
2
e
e
(cos d t p
sin d t p ) 100%
n t p
(cos
1
sin ) 100%
dc(t ) / dt 0
则
故
n e
nt p
sin(d t p ) d e
tan(d t p )
nt p
cos(d t p ) 0
2
1
tan
到达第一个峰值时应有
d t p 0, , 2 ,3
d t p
s1 , s2 jn 是一对共轭纯虚数根。
三、二阶系统的单位阶跃响应
对于单位阶跃输入
r (t ) 1(t )
1 R( s) s
于是
2 n 1 C ( s) 2 2 s 2n s n s
由拉氏反变换可以得到二阶系统的单位阶跃响应为
c(t ) L1[C ( s)] 下面按阻尼比分别讨论。
欠阻尼系统单位阶跃响应为
c(t ) 1 e nt cos d t
n t e sin d t d
n
1 e nt (cos d t
1
2
sin d t )
(t 0)
或写为
c(t ) 1 e nt 1
2
( 1
解得 t 1/ n 。 整个暂态过程中,临界阻尼系统阶跃响应都是单调 增长的没有超调。如以达到稳态值的 95% 所经历的时 间做为调整时间,则
自动控制原理-二阶系统的响应

荡。
0
Re
t × − jωn
c.∵e(t) = r(t) −c(t) =
1
1−ζ
2
e−ζωnt
sin(ωdt
+
β)
8
∴ess = e(∞) = 0
即系统带有一个积分环节,对单位阶跃输 入,稳态误差为零。
2、临界阻尼情况 (ζ = 1)
此时
G(S)
=
C(S) R(S)
=
(S
ωn2 + ωn )2
而
R(S)
即它们是 c(t)的包络线: 1 − ζ 2
23
包络线的时间常数为:
T= 1
ζωn
可用包络线代替响应曲线,求出近似调
整时间,即
ts
(5%
)
=
3
ζω
n
(0 < ζ < 0.9)
ts
(2%)=
4
ζωn
(0 < ζ < 0.9)
24
调整时间与闭环极点与虚轴的距离成反比, 极点离虚轴越远,调整时间越短。
b.若 ζ >> 1, S1 << S2 , 此时系统可用
一阶系统来近似,即
C(S) = S1 R(S) S + S1
ts
=
3 S1
(5%)
12
4、负阻尼情况 (ζ < 0)
此时,系统响应表达式的各指数项均为 正指数,其阶跃响应是发散的:
h(t)
h(t)
0
t
0
t
5、二阶系统在各种阻尼比下的h(t)
13
讨论:
a.阻尼比 ζ 是二阶系统最重要的特征参数, 只要知道 ζ 的大小,而不必求解方程,就
二阶系统的时域响应与极点的关系-概述说明以及解释

二阶系统的时域响应与极点的关系-概述说明以及解释1.引言1.1 概述二阶系统是一类常见的控制系统,其具有两个自由度。
在控制理论中,了解二阶系统的时域响应与极点的关系对于系统分析和设计非常重要。
本文旨在通过探讨二阶系统的时域响应与极点的关系,揭示出其内在的数学规律和工程应用。
在本文中,我们会对二阶系统进行定义和特点的介绍,然后重点关注时域响应与极点之间的联系。
二阶系统的时域响应是指系统在时域上对输入信号的响应情况,它包括了系统的过渡过程、稳定过程和超调量等重要指标。
而系统的极点则是描述系统动态特性的重要参数,它们决定了系统的稳定性、阻尼性和振荡频率等方面。
在本文的后续内容中,我们将通过实例和数学分析,详细探讨二阶系统的时域响应与极点之间的关系。
我们将会介绍不同类型的二阶系统以及它们的特点,在此基础上,深入研究时域响应与极点之间的对应关系。
通过了解二阶系统的时域响应与极点的关系,我们可以更好地理解和分析控制系统的动态特性,为系统设计和性能调整提供理论依据和指导。
对于工程实践中的控制系统设计和优化,这一关系的理解具有重要的实际应用意义。
接下来的内容将重点聚焦于系统的定义和特点,以及时域响应与极点之间的关系,希望读者能够通过本文对二阶系统有更全面、深入的了解。
1.2文章结构1.2 文章结构本文将围绕二阶系统的时域响应与极点的关系展开讨论。
文章分为引言、正文和结论三个部分。
引言部分首先对二阶系统进行概述,介绍了其定义和特点。
随后,本节将阐述文章的结构安排,为读者提供对接下来内容的整体了解。
最后,明确本文的目的,即通过分析二阶系统时域响应与极点之间的关系,探索出对二阶系统的应用和意义。
正文部分将详细探讨二阶系统的时域响应与极点之间的关系。
首先,将对二阶系统的定义和特点进行阐述,以便读者对系统本身有清晰的认识。
然后,我们将深入研究时域响应和极点之间的关系,并通过理论分析和实例说明,阐释二阶系统响应特性与极点位置之间的关联。
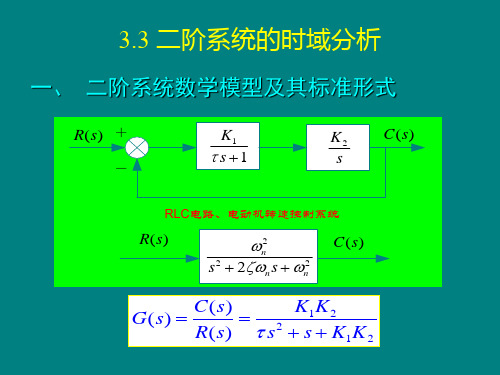
二阶系统的时域分析二阶系统的数学模型

二阶系统的数学模型
动态结构图
开环传递函数
R(s)
-
G(s)
C(s)
G(s)
n2
s(s 2n )
闭环传递函数
(s)
s2
n2 2ns
n2
ζ为系统的阻尼比;ωn为无阻尼振荡频率,简 称固有频率(也称自然振荡频率)
二阶系统的时域分析
二阶系统的闭环特征方程闭环极点
s2 2ns n2 0 s1,2 n n 2 1
阻尼比对系统的影响
0 2
0.1 1.8 0.2 1.6
1.4
0.3 1.2
0.4 1
Step Response
0.5 0.6 0.7 0.8
Amplitude
0.8
0.6
1.0
0.4
1.5
0.2
2.5
0
0
2
4
6
8
10
12
14
Time (sec)
二阶系统的时域分析
h' (t) ne nt (cosdt
1
2
sin dt)
d e nt ( sin dt
1
2
cos d t )
二阶系统的时域分析
欠阻尼二阶系统阶跃响应的性能指标
2.峰值时间tp 代入:d n 1 2
h'
(th)
' (t)ne(
n
1
2tcons 2
d tn
12n
1 2
2e)e ntnst isnindt d
曲线的不连续性,是由于ζ值的微小变化可引起调节 时间显著变化而造成的。
近似计算时,常用阻尼正弦振荡的包络线衰减到误差
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
闭环传递函数
5K 5K Φ( s ) = 2 s + 5s + 5 K
其中阻尼比和自然振荡角频率分别为
ξ=
10 R 10 , ϖ n = 10 40 R
观察阶跃响应? 令R=10K, 40K, 160K经检查线路已经正确搭接后再上电开始实验,布 线时严禁带电进行操作。 不要过于频繁得开启电源,重新开启和上一次断开之间得 时间应大于30 秒。 切勿把电阻、电容等掉进箱子左侧,以免烧坏箱子。 对于搭线被控对象时,输入和反馈回路中的电阻尽可能利 用实验板的电位器来实现。 做完实验后,应将导线及元器件按实验前的位置放好,千 万不要散乱的放在机箱中,以免下次做实验引起短路。
实验二 二阶系统的过渡过程
根据 ξ 的不同取值,二阶系统有以下几种工作状态: (1)当 0 < ξ < 1 ,此时二阶系统称为欠阻尼 欠阻尼状态。 欠阻尼 (2)当ξ = 1 ,此时二阶系统称为临界阻尼 临界阻尼状态。 临界阻尼 (3)当ξ > 1 ,此时二阶系统称为过阻尼 过阻尼状态。 过阻尼 (4)当ξ = 0 ,此时二阶系统称为无阻尼 无阻尼状态,系统 无阻尼 单位阶跃响应为等幅振荡。 那种状态最好? 那种状态最好?
自动控制原理实验
实验二 二阶系统的过渡过程
1 实验目的
1)学习自动控制系统动态性能指标的测试技术及系统 学习自动控制系统动态性能指标的测试技术及系统 动态性能指标 阶跃响应曲线的测试方法。 阶跃响应曲线的测试方法。
ζ 2)研究二阶系统的两个重要参数, 和 T 对系统动态 研究二阶系统的两个重要参数, 品质的影响。 品质的影响。
R i = 200KΩ, R f =280KΩ, (R,C)=(470KΩ,1uF),(1MΩ,1uF),(470KΩ, 4.7uF)
实验二 二阶系统的过渡过程
参数选择方案2 参数选择方案2
(1)时间常数 不变, (1)时间常数 T 不变,改变系统的阻尼比
R=1MΩ, C=1uF, R i = 100 K Ω, 调节R f =100KΩ,200KΩ,500KΩ
实验二 二阶系统的过渡过程
1 内环传递函数 ϕ ( s ) = , Ts + α
1 闭环传递函数 φ ( s ) = 2 2 = , T s + α Ts + 1 s 2 + α s + 1 T T2 1 T2
1 阻尼系数ξ = , 自然振荡角频率ωn = 2 T
α
实验二 二阶系统的过渡过程
α
图2.3. 二阶系统的模拟电路图
3)观察在不同参数下,二阶系统的阶跃响应曲线,并 观察在不同参数下,二阶系统的阶跃响应曲线, 测出超调量 σ % 和调节时间 t s。 4)定量分析 ζ 和 T 与超调量σ % ,调节时间 的关系。 t s的关系。
2 实验仪器设备
1)TDN-AC/ACS自动控制原理模拟实验机 TDN-AC/ACS自动控制原理模拟实验机 计算机(配虚拟示波器及Matlab软件) Matlab软件 2)计算机(配虚拟示波器及Matlab软件) PCI1710数据采集卡 3)PCI1710数据采集卡 4)万用表 电阻、 5)电阻、电容及联线导线 一台 一台 一块 一块 若干
实验二 二阶系统的过渡过程
4 实验原理
ωn2 s( s + 2ζωn )
图2.1.典型二阶系统方框图 2.1.典型二阶系统方框图
ωn 2 闭环传递函数: 闭环传递函数: Φ( s) = 2 s + 2ζωn s + ωn 2
系统的动态性能指标主要有: 系统的动态性能指标主要有: 动态性能指标主要有
K K K T2 开环传递函数:G ( s ) = , = 1 , 闭环传递函数:G ( s ) = K 1 K s(T2 s + 1) T1 s2 + s + T2 T2
实验二 二阶系统的过渡过程
方案2 方案2
图2.5. 另一种在模拟机上实现的二阶系统的方框图
实验二 二阶系统的过渡过程
实验中选择如下的参数
实验二 二阶系统的过渡过程
5 实验步骤及实验记录与分析
通过搭建实验电路,观测在不同参数作用下,记录系统在不 通过搭建实验电路,观测在不同参数作用下, 同阻尼下过渡过程的阶跃相应曲线,并记录性能指标。 同阻尼下过渡过程的阶跃相应曲线,并记录性能指标。
实验二 二阶系统的过渡过程
6 思考题
1)在模拟系统中若阶跃输入幅值过大,会产生什么结果? 在模拟系统中若阶跃输入幅值过大,会产生什么结果? 2)在模拟仿真中为什么要多增一个1:1的比例环节? 在模拟仿真中为什么要多增一个1 的比例环节? 3)在模拟系统中如何实现负反馈,如何实现单位负反馈? 在模拟系统中如何实现负反馈,如何实现单位负反馈?
实验二 二阶系统的过渡过程
7 实验报告要求
1)写明实验线路及原始数据。要有准确的实验记录(包 写明实验线路及原始数据。要有准确的实验记录( 括测量参数)与理论值作以比较。 括测量参数)与理论值作以比较。 2)对实验中出现的问题及现象要有准确的描述和分析。 对实验中出现的问题及现象要有准确的描述和分析。 3)推导模拟电路的闭环传递函数,并确定ωn、ξ和R、C 推导模拟电路的闭环传递函数,并确定ωn、 ωn 的关系。 的关系。 4)回答实验思考题,写出本实验的体会及建议。 回答实验思考题,写出本实验的体会及建议。
其中 α =
Rf Ri
实验二 二阶系统的过渡过程
参数选择方案1 参数选择方案1
(1)时间常数 不变, (1)时间常数 T 不变,改变系统的阻尼比
R=500KΩ,C=2uF, R i = 200KΩ, 调节R f =200KΩ,400KΩ,600KΩ
(2)阻尼比不变,改变时间数 (2)阻尼比不变,改变时间数 T 阻尼比不变
(2)阻尼比不变,改变时间数 (2)阻尼比不变,改变时间数 T 阻尼比不变
R i = 100KΩ, R f =140KΩ, (R,C)=(470KΩ,1uF),(1MΩ, 1uF),(470KΩ, 4.7uF)
实验二 二阶系统的过渡过程
方案2 方案2
1 T1s
K1 T2 s + 1
图2.4. 另一种在模拟机上实现的二阶系统的方框图
σ% = e
tp =
−
ζπ
1−ζ 2
×100%
π ωn 1− ζ 2
ts ≈
3
ζωn
4
∆ = 5%
π −β tr = ωn 1−ζ 2
ts ≈
ζωn
∆ = 2%
实验二 二阶系统的过渡过程
方案1 方案1
1 Ts
1 T s
α
图2.2.一种便于在模拟机上实现的二阶系统的方框图 2.2.一种便于在模拟机上实现的二阶系统的方框图
实验二 二阶系统的过渡过程
3 实验内容 1)根据电路图搭建实验电路。 1)根据电路图搭建实验电路。 根据电路图搭建实验电路 2)保持 不变, 2)保持 T 不变,改变阻尼比 ζ ,观察过渡过程曲 线的变化情况。 线的变化情况。 3)保持 不变, 3)保持ζ 不变,改变系统的时间常数 T ,观察过 渡过程曲线的变化情况。 渡过程曲线的变化情况
