2021年转动惯量计算折算公式

合集下载

如何计算转动惯量的？

对于细杆当回转轴过杆的中点并垂直于杆时；J=m(L^2)/12其中m是杆的质量，L是杆的长度。

当回转轴过杆的端点并垂直于杆时：J=m(L^2)/3其中m是杆的质量，L是杆的长度。

对于圆柱体当回转轴是圆柱体轴线时；J=m(r^2)/2其中m是圆柱体的质量，r是圆柱体的半径。

对于细圆环当回转轴通过中心与环面垂直时，J=mR^2；当回转轴通过边缘与环面垂直时，J=2mR^2；R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时，J=﹙1/2﹚mR^2；当回转轴通过边缘与盘面垂直时，J=﹙3/2﹚mR^2；R为其半径对于空心圆柱当回转轴为对称轴时，J=﹙1/2﹚m[（R1）^2+（R2）^2]；R1和R2分别为其内外半径。

对于球壳当回转轴为中心轴时，J=﹙2/3﹚mR^2；当回转轴为球壳的切线时，J=﹙5/3﹚mR^2；R为球壳半径。

对于实心球体当回转轴为球体的中心轴时，J=﹙2/5﹚mR^2；当回转轴为球体的切线时，J=﹙7/5﹚mR^2；R为球体半径对于立方体当回转轴为其中心轴时，J=﹙1/6﹚mL^2；当回转轴为其棱边时，J=﹙2/3﹚mL^2；当回转轴为其体对角线时，J=（3/16）mL^2；L为立方体边长。

只知道转动惯量的计算方式而不能使用是没有意义的。

下面给出一些（绕定轴转动时）的刚体动力学公式。

角加速度与合外力矩的关系：角加速度与合外力矩式中M为合外力矩，β为角加速度。

可以看出这个式子与牛顿第二定律是对应的。

角动量：角动量刚体的定轴转动动能：转动动能注意这只是刚体绕定轴的转动动能，其总动能应该再加上质心动能。

只用E=（1/2）mv^2不好分析转动刚体的问题，是因为其中不包含刚体的任何转动信息，里面的速度v只代表刚体的质心运动情况。

由这一公式，可以从能量的角度分析刚体动力学的问题。

转动惯量(Moment of Inertia)是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。

(完整word版)转动惯量计算公式

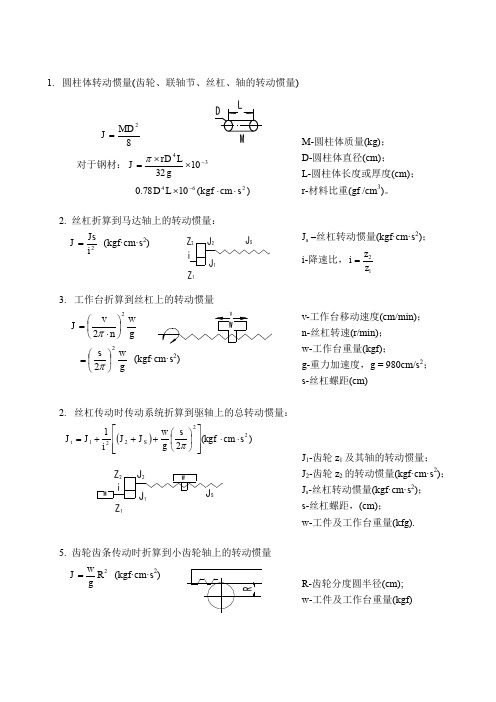
1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材：341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg)； D-圆柱体直径(cm)； L-圆柱体长度或厚度(cm)； r-材料比重(gf /cm 3)。

2. 丝杠折算到马达轴上的转动惯量：2i Js J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2)； i-降速比，12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min)； n-丝杠转速(r/min)； w-工作台重量(kgf)；g-重力加速度，g = 980cm/s 2； s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量：())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量； J 2-齿轮z 2的转动惯量(kgf·cm·s 2)； J s -丝杠转动惯量(kgf·cm·s 2)； s-丝杠螺距，(cm)； w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1，J 2-分别为Ⅰ轴，Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2)；R-齿轮z 分度圆半径(cm)； w-工件及工作台重量(kgf)。

刚体转动惯量计算公式

刚体转动惯量计算公式刚体转动惯量这玩意儿，在物理学里可是个挺重要的概念。

咱们先来瞧瞧啥是刚体转动惯量。

简单说，刚体转动惯量就是衡量刚体转动时惯性大小的一个物理量。

想象一下，你转一个大圆盘和转一个小圆盘，是不是感觉转大圆盘更费劲？这就是因为大圆盘的转动惯量大呀！那刚体转动惯量咋算呢？这就有个计算公式啦。

对于一个绕定轴转动的刚体，其转动惯量 I 等于各个质量元的质量乘以它到转轴距离的平方的总和。

用数学式子表示就是：I = ΣΔmiri² 。

比如说，有一个均匀的细棒，长度为 L ，质量为 M ，绕通过一端且垂直于棒的轴转动。

那这时候转动惯量 I 就等于 1/3 ML²。

我还记得有一次给学生们讲这个知识点的时候，有个小家伙一脸迷茫地问我：“老师，这转动惯量到底有啥用啊？”我笑着给他举了个例子。

我说：“你看啊，咱们骑自行车，车轮就是个刚体。

如果车轮的转动惯量大，那你起步的时候是不是就得费更大的劲儿？但是一旦转动起来，保持转动就相对容易些。

这就好比一个大胖子跑步，一开始跑起来难，但跑起来后惯性大，停下来也不容易。

”这小家伙听完，眼睛一下子亮了，好像明白了点什么。

再比如说一个圆环，质量为 M ，半径为 R ，绕通过圆心且垂直于圆环平面的轴转动，转动惯量就是 MR²。

还有那种质量分布不均匀的情况，就得把刚体分成很多小块，分别计算每一小块的转动惯量，然后再加起来。

这就有点像咱们做拼图，一块一块拼出最终的结果。

在实际生活中，转动惯量的应用可多啦。

像工厂里的大型机器轮子，设计的时候就得考虑转动惯量，不然运转起来可就麻烦喽。

总之，刚体转动惯量计算公式虽然看起来有点复杂，但只要咱们多琢磨琢磨，多结合实际例子想想，就能慢慢搞清楚啦。

就像解一道难题，一开始觉得难，多尝试几次，说不定就豁然开朗啦！希望大家都能把这个知识点掌握好，在物理学的世界里畅游无阻！。

转动惯量的三个基本公式

转动惯量的三个基本公式说到转动惯量，可能不少朋友会觉得这东西听起来挺复杂，其实没那么神秘。

就好像一个人在旋转的时候，越重的东西转起来越费劲，你能想象一个大胖子在冰面上转圈圈，哎呀，那可真是要多困难有多困难。

而转动惯量就是用来描述这种“转动困难”的一个重要概念。

它就像一个“老大哥”，告诉我们物体在转动时的“任性程度”。

咱们就聊聊转动惯量的三个基本公式，简单点说，就是让大家明白这个东西的“真面目”。

首先呢，有一个超级简单的公式，叫做 (I = m cdot r^2)。

这里的 (I) 就是转动惯量，(m) 是物体的质量，(r) 是物体到旋转轴的距离。

想象一下你拿着一个轻巧的小球，往旋转轴一靠，它的转动惯量就小得可怜；可是如果你换成一个大木头块，嘿，那就完全是另一回事了！大木头块离旋转轴远，转动起来绝对是困难重重。

要是你在旋转木头的时候，还得小心别让它翻掉，那场面可真是笑话一场。

接着咱们来聊聊第二个公式，这个就有点儿意思了。

公式是 (I = frac{1{2 m r^2)，这是个普遍适用的公式，特别适合那些像圆盘、圆筒这样形状的物体。

比如说你在滑冰场看到的圆形冰盘，滑起来就特别顺畅，原因就是它的转动惯量相对较小。

这个公式里的 ( frac{1{2 ) 就是说，咱们把它的重量和半径的平方结合起来，结果就让这个冰盘转得轻松无比。

想想看，要是你在玩飞盘，飞盘轻巧又好转，这不就是得益于它的转动惯量吗？再来就是第三个公式，稍微复杂一点，但也不复杂到哪去。

这个公式是 (I =frac{2{5 m r^2)，主要适用于球形物体。

比如篮球，哦，那可是个家喻户晓的例子。

你在球场上投篮的时候，那个球转起来就像个小旋风，飞得又快又稳。

这是因为篮球的转动惯量比其他形状的物体要小，更容易在空中旋转。

你要是仔细观察，就会发现球转动的时候，那种流畅的感觉，简直让人心醉神迷。

说到这里，可能有朋友会问，转动惯量跟生活有什么关系呢？嘿，咱们日常生活中处处可见。

常见转动惯量计算公式

常见转动惯量计算公式转动惯量是描述物体转动惯性的物理量，在物理学中有着重要的地位。

那咱就来聊聊常见的转动惯量计算公式。

先来说说转动惯量的定义哈。

它可以理解为物体对于旋转运动的“抗拒程度”。

想象一下，一个巨大的飞轮和一个小小的陀螺，让它们转起来，明显能感觉到飞轮更难转动起来，也更难停下，这就是因为飞轮的转动惯量大。

常见的转动惯量计算公式里，对于一个质点，其转动惯量等于质点的质量乘以质点到转轴距离的平方。

这就好比我们去推一个离转轴远的球比推一个离转轴近的球更费劲。

再来说说均匀细棒绕垂直于棒的中心轴转动的情况。

假设细棒长度为 L ，质量为 m ，那转动惯量就等于 1/12 * m * L²。

我记得之前给学生们讲这个的时候，有个调皮的孩子就问我：“老师，这细棒要是变成金箍棒，是不是转动惯量就大得吓人啦？”全班都被他逗乐了。

还有圆盘绕中心轴转动的情况。

假如圆盘半径为 R ，质量为 M ，其转动惯量就是 1/2 * M * R²。

这就好像我们转一个大圆盘和转一个小圆盘，大圆盘明显更“稳重”，不容易被转动。

另外，对于圆环绕中心轴转动，转动惯量是 M * R²，这里的 M 是圆环的质量，R 是圆环的半径。

在实际生活中，转动惯量的概念也无处不在。

就像骑自行车，车轮的转动惯量会影响骑行的感受。

车轮大而且重的自行车，起步的时候会感觉比较吃力，但一旦速度起来了，保持稳定就相对容易些，这就是因为大而重的车轮转动惯量大。

在工程领域，转动惯量的计算更是至关重要。

比如设计汽车的发动机曲轴，就得精确计算转动惯量，以确保发动机运转的平稳性和可靠性。

总之，转动惯量的计算公式虽然看起来有些复杂，但只要我们多结合实际去理解，就会发现它们其实也没那么难。

希望大家都能掌握这些常见的转动惯量计算公式，更好地理解我们周围的物理世界。

转动惯量计算折算公式

转动惯量计算折算公式
转动惯量（即转动惯性矩）是描述物体对转动运动的惯性的物理量，
它可以用公式I=mr^2来计算，其中I是转动惯量，m是物体的质量，r是
物体的转动半径。

然而，在实际问题中，物体的形状往往是复杂的，不可能直接通过上
述公式来计算转动惯量。

为了解决这个问题，我们可以通过一些折算公式
来将复杂物体的转动惯量转换为一些简单形状的转动惯量之和。

以下是一些常见的折算公式：
1.对于长方体：
-绕通过质心垂直于一条边的转动轴转动：I=(1/12)*m*(a^2+b^2)，
其中m是质量，a和b是长方体的两个边长。

-绕通过质心垂直于两条平行边的转动轴转动：I=(1/3)*m*(a^2+b^2)，其中m是质量，a和b是长方体的两个边长。

2.对于球体：
-绕通过质心的任意轴转动：I=(2/5)*m*r^2，其中m是质量，r是球
体的半径。

3.对于圆环：
-绕通过圆环中心的垂直于其平面的转动轴转动：I=m*r^2，其中m是
质量，r是圆环的半径。

4.对于圆盘：
-绕通过圆盘中心的垂直于其平面的转动轴转动：I=(1/2)*m*r^2，其中m是质量，r是圆盘的半径。

5.对于薄杆（在转动轴与薄杆所在直线垂直的情况下）：
-绕通过薄杆中心的转动轴转动：I=(1/12)*m*L^2，其中m是质量，L 是薄杆的长度。

这些折算公式可以帮助我们将复杂物体的转动惯量转换为一些简单形状的转动惯量之和，从而简化计算过程。

在实际应用中，我们可以根据物体的形状选择合适的折算公式来计算转动惯量，从而更好地描述物体的转动运动。

转动惯量公式

nema标准中的计算是如下（转化公式）：J=A×0.055613×（Pn^0.95）÷（n/1000）^2.4-0.004474×（Pn^1.5）÷（n/1000）^1.8A小于等于1800rpm时取24，A大于1800rpm时取27 Pn为功率（kw） n 为同步转速高压电动机在设计时，要求计算出转子的转动惯量。

下面对计算方法做一分析。

转动惯量是物体在转动时惯性的度量，它不仅与物体质量的大小有关，还与物体质量分体情况有关。

机械工程师手册给出了一些简单形状物体的转动惯量。

1、圆柱体沿轴线转动惯量：Kg•m2 (1)式中：M —圆柱体质量KgR —圆柱体外径半径 m2、空心圆柱体沿轴线转动惯量：Kg•m2 (2)式中： M —空心圆柱体质量KgR —空心圆柱体外半径 mr —空心圆柱体内半径m3、薄板沿对称线转动惯量：Kg•m2 (3)式中：M —薄板质量Kga —薄板垂直于轴线方向的宽度m物体的转动惯量除了用J表示外，在工程上有的用物体的重量G和物体的回转直径D的平方的乘积GD2来表示，也称为物体的飞轮力矩或惯量矩，单位N•m2或Kg f m2。

物体的飞轮力矩GD2和转动惯量J之间的关系，用下式表示：N•m2 (4)式中：g —重力加速度 g=9.81 m/s2将重力单位N化为习惯上的重力单位Kgf ，则（4）变为：Kg f m2 (5)由以上公式，可以对鼠笼型高压电机的转动惯量进行计算。

计算时，将高压电机转子分解为转子铁心（包括导条和端环）、幅铁、转轴三部分，分别算出各部分的Jn，各部分的转动惯量相加即得电机的转动惯量J。

如需要，按（5）式换算成飞轮力矩GD2。

一般产品样本中要求给定的是转动惯量J，兰州引进的电磁设计程序计算出的是飞轮力矩GD2。

计算程序如下：1、转子铁心的转动惯量，按空心圆柱公式（2）进行计算，考虑导条端环度大小的因素，以系数c进行修正。

转动惯量积分公式

转动惯量积分公式
转动惯量积分公式是用于计算刚体转动惯量的公式，它在物理学中具有重要的应用价值。

在力学中，转动惯量是一个物体在绕某一轴旋转时所具有的惯性量度，它与物体的形状、质量分布以及旋转轴的位置有关。

转动惯量的计算涉及到对物体的每一小部分的质量、位置及旋转轴的距离的分析，因此需要使用积分公式。

转动惯量积分公式可以表示如下：
I = ∫rdm
其中，I表示转动惯量的大小，r表示物体的质心到旋转轴的距离，dm表示物体的质量微元。

对于简单的几何形状的物体，可以使用公式求解其转动惯量。

例如，对于一个密度均匀的圆环，其转动惯量可以表示为：
I = MR
其中，M为圆环的质量，R为圆环的半径。

对于其他形状的物体，可以将其分解成一系列小的质量微元，然后使用转动惯量积分公式求解。

在实际应用中，转动惯量是一个很重要的参数，它可以用来描述物体的惯性特性以及旋转的稳定性。

例如，在飞行器设计中，需要考虑飞行器的转动惯量，以保证其稳定性和控制性能。

在机械设计中，转动惯量也是一个重要的参数，用于设计传动系统和运动控制系统。

总之，转动惯量积分公式是物理学中一个重要的公式，它可以用于计算刚体的转动惯量，具有广泛的应用价值。

有关转动惯量的公式

有关转动惯量的公式转动惯量这个概念，在物理学中可是相当重要的哟！咱先来说说转动惯量到底是啥。

简单来讲，转动惯量就是描述物体转动时惯性大小的一个物理量。

就好像你要推动一个大胖子和一个小瘦子，大胖子动起来更费劲，那大胖子就相当于有更大的转动惯量。

那转动惯量的公式是啥呢？一般来说，对于一个质点，它的转动惯量 I = mr²，这里的 m 是质点的质量，r 是质点到转轴的距离。

如果是一个连续分布的物体，那计算转动惯量就得积分啦。

比如说一个均匀的细圆环，绕着圆心轴转动，它的转动惯量 I = mR²，这里的m 是圆环的质量，R 是圆环的半径。

再比如一个均匀的圆盘，绕着通过圆心且垂直于盘面的轴转动，转动惯量 I = ½ mR²。

给大家讲个我曾经遇到的事儿吧。

有一次我带着学生们做物理实验，就是研究不同形状物体的转动惯量。

我们准备了各种奇奇怪怪的东西，有小木板、塑料圆盘，还有用铁丝弯成的各种形状。

其中有一组同学，他们在测量一个不规则形状木板的转动惯量时，怎么算都不对。

我过去一看，好家伙，他们测量距离的时候量错了，把到边缘的距离当成了到转轴的距离。

我让他们重新量，最后终于算对了，那几个孩子开心得不行，我看着也觉得特有成就感。

其实在生活中，转动惯量的应用可多了去了。

就像我们骑的自行车，车轮的转动惯量就对骑行有影响。

车轮质量大、半径大，转动惯量就大，骑起来启动的时候就比较费劲，但是一旦跑起来保持速度就相对容易。

还有汽车的轮子也是同样的道理，大轮子和小轮子的转动惯量不同，对汽车的加速、制动都有影响。

在工程领域，转动惯量更是重要。

比如说设计发动机的飞轮，就得考虑转动惯量，要是设计不好，机器运转起来就不顺畅。

总之，转动惯量这个概念虽然有点抽象，但只要我们多琢磨、多联系实际，就能发现它真的无处不在，对我们理解和解决很多问题都有很大的帮助。

希望大家通过对转动惯量公式的学习，能更好地探索物理世界的奥秘，发现更多有趣的现象和规律！。

力矩做功计算公式转动惯量

力矩做功计算公式转动惯量转动惯量，也称为惯性矩或转动惯性，是描述物体对转动运动的惯性大小的物理量。

它与物体的质量分布和旋转轴的位置有关，是描述物体对转动运动的惯性大小的物理量。

在物理学中，转动惯量的概念对于描述物体在转动运动中的惯性大小非常重要，它是描述物体在转动运动中的惯性大小的物理量。

转动惯量的计算公式是：\[ I = \int r^2 dm \]其中，I表示转动惯量，r表示离转轴的距离，dm表示质量元素。

对于连续分布的质量，转动惯量的计算可以通过积分来进行。

对物体进行积分，可以得到物体对于某一轴的转动惯量。

转动惯量的计算是对物体的质量分布和旋转轴的位置进行分析，从而得到物体对于某一轴的转动惯量。

转动惯量的计算公式可以用于计算物体在转动运动中的惯性大小。

在物理学中，转动惯量是描述物体在转动运动中的惯性大小的物理量。

对于不同形状和质量分布的物体，其转动惯量的计算方法也不同。

对于简单的几何形状，可以通过几何方法来计算转动惯量；对于复杂的质量分布，可以通过积分来计算转动惯量。

转动惯量的计算公式在物理学中有着广泛的应用。

在工程学和物理学中，转动惯量的计算是对于物体在转动运动中的惯性大小进行分析的重要方法。

通过计算转动惯量，可以得到物体在转动运动中的惯性大小，从而对物体的转动运动进行分析和研究。

转动惯量的计算公式是描述物体在转动运动中的惯性大小的重要方法。

通过计算转动惯量，可以得到物体在转动运动中的惯性大小，从而对物体的转动运动进行分析和研究。

转动惯量的计算公式在工程学和物理学中有着广泛的应用，对于不同形状和质量分布的物体，其转动惯量的计算方法也不同。

转动惯量的计算公式在物理学中有着广泛的应用。

在工程学和物理学中，转动惯量的计算是对于物体在转动运动中的惯性大小进行分析的重要方法。

通过计算转动惯量，可以得到物体在转动运动中的惯性大小，从而对物体的转动运动进行分析和研究。

在物理学中，转动惯量的计算公式是描述物体在转动运动中的惯性大小的重要方法。

转动惯量计算公式

转动惯量计算公式转动惯量（也称为惯性矩或转动惯性）是物体抵抗转动的能力的度量，是物体转动时的一项重要物理性质。

在机械工程、物理学、航空航天等领域中，转动惯量的计算是解决相关问题的关键。

转动惯量可以通过各种形状的物体的质量分布来计算，例如直线、薄片、圆筒、球体等。

不同形状的物体转动惯量的计算公式也有所不同。

在本文中，我们将介绍几种常见形状的物体的转动惯量计算公式。

1. 直线的转动惯量计算公式当物体是一个直线时，其转动惯量可以用关于质量和长度的公式来计算。

以下是直线转动惯量的计算公式：•绕质心轴的转动惯量：$I = \\frac{1}{3} m l^2$•绕端点轴的转动惯量：$I = \\frac{1}{12} m l^2$其中，I是转动惯量，I是物体的质量，I是直线的长度。

2. 圆筒的转动惯量计算公式圆筒是一种常见的物体形状，例如水桶、轮胎等。

对于圆筒的转动惯量计算，有以下公式：•绕质心轴的转动惯量：$I = \\frac{1}{2} m r^2$•绕圆轴的转动惯量：I=II2其中，I是转动惯量，I是圆筒的质量，I是圆筒的半径。

3. 薄片的转动惯量计算公式薄片是一个平面形状的物体，例如纸片、金属片等。

对于薄片的转动惯量计算，有以下公式：•绕质心轴的转动惯量：$I = \\frac{1}{4} m a^2$•绕边缘轴的转动惯量：$I = \\frac{1}{3} m a^2$其中，I是转动惯量，I是薄片的质量，I是薄片的边长。

4. 球体的转动惯量计算公式球体是一个球形物体，例如篮球、乒乓球等。

对于球体的转动惯量计算，有以下公式：•绕质心轴的转动惯量：$I = \\frac{2}{5} m r^2$•绕直径轴的转动惯量：$I = \\frac{2}{3} m r^2$其中，I是转动惯量，I是球体的质量，I是球体的半径。

5. 其他形状的转动惯量计算公式除了上述常见形状的物体，其他形状的转动惯量计算公式也可以通过积分或者几何关系得到。

转动惯量计算

转动惯量计算1. 简介转动惯量是描述物体绕轴旋转时所表现出的惯性大小的物理量。

在实际应用中，计算物体的转动惯量对于设计机械系统和工程结构有着重要的作用。

本文将介绍转动惯量的定义、计算方法以及一些常见形状物体的转动惯量计算公式。

2. 转动惯量的定义转动惯量（或称作转动惯性矩）表示了物体绕特定轴旋转时所表现出的惯性大小。

当物体绕轴旋转时，自身的质量分布会导致不同部分对旋转运动的阻碍程度不同。

转动惯量用来描述物体抵抗旋转运动的特性，它与物体的质量分布以及旋转轴的位置和方向有关。

3. 转动惯量的计算方法物体的转动惯量可以通过不同的方法来计算，具体的计算方法取决于物体的形状和轴的位置。

下面将介绍几个常见形状物体的转动惯量计算公式。

3.1 点质量的转动惯量对于一个处于轴上的点质量，其转动惯量可以表示为：I = m * r^2其中，I表示转动惯量，m表示质量，r表示距离旋转轴的距离。

3.2 细长杆的转动惯量对于一个质量均匀分布的细长杆，其转动惯量可以表示为：I = (1/3) * m * L^2其中，I表示转动惯量，m表示质量，L表示杆的长度。

3.3 圆环的转动惯量对于一个质量均匀分布的圆环，其转动惯量可以表示为：I = m * R^2其中，I表示转动惯量，m表示质量，R表示圆环的半径。

4. 应用举例以下是几个常见物体的转动惯量计算示例：4.1 球体的转动惯量对于一个质量均匀分布的球体，其转动惯量可以表示为：I = (2/5) * m * R^2其中，I表示转动惯量，m表示质量，R表示球体的半径。

4.2 圆盘的转动惯量对于一个质量均匀分布的圆盘，其转动惯量可以表示为：I = (1/2) * m * R^2其中，I表示转动惯量，m表示质量，R表示圆盘的半径。

4.3 矩形板的转动惯量对于一个质量均匀分布的矩形板，其转动惯量可以表示为：I = (1/12) * m * (a^2 + b^2)其中，I表示转动惯量，m表示质量，a和b分别表示矩形板的长和宽。

转动惯量二重积分公式

转动惯量二重积分公式转动惯量是描述刚体旋转惯性特性的物理量，它在物理学和工程学中有着重要的应用。

转动惯量可以通过求解转动惯量二重积分公式来计算得到。

本文将详细介绍转动惯量二重积分公式的概念和应用。

让我们来了解一下转动惯量的定义。

转动惯量表示物体绕轴旋转时的惯性大小，它的计算公式是I = ∫r^2 dm。

其中，I是转动惯量，r 是物体离轴距离，dm是物体的微小质量。

转动惯量二重积分公式可以应用于各种不规则形状的物体。

例如，对于一个平面形状的物体，可以将其分解为无数个微小的质量元素，然后使用转动惯量二重积分公式对每个质量元素进行求和，最终得到整个物体的转动惯量。

对于一个平面形状的物体，转动惯量二重积分公式可以表示为I = ∬r^2 dm。

其中，r是物体上的某一点到轴的距离，dm是该点的微小质量。

通过对整个物体进行积分，可以得到物体的总转动惯量。

接下来，我们来看一个具体的例子。

假设有一个半径为R的圆盘，质量均匀分布在整个圆盘上。

我们想要计算这个圆盘的转动惯量。

我们将圆盘分解为无数个微小的质量元素。

假设圆盘上的一个微小质量元素位于圆盘上的点(x, y)，则该点到轴的距离可以表示为r = √(x^2 + y^2)。

然后，我们可以使用转动惯量二重积分公式来计算每个质量元素的转动惯量。

即I = ∬r^2 dm。

在这个例子中，质量元素的微小质量可以表示为dm = ρ dA，其中ρ是圆盘的面密度，dA是质量元素的面积。

将r和dm代入转动惯量二重积分公式，我们可以得到I = ∬(x^2 + y^2)ρ dA。

接下来，我们需要确定积分的范围。

由于整个圆盘是半径为R的圆，我们可以将积分范围限定在圆的内部。

即积分范围为x^2 + y^2 ≤ R^2。

我们可以将转动惯量二重积分公式代入积分范围，计算出整个圆盘的转动惯量。

具体的计算过程可能较为复杂，但通过数学工具和计算软件，可以快速得到结果。

通过以上的例子，我们可以看到转动惯量二重积分公式在计算转动惯量时的重要性和应用价值。

高等数学转动惯量计算公式

高等数学转动惯量计算公式转动惯量是描述物体对旋转运动的惯性的物理量，它与物体的质量分布、形状以及旋转轴的位置有关。

在高等数学中，转动惯量的计算是一个重要的内容，可以通过不同的公式来求解。

本文将对转动惯量的计算公式进行详细介绍，并提供一些实际问题的解决思路，帮助读者更好地理解和应用这些公式。

一、转动惯量的定义和基本概念转动惯量是描述物体对旋转运动惯性的物理量，用字母I表示。

它与质量分布和旋转轴的位置有关。

当物体绕一个轴线旋转时，旋转轴到物体的每个质点都有一个距离，这个距离与质点的质量成正比，用r表示。

转动惯量的定义公式为：I = ∑mᵢrᵢ²其中，mᵢ表示每个质点的质量，rᵢ表示旋转轴到该质点的距离。

二、转动惯量的计算公式及应用1. 刚体的转动惯量对于刚体来说，可以通过对各个质点的转动惯量进行求和，得到整个刚体的转动惯量。

当刚体的质量分布均匀时，可以使用以下公式进行计算：I = MR²其中，M表示刚体的质量，R表示围绕旋转轴的平行轴距离。

这个公式适用于质点系、棒、圆环等等旋转的刚体。

2. 平行轴定理和垂直轴定理平行轴定理和垂直轴定理是转动惯量的两个重要定理。

它们通过简化计算，使得转动惯量的求解更加方便。

- 平行轴定理：如果已知物体绕通过质心的轴的转动惯量为I₀，在平行于该轴且与质心所在平面距离为h的轴上的转动惯量为I₁，则物体围绕与质心平行轴的转动惯量I₂可以表示为：I₂ = I₀ + mh²其中，m表示物体的总质量。

- 垂直轴定理：如果已知物体绕通过质心轴的转动惯量为I₀，在与质心所在直线垂直且过该直线上某点P的轴上的转动惯量为I₁，则物体围绕通过该直线的转动惯量I₂可以表示为：I₂ = I₀ + MP²其中，M表示物体的总质量，P表示物体上任意一点到该直线的距离。

这两个定理在实际问题中的应用较为广泛，可以较快地求解旋转物体的转动惯量。

三、实际问题解决思路转动惯量的计算在物体的旋转运动以及力矩的分析中起到了关键作用。

转动惯量手动计算公式

转动惯量1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材：341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg)； D-圆柱体直径(cm)； L-圆柱体长度或厚度(cm)； r-材料比重(gf /cm 3)。

2. 丝杠折算到马达轴上的转动惯量：2iJs J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2)； i-降速比，12z z i =3. 工作台折算到丝杠上的转动惯量gw22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min)； n-丝杠转速(r/min)； w-工作台重量(kgf)；g-重力加速度，g = 980cm/s 2； s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量：())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量； J 2-齿轮z 2的转动惯量(kgf·cm·s 2)； J s -丝杠转动惯量(kgf·cm·s 2)； s-丝杠螺距，(cm)； w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1，J 2-分别为Ⅰ轴，Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2)；R-齿轮z 分度圆半径(cm)； w-工件及工作台重量(kgf)。

惯量的计算公式

惯量的计算公式惯量是物理学中一个比较重要的概念，特别是在研究物体的旋转运动时。

那咱就来好好聊聊惯量的计算公式。

咱先来说说惯量到底是啥。

比如说，你转动一个大圆盘和一个小圆盘，明显感觉大圆盘更难转动起来，也更难让它停下。

这就是因为大圆盘的惯量大呀！惯量的计算公式呢，对于一个质点，它的转动惯量 I 等于 mr²，这里的 m 是质点的质量，r 是质点到转轴的距离。

要是一个物体不是一个简单的质点，而是一个有形状、有大小的物体，那计算惯量就稍微复杂点啦。

比如说一个均匀的细圆环，它绕着中心轴旋转的转动惯量是 mR²；一个均匀的圆盘，绕着中心轴旋转的转动惯量是 1/2 mR²。

我记得之前给学生们讲这个知识点的时候，有个特别有趣的事儿。

有个小家伙特别积极，每次我讲完一个公式，他都瞪大眼睛，好像要把这公式吃进去似的。

我出了一道关于圆盘惯量计算的题，让大家在课堂上做。

这小家伙刷刷刷就开始动笔，结果算错了。

我走到他身边，看他一脸困惑，就给他指出来，原来是他把半径的平方算错啦。

然后我一点点给他重新讲了一遍，看着他恍然大悟的样子，我心里那叫一个满足。

咱再来说说惯量在实际生活中的应用。

像汽车的轮子，质量越大，半径越大，惯量就越大。

启动的时候就需要更多的力，但是跑起来之后保持速度就相对容易些。

还有那种大型的旋转机械，比如风力发电机的叶片，在设计的时候就得好好考虑惯量的问题，要不然转动起来可费劲啦。

对于复杂形状的物体，计算惯量可能就得用到积分的知识啦。

这对于高中生来说可能有点难，但是别怕，只要把基础的概念搞清楚，以后再学高深的知识就会轻松很多。

总之，惯量的计算公式虽然看起来有点复杂，但是只要多做几道题，多联系实际想想，就能掌握得很好啦。

希望大家都能把这个知识点吃得透透的，以后遇到相关的问题都能轻松解决！。

转动惯量数学积分公式

转动惯量数学积分公式转动惯量这个概念在物理学中可有着不小的分量呢，尤其是涉及到数学积分公式的时候，那更是充满了挑战和趣味。

咱们先来说说啥是转动惯量。

想象一下，一个圆盘在旋转，不同位置的质点对旋转的影响是不一样的。

离旋转中心远的质点，转起来就更费劲，而离得近的就相对轻松些。

转动惯量就是用来衡量这种“费劲”程度的物理量。

那转动惯量的数学积分公式到底是啥样的呢？其实就是通过积分来把物体上每个微小部分的质量和它到旋转轴距离的平方乘起来，然后再把所有这些乘积加起来。

这听起来有点复杂，对吧？我给您举个例子。

比如说有一个均匀的圆环，咱们来算算它的转动惯量。

假设圆环的半径是 R ，质量是 M 。

咱们把圆环分成很多很小很小的段，每一段的长度可以看作是 dl ，对应的质量就是 dM 。

因为圆环是均匀的，所以dM = M * dl / (2πR) 。

而这一小段到旋转中心的距离就是 R ，所以它对转动惯量的贡献就是 R² * dM 。

把整个圆环上所有这样的小段加起来，就是积分：∫ R² * dM ，从 0 到2πR 。

经过一番计算，就能得到圆环的转动惯量是 M *R²。

再比如说一个实心的圆柱体，要算它的转动惯量就更复杂一点啦。

得考虑不同半径处的质量分布。

在学习转动惯量数学积分公式的过程中，我想起自己上学那会，有一次物理课上，老师让我们分组讨论一个关于转动惯量的难题。

我们小组几个人围在一起，抓耳挠腮，各种比划和计算。

一开始，大家都有点懵，你一言我一语，思路乱得像一团麻。

但是慢慢地，我们从最基本的概念入手，一点一点地理清思路。

当最终算出正确答案的时候，那种成就感简直爆棚！那时候我就深深体会到，物理这门学科，虽然有时候让人头疼，但只要肯钻研，就能发现其中的乐趣。

总之，转动惯量的数学积分公式虽然有点复杂，但只要咱们耐心琢磨，多做几道题，多想想其中的道理，就能掌握它。

这不仅能帮助我们解决物理问题，还能锻炼咱们的思维能力呢！所以呀，别害怕这些公式，勇敢地去探索它们背后的奥秘吧！。

机械设计转动惯量计算公式

1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材：341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量（kg ）； D —圆柱体直径(cm)； L —圆柱体长度或厚度（cm ）； r —材料比重(gf /cm 3）。

2。

丝杠折算到马达轴上的转动惯量：2i Js J = （kgf·cm·s 2） J s –丝杠转动惯量（kgf·cm·s 2）； i-降速比，12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J πg w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2） v -工作台移动速度(cm/min ）； n —丝杠转速（r/min); w —工作台重量（kgf ）； g-重力加速度,g = 980cm/s 2； s —丝杠螺距（cm ）2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm(kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs JJ iJ J S tJ 1-齿轮z 1及其轴的转动惯量； J 2-齿轮z 2的转动惯量（kgf·cm·s 2）； J s -丝杠转动惯量(kgf·cm·s 2）； s-丝杠螺距，(cm ）； w —工件及工作台重量(kfg ）.5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2）R —齿轮分度圆半径（cm); w-工件及工作台重量(kgf ）6。

齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1，J 2-分别为Ⅰ轴，Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2)；R —齿轮z 分度圆半径(cm)； w —工件及工作台重量（kgf ）。

转动惯量计算折算公式

2. 丝杠折算到马达轴上的转动惯量：2iJs J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2)； i-降速比，12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min)； n-丝杠转速(r/min)； w-工作台重量(kgf)；g-重力加速度，g = 980cm/s 2； s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量：())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量； J 2-齿轮z 2的转动惯量(kgf·cm·s 2)； J s -丝杠转动惯量(kgf·cm·s 2)； s-丝杠螺距，(cm)； w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1，J 2-分别为Ⅰ轴，Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2)；R-齿轮z 分度圆半径(cm)； w-工件及工作台重量(kgf)。