2021年湖南省中考数学一轮复习课时训练(20) 全等三角形
专题19 全等三角形-2021年中考数学一轮复习精讲+热考题型(解析版)
专题19 全等三角形【知识要点】知识点1 全等三角形及其性质全等图形概念：能完全重合的图形叫做全等图形.特征：①形状相同。
②大小相等。
③对应边相等、对应角相等。
全等三角形概念：两个能完全重合的三角形叫做全等三角形.小结：把两个全等三角形重合到一起，重合的顶点叫做对应顶点，重合的边叫做对应边，重合的角叫做对应角.表示方法：全等用符号“≌”，读作“全等于”。
书写三角形全等时，要注意对应顶点字母要写在对应位置上。
全等变换定义：只改变图形的位置，而不改变图形的形状和大小的变换。
变换方式（常见）：平移、翻折、旋转。
全等三角形的性质：对应边相等，对应角相等。
知识点2：全等三角形的判定（重点）注：①判定两个三角形全等必须有一组边对应相等；②全等三角形周长、面积相等．证题的思路（重点）：知识点3 角平分线角平分线的性质定理：角平分线上的点到角两边的距离相等；判定定理：到角两边距离相等的点在角的平分线上．三角形中角平分线的性质：三角形的三条角平分线相交于一点，并且这点到三条边距离相等。
【考查题型】考查题型一全等三角形的性质典例1．如图，若△ABC≌△ADE，则下列结论中一定成立的是（）A．AC＝DE B．∠BAD＝∠CAEC．AB＝AE D．∠ABC＝∠AED【答案】B【详解】根据全等三角形的性质即可得到结论．【解答】解：∵△ABC≌△ADE，∴AC＝AE，AB＝AD，∠ABC＝∠ADE，∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE．故A，C，D选项错误，B选项正确，故选：B．变式1-1．三个全等三角形按如图的形式摆放，则∠1+∠2+∠3的度数是（）A．90B．120C．135D．180【答案】D【分析】根据全等三角形的性质和三角形的内角和定理和三角形的外角可得∠1+∠2+∠3+∠4+∠5+∠6=360〬,∠5+∠7+∠8=180°，即∠1+∠2+∠3=360°-180°.【详解】∵图中是三个全等三角形，∴∠4=∠8, ∠6=∠7,又∵三角形ABC的外角和=∠1+∠2+∠3+∠4+∠5+∠6=360〬,又∠5+∠7+∠8=180°，∴∠1+∠2+∠3=360°-180°=180°.故选D变式1-2．如图所示，△ABD≌△CDB，下面四个结论中，不正确的是（）A．△ABD和△CDB的面积相等B．△ABD和△CDB的周长相等C．∠A+∠ABD＝∠C+∠CBD D．AD∥BC，且AD＝BC【答案】C【分析】通过全等三角形的性质进行逐一判断即可．【详解】A、∵△ABD≌△CDB，∴△ABD和△CDB的面积相等，故本选项错误；B、∵△ABD≌△CDB，∴△ABD和△CDB的周长相等，故本选项错误；C、∵△ABD≌△CDB，∴∠A＝∠C，∠ABD＝∠CDB，∴∠A+∠ABD＝∠C+∠CDB≠∠C+∠CBD，故本选项正确；D、∵△ABD≌△CDB，∴AD＝BC，∠ADB＝∠CBD，∴AD∥BC，故本选项错误；故选：C．考查题型二全等三角形的判定-SSS∆≅∆的依据是典例2．用直尺和圆规作一个角的角平分线的示意图如图所示，其中说明COE DOE（）A．SSS B．SAS C．ASA D．AAS【答案】A【分析】根据角平分线的作法可知CO=DO，EO=EO，EC=ED，符合三角形全等的判定方法中的SSS，可∆≅∆．证COE DOE【详解】解：由作法知CO=DO，EO=EO，EC=ED，∆≅∆（SSS），∴COE DOE故选：A．变式2-1．在平面直角坐标系xOy中，点A（﹣3，0），B（2，0），C（﹣1，2），E（4，2），如果△ABC与△EFB全等，那么点F的坐标可以是（）A．（6，0）B．（4，0）C．（4．﹣2）D．（4，﹣3）【答案】D【分析】画出平面直角坐标系，利用全等三角形的性质以及坐标与图形的性质得出符合题意的答案．【详解】解：如图所示：△ABC 与△EFB 全等，点F 的坐标可以是：(4，﹣3)．故选：D ．变式2-2．如图，在四边形ABCD 中，90B D ∠=∠=︒，点E ，F 分别在AB ，AD 上，AE AF =，CE CF =，求证：CB CD =．【答案】见解析【分析】连接AC ，证明△ACE ≌△ACF ，得到∠CAE=∠CAF ，再利用角平分线的性质定理得到CB=CD ．【详解】解：连接AC ，∵AE=AF ，CE=CF ，AC=AC ，∴△ACE ≌△ACF （SSS ），∴∠CAE=∠CAF ，∵∠B=∠D=90°，∴CB=CD ．变式2-3．人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法：已知：AOB∠求作：AOB∠的平分线做法：（1）以O为圆心，适当长为半径画弧，交OA于点M，交OB于点N，（2）分别以点M，N为圆心，大于12MN的长为半径画弧，两弧在AOB∠的内部相交于点C（3）画射线OC，射线OC即为所求．请你根据提供的材料完成下面问题：（1）这种作已知角平分线的方法的依据是__________________(填序号)．①SSS②SAS③AAS④ASA（2）请你证明OC为AOB∠的平分线．【答案】（1）①；（2）证明见解析【分析】（1）根据作图的过程知道：OM=ON，OC=OC，CM=CM，由“SSS”可以证得△EOC≌△DOC；（2）根据作图的过程知道：OM=ON，OC=OC，CM=CM，由全等三角形的判定定理SSS可以证得△EOC ≌△DOC，从而得到OC为AOB∠的平分线．【详解】（1）根据作图的过程知道：OM=ON，OC=OC，CM=CM，所以由全等三角形的判定定理SSS可以证得△EOC≌△DOC，从而得到OC为AOB∠的平分线；故答案为：①；（2）如图，连接MC 、NC ．根据作图的过程知，在△MOC 与△NOC 中，OM ON OC OC CM CN ⎧⎪⎨⎪⎩＝＝＝，∴△MOC ≌△NOC （SSS ），∠AOC=∠BOC ，∴OC 为AOB ∠的平分线．考查题型三 全等三角形的判定-SAS典例3．如图，已知,AB DC ABC DCB =∠=∠．能直接判断ABC DCB △≌△的方法是（ ）A ．SASB ．AASC ．SSSD ．ASA【答案】A 【分析】根据三角形全等的判定定理解答.【详解】在△ABC 和△DCB 中，AB DC ABC DCB BC CB =⎧⎪∠=∠⎨⎪=⎩,∴ABC DCB △≌△(SAS),故选：A.变式3-1．如图所示，将两根钢条AA’、BB’的中点O 连在一起，使AA’、BB’可以绕着点O自由旋转，就做成了一个测量工件，则A’B’的长等于内槽宽AB ，那么判定△OAB ≌△OA’B’的理由是（ ）A ．边角边B ．角边角C ．边边边D ．角角边【答案】A 【分析】根据线段中点的定义可得,AO A O BO B O ''==，进一步即可根据SAS 证明△OAB ≌△OA B ''，于是可得答案．【详解】解：∵点O 是AA '和BB '的中点，∴,AO A O BO B O ''==，在△OAB 和△OA B ''中，∵,,AO A O AOB A OB BO B O ''''=∠=∠=，∴△OAB ≌△OA B ''（SAS ）．故选：A ．变式3-2．如图，已知//AB CD ，AB CD =，BE CF =．求证：（1）ABF DCE ∆≅∆；（2）//AF DE ．【答案】（1）证明见详解；（2）证明见解析．【分析】（1）先由平行线的性质得∠B=∠C ，从而利用SAS 判定△ABF ≌△DCE ；（2）根据全等三角形的性质得∠AFB=∠DEC ，由等角的补角相等可得∠AFE=∠DEF ，再由平行线的判定可得结论．【详解】证明：（1）∵AB ∥CD ，∴∠B=∠C ，∵BE=CF ，∴BE-EF=CF-EF ，即BF=CE ，在△ABF 和△DCE 中，==AB CD B C BF CE =⎧⎪∠∠⎨⎪⎩∴△ABF ≌△DCE （SAS ）；（2）∵△ABF ≌△DCE ，∴∠AFB=∠DEC ，∴∠AFE=∠DEF ，∴AF ∥DE ．变式3-3．已知：如图，点A 、B 、C 、D 在一条直线上，//,,EA FB EA FB AB CD ==．（1）求证：E F ∠=∠；（2）若40,80A D ∠=︒∠=︒，求E ∠的度数．【答案】（1）见解析；（2）60°【分析】（1）根据已知条件证明△ACE ≌△BDF ，即可得到结论；（2）根据全等三角形的性质得到∠D=∠ACE=80°，再利用三角形内角和定理求出结果.【详解】解：（1）∵AE ∥BF ，∴∠A=∠DBF ，∵AB=CD ，∴AB+BC=CD+BC ，即AC=BD ，又∵AE=BF ，∴△ACE ≌△BDF （SAS ），∴∠E=∠F ；（2）∵△ACE ≌△BDF ，∴∠D=∠ACE=80°，∵∠A=40°，∴∠E=180°-∠A-∠ACE=60°.考查题型四 全等三角形的判定-AAS典例4．如图，AB CD ⊥，且AB CD =.E 、F 是AD 上两点，CE AD ⊥，BF AD ⊥.若CE a =，BF b =，EF c =，则AD 的长为（ ）A ．a c +B ．b c +C ．a b c -+D ．a b c +-【答案】D【解析】如图,∵AB ⊥CD,CE ⊥AD,∴∠1=∠2,又∵∠3=∠4,∴180°-∠1-∠4=180°-∠2-∠3,即∠A=∠C.∵BF ⊥AD,∴∠CED=∠BFD=90°,∵AB=CD,∴△ABF ≌△CDE,∴AF=CE=a,ED=BF=b,又∵EF=c,∴AD=a+b-c.故选:D.变式4-1．如图，D 是AB 上一点，DF 交AC 于点E ，DE FE =，//FC AB ，若4AB =，3CF =，则BD 的长是( )A ．0.5B ．1C ．1.5D ．2【答案】B 【分析】根据平行线的性质，得出A FCE ∠=∠，ADE F ∠=∠，根据全等三角形的判定，得出ADE CFE ∆≅∆，根据全等三角形的性质，得出AD CF =，根据4AB =，3CF =，即可求线段DB 的长．【详解】∵//CF AB ，∴A FCE ∠=∠，ADE F ∠=∠，在ADE ∆和FCE ∆中A FCE ADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()ADE CFE AAS ∆≅∆，∴3AD CF ==，∵4AB =，∴431DB AB AD =-=-=.故选B ．变式4-2．△BDE 和△FGH 是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内．若求五边形DECHF的周长，则只需知道（）A．△ABC的周长B．△AFH的周长C．四边形FBGH的周长D．四边形ADEC的周长【答案】A【分析】由等边三角形的性质和三角形的内角和定理可得：FH＝GH，∠ACB＝∠A＝60°，∠AHF＝∠HGC，进而可根据AAS证明△AFH≌△CHG，可得AF＝CH，然后根据等量代换和线段间的和差关系即可推出五边形DECHF的周长＝AB+BC，从而可得结论．【详解】解：∵△GFH为等边三角形，∴FH＝GH，∠FHG＝60°，∴∠AHF+∠GHC＝120°，∵△ABC为等边三角形，∴AB＝BC＝AC，∠ACB＝∠A＝60°，∴∠GHC+∠HGC＝120°，∴∠AHF＝∠HGC，∴△AFH≌△CHG（AAS），∴AF＝CH．∵△BDE和△FGH是两个全等的等边三角形，∴BE＝FH，∴五边形DECHF的周长＝DE+CE+CH+FH+DF＝BD+CE+AF+BE+DF＝（BD+DF+AF）+（CE+BE），＝AB+BC．∴只需知道△ABC的周长即可．故选：A．变式4-3．如图，AC是∠BAE的平分线，点D是线段AC上的一点，∠C＝∠E，AB＝AD．求证：BC＝DE．【答案】见解析【分析】根据角平分线的性质证明△BAC≌△DAE，即可得到结果；【详解】证明：∵AC是∠BAE的平分线，∴∠BAC＝∠DAE，∵∠C＝∠E，AB＝AD．∴△BAC≌△DAE（AAS），∴BC＝DE．变式4-4．如图，在△ABC中，AB＝AC，点D、E分别是线段BC、AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．（1）求证：△BDE≌△F AE；（2）求证：四边形ADCF为矩形．【答案】（1）见解析；（2）见解析【分析】（1）首先根据平行线的性质得到∠AFE =∠DBE ，再根据线段中点的定义得到AE =DE ，根据全等三角形的判定定理即可得到结论；（2）根据全等三角形的性质得到AF =BD ，推出四边形ADCF 是平行四边形，根据等腰三角形的性质得到∠ADC =90°，于是得到结论．【详解】（1）证明：∵AF ∥BC ，∴∠AFE =∠DBE ，∵E 是线段AD 的中点，∴AE =DE ，∵∠AEF =∠DEB ，∴BDE FAE ≅△△（AAS ）；（2）证明：∵BDE FAE ≅△△，∴AF =BD ，∵D 是线段BC 的中点，∴BD =CD ，∴AF =CD ，∵AF ∥CD ，∴四边形ADCF 是平行四边形，∵AB =AC ，∴AD BC ⊥，∴∠ADC =90°，∴四边形ADCF 为矩形．考查题型五 全等三角形的判定-ASA典例5．如图，EF 过▱ABCD 对角线的交点O ，交AD 于E ，交BC 于F ，若▱ABCD 的周长为18，1.5OE =，则四边形EFCD 的周长为( )A ．14B ．13C ．12D ．10【答案】C 【详解】∵平行四边形ABCD ，∴AD ∥BC ，AD =BC ，AO =CO ，∴∠EAO =∠FCO ，∵在△AEO 和△CFO 中，AEO CFO AO COAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△AEO ≌△CFO ，∴AE =CF ，EO =FO =1.5，∵C 四边形ABCD =18，∴CD +AD =9，∴C 四边形CDEF =CD +DE +EF +FC =CD +DE +EF +AE =CD +AD +EF =9+3=12.故选C.变式5-1．如图，在四边形ABCD 中，//AD BC ，90D ∠=，8AD =，6BC =，分别以点A ，C 为圆心，大于12AC 长为半径作弧，两弧交于点E ，作射线BE 交AD 于点F ，交AC 于点O ．若点O 是AC 的中点，则CD 的长为（ ）A．B ．6 C．D ．8【答案】A【分析】连接FC ，根据基本作图，可得OE 垂直平分AC ，由垂直平分线的性质得出AF =FC ．再根据ASA 证明△FOA ≌△BOC ，那么AF =BC =3，等量代换得到FC =AF =3，利用线段的和差关系求出FD =AD -AF =1．然后在直角△FDC 中利用勾股定理求出CD 的长．【详解】解：如图，连接FC ，∵点O 是AC 的中点，由作法可知，OE 垂直平分AC ，∴AF =FC ．∵AD ∥BC ，∴∠F AO =∠BCO ．在△FOA 与△BOC 中，FAO BCO OA OCAOF COB ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝ ， ∴△FOA ≌△BOC （ASA ），∴AF =BC =6，∴FC =AF =6，FD =AD -AF =8-6=2．在△FDC 中，∵∠D =90°，∴CD 2+DF 2=FC 2，∴CD 2+22=62，∴CD=故选：A ．变式5-2．如图，AB ＝AC ，AB ⊥AC ，AD ⊥AE ，且∠ABD ＝∠ACE .求证：BD ＝CE .【答案】见解析.【分析】先求出∠CAE ＝∠BAD 再利用ASA 证明△ABD ≌△ACE ，即可解答【详解】∵AB ⊥AC ，AD ⊥AE ，∴∠BAE +∠CAE ＝90°，∠BAE +∠BAD ＝90°，∴∠CAE ＝∠BAD .又AB ＝AC ，∠ABD ＝∠ACE ，∴△ABD ≌△ACE (ASA).∴BD ＝CE .变式5-2．如图，点C 在线段BD 上，且AB ⊥BD ，DE ⊥BD ，AC ⊥CE ，BC=DE ，求证：AB=CD ．【答案】详见解析【分析】根据AB ⊥BD ，DE ⊥BD ，AC ⊥CE ，可以得到90ABC CDE ACB ︒∠=∠=∠=，90ACB ECD ︒∠+∠=，90ECD CED ︒∠+∠=，从而有ACB CED ∠=∠，可以验证ABC ∆和CDE ∆全等，从而得到AB =CD ．【详解】证明：∵AB BD ⊥，DE BD ⊥，AC CE ⊥∴90ABC CDE ACB ︒∠=∠=∠=∴90ACB ECD ︒∠+∠=，90ECD CED ︒∠+∠=∴ACB CED ∠=∠在ABC ∆和CDE ∆中ACB CED BC DEABC CDE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABC ∆≌CDE ∆故AB CD =．考查题型六 全等三角形的判定-HL典例6．如图，∠B ＝∠E ，BF ＝EC ，AC ∥DF ．求证：△ABC ≌△DEF ．【答案】证明见解析【分析】首先利用平行线的性质得出∠ACB ＝∠DFE ，进而利用全等三角形的判定定理ASA ，进而得出答案．【详解】证明：∵AC ∥DF ，∴∠ACB ＝∠DFE ，∵BF ＝CE ，∴BC ＝EF ，在△ABC 和△DEF 中，B E BC EFACB DFE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABC ≌△DEF （ASA ）．变式6-1．已知：如图，AB=CD ，DE ⊥AC ，BF ⊥AC ，E ，F 是垂足，AE=CF ．求证：△ABF ≌△CDE【答案】见解析.【分析】根据HL 即可判定Rt △ABF ≌Rt △CDE .【详解】证明：∵DE ⊥AC ，BF ⊥AC ，∴∠AFB =∠CED =90°，∵AE=CF ，∴AF=CE ，在Rt △ABF 和Rt △CDE 中，AB CD AF CE=⎧⎨=⎩ ∴Rt △ABF ≌Rt △CDE （HL ）.考查题型七 判定三角形全等的的条件典例7．如图，点E 在菱形ABCD 的AB 边上，点F 在BC 边的延长线上，连接CE ，DF ，对于下列条件：①BE CF =；②,CE AB DF BC ⊥⊥；③CE DF =；④BCE CDF ∠=∠，只选其中一个添加，不能确定BCE CDF ∆≅∆的是（ ）A ．①B ．②C ．③D ．④【答案】C 【分析】根据菱形的性质和全等三角形的判定定理即可得到结论． 【详解】解：四边形ABCD 是菱形，BC CD ∴=，//AB CD ，B DCF ∴∠=∠， ①添加BE CF =，()BCE CDF SAS ∴∆≅∆， ②添加CE AB ⊥，DF BC ⊥，90CEB F ∴∠=∠=︒，()BCE CDF AAS ∴∆≅∆， ③添加CE DF =，不能确定BCE CDF ∆≅∆； ④添加BCE CDF ∠=∠，()BCE CDF ASA ∴∆≅∆，故选：C ．变式7-1．如图，等腰△ABC 中，点D ，E 分别在腰AB ，AC 上，添加下列条件，不能判定ABE △≌ACD △的是（ ）A ．AD AE =B ．BE CD =C ．ADC AEB ∠=∠D ．DCB EBC ∠=∠【答案】B【分析】根据全等三角形的判定方法逐项判断即得答案．【详解】解： A 、若添加AD AE =，由于AB =AC ，∠A 是公共角，则可根据SAS 判定ABE △≌ACD △，故本选项不符合题意；B 、若添加BE CD =，不能判定ABE △≌ACD △，故本选项符合题意；C 、若添加ADC AEB ∠=∠，由于AB =AC ，∠A 是公共角，则可根据AAS 判定ABE △≌ACD △，故本选项不符合题意；D 、若添加DCB EBC ∠=∠，∵AB =AC ，∴∠ABC =∠ACB ，∴∠ABE =∠ACD ，由于∠A 是公共角，则可根据ASA 判定ABE △≌ACD △，故本选项不符合题意．故选：B ．变式7-2．如图，四边形ABCD 是菱形，E 、F 分别是BC 、CD 两边上的点，不能保证．．．．ABE △和ADF 一定全等的条件是（ ）A ．BAF DAE ∠=∠B ．EC FC =C ．AE AF =D ．BE DF =【答案】C 【分析】根据菱形的性质结合全等三角形的判定方法，对各选项分别判断即可得解．【详解】∵四边形ABCD 是菱形，∴AB=BC=CD=DA ，BAD C ∠=∠，B D ∠=∠，如果BAF DAE ∠=∠，∴BAF EAF DAE EAF ∠∠∠∠-=-，即BAE DAF ∠=∠，∵BAE DAF AB DA B D ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴ABE △≅ADF (ASA )，故A 正确；如果EC=FC ，∴BC-EC=CD-FC ，即BE=DF ，∵AB DA B D BE DF =⎧⎪∠=∠⎨⎪=⎩，∴ABE △≅ADF (SAS )，故B 正确；如果AE=AF ，∵AB=DA ，B D ∠=∠，是SSA ，则不能判定ABE △和ADF 全等，故C 错误；如果BE DF =，则AB DA B D BE DF =⎧⎪∠=∠⎨⎪=⎩，∴ABE △≅ADF (SAS )，故D 正确；故选：C．考查题型八全等三角形综合问题典例8．如图AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．（1）求证AD=AE；（2）连接OA，BC，试判断直线OA，BC的关系并说明理由．【答案】（1）证明见解析；（2）互相垂直，证明见解析【分析】（1）根据AAS推出△ACD≌△ABE，根据全等三角形的性质得出即可；（2）证Rt△ADO≌Rt△AEO，推出∠DAO=∠EAO，根据等腰三角形的性质推出即可．【详解】（1）证明：∵CD⊥AB，BE⊥AC，∴∠ADC=∠AEB=90°，△ACD和△ABE中，∵ADC AEBCAD BAE AB AC∠∠⎧⎪∠∠⎨⎪⎩＝＝＝∴△ACD≌△ABE（AAS），∴AD=AE．（2）猜想：OA⊥BC．证明：连接OA、BC，∵CD ⊥AB ，BE ⊥AC ，∴∠ADC=∠AEB=90°．在Rt △ADO 和Rt △AEO 中，∵OA OA AD AE ⎧⎨⎩＝＝ ∴Rt △ADO ≌Rt △AEO （HL ）．∴∠DAO=∠EAO ，又∵AB=AC ，∴OA ⊥BC ．变式8-1．如图，AC BC ⊥，DC EC ⊥，AC BC =．DC EC =，AE 与BD 交于点F ．（1）求证：AE BD =；（2）求AFD ∠的度数．【答案】（1）见解析（2）90°【分析】（1）根据题意证明△ACE ≌△BCD 即可求解；（2）根据三角形的内角和及全等三角形的性质即可得到AFD ∠的度数．【详解】（1）∵AC BC ⊥，DC EC ⊥，∴∠ACB=∠ECD=90°∴∠ACB+∠BCE=∠ECD+∠BCE即∠ACE=∠BCD又AC BC =．DC EC =∴△ACE ≌△BCD∴AE BD =（2）∵△ACE ≌△BCD∴∠A=∠B设AE 与BC 交于O 点,∴∠AOC=∠BOF∴∠A+∠AOC+∠ACO=∠B+∠BOF+∠BFO=180°∴∠BFO=∠ACO=90°故AFD ∠=180°-∠BFO=90°．变式8-2．如图，在△ABC 和△DCE 中，AC ＝DE ，∠B ＝∠DCE ＝90°，点A ，C ，D 依次在同一直线上，且AB ∥DE ．（1）求证：△ABC ≌△DCE ；（2）连结AE ，当BC ＝5，AC ＝12时，求AE 的长．【答案】（1）见解析；（2）13【分析】根据题意可知，本题考查平行的性质，全等三角形的判定和勾股定理，根据判定定理，运用两直线平行内错角相等再通过AAS 以及勾股定理进行求解．【详解】解：（1）∵//AB DE∴BAC CDE ∠=∠在△ABC 和△DCE 中B DCE BAC CDE AC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DCE（2）由（1）可得BC =CE =5在直角三角形ACE 中13AE ===变式8-3．如图，AC 是四边形ABCD 的对角线，∠1＝∠B ，点E 、F 分别在AB 、BC 上，BE ＝CD ，BF ＝CA ，连接EF ．（1）求证：∠D ＝∠2；（2）若EF ∥AC ，∠D ＝78°，求∠BAC 的度数．【答案】（1）证明见解析；（2）78°．【分析】（1）由“SAS ”可证△BEF ≌△CDA ，可得∠D ＝∠2；（2）由（1）可得∠D ＝∠2＝78°，由平行线的性质可得∠2＝∠BAC ＝78°．【详解】证明：（1）在△BEF 和△CDA 中，1BE CD B BF CA =⎧⎪∠=∠⎨⎪=⎩，∴△BEF ≌△CDA （SAS ），∴∠D ＝∠2；（2）∵∠D ＝∠2，∠D ＝78°，∴∠D ＝∠2＝78°，∵EF ∥AC ，∴∠2＝∠BAC ＝78°．变式8-4．如图，在三角形ABC 中，点D 是BC 上的中点，连接AD 并延长到点E ，使DE AD =，连接CE ．（1）求证：ABD ECD ∆≅∆（2）若ABD ∆的面积为5，求ACE ∆的面积．【答案】（1）详见解析；（2）10．【分析】（1）根据中点定义、对顶角相等以及已知条件运用SAS 即可证明；（2）先根据三角形中点的性质和全等三角形的性质得到ABD ACD S S =、ABD ECD S S =，再结合5ABD S =以及ACE ACD ECD S S S =+解答即可．【详解】证明：（1）∵D 是BC 的中点，∴BD=CD在△ABD 和△CED 中，BD CD ADB CED AD ED =⎧⎪∠=∠⎨⎪=⎩所以ABD ECD ∆≅∆；(2)∵在△ABC 中，D 是BC 的中点∴ABD ACD S S =ABD ECD ∆≅∆ABD ECD S S ∴=∵5ABD S =5510ACE ACD ECD S S S ∴=+=+=．答：三角形ACE 的面积为10．考查题型九 角平分线的性质定理典例9．如图，已知在△ABC 中，CD 是AB 边上的高线，BE 平分∠ABC ，交CD 于点E ，BC=5，DE=2，则△BCE 的面积等于（ ）A ．10B ．7C ．5D ．4【答案】C 【解析】试题分析：如图，过点E 作EF ⊥BC 交BC 于点F,根据角平分线的性质可得DE=EF=2,所以△BCE 的面积等于1152522BC EF ⨯⨯=⨯⨯=,故答案选C ．变式9-1．如图，AB ∥CD ，AD 平分∠BAC ，若∠BAD=70°，则∠ACD 的度数为( )A ．40°B ．35°C ．50°D ．45°【答案】A 【解析】试题分析：已知AD 平分∠BAC ，∠BAD=70°，根据角平分线定义求出∠BAC=2∠BAD=140°，再由AB ∥CD ，所以∠ACD=180°﹣∠BAC=40°，故选A ．变式9-2．如图，在△ABC 中，∠C ＝90°，以点B 为圆心，以适当长为半径画弧交AB 、BC 于P 、Q 两点，再分别以点P ，Q 为圆心，大于12PQ 的长为半径画弧，两弧相交于点N ，射线BN 交AC 于点D ．若AB ＝10，AC ＝8，则CD 的长是（ ）A ．2B ．2.4C ．3D ．4【答案】C 【分析】作DE ⊥AB 于E ，根据角平分线的性质得到DE DC ＝，设DE DC x ＝＝ ，根据ABD ∆的面积公式列方程计算即可．【详解】解：如图所示，作DE ⊥AB 于E ，∵10890AB AC C ∠︒＝，＝，＝ ，∴6BC ＝ ，由基本尺规作图可知，BD 是△ABC 的角平分线，∵∠C ＝90°，DE ⊥AB ，∴可设DE DC x ＝＝ ， ∴1122ABD SAB DE AD BC =⨯⨯=⨯⨯， 即11108622x x ⨯⨯=⨯⨯（﹣）， 解得3x = ，即3CD = ，故选C ．变式9-3．三条公路将A 、B 、C 三个村庄连成一个如图的三角形区域，如果在这个区域内修建一个公园，要使公园到三条公路的距离相等，那么这个公园应建的位置是（ ）A．三条高线的交点B．三条中线的交点C．三条角平分线的交点D．三边垂直平分线的交点【答案】C【分析】根据角平分线上的点到角的两边的距离相等解答即可．【详解】在这个区域内修建一个公园，要使公园到三条公路的距离相等，根据角平分线的性质，公园应建在∠A、∠B、∠C的角平分线的交点处.故选C.考查题型十角平分线的判定定理典例10．如图，Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，AB=10，S△ABD=15，则CD的长为（）A．3B．4C．5D．6【答案】A【详解】作DE⊥AB于E，∵AB=10，S△ABD =15，∴DE=3，∵AD平分∠BAC,∠C=90°，DE⊥AB，∴DE=CD=3，故选A.变式10-1．如图，PA 、PB 分别切⊙O 于A 、B ，60APB ∠=，⊙O 半径为2，则PA 的长为（ ）A ．3B ．4C ．D ．【答案】C 【分析】连接PO 、AO 、BO ，由角平分线的判定定理得，PO 平分∠APB ，则∠APO=30°，得到PO=4，由勾股定理，即可求出PA.【详解】解：连接PO 、AO 、BO ，如图：∵PA 、PB 分别切⊙O 于A 、B ，∴PA AO ⊥，PB BO ⊥，AO=BO ，∴PO 平分∠APB ，∴∠APO=116022APB ∠=⨯︒=30°， ∵AO=2，∠PAO=90°，∴PO=2AO=4，由勾股定理，则PA ==故选：C.变式10-2．如图，已知P 是∠AOB 的平分线上的一点，∠AOB ＝60°，PD ⊥OA ，M 是OP 的中点，点C 是OB 上的一个动点，若PC 的最小值为3 cm ，则MD 的长度为( )A ．3cmB ．C ．2cmD ．【答案】A 【分析】根据垂线段最短、角平分线的性质求出PD ，根据直角三角形的性质解答．【详解】作PC ⊥OB 于C ，则此时PC 最小，∵P 是∠AOB 的角平分线上的一点，PD ⊥OA ，PC ⊥OB ，∴PD=PC=3，∠AOP=30°，∴OP=2PD=6，∵PD ⊥OA ，M 是OP 的中点，∴DM=12OP=3， 故选A ．变式10-3．如图，已知ABC 和ADE 都是等腰三角形，90BAC DAE ∠=∠=︒，,BD CE 交于点F ，连接AF ，下列结论：①BD CE =；②BF CF ⊥；③AF 平分CAD ∠；④45AFE ∠=︒．其中正确结论的个数有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C 【分析】①证明△BAD ≌△CAE,再利用全等三角形的性质即可判断；②由△BAD ≌△CAE 可得∠ABF=∠ACF ，再由∠ABF+∠BGA=90°、∠BGA=∠CGF 证得∠BFC=90°即可判定；③分别过A 作AM ⊥BD 、AN ⊥CE,根据全等三角形面积相等和BD=CE ，证得AM=AN,即AF 平分∠BFE,即可判定；④由AF 平分∠BFE结合BF CF⊥即可判定．【详解】解：∵∠BAC=∠EAD∴∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE 在△BAD和△CAE中AB=AC, ∠BAD=∠CAE,AD=AE∴△BAD≌△CAE∴BD=CE故①正确；∵△BAD≌△CAE∴∠ABF=∠ACF∵∠ABF+∠BGA=90°、∠BGA=∠CGF∴∠ACF+∠BGA=90°,∴∠BFC=90°故②正确；分别过A作AM⊥BD、AN⊥CE垂足分别为M、N ∵△BAD≌△CAE∴S△BAD=S△CAE,∴1122BD AM CE AN ⋅=⋅∵BD=CE∴AM=AN∴AF平分∠BFE，无法证明AF平分∠CAD．故③错误；∵AF 平分∠BFE ，BF CF ⊥ ∴45AFE ∠=︒故④正确．故答案为C ．。
2021年中考数学专题复习：全等三角形(二)
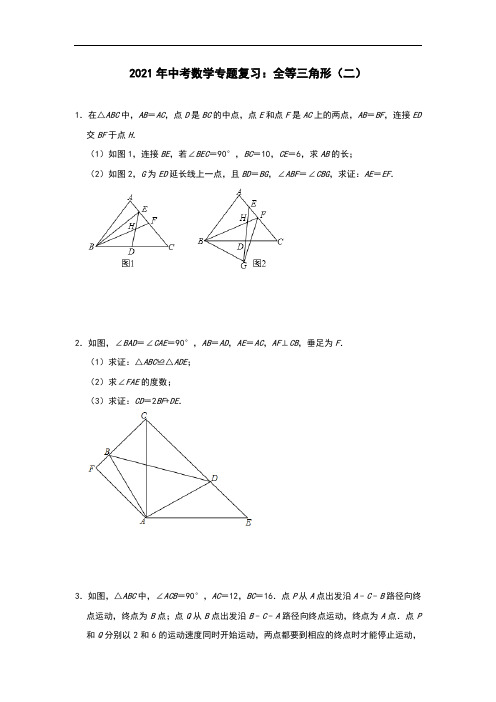
2021年中考数学专题复习：全等三角形（二）1．在△ABC中，AB＝AC，点D是BC的中点，点E和点F是AC上的两点，AB＝BF，连接ED 交BF于点H．（1）如图1，连接BE，若∠BEC＝90°，BC＝10，CE＝6，求AB的长；（2）如图2，G为ED延长线上一点，且BD＝BG，∠ABF＝∠CBG，求证：AE＝EF．2．如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF⊥CB，垂足为F．（1）求证：△ABC≌△ADE；（2）求∠FAE的度数；（3）求证：CD＝2BF+DE．3．如图，△ABC中，∠ACB＝90°，AC＝12，BC＝16．点P从A点出发沿A﹣C﹣B路径向终点运动，终点为B点；点Q从B点出发沿B﹣C﹣A路径向终点运动，终点为A点．点P 和Q分别以2和6的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．问：点P运动多少时间时，△PEC与QFC全等？请说明理由．4．如图，在△ABC中，∠ABC＝60°，AD、CE分别平分∠BAC、∠ACB，求证：AC＝AE+CD．5．如图，△ABC和△EBD中，∠ABC＝∠DBE＝90°，AB＝CB，BE＝BD，连接AE，CD，AE与CD交于点M，AE与BC交于点N．（1）求证：AE＝CD；（2）求证：AE⊥CD；（3）连接BM，有以下两个结论：①BM平分∠CBE；②MB平分∠AMD．其中正确的有（请写序号，少选、错选均不得分）．6．已知△ABC为等边三角形，点D为直线BC上一动点（点D不与点B，点C重合）．以AD 为边作等边三角形ADE，连接CE．（1）如图1，当点D在边BC上时．①求证：△ABD≌△ACE；②直接判断结论BC＝DC+CE是否成立（不需证明）；（2）如图2，当点D在边BC的延长线上时，其他条件不变，请写出BC，DC，CE之间存在的数量关系，并写出证明过程．7．已知，如图△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD 相交于点F．求证：（1）BF＝AC；（2）CE＝BF．8．在平面直角坐标系中，A（7，0），B（0，7）．（1）如图1，P是AB上一点且＝，求P点坐标；（2）如图2，D为OA上一点，AC∥OB且∠CBO＝∠DCB，求∠CBD的度数；（3）如图3，E为OA上一点，OF⊥BE于F，若∠EOF＝∠ABE，求的值9．如图，点A、C、D、B在同一条直线上，且AC＝BD，∠A＝∠B，∠E＝∠F．（1）求证：△ADE≌△BCF；（2）若∠BCF＝65°，求∠DMF的度数．10．阅读探索题：（1）如图1，OP是∠MON的平分线，以O为圆心任意长为半径作弧，分别交射线ON、OM 于C、B两点，在射线OP上任取一点A（点O除外），连接AB、AC．求证：△AOB≌△AOC．（2）请你参考以上方法，解答下列问题：如图2，在 Rt△ABC中，∠ACB＝90°，∠A＝60°，CD平分∠ACB，试判断BC和AC、AD 之间的数量关系并证明．11．如图所示，一个四边形纸片ABCD，∠B＝∠D＝90°，把纸片按如图所示折叠，使点B 落在AD边上的B′点，AE是折痕．（1）试判断B′E与DC的位置关系；（2）如果∠C＝130°，求∠AEB的度数．12．如图，点C在线段AB上，AD∥EB，AC＝BE，AD＝BC．CF平分∠DCE．求证：（1）△ACD≌△BEC；（2）CF⊥DE．13．请将下面的说理过程和理由补充完整．如图，点B，E，C，F在一条直线上，BE＝CF，AB∥DE，AB＝DE，说明AC＝DF．解：∵BE＝CF，（已知）∴BE+EC＝CF+ ．（等式的性质）即BC＝．∵AB∥DE，（已知）．∴∠B＝．（）又∵AB＝DE，（已知）∴△ABC≌△DEF．（）∴AC＝DF．（）14．如图1，在△ABC中，AB＝AC，点D是BC的中点，点E在AD上．（1）求证：∠ABE＝∠ACE；（2）如图2，若BE的延长线交AC于点F，CE的延长线交AB于点G．求证：EF＝EG．15．已知，在△ABC中，AC＝BC．分别过A，B点作互相平行的直线AM和BN．过点C的直线分别交直线AM，BN于点D，E．（1）如图1．若CD＝CE．求∠ABE的大小；（2）如图2．∠ABC＝∠DEB＝60°．求证：AD+DC＝BE．参考答案1．解：（1）如图1，连接AD，∵AB＝AC，点D是BC的中点，∴AD⊥BC∵∠BEC＝90°，BC＝10，CE＝6，∴BE＝＝＝8设AB＝x，则AE＝x﹣6∵AE2+BE2＝AB2，即（x﹣6）2+82＝x2，解得：x＝，∴AB＝，（2）证明：如图2，连接BE，∵BD＝BG∴∠BDG＝∠BGD∵AB＝BF，∴∠A＝∠AFB∵∠ABF＝∠CBG，∴∠BDG＝∠A∴∠EDC＝∠BDG＝∠A∵∠A+∠ABC+∠C＝∠EDC+∠CED+∠C＝180°∴∠CED＝∠ABC∵AB＝AC∴∠C＝∠ABC∴∠C＝∠CED∴DE＝DC∵点D是BC的中点，∴BD＝DC∴DE＝DC＝BD∴∠BED＝∠EBD∵∠BED+∠EBD+∠C+∠CED＝180°，即2∠BED+2∠CED＝180°∴∠BED+∠CED＝90°∴BE⊥AF∵BA＝BF∴AE＝EF2．证明：（1）∵∠BAD＝∠CAE＝90°，∴∠BAC+∠CAD＝90°，∠CAD+∠DAE＝90°，∴∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS）；（2）∵∠CAE＝90°，AC＝AE，∴∠E＝45°，由（1）知△BAC≌△DAE，∴∠BCA＝∠E＝45°，∵AF⊥BC，∴∠CFA＝90°，∴∠CAF＝45°，∴∠FAE＝∠FAC+∠CAE＝45°+90°＝135°；（3）延长BF到G，使得FG＝FB，∵AF⊥BG，∴∠AFG＝∠AFB＝90°，在△AFB和△AFG中，，∴△AFB≌△AFG（SAS），∴AB＝AG，∠ABF＝∠G，∵△BAC≌△DAE，∴AB＝AD，∠CBA＝∠EDA，CB＝ED，∴AG＝AD，∠ABF＝∠CDA，∴∠G＝∠CDA，∵∠GCA＝∠DCA＝45°，在△CGA和△CDA中，，∴△CGA≌△CDA（AAS），∴CG＝CD，∵CG＝CB+BF+FG＝CB+2BF＝DE+2BF，∴CD＝2BF+DE．3．解：∵△PEC≌△QFC，∴斜边CP＝CQ，有四种情况：①P在AC上，Q在BC上，，CP＝12﹣2t，CQ＝16﹣6t，∴12﹣2t＝16﹣6t，∴t＝1；②P、Q都在AC上，此时P、Q重合，∴CP＝12﹣2t＝6t﹣16，∴t＝3.5；③P到BC上，Q在AC时，此时不存在；理由是：16÷6×2＜12，Q到AC上时，P点也在AC上；④当Q到A点（和A重合），P在BC上时，∵CP＝CQ＝AC＝12．CP＝12﹣2t，∴2t﹣12＝12，∴t＝12符合题意；答：点P运动1或3.5或12时，△PEC与△QFC全等．4．证明：在AC上取AF＝AE，连接OF，∵AD平分∠BAC、∴∠EAO＝∠FAO，在△AEO与△AFO中，∴△AEO≌△AFO（SAS），∵AD、CE分别平分∠BAC、∠ACB，∴∠ECA+∠DAC＝∠ACB+∠BAC＝（∠ACB+∠BAC）＝（180°﹣∠B）＝60°则∠AOC＝180°﹣∠ECA﹣∠DAC＝120°；∴∠AOC＝∠DOE＝120°，∠AOE＝∠COD＝∠AOF＝60°，则∠COF＝60°，∴∠COD＝∠COF，∴在△FOC与△DOC中，，∴△FOC≌△DOC（ASA），∴DC＝FC，∵AC＝AF+FC，∴AC＝AE+CD．5．（1）证明：∵∠ABC＝∠DBE，∴∠ABC+∠CBE＝∠DBE+∠CBE，即∠ABE＝∠CBD，在△ABE和△CBD中，，∴△ABE≌△CBD，∴AE＝CD．（2）∵△ABE≌△CBD，∴∠BAE＝∠BCD，∵∠NMC＝180°﹣∠BCD﹣∠CNM，∠ABC＝180°﹣∠BAE﹣∠ANB，∵∠ABC＝90°，∴∠NMC＝90°，∴AE⊥CD．（3）结论：②理由：作BK⊥AE于K，BJ⊥CD于J．∵△ABE≌△CBD，∴AE＝CD，S△ABE ＝S△CDB，∴•AE•BK＝•CD•BJ，∴BK＝BJ，∵作BK⊥AE于K，BJ⊥CD于J，∴BM平分∠AMD．不妨设①成立，则△CBM≌△EBM，则AB＝BD，显然不可能，故①错误．故答案为②．6．解：（1）①∵△ABC和△ADE是等边三角形，∴∠BAC＝∠DAE＝60°，AB＝BC＝AC，AD＝DE＝AE．∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠BAD＝∠EAC．在△ABD和△ACE中，∴△ABD≌△ACE（SAS）．②∵△ABD≌△ACE，∴BD＝CE．∵BC＝BD+CD，∴BC＝CE+CD．（2）BC+CD＝CE．∵△ABC和△ADE是等边三角形，∴∠BAC＝∠DAE＝60°，AB＝BC＝AC，AD＝DE＝AE．∴∠BAC+∠DAC＝∠DAE+∠DAC，∴∠BAD＝∠EAC．在△ABD和△ACE中，∴△ABD≌△ACE（SAS）．∴BD＝CE．∵BD＝BC+CD，∴CE＝BC+CD；7．（1）证明：∵CD⊥AB，BE⊥AC，∴∠BDC＝∠ADC＝∠AEB＝90°，∴∠A+∠ABE＝90°，∠ABE+∠DFB＝90°，∴∠A＝∠DFB，∵∠ABC＝45°，∠BDC＝90°，∴∠DCB＝90°﹣45°＝45°＝∠DBC，∴BD＝DC，在△BDF和△CDA中∵，∴△BDF≌△CDA（AAS），∴BF＝AC；（2）证明：∵BE⊥AC，∴∠AEB＝∠CEB，∵BE平分∠ABC，∴∠ABE＝∠CBE，在△AEB和△CEB中∵，∴△AEB≌△CEB（ASA），∴AE＝CE，即CE＝AC，∵由（1）知AC＝BF，∴CE＝BF．8．解：（1）作PG⊥x轴于G，PN⊥y轴于N，∵A（7，0），B（0，7），∴OA＝7，OB＝7，∵PG⊥x轴，∴PG∥OB，∴△AGP∽△AOB，∴＝，即＝，解得，PG＝3，同理，PN＝4，∴P点坐标为（4，3）；（2）作BG⊥AC交AC的延长线于G，作BH⊥CD于H，∴四边形BOAG为矩形，∴BO＝BG，∵OA＝OB，∴矩形BOAG为正方形，∵AC∥OB，∴∠CBO＝∠BCG，∵∠CBO＝∠DCB，∴∠BCG＝∠DCB，在△BCH和△BCG中，，∴△BCH≌△BCG（AAS），∴∠CBH＝∠CBG，BG＝BH，∴BO＝BH，在Rt△BOD和Rt△BHD中，，∴Rt△BOD≌Rt△BHD（HL），∴∠BOD＝∠HOD，∴∠CBD＝∠DBH+∠CBH＝∠OBG＝45°；（3）∵OA＝OB，∴∠ABO＝∠BAO＝45°，∵∠BEO＝∠BAE+∠ABE＝45°+∠EOF，∵OF⊥BE，∴∠BEO+∠EOF＝90°，∴∠BEO＝67.5°，∠EOF＝22.5°，则∠OBE＝22.5°，作∠BOP＝∠OBE＝22.5°，则PB＝PO，∠OPF＝45°，设OF＝a，则PF＝OF＝a，由勾股定理得，OP＝a，∴PB＝a，∴BF＝a+a，∵∠BOP＝∠OBE，∠OFB＝∠EFO＝90°，∴△OFB∽△EFO，∴EF＝＝a﹣a，∴＝＝2．9．证明：如图所示：（1）∵AD＝AC+CD，BC＝BD+CD，AC＝BD，∴AD＝BC，在△AED和△BFC中，，∴△AED≌△BFC（AAS），（2）∵△AED≌△BFC，∴∠ADE＝∠BCF，又∵∠BCF＝65°，∴∠ADE＝65°，又∵∠ADE+∠BCF＝∠DMF∴∠DMF＝65°×2＝130°．10．（1）证明：在△AOB和△AOC中，，∴△AOB≌△AOC（SAS）．（2）在CB上截取CE＝CA，∵CD平分∠ACB，∴∠ACD＝∠BCD，在△ACD和△ECD中，，∴△ACD≌△ECD（SAS），∴∠CAD＝∠CED＝60°，∵∠ACB＝90°，∴∠B＝30°，∴∠EDB＝30°，即∠EDB＝∠B，∴DE＝EB，∵BC＝CE+BE，∴BC＝AC+DE，∴BC＝AC+AD．11．解：（1）由于AB′是AB的折叠后形成的，∠AB′E＝∠B＝∠D＝90°，（2）∵折叠，∴△ABE≌△AB′E，∴∠AEB′＝∠AEB，即∠AEB＝∠BEB′，∵B′E∥DC，∴∠BEB′＝∠C＝130°，∴∠AEB＝∠BEB′＝65°．12．证明：（1）∵AD∥BE，∴∠A＝∠B，在△ACD和△BEC中，∴△ACD≌△BEC（SAS）；（2）∵△ACD≌△BEC，∴CD＝CE，又∵CF平分∠DCE，∴CF⊥DE．13．解：∵BE＝CF，（已知）∴BE+EC＝CF+EC（等式的性质）即BC＝EF．∵AB∥DE，（已知）∴∠B＝∠DEF．（两直线平行，同位角相等）又∵AB＝DE，（已知）∴△ABC≌△DEF（SAS）∴AC＝DF．（全等三角形对应边相等）故答案为：EC；EF；∠DEF；两直线平行，同位角相等；SAS；全等三角形对应边相等．14．解：（1）证明：∵点D是BC的中点，在△ABD和△ACD中，，∴△ABD≌△ACD（SSS），∴∠BAD＝∠CAD，在△ABE和△ACE中，，∴△ABE≌△ACE（SAS），∴∠ABE＝∠ACE；（2）如图，由（1）知，△ABE≌△ACE，∴BE＝CE，∠ABE＝∠ACE，在△BEG和△CEF中，，∴△BEG≌△CEF（ASA），∴EG＝EF．15．（1）解：如图1，延长AC交BN于点F，∵AM∥BN，∴∠DAF＝∠AFB，在△ADC和△FEC中，，∴△ADC≌△FEC（AAS），∵AC＝BC，∴BC＝AC＝FC＝AF，∴△ABF是直角三角形，∴∠ABE＝90°；（2）证明：如图2，在EB上截取EH＝EC，连CH，∵AC＝BC，∠ABC＝60°，∴△ABC为等边三角形，∵∠DEB＝60°，∴△CHE是等边三角形，∴∠CHE＝60°，∠HCE＝60°，∴∠BHC＝120°，∵AM∥BN，∴∠ADC+∠BEC＝180°，∴∠ADC＝120°，∴∠DAC+∠DCA＝60°，又∵∠DCA+∠ACB+∠BCH+∠HCE＝180°，∴∠DCA+∠BCH＝60°，∴∠DAC＝∠BCH，在△DAC与△HCB中，，∴△DAC≌△HCB（AAS），∴AD＝CH，DC＝BH，又∵CH＝CE＝HE，∴BE＝BH+HE＝DC+AD，即AD+DC＝BE．。
2021年中考数学一轮单元复习12全等三角形(含参考答案)
中考数学一轮单元复习：全等三角形一、选择题1.已知图中的两个三角形全等，则∠1等于（）A.50°B.58°C.60°D.72°2.若△ABC≌△DEF，且△ABC的周长为20，AB=5，BC=8，则DF长为（）.A.5B.8C.7D.5或83.如图，△ABC≌△ADE，∠B=80°，∠C=30°，∠DAC=35°，则∠EAC的度数为（）A. 40°B.30°C.35°D.25°4.如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（）A.CB=CDB.∠BAC=∠DACC.∠BCA=∠DCAD.∠B=∠D=90°5.边长都为整数的△ABC≌△DEF,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为偶数,则 DF的取值为（）A.3B.4C.5D.3或4或56.△ABC与△DFE是全等三角形，A与D对应，B与F对应，则按标有字母的线段计算，图中相等的线段有（）A.1组B.2组C.3组D.4组7.如图已知△ABE≌△ACD, AB=AC, BE=CD，∠B=40°,∠AEC=120°则∠DAC的度数为（）A.80°B.70°C.60°D.50°8.在△ABC中，AB=8，AC=6，则BC边上的中线AD的取值范围是（）。
A．6＜AD＜8 B．2＜AD＜14 C．1＜AD＜7 D．无法确定9.如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（）A．△ACE≌△BCD B．△BGC≌△AFC C．△DCG≌△ECF D．△ADB≌△CEA二、填空题10.已知△ABC≌△A′B′C′，∠A=∠A′，∠B=∠B′，∠C=70°，AB=15cm，则∠C′=_________，A′B′=__________．11.如果△ABC≌△DEF，且△ABC的周长是100cm，A、B分别与D、E对应，并且AB=30cm，DF=25cm，则BC的长等于_____cm.12.如图，△ABC≌△DEF，A与D，B与E分别是对应顶点，∠B=60°，∠A=68°，AB=13cm，则∠F= 度，DE= cm．13.如图，△ABC是不等边三角形，DE=BC，以D，E为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以画出个.14.如图EB交AC于M，交FC于D，AB交FC于N，∠E=∠F=90°，∠B=∠C，AE=AF．给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN．其中正确的结论有（填序号）．15.如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D．若BD：DC=3：2，点D到AB的距离为6，则BC的长是．16.如图所示，BD是∠ABC的平分线，DE⊥AB于点E，AB=36cm，BC=24cm，S△ABC=144cm，则DE的长是．三、解答题17.如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数.18.如图，AC=AE，∠1=∠2，AB=AD．求证：BC=DE．19.如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C，求证：AF=DE．20.已知△ABN和△ACM位置如图所示，AB=AC，∠1=∠2，∠M=∠N．求证：AD=AE．21.如图所示，已知AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．22.如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD.(1)求证：△BCE≌△DCF；(2)求证：AB+AD=2AE.参考答案1.B2.C3.C4.C.5.B6.D7.A8.C9.D10.答案为：700,15㎝11.答案为：45；12.答案为：52，13．13.答案为：4.14.答案为：①②③．15.答案为：15．16.答案为：4.8cm．17.解：∵△ABC≌△ADE，∴∠DAE=∠BAC=（∠EAB﹣∠CAD）=.∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°∠DGB=∠DFB﹣∠D=90°﹣25°=65°.综上所述：∠DFB=90°，∠DGB=65°.18.证明：∵∠1=∠2，∴∠CAB=∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS），∴BC=DE．19.证明：∵BE=CF，∴BE+EF=CF+EF，即BF=CE，在△ABF和△DCE中，，∴△ABF≌△DCE(SAS)∴AF=DE．20.证明：∵∠M=∠N，∴∠MDO=∠NEO，∴∠BDA=∠CEA，∴在△ABD和△ACE中，∵，∴△ABD≌△ACE（AAS），∴AD=AE．21.证明：连接AD，在△ACD和△ABD中，，∴△ACD≌△ABD（SSS），∴∠EAD=∠FAD，即AD平分∠EAF，∵DE⊥AE，DF⊥AF，∴DE=DF．22. (1)证明：∵AC是角平分线，CE⊥AB于E，CF⊥AD于F，∴CE=CF，∠F=∠CEB=90°，在Rt△BCE和Rt△DCF中，∴△BCE≌△DCF；(2)解：∵CE⊥AB于E，CF⊥AD于F，∴∠F=∠CEA=90°，在Rt△FAC和Rt△EAC中，，∴Rt△FAC≌Rt△EAC，∴AF=AE，∵△BCE≌△DCF，∴BE=DF，∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.。
2021年九年级数学中考一轮复习——几何专题：全等三角形性质与判定(三)
2021年九年级数学中考复习——几何专题：全等三角形性质与判定（三）1．如图，在△ABC中，AB＝AC，∠A＝108°，BE平分∠ABC交AC于点E，求证：BC＝AB+CE．2．如图2，△ABC中，∠B＝∠C，若∠A＝70°，求∠B的度数．3．如图，在△ABC中，AD⊥BC于点D，AD＝BD，点E是线段AD上一点，且ED＝CD，连接BE交AC于点F．（1）求证：∠CBF＝∠DAC；（2）若BD＝3，BF＝，求△BAF的周长．4．如图，△ABC中，AD既是中线，又是角平分线，DE⊥AB于点E，DF⊥AC于点F．（1）求证：△BDE≌△CDF；（2）你认为AD还是△ABC的高吗？如果是，请给出证明；如果不是，请说明理由．5．已知：D，A，E三点都在直线m上，在直线m的同一侧作△ABC，使AB＝AC，连接BD，CE．（1）如图①，若∠BAC＝90°，BD⊥m，CE⊥m，求证：△ABD≌△ACE；（2）如图②，若∠BDA＝∠AEC＝∠BAC，请判断BD，CE，DE三条线段之间的数量关系，并说明理由．6．已知：如图，点A、B、C、D在一条直线上，AE∥DF，AE＝DF，AB＝CD．（1）求证：∠E＝∠F；（2）若∠D＝28°，∠ECA＝100°，求∠F的度数．7．如图1，在△ABC中，AE⊥BC于点E，AE＝BE，D是AE上的一点，且DE＝CE，连接BD，CD．（1）试判断BD与AC的位置关系和数量关系，并说明理由；（2）如图2，若将△DCE绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由．8．已知，在△ABC中，D是AC上一点，BF交AC于点E，连接DF．（1）如图1，BE＝EF，AB∥DF．求证：AE＝DE；（2）如图2，点D与点C重合，∠A＝90°，∠ACB＝∠ECF，∠F＝∠AEB．若CE＝3，BC＝5，求AC的长．9．如图，AB＝CD，AE⊥BC于E，DF⊥BC于F，AE＝DF．求证：（1）CE＝BF；（2）AB∥CD．10．如图，在△ACD和△BCE中，AC＝BC，AD＝BE，CD＝CE，∠ACE＝55°，∠BCD＝155°，AD与BE相交于点P，求∠ACB的度数．参考答案1．证明：如图，在BC上取BA′＝BA，连接EA′，∵∠A＝108°，AB＝AC，∴∠ABC＝∠ACB＝36°，∵BE平分∠ABC，∴∠ABE＝∠CBA＝18°，在△ABE与△A′BE中，，∴△ABE≌△A′BE（SAS），∴∠BA′E＝∠A＝108°，∴∠EA′C＝72°，∴∠A′EC＝72°，∴∠A′EC＝∠CA′E，∴CE＝CA′，∴BC＝BA′+EC＝AB+EC＝AC+EC．2．（1）证明：∵C是线段AB的中点，∴AC＝CB，在△ACD和△CBE中，∵，∴△ACD≌△CBE（SSS）；（2）解：△ABC中，∠A+∠B+∠C＝180°，∵∠B＝∠C，∴70°+∠B+∠B＝180°，∴∠B＝55°．3．解：（1）证明：∵AD⊥BC，∴∠ADC＝∠ADB＝90°，在△ACD和△BED中，，∴△ACD≌△BED（SAS），∴∠DAC＝∠CBF；（2）∵AD⊥BC，AD＝BD＝3，∴AB＝＝3，∵∠DAC＝∠CBF，∴∠DAC+∠C＝∠CBF+∠C＝90°，∴∠AFB＝90°，∴AF＝＝2，∴△BAF的周长为：AB+BF+AF＝3++2．4．（1）证明：∵AD既是中线，又是角平分线，DE⊥AB，DF⊥AC，∴BD＝CD，DE＝DF，∠DEB＝∠DFC＝90°，在Rt△BDE和Rt△CDF中，，∴Rt△BDE≌Rt△CDF（HL）；（2）AD还是△ABC的高，证明：由（1）△BDE≌△CDF，∴∠B＝∠C，∵AD既是中线，又是角平分线，∴BD＝CD，∠BAD＝∠CAD，在△BAD和△CAD中，，∴△BAD≌△CAD（AAS），∴∠ADB＝∠ADC，∵∠ADB+∠ADC＝180°，∴∠ADB＝∠ADC＝90°，即AD还是△ABC的高．5．解：（1）证明：如图①，∵D，A，E三点都在直线m上，∠BAC＝90°，∴∠BAD+∠CAE＝90°，∵BD⊥m，CE⊥m，∴∠ADB＝∠CEA＝90°，∴∠BAD+∠ABD＝90°，∴∠ABD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（AAS）；（2）DE＝BD+CE．理由是：如图②，∵∠BDA＝∠AEC＝∠BAC，∴由三角形内角和及平角性质，得：∠BAD+∠ABD＝∠BAD+∠CAE＝∠CAE+∠ACE，∴∠ABD＝∠CAE，∠BAD＝∠ACE，在△ABD和△ACE中，，∴△ABD≌△ACE（ASA），∴BD＝AE，AD＝CE，∴DE＝AD+AE＝BD+CE．6．（1）证明：∵AE∥DF，∴∠A＝∠D，∵AB＝CD，∴AB+BC＝CD+BC，∴AC＝DB，在△EAC和△FDB中，，∴△EAC≌△FDB（SAS），∴∠E＝∠F；（2）解：由（1）得：△EAC≌△FDB，∴∠ECA＝∠FBD＝100°，∴∠F＝180°﹣∠D﹣∠FBD＝180°﹣28°﹣100°＝52°．7．解：（1）BD＝AC，BD⊥AC，理由：延长BD交AC于F．∵AE⊥BC，∴∠AEB＝∠AEC＝90°，在△BED和△AEC中，，∴△BED≌△AEC（SAS），∴BD＝AC，∠DBE＝∠CAE，∵∠BED＝90°，∴∠EBD+∠BDE＝90°，∵∠BDE＝∠ADF，∴∠ADF+∠CAE＝90°，∴∠AFD＝180°﹣90°＝90°，∴BD⊥AC；（2）结论不发生变化，理由是：设AC与DE相交于点O，∵∠BEA＝∠DEC＝90°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC（SAS），∴BD＝AC，∠BDE＝∠ACE，∵∠DEC＝90°，∴∠ACE+∠EOC＝90°，∵∠EOC＝∠DOF，∴∠BDE+∠DOF＝90°，∴∠DFO＝180°﹣90°＝90°，∴BD⊥AC．8．（1）证明：∵AB∥DF，∴∠A＝∠EDF，在△ABE和△DFE中，，∴△ABE≌△DFE（AAS），∴AE＝DE；（2）解：过B作BH∥DF交CA的延长线于点H，∴∠HBE＝∠F＝∠AEB，∠H＝∠ACF＝ACB，∴BH＝EH＝BC＝5，∵CE＝3，∴CH＝HE+CE＝8，又∠BAD＝90°，∴CA＝HA＝CH＝4．9．（1）证明：∵AE⊥BC，DF⊥BC，∴∠AEB＝∠DFC＝90°，在Rt△ABE和Rt△CDF中，，∴Rt△ABE≌Rt△CDF（HL），∴BE＝CF，∴BE﹣EF＝CF﹣EF，∴CE＝BF；（2）∵Rt△ABE≌Rt△CDF，∴∠B＝∠C，∴AB∥CD．10．解：在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴∠ACD＝∠BCE，∴∠ACD﹣∠ACE＝∠BCE﹣∠ACE，即∠DCE＝∠ACB，∴∠ACB＝（∠BCD﹣∠ACE）＝（155°﹣55°）＝50°．。
中考数学 一轮训练：全等三角形 附答案
2020-2021 中考数学一轮训练：全等三角形一、选择题1. 如图，PD⊥AB，PE⊥AC，垂足分别为D，E，且PD＝PE，则△APD与△APE全等的理由是()A．SAS B．AAA C．SSS D．HL2. 如图，P为OC上一点，PM⊥OA，PN⊥OB，垂足分别为M，N，PM＝PN，∠BOC＝30°，则∠AOB的度数为()A．30°B．45°C．60°D．50°3. 如图，BE⊥AC，CF⊥AB，垂足分别是E，F.若BE＝CF，则图中全等三角形有()A．1对B．2对C．3对D．4对4. 根据下列条件，能画出唯一的△ABC的是()A．AB＝3，BC＝4，AC＝8 B．AB＝4，BC＝3，∠A＝30°C．AB＝5，AC＝6，∠A＝50°D．∠A＝30°，∠B＝70°，∠C＝80°5. 如图所示，已知△ABC≌△ADE，BC的延长线交DE于点F，∠B=∠D=25°，∠ACB=∠AED=105°，∠DAC=10°，则∠DFB的度数为 ()A.40°B.50°C.55°D.60°6. 如图，AB⊥CD，且AB＝CD.E，F是AD上两点，CE⊥AD，BF⊥AD.若CE ＝a，BF＝b，EF＝c，则AD的长为()A．a＋c B．b＋cC．a－b＋c D．a＋b－c7. 如图，△ACB≌△A'CB'，∠ACA'=30°，则∠BCB'的度数为()A.20°B.30°C.35°D.40°8. 如图，平面上到两两相交的三条直线a，b，c的距离相等的点一共有()A．4个B．3个C．2个D．1个二、填空题9. 如图，△ABC≌△A′B′C′，其中∠A＝36°，∠C′＝24°，则∠B＝________.10. 如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE交于点H，请你添加一个适当条件：________，使△AEH≌△CEB.11. 如图，△ABC≌△ADE，BC的延长线交DE于点G，∠CAB=54°，∠DAC=16°，则∠DGB=°.12. 在平面直角坐标系xOy中，已知点A，B的坐标分别为(2，0)，(2，4)，若以A，B，P为顶点的三角形与△ABO全等，则点P的坐标为________________________．13. 已知△ABC的三边长分别为6，7，10，△DEF的三边长分别为6，3x-2，2x-1.若这两个三角形全等，则x的值为.14. 如图，四边形ABCD的对角线AC，BD相交于点O，△ABO≌△ADO.有下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的序号是.15. 如图，在△ABC中，∠ACB=120°，BC=4，D为AB的中点，DC⊥BC，则△ABC 的面积是.16. 如图，在△ABC中，∠C＝90°，AC＝BC，AD是∠BAC的平分线，DE⊥AB，垂足为E.若△DBE的周长为20，则AB＝________．三、解答题17. 如图2-Z-20，C是AB的中点，AD=CE，CD=BE.求证:∠A+∠ECA=180°.18. 如图，已知△ACF≌△DBE，且点A，B，C，D在同一条直线上.若AD=16，BC=10，求AB的长.19. 如图，AC∥BE，点D在BC上，AB＝DE，∠ABE＝∠CDE.求证：DC＝BE－AC.20. 如图，BE，CF都是△ABC的高，在BE上截取BD＝AC，在射线CF上截取CG＝AB，连接AG，AD.求证：(1)△BAD≌△CGA；(2)AD⊥AG.21. 在矩形ABCD中，AD＝4，M是AD的中点，点E是线段AB上一点，连接EM并延长交线段CD的延长线于点F.(1)如图①，求证：△AEM ≌△DFM；(2)如图②，若AB＝2，过点M作MG⊥EF交线段BC于点G，求证：△GEF是等腰直角三角形；(3)如图③，若AB＝23，过点M作MG⊥EF交线段BC的延长线于点G，若MG=nME，求n的值.22. 已知：在等边△ABC中，D、E分别是AC、BC上的点，且∠BAE＝∠CBD ＜60°，DH⊥AB，垂足为点H.(1)如图①，当点D、E分别在边AC、BC上时，求证：△ABE≌△BCD；(2)如图②，当点D、E分别在AC、CB延长线上时，探究线段AC、AH、BE的数量关系；(3)在(2)的条件下，如图③，作EK∥BD交射线AC于点K，连接HK，交BC于点G，交BD于点P，当AC＝6，BE＝2时，求线段BP的长．2020-2021 中考数学 一轮训练：全等三角形-答案一、选择题 1. 【答案】D2. 【答案】C[解析] ∵点P 在OC 上，PM ⊥OA ，PN ⊥OB ，PM ＝PN ，∴OC 是∠AOB 的平分线．∵∠BOC ＝30°，∴∠AOB ＝60°.3. 【答案】C[解析] ①∵BE ⊥AC ，CF ⊥AB ，∴∠CFB ＝∠BEC ＝90°.在Rt △BCF 和Rt △CBE 中，⎩⎨⎧CF ＝BE ，BC ＝CB ，∴Rt △BCF ≌Rt △CBE(HL)．②∵BE ⊥AC ，CF ⊥AB ，∴∠AFC ＝∠AEB ＝90°.在△ABE 和△ACF 中，⎩⎨⎧∠AEB ＝∠AFC ，∠A ＝∠A ，BE ＝CF ，∴△ABE ≌△ACF(AAS)． ③设BE 与CF 相交于点O. ∵BE ⊥AC ，CF ⊥AB ， ∴∠OFB ＝∠OEC ＝90°.∵△ABE ≌△ACF ，∴AB ＝AC ，AE ＝AF. ∴BF ＝CE.在△BOF 和△COE 中，⎩⎨⎧∠OFB ＝∠OEC ，∠BOF ＝∠COE ，BF ＝CE ，∴△BOF ≌△COE(AAS)．4. 【答案】C[解析] 对于选项A 来说，AB ＋BC<AC ，不能画出△ABC ；对于选项B来说，可画出△ABC为锐角三角形或者钝角三角形；对于选项C来说，已知两边及其夹角，△ABC是唯一的；对于选项D来说，△ABC的形状可确定，但大小不确定．5. 【答案】D[解析] 因为△ABC≌△ADE，∠B=∠D=25°，∠ACB=∠AED=105°，所以∠CAB=∠EAD=180°-105°-25°=50°.所以∠DAB=∠CAB+∠DAC=60°.由图易得∠DFB=∠DAB=60°.6. 【答案】D[解析] ∵AB⊥CD，CE⊥AD，BF⊥AD，∴∠CED＝∠AFB＝90°，∠A＝∠C.又∵AB＝CD，∴△CED≌△AFB.∴AF＝CE＝a，DE＝BF＝b，DF ＝DE－EF＝b－c.∴AD＝AF＋DF＝a＋b－c.故选D.7. 【答案】B[解析] 由△ACB≌△A'CB'，得∠ACB=∠A'CB'.由等式的基本性质，得∠ACB-∠A'CB=∠A'CB'-∠A'CB.所以∠BCB'=∠ACA'=30°.8. 【答案】A[解析] 如图，到三条直线a，b，c的距离相等的点一共有4个．二、填空题9. 【答案】120°【解析】由于△ABC≌△A′B′C′，∴∠C＝∠C′＝24°，在△ABC 中，∠B＝180°－24°－36°＝120°.10. 【答案】AH＝CB(符合要求即可)【解析】∵AD⊥BC，CE⊥AB，垂足分别为点D、E，∴∠BEC＝∠AEC＝90°，在Rt△AEH中，∠EAH＝90°－∠AHE，在Rt△HDC中，∠ECB＝90°－∠DHC，∵∠AHE＝∠DHC，∴∠EAH＝∠ECB，∴根据AAS添加AH＝CB或EH＝EB；根据ASA添加AE＝CE.可证△AEH≌△CEB.故答案为：AH＝CB或EH＝EB或AE＝CE均可．11. 【答案】70[解析] ∵△ABC≌△ADE，∴∠B=∠D.∵∠GFD=∠AFB，∴∠DGB=∠F AB.∵∠F AB=∠DAC+∠CAB=70°，∴∠DGB=70°.12. 【答案】(4，0)或(4，4)或(0，4)13. 【答案】4[解析] ∵△ABC的三边长分别为6，7，10，△DEF的三边长分别为6，3x-2，2x-1，这两个三角形全等，∴3x-2=10，2x-1=7，解得x=4;还可以是3x-2=7，2x-1=10，这种情况不成立.14. 【答案】①②③[解析] 由△ABO≌△ADO，得AB=AD，∠AOB=∠AOD=90°，∠BAC=∠DAC.又因为AC=AC，所以△ABC≌△ADC，则CB=CD.所以①②③正确.15. 【答案】8[解析]∵DC⊥BC，∴∠BCD=90°.∵∠ACB=120°，∴∠ACD=30°.延长CD到H使DH=CD，∵D为AB的中点，∴AD=BD.在△ADH与△BDC中，∴△ADH≌△BDC(SAS)，∴AH=BC=4，∠H=∠BCD=90°.∵∠ACH=30°，∴CH=AH=4，∴CD=2，∴△ABC的面积=2S△BCD=2××4×2=8.16. 【答案】20[解析] 由角平分线的性质可得CD＝DE.易证Rt△ACD≌Rt△AED，则AC＝AE，DE＋DB＝CD＋DB＝BC＝AC＝AE，故DE＋DB＋EB ＝AE＋EB＝AB.三、解答题17. 【答案】证明:∵C是AB的中点，∴AC=CB.在△ACD 和△CBE 中，∴△ACD ≌△CBE (SSS). ∴∠A=∠ECB.∴AD ∥CE.∴∠A+∠ECA=180°.18. 【答案】解:∵△ACF ≌△DBE ，∴AC=DB.∴AC-BC=DB-BC ，即AB=CD. ∵AD=16，BC=10， ∴AB=CD=(AD-BC )=3.19. 【答案】证明：∵AC ∥BE ，∴∠C ＝∠DBE ，∠A ＋∠ABE ＝180°. ∵∠BDE ＋∠CDE ＝180°，∠ABE ＝∠CDE ， ∴∠A ＝∠BDE.在△ABC 和△DEB 中，⎩⎨⎧∠C ＝∠DBE ，∠A ＝∠BDE ，AB ＝DE ，∴△ABC ≌△DEB(AAS)． ∴AC ＝DB ，BC ＝EB. 又∵DC ＝BC －BD ， ∴DC ＝BE －AC.20. 【答案】证明：(1)∵BE ，CF 都是△ABC 的高， ∴∠ABE ＋∠BAC ＝90°，∠ACF ＋∠BAC ＝90°. ∴∠ABE ＝∠ACF.在△BAD 和△CGA 中，⎩⎨⎧AB ＝GC ，∠ABD ＝∠GCA ，BD ＝CA ，∴△BAD ≌△CGA(SAS)．(2)∵△BAD ≌△CGA ，∴∠G ＝∠BAD. ∵∠AFG ＝90°，∴∠GAD ＝∠BAD ＋∠BAG ＝∠G ＋∠BAG ＝90°.∴AD ⊥AG .21. 【答案】(1)证明：∵四边形ABCD 是矩形， ∴∠EAM ＝∠FDM ＝90°， ∵M 是AD 的中点， ∴AM ＝DM ，在△AME 和△DMF 中，⎩⎨⎧∠A ＝∠FDBAM ＝DM∠AME ＝∠DMF， ∴△AEM ≌△DFM (ASA)；(2)证明：如解图①，过点G 作GH ⊥AD 于H ，解图①∵∠A ＝∠B ＝∠AHG ＝90°， ∴四边形ABGH 是矩形， ∴GH ＝AB ＝2， ∵M 是AD 的中点，∴AM ＝12AD ＝2，∴AM ＝GH ， ∵MG ⊥EF ，∴∠GME ＝90° ∴∠AME ＋∠GMH ＝90°. ∵∠AME ＋∠AEM ＝90°， ∴∠AEM ＝∠GMH ， 在△AEM 和△HMG 中，⎩⎨⎧AM ＝GH∠AEM ＝∠GMH ∠A ＝∠AHG， ∴△AEM ≌△HMG ，∴ME ＝MG ，∴∠EGM ＝45°，由(1)得△AEM ≌△DFM ，∴ME ＝MF ，∵MG ⊥EF ，FMG EMG ≌△△∴，∴GE ＝GF ，∴∠EGF ＝2∠EGM ＝90°，∴△GEF 是等腰直角三角形．(3)解：如解图②，过点G 作GH ⊥AD 交AD 延长线于点H ，解图②∵∠A ＝∠B ＝∠AHG ＝90°，∴四边形ABGH 是矩形，∴GH ＝AB ＝23，∵MG ⊥EF ，∴∠GME ＝90°，∴∠AME ＋∠GMH ＝90°，∵∠AME ＋∠AEM ＝90°，∴∠AEM ＝∠GMH ，又∵∠A ＝∠GHM ＝90°，∴△AEM ∽△HMG ，∴EM MG ＝AM GH ，在Rt △GME 中，tan ∠MEG ＝MG EM ＝ 3.∴n =322. 【答案】 (1)证明：∵△ABC 为等边三角形，∴∠ABC ＝∠C ＝∠CAB ＝60°，AB ＝BC ，在△ABE 和△BCD 中，⎩⎨⎧∠BAE ＝∠CBDAB ＝BC∠ABE ＝∠BCD，∴△ABE ≌△BCD (ASA)；(2)解：∵△ABC 为等边三角形，∴∠ABC ＝∠CAB ＝60°，AB ＝BC ，∴∠ABE ＝∠BCD ＝180°－60°＝120°.∴在△ABE 和△BCD 中，⎩⎨⎧∠BAE ＝∠CBDAB ＝BC∠ABE ＝∠BCD， ∴△ABE ≌△BCD (ASA)，∴BE ＝CD .∵DH ⊥AB ，∴∠DHA ＝90°，∵∠CAB ＝60°，∴∠ADH ＝30°，∴AD ＝2AH ，∴AC ＝AD －CD ＝2AH －BE ；(3)解：如解图，作DS ⊥BC 延长线于点S ，作HM ∥AC 交BC 于点M ，解图∵AC ＝6，BE ＝2，∴由(2)得AH ＝4，BH ＝2,与(1)同理可得BE ＝CD ＝2，CE ＝8，∵∠SCD ＝∠ACB ＝60°，∴∠CDS ＝30°，∴CS ＝1，SD ＝3，BS ＝7，∵BD 2＝BS 2＋SD 2＝72＋(3)2，∴BD ＝213，∵EK ∥BD ，∴△CBD ∽△CEK ，∴CB CE ＝CD CK ＝BD EK ，∴CK ＝CD ·CE CB ＝2×86＝83，EK ＝CE ·BD CB ＝8×2136＝8133. ∵HM ∥AC ，∴∠HMB ＝∠ACB ＝60°，∴△HMB 为等边三角形，BM ＝BH ＝HM ＝2， CM ＝CB －BM ＝4，又∵HM ∥AC ，∴△HMG ∽△KCG ，∴HM KC ＝MGCG ，即382＝MG4－MG ，∴MG ＝127，BG ＝267，EG ＝407，∵EK ∥BD ，∴△GBP ∽△GEK ，∴BP EK ＝GBGE ， ∴BP ＝261315.。
2025年湖南中考数学一轮复习考点研析 第四章 三角形技法2 全等三角形的常见模型
∠A=∠D.请你从中任选一个条件,使△ABC≌△DEF,并写出证明过程.
解:答案不唯一,如选择条件②.证明如下:
∵BE=CF,
∴BE＋EC=CF＋EC,即BC=EF.
= ,
在△ABC和△DEF中,ቐ∠ = ∠,
证:△BDC≌△CEB.
证明:∵AB=AC,∴∠DBC=∠ECB.
∵AD=AE,∴AB－AD=AC－AE,即DB=EC.
= ,
在△DBC和△ECB中,ቐ∠ = ∠,∴△BDC≌△CEB(SAS).
= ,
证明
3.如图,AD⊥AE,AB⊥AC,∠B=∠C,AB=AC.求证:△ABD≌△ACE.
= ,
∴△ACE≌△DCB(SAS),∴∠CAM=∠CDN.
∵ ∠ MDP ＋ ∠ DMP ＋ ∠ MPD= ∠ CAM ＋ ∠ AMC ＋
∠ACM=180°,∠MDP=∠CAM,∠DMP=∠AMC,
∴∠APD=∠ACM=模型类别
一线三等
已知条件
图示
相关结论
腰三角形
已知条件
CA=CB,CD=CE,
∠ACB=∠DCE
图示
相关结论
△BCD≌△ACE
4.如图,在△ABC和△ADE中,AB=AD,AC=AE,∠BAD=∠CAE,DE分别交BC,AC
于点F,G.
(1)求证:∠C=∠E.
(2)若∠CAE=24°,求∠EFC的度数.
(1)证明:∵∠BAD=∠CAE,
2025年湖南中考数学一轮复习考点研析
第一部分 考点研析
第四章 三角形
技法2 全等三角形的常见模型
2021年中考数学真题 三角形及全等三角形(共40题)-(原卷版)
16三角形及全等三角形（共40题）姓名：__________________ 班级：______________ 得分：_________________一、单选题1．（2021·湖南岳阳市·中考真题）下列命题是真命题的是（）A．五边形的内角和是720︒B．三角形的任意两边之和大于第三边C．内错角相等D．三角形的重心是这个三角形的三条角平分线的交点2．（2021·山东临沂市·中考真题）如图，在//AB CD中，40∠，∠=︒，CB平分DCEAEC则ABC∠的度数为（）A．10︒B．20︒C．30D．40︒3．（2021·陕西中考真题）如图，点D、E分别在线段BC、AC上，连接AD、BE．若∠=︒，50∠=︒，则1∠的大小为（）BC35A∠=︒，25A．60°B．70°C．75°D．85°4．（2021·四川乐山市·中考真题）如图，已知直线1l、2l、3l两两相交，且13l l⊥．若α=︒，则β的度数为（）50A ．120︒B ．130︒C ．140︒D ．150︒5．（2021·安徽中考真题）两个直角三角板如图摆放，其中90BAC EDF ∠=∠=︒，45E ∠=︒，30C ∠=︒，AB 与DF 交于点M ．若//BC EF ，则BMD ∠的大小为（ ）A ．60︒B ．67.5︒C ．75︒D ．82.5︒6．（2021·江苏扬州市·中考真题）如图，点A 、B 、C 、D 、E 在同一平面内，连接AB 、BC 、CD 、DE 、EA ，若100BCD ∠=︒，则A B D E ∠+∠+∠+∠=（ ）A ．220︒B ．240︒C ．260︒D ．280︒7．（2021·河北中考真题）定理：三角形的一个外角等于与它不相邻的两个内角的和．已知：如图，ACD ∠是ABC 的外角．求证：ACD A B ∠=∠+∠．下列说法正确的是（ ）A ．证法1还需证明其他形状的三角形，该定理的证明才完整B ．证法1用严谨的推理证明了该定理C ．证法2用特殊到一般法证明了该定理D ．证法2只要测量够一百个三角形进行验证，就能证明该定理8．（2021·四川泸州市·中考真题）在锐角ABC 中，∠A ，∠B ，∠C 所对的边分别为a ，b ，c ，有以下结论：2sinA sinB sinCa cb R ===（其中R 为ABC 的外接圆半径）成立．在ABC 中，若∠A =75°，∠B =45°，c =4，则ABC 的外接圆面积为（ ）A ．163πB ．643πC ．16πD ．64π9．（2021·重庆中考真题）如图，在ABC和DCB中，ACB DBC∠=∠，添加一个条件，不能．．证明ABC和DCB全等的是（）A．ABC DCB∠=∠B．AB DC=C．AC DB=D．A D∠=∠10．（2021·重庆中考真题）如图，点B，F，C，E共线，∠B=∠E，BF=EC，添加一个条件，不等判断∠ABC∠∠DEF的是（）A．AB=DE B．∠A=∠D C．AC=DF D．AC∠FD 11．（2021·浙江嘉兴市·中考真题）将一张三角形纸片按如图步骤∠至∠折叠两次得图∠，然后剪出图∠中的阴影部分，则阴影部分展开铺平后的图形是（）A．等腰三角形B．直角三角形C．矩形D．菱形12．（2021·四川遂宁市·中考真题）下列说法正确的是（）A．角平分线上的点到角两边的距离相等B．平行四边形既是轴对称图形，又是中心对称图形C．在代数式1a ，2x，xπ，985，42ba+，13y+中，1a，xπ，42ba+是分式D．若一组数据2、3、x、1、5的平均数是3，则这组数据的中位数是4 13．（2021·湖南娄底市·中考真题）2,5,m是某三角形三边的长，则22(3)(7)m m-+-等于（）A．210m-B．102m-C．10D．414．（2021·山东泰安市·中考真题）如图，直线//m n，三角尺的直角顶点在直线m 上，且三角尺的直角被直线m平分，若160∠=︒，则下列结论错误的是（）A．275∠=︒B．345∠=︒C．4105∠=︒D．5130∠=︒15．（2021·四川资阳市·中考真题）如图，已知直线//,140,230m n∠=︒∠=︒，则3∠的度数为（）A．80︒B．70︒C．60︒D．50︒16．（2021·海南中考真题）如图，已知//a b，直线l与直线a b、分别交于点A B、，分别以点A B、为圆心，大于12AB的长为半径画弧，两弧相交于点M N、，作直线MN，交直线b于点C，连接AC，若140∠=︒，则ACB∠的度数是（）A ．90︒B ．95︒C ．100︒D ．105︒17．（2021·四川广元市·中考真题）观察下列作图痕迹，所作线段CD 为ABC 的角平分线的是（ ）A ．B ．C ．D ．二、填空题18．（2021·河北中考真题）下图是可调躺椅示意图（数据如图），AE 与BD 的交点为C ，且A ∠，B ，E ∠保持不变．为了舒适，需调整D ∠的大小，使110EFD ∠=︒，则图中D ∠应___________（填“增加”或“减少”）___________度．19．（2021·江苏苏州市·中考真题）如图．在Rt ABC △中，90C ∠=︒，AF EF =．若72CFE ∠=︒，则B ∠=______．20．（2021·浙江中考真题）为庆祝中国共产党建党100周年，某校用红色灯带制作了一个如图所示的正五角星（,,,,A B C D E 是正五边形的五个顶点），则图中A ∠的度数是_______度．21．（2021·江苏连云港市·中考真题）如图，BE 是ABC 的中线，点F 在BE 上，延长AF 交BC 于点D ．若3BF FE =，则BD DC=______．22．（2021·四川遂宁市·中考真题）如图，在∠ABC中，AB＝5，AC＝7，直线DE 垂直平分BC，垂足为E，交AC于点D，则∠ABD的周长是_____ ．23．（2021·云南中考真题）已知ABC的三个顶点都是同一个正方形的顶点，ABC∠的平分线与线段AC交于点D．若ABC的一条边长为6，则点D到直线AB的距离为__________．24．（2021·广西柳州市·中考真题）若长度分别为3，4，a的三条线段能组成一个三角形，则整数a的值可以是________．（写出一个即可）25．（2021·四川成都市·中考真题）如图，在Rt ABC中，90,C AC BC∠=︒=，按以下步骤作图：∠以点A为圆心，以任意长为半径作弧，分别交,AC AB于点M，N；∠分别以M，N为圆心，以大于12MN的长为半径作弧，两弧在BAC∠内交于点O；∠作射线AO，交BC于点D．若点D到AB的距离为1，则BC的长为_______．三、解答题26．（2021·陕西中考真题）如图，//=，点E在BC上，且BE AC=．求BD AC，BD BC证：D ABC∠=∠．27．（2021·湖南衡阳市·中考真题）如图，点A、B、D、E在同一条直线上，=．求证：ABC DEFAB DE AC DF BC EF,//,//△≌△．28．（2021·四川乐山市·中考真题）如图，已知AB DC=，A D∠=∠，AC与DB相交于点O，求证：OBC OCB∠=∠．29．（2021·四川泸州市·中考真题）如图，点D在AB上，点E在AC上，AB=AC，∠B=∠C，求证：BD=CE30．（2021·云南中考真题）如图，在四边形ABCD中，,,==与BD相AD BC AC BD AC交于点E．求证：DAC CBD∠=∠．31．（2021·四川遂宁市·中考真题）如图，在平行四边形ABCD中，对角线AC与BD相交于点O，过点O的直线EF与BA、DC的延长线分别交于点E、F．（1）求证：AE＝CF；（2）请再添加一个条件，使四边形BFDE是菱形，并说明理由．32．（2021·江苏连云港市·中考真题）在数学兴趣小组活动中，小亮进行数学探究活动．（1）ABC是边长为3的等边三角形，E是边AC上的一点，且1AE=，小亮以BE为边作等边三角形BEF，如图1，求CF的长；（2）ABC是边长为3的等边三角形，E是边AC上的一个动点，小亮以BE为边作等边三角形BEF，如图2，在点E从点C到点A的运动过程中，求点F所经过的路径长；（3）ABC是边长为3的等边三角形，M是高CD上的一个动点，小亮以BM为边作等边三角形BMN，如图3，在点M从点C到点D的运动过程中，求点N所经过的路径长；（4）正方形ABCD的边长为3，E是边CB上的一个动点，在点E从点C到点B 的运动过程中，小亮以B为顶点作正方形BFGH，其中点F、G都在直线AE上，如图4，当点E到达点B时，点F、G、H与点B重合．则点H所经过的路径长为______，点G所经过的路径长为______．33．（2021·四川乐山市·中考真题）在等腰ABC中，AB AC=，点D是BC边上一点（不与点B、C重合），连结AD．（1）如图1，若60C∠=°，点D关于直线AB的对称点为点E，结AE，DE，则BDE∠= ________；（2）若60C∠=°，将线段AD绕点A顺时针旋转60︒得到线段AE，连结BE．∠在图2中补全图形；∠探究CD与BE的数量关系，并证明；（3）如图3，若AB ADkBC DE==，且ADE C∠=∠，试探究BE、BD、AC之间满足的数量关系，并证明．34．（2021·安徽中考真题）如图1，在四边形ABCD中，ABC BCD∠=∠，点E在边BC上，且//AE CD，//DE AB，作CF//AD交线段AE于点F，连接BF．（1）求证：ABF EAD△≌△；（2）如图2，若9AB=，5CD=，ECF AED∠=∠，求BE的长；（3）如图3，若BF的延长线经过AD的中点M，求BEEC的值．35．（2021·重庆中考真题）如图，四边形ABCD为平行四边形，连接AC，且=．请用尺规完成基本作图：作出BAC2AC AB∠的角平分线与BC交于点E．连接BD交AE于点F，交AC于点O，猜想线段BF和线段DF的数量关系，并证明你的猜想．（尺规作图保留作图痕迹，不写作法）36．（2021·浙江温州市·中考真题）如图，BE是ABC的角平分线，在AB上取点D，使DB DE=．（1）求证：//DE BC．（2）若65∠=︒，求EBC∠的度数．∠=︒，45AEDA37．（2021·江苏无锡市·中考真题）已知：如图，AC，DB相交于点O，AB DC=，ABO DCO ∠=∠．求证：（1）ABO DCO △≌△；（2）OBC OCB ∠=∠．38．（2021·福建中考真题）如图，在ABC 中，D 是边BC 上的点，,⊥⊥DE AC DF AB ，垂足分别为E ，F ，且,DE DF CE BF ==．求证：B C ∠=∠．39．（2021·四川南充市·中考真题）如图，90BAC ∠=︒，AD 是BAC ∠内部一条射线，若AB AC =，BE AD ⊥于点E ，CF AD ⊥于点F ．求证：AF BE =．40．（2021·浙江中考真题）已知在ACD △中，Р是CD 的中点，B 是AD 延长线上的一点，连结,BC AP ．（1）如图1，若90,60,,3ACB CAD BD AC AP ︒∠=︒∠===，求BC 的长． （2）过点D 作//DE AC ，交AP 延长线于点E ，如图2所示．若60,CAD BD AC ∠︒==，求证：2BC AP =．（3）如图3，若45CAD ∠=︒，是否存在实数m ，当BD mAC =时，2BC AP =？若存在，请直接写出m 的值；若不存在，请说明理由．。
2021中考数学 全等三角形 专题训练(含答案)
2021中考数学全等三角形专题训练一、选择题1. 如图，要用“SAS”证明△ABC≌△ADE，若已知AB＝AD，AC＝AE，则还需添加条件()A．∠B＝∠D B．∠C＝∠EC．∠1＝∠2 D．∠3＝∠42. 如图所示，∠C＝∠D＝90°，若要用“HL”判定Rt△ABC与Rt△ABD全等，则可添加的条件是()A．AC＝AD B．AB＝ABC．∠ABC＝∠ABD D．∠BAC＝∠BAD3. 下列三角形中全等的是()A．①②B．②③C．③④D．①④4. 如图，小强画了一个与已知△ABC全等的△DEF，他画图的步骤是：(1)画DE ＝AB；(2)在DE的同旁画∠HDE＝∠A，∠GED＝∠B，DH，EG相交于点F，小强画图的依据是()A．ASA B．SASC．SSS D．AAS5. 如图，点B，E在线段CD上，若∠C=∠D，则添加下列条件，不一定能使△ABC≌△EFD的是()A.BC=FD，AC=EDB.∠A=∠DEF，AC=EDC.AC=ED，AB=EFD.∠A=∠DEF，BC=FD6. 如图，有两个长度相同的滑梯靠在一面墙上，已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，且左边的滑梯与地面的夹角∠ABC＝35°，则右边的滑梯与地面的夹角∠DFE等于()A．60°B．55°C．65°D．35°7. 如图，平面上到两两相交的三条直线a，b，c的距离相等的点一共有()A．4个B．3个C．2个D．1个8. 现已知线段a，b(a<b)，∠MON=90°，求作Rt△ABO，使得∠O=90°，OA=a，AB=b.小惠和小雷的作法分别如下:小惠:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点A为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.小雷:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点O为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.则下列说法中正确的是()A.小惠的作法正确，小雷的作法错误B.小雷的作法正确，小惠的作法错误C.两人的作法都正确D.两人的作法都错误二、填空题9. 如图，△ABC≌△ADE，BC的延长线交DE于点G，∠CAB=54°，∠DAC=16°，则∠DGB=°.10. 如图，已知CD＝CA，∠1＝∠2，要使△ECD≌△BCA，需添加的条件是__________(只需写出一个条件)．11. 要测量河岸相对两点A，B之间的距离，已知AB垂直于河岸BF，先在BF 上取两点C，D，使CD＝CB，再过点D作BF的垂线段DE，使点A，C，E在一条直线上，如图，测出DE＝20米，则AB的长是________米．12. 如图，D为Rt△ABC中斜边BC上的一点，且BD=AB，过点D作BC的垂线，交AC于点E.若AE=12 cm，则DE的长为cm.13. 如图，要测量河岸相对两点A，B之间的距离，从B点沿与AB成90°角方向，向前走50米到C处立一根标杆，然后方向不变继续向前走50米到D处，在D 处转90°沿DE方向再走17米到达E处，这时A，C，E三点在同一直线上，则A，B之间的距离为________米．14. 如图，在△ABC中，∠ACB=120°，BC=4，D为AB的中点，DC⊥BC，则△ABC 的面积是.15. 如图，在Rt△ABC中，∠C=90°，E为AB的中点，D为AC上一点，BF∥AC，交DE的延长线于点F，AC=6，BC=5，则四边形FBCD周长的最小值是.三、解答题16. 已知：如图，点C，F在AD上，AF＝DC，∠B＝∠E，∠A＝∠D.求证：AB ＝DE.17. 已知，如图，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点．(1)求证：△ACE ≌△BCD ； (2)求证：2CD 2＝AD 2＋DB 2.18. 如图，A ，B两点分别在射线OM ，ON 上，点C 在∠MON 的内部且CA ＝CB ，CD ⊥OM ，CE ⊥ON ，垂足分别为D ，E ，且AD ＝BE . (1)求证：OC 平分∠MON ；(2)如果AO ＝10，BO ＝4，求OD 的长．2021中考数学 全等三角形 专题训练-答案一、选择题1. 【答案】C[解析] 还需添加条件∠1＝∠2.理由：∵∠1＝∠2，∴∠1＋∠EAC ＝∠2＋∠EAC ，即∠BAC ＝∠DAE. 在△ABC 和△ADE 中，⎩⎨⎧AB ＝AD ，∠BAC ＝∠DAE ，AC ＝AE ，∴△ABC ≌△ADE(SAS)．2. 【答案】A3. 【答案】A[解析] ①②符合证明三角形全等的判定方法“SAS”．③④中相等的角所对的边不相等，所以不可能全等．故选A.4. 【答案】A5. 【答案】C[解析] A .添加BC=FD ，AC=ED ，可利用“SAS”判定△ABC ≌△EFD ;B .添加∠A=∠DEF ，AC=ED ，可利用“ASA”判定△ABC ≌△EFD ; C .添加AC=ED ，AB=EF ，不能判定△ABC ≌△EFD ;D .添加∠A=∠DEF ，BC=FD ，可利用“AAS”判定△ABC ≌△EFD.6. 【答案】B [解析] 在Rt △ABC 和Rt △DEF 中，⎩⎨⎧BC ＝EF ，AC ＝DF ，∴Rt △ABC ≌Rt △DEF(HL)． ∴∠DEF ＝∠ABC ＝35°. ∴∠DFE ＝90°－35°＝55°.7. 【答案】A[解析] 如图，到三条直线a ，b ，c 的距离相等的点一共有4个．8. 【答案】A[解析] AB=b ，AB 是斜边，小惠作的斜边长是b 符合条件，而小雷作的是一条直角边长是b.故小惠的作法正确，小雷的作法错误.二、填空题9. 【答案】70 [解析] ∵△ABC ≌△ADE ，∴∠B=∠D.∵∠GFD=∠AFB ，∴∠DGB=∠F AB.∵∠F AB=∠DAC+∠CAB=70°，∴∠DGB=70°.10. 【答案】答案不唯一，如CE ＝CB [解析] 由∠1＝∠2，可得∠DCE ＝∠ACB ，又∵CD ＝CA ，∴添加CE ＝CB ，可根据“SAS”判定两个三角形全等．11. 【答案】2012. 【答案】12[解析] 如图，连接BE.∵D 为Rt △ABC 中斜边BC 上的一点，过点D 作BC 的垂线，交AC 于点E ，∴∠A=∠BDE=90°. 在Rt △DBE 和Rt △ABE 中，∴Rt △DBE ≌Rt △ABE (HL).∴DE=AE.∵AE=12 cm ，∴DE=12 cm .13. 【答案】17[解析] 在△ABC 和△EDC 中，⎩⎨⎧∠ABC ＝∠EDC ＝90°，BC ＝DC ，∠ACB ＝∠ECD ，∴△ABC ≌△EDC(ASA)． ∴AB ＝ED ＝17米．14. 【答案】8[解析]∵DC ⊥BC ，∴∠BCD=90°. ∵∠ACB=120°， ∴∠ACD=30°.延长CD 到H 使DH=CD ， ∵D 为AB 的中点， ∴AD=BD.在△ADH与△BDC中，∴△ADH ≌△BDC (SAS)， ∴AH=BC=4，∠H=∠BCD=90°. ∵∠ACH=30°， ∴CH=AH=4，∴CD=2，∴△ABC 的面积=2S △BCD =2××4×2=8.15. 【答案】16 [解析] ∵BF ∥AC ，∴∠EBF=∠EAD. 在△BFE 和△ADE 中，∴△BFE ≌△ADE (ASA).∴BF=AD.∴BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD. ∵当FD ⊥AC 时，FD 最短，此时FD=BC=5， ∴四边形FBCD 周长的最小值为5+11=16.三、解答题16. 【答案】证明：∵AF ＝DC ，∴AC ＝DF.在△ABC 和△DEF 中，⎩⎨⎧∠A ＝∠D ，∠B ＝∠E ，AC ＝DF ，∴△ABC ≌△DEF(AAS)．∴AB ＝DE.17. 【答案】13证明：(1)∵△ACB 和△ECD 都是等腰直角三角形，∴CD ＝CE ，AC ＝BC ，∠ECD ＝∠ACB ＝90°，∴∠ECD －∠ACD ＝∠ACB －∠ACD ，即∠ACE ＝∠BCD ，(1分) 在△ACE 与△BCD 中，⎩⎨⎧EC ＝DC∠ACE ＝∠BCD AC ＝BC，(3分) ∴△ACE ≌△BCD(SAS )．(4分) (2)∵△ACE ≌△BCD ，∴AE ＝BD ，∠EAC ＝∠B ＝45°，(6分) ∴∠EAD ＝∠EAC ＋∠CAD ＝90°， 在Rt △EAD 中，ED 2＝AD 2＋AE 2， ∴ED 2＝AD 2＋BD 2，(8分) 又ED 2＝EC 2＋CD 2＝2CD 2， ∴2CD 2＝AD 2＋DB 2.(10分)18. 【答案】解：(1)证明：∵CD ⊥OM ，CE ⊥ON ， ∴∠CDA ＝∠CEB ＝90°.在Rt △ACD 与Rt △BCE 中，⎩⎨⎧CA ＝CB ，AD ＝BE ，∴Rt △ACD ≌Rt △BCE(HL)． ∴CD ＝CE.又∵CD ⊥OM ，CE ⊥ON ，∴OC 平分∠MON. (2)在Rt △ODC 与Rt △OEC 中，⎩⎨⎧CD ＝CE ，OC ＝OC ，∴Rt △ODC ≌Rt △OEC. ∴OD ＝OE. 设BE ＝x.∵BO ＝4，∴OE ＝OD ＝4＋x. ∵AD ＝BE ＝x ，∴AO ＝OD ＋AD ＝4＋2x ＝10. ∴x ＝3.∴OD ＝4＋3＝7.。
全等三角形知识点演练(5大核心考点,91题)讲练)2023年中考数学一轮大单元复习
专题4.3 全等三角形考点1：全等形和全等三角形性质例1．（1）（2022秋·江苏连云港·八年级校考阶段练习）下列图标中，不是由全等图形组合成的是（）A．B．C．D．（2）（2023秋·浙江台州·八年级统考期末）如图，△ABC≌△DEF，且∠A=55°，∠B=75°，则∠F=______°．（3）（2022秋·湖南岳阳·八年级校考期中）如图，△ABC≌△DEC，点B、C、D在同一直线上，且BD=12，AC=7，则CE长为____________．知识点训练1．（2023秋·河北邢台·八年级统考期末）与下图全等的图形是（）A．B．C．D．2．（2020秋·江苏常州·八年级常州市清潭中学校考期中）找出下列各组图中的全等图形（）A．②和⑥B．②和⑦C．③和④D．⑥和⑦3．（2022秋·福建龙岩·八年级统考期末）如图，△DBC≌△ECB，且BE与CD相交于点A，下列结论错误的是（）A．BE=CD B．AB=ACC．∠D=∠E D．BD=AE4．（2023秋·四川自贡·八年级统考期末）如图所示，△ABC≌△AEF，∠B=∠E，有以下结论：①AC=AE；②EF=BC；③∠EAB=∠FAC；④∠EFA=∠AFC．其中正确的个数是（）5．（河北省唐山市2022-2023学年八年级上学期期末考试数学试题）如图，△ABC≌△DEC，点B，C，D在同一条直线上，且CE=1，CD=3，则BD的长是（）A．1.5B．2C．3.5D．46．（2023秋·四川南充·八年级统考期末）如图，点A，E，C在同一直线上，△ABC≌△DEC，AE=3，CD=8，则BC的长为（）A．3B．5C．8D．117．（2023秋·天津·八年级统考期末）如图，已知△ABC≌△DEF，CD平分∠BCA，DF与BC交于点G．若∠A=26°，∠CGF=83°，则∠E的度数是（）A．34°B．36°C．38°D．40°8．（2022秋·河南许昌·八年级统考期中）如图所示的图案是由全等的图形拼成的，其中AD=0.8，BC=1.6，则AF=（）9．（2022秋·山东菏泽·八年级统考期中）下列说法正确的是（）A．形状相同的两个三角形全等B．三个角都分别相等的两个三角形全等C．完全重合的两个三角形全等D．所有的等边三角形全等10．（2022秋·山东烟台·七年级统考期中）下列说法：①角是轴对称图形；②等腰三角形有三条对称轴；③关于某直线成轴对称的两个三角形全等；④两个全等三角形一定关于某条直线成轴对称．其中正确的个数是（）A．1个B．2个C．3个D．4个11．（2022秋·江苏宿迁·八年级统考期中）如图所示的网格是由9个相同的小正方形拼成的，图形的各个顶点均为格点，则∠1−∠2−∠3的度数为（）．A．30°B．45°C．55°D．60°12．（2023·福建南平·统考一模）如图，在△ABC中，∠BAC=135°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E．当点A、D、E在同一条直线上时，下列结论不正确．．．的是（）A．△ABC≌△DEC B．AE=AB+CDC．AD=√2AC D．AB⊥AE13．（2021秋·陕西商洛·八年级统考期末）在平面直角坐标系内，点O为坐标原点，A(−4,0)，B(0,3)．若在该坐标平面内有一点P（不与点A、B、O重合）为一个顶点的直角三角形与Rt△ABO全等，且这个以点P 为顶点的直角三角形与Rt△ABO有一条公共边，则所有符合条件的三角形个数为（）A．3个B．4个C．6个D．7个14．（2023秋·云南曲靖·八年级统考期末）如图，在平面直角坐标系中，点A的坐标为(3,0)，点B的坐标为(0,6)，点C在x轴上运动（不与点A重合），点D在y轴上运动（不与点B重合），当以点C、O、D为顶点的三角形与△AOB全等时，则点D的坐标为______．15．（2023秋·江苏镇江·八年级统考期末）如图，△AOD≌△BOC，∠A=30°，∠C=50°，∠AOC=150°，则∠COD=______°．16．（2023秋·四川南充·八年级统考期末）如图，△ABC绕点C旋转得到△DEC，点E在边AB上，若∠B=75°，则∠ACD的度数是_________．考点2：全等三角形的判定及应用例2．（1）（2023秋·山东威海·七年级统考期末）为了测量湖的宽度AB，小明同学先从A点走到点O处，再继续向前走相同的距离到达点C（即OC=OA），然后从点C沿与AB平行的方向，走到与点O，B共线的点D处，测量C，D间的距离就是湖的宽度．下列可以判断△OCD≌△OAB的是（）A．SSS B．SSA C．SAS D．ASA（2）（2023秋·黑龙江齐齐哈尔·八年级统考期末）如图，已知∠CAE=∠DAB，AC=AD，请你再添加一个条件：___________，使△ABC≌△AED．（3）（2023秋·江苏徐州·八年级统考期末）根据下列条件，能确定△ABC（存在且唯一）的是（）A．AB=2，BC=3，AC=6B．AC=4，BC=3，∠A=60°C．AB=5，BC=3，∠B=30°D．∠A=45°，∠B=45°，∠C=90°（4）（2023秋·广东汕头·八年级统考期末）如图，在△ABC中，∠ACB=65°，∠BAC=70°，AD⊥BC于点D，BM⊥AC于点M，AD与BM交于点P，则∠BPC=______．例3（2022秋·浙江宁波·八年级校考期末）如图，在Rt△ABC中，AB=BC，∠ABC=90°，BO⊥AC于点O，P是OC的中点，D是BC延长线上一点，满足PB=PD．(1)求证∠1=∠2；(2)探究CD与AP之间的数量关系，并给出证明．例4．（2023秋·黑龙江齐齐哈尔·八年级统考期末）综合与实践【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图（1），△ABC中，AB=8，AC=6，求BC边上的中线AD的取值范围，经过组内合作交流．小明得到了如下的解决方法：延长AD到点E，使DE=AD请根据小明的方法思考：(1)由已知和作图得到△ADC≌△EDB的理由是（）A．SSS B．SAS C．AAS D．HL(2)求得AD的取值范围是___________．【感悟】解题时，条件中若出现“中点”、“中线”字样，可以考虑倍长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【问题解决】(3)如图（2），AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF．求证：AC=BF．知识点训练1．（2022秋·浙江温州·八年级校考期中）如图，在Rt△ABC中，∠ACB=90∘,∠ABC=25∘，O为斜边中点，将线段OA绕点O逆时针旋转a(0∘<α<90∘)至OP，若CB=CP，则α的值为（）A．80∘B．65∘C．50∘D．40∘2．（2023秋·山东威海·七年级统考期末）如图，△ABC和△BDE都是等边三角形，点A，D，E在同一条直线上，BE=2，CE=4，则AE=（）A．6B．5C．8D．73．（海南省海口市（部分校）2022-2023学年八年级上学期期末检测数学试题（A））如图，直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为3，等腰直角△ABC的三个顶点A、B、C分别在直线l2、l1、l3上，∠ACB=90°，则△ABC的面积为（）D．25A．10B．12C．2524．（2022秋·黑龙江双鸭山·八年级统考期末）如图所示的网格是由9个相同的小正方形拼成的，图形的各个顶点均为格点，则∠2+∠3的度数为（）A．30°B．45°C．55°D．60°5．（2022秋·安徽黄山·八年级统考期末）如图，已知等边△ABC和等边△BPE，点P在BC的延长线上，EC的延长线交AP于点M，连接BM，有下列结论：①AP=CE；②∠PME=60°；③MB平分∠AME；④AM+MC=BM，其中正确的结论是（）A．①②③B．①②④C．①③④D．①②③④6．（2022秋·山西吕梁·八年级统考期末）如图，点E，F在线段AC上，AE=CF，AD⊥DF，CB⊥BE，要根据“HL”证明Rt△ADF≌Rt△CBE，则还需添加的一个条件是（）A．AF=CE B．∠A=∠C C．AD=CB D．AD∥BC7．（2023·全国·九年级专题练习）如图，点O为△ABC的内心，∠B=60°，BM≠BN，点M，N分别为AB，BC上的点，且OM=ON．甲、乙、丙三人有如下判断：甲：∠MON=120°；乙：四边形OMBN的面积为定值；丙：当MN⊥BC时，△MON的周长有最小值．则下列说法正确的是（）A．只有甲正确B．只有乙错误C．乙、丙都正确D．只有丙错误8．（2023秋·浙江台州·八年级统考期末）如图，AB与CD相交于点O，且OA=OB，添加下列选项中的一个条件，不能判定△AOC和△BOD全等的是（）A．OC=ODB．∠A=∠BC．AC=BDD．AC∥BD9．（2023秋·浙江台州·八年级统考期末）如图，射线OC为∠AOB的平分线，点M，N分别是边OA，OB上的两个定点，且OM<ON，点P在OC上，满足PM=PN的点P的个数有（）A．0个B．1个C．2个D．无数个10．（2023秋·河南新乡·八年级统考期末）在△ABC和△DEF中，已知AB=DE，∠A=∠D，下列条件：①AC= DF；②∠B=∠E；③∠C=∠F；④BC=EF．其中一定能判定△ABC≌△DEF的个数为（）A．1B．2C．3D．411．（2022秋·四川广安·八年级统考期末）如图，AB=DC，若要用“SSS”证明△ABC≌△DCB，需要补充一个条件，这个条件是__________．12．（2022秋·福建莆田·八年级统考期末）数学社团活动课上，甲乙两位同学玩数学游戏．游戏规则是：两人轮流对△ABC及△A′B′C′的对应边或对应角添加一组等量条件（点A′，B′，C′分别是点A，B，C的对应点），某轮添加条件后，若能判定△ABC与△A′B′C′全等，则当轮添加条件者失败，另一人获胜．1甲AB=A′B′=2cm2乙∠A=∠A′=35°3甲…上表记录了两人游戏的部分过程，则下列说法正确的是___________．（填写所有正确结论的序号）①若第3轮甲添加∠C=∠C′=45°，则甲获胜；②若第3轮甲添加BC=B′C′=3cm，则甲必胜；③若第2轮乙添加条件修改为∠A=∠A′=90°，则乙必胜；④若第2轮乙添加条件修改为BC=B′C′=3cm，则此游戏最多4轮必分胜负．13．（2023秋·山东淄博·七年级统考期末）如图，点C，E，B，F在同一条直线上，AB=DE，AC=DF，BF=CE．说明AC∥DF．14．（2023秋·江苏南京·八年级统考期末）如图AB=AD,CB=CD,AC,BD相交于点E．(1)求证△ABC≅△ADC；(2)求证BE=DE．15．（2022秋·山西吕梁·八年级统考期末）如图，△ABC是等边三角形，点D，E分别在BC，CA的延长线上，且CD=AE．求证：∠D=∠E．16．（2023秋·广东汕头·八年级统考期末）如图，已知点O在等边△ABC的内部，∠AOB=105°，∠BOC=α，以OC为边作等边△COD，连接AD．(1)求证：AD=BO；(2)当α=150∘时，试判断△AOD的形状，并说明理由；17．（2023秋·江苏南京·八年级统考期末）如图，在四边形ABCD中，连接BD，AB∥CD，且AB=CD．(1)求证：△ABD≅△CDB；(2)若AB=BD，∠ABD=48°，求∠C的度数．18．（2023秋·浙江宁波·八年级校考期末）如图，在四边形ABCD中，P为CD边上的一点，BC∥AD．AP、BP 分别是∠BAD、∠ABC的角平分线．(1)若∠BAD=70°，则∠ABP的度数为_______，∠APB的度数为____________；(2)求证：AB=BC+AD；(3)设BP=3a，AP=4a，过点P作一条直线，分别与AD，BC所在直线交于点E、F，若AB=EF，直接写出AE的长（用含a的代数式表示）考点3：角平分线性质定理和逆定理例5.（2023秋·广东汕头·八年级统考期末）如图，DE⊥AB于点E，DF⊥AC于点F，若BD=CD,BE=CF．(1)求证：AD 平分∠BAC ；(2)请猜想AB +AC 与AE 之间的数量关系，并给予证明．例6.（2022秋·湖北武汉·八年级校考期末）如图，在△ABC 中，E 是BC 中垂线上一点，EM ⊥AB 于M ，EN ⊥AC 于N ，BM =CN ．求证：AE 平分∠BAC ．知识点训练1．（2022秋·贵州铜仁·九年级统考期中）如图，在平面直角坐标系中，△OAB 的顶点B 的坐标为(6,0)，OC 平分∠AOB 交AB 于点C ，反比例函数y =k x (x >0)的图象经过点A ，C ．若S △AOC :S △BOC =2:3，则k 的值为（ ）A ．5√716B ．45√716C ．454D ．916 2．（2023秋·山东济宁·八年级统考期末）如图，Rt △ABC 中，∠C =90°，∠ABC =60°，以顶点B 为圆心、适当长为半径作弧，在边BC 、BA 上截取BE 、BD ；然后分别以点D 、E 为圆心、以大于DE 的长为半径作弧，两弧在∠CBA 内交于点F ；作射线BF 交AC 于点G ．若AC =6，P 为边AB 上一动点，则GP 的最小值为（ ）A．3B．2C．1D．无法确定3．（2023秋·山东淄博·七年级统考期末）如图，已知AB=AC，∠A=36°，AB的垂直平分线MD交AC于点D，AB于点M，以下结论：①△BCD是等腰三角形；②BD是△ACB的角平分线；③△BCD的周长C△BCD=AC+ BC；④△ADM≌△BCD．正确的有（）A．①③B．①②C．①②③D．③④4．（2023秋·黑龙江牡丹江·八年级统考期末）如图，已知△ABC和△ADE都是等腰直角三角形，∠BAC=∠EAD=90°，BD，CE交于点F，连接AF，下列结论：①BD=CE；②∠AEF=∠ADF；③BD⊥CE；④AF 平分∠CAD；⑤∠AFE=45°，其中结论正确的序号是（）A．①②③④B．①②④⑤C．①③④⑤D．①②③⑤5．（2022秋·福建泉州·八年级统考期末）小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（）A．角的内部到角两边距离相等的点在这个角的平分线上．B．角平分线上的点到角两边的距离相等．C．三角形三个内角的平分线交于同一个点．D．三角形三个内角的平分线的交点到三条边的距离相等．6．（2023秋·河北邢台·八年级统考期末）如图，在△ABC中，∠BAC=60°，角平分线BE，CD相交于点P，若AP=4，AC=6，则S△APC=（）．A．4B．6C．12D．247．（2023秋·江苏泰州·八年级统考期末）已知，如图，△ABC中，∠ABC=48°，∠ACB=84°，点D、E分别在BA、BC延长线上，BP平分∠ABC，CP平分∠ACE，连接AP，则∠PAC的度数为（）A．45°B．48°C．60°D．66°8．（2023秋·河北沧州·八年级统考期末）如图，在△AOB和△COD中，OA=OB,OC=OD,OA<OC,∠AOB=∠COD=108∘，连接AC，BD交于点M，连接OM．甲、乙、丙三人的说法如下，下列判断正确的是（）甲：AC=BD；乙：∠CMD>∠COD；丙：MO平分∠BMCA．乙错，丙对B．甲和乙都对C．甲对，丙错D．甲错，丙对9．（2023秋·重庆大足·八年级统考期末）如图，△ABC的三边AC、BC、AB的长分别是8、12、16，点O是△ABC三条角平分线的交点，则S△OAB:S△OBC:S△OAC的值为（）A．4:3:2B．5:3:2C．2:3:4D．3:4:510．（2022秋·甘肃庆阳·八年级统考期中）庆阳市是传统的中药材生产区，优越的地理气候条件形成了较独特的资源禀赋，孕育了丰富的中药植物资源和优良品种，素有“天然药库”“中药之乡”的美称．如图，三条公路把A、B、C三个盛产中药材的村庄连成一个三角形区域，此地区决定在这个三角形区域内修建一个中药材批发市场，要使批发市场到三条公路的距离相等，则这个批发市场应建在（）A．三角形的三条中线的交点处B．三角形的三条角平分线的交点处C．三角形的三条高的交点处D．以上位置都不对11．（2022秋·海南海口·八年级校联考期末）如图，在△ABC中，∠A=90°，BD平分∠ABC，BC=12，AD=4，则△DBC的面积为__________．12．（2023·湖南衡阳·校考一模）如图所示，点O在一块直角三角板ABC上（其中∠ABC=30°），OM⊥AB于点M，ON⊥BC于点N，若OM=ON，则∠ABO=_______度．13．（2023秋·湖北省直辖县级单位·八年级统考期末）如图，△ABC与△BDE都为等边三角形，连接AE与CD，延长AE交CD于点F，连接FB．给出下面四个结论：①AE=CD；②∠AFC=60°；③BF平分∠EBD；④FB 平分∠EFD.其中所有正确结论的序号是__________．14．（2023春·浙江金华·八年级浙江省义乌市后宅中学校考阶段练习）已知：OP平分∠MON，点A，B分别在边OM，ON上，且∠OAP+∠OBP=180°．(1)如图1，当∠OAP=90°时，求证：OA=OB；(2)如图2，当∠OAP<90°时，作PC⊥OM于点C．求证：①PA=PB；②请直接写出OA，OB，AC之间的数量关系．15．（2022春·广东茂名·八年级统考期中）如图，在Rt△ABC中，∠A=90°，∠B=30°，CM平分∠ACB交AB 于点M，过点M作MN∥BC交AC于点N，若AN=1，求BC的长．考点4：线段垂直平分线性质定理和逆定理例7. (1)（2023秋·浙江宁波·八年级宁波市第七中学校考期末）如图，△ABC中，AB<AC<BC，如果要使用尺规作图的方法在BC上确定一点P，使PA＋PB=BC，那么符合要求的作图痕迹是（）A．B．C．D．(2)（2023秋·云南曲靖·八年级统考期末）如图，在△ABC中，∠BAC=110°，EF是边AB的垂直平分线，垂足为E，交BC于F．MN是边AC的垂直平分线，垂足为M，交BC于N．连接AF、AN则∠FAN的度数是（）A．70B．55C．40D．30(3)（2022秋·新疆乌鲁木齐·八年级校考期末）电信部门要再S区修建一座手机信号发射塔，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条高速公路OC，OD的距离也必须相等，则发射塔应建在（）A．∠COD的平分线上任意某点处B．线段AB的垂直平分线上任意某点处C．∠COD的平分线和线段AB的交点处D．∠COD的平分线和线段AB垂直平分线的交点处例8.（2023春·重庆沙坪坝·八年级重庆南开中学校考开学考试）如图，在△ABC中，EF是AB的垂直平分线，AD⊥BC于点D，且D为CE的中点．(1)求证：BE=AC；(2)若∠C=70°，求∠BAC的度数．知识点训练1．（2022秋·海南海口·八年级校联考期末）如图，在△ABC中，DE垂直平分BC，若AB=6，AC=8，则△ABD 的周长等于（）A．11B．13C．14D．162．（2023秋·河南南阳·八年级统考期末）如图，等腰△ABC的底边BC长为6，面积是24，E为腰AB的垂直平分线MN上一动点．点D为BC的中点，则△BDE的周长的最小值为（）A．6B．8C．10D．113．（2023秋·福建泉州·八年级校联考期末）如图，根据尺规作图的痕迹，计算∠α的度数为（）A．56∘B．68∘C．28∘D．34∘4．（2023秋·山东东营·八年级统考期末）如图，平行四边形ABCD的对角线AC、BD交于点O，DE平分∠ADCAB，连接OE．下列结论：①S▱ABCD=AD⋅BC；②DB平分∠CDE；③AO=交AB于点E，∠BCD=60°，AD=12DE；④OE垂直平分BD．其中正确的个数有（）A．1个B．2个C．3个D．4个5．（2022秋·河北石家庄·八年级统考期末）如图，在△ABC中，AB=AC，尺规作图：（1）分别以B，C为圆心，BC长为半径作弧，两弧交于点D；（2）连接AD，BD，CD，AD与BC交于点E，则下列结论中错误的是（）A．△ABD≌△ACD B．△DBE≌△DCEC．△BCD是等边三角形D．BC垂直平分AD6．（2023秋·黑龙江牡丹江·八年级统考期末）如图，在△ABC中，∠ACB=90°，∠A=75°，DE垂直平分AB，交AB于点D，交BC于点E，若BE=8cm，则AC为______cm．7．（2023秋·重庆万州·八年级统考期末）如图，在△ABC中，边AC的垂直平分线交BC于点D，交AC于点E，连接AD，若AD是∠BAC的角平分线，且AB=AD时，则∠B=___________°．8．（2023秋·山东淄博·七年级统考期末）如图，已知AB是线段CD的垂直平分线，垂足为点F．E是AB上的一点，∠CEF=30°，CF=2．试求△CED的周长．9．（2022秋·山西吕梁·八年级统考期末）如图，在△ABC中，AB=BC，EF是AB的垂直平分线，交AB于点E，交BC于点F．(1)按要求作图：作∠ABC的平分线BD，交AC于点D，交EF于点O，连接OA，OC（尺规作图，保留痕迹，不写作法）；(2)求证：点O在BC的垂直平分线上；(3)若∠CBD=20°，求∠COF的度数．10．（2023秋·黑龙江齐齐哈尔·八年级统考期末）如图，∠AOB=30°，M，N分别是射线OA,OB上的动点，OP平分∠AOB，OP=9，则△PMN的周长的最小值为（）C．6D．27A．9B．9211．（2022秋·山东临沂·八年级校考期末）.如图，电信部门要在S区修建一座电视信号发射塔．按照设计要求，发射塔到两个城镇A，B距离必须相等，到两条高速公路m和n的距离也必须相等．发射塔应修建在什么位置？在图上标出它的位置．（保留作图痕迹）12．（2023·全国·九年级专题练习）如图，∠HAB=30°，点B与点C关于射线AH对称，连接AC．D点为射线AH 上任意一点，连接CD．将线段CD绕点C顺时针旋转60°，得到线段CE，连接BE．(1)求证：直线EB是线段AC的垂直平分线；(2)点D是射线AH上一动点，请你直接写出∠ADC与∠ECA之间的数量关系．13．（2023秋·山西运城·九年级统考期末）综合与实践问题情境：课堂上老师展示了一张直角三角形纸片．请同学们进行折纸活动，已知在Rt△ABC中．∠ACB=90°，点D、F分别是BC、AB上的一点．连接DF．(1)如图1．小红将△BDF 沿直线DF 折叠，点B 恰好落在BC 上点E 处，若S △BDF S 四边形ACEF=17，则DEDC的值______．(2)如图2，小明将△BDF 沿直线DF 折叠，点B 落在AC 上点E 处，若FE ⊥AC ，求证：四边形BDEF 是菱形； (3)如图3．小亮将△BDF 沿直线DF 折叠，点B 落在AC 延长线上点E 处，且EF 平分∠AED ，若AC =3，BC =4，求CE 的长．14．（2023秋·江苏南京·八年级统考期末）（1）如图1，在△ABC 中，∠A =30°，∠C =90°．求证BC =12AB ．①补全证明过程．证明：如图2，取AB 中点D ，连接CD ． ∴BD =AD =12AB ．在△ABC 中，∠C =90°， ∴______； ∴CD =BD ． 又∠A =30°，∴∠B =90°−∠A =60°． ∴△BCD 为______三角形． ∴BC =BD =12AB ．②请用文字概括①所证明的命题：____________．（2）如图3，某市三个城镇中心D，E，F恰好分别位于一个等边三角形的三个顶点处，在三个城镇中心之间铺设通信光缆，以城镇D为出发点设计了三种连接方案：方案1：DE+EF；方案2：DG+EF（G为EF的中点）；方案3：OD+OE+OF（O为△DEF三边的垂直平分线的交点）．①设DE=6，通过计算，比较三种连接方案中铺设的光缆长度的长短；②不计算，比较三种连接方案中铺设的光缆长度的长短，并说明理由．15．（2023秋·河南洛阳·八年级统考期末）我们已经知道线段是轴对称图形，线段的垂直平分线是线段的对称轴，如图1，直线MN是线段AB的垂直平分线，P是MN上任一点，连接PA、PB，将线段AB沿直线MN对称，我们发现PA与PB完全重合，由此即有：线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等．解答下列问题：(1)请你结合图形把已知和求证补充完整，并写出证明过程．已知：如图1，MN⊥AB，垂足为点C，______，点P是直线MN上的任意一点．求证：______．(2)证明：如图2，CD是线段AB垂直平分线，则∠CAD与∠CBD有何关系？请说明理由．考点5：全等三角形的综合问题例9.（2023秋·河南南阳·八年级统考期末）如图，在△ABC中，∠ACB=90°，CE⊥AB于点E，AD=AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G．(1)求证：DF∥BC；(2)若AE=6，CE=8，求线段GF的长．例10.（2022秋·湖北黄冈·八年级统考期末）已知OM是∠AOB的平分线，点P是射线OM上一定点，点C、D分别在射线OA、OB上，连接PC、PD．(1)如图①，当PC⊥OA，PD⊥OB时，则PC与PD的数量关系是___________；(2)如图②，点C、D在射线OA、OB上滑动，且∠AOB=90∘，当PC⊥PD时，PC与PD在（1）中的数量关系还成立吗？请说明理由．(3)在问题（2）中，若OC+OD=6，则四边形ODPC的面积S是否为定值？若是，请求出该定值，若不是，请说明理由．知识点训练1．（2022秋·河南商丘·八年级统考期中）如图，在△ABC中，∠ABC=90°，D,E分别为边AC,BC上一点，连接BD,DE．已知AB=BE,AD=DE．(1)求证：BD平分∠ABC；(2)若∠A=55°，求证：∠CDE=14∠ADB．2．（2023秋·湖北荆州·八年级统考期末）如图，在△ABC中，BC=2AB，D是AC上一点，∠ABD=20°，E 是BD上一点，EA⊥AB，EB=EC．(1)求证：BD平分∠ABC；(2)求∠DEC的度数．3．（2023秋·重庆长寿·九年级统考期末）在图（1）至图（2）中，直线MN与线段AB相交于点O，∠1=∠2=45°．(1)如图（1），若AO=OB，请写出AO与BD的数量关系和位置关系；(2)将图（1）中的MN绕点O顺时针旋转得到图（2），其中AO=OB．求证：AC=BD，AC⊥BD．4．（2023秋·重庆万州·八年级统考期末）小明在物理课上学习了发声物体的振动实验后，对其作了进一步的探究：在一个支架的横杆点O处用一根细绳悬挂一个小球A，小球A可以自由摆动，如图，OA表示小球静止时的位置．当小明用发声物体靠进小球时，小球从OA摆到OB位置，此时过点B作BD⊥OA于点D，当小球摆到OC位置时，OB与OC恰好垂直（图中的A、B、O、C在同一平面上），过点C作CE⊥OA于点E，测得CE=15cm,AD=2cm．(1)试说明OE=BD；(2)求DE的长．5．（2022秋·海南海口·八年级校联考期末）如图1，在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，∠MDN=90°，将∠MDN绕点D顺时针旋转，它的两边分别交AB、AC于点E、F．(1)求证：△BDE≌△ADF；(2)如图2，若DM=DN，连接BM、NA，求证：BM=AN．6．（2023秋·江苏宿迁·八年级统考期末）如图，已知AC平分∠BAF，CE⊥AB于点E，CF⊥AF于点F，且BC= DC．(1)求证：BE=DF；(2)若AB=21，AD=9，求DF的长．7．（2023秋·广西南宁·九年级统考期末）如图，将矩形ABCD绕点B旋转得到矩形BEFG，点E在AD上，延长DA交GF于点H.(1)求证：△ABE≅△FEH；(2)连接BH，若∠EBC=30°，求∠ABH的度数．8．（2023秋·山东威海·七年级统考期末）在四边形ABDE中，点C是BD边的中点．(1)如图①，AC平分∠BAE，∠ACE=90°，写出线段AE，AB，DE间的数量关系及理由；(2)如图②，AC平分∠BAE，EC平分∠AED，∠ACE=120°，写出线段AB，BD，DE，AE间的数量关系及理由．9．（2022秋·广西柳州·八年级统考期末）在平面直角坐标系中，点O为坐标原点，A(a,0)，B(0,b)，且a，b满足(a−3)2+|b−3|=0，连接AB．(1)求点A，B点的坐标；(2)如图1，动点C从点O出发，以1个单位/秒的速度沿y轴正半轴运动，运动时间为t秒(0<t<3)，连接AC，过点C作CD⊥AC，且CD=CA，点D在第一象限，请用含有t的式子表示点D的坐标；(3)在（2）的条件下，如图2，连接并延长DB交x轴于点E，连接AD和AB，过点B作线段BF交x轴于点F，使得∠OBF=∠DCB，已知此时点F的坐标为(−1,0)，求△ADE的面积．10．（2023秋·福建福州·八年级统考期末）在平面直角坐标系xOy中，点A(0,a)，B(b,0)，C(c,0)，点D在第四象限，其中a>0，b<0，c>0，∠BAC+∠BDC=180°，AC⊥CD．(1)如图1，求证：∠BAO=∠CBD；(2)若|a−c|+b2+6b+9=0，且AB=BD．①如图1，求四边形ACDB的面积；（用含a的式子表示）②如图2，BD交y轴于点E，连接AD，当E关于AD的对称点K落在x轴上时，求CK的长．。
湖南省201x年中考数学总复习 第四单元 三角形 课时训练20 全等三角形练习
全等三角形20全等三角形限时:30分钟夯实基础1.下列结论正确的是()A.形状相同的两个图形是全等图形B.全等图形的面积相等C.对应角相等的两个三角形全等D.两个等边三角形全等2.如图K20-1,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是()图K20-1A.∠B=∠E,BC=EFB.BC=EF,AC=DFC.∠A=∠D,∠B=∠ED.∠A=∠D,BC=EF3.如图K20-2,点A,E,F,D在同一直线上.若AB∥CD,AB=CD,AE=FD,则图中的全等三角形有()图K20-2A.1对B.2对C.3对D.4对4.在如图K20-3所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC有一条公共边且全等的所有格点三角形的个数是 ()图K20-3A.1B.2C.3D.45.如图K20-4,在五边形ABCDE中,有一正三角形ACD.若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为()图K20-4A.115°B.120°C.125°D.130°6.[xx·荆州]已知:∠AOB.求作:∠AOB的平分线.作法:如图K20-5,①以点O为圆心,适当长为半径画弧,分别交OA,OB于点M,N;②分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB内部交于点C;③画射线OC.射线OC即为所求.上述作图用到了全等三角形的判定方法,这个方法是.图K20-57.如图K20-6,AB∥CF,E为DF的中点,AB=10,CF=6,则BD= .图K20-68.[xx·哈尔滨]如图K20-7,已知△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE 与DC交于点M,BD与AC交于点N.(1)如图①,求证:AE=BD;(2)如图②,若AC=DC,在不添加任何辅助线的情况下,请直接写出图②中四对全等的直角三角形.图K20-79.如图K20-8,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.(1)求证:AB=CD;(2)若AB=CF,∠B=30°,求∠D的度数.图K20-8能力提升10.[xx·河北]已知:如图K20-9,点P在线段AB外,且PA=PB.求证:点P在线段AB的垂直平分线上.在证明该结论时,需添加辅助线,则作法不正确的是()图K20-9A.作∠APB的平分线PC交AB于点CB.过点P作PC⊥AB于点C且AC=BCC.取AB的中点C,连接PCD.过点P作PC⊥AB,垂足为C11.如图K20-10,已知△ABC三个内角的平分线交于点O,延长BA到点D,使AD=AO,连接DO.若BD=BC,∠ABC=54°,BCA的度数为.图K20-1012.[xx·娄底]如图K20-11,在等腰直角三角形ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°.若ED的长为m,则△BEF的周长是(用含m的代数式表示).图K20-1113.[xx·宜昌]如图K20-12①,已知AB=AC,D为∠BAC的平分线上一点,连接BD,CD;如图②,已知AB=AC,D,E为∠BAC 的平分线上两点,连接BD,CD,BE,CE;如图③,已知AB=AC,D,E,F为∠BAC的平分线上三点,连接BD,CD,BE,CE,BF,CF;…,依此规律,第n个图形中有全等三角形的对数是.图K20-12拓展练习14.[xx·滨州]如图K20-13,已知在△ABC中,∠A=90°,AB=AC,点D为BC的中点.(1)如图①,若点E,F分别为AB,AC上的点,且DE⊥DF,求证:BE=AF.(2)若点E,F分别为AB,CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.图K20-13参考答案1.B2.D3.C4.D5.C[解析] 在正三角形ACD中,AC=AD,∠ACD=∠ADC=∠CAD=60°.∵AB=DE,BC=AE,∴△ABC≌△DEA.∴∠B=∠E=115°,∠ACB=∠EAD,∠BAC=∠ADE.∴∠ACB+∠BAC=∠BAC+∠DAE=180°-115°=65°.∴∠BAE=∠BAC+∠DAE+∠CAD=65°+60°=125°.故选C.6.SSS7.48.解:(1)证明:∵△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,∴AC=BC,DC=EC.∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE.在△ACE和△BCD中,∴△ACE≌△BCD(SAS).∴AE=BD.(2)∵AC=DC,∴AC=CD=EC=CB.∴△ACB≌△DCE(SAS).由(1)可知,∠AEC=∠BDC,∠EAC=∠DBC,∴∠DOM=90°.∵∠AEC=∠CAE=∠CBD,∴△EMC≌△BNC(ASA).∴CM=CN.∴DM=AN,△AON≌△DOM(AAS).∵AB=DE,AO=DO,∴Rt△AOB≌Rt△DOE(HL).9.解:(1)证明:∵AB∥CD,. ∴∠B=∠C.又∵AE=DF,∠A=∠D,∴△ABE≌△DCF.∴AB=CD.(2)∵AB=CF,AB=CD,∴DC=CF.∴∠D=∠CFD.∵∠C=∠B=30°,∴∠D=75°.10.B11.42°12.m+2[解析] 如图所示,连接BD.在等腰直角三角形ABC中,点D是AC的中点,∴BD⊥AC.∴BD=AD=CD,∠DBC=∠A=45°,∠ADB=90°.∵∠EDF=90°,∴∠ADE=∠BDF.在△ADE和△BDF中,∴△ADE≌△BDF(ASA).∴AE=BF,DE=DF.在Rt△DEF中,DF=DE=m.∴EF=DE=m.∴△BEF的周长为BE+BF+EF=BE+AE+EF=AB+EF=2+m.13.[解析] 当有一点D时,有1对全等三角形;当有两点D,E时,有3对全等三角形;当有三点D,E,F时,有6对全等三角形;当有四点时,有10对全等三角形;…;当有n个点时,图中有对全等三角形.14.解:(1)证明:如图①,连接AD.①∵∠BDA=∠EDF=90°,∴∠BDE+∠EDA=∠EDA+∠ADF.∴∠BDE=∠ADF.∵D为BC的中点,△ABC是等腰直角三角形,∴BD=AD,∠B=∠DAC=45°,∴△BDE≌△ADF(ASA).∴BE=AF.(2)BE=AF.理由如下:如图②,连接AD.②. ∵∠BDA=∠EDF=90°,∴∠BDE+∠BDF=∠BDF+∠ADF.∴∠BDE=∠ADF.∵D为BC的中点,△ABC是等腰直角三角形,∴BD=AD,∠ABC=∠DAC=45°,∴∠EBD=∠FAD=180°-45°=135°.∴△BDE≌△ADF(ASA).∴BE=AF.如有侵权请联系告知删除，感谢你们的配合！如有侵权请联系告知删除，感谢你们的配合！。
2021年中考数学复习考点专项训练——全等三角形
2021中考数学复习考点专项训练——全等三角形一、选择题1. 如图所示，在∠AOB的两边上截取AO＝BO，OC＝OD，连接AD、BC交于点P，连接OP，则下列结论正确的是()①△APC≅△BPD②△ADO≅△BCO③△AOP≅△BOP④△OCP≅△ODPA.②③④B.①②③C.①②③④D.①③④2．如图，已知∠1＝∠2，要说明△ABD≌△ACD，还需从下列条件中选一个，错误的选法是（）A．∠ADB＝∠ADC B．∠B＝∠C C．DB＝DC D．AB＝AC3. 如图，已知在△ABC和△DEF中，∠A=∠D=90∘，则下列条件中不能判定△ABC和△DEF全等的是（）A.AB=DE,AC=DFB.∠C=∠F,∠B=∠EC.AB=DE,BC=EFD.∠C=∠F,BC=EF4．下列条件不可以判定两个直角三角形全等的是（）A．两条直角边对应相等B．两个锐角对应相等C．一条直角边和它所对的锐角对应相等D．一个锐角和锐角所对的直角边对应相等5.如图，已知△ABC≌△ADE若∠B=80°，∠C=30°，∠DAC=35°，则∠EAC的度数为( )A.40°B.35°C.30°D.25°6. 如图，∠ABC=∠ABD，还应补充一个条件，才能推出△ABC≅△ABD，补充下列其中一个条件后，不一定能推出△ABC≅△ABD的是( )A.AC=ADB.BC=BDC.∠CAB=∠DABD.∠ACB=∠ADB7. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，要说明∠D′O′C′=∠DOC，需要证明△D′O′C′≅△DOC，则这两个三角形全等的依据是()A.边边边B.边角边C.角边角D.角角边8.已知△ABC和△DEF，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②AB=DE，∠B=∠E，BC=EF；③∠B=∠E，BC=EF，∠C=∠F；④AB=DE，AC=DF，∠B=∠E其中能使△ABC≌△DEF的共有( )A.1组B.2组C.3组D.4组9.在△ABC和△A′B′C′中，已知∠A=∠A′，AB=A′B′，在下面判断中错误的是（）A、若添加条件AC=A′C′，则△ABC≌△A′B′C′B、若添加条件BC=B′C′，则△ABC≌△A′B′C′C、若添加条件∠B=∠B′，则△ABC≌△A′B′C′D、若添加条件∠C=∠C′，则△ABC≌△A′B′C′10．如图，已知△ABC≌△ADC，∠B＝30°，∠BAC＝23°，则∠ACD的度数为（）A．120°B．125°C．127°D．104°11. 如图①，已知∠ABC，用尺规作它的角平分线．如图②，步骤如下：第一步：以B为圆心，以a为半径画弧，分别交射线BA，BC于点D，E；第二步：分别以D，E为圆心，以b为半径画弧，两弧在∠ABC内部交于点P；第三步：画射线BP，射线BP即为所求．下列叙述不正确的是( )A.a>0B.作图的原理是构造SSS三角形全等C.由第二步可知，DP=EPDE的长D.b<1212.如图△ABC中，∠C=90°，AB=2BC，D为AB中点过点D作DE⊥AB交AC于点E，下列结论：①CE=DE；②AE=BC；③∠B=2∠A；④∠A=30°中正确个数为（）A、1个B、2个C、3个D、4个13. 如图，已知AD是△ABC的BC边上的高，下列能使△ABD≅△ACD的条件是( )A.AB=ACB.∠BAC=90∘C.BD=ACD.∠B=45∘14.工人师傅常用角尺平分一个任意角，做法是：如图在∠AOB的边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，得到∠AOB的平分线OP，做法中用到三角形全等的判定方法是（）A、SSSB、SASC、ASAD、HL15. 如图，AD是△ABC的角平分线，且AB:AC=√3:√2，则△ABD与△ACD的面积之比为（）A.3:2B.√3:√2C.2:3D.√2:√3二．填空题16. 如图，△ABC中，AB＝AC，D、E是BC边上两点，AD＝AE，BE＝6，DE＝4，则EC＝________．17. 如图，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，S△ABC＝7，DE＝2，AB＝4，则AC的长是________．18.如图，D为Rt△ABC斜边BC上的一点，且BD=BA，过点D作BC的垂线，交AC于点E。
中考数学一轮复习《全等三角形》练习题(含答案)
中考数学一轮复习《全等三角形》练习题（含答案）(建议答题时间：60分钟)基础过关1. 如图，点E，F在线段BC上，△ABF与△DCE全等，点A与点D，点B与点C是对应顶点，AF与DE交于点M，则∠DCE＝()A. ∠BB. ∠AC. ∠EMFD. ∠AFB第1题图第2题图2. (人教八上第44页11题改编)如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是()A. AB＝DEB. AC＝DFC. ∠A＝∠DD. BF＝EC3. 如图，△ABC中，AB＝AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等三角形的对数是()A. 1对B. 2对C. 3对D. 4对第3题图第4题图第5题图4. 注重开放探究(2017怀化)如图，AC＝DC，BC＝EC，请你添加一个适当的条件：____________________________，使得△ABC≌△DEC.5. 如图，AB∥CF，E为DF的中点，AB＝10，CF＝6，则BD＝________.6. 如图，在△ABC中，分别以AC、BC为边作等边三角形ACD和等边三角形BCE，连接AE、BD交于点O，则∠AOB的度数为________．第6题图7. (2017福建)如图，点B，E，C，F在一条直线上，AB＝DE，AC＝DF，BE＝CF，求证：∠A＝∠D.第7题图8. (2017武汉)如图，点C、F、E、B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．第8题图9. (2017南充)如图，DE⊥AB，CF⊥AB，垂足分别是点E、F，DE＝CF，AE＝BF，求证：AC∥BD.第9题图10. (2017重庆巴南区期中检测)如图，在四边形ABCD中，点E在对角线AC上，AB∥DE，∠ACB＝∠ADE，AB＝EA，求证：AC＝ED.第10题图11. (人教八上第44页4题改编)如图所示，已知∠1＝∠2，请你添加一个条件，证明：AB＝AC.(1)你添加的条件是________________；(2)请写出证明过程．第11题图12. (2017重庆一中期中考试)如图，AF∥DE，点B、C在线段AD上，且∠E＝∠F，连接FC、EB，延长EB交AF于点G.(1)求证：BE∥CF；(2)若CF＝BE，求证：AB＝CD.第12题图13. (2017苏州)如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O.(1)求证：△AEC≌△BED；(2)若∠1＝42°，求∠BDE的度数．第13题图14. (2017哈尔滨)已知，△ACB和△DCE都是等腰直角三角形，∠ACB＝∠DCE ＝90°，连接AE、BD交于点O.AE与DC交于点M，BD与AC交于点N.(1)如图①，求证：AE＝BD；(2)如图②，若AC＝DC，在不添加任何辅助线的情况下，请直接写出图②中四对全等的直角三角形．第14题图满分冲关1. (2017滨州)如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补．若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：(1)PM＝PN恒成立；(2)OM＋ON的值不变；(3)四边形PMON的面积不变；(4)MN的长不变，其中正确的个数为()A. 4B. 3C. 2D. 1第1题图第2题图2. (2018原创) 如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC 交ED的延长线于点F，若BC恰好平分∠ABF，AE＝2BF.给出下列四个结论：①DE＝DF；②DB＝DC；③AD⊥BC；④AC＝3BF，其中正确的结论共有()A. 4个B. 3个C. 2个D. 1个3. (2017新疆建设兵团)如图，在四边形ABCD中，AB＝AD，CB＝CD，对角线AC，BD相交于点O，下列结论中：①∠ABC＝∠ADC；②AC与BD互相平分；③AC，BD分别平分四边形ABCD的两组对角；④四边形ABCD的面积S＝12AC·BD，正确的是________．(填写所有正确结论的序号)第3题图4. (2017温州)如图，在五边形ABCDE中，∠BCD＝∠EDC＝90°，BC＝ED，AC ＝AD.(1)求证：△ABC≌△AED；(2)当∠B＝140°时，求∠BAE的度数．第4题图5. (2017荆门)如图，在Rt△ACB中，∠ACB＝90°，点D是AB的中点，点E是CD的中点，过点C作CF∥AB交AE的延长线于点F.(1)求证：△ADE≌△FCE；(2)若∠DCF＝120°，DE＝2，求BC的长．第5题图6. (2017齐齐哈尔)如图，在△ABC中，AD⊥BC于D，BD＝AD，DG＝DC，E，F分别是BG，AC的中点．(1)求证：DE＝DF，DE⊥DF；(2)连接EF，若AC＝10，求EF的长．第6题图7. (2017德阳)如图，在平行四边形ABCD中，E、F分别是AB、BC的中点，CE ⊥AB，垂足为E，AF⊥BC，垂足为F，AF与CE相交于点G.(1)证明：△CFG≌△AEG；(2)若AB＝4，求四边形AGCD的对角线GD的长．第7题图8. (2017北京)在等腰直角△ABC中，∠ACB＝90°，P是线段BC上一动点(与点B，C不重合)，连接AP，延长BC至点Q，使得CQ＝CP，过点Q作QH⊥AP于点H，交AB于点M.(1)若∠P AC＝α，求∠AMQ的大小(用含α的式子表示)；(2)用等式表示线段MB与PQ之间的数量关系，并证明．第8题图9. (2018原创)已知△ABC和△ADE都是等边三角形，点B，D，E在同一条直线上．(1)如图①，当AC⊥DE，且AD＝2时，求线段BC的长度；(2)如图②，当CD⊥BE时，取线段BC的中点F，线段DC的中点G，连接DF，EG，求证：DF＝EG.第9题图答案基础过关 1. A 2. C3. D 【解析】∵AB ＝AC ，D 为BC 中点，∴CD ＝BD ，∠BDO ＝∠CDO ＝90°，在△ABD 和△ACD 中，⎩⎨⎧AB ＝AC AD ＝AD BD ＝CD ，∴△ABD ≌△ACD (SSS )，∵EF 垂直平分AC ，∴OA ＝OC ，AE ＝CE ，在△AOE 和△COE 中，⎩⎨⎧OA ＝OCOE ＝OE AE ＝CE ，∴△AOE ≌△COE (SSS )； 在△BOD 和△COD 中，⎩⎨⎧BD ＝CD∠BDO ＝∠CDO OD ＝OD ，∴△BOD ≌△COD (SAS )；在△AOC和△AOB 中，⎩⎨⎧AC ＝ABOA ＝OA OC ＝OB，∴△AOC ≌△AOB (SSS )．4. AB ＝DE (答案不唯一)5. 4 【解析】∵AB ∥CF ，∴∠ADE ＝∠CFE ，∵E 是DF 的中点，∴DE ＝EF ，在△ADE 与△CFE 中，⎩⎨⎧∠ADE ＝∠CFEDE ＝FE∠AED ＝∠CEF，∴△ADE ≌△CFE (ASA )，∴AD ＝CF ，∵AB ＝10，CF ＝6，∴BD ＝AB －AD ＝10－6＝4.6. 120° 【解析】∵△ACD 和△BCE 均为等边三角形，∴∠DCA ＝∠BCE ＝60°，AC ＝DC ，BC ＝EC ，∴∠DCB ＝∠DCA ＋∠ACB ＝∠BCE ＋∠ACB ＝∠ACE ，∴△DCB ≌△ACE (SAS )，∴∠CDB ＝∠CAE ，∴∠AOB ＝∠DAO ＋∠ADO ＝∠DAC ＋∠CAE ＋∠ADC －∠CDB ＝∠ADC ＋∠DAC ＝120°.7. 证明：∵BE ＝CF ， ∴BC ＝EF ，在△ABC 和△DEF 中，⎩⎨⎧AB ＝DE AC ＝DF BC ＝EF，∴△ABC ≌△DEF (SSS )， ∴∠A ＝∠D .8. 解：CD ∥AB ，CD ＝AB . 证明： ∵CE ＝BF ， ∴CF ＝BE ，又∵∠CFD ＝∠BEA ，DF ＝AE ， ∴△CFD ≌△BEA (SAS )， ∴CD ＝AB ，∠C ＝∠B ， ∴CD ∥AB .9. 证明：∵DE ⊥AB ，CF ⊥AB ， ∴∠BED ＝∠AFC ＝90°， 又∵AE ＝BF ， ∴AE ＋EF ＝BF ＋EF ， ∴AF ＝BE .在△ACF 和△BDE 中，⎩⎨⎧AF ＝BE∠AFC ＝∠BED CF ＝DE，∴△ACF ≌△BDE (SAS )， ∴∠A ＝∠B ， ∴AC ∥BD .10. 证明：∵AB ∥DE ， ∴∠BAC ＝∠AED ，在△ABC 和△EAD 中，⎩⎨⎧∠ACB ＝∠ADE∠BAC ＝∠AED AB ＝EA，∴△ABC ≌△EAD (AAS )， ∴AC ＝ED .11. (1)解：∠B ＝∠C 或∠ADB ＝∠ADC 等；(2)证明：若添加的条件为∠B ＝∠C ，在△ABD 和△ACD 中，⎩⎨⎧∠B ＝∠C∠1＝∠2AD ＝AD，∴△ABD ≌△ACD (AAS )， ∴AB ＝AC ；若添加的条件为∠ADB ＝∠ADC ，在△ABD 和△ACD 中，⎩⎨⎧∠1＝∠2AD ＝AD ∠ADB ＝∠ADC，∴△ABD ≌△ACD (ASA )， ∴AB ＝AC .12. 证明：(1)∵AF ∥DE ， ∴∠E ＝∠AGE ， ∵∠E ＝∠F ， ∴∠F ＝∠AGE ， ∴BE ∥CF ； (2)∵AF ∥DE ∴∠A ＝∠D ，在△ACF 和△DBE 中，⎩⎨⎧∠A ＝∠D∠F ＝∠E CF ＝BE，∴△ACF ≌△DBE (AAS )， ∴AC ＝DB ， ∴AB ＝CD .13. (1)证明：∵AE 和BD 相交于点O ， ∴∠AOD ＝∠BOE ，在△AOD 和△BOE 中，∠A ＝∠B ， ∴∠BEO ＝∠2， 又∵∠1＝∠2， ∴∠1＝∠BEO ， ∴∠AEC ＝∠BED ，在△AEC 和△BED 中，⎩⎨⎧∠A ＝∠BAE ＝BE ∠AEC ＝∠BED，∴△AEC ≌△BED (ASA )； 解：(2)∵△AEC ≌△BED ， ∴EC ＝ED ，∠C ＝∠BDE ，在△EDC 中 ，∵EC ＝ED ，∠1＝42°， ∴∠C ＝∠EDC ＝69°， ∴∠BDE ＝∠C ＝69°.14. (1)证明：∵△ACB 和△DCE 均为等腰直角三角形，∠ACB ＝∠DCE ＝90°， ∴AC ＝BC ，DC ＝EC ，∠ACB ＋∠ACD ＝∠DCE ＋∠ACD ， ∴∠BCD ＝∠ACE ， ∴△ACE ≌△BCD (SAS )， ∴AE ＝BD ；(2)解：△ACB ≌△DCE ，△AON ≌△DOM ，△AOB ≌△DOE ，△NCB ≌△MCE . 满分冲关1. B 【解析】如解图，过点P 分别作OA 、OB 的垂线PC 、PD ，根据角平分线的性质可得PC ＝PD ，∵OP 一定，∴OC ＝OD .∵∠AOB 是定角，∠MPN 与∠AOB 互补，∴∠MPN 也为定角．∵∠CPD 与∠AOB 也互补，∴∠MPN ＝∠CPD ，∴∠MPC ＝∠NPD ，∴△MPC ≌△NPD (ASA )，∴CM ＝DN ，MP ＝NP .故(1)正确；∵OM ＋ON ＝OC ＋CM ＋OD －DN ，∴OM ＋ON ＝OC ＋OD ，∵OC ＝OD 为定长，∴OM ＋ON 为定长．故(2)正确；∵△MPC ≌△NPD ，∴S四边形MONP＝S △CMP ＋S四边形CONP＝S △NPD ＋S 四边形CONP ＝S 四边形CODP .∴四边形MONP 面积为定值．故(3)正确；∵Rt △MPC 中，MP 为斜边，CP 为直角边，∴可设MP ＝kCP ，∴PN ＝kDP ，∵∠MPN ＝∠CPD ，∴△MPN ∽△CPD ，其相似比为k ，∴MN ＝kCD ，当点M 与点C 重合，点N 和点D 重合时，MN ＝CD ，当点M 与点C 不重合，点N 与点D 不重合时，MN ≠CD ，∴MN 的长度在发生变化．故(4)错误．第1题解图2. A 【解析】∵BF ∥AC ，∴∠C ＝∠CBF ，∵BC 平分∠ABF ，∴∠ABC ＝∠CBF ，∴∠C ＝∠ABC ，∴AB ＝AC ，∵AD 是△ABC 的角平分线，∴BD ＝CD ，AD ⊥BC ，故②③正确，在△CDE 与△BDF 中，⎩⎨⎧∠C ＝∠CBF CD ＝BD ∠EDC ＝∠BDF，∴△CDE ≌△BDF (ASA )，∴DE ＝DF ，CE ＝BF ，故①正确；∵AE ＝2BF ，∴AC ＝3BF ，故④正确．故选A .3. ①④【解析】在△ABC 与△ADC 中，⎩⎨⎧AB ＝ADBC ＝DC AC ＝AC，∴△ABC ≌△ADC (SSS )，∴∠ABC ＝∠ADC ，故①正确；∵△ABC ≌△ADC ，∴∠BAC ＝∠DAC ，∠BCA ＝∠DCA ，∴AC 平分∠BAD 、∠BCD ，故③错误；又∵AB ＝AD ，∠BAC ＝∠DAC ，∴OB ＝OD ，∴AC ，BD 互相垂直，但不平分，故②错误；∵AC ，BD 互相垂重，∴四边形ABCD 的面积S ＝12AC ·BO ＋12AC ·OD ＝12AC ·BD .故④正确，综上所述，正确的结论是①④. 4. (1)证明：∵AC ＝AD ， ∴∠ACD ＝∠ADC ，∴∠BCD －∠ACD ＝∠EDC －∠ADC 即∠BCA ＝∠EDA ，在△ABC 与△AED 中，BC ＝ED ，∠BCA ＝∠EDA ，AC ＝AD ， ∴△ABC ≌△AED (SAS )； (2)解：∵△ABC ≌△AED ， ∴∠E ＝∠B ＝140°，∵五边形ABCDE 内角和为(5－2)×180°＝540°，∴∠BAE ＝540°－2×90°－2×140°＝80°. 5. (1)证明：∵点E 是CD 的中点， ∴DE ＝CE ， ∵AB ∥CF ， ∴∠BAF ＝∠AFC ，在△ADE 与△FCE 中，⎩⎨⎧∠DAE ＝∠CFE ∠AED ＝∠FEC DE ＝CE，∴△ADE ≌△FCE (AAS )； (2)解：由(1)知CD ＝2DE ， ∵DE ＝2， ∴CD ＝4，在Rt △ABC 中，点D 为AB 的中点， ∴AB ＝2CD ＝8，AD ＝CD ＝12AB . ∵AB ∥CF ，∴∠BDC ＝180°－∠DCF ＝180°－120°＝60°， ∴∠DAC ＝∠ACD ＝12∠BDC ＝12×60°＝30°， ∴在Rt △ABC 中，BC ＝12AB ＝12×8＝4. 6. (1)证明：∵AD ⊥BC ， ∴∠ADB ＝∠ADC ＝90°，在△BDG 和△ADC 中，⎩⎨⎧BD ＝AD∠BDG ＝∠ADC DG ＝DC，∴△BDG ≌△ADC (SAS )， ∴BG ＝AC ，∠BGD ＝∠C ，∵∠ADB ＝∠ADC ＝90°，E ，F 分别是BG ，AC 的中点， ∴DE ＝12BG ＝EG ，DF ＝12AC ＝AF ，∴DE ＝DF ，∠EDG ＝∠EGD ，∠FDA ＝∠F AD ， ∴∠EDG ＋∠FDA ＝90°，∴DE ⊥DF ； (2)解：∵AC ＝10， ∴DE ＝DF ＝5，由勾股定理得，EF ＝DE 2＋DF 2＝5 2. 7. (1)证明：∵E 是AB 的中点，且CE ⊥AB ， ∴CA ＝CB .∵F 是BC 的中点，且AF ⊥BC ， ∴AB ＝AC ， ∴AB ＝AC ＝BC ，∴12AB ＝12BC ，∴AE ＝CF ，在△CFG 和△AEG 中，⎩⎨⎧∠CGF ＝∠AGE∠CFG ＝∠AEG CF ＝AE，∴△CFG ≌△AEG (AAS )； (2)解：如解图，连接GD ，第7题解图∵AB ＝AC ＝BC ，∴△ABC 为等边三角形，从而△CAD 也为等边三角形， ∵AF ⊥BC ，∴∠GAC ＝∠EAF ＝30°， 又∵AE ＝12AB ＝2， ∴在Rt △AEG 中，AG ＝23AE ＝433， ∵∠GAD ＝∠GAC ＋∠CAD ＝90°，∴在Rt △ADG 中，根据勾股定理得：GD 2＝AG 2＋AD 2，即GD 2＝(433)2＋42，∴GD 2＝643， ∴GD ＝833.8. 解：(1) ∵∠ACP ＝90°，∴在Rt △ACP 中，∠CAP ＋∠APC ＝90°， ∵HQ ⊥AP ,∴在Rt △HPQ 中，∠Q ＋∠HPQ ＝90°， 又∵∠APC ＝∠HPQ ，∠CAP ＝α， ∴∠Q ＝α，又∵在等腰Rt △ABC 中，∠B ＝∠BAC ＝45°， ∴∠AMQ ＝∠B ＋∠Q ＝45°＋α； (2)PQ ＝2BM .证明：如解图，连接AQ ，过点M 作MN ⊥BQ 于点N .第8题解图∵∠ACP ＝90°，CQ ＝CP ，∠CAP ＝α， ∴∠CAQ ＝∠CAP ＝α，AP ＝AQ ，PQ ＝2CP ， 又∵∠BAC ＝45°，∴∠MAQ ＝∠BAC ＋∠CAQ ＝45°＋α＝∠AMQ ， ∴AQ ＝MQ ， ∴AP ＝MQ ， 又∵MN ⊥BQ ， ∴∠ACP ＝∠QNM ＝90°.在Rt △APC 和Rt △QMN 中，⎩⎨⎧∠CAP ＝∠NQM∠ACP ＝∠QNM ＝90°AP ＝MQ，∴Rt △APC ≌Rt △QMN (AAS )， ∴CP ＝MN ，∴PQ ＝2MN ， 又∵在Rt △BMN 中，∠B ＝45°， ∴BM ＝2MN ，∴PQ ＝2BM .9. (1)解：∵△ABC 和△ADE 都是等边三角形，AC ⊥DE ，AD ＝2， ∴BC ＝AC ，DE ＝AD ＝2，DF ＝12DE ＝1，AF ＝CF ， ∴AF ＝AD 2－DF 2＝3， ∴AC ＝2AF ＝23，∴BC ＝23； (2)证明：连接CE ，FG ，如解图所示：第9题解图∵△ABC 和△ADE 都是等边三角形，点B ，D ，E 同一在一条直线上． ∴AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ＝∠AED ＝60°， ∴∠ADB ＝120°，∠BAD ＝∠CAE ，在△ABD 和△ACE 中，⎩⎨⎧AB ＝AC∠BAD ＝∠CAE AD ＝AE，∴△ABD ≌△ACE (SAS )，∴BD ＝CE ，∠AEC ＝∠ADB ＝120°， ∴∠CED ＝∠AEC －∠AED ＝60°， ∵CD ⊥BE ， ∴∠DCE ＝30°， ∴DE ＝12CE ，∵线段BC的中点为F，线段DC的中点为G，∴FG∥BD，FG＝12BD，∴FG∥DE，FG＝DE，∴四边形DFGE是平行四边形，∴DF＝EG.。
湖南省2021年中考数学总复习第四单元三角形课时训练20全等三角形练习
全等三角形20 全等三角形限时:30分钟夯实根底1.以下结论正确的选项是()A.形状一样的两个图形是全等图形B.全等图形的面积相等C.对应角相等的两个三角形全等D.两个等边三角形全等2.如图K20-1,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是()图K20-1A.∠B=∠E,BC=EFB.BC=EF,AC=DFC.∠A=∠D,∠B=∠ED.∠A=∠D,BC=EF3.如图K20-2,点A,E,F,D在同一直线上.假设AB∥CD,AB=CD,AE=FD,那么图中的全等三角形有()图K20-2A.1对B.2对C.3对D.4对4.在如图K20-3所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),那么与△ABC有一条公共边且全等的所有格点三角形的个数是()图K20-3A.1B.2C.3D.45.如图K20-4,在五边形ABCDE中,有一正三角形ACD.假设AB=DE,BC=AE,∠E=115°,那么∠BAE的度数为()图K20-4A.115°B.120°C.125°D.130°6.[2021·荆州] :∠AOB.求作:∠AOB的平分线.MN的长为作法:如图K20-5,①以点O为圆心,适当长为半径画弧,分别交OA,OB于点M,N;②分别以点M,N为圆心,大于12半径画弧,两弧在∠AOB内部交于点C;③画射线OC.射线OC即为所求.上述作图用到了全等三角形的判定方法,这个方法是.图K20-57.如图K20-6,AB∥CF,E为DF的中点,AB=10,CF=6,那么BD= .图K20-68.[2021·哈尔滨] 如图K20-7,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC 交于点M,BD与AC交于点N.(1)如图①,求证:AE=BD;(2)如图②,假设AC=DC,在不添加任何辅助线的情况下,请直接写出图②中四对全等的直角三角形.图K20-79.如图K20-8,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.(1)求证:AB=CD;(2)假设AB=CF,∠B=30°,求∠D的度数.图K20-8能力提升10.[2021·河北] :如图K20-9,点P在线段AB外,且PA=PB.求证:点P在线段AB的垂直平分线上.在证明该结论时,需添加辅助线,那么作法不正确的选项是()图K20-9A.作∠APB的平分线PC交AB于点CB.过点P作PC⊥AB于点C且AC=BCC.取AB的中点C,连接PCD.过点P作PC⊥AB,垂足为C11.如图K20-10,△ABC三个内角的平分线交于点O,延长BA到点D,使AD=AO,连接DO.假设BD=BC,∠ABC=54°,那么∠BCA的度数为.图K20-1012.[2021·娄底] 如图K20-11,在等腰直角三角形ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°.假设ED的长为m,那么△BEF的周长是(用含m的代数式表示).图K20-1113.[2021·宜昌] 如图K20-12①,AB=AC,D为∠BAC的平分线上一点,连接BD,CD;如图②,AB=AC,D,E为∠BAC的平分线上两点,连接BD,CD,BE,CE;如图③,AB=AC,D,E,F为∠BAC的平分线上三点,连接BD,CD,BE,CE,BF,CF;…,依此规律,第n 个图形中有全等三角形的对数是.图K20-12拓展练习14.[2021·滨州] 如图K20-13,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.(1)如图①,假设点E,F分别为AB,AC上的点,且DE⊥DF,求证:BE=AF.(2)假设点E,F分别为AB,CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.图K20-13参考答案1.B2.D3.C4.D5.C[解析] 在正三角形ACD中,AC=AD,∠ACD=∠ADC=∠CAD=60°.∵AB=DE,BC=AE,∴△ABC≌△DEA.∴∠B=∠E=115°,∠ACB=∠EAD,∠BAC=∠ADE.∴∠ACB+∠BAC=∠BAC+∠DAE=180°-115°=65°.∴∠BAE=∠BAC+∠DAE+∠CAD=65°+60°=125°.应选C.6.SSS7.48.解:(1)证明:∵△ACB 和△DCE 都是等腰直角三角形,∠ACB=∠DCE=90°, ∴AC=BC ,DC=EC.∴∠ACB+∠ACD=∠DCE+∠ACD , 即∠BCD=∠ACE. 在△ACE 和△BCD 中,{AA =AA ,∠AAA =∠AAA ,AA =AA ,∴△ACE ≌△BCD (SAS). ∴AE=BD. (2)∵AC=DC , ∴AC=CD=EC=CB. ∴△ACB ≌△DCE (SAS).由(1)可知,∠AEC=∠BDC ,∠EAC=∠DBC , ∴∠DOM=90°. ∵∠AEC=∠CAE=∠CBD , ∴△EMC ≌△BNC (ASA).∴CM=CN. ∴DM=AN ,△AON ≌△DOM (AAS). ∵AB=DE ,AO=DO ,∴Rt △AOB ≌Rt △DOE (HL). 9.解:(1)证明:∵AB ∥CD ,∴∠B=∠C. 又∵AE=DF ,∠A=∠D , ∴△ABE ≌△DCF. ∴AB=CD.(2)∵AB=CF ,AB=CD , ∴DC=CF. ∴∠D=∠CFD. ∵∠C=∠B=30°, ∴∠D=75°. 10.B 11.42°12.√2m+2 [解析] 如下图,连接BD.在等腰直角三角形ABC 中,点D 是AC 的中点, ∴BD ⊥AC.∴BD=AD=CD ,∠DBC=∠A=45°,∠ADB=90°. ∵∠EDF=90°, ∴∠ADE=∠BDF.在△ADE 和△BDF 中,{∠A =∠AAA ,AA =AA ,∠AAA =∠AAA ,∴△ADE ≌△BDF (ASA).∴AE=BF,DE=DF.在Rt△DEF中,DF=DE=m.∴EF=√2DE=√2m.∴△BEF的周长为BE+BF+EF=BE+AE+EF=AB+EF=2+√2m.[解析] 当有一点D时,有1对全等三角形;当有两点D,E时,有3对全等三角形;当有三点D,E,F时,有6对13.A(A+1)2对全等三角形.全等三角形;当有四点时,有10对全等三角形;…;当有n个点时,图中有A(A+1)214.解:(1)证明:如图①,连接AD.①∵∠BDA=∠EDF=90°,∴∠BDE+∠EDA=∠EDA+∠ADF.∴∠BDE=∠ADF.∵D为BC的中点,△ABC是等腰直角三角形,∴BD=AD,∠B=∠DAC=45°,∴△BDE≌△ADF(ASA).∴BE=AF.(2)BE=AF.理由如下:如图②,连接AD.②∵∠BDA=∠EDF=90°,∴∠BDE+∠BDF=∠BDF+∠ADF.∴∠BDE=∠ADF.∵D为BC的中点,△ABC是等腰直角三角形, ∴BD=AD,∠ABC=∠DAC=45°,∴∠EBD=∠FAD=180°-45°=135°.∴△BDE≌△ADF(ASA).∴BE=AF.。
2021年九年级数学中考复习分类专题：全等三角形的判定综合练
2021年九年级数学中考复习分类专题：全等三角形的判定综合练一．选择题1．在△ABC和△DEF中，给出下列四组条件：①AB＝DE，BC＝EF，AC＝DF；②AB＝DE，∠B＝∠E，BC＝EF；③∠B＝∠E，BC＝EF，∠C＝∠F；④∠A＝∠D，∠B＝∠E，∠C＝∠F；其中，能使△ABC≌△DEF的条件共有（）A．1组B．2组C．3组D．4组2．下列说法正确的是（）A．全等三角形是指面积相等的三角形B．全等三角形是指能完全重合的三角形C．周长相等的三角形是全等三角形D．所有的等边三角形都是全等三角形3．下列各图中a、b、c为△ABC的边长，根据图中标注数据，判断甲、乙、丙、丁四个三角形和如图△ABC不一定全等的是（）A．B．C．D．4．如图，△ABC和△DEC中，已知AB＝DE，还需添加两个条件才能使△ABC≌△DEC，不正确的是（）A．BC＝EC，∠B＝∠E B．BC＝EC，AC＝DCC．AC＝DC，∠A＝∠D D．BC＝EC，∠A＝∠D5．已知：如图，AC＝DE，∠1＝∠2，要使△ABC≌△DFE，需添加一个条件，则添加的条件以及相应的判定定理合适的是（）A．∠A＝∠D（ASA）B．AB＝DF（SAS）C．BC＝FE（SSA）D．∠B＝∠F（ASA）6．点D、E分别在线段AB、AC上，CD与BE相交于点O，已知AE＝AD，添加以下哪一个条件不能判定△ABE≌△ACD（）A．∠B＝∠C B．∠BEA＝∠CDA C．BE＝CD D．AB＝AC7．如图，∠E＝∠F＝90°，∠B＝∠C，AE＝AF，下列结论：①EM＝NF；②NC＝FN；③∠FAN ＝∠EAM；④△ACN≌△ABM．其中正确的有（）A．1个B．2个C．3个D．4个8．在如图所示的6×6网格中，△ABC是格点三角形（即顶点恰好是网格线的交点），则与△ABC有一条公共边且全等（不含△ABC）的所有格点三角形的个数是（）A．3个B．4个C．6个D．7个9．如图，AC＝BC，AD＝BD，这个图形叫做“筝形”，数学兴趣小组几名同学探究出关于它的如下结论：①△ACD≌△BCD；②AO＝BO；③AB⊥CD；④△AOC≌△BOC；⑤“筝形”是轴对称图形．其中正确的结论有（）A．2个B．3个C．4个D．5个10．如图，△ABC、△ADE、△DFG均为等边三角形，C、E、F三点共线，且E是CF的中点，下列结论：①△ADG≌△EDF；②△AEC为等腰三角形；③DF＝AD+GE；④∠BAG＝∠BCE；⑤∠GEB＝60°，其中正确的个数为（）A．2 B．3 C．4 D．5二．填空题11．如图，点B、F、C、E在一条直线上，已知AB＝DE，AC＝DF，请你添加一个适当的条件，根据SSS可判定△ABC≌△DEF．12．如图，已知AB＝DE，∠B＝∠E，添加下列哪个条件可以利用SAS判断△ABC≌△DEC．正确的是：．①∠A＝∠D；②BC＝EC；③AC＝DC；④∠BCE＝∠ACD．13．在平面直角坐标系中，已知点A，B的坐标分别是（2，0），（4，2），若在x轴下方有一点P，使以O，A，P为顶点的三角形与△OAB全等，则满足条件的P点的坐标是．14．如图，在△ABC中，点E、F分别是AB、AC边上的点，EF∥BC，点D在BC边上，连接DE、DF，请你添加一个条件，使△BED≌△FDE．15．如图，∠C＝90°，AC＝20，BC＝10，AX⊥AC，点P和点Q同时从点A出发，分别在线段AC和射线AX上运动，且AB＝PQ，当AP＝时，以点A，P，Q为顶点的三角形与△ABC全等．16．在直角坐标系中，已知A（6，0）、F（3，0），C（0，2），在△AOC的边上取两点P、Q（点Q是不同于点F的点），若以O、P、Q为顶点的三角形与△OFP全等，则符合条件的点P的坐标为．三．解答题17．在△ABC中，AB＝AC，BD＝CE，CD⊥AB于点D，BE⊥AC于点E．（1）如图1，求证：△ABE≌△ACD；（2）如图2，BE与CD交于点O，连接AO，直接写出图中所有的全等三角形（△ABE≌△ACD除外）．18．已知：点A，D，C在同一条直线上，AB∥CE，AC＝CE，∠ACB＝∠E，求证：△ABC≌△CDE．19．如图，△ABC和△ADE都是等腰直角三角形，AB＝AC，AD＝AE，连结BD、CE；求证：△ABD与△ACE全等．20．如图，在△ABC中，BD，CE分别是AC，AB边上的高，在BD上截取BF＝AC，延长CE至点G使CG＝AB，连接AF，AG．（1）如图1，求证：AG＝AF；（2）如图2，若BD恰好平分∠ABC，过点G作GH⊥AC交CA的延长线于点H，请直接写出图中所有的全等三角形并用全等符号连接．21．如图，在△ABC中，AB＝AC，D是边BC延长线上一点，连结AD．AE∥BD，∠BAC＝∠DAE，连接CE交AD于点F．（1）若∠D＝36°，求∠B的度数；（2）若CA平分∠BCE，求证：△ABD≌△ACE．参考答案一．选择题1．解：①AB＝DE，BC＝EF，AC＝DF，可根据SSS判定△ABC≌△DEF；②AB＝DE，∠B＝∠E，BC＝EF，可根据SAS判定△ABC≌△DEF；③∠B＝∠E，BC＝EF，∠C＝∠F，可根据ASA判定△ABC≌△DEF；④∠A＝∠D，∠B＝∠E，∠C＝∠F，不能判定△ABC≌△DEF；故选：C．2．解：A、面积相等的两个三角形不一定是全等三角形，本说法错误；B、全等三角形是指能完全重合的三角形，故本选项正确；C、所有周长相等的三角形不一定都是全等三角形，本说法错误；D、所有的等边三角形形状都相同，大小与边长有关，边长不相等，则不能够重合，所以不一定是全等三角形，本说法错误；故选：B．3．解：∵∠B＝70°，∠C＝50°，∴∠A＝180°﹣70°﹣50°＝60°，根据“SAS”判断图乙中的三角形与△ABC全等；根据“AAS”判断图丙中的三角形与△ABC全等；根据“SSS”判断图丙中的三角形与△ABC全等．根据“SSA”无法判断图甲中的三角形与△ABC全等．故选：A．4．解：∵AB＝DE，∴当BC＝EC，∠B＝∠E时，满足SAS，可证明△ABC≌△DEC，故A可以；当BC＝EC，AC＝DC时，满足SSS，可证明△ABC≌△DEC，故B可以；当AC＝DC，∠A＝∠D时，满足SAS，可证明△ABC≌△DEC，故C可以；当BC＝EC，∠A＝∠D时，在△ABC中是ASS，在△DEC中是ASS，故不能证明△ABC≌△DEC，故D不可以；故选：D．5．解：A、添加条件∠A＝∠D判定△ABC≌△DFE用的判定方法是ASA，故原题说法正确；B、添加条件AB＝DF不能判定△ABC≌△DFE，故原题说法错误；C、添加条件BC＝FE判定△ABC≌△DFE用的判定方法是SAS，故原题说法错误；D、添加条件∠B＝∠F判定△ABC≌△DFE用的判定方法是AAS，故原题说法错误；故选：A．6．解：A．由AE＝AD、∠A＝∠A、∠B＝∠C可依据“AAS”判定△ABE≌△ACD，此选项不符合题意；B．由AE＝AD、∠A＝∠A、∠BEA＝∠CDA可依据“ASA”判定△ABE≌△ACD，此选项不符合题意；C．由BE＝CD、AE＝AD、∠A＝∠A不能判定△ABE≌△ACD，此选项符合题意；D．由AE＝AD、∠A＝∠A、AB＝AC可依据“SAS”判定△ABE≌△ACD，此选项不符合题意；故选：C．7．解：在△AEB和△AFC中，，∴△AEB≌△AFC（AAS），∴∠EAB＝∠FAC，EB＝CF，AB＝AC，∴∠EAM＝∠FAN，故③正确，在△AEM和△AFN中，，∴△AEM≌△AFN（ASA），∴EM＝FN，AM＝AN，故①正确，∵AC＝AB，∴CM＝BN，得不出△ANC与△AFN全等，故②错误，在△ACN和△ABM中，，∴△ACN≌△ABM，故④正确，故①③④正确，故选：C．8．解：如图所示：一共有7个符合题意的点．故选：D．9．解：在△ACD和△BCD中，，∴△ACD≌△BCD（SSS），①结论正确；∵AC＝BC，AD＝BD，∴CD是线段AB的垂直平分线，∴AO＝BO，AB⊥CD，②③结论正确；在△AOC和△BOC中，，∴△AOC≌△BOC（SSS），④结论正确；“筝形”沿直线CD折叠，直线两旁的部分能够互相重合，∴“筝形”是轴对称图形，⑤结论正确；故选：D．10．解：∵△ADE、△DFG，△ABC为等边三角形，∴DA＝DE，DG＝DG，∠ADE＝∠FGD＝∠AED＝∠ACB＝∠DAE＝∠BAC＝60°，∴∠ADG＝∠EDF，∠DAB＝∠CAE，∴△ADG≌△EDF（SAS），故①正确∴∠DEF＝∠DAG，∵∠DEF+∠AED＝∠EAC+∠ACE＝∠EAC+∠ABC﹣∠BCF，∴∠EAC﹣∠DEF＝∠BCF，∵∠BAG＝∠DAB﹣∠DAG＝∠CAE﹣∠DEF，∴∠BAG＝∠BCF，故④正确，∵DF+EG＝DG+GE≥DE，∴DF+GE≠AD，故③错误．设AG交CF于点O，DG交CF于K．∵△ADG≌△EDF，∴∠OGK＝∠FKD，EF＝AG，∵∠GKO＝∠FKD，∴∠GOK＝∠FDK＝60°，∴∠AOC＝∠GOK＝∠ABC＝60°，∴∠BAG＝∠BCE，∵EF＝CE，∴AG＝CE，∵AB＝CB，∴△BAG≌△BCE（SAS），∴BG＝BE，∠ABG＝∠CBE，∴∠EBC＝∠ABC＝60°，∴△EBG是等边三角形，∴∠EGB＝60°，故⑤正确，无法判断AC＝EC或AE＝EC或AE＝EC，故△ACE不一定是等腰三角形，故②错误，故选：B．二．填空题（共6小题）11．解：适合的条件是BC＝EF，理由是：∵在△ABC和△DEF中，∴△ABC≌△DEF（SSS），故答案为：BC＝EF．12．解：∵AB＝DE，∠B＝∠E，∴添加①∠A＝∠D，利用ASA得出△ABC≌△DEC；∴添加②BC＝EC，利用SAS得出△ABC≌△DEC；∴添加④∠BCE＝∠ACD，得出∠ACB＝∠DCE，利用AAS得出△ABC≌△DEC；故答案为：②．13．解：如图所示：在x轴下方有一点P，使以O，A，P为顶点的三角形与△OAB全等，则满足条件的P点的坐标是：（﹣2，﹣2）或（4，﹣2）．故答案为：（﹣2，﹣2）或（4，﹣2）．14．解：由题意：DE＝ED，∠DEF＝∠EDB，∴根据SAS可以添加DB＝EF，根据AAS，ASA可以添加∠BED＝∠EDF或DF∥AB或∠B＝∠EFD，故答案为BD＝EF（或∠BED＝∠EDF或DF∥AB或∠B＝∠EFD）15．解：∵AX⊥AC，∴∠PAQ＝90°，∴∠C＝∠PAQ＝90°，分两种情况：①当AP＝BC＝10时，在Rt△ABC和Rt△QPA中，，∴Rt△ABC≌Rt△QPA（HL）；②当AP＝CA＝20时，在△ABC和△PQA中，，∴Rt△ABC≌Rt△PQA（HL）；综上所述：当点P运动到AP＝10或20时，△ABC与△APQ全等；故答案为：10或20．16．解：①如图1，过点F作FP⊥OA，垂足为P，过点P作PQ⊥OC，垂足为Q，连接OP，此时△OFP≌PQO，∵A（6，0）、F（3，0），∴PF、PQ是△OAC的中位线，∴PQ＝OA＝3，PF＝OC＝，∴P（3，），②如图2，由①可知，点P、Q位置互换，亦满足题意，此时，P（0，），③如图3，作∠AOC的平分线交AC于点P，在OC上截取OQ＝OF＝3，连接PF、PQ，此时△OFP≌OQP，过点P作PM⊥OA，垂足为M，PN⊥OC，垂足为N，则PM＝PN，由三角形面积公式得，OA•PM+OC•PN＝AO•OC，即，6PM+2PM＝6×2，∴PM＝PN＝3﹣3，∴点P（3﹣3，3﹣3），④如图4，在AC上截取AP＝6＝OA，取AP的中点Q，则PQ＝OF＝3，过点P作PB⊥OA，垂足为B，在Rt△ABP中，PB＝AP＝3，AB＝×AP＝3，∴OB＝OA﹣AB＝6﹣3，∴点P（6﹣3，3），故答案为：（3，）或（0，）或（3﹣3，3﹣3）或（6﹣3，3）．三．解答题（共5小题）17．（1）证明：∵AB＝AC，BD＝CE，∴AB﹣BD﹣AC﹣CE，∴AD＝AE，∵CD⊥AB，BE⊥AC，∴∠AEB＝∠ADC＝90°，在Rt△ABE和Rt△ACD中，∴Rt△ABE≌Rt△ACD（HL）；（2）解：∵Rt△ABE≌Rt△ACD，∴∠ABE＝∠ACD，在△DOB和△EOC中，∴△DOB≌△EOC（AAS），∴OB＝OC，DO＝EO，∴∠EBC＝∠DCB，OD+OC＝OE+OB，∴DC＝BE，在△BEC和△CDB中，∴△BEC≌△CDB（SAS），在△ABOHE△ACO中，∴△ABO≌△ACO（SSS），在△ADO和△AEO中，∴△ADO≌△AEO（SSS），即全等三角形有：△DOB≌△EOC，△BEC≌△CDB，△ABO≌△ACO，△ADO≌△AEO．18．证明：∵AB∥CE，∴∠A＝∠ECD．∵在△ABC和△CDE中，，∴△ABC≌△CDE（ASA）．19．证明：∵△ABC和△ADE都是等腰直角三角形，AB＝AC，AD＝AE，∴∠BAC＝∠DAE＝90°，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△ABD和△ACE中，∴△ABD≌△ACE（SAS），即△ABD与△ACE全等．20．证明：（1）∵BD、CE分别是AC、AB两条边上的高，∴∠AEC＝∠ADB＝90°，∴∠ABD+∠BAD＝∠ACE+∠CAE＝90°，∴∠ABD＝∠ACG，在△AGC与△FAB中，，∴△AGC≌△FAB（SAS），∴AG＝AF；（2）图中全等三角形有△AGC≌△FAB，由得出△CGH≌△BAD，由得出Rt△AGH≌Rt△FAD，△ABD≌△CBD；△CBD≌△GCH．21．解：（1）∵AE∥BD，∴∠DAE＝∠BAC，∵∠DAE＝∠BAC，∴∠D＝∠BAC＝36°，∵AB＝AC，∴∠B＝∠ACB，∴∠B＝＝＝72°．（2）证明：∵CA平分∠BCE，∴∠BCA＝∠ACE，∵∠B＝∠ACB，∴∠B＝∠ACE，∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（ASA）．。
2021年中考数学专项训练： 全等三角形(含答案)
一、选择题10.(2020·宁波)△BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道A．△ABC的周长B．△AFH的周长C．四边形FBGH的周长D．四边形ADEC的周长{答案}A{解析}本题考查了全等三角形的判定和性质，等边三角形的性质，五边形DECHF的周长为DE＋CE＋CH＋FH ＋DF，∵△ABC和△FGH是两个等边三角形，∴△AFH≌△CHG，∴CH＝AF．∵△BDE和△FGH是两个全等的等边三角形，∴DE＝FH＝BD＝BE，∴DE＋CE＋CH＋FH＋DF＝BE＋CE＋CH＋BD＋DF＝BC＋BF＋CH＝BC＋BA，∴只需要知道△ABC的周长就可以求得五边形DECHF的周长，因此本题选A．（2020·四川甘孜州）9．如图，等腰△ABC中，点D，E分别在腰AB，AC上，添加下列条件，不能判定△ABE ≌△ACD的是( )A．AD＝AE B．BE＝CD C．∠ADC＝∠AEB D．∠DCB＝∠EBC{答案}B{解析}本题考查了全等三角形的判定．由全等三角形的判定“SAS”、“AAS”、“ASA”可得，添加选项A、C、D都能判定两三角形全等；而添加选项B则不能判定两三角形全等，故选B．7．（2020·绵阳）如图，在四边形ABCD中，∠A＝∠C＝90°，DF∥BC，∠ABC的平分线BE交DF于点G，GH⊥DF，点E恰好为DH的中点．若AE＝3，CD＝2，则GH＝（）A．1 B．2 C．3 D．4{答案}B{解析}延长HG交BC于点M．∴DF∥BC，GH⊥DF，∴∠GMC＝∠MGD＝∠C＝90°，∴四边形GMCD为矩形，∴MG＝CD＝2，∴BE平分∠ABC，∴∠ABE＝∠EBC，又∴∠A＝∠BMG＝90°，∴△ABE∽△MBG，∴＝＝，∴BG＝2EG，∴∠HGD＝90°，点E为DH的中点，∴DH＝2EG＝2ED，∴DH＝BG，∴EG＝ED，∴∠EGD＝∠EDG,∴DF∥BC，∴∠EGD＝∠GBM,∴∠EDG＝∠GBM,又∴∠HGD＝∠BMG＝90°，∴△DHG≌△BGM，∴HG＝GM＝2．故选项B正确．BEBGAEMG238．（2020·鄂州）如图，在△AOB 和△COD 中，OA ＝OB ，OC ＝OD ，OA ＜OC ，36AOB COD ︒∠=∠=．连接AC 、BD 交于点M ，连接OM ．下列结论：①36AMB ︒∠=；②AC BD =；③OM 平分AOD ∠；④MO 平分AMD ∠其中正确的结论个数有（ ）个． A ．4 B ．3 C ．2 D ．1 {答案}B{解析}本题考查了全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识；证明三角形全等是解题的关键．由SAS 证明△AOC ≌△BOD ，得到∠OAC ＝∠OBD ，由三角形的外角性质得：∠AMB ＋∠OBD ＝∠AOB ＋∠OAC ，得出∠AMB ＝∠AOB ＝36°，①正确；根据全等三角形的性质得出∠OCA ＝∠ODB ，AC ＝BD ，②正确；作OG ⊥AC 于G ，OH ⊥BD 于H ，如图所示：则∠OGC ＝∠OHD ＝90°，由AAS 证明△OCG ≌△ODH （AAS ），得出OG ＝OH ，由角平分线的判定方法得出MO 平分AMD ∠，④正确；由∠AOB ＝∠COD ，得出当∠DOM ＝∠AOM 时，OM 才平分∠BOC ，假设∠DOM ＝∠AOM ，由△AOC ≌△BOD 得出∠COM ＝∠BOM ，由MO 平分∠BMC 得出∠CMO ＝∠BMO ，推出△COM ≌△BOM ，得OB ＝OC ，而OA ＝OB ，所以OA ＝OC ，而OA OC <，故③错误；即可得出结论． 正确的有①②④； 故选B ．11．如图，在中，，将绕点C 顺时针旋转得到，使点B 的对应点E 恰好落在边上，点A 的对应点为D ，延长交于点F ，则下列结论一定正确的是（ ）ABC 90ACB ∠=︒ABC DEC AC DE ABA. B. C. D.{答案}D{解析}本题考查旋转的性质以及全等三角形的性质，证明过程常用角的互换、直角互余作为解题工具，另外证明题当中反证法也极为常见，需要熟练利用．可通过旋转的性质得出△ABC与△DEC全等，故可判断A选项；可利用相似的性质结合反证法判断B，C选项；最后根据角的互换，直角互余判断D选项．由已知得：△ABC△DEC，则AC=DC，∠A=∠D，∠B=∠CED，故A选项错误；∵∠A=∠A，∠B=∠CED=∠AEF，故△AEF△ABC，则，假设BC=EF，则有AE=AB，由图显然可知AE AB，故假设BC=EF不成立，故B选项错误；假设∠AEF=∠D，则∠CED=∠AEF=∠D，故△CED为等腰直角三角形，即△ABC为等腰直角三角形，因为题干信息△ABC未说明其三角形性质，故假设∠AEF=∠D不一定成立，故C选项错误；∵∠ACB=90°，∴∠A+∠B=90°．又∵∠A=∠D，∴∠B+∠D=90°．故AB⊥DF，D选项正确．故选：D．7．（2020·淄博）如图，若△ABC≌△ADE，则下列结论中一定成立的是（）A．AC＝DE B．∠BAD＝∠CAE C．AB＝AE D．∠ABC＝∠AED【解析】∵△ABC≌△ADE，∴AC＝AE，AB＝AD，∠ABC＝∠ADE，∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE．故A，C，D选项错误，B选项正确，故选：B．6.（2020·永州）如图，已知,AB DC ABC DCB=∠=∠．能直接判断ABC DCB△≌△的方法是（）AC DE=BC EF=AEF D∠=∠AB DF⊥≅EF AEBC AB≠A. SASB. AASC. SSSD. ASA【答案】A【详解】在△ABC和△DCB中，AB DCABC DCBBC CB=⎧⎪∠=∠⎨⎪=⎩,∴ABC DCB△≌△(SAS),故选：A.7．（2020·邵阳）如图，四边形ABCD是平行四边形，点E,B,D,F在同一条直线上，请添加一个条件使得△ABE ≌△CDF,下列不正确的是（）A.AE=CFB.∠AEB=∠CFDC.∠EAB=∠FCDD.BE=DF{答案} A{解析}本题考查了平行四边形的性质、全等三角形的判定和性质等知识，∴四边形ABCD是平行四边形，∴AB=CD，AB∴CD，∴∴ABD=∴BDC，∴∴ABE+∴ABD=∴BDC+∴CDF，∴∴ABE=∴CDF，A.若添加AE CF=，则无法证明ABE CDF△≌△，故A错误；B.若添加AEB CFD∠=∠，运用AAS可以证明ABE CDF△≌△，故选项B正确；C.若添加EAB FCD∠=∠，运用ASA可以证明ABE CDF△≌△，故选项C正确；D.若添加BE DF=，运用SAS可以证明ABE CDF△≌△，故选项D正确．因此本题选A．二、填空题 18．（2019·上海）在△ABC 和△A 1B 1C 1中，已知∠C ＝∠C 1＝90°，AC ＝A 1C 1＝3，BC ＝4，B 1C 1＝2，点D 、D 1分别在边AB 、A 1B 1上，且△ACD ≌△C 1A 1D 1，那么AD 的长是 ． {答案}53{解析}如图，∵在∴ABC 和∴A1B1C1中，∠C ＝∠C1＝90°，AC ＝A1C1＝3，BC ＝4，B1C1＝2， ∴AB5，设AD ＝x ，则BD ＝5－x ，∵△ACD ≌△C1A1D1，∴C1D1＝AD ＝x ，∠A1C1D1＝∠A ，∠A1D1C1＝∠CDA ， ∴∠C1D1B1＝∠BDC ，∵∠B ＝90°－∠A ，∠B1C1D1＝90°－∠A1C1D1，∴∠B1C1D1＝∠B ，∴△C1B1 D1∽△BCD ， ∴1111BD BC C D C B =，即5x x-＝2，解得x ＝53.∴AD 的长为53. 13．（2020·黑龙江龙东）如图，Rt∴ABC 和Rt∴EDF 中，BC ∴DF ，在不添加任何辅助线的情况下，请你添加一个条件 ，使Rt∴ABC 和Rt∴EDF 全等．{答案} AB ＝ED 答案不唯一．{解析}本题考查了三角形全等的条件，解：∴Rt∴ABC 和Rt∴EDF 中，∴∴BAC ＝∴DEF ＝90°，∴BC∴DF ，∴∴DFE ＝∴BCA ，∴添加AB ＝ED ，在Rt∴ABC 和Rt∴EDF 中{∠DFE =∠BCA∠DEF =∠BAC AB =ED，∴Rt∴ABC∴Rt∴EDF （AAS ），故答案为：AB ＝ED 答案不唯一． 14．（2020·北京）在△ABC 中，AB =AC ，点D 在BC 上（不与点B ，C 重合）.只需添加一个条件即可证明△ABD ≌△ACD ，这个条件可以是 （写出一个即可）． {答案}答案不唯一，∠BAD =∠CAD 或者BD =CD 或AD ⊥BC{解析}根据等腰三角形三线合一的性质可得，要使△ABD ≌△ACD ，则可以填∠BAD =∠CAD 或者BD =CD 或AD ⊥BC 均可．13．（2020·齐齐哈尔如图，已知在△ABD 和△ABC 中，∠DAB ＝∠CAB ，点A 、B 、E 在同一条直线上，若使△ABD ≌△ABC ，则还需添加的一个条件是 ．（只填一个即可） {答案} AD ＝AC （∠D ＝∠C 或∠ABD ＝∠ABC 等）{解析}利用全等三角形的判定方法添加条件．∵∠DAB ＝∠CAB ，AB ＝AB ， ∴当添加AD ＝AC 时，可根据“SAS ”判断△ABD ≌△ABC ； 当添加∠D ＝∠C 时，可根据“AAS ”判断△ABD ≌△ABC ； 当添加∠ABD ＝∠ABC 时，可根据“ASA ”判断△ABD ≌△ABC ． 故答案为AD ＝AC （∠D ＝∠C 或∠ABD ＝∠ABC 等）．14．（2020·怀化）如图，在△ABC 和△ADC 中，AB ＝AD ，BC ＝DC ，∠B ＝130°，则∠D ＝ °．{答案}130{解析}根据全等三角形的判定定理得出△ABC ≌△ADC ，根据平行线的性质得出∠D ＝∠B ，代入求出即可． 证明：∵在△ADC 和△ABC 中 {AD =AB AC =AC CD =CB， ∴△ABC ≌△ADC （SSS ）， ∴∠D ＝∠B ， ∵∠B ＝130°， ∴∠D ＝130°， 故答案为：130．15．（2020·抚顺本溪辽阳）如图，在△ABC 中，M ，N 分别是AB 和AC 的中点，连接MN ，点E 是CN 的中点，连接ME 并延长，交BC 的延长线于点D ，若BC ＝4，则CD 的长为 ．{答案}2{解析}本题可根据三角形中位线定理，及三角形全等的知识求解．∵M ，N 分别是AB 和AC 的中点，∴MN ＝12BC ＝2，MN ∥BC ．∴∠NME ＝∠D ，∵NE ＝CE ，∠NEM ＝∠CED ，∴△NEM ≌△CED ，∴CD ＝MN ＝2．三、解答题 18．（2020·温州） 如图,在△ABC 和△DCE 中,AC ＝DE ,∠B ＝∠DCE ＝90° ,点A ,C ,D 依次在同一直线上,且AB // DE .(1)求证:△ABC ≌△DCE .(2)连结AE ,当BC ＝5,AC ＝12时,求AE 的长.{解析}本题考查了平行线的性质、全等三角形的判定、勾股定理等知识．（1）由AB//DE,得到∠BAC ＝∠D. 又因为∠B ＝∠DCE ＝90°,AC ＝DE ，所以△ABC ≌△DCE(AAS).（2）由（1）知BC ＝CE ，从而在Rt △ACE 中，利用勾股定理求AE.E ADBCMN E CB A{答案}解：(1): AB//DE,∴∠BAC＝∠D. 又∵∠B＝∠DCE＝90°,AC＝DE,∴△ABC≌△DCE(AAS).(2)由（1）知△ABC≌△DCE,∴CE＝BC＝5.在Rt△ACE中，∵AC＝12, CE＝5,2251213 AE∴=+=.21．（2020台州）如图，已知AB＝AC，AD＝AE，BD和CE相交于点O．（1）求证：△ABD≌△ACE；（2）判断△BOC的形状，并说明理由．【分析】（1）由“SAS”可证△ABD≌△ACE；（2）由全等三角形的性质可得∠ABD＝∠ACE，由等腰三角形的性质可得∠ABC＝∠ACB，可求∠OBC＝∠OCB，可得BO＝CO，即可得结论．【解答】证明：（1）∵AB＝AC，∠BAD＝∠CAE，AD＝AE，∴△ABD≌△ACE（SAS）；（2）△BOC是等腰三角形，理由如下：∵△ABD≌△ACE，∴∠ABD＝∠ACE，∵AB＝AC，∴∠ABC＝∠ACB，∴∠ABC﹣∠ABD＝∠ACB﹣∠ACE，∴∠OBC＝∠OCB，∴BO＝CO，∴△BOC是等腰三角形．20．（2020·铜仁）如图，∠B＝∠E，BF＝EC，AC∥DF．求证：△ABC≌△DEF．{解析}由已知条件“BF＝EC”结合图形可知：BC＝EF，欲证△ABC≌△DEF，目前已经知道的条件是一边（BF＝EC）、一角（∠B＝∠E），所以可以考虑全等三角形的判定定理AAS、SAS或ASA，再次分析已知条件，发现由AC∥DF可得出∠ACB＝∠DFE，所以考虑由ASA定理证得结果．{答案}证明：∵AC∥DF，∴∠ACB＝∠DFE.又∵BF＝CE，∴BC＝EF.在△ABC和△DEF中，∵，∴△ABC≌△DEF（ASA）．26．（2020·常德）已知D是RR△RRR斜边AB的中点，∠RRR=90°，∠RRR=30°，过点D作Rt△RRR使∠RRR=90°，∠RRR=30°，连接CE并延长CE到点P，使RR=RR，连接BE，FP，BP，设BC与DE交于M，PB与EF交于N．(1)如图1，当D，B，F共线时，求证：①RR=RR；②∠RRR=30°；(2)如图2，当D，B，F不共线时，连接BF，求证：∠RRR+∠RRR=30°．{解析} (1)①证明△CBP是直角三角形，根据直角三角形斜边上的中线等于斜边的一半可得结论；②根据同位角相等可得BC//EF，由平行线的性质得BP⊥EF，可得EF是线段BP的垂直平分线，根据等腰三角形三线合一的性质可得∠PFE=∠BFE=30°；(2)如图2，延长DE到Q，使EQ=DE，连接CD，PQ，FQ，证明△QEP≌△DEC(SAS)，则PQ=DC=DB，由QE=DE，∠DEF=90°，知EF是DQ的垂直平分线，证明△FQP≌△FDB(SAS)，再由EF是DQ的垂直平分线，可得结论．{答案}解：证明(1)①∵∠ACB=90°，∠ABC=30°，∴∠A=90°−30°=60°，同理∠EDF=60°，∴∠A=∠EDF=60°，∴AC//DE，∴∠DMB=∠ACB=90°，∵D是Rt△ABC斜边AB的中点，AC//DM，∴BMBC =BDAB=12，即M是BC的中点，∵EP=CE，即E是PC的中点，∴ED//BP，∴∠CBP=∠DMB=90°，∴△CBP是直角三角形，∴BE=12PC=EP；②∵∠ABC=∠DFE=30°，∴BC//EF，由①知：∠CBP=90°，∴BP⊥EF，∵EB=EP，∴EF是线段BP的垂直平分线，∴PF=BF，∴∠PFE=∠BFE=30°；(2)如图2，延长DE到Q，使EQ=DE，连接CD，PQ，FQ，∵EC=EP，∠DEC=∠QEP，∴△QEP≌△DEC(SAS)，则PQ=DC=DB，∵QE=DE，∠DEF=90°∴EF是DQ的垂直平分线，∴QF=DF，∵CD=AD，∴∠CDA=∠A=60°，∴∠CDB=120°，∴∠FDB=120°−∠FDC=120°−(60°+∠EDC)=60°−∠EDC=60°−∠EQP=∠FQP，∴△FQP≌△FDB(SAS)，∴∠QFP=∠BFD，∵EF是DQ的垂直平分线，∴∠QFE=∠EFD=30°，∴∠QFP+∠EFP=30°，∴∠BFD+∠EFP=30°．25．（2020·黔东南州）如图1，△ABC和△DCE都是等边三角形．探究发现（1）△BCD与△ACE是否全等？若全等，加以证明；若不全等，请说明理由．拓展运用（2）若B、C、E三点不在一条直线上，∠ADC＝30°，AD＝3，CD＝2，求BD的长．（3）若B、C、E三点在一条直线上（如图2），且△ABC和△DCE的边长分别为1和2，求△ACD的面积及AD的长．{解析}（1）依据等式的性质可证明∠BCD＝∠ACE，然后依据SAS可证明△ACE≌△BCD；（2）由（1）知：BD＝AE，利用勾股定理计算AE的长，可得BD的长；（3）如图2，过点A作AF⊥CD于F，先根据平角的定义得∠ACD＝60°，利用特殊角的三角函数可得AF的长（也可以利用含30度角的直角三角形的性质），由三角形面积公式可得△ACD的面积，最后根据勾股定理可得AD的长．{答案}解：（1）全等.理由是：∵△ABC和△DCE都是等边三角形，∴AC＝BC，DC＝EC，∠ACB＝∠DCE＝60°，∴∠ACB+∠ACD＝∠DCE+∠ACD，即∠BCD＝∠ACE，在△BCD和△ACE中，{CD=CE∠BCD=∠ACEBC=AC，∴△ACE≌△BCD（SAS）；（2）如图3，由（1）得：△BCD≌△ACE，∴BD ＝AE ，∵△DCE 都是等边三角形，∴∠CDE ＝60°，CD ＝DE ＝2， ∵∠ADC ＝30°，∴∠ADE ＝∠ADC+∠CDE ＝30°+60°＝90°，在Rt △ADE 中，AD ＝3，DE ＝2，∴AE =√AD 2+DE 2=√9+4=√13，∴BD =√13； （3）如图2，过A 作AF ⊥CD 于F ，∵B 、C 、E 三点在一条直线上，∴∠BCA+∠ACD+∠DCE ＝180°，∵△ABC 和△DCE 都是等边三角形，∴∠BCA ＝∠DCE ＝60°，∴∠ACD ＝60°， 在Rt △ACF 中，sin ∠ACF =AFAC ，∴AF ＝AC ×sin ∠ACF ＝1×√32=√32， ∴S △ACD =12×CD ×AF =12×2×√32=√32，∴CF ＝AC ×cos ∠ACF ＝1×12=12，FD ＝CD ﹣CF ＝2−12=32，在Rt △AFD 中，AD2＝AF2+FD2=(√32)2+(32)2=3，∴AD =√3．23．（2020·安徽）如图1，已知四边形ABCD 是矩形，点E 在BA 的延长线上，AE ＝AD .EC 与BD 相交于点G ，与AD 相交于点F ，AF ＝AB . (1)求证：BD ⊥EC ；(2)若AB ＝1，求AE 的长；(3)如图2，连接AG ，求证：EG -DG ＝2AG .图1 图2{解析}(1)证明△AEF ≌△ADB ，结合已知条件，等量代换求∠EGB ＝90°即可； (2)证明△AEF ∽△DCF ，代入已知与等量，转化成方程求解；(3)以AG 为腰构造等腰直角三角形，将EG 、DG 和2AG 转化到同一条直线中求解.{答案}(1)证明:因为四边形ABCD 是矩形，点E 在BA 的延长线上，所以∠EAF ＝∠DAB ＝90°，又AE ＝AD ，AF ＝AB ，所以△AEF ≌△ADB ，∠AEF ＝∠ADB.所以∠GEB ＋∠GBE ＝∠ADB ＋∠ABD ＝90°，即∠EGB ＝90°，故BD ⊥EC.(2)解:由矩形性质知 AE//CD.所以∠AEF ＝∠DCF ，∠EAF ＝∠CDF,所以△AEF ∽△DCF ，AE AFDC DF =，即AE DF ＝AF DC.设AE ＝AD ＝a(a>0)，则有a (a －1)＝1，化简得a 2－a －1＝0，解得a ＝15+ 或15- (舍)，所以AE 的长为15+.(3)证明:方法一:如图1，在线段EG 上取点P ，使得EP ＝DG ，在△AEP 与△ADG 中，AE ＝AD ，∠AEP ＝∠ADG ，EP ＝DG ，所以△AEP ≌△ADG ，所以AP ＝AG ，∠EAP ＝∠DAG ， 所以∠PAG ＝∠PAD ＋∠DAG ＝∠PAD ＋∠EAP ＝∠DAE ＝90°，△PAG 为等腰直角三角形. 于是EG －DG ＝EG －EP ＝PG ＝2AG.方法二，如图2，过点A 作AG 的垂线，与DB 的延长线交于点Q.在△AEG 与△ADQ 中，G CE D FG CE BA D FAE ＝AD ，∠AEG ＝∠ADQ ，∠EAG ＝90°＋∠DAG ＝∠DAQ ，所以△AEG ≌△ADQ ， 所以EG ＝DQ ，AG ＝AQ ，△AGQ 为等腰直直角三角形，于是EG －DG ＝DQ －DG ＝QG图1 图224．（2020·哈尔滨）已知：在△ABC 中，AB ＝AC ，点D 、点E 在边BC 上，BD ＝CE ，连接AD 、AE . （1）如图1，求证：AD ＝AE ；（2）如图2，当∠DAE ＝∠C ＝45°时，过点B 作BF ∥AC 交AD 的延长线于点F ，在不添加任何辅助线的情况下，请直接写出图2中的四个等腰三角形，使写出的每个等腰三角形的顶角都等于45°.{解析}本题考查了全等判定与等腰三角形判定，（1）只需要证明△ABD ≌ △ACE 即可得出结论，（2）根据（1）中的结论知道△ADE 中∠DAE ＝45°，AD ＝AE ，所以45°和∠ADE 或∠AED 的所有相等的角所在三角形为符合条件的三角形．{答案} (1)证明:如图1∵AB ＝AC ∴∠ABC ＝∠ACB ∵BD ＝CE ∴△ABD ≌ △ACE ∴AD ＝AE (2)如图2 △ADE △BDF △BAE △CAD23（2020·江苏徐州）如图，AC ⊥BC ，DC ⊥EC ，AC =BC ，DC =EC ，AE 与BD 交于点F . （1）求证：AE =BD ； （2）求∠AFD 的度数. （第23题）{解析} （1）先利用边角边证明△ACE ≌△BCD ，然后由全等三角形的性质得到AE=BD ；（2）利用全等三角形的性质以及三角形的内角和定理来进行证明.{答案}解：（1）∵AC ⊥CB ，CD ⊥EC ，∴∠ACB=∠ECD=90˚,∴∠ACE=∠BCD ，在△ACE 和△BCD 中，AC BC ACE BCD CE CD =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD ，∴AE=BD.（2）∵△ACE ≌△BCD ，∴∠A=∠B ，∵∠AGC=∠BGF ，∴∠BFA=∠ACB=90˚，∴∠AFD=∠BFA=90˚.26.（2020·苏州）问题1：如图①，在四边形ABCD 中，90B C ∠=∠=︒，P 是BC 上一点，PA PD =，90APD ∠=︒.A求证：AB CD BC+=.问题2：如图②，在四边形ABCD中，45B C∠=∠=︒，P是BC上一点，PA PD=，90APD∠=︒.求ABCCDB+的值.{解析}问题1：证法一：证明ABP PCD∆∆≌；证法二：根据三角函数求解；问题2：分别过点A、D作BC的垂线，垂足为E、F转化为问题1求解。
2021年九年级中考数学 专题训练：全等三角形(含答案)
2021 中考数学专题训练：全等三角形一、选择题1. 下列各图中a，b，c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC 全等的是()A.甲和乙B.乙和丙C.甲和丙D.只有丙2. 如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能．．判定△ABE≌△ACD()A. ∠B＝∠CB. AD＝AEC. BD＝CED. BE＝CD3. 如图，AB⊥CD，且AB=CD.E，F是AD上两点，CE⊥AD，BF⊥AD.若CE=a，BF=b，EF=c，则AD的长为()A.a+cB.b+cC.a-b+cD.a+b-c4. 如图，在△ABC和△DEC中，已知AB＝DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是()A．BC＝EC，∠B＝∠E B．BC＝EC，AC＝DCC ．BC ＝DC ，∠A ＝∠D D ．∠B ＝∠E ，∠A ＝∠D5. (2019•临沂)如图，D 是AB 上一点，DF 交AC 于点E ，DE FE =，FC AB ∥，若4AB =，3CF =，则BD 的长是A ．0.5B ．1C ．1.5D ．26. 如图，已知点A ，B ，C ，D 在同一条直线上，△AEC ≌△DFB.如果AD=37 cm ，BC=15 cm ，那么AB 的长为 ( )A .10 cmB .11 cmC .12 cmD .13 cm7. 如图，AB ⊥BC ，BE ⊥AC ，垂足分别为B ，E ，∠1=∠2，AD=AB ，则下列结论正确的是( )A .∠1=∠EFDB .BE=EC C .BF=CD D .FD ∥BC8. 如图为6个边长相等的正方形的组合图形，则∠1＋∠2＋∠3等于( )A ．90°B ．120C ．135°D ．150°9. 如图，点G 在AB 的延长线上，∠GBC ，∠BAC 的平分线相交于点F ，BE ⊥CF于点H .若∠AFB ＝40°，则∠BCF 的度数为( )A．40°B．50°C．55°D．60°10. 如图，∠AOB＝120°，OP平分∠AOB，且OP＝2.若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有()A. 1个B. 2个C. 3个D. 3个以上二、填空题11. 如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE交于点H，请你添加一个适当条件：________，使△AEH≌△CEB.12. 如图，已知点B，C，F，E在同一直线上，∠1＝∠2，∠A＝∠D，要使△ABC≌△DEF，还需添加一个条件，这个条件可以是____________(只需写出一个)．13. 如图，在△ABC中，∠C＝90°，∠CAB＝50°，按以下步骤作图：①以点A 为圆心，小于AC的长为半径画弧，分别交AB，AC于点E，F；②分别以点E，F为圆心，大于12EF的长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D，则∠ADC的度数为________．14. 如图，已知AC＝FE，BC＝DE，点A，D，B，F在同一直线上，要使△ABC≌△FDE，还需添加一个．．条件，这个条件可以是__________(填一个即可)．15. (2019•南通)如图，△ABC中，AB=BC，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF，若∠BAE=25°，则∠ACF=__________度．16. 如图，在△ABC中，∠C＝90°，AC＝BC，AD是∠BAC的平分线，DE⊥AB，垂足为E.若△DBE的周长为20，则AB＝________．17. 如图所示，已知AD∥BC，则∠1＝∠2，理由是________________；又知AD ＝CB，AC为公共边，则△ADC≌△CBA，理由是______，则∠DCA＝∠BAC，理由是__________________，则AB∥DC，理由是________________________________．18. 如图，P是△ABC外的一点，PD⊥AB交BA的延长线于点D，PE⊥AC于点E，PF⊥BC交BC的延长线于点F，连接PB，PC.若PD＝PE＝PF，∠BAC＝64°，则∠BPC的度数为________．三、解答题19. 如图，AB=AD，BC=DC，点E在AC上.(1)求证:AC平分∠BAD;(2)求证:BE=DE.20. 如图，AD∥BC，AB⊥BC于点B，连接AC，过点D作DE⊥AC于点E，过点B作BF⊥AC于点F.(1)若∠ABF＝63°，求∠ADE的度数；DE＝BF＋EF.21. 如图②，在△ABC中，AB＝AC，AB＞BC，点D在边BC上，且CD＝2BD，点E，F在线段AD上，∠1＝∠2＝∠BAC.若△ABC的面积为15，求△ABE与△CDF的面积之和．2021 中考数学 专题训练：全等三角形-答案一、选择题1. 【答案】B [解析]依据SAS 全等判定可得乙三角形与△ABC 全等;依据AAS 全等判定可得丙三角形与△ABC 全等，不能判定甲三角形与△ABC 全等.故选B .2. 【答案】D【解析】A.当∠B ＝∠C 时，在△ABE 与△ACD 中，⎩⎨⎧∠A ＝∠AAB ＝AC ∠B ＝∠C，∴△ABE ≌△ACD (ASA)；B.当AD ＝AE 时，在△ABE 与△ACD 中，⎩⎨⎧AB ＝AC∠A ＝∠A AE ＝AD，∴△ABE ≌△ACD (SAS)；C.当BD ＝CE 时，∵AB ＝AC ，∴AD ＝AE ，在△ABE与△ACD 中，⎩⎨⎧AB ＝AC∠A ＝∠A AE ＝AD，∴△ABE ≌△ACD (SAS)；D.当BE ＝CD 时，在△ABE与△ACD 中，有AB ＝AC ，BE ＝BD ，∠A ＝∠A ，只满足两边及一对角对应相等的两个三角形不一定全等．故选D.3. 【答案】D [解析]∵AB ⊥CD ，CE ⊥AD ，BF ⊥AD ， ∴∠CED=∠AFB=90°，∠A=∠C ， 又∵AB=CD ，∴△CED ≌△AFB，∴AF=CE=a ，DE=BF=b ，DF=DE -EF=b -c ， ∴AD=AF +DF=a +b -c ，故选D .4. 【答案】C5. 【答案】B【解析】∵CF AB ∥，∴A FCE ∠=∠，ADE F ∠=∠，在ADE △和FCE △中，A FCE ADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ADE CFE △≌△，∴3AD CF ==，∵4AB =，∴431DB AB AD =-=-=．故选B ．6. 【答案】B[解析] ∵△AEC ≌△DFB ，∴AC=DB.∴AC-BC=DB-BC ，即AB=CD. ∵AD=37 cm ，BC=15 cm ， ∴AB==11(cm).7. 【答案】D[解析] 在△AFD 和△AFB 中，∴△AFD ≌△AFB. ∴∠ADF=∠ABF . ∵AB ⊥BC ，BE ⊥AC ， ∴∠BEC=∠ABC=90°.∴∠ABF+∠EBC=90°，∠C+∠EBC=90°. ∴∠ADF=∠ABF=∠C. ∴FD ∥BC.8. 【答案】C[解析] 在图中容易发现全等三角形，将∠3转化为与其相等的对应角后可以看出∠3与∠1互余．故∠1＋∠3＝90°.易得∠2＝45°，故∠1＋∠2＋∠3＝135°.9. 【答案】B[解析] 如图，过点F 分别作FZ ⊥AE 于点Z ，FY ⊥CB 于点Y ，FW ⊥AB 于点W.∵AF平分∠BAC，FZ⊥AE，FW⊥AB，∴FZ＝FW.同理FW＝FY.∴FZ＝FY.又∵FZ⊥AE，FY⊥CB，∴∠FCZ＝∠FCY.由∠AFB＝40°，易得∠ACB＝80°.∴∠ZCY＝100°.∴∠BCF＝50°.10. 【答案】D【解析】如解图，①当OM1＝2时，点N1与点O重合，△PMN 是等边三角形；②当ON2＝2时，点M2与点O重合，△PMN是等边三角形；③当点M3，N3分别是OM1，ON2的中点时，△PMN是等边三角形；④当取∠M1PM4＝∠OPN4时，易证△M1PM4≌△OPN4(SAS)，∴PM4＝PN4，又∵∠M4PN4＝60°，∴△PMN是等边三角形，此时点M，N有无数个，综上所述，故选D.二、填空题11. 【答案】AH＝CB(符合要求即可)【解析】∵AD⊥BC，CE⊥AB，垂足分别为点D、E，∴∠BEC＝∠AEC＝90°，在Rt△AEH中，∠EAH＝90°－∠AHE，在Rt△HDC中，∠ECB＝90°－∠DHC，∵∠AHE＝∠DHC，∴∠EAH＝∠ECB，∴根据AAS添加AH＝CB或EH＝EB；根据ASA添加AE＝CE.可证△AEH≌△CEB.故答案为：AH＝CB或EH＝EB或AE＝CE均可．12. 【答案】AB＝DE(答案不唯一)13. 【答案】65°14. 【答案】答案不唯一，如∠C＝∠E或AB＝FD等15. 【答案】70【解析】∵∠ABC=90°，AB=AC，∴∠CBF=180°–∠ABC=90°，∠ACB=45°，在Rt△ABE和Rt△CBF中，AB CBAE CF=⎧⎨=⎩，∴Rt△ABE≌Rt△CBF，∴∠BCF=∠BAE=25°，∴∠ACF=∠ACB+∠BCF=45°+25°=70°，故答案为：70．16. 【答案】20[解析] 由角平分线的性质可得CD＝DE.易证Rt△ACD≌Rt△AED，则AC＝AE，DE＋DB＝CD＋DB＝BC＝AC＝AE，故DE＋DB＋EB ＝AE＋EB＝AB.17. 【答案】两直线平行，内错角相等SAS全等三角形的对应角相等内错角相等，两直线平行18. 【答案】32°[解析] ∵PD＝PE＝PF，PD⊥AB交BA的延长线于点D，PE⊥AC 于点E，PF⊥BC交BC的延长线于点F，∴CP平分∠ACF，BP平分∠ABC.∴∠PCF＝12∠ACF，∠PBF＝12∠ABC.∴∠BPC＝∠PCF－∠PBF＝12(∠ACF－∠ABC)＝12∠BAC＝32°.三、解答题19. 【答案】证明:(1)在△ABC与△ADC中，∴△ABC≌△ADC(SSS)，∴∠BAC=∠DAC，即AC平分∠BAD. (2)由(1)知∠BAE=∠DAE.在△BAE与△DAE中，∴△BAE≌△DAE(SAS)，∴BE=DE.20. 【答案】解：(1)∵AD∥BC，AB⊥BC，∴∠ABC＝∠BAD＝90°.∵DE⊥AC，BF⊥AC，∴∠BFA＝∠AED＝90°.∴∠ABF＋∠BAF＝∠BAF＋∠DAE＝90°. ∴∠DAE＝∠ABF＝63°.∴∠ADE＝27°.(2)证明：由(1)得∠DAE ＝∠ABF ，∠AED ＝∠BFA ＝90°.在△DAE 和△ABF 中，⎩⎨⎧∠DAE ＝∠ABF ，∠AED ＝∠BFA ，AD ＝BA ，∴△DAE ≌△ABF(AAS)． ∴AE ＝BF ，DE ＝AF.∴DE ＝AF ＝AE ＋EF ＝BF ＋EF.21. 【答案】∵∠1＝∠2＝∠BAC ，且∠1＝∠BAE ＋∠ABE ，∠2＝∠CAF ＋∠ACF ，∠BAC ＝∠BAE ＋∠CAF ，∴∠BAE ＝∠ACF ，∠ABE ＝∠CAF.在△ABE 和△CAF 中，⎩⎨⎧∠BAE ＝∠ACF ，AB ＝CA ，∠ABE ＝∠CAF ，∴△ABE ≌△CAF(ASA)． ∴S △ABE ＝S △CAF .∴S △ABE ＋S △CDF ＝S △CAF ＋S △CDF ＝S △ACD . ∵CD ＝2BD ，△ABC 的面积为15， ∴S △ACD ＝10. ∴S △ABE ＋S △CDF ＝10.。
2021年中考数学复习微专题《全等三角形》解答题高频题型练习(旋转全等模型、对角互补模型、半角模型
2021年中考数学复习微专题《全等三角形》解答题高频题型精准练1. 如图，OE平分∠AOB，EF//OB，EC⊥OB．(1)求证：OF=EF(2)若∠BOE=15°，EC=5求：OF的值．2. 如图，点F、B、E、C在同一直线上，并且BF＝CE，∠ABC＝∠DEF．能否由上面的已知条件证明△ABC≌△DEF？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使△ABC≌△DEF，并给出证明．提供的三个条件是：①AB＝DE; ②AC＝DF; ③AC∥DF．F3. 如图，△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，∠BPC=40°，则∠CAP=________．4. 已知：如图，∠B=∠C=90°，M是BC的中点，且DM平分∠ADC．(1)求证：AM平分∠DAB．(2)试说明线段DM与AM有怎样的位置关系？并证明你的结论．5. 如图，CA=CB，CD=CE，∠ACB=∠DCE=40°，AD、BE交于点H，连接CH，求∠CHE的度数.6. 如图，在△ABC和△ADE中，AC=AB，AE=AD，∠CAB=∠EAD=90°(1)求证：CE=BD；(2)求证：CE⊥BD．7. 如图：在△ABC中，∠ACB=90°，AC=BC，过点C在△ABC外作直线MN，AM ⊥MN于M，BN⊥MN于N．(1)求证：MN=AM+BN．(2)若过点C在△ABC内作直线MN，AM⊥MN于M，BN⊥MN于N，则AM、BN与MN 之间有什么关系？请说明理由．8. 如图，∠BAD=∠CAE=90°，AB=AD，AC=AE，AF⊥CF，垂足为F．(1)求证：△ABC≅△ADE；(2)求证：CA平分∠ECF；(3)请指出CE与AF有怎样的数量关系，并说明理由．9. 在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F.试探究线段AB与AF、CF之间的数量关系，并证明你的结论.10. 如图，在正方形ABCD中，EE、F分别是边BC、CD上的点，∠EAF=45°，△ECF的周长为8，求正方形ABCD的面积.11. 已知，如图，△ABC的边BC的中点为点N，过点A的任一直线AD⊥BD于D，CE⊥AD于E，求证：NE=ND.12. 图1、图2中，点C为线段AB上一点，△ACM与△CBN都是等边三角形．（1）如图1，线段AN与线段BM是否相等？证明你的结论；（2）如图2，AN与MC交于点E，BM与CN交于点F，探究△CEF的形状，并证明你的结论．13. 如图①，将一个边长为2的正方形ABCD 和一个长为2，宽为1的矩形CEFD 拼在一起，构成一个大的矩形ABEF 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课时训练(二十)全等三角形
夯实基础
1.[2020·岳阳平江模拟]如图K20-1,将两根钢条AA',BB'的中点O连在一起,使AA',BB'可以绕着点O自由转动,就做成了一个测量工件,由三角形全等得出A'B'的长等于内槽宽AB的长,那么判定△OAB≌△OA'B'的理由是()
图K20-1
A.边角边
B.角边角
C.边边边
D.角角边
2.[2018·南京]如图K20-2,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD 的长为()
图K20-2
A.a+c
B.b+c
C.a-b+c
D.a+b-c
3.[2019·三明]如图K20-3,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,交AC于点D,DE⊥AB于点E,下列四个结论:①DE=DC;②BE=BC;③AD=DC;④△BDE≌△BDC.其中正确的有()
图K20-3
A.1个
B.2个
C.3个
D.4个
4.[2020·北京]如图K20-4,在△ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明△ABD ≌△ACD,这个条件可以是.(写出一个即可)
图K20-4
5.[2020·伊春]如图K20-5,Rt△ABC和Rt△EDF中,BC∥DF,在不添加任何辅助线的情况下,请你添加一个条件(答案不唯一),使Rt△ABC和Rt△EDF全等.
图K20-5
6.[2018·荆州]已知:∠AOB,求作:∠AOB的平分线.作法:①以点O为圆心,适当长为半径画弧,分别交OA,OB于点
MN的长为半径画弧,两弧在∠AOB内部交于点C;③画射线OC,射线OC即M,N;②分别以点M,N为圆心,大于1
2
为所求.上述作图用到了全等三角形的判定方法,这个方法是.
图K20-6
7.[2020·齐齐哈尔]如图K20-7,已知在△ABD和△ABC中,∠DAB=∠CAB,点A,B,E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是.(只填一个即可)
图K20-7
8.[2019·广州]如图K20-8,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌△CFE.
图K20-8
9.[2020·吉林]如图K20-9,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
图K20-9
10.[2019·桂林]如图K20-10,AB=AD,BC=DC,点E在AC上.
(1)求证:AC平分∠BAD;
(2)求证:BE=DE.
图K20-10
11.[2019·莱芜]如图K20-11,已知等边三角形ABC,CD⊥AB于D,AF⊥AC,E为线段CD上一点,且CE=AF,连接BE,BF,EG⊥BF于G,连接DG.
(1)求证:BE=BF;
(2)试说明DG与AF的位置关系和数量关系.
图K20-11
拓展提升
12.[2020·凉山州]如图K20-12,点P,Q分别是等边三角形ABC边AB,BC上的动点(端点除外),点P,点Q以相同的速度,同时从点A,点B出发.
(1)如图①,连接AQ,CP.求证:△ABQ≌△CAP.
(2)如图①,当点P,Q分别在AB,BC边上运动时,AQ,CP相交于点M,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
(3)如图②,当点P,Q在AB,BC的延长线上运动时,直线AQ,CP相交于M,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
图K20-12
【参考答案】
1.A
2.D [解析]∵AB ⊥CD ,CE ⊥AD ,BF ⊥AD ,∴∠CED=∠AFB=90°,∠A=∠C ,又AB=CD ,∴△CED ≌△AFB ,∴AF=CE=a ,DE=BF=b ,∴DF=DE -EF=b -c ,∴AD=AF+DF=a+b -c ,故选D .
3.C [解析]∵∠ACB=90°,BD 是∠ABC 的平分线,DE ⊥AB ,∴DE=DC ,故①正确; 又∵∠C=∠BED=90°,BD=BD ,∴Rt △BCD ≌Rt △BED (HL),故④正确;∴BE=BC ,故②正确; ∵Rt △ADE 中,AD>DE=CD ,∴AD=DC 不成立,故③错误.
4.答案不唯一,如∠BAD=∠CAD 或BD=CD 或AD ⊥BC [解析]根据等腰三角形三线合一的性质,要使△ABD ≌△ACD ,则可以填∠BAD=∠CAD 或BD=CD 或AD ⊥BC.
5.AB=ED
6.SSS
7.AD=AC (或∠D=∠C 或∠ABD=∠ABC 等) 8.证明:∵FC ∥AB ,∴∠A=∠FCE ,∠ADE=∠F .
在△ADE 与△CFE 中,{∠A =∠FCE ,
∠ADE =∠F ,DE =EF ,∴△ADE ≌△CFE (AAS).
9.证明:∵DE ∥AC ,∴∠EDB=∠A. 在△DEB 与△ABC 中,{DE =AB ,
∠EDB =∠A ,BD =CA ,
∴△DEB ≌△ABC (SAS).
10.证明:(1)在△ABC 与△ADC 中,{AB =AD ,
AC =AC ,BC =DC ,∴△ABC ≌△ADC (SSS),∴∠BAC=∠DAC ,
即AC 平分∠BAD. (2)由(1)得∠BAE=∠DAE ,
在△BAE与△DAE中,{BA=DA,
∠BAE=∠DAE, AE=AE,
∴△BAE≌△DAE(SAS),∴BE=DE.
11.解:(1)证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=∠ABC=60°,∵CD⊥AB,∴BD=AD,∠BCD=30°,
∵AF⊥AC,∴∠F AC=90°,
∴∠F AB=∠F AC-∠BAC=30°,
∴∠F AB=∠ECB,又∵AB=BC,AF=CE,
∴△ABF≌△CBE(SAS),∴BF=BE.
(2)AF=2GD,AF∥DG.
理由如下:连接EF,
∵△ABF≌△CBE,
∴∠ABF=∠CBE,BE=BF,
∵∠ABE+∠EBC=60°,
∴∠ABE+∠ABF=60°,
∴△BEF是等边三角形,
∵GE⊥BF,
∴BG=FG,∵BD=AD,∴AF=2GD,AF∥DG.
12.解:(1)证明:∵△ABC是等边三角形,
∴∠ABQ=∠CAP=60°,AB=CA,
又∵点P,Q运动速度相同,
∴AP=BQ,∴△ABQ≌△CAP(SAS).
(2)点P,Q在AB,BC边上运动的过程中,∠QMC的大小不变.理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,
∵∠QMC是△ACM的外角,
∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC.
∵∠BAC=60°,∴∠QMC=60°.
(3)点P,Q在AB,BC的延长线上运动时,∠QMC的大小不变.理由:易得△ABQ≌△CAP,∴∠BAQ=∠ACP,
∵∠QMC是△APM的外角,∴∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°-∠P AC=180°-60°=120°.。