[工学]2离散时间信号和系统的时域分析
实验二 离散时间信号的时域分析
实验二 离散时间信号的时域分析1.实验目的（1）学习MA TLAB 软件及其在信号处理中的应用，加深对常用离散时间信号的理解。
（2）利用MA TLAB 产生常见离散时间信号及其图形的显示，进行简单运算。
（3）熟悉MA TLAB 对离散信号的处理及其应用。
2.实验原理离散时间信号是时间为离散变量的信号。
其函数值在时间上是不连续的“序列”。
（1）单位抽样序列⎩⎨⎧=01)(n δ 00≠=n n 如果序列在时间轴上面有K 个单位的延迟，则可以得到)(k n -δ，即：1,()0,n k n k n kd ì=ïï-=íï¹ïî 该序列可以用MA TLAB 中的zeros 函数来实现。
（2）正弦序列)/2sin()(ϕπ+=Fs fn A n x可以利用sin 函数来产生。
（3）指数序列()(),n x n a n a R e =在MA TLAB 中通过：0:1;n N =-和.^;x a n =来实现。
3.实验内容及其步骤（1）复习有关离散时间信号的有关内容。
（2）通过程序实现上述几种信号的产生，并进行简单的运算操作。
单位抽样序列⎩⎨⎧=01)(n δ 00≠=n n 参考：% Generation of a Unit Sample Sequenceclf;% Generate a vector from -10 to 20n = -10:20;% Generate the unit sample sequenceu = [zeros(1,10) 1 zeros(1,20)];% Plot the unit sample sequencestem(n,u);xlabel('Time index n');ylabel('Amplitude');title('Unit Sample Sequence');axis([-10 20 0 1.2]);如果序列在时间轴上面有K 个单位的延迟，则可以得到)(k n -δ，即：1,()0,n k n k n kd ì=ïï-=íï¹ïî ，通过程序来实现如下所示结果。
实验2离散时间LTI系统的时域分析
实验二 离散时间LTI 系统的时域分析一 实验目的（1） 学会运用MATLAB 求解离散时间系统的零状态响应；（2） 学会运用MATLAB 求解离散时间系统的单位取样响应；（3） 学会运用MATLAB 求解离散时间系统的卷积和。
二 实验原理及实例分析1、离散时间系统的响应离散时间LTI 系统可用线性常系数差分方程来描述，即∑∑==-=-Mj jN i i j n x b i n y a 00)()( （1） 其中，i a （0=i ，1，…，N ）和j b （0=j ，1，…，M ）为实常数。
MATLAB 中函数filter 可对式（1）的差分方程在指定时间范围内的输入序列所产生的响应进行求解。
函数filter 的语句格式为y = filter (b , a , x )其中，x 为输入的离散序列；y 为输出的离散序列；y 的长度与x 的长度一样；b 与a 分别为差分方程右端与左端的系数向量。
【实例1】 已知某LTI 系统的差分方程为)1(2)()2(2)1(4)(3-+=-+--n x n x n y n y n y试用MATLAB 命令绘出当激励信号为)()2/1()(n u n x n=时，该系统的零状态响应。
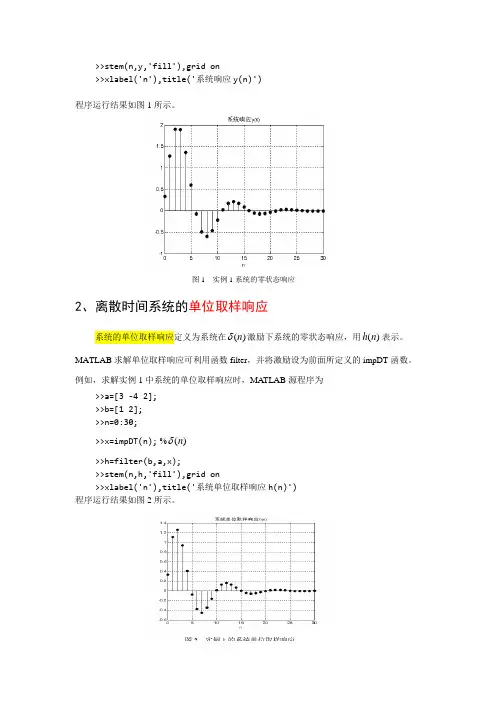
解：MATLAB 源程序为>>a=[3 -4 0 2];>>b=[1 2]; >>n=0:30;>>x=(1/2).^n;>>y=filter(b,a,x);>>stem(n,y,'fill'),grid on>>xlabel('n'),title('系统响应y(n)')程序运行结果如图1所示。
2、离散时间系统的单位取样响应系统的单位取样响应定义为系统在)(n δ激励下系统的零状态响应，用)(n h 表示。
MATLAB 求解单位取样响应可利用函数filter ，并将激励设为前面所定义的impDT 函数。
离散时间信号的时域分析实验报告
离散时间信号的时域分析实验报告实验报告：离散时间信号的时域分析一、实验目的本实验旨在通过MATLAB软件，对离散时间信号进行时域分析，包括信号的显示、基本运算（如加法、减法、乘法、反转等）、以及频域变换（如傅里叶变换）等，以加深对离散时间信号处理的基本概念和原理的理解。
二、实验原理离散时间信号是在时间轴上离散分布的信号，其数学表示为离散时间函数。
与连续时间信号不同，离散时间信号只能在特定的时间点取值。
离散时间信号的时域分析是研究信号的基本属性，包括幅度、时间、频率等。
通过时域分析，我们可以对信号进行各种基本运算和变换，以提取有用的信息。
三、实验步骤1.信号生成：首先，我们使用MATLAB生成两组简单的离散时间信号，一组为正弦波，另一组为方波。
我们将这些信号存储在数组中，以便后续分析和显示。
2.信号显示：利用MATLAB的绘图功能，将生成的信号在时域中显示出来。
这样，我们可以直观地观察信号的基本属性，包括幅度和时间关系。
3.基本运算：对生成的信号进行基本运算，包括加法、减法、乘法、反转等。
将这些运算的结果存储在新的数组中，并绘制出运算后的信号波形。
4.傅里叶变换：使用MATLAB的FFT（快速傅里叶变换）函数，将信号从时域变换到频域。
我们可以得到信号的频谱，进而分析信号的频率属性。
5.结果分析：对上述步骤得到的结果进行分析，包括比较基本运算前后的信号波形变化，以及傅里叶变换前后的频谱差异等。
四、实验结果1.信号显示：通过绘制图形，我们观察到正弦波和方波在时域中的波形特点。
正弦波呈现周期性的波形，方波则呈现明显的阶跃特性。
2.基本运算：通过对比基本运算前后的信号波形图，我们可以观察到信号经过加法、减法、乘法、反转等运算后，其波形发生相应的变化。
例如，两个信号相加后，其幅度和时间与原信号不同。
反转信号则使得波形在时间轴上反向。
3.傅里叶变换：通过FFT变换，我们将时域中的正弦波和方波转换到频域。
正弦波的频谱显示其频率为单一的直流分量，方波的频谱则显示其主要频率分量是直流分量和若干奇数倍的谐波分量。
(信息与通信)第七章离散时间系统的时域分析2
稳定性分析的应用
稳定性分析在离散时间系统中的应用非常广 泛。例如，在数字信号处理中，稳定性分析 可以帮助我们判断数字滤波器的性能和稳定 性；在控制系统分析中，稳定性分析是判断 系统能否正常工作的关键；在图像处理中， 稳定性分析可以帮助我们判断图像处理算法 的性能和稳定性。
此外，稳定性分析还可以应用于其他领域， 如金融、交通等。在这些领域中，稳定性分 析可以帮助我们理解和预测系统的行为，从
数字电视、数字广播、卫星通 信、移动通信等。
计算机控制系统
计算机控制的生产线、机器人 、智能家居等。
科学计算
数值计算、模拟仿真等。
02
离散时间系统的时域分析方法
差分法
01
差分法是通过离散时间信号的差分运算来分析系统的
特性。
02
差分方程是描述离散时间系统动态行为的基本工具，
通过求解差分方程可以得到系统的输出响应。
离散时间系统的仿真工具与技术
数学软件仿真
使用数学软件（如MATLAB、Simulink等）进行离散时间系统的建 模和仿真，可以进行系统性能分析和优化。
硬件描述语言仿真
使用硬件描述语言（如Verilog、VHDL等）进行离散时间系统的建 模和仿真，可以模拟硬件实现并进行验证。
模拟器仿真
使用模拟器（如QEMU、ModelSim等）进行离散时间系统的仿真， 可以模拟实际硬件运行环境，进行系统测试和验证。
对比分析
将离散时间系统的性能与其他同类系统进行对比， 以评估其优劣。
性能优化策略
01
算法优化
改进或优化离散时间系统的算法， 以提高其性能。
并行处理
利用并行处理技术，提高离散时间 系统的处理速度和效率。
03
6.离散时间信号与系统的时域分析
0, n 1 1 z ( n) x ( n) y ( n) , n 1 2 1 n 1 ( 2 )( n 1)( 2 ) , n 0
6 线性时不变离散系统的时域分析
5. 累加 设某一序列为x(n),则x(n)的累加序列 y(n)定义为
y ( n)
k
x(k ) x(n) * u(n)
n
根据上述性质可以推得以下结论：
f (n n1 ) * (n n2 ) f (n n1 n2 )
6 线性时不变离散系统的时域分析
例 已知 x1 (n) (n) 3 (n 1) 2 (n 2) x2 (n) u(n) u(n 3) 试求信号 x (n) ，它满足 x(n) x1 (n) x2 (n) 解：可利用上面讲述的性质求解。
1 1/ 2 1/4 -2 -1 0 1 1/8 ... 2
n
x(-n) 1 1/2 1/8 1/4 ... -2 -1 0
1
2
n
6 线性时不变离散系统的时域分析
3.序列的加减 两序列的加、减是指同序号(n)的序列值逐项对 应相加得一新序列。
6 线性时不变离散系统的时域分析
例：
x(n) 1 1/2 1/4 -2 -1 0 y(n) 2 1 1/4 1/2 1 2 n …
6 线性时不变离散系统的时域分析
2.单位阶跃序列
u（n）
1, u ( n) 0,
n0 n0
u(n)
...
-1 0 1 2 3 n
(n) u (n) u (n) u (n 1)
m 0
u (n) (n m) (n) (n 1) (n 2)
第2章 连续时间信号和离散时间信号的时域分析
第2章 连续时间信号和离散时间信号的时域分析
2．单位冲激信号 1) 单位冲激信号(Delta函数)的定义
∞ δ (t )dt = 1 ∫ ∞ (2-14) δ (t ) = 0 t ≠ 0 冲激信号用箭头表示，如图2.8(a)所示。冲激信号具有强度，其
强度就是冲激信号对时间的定积分值。在图中以括号注明，以与信 号的幅值相区分。 冲激信号可以延时至任意时刻 t0 ，以符号 δ (t t 0 ) 表示，定义 为
Ae st = Ae(σ + jω
0 )t
= Aeσ t cos(ω0 t ) + jAeσ t sin(ω0 t )
(2-8)
式(2-8)表明，一个复指数信号可以分解为实部﹑虚部两部分。 实部﹑虚部分别为幅度按指数规律变化的正弦信号。若 σ < 0 ，复指 数信号的实部﹑虚部为减幅正弦信号，波形如图2.4(a)﹑(b)所示。 若 σ > 0 ，其实部﹑虚部为增幅正弦信号，波形如图2.4(c)﹑(d)所 示。
第2章 连续时间信号和离散时间信号的时域分析
4．抽样函数 抽样函数是指 sin t 与 t 之比构成的函数，其定义如下：
sin t Sa(t ) = t
抽样函数的波形如图2.5所示。
(2-10)
图2.5 抽样函数的波形 抽样函数具有以下性质：
Sa(0) = 1， Sa(kπ) = 0 ，k
= ±1, ±2,L ∫∞ Sa(t )dt = π
第2章 连续时间信号和离散时间信号的时域分析
应用阶跃信号与延时阶跃信号，可以表示任意的矩形波脉冲信号。 例如，图2.7(a)所示的矩形波信号可由图2.7(b)表示,即 :
f (t ) = u (t T ) u (t 3T )
离散时间信号与系统的时域分析实验报告
离散时间信号与系统的时域分析实验报告报告⼆：⼀、设计题⽬1．绘制信号)()(1k k f δ=和)2()(2-=k k f δ的波形2.绘制直流信号)()(1k k f ε=和)2(2-=k f ε的波形3绘制信号)()(6k G k f =的波形⼆实验⽬的1．掌握⽤MATLAB 绘制离散时间信号（序列）波形图的基本原理。
2．掌握⽤MATLAB 绘制典型的离散时间信号（序列）。
3．通过对离散信号波形的绘制与观察，加深理解离散信号的基本特性。
三、设计原理离散时间信号(也称为离放序列)是指在时间上的取值是离散的，只在⼀些离放的瞬间才有定义的,⽽在其他时间没有定义，简称离放信号(也称为离散序列) 序列的离散时间间隔是等间隔(均匀)的，取时间间隔为T.以f(kT)表⽰该离散序列,k 为整数(k=0,±1.±2，...)。
为了简便，取T=1.则f(kT)简记为f(k)， k 表⽰各函数值在序列中出现的序号。
序列f(k)的数学表达式可以写成闭合形式,也可逐⼀列出f(k)的值。
通常,把对应某序号K0的序列值称为序列的第K0个样点的“样点值”。
四、设计的过程及仿真1clear all; close all; clc;k1=-4;k2=4;k=k1:k2;n1=0;n2=2;f1=[(k-n1)==0];f2=[(k-n2)==0];subplot(1,2,1)stem(k,f1,'fill','-k','linewidth',2);xlabel('k');ylabel('f_1(k)');title('δ(k)')axis([k1,k2,-0.1,1.1]);subplot(1,2,2)stem(k,f2,'filled','-k','linewidth',2);ylabel('f_2(k)');title('δ(k-2)')axis([k1,k2,-0.1,1.1]);程序运⾏后，仿真绘制的结果如图所⽰:2c lear all; close all; clc;k1=-2;k2=8;k=k1:k2;n1=0;n2=2; %阶跃序列开始出现的位置f1=[(k-n1)>=0]; f2=[(k-n2)>=0];subplot(1,2,1)stem(k,f1,'fill','-k','linewidth',2);xlabel('k');ylabel('f_1(k)');title('ε(k)')axis([k1,k2+0.2,-0.1,1.1])subplot(1,2,2)stem(k,f2,'filled','-k','linewidth',2);xlabel('k');ylabel('f_2(k)');title('ε(k-2)')axis([k1,k2+0.2,-0.1,1.1]);程序运⾏后，仿真绘制的结果如图所⽰:3clear all; close all; clc;k1=-2;k2=7;k=k1:k2; %建⽴时间序列n1=0;n2=6; f1=[(k-n1)>=0];f2=[(k-n2)>=0];f=f1-f2;stem(k,f,'fill','-k','linewidth',2);xlabel('k');ylabel('f(k)');title('G_6(k)')axis([k1,k2,-0.1,1.1]);程序运⾏后，仿真绘制的结果如图所⽰:五、设计的结论及收获实现了⽤matlab绘制离散时间信号, 通过对离散信号波形的绘制与观察，加深理解离散信号的基本特性。
数字信号处理知识点
《数字信号处理》辅导一、离散时间信号和系统的时域分析 （一） 离散时间信号（1）基本概念信号：信号传递信息的函数也是独立变量的函数，这个变量可以是时间、空间位置等。
连续信号：在某个时间区间，除有限间断点外所有瞬时均有确定值。
模拟信号：是连续信号的特例。
时间和幅度均连续。
离散信号：时间上不连续，幅度连续。
常见离散信号——序列。
数字信号：幅度量化，时间和幅度均不连续。
（2）基本序列（课本第7——10页）1）单位脉冲序列 1,0()0,0n n n δ=⎧=⎨≠⎩ 2）单位阶跃序列 1,0()0,0n u n n ≥⎧=⎨≤⎩3）矩形序列 1,01()0,0,N n N R n n n N ≤≤-⎧=⎨<≥⎩ 4）实指数序列 ()n a u n5）正弦序列 0()sin()x n A n ωθ=+ 6）复指数序列 ()j n n x n e e ωσ= （3）周期序列1）定义：对于序列()x n ，若存在正整数N 使()(),x n x n N n =+-∞<<∞ 则称()x n 为周期序列，记为()x n ，N 为其周期。
注意正弦周期序列周期性的判定（课本第10页）2）周期序列的表示方法： a.主值区间表示法 b.模N 表示法 3）周期延拓设()x n 为N 点非周期序列，以周期序列L 对作()x n 无限次移位相加，即可得到周期序列()x n ，即()()i x n x n iL ∞=-∞=-∑当L N ≥时，()()()N x n x n R n = 当L N <时，()()()N x n x n R n ≠（4）序列的分解序列共轭对称分解定理：对于任意给定的整数M ，任何序列()x n 都可以分解成关于/2c M =共轭对称的序列()e x n 和共轭反对称的序列()o x n 之和，即()()(),e o x n x n x n n =+-∞<<∞并且1()[()()]2e x n x n x M n *=+- 1()[()()]2o x n x n x M n *=--（4）序列的运算 1）基本运算2）线性卷积：将序列()x n 以y 轴为中心做翻转，然后做m 点移位，最后与()x n 对应点相乘求和——翻转、移位、相乘、求和定义式： 1212()()()()()m y n x m x n m x n x n ∞=-∞=-=*∑线性卷积的计算：A 、图解 B 、解析法C 、不进位乘法（必须掌握）3）单位复指数序列求和（必须掌握）/2/2/2/2/2/21/2/2/2/2/2/2(1)/21()()/(2)1()()/(2)sin(/2)sin(/2)j N j N j N j N j N j N j N N j nj j j j j j j n j N e e e e e e e j ee e e e e e e j N e ωωωωωωωωωωωωωωωωωω------------=-----===---=∑如果2/k N ωπ=，那么根据洛比达法则有sin(/2)(0)(0)(()())sin(/2)N N k N N k N ωδδω===或可以结合作业题3.22进行练习（5）序列的功率和能量能量：2|()|n E x n ∞=-∞=∑功率：21lim |()|21NN n NP x n N →∞=-=+∑ （6）相关函数——与随机信号的定义运算相同（二） 离散时间系统1．系统性质 （1）线性性质定义：设系统的输入分别为1()x n 和2()x n ，输出分别为1()y n 和2()y n ，即1122()[()],()[()]y n T x n y n T x n ==统的输对于任意给定的常数a 、b ，下式成立1212()[()()]()()y n T ax n bx n a y n by n =+=+则该系统服从线性叠加原理，为线性系统，否则为非线性系统。
离散信号与系统的时域和频域分析
h(k n) an1h(k n 1) an2h(k n 2) ... a0h(k ) 0 K>0时， n 齐次差分方程解： k
h(k ) [ ci ( ) ] (k )
离散信号与系统分析
开始
下一页
结束
本章说明
与连续信号与系统相比较，离散系统的数学描述是激励响应的差分方 程，其系统分析求响应实质是求解描述离散系统的差分方程。离散系 统的零状态响应可以用卷积和来求取。 时域分析： 1.掌握离散信号与系统的基本概念。 2.熟悉并掌握常用基本信号的描述、特性、运算与变换。 3.深刻理解采样定理的意义、内容及应用。 4.掌握离散系统的数学描述方法—差分方程及模拟图 5.掌握离散系统的时域分析—经典法求零输入响应、零状态响应。 6.熟悉卷积和法及其主要性质并会应用卷积和法求零状态响应。
4、图解法卷积
①变量代换 f1(n) 变成f1(k) f2(n) 变成f2( ②反折其中之一信号 ③将反折信号移位 m f2(-k) f2(m-k) 以k代n
④e将平移后的f2(m-k)与对应的f1(k)相乘 ⑤将各乘积值相加可画出全部y(m) ⑥重复步骤③到⑤可画出全部y(n) 5、系统零状态响应为
5、序列的运算
④差分：离散信号的差分运算 f (k ) f (k 1) f (k ) 前向差分： f (k ) f (k ) f (k 1) 后向差分： ⑤反折：将离散信号以纵轴为对称轴反折（转） ⑥压扩：将离散信号中f（k）的自变量k置换为ak得到的过程称为信号的尺 度变换 注意：不存在非整数ak的值！ ⑦求和：离散信号的求和运算是对某一离散信号进行历史推演的求和过程。
实验二离散时间系统的时域分析实验
数字信号处理——实验二武汉工程大学电气信息学院通信工程红烧大白兔一、实验目的1、在时域中仿真离散时间系统，进而理解离散时间系统对输入信号或延时信号进行简单运算处理，生成具有所需特性的输出信号的方法。
2、仿真并理解线性与非线性、时变与时不变等离散时间系统。
3、掌握线性时不变系统的冲激响应的计算并用计算机仿真实现。
4、仿真并理解线性时不变系统的级联、验证线性时不变系统的稳定特性。
二、实验设备计算机，MATLAB语言环境三、实验根底理论1、系统的线性线性性质表现为系统满足线性叠加原理：假设某一输入是由N个信号的加权和组成的，输出就是由系统对这N个信号中每一个的响应的相应加权和组成的。
设x1〔n〕和〔n〕分别作为系统的输入序列，其输出分别用y1(n)和y2(n)表示，即Y1(n)=T[x1(n)],y2(n)=T[x2(n)]假设满足T[a1x1(n)+a2x2(n)]=a1y1(n)+a2y2(n)x2那么那么该系统服从线性叠加原理，或者称为该系统为线性系统。
2、系统的时不变特性假设系统的变换关系不随时间变化而变化，或者说系统的输出随输入的移位而相应移位但形状不变，那么称该系统为时不变系统。
对于时不变系统，假设y(n)=T[x(n)]那么T[x(n-m)]=y(n-m)3、系统的因果性系统的因果性既系统的可实现性。
如果系统n时刻的输出取决于n时刻及n时刻以前的输入，而和以后的输入无关，那么该系统是可实现的，是因果系统。
系统具有因果性的充分必要条件是h(n)=0,n<04、系统的稳定性稳定系统是指有界输入产生有界输出〔BIBO)的系统。
如果对于输入序列x(n),存在一个不变的正有限值M，对于所有n值满足|x(n)|≤M<∞那么称该输入序列是有界的。
稳定性要求对于每个有界输入存在一个不变的正有限值K，对于所有n值，输出序列y(n)满足|y(n)|≤K<∞系统稳定的充分必要条件是系统的单位取样响应绝对可和，用公式表示为|h(n)|n5、系统的冲激响应设系统输入x(n)=δ(n)，系统输出y(n)的初始状态为零，这时系统输出用即h(n)=T[δ(n)]那么称h(n)为系统的单位脉冲响应。
离散时间系统的时域特性分析
离散时间系统的时域特性分析离散时间系统是指输入和输出均为离散时间信号的系统，如数字滤波器、数字控制系统等。
时域分析是研究系统在时间上的响应特性，包括系统的稳定性、响应速度、能否达到稳态等。
在时域分析中，我们通常关注系统的单位采样响应、阶跃响应和脉冲响应。
1. 单位采样响应单位采样响应是指当输入信号为单位脉冲序列时，系统的输出响应。
在时间域上，单位脉冲序列可以表示为:$$ u[n] = \begin{cases}1 & n=0\\ 0 & n \neq 0\end{cases} $$系统的单位采样响应可以表示为:$$ h[n] = T\{ \delta[n]\} $$其中，$T\{\}$表示系统的传输函数，$\delta[n]$表示单位脉冲序列。
通常情况下，我们可以通过借助系统的差分方程求得系统的单位采样响应。
对于一种具有一阶差分方程的系统，其单位采样响应可以表示为:2. 阶跃响应其中，$\alpha$为系统的传递常数。
3. 脉冲响应脉冲响应是指当输入信号为任意离散时间信号时，系统的输出响应。
其主要思路是通过将任意输入信号拆解成单位脉冲序列的线性组合，进而求得系统的输出响应。
设输入信号为$x[n]$，系统的脉冲响应为$h[n]$，则系统的输出信号$y[n]$可以表示为:$$ y[n] = \sum_{k=-\infty}^{\infty} x[k]h[n-k] $$在实际计算中，通常采用卷积算法实现脉冲响应的计算，即将输入信号和脉冲响应进行卷积运算。
总之，时域特性分析是对离散时间系统进行分析和设计时的基础。
对于实际工程应用中的系统，需要综合考虑其时域和频域特性，进而选择合适的滤波器结构、控制算法等来实现系统的优化设计。
离散信号与系统的时域分析
连续时间信号，在数学上可以表示为连续时间变量t的函 数。这类信号 的特点是：在时间定义域内，除有限个不连续 点外， 对任一给定时刻都对应有确定的信号值。 离散时间信号，简称离散信号，它是离散时间变量 tk(k=0,±1, ±2, …)的函数。信号仅在规定的离散时间点上 有意义，而在其它时间则没有定义。
1
(k－k 0 )
1
o
k 0 －1 k 0 k 0 ＋1 (a )
k
－k 0 － 1 －k 0 －k 0 ＋ 1 (b )
o
k
2. 正弦序列 正弦序列的一般形式为 由于
f (k ) A cos(0k )
f ( k ) A cos(0k ) A cos(0k 2m ) 2 m A cos0 k 0
5.2.2 卷积和的性质
性质1 离散信号的卷积和运算服从交换律、结合律和 分配律，即
f1 (k ) f 2 (k ) f 2 (k ) f1 (k )
f1 (k ) [ f 2 (k ) f 3 (k )] [ f1 (k ) f 2 (k )] f 3 (k )
f1 (k ) [ f 2 (k ) f 3 (k )] f1 (k ) f 2 (k ) f1 (k ) f 3 (k )
第五章 离散信号与系统 的时域分析
引 言
连续时间系统：这类系统用于传输和处理连续时间信号
离散系统：用于传输和处理离散时间信号的系统称为离散时间系
统，数字计算机是典型的离散系统例子，数据控制系统和数字通
信系统的核心组成部分也都是离散系统。
混合系统：连续系统与离散系统组合起来使用。
5.1 离散时间基本信号
信号与系统第五章 离散信号与系统的时域分析
f1(k) f (n)
6
n
3 2
1
1 1 2 3 k
3
1
1 1 2 3 4 k
《信号与系统》SIGNALS AND SYSTEMS
返回
ZB
5.1.3 常用的离散信号
(k)
1. 单位函数 (k)
(k)
1 0
k0 k0
1
1 1 2 3 k
(k n)
(k
n)
1 0
k n kn
1
1 0 1 2 n k
整理，得 y(k 2) 3y(k 1)＋2y(k)＝0
《信号与系统》SIGNALS AND SYSTEMS ZB
例：每月存入银行 A 元，设月息为 ，试确定第 k 次存
款后应有的存款额 y(k) 的方程。
解：第 k＋1 次存入后应有的存款额为
A y(k) y(k)
即 y(k 1) y(k) y(k) A
(1) 筛选特性 f (k) (k n) f (n)
k
(2) 加权特性 f (k) (k n) f (n) (k n)
应用此性质，可以把任意离散信号 f (k) 表示为一系 列延时单位函数的加权和，即
f (k) f (2) (k 2) f (1) (k 1)
返回《信号f与(0)系 (统k) 》fS(1IG) N(kAL1)SANDSnYSTfE(Mn)S
一阶后向差分
f (k) f (k) f (k 1)
二阶后向差分
f (k) 2 f (k) f (k) f (k 1)
《信号与系统》SIGf (Nk)AL2SfA(kND1)SYfS(TkEM2)S
返回
ZB
6. 序列的求和（累加） (对应于连续信号的积分)
离散信号与系统的时域分析实验报告
离散信号与系统的时域分析实验报告1. 引言离散信号与系统是数字信号处理中的重要基础知识，它涉及信号的采样、量化和表示，以及离散系统的描述和分析。
本实验通过对离散信号在时域下的分析，旨在加深对离散信号与系统的理解。
在实验中，我们将学习如何采样和显示离散信号，并通过时域分析方法分析信号的特性。
2. 实验步骤2.1 信号的采样与显示首先，我们需要准备一个模拟信号源，例如函数发生器，来产生一个连续时间域的模拟信号。
通过设置函数发生器的频率和振幅，我们可以产生不同的信号。
接下来，我们需要使用一个采样器来对模拟信号进行采样，将其转化为离散时间域的信号。
使用合适的采样率，我们可以准确地获取模拟信号的离散样本。
最后，我们将采样后的信号通过合适的显示设备进行显示，以便观察和分析。
2.2 信号的观察与分析在实验中，我们可以选择不同类型的模拟信号，例如正弦波、方波或脉冲信号。
通过观察采样后的离散信号，我们可以观察到信号的周期性、频率、振幅等特性。
通过对不同频率和振幅的信号进行采样，我们可以进一步研究信号与采样率之间的关系，例如采样定理等。
2.3 信号的变换与滤波在实验中，我们可以尝试对采样后的离散信号进行变换和滤波。
例如，在频域下对信号进行离散傅里叶变换（DFT），我们可以将时域信号转换为频域信号，以便观察信号的频谱特性。
通过对频谱进行分析，我们可以观察到信号的频率成分和能量分布情况。
此外，我们还可以尝试使用不同的数字滤波器对离散信号进行滤波，以提取感兴趣的频率成分或去除噪声等。
3. 实验结果与分析通过实验，我们可以得到许多有关离散信号与系统的有趣结果。
例如，在观察信号的采样过程中，我们可以发现信号频率大于采样率的一半时，会发生混叠现象，即信号的频谱会发生重叠，导致采样后的信号失真。
而当信号频率小于采样率的一半时，可以还原原始信号。
此外，我们还可以观察到在频域下，正弦波信号为离散频谱，而方波信号则有更多的频率成分。
4. 结论通过本实验，我们对离散信号与系统的时域分析有了更深入的理解。
第2章 离散时间信号与系统的变换域分析
bi z i
M
因此，X(z)可以展成以下部分分式形式
r Ak Ck n X ( z ) Bn z 1 1 zk z (1 zi z 1 ) k n 0 k 1 k 1 M N N r
其中，M≥N时，才存在Bn；Zk为X(z)的各单极点， Zi为X(z)的一个r阶极点。而系数Ak，Ck 分别为： A Re s[ X ( z ) ] z z zk k 1 d r k r x( z ) Ck r k [( z zi ) (r k )! dz z zz ,
X ( z)
0
n
0
n2 n
n
x ( n) z
n
n2
n
x ( n) z
x ( n) z
n 1
n2
n
14
第二项为有限长序列,其收敛域 0 z ; 第一项为z的正幂次级数，根据阿贝尔定理, 其收敛域为 0 z Rx ; R x 为最大收敛半径 .
i
k 1, 2r 29
分别求出各部分分式的z反变换（可查 P39 表2-1-1），然后相加即得X(z)的z反变换。
[例2-5]利用部分分式法，求X ( z) 1 (1 2 z 1 ) (1 0.5z 1 ) , z 2 的z反变换。 解：
1 z X ( z) 1 1 (1 2 z )(1 0.5 z ) ( z 2)( z 0.5) X ( z) z A1 A2 z ( z 2)( z 0.5) z 2 z 0.5
对采样信号 进行拉普拉斯变换
x a (t )
n
x (nT ) (t nT )
第2章 时域离散信号和系统的频域分析
X (z)
n
x ( n) z n x ( n) z n
n0
n
x ( n) z n
因而其收敛域应该是右边序列与左边序列收敛域的重叠部分。 等式右边第一项为右边序列，其收敛域为|z|>Rx-; 第二项为左边序 列，其收敛域为|z|<Rx+。如果Rx-<Rx+，则存在公共收敛区域，X(z)
n 0
n n
1 (az ) 1 az 1 n 0
1 n
|z|>|a|
这是一个无穷项的等比级数求和，只有在 |az-1|<1即|z|>|a|处收敛如图所示。故得到以上
1 z 闭合形式的表达式，由于 ，故 1 az 1 z a
jIm[z]
|a|
a
o
在z=a处有一极点(用“×”表示)，在z=0处有
4
第2章
时域离散信号和系统的频域分析
2.5 序列的Z 变换
2.5.1
ˇ
Z变换的定义 一个离散序列x(n)的Z变换定义为
X (z)
‵ 式中，z是一个复变量，它所在的复平面称为Z平 面。我们常用Z［x(n)］表示对序列x(n)进行Z 变换，也即
n
x ( n) z
n
（2.5.1）
Z[ x(n)] X ( z )
Re[z]
一个零点(用“○”表示)，收敛域为极点所
在圆|z|=|a|的外部。
18
第2章
时域离散信号和系统的频域分析
收敛域上函数必须是解析的，因此收敛域内不允许有极点存在。 所以，右边序列的Z变换如果有N个有限极点｛z1,z2,…,zN｝存在，
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
h
11
1.3 序列的周期性
定义 如何判断？
h
12
1.4 序列的简单运算
常 规 运 算
(四则运算)
线性运算 乘除运算
数 差分运算 学 运 算 累加运算
波
时移运算
形
变
压扩运算
换
反褶运算
相
卷积运算
互
运
算
相关运算
h
13
1.4 序列的简单运算
1）相加 z(n)x(n)y(n)
逐 项 对 应 相 加
a 1 3 210 1 2 3 45 n
fnann an n0,1,2,... a为实数
0 n1,2,...
h
10
1.2 典型离散信号
6）正弦型序列：
x(n) x(n)Asin(n0)
3 21 0 1 2 3 45 n
7）复指数序列：
x ( n ) e ( j 0 ) n x ( n ) e j e n e j o n e n ( c o s 0 n j s i n 0 n )
１）单位样值序列（单位冲激序列）：
(n)
(ni)
1 0 1 23 n
1 0 1 23 i n
(n) 10,,
n0 n0
(ni) 10,,
ni ni
h
7
1.2 典型离散信号
2）单位阶跃序列：
u(n)
u(ni)
3 21 0 1 2 3 45 n
3 21 0 1 i
n
(n)
1, 0,
n0 n0
(ni) 10 nnii
➢定义
序列：信号的时间函数只在某些离散瞬时nT 有定义值。
样值：序号为n的函数值x(n)称为在第n个样 点的样值。
h
5
1.1 离散时间信号概念
➢表示法
✓指针表示法 x(n) x(1) x(0) x(1) x(2)
✓图解表示： n——横坐标并取整数; x(n) ——纵坐标;
h
6
1.2 典型离散信号
线性系统：均匀性和叠加性。
设两对激励与响应x1(n)y1(n), x2(n)y2(n) 则c1x1(n)c2x2(n)c1y1(n)c2y2(n)
x 1 ( n ) 离散时间系统 y 1 ( n ) x 2 ( n ) 离散时间系统 y 2 ( n )
c1x1(n)c2x2(n)
c1y1(n)c2y2(n)
h
20
第二节 离散时间系统
h
21
2 离散时间系统
2.1 离散时间系统的概念 2.2 线性移（时）不变系统 2.3 单位样值（冲激）响应与卷积和 2.4 系统的因果性和稳定性
h
22
2.1 离散时间系统的概念
离散时间系统表示对输入序列的运算。
x(n)
离散时间系统
y(n)
T[x(n)]
h
23
2.2 线性移不变系统
离散时间系统
h
24
2.2 线性移不变系统
移不变系统
设 激 励 与 响 应 x ( n ) y ( n ) ,则 x ( n N ) y ( n N )
x(n)
y(n)
x(n)
y(n)
离散时间系统
0 1 23 n
0 1 23
n
x(nN)
0 1 23
y(nN)
x(n-N)
y(n-N)
离散时间系统
离散时间系统 的时域分析
h
1
主要内容
1.离散时间信号——序列 2.离散时间系统 3.离散时间系统的数学模型
h
2
第一节 离散时间信号
——序列
h
3
1 离散时间信号——序列
离散时间信号概念 典型离散信号（常用序列） 序列的周期性 序列的简单运算 离散信号的分解
h
4
1.1 离散时间信号概念
两 序 列 的 样 值 = = = = = = =新 序 列
2）相乘 z(n)x(n)y(n)
逐 项 对 应 相 乘
两 序 列 的 样 值 =======新 序 列
3）延时 z(n)x(nm)
逐 项 依 次 左 移 或 右 移 m 位
原 序 列 ============新 序 列
4）反褶 z(n)x(n)
1.4 序列的简单运算
5）尺度变换 z(n)x(an)
n 轴 上 压 缩 或 扩 展
原 序 列 的 波 形 = = = = = = = = = 新 序 列
需按规律去除某些点（压缩时a无法除尽的样点） 或补足相应的零值（扩展时多出的样点）
h
16
1.4 序列的简单运算
x ( n ) 波 形 如 图 所 示 , 分 别 画 出 x ( 2 n ) 、 x ( n / 2 ) 的 波 形
h
8
1.2 典型离散信号
3）矩形序列：
RN (n)
1, RN(n)0,
0nN1 其它n
3 21 0 1 2 N1N n
4）斜变序列：
x (n )
x(n)n(n)0n nn 00
3 21 0 1 2 N1 N n
h
9
1.2 典型Leabharlann 散信号5）单边实指数序列：
x(n)
a 1
x(n)
3 21 0 1 2 3 45 n
8）能量
E
xn 2
n
绝 对 值 平 方 和
序 列 中 所 有 样 值 = = = = = = = 能 量
h
19
1.5 离散信号的分解
常用分解法： x(n) x(m)(nm) m 其 中 x(m )(nm ) x 0( n) m m n n
将任意序列表示为加权、延迟的单位样值信号之和。
序列样值与其前面相邻的样值相减 后向差分
x(n )x(n )x(n 1 )
2x(n ) x(n )x(n ) 2 x(n 1 )x(n 2 )
序列样值与其后面相邻的样值相减
h
18
1.4 序列的简单运算
7）累加
n
z(n) x(k) k
累 加 至 第 n 样 点
原 序 列 中 所 有 样 值 = = = = = = = 新 序 列
0
n
h
1 23
n
25
2.2 线性移不变系统
线性移不变系统
如果信号是以离散时间作为自变量的，那 么就是线性时不变系统（LTI，Linear timeinvariant）。
x(n)
x(2n)
6
6
5
5
4
4
抽取
3
3
2
2
1
1
-3 -2 -1 0 1 2 3 4 5 6 n x(n/2) 6
5
4
3
2
1
h
-1 0 1 2 3 4 n
插值
17
-3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 n
1.4 序列的简单运算
6）差分
前向差分
x(n )x(n 1 )x(n )
相 对 纵 轴 反 折 波 形
原 序 列 = = = = = h = = = =新 序 列14
x(n)
1 2
(1
2)n
,
n 1
0,
n 1
x(n) 1
1/2 1/4 1/8
-2 -1 0 1 2 n
x(n+1) 1
1/2
1/4 1/8
-2 -1 0 1
n
x(－n)
1
1/2 1/4 1/8
-2 -1 0 1 2 n