矢量数据模型
合集下载
地理信息系统第三四章作业
1 、试分析 GIS 的几种主要的数据模型各自的优缺点。
答：GIS主要的数据模型有：矢量数据模型、栅格数据模型、矢量-栅格一体化数据模型、镶嵌数据模型、面向对象数据模型。
矢量数据模型：优点：1.便于面向现象(土壤类、土地利用单元等)；2.数据结构紧凑、冗余度低；3.有利于网络分析；4.图形显示质量好、精度高。
缺点：1.数据结构复杂；2.软件与硬件的技术要求比较高；3.多边形叠合等分析比较困难；4.显示与绘图成本比较高。
栅格数据模型：优点：1.数据结构简单；2.空间分析和地理现象的模拟均比较容易；3.有利于与遥感数据的匹配应用和分析；4.输出方法快速，成本比较低廉。
缺点：1.图形数据量大；2.投影转换比较困难；3.栅格地图的图形质量相对较低；4.现象识别的效果不如矢量方法。
2 、简述栅格数据压缩编码的几种方式和各自优缺点。
答：1.游程长度编码结构优缺点：对于游程长度编码，区域越大，数据的相关性越强，则压缩越大，适用于类型区域面积较大的专题图，而不适合于类型连续变化或类别区域分散的分类图（压缩比与图的复杂程度成反比）。
这种编码在栅格加密时，数据量不会明显增加，压缩率高，并最大限度地保留原始栅格结构，编码解码运算简单，且易于检索，叠加，合并等操作，这种编码应用广泛。
2. 块码结构优缺点：具有可变分辨率，即当属性变化小时图块大，对于大块图斑记录单元大，分辨率低，压缩比高。
小块图斑记录单元小，分辨率高，压缩比低。
所以，与行程编码类似，随图形复杂程度的提高而降低分辨率。
3. 链式编码（弗里曼编码或边界链码）优缺点：可以有效的压缩栅格数据，特别是对计算面积、长度、转折方向和凹凸度等运算十分方便。
缺点是对边界做合并和插入等修改，编辑比较困难。
这种结构有些类似矢量结构，但不具有区域的性质，因此对区域空间分析运算比较困难。
4. 四叉树编码优缺点：对于团块图像，四叉树表示法占用空间要少得多，四叉树表示法基本上是一种非冗余表示法。
第三章空间数据模型第3节矢量数据模型
(xn,yn) (x(1x,ny,1y)n) (x1,y1)
(a) (xn,yn)
(b)
(xn,yn)
A
KI
H
J
BC
G
FE
D
(c)
第三章空间数据模型第3节矢量数据模型
一维矢量具有方向、长度
方向：即有起始结点和终止结点
长度：可以用以下方式表达：
引入欧氏空间的距离概念：
n
长度 [(xi xi1)2 ( yi yi1)2 ]1/2 i2
一．基本概念 二．关系数据模型和关系表 三．矢量数据模型（ Spaghetti Model ） 四．矢量数据模型（拓扑数据模型）
第三章空间数据模型第3节矢量数据模型
一、基本概念
• 现实世界和矢量表达 • 位置和边界被清楚地记录 • 对象可以被识别 • 属性值与对象相联系 • 空间关系可以清晰表达
第三章空间数据模型第3节矢量数据模型
(1) 地理要素被当成单个对象对待
空间边界可以被清晰的编码
(2)对象之间没有关系
要素间的空间拓扑不被记录
第三章空间数据模型第3节矢量数据模型
矢量表达法
• 不同的空间特征具有不同的矢量维数
– 0维矢量-点：即空间中的一个点，没有大小、 方向，二维和三维欧氏空间中为：（x,y),(x,y,z)
– 一维矢量-线：空间中的线划要素或空间对象间 的边界，也称为弧段、链
用的概念，是三维空间中曲面法向矢量的 另外一种描述方法
第三章空间数据模型第3节矢量数据模型
空间曲面
• 矢量实现方法多样 • 常用等值线法、剖面法
第三章空间数据模型第3节矢量数据模型
三维矢量-体
• 指三维空间中的实体
4.2矢量数据模型
5
f
2
b3
g
6
拓扑关系表见书66、67 页；应 用。
五、三维数据结构
• 对于地下矿体分布、大气流场在某一 时刻的状态等，需要一种能描述真三 维的数据结构来表达。
• 三维数据结构一般用八叉树结构编码。
八叉树结构编码
• 它是在四叉树结构直接发展而来的，其原 理是将空间区域不断地分解为八个同样大 小的区域，一直到同一区域的属性单一为 止。
一、基本概念
• 1、矢量数据： 地图图形离散化成计算机能 识别和处理的数据。代表地 图图形的各离散点的平面坐 标。
• 2、空间数据： 地图数据大多反映空间地物的地
理分布，具有空间定位的性质。
3、属性数据
• 用来描述地物的质量和数量特征的 数据。
二、基本表示方法
点——用一坐标对表示：（X,Y）; 线——用一串有序的坐标对表示：
（X1,Y1）、 （X2,Y2）…（Xn,Yn） 面——用一串有序的但首尾坐标相同的x,y
坐标表示其轮廓范围：即（X1,Y1）、 （X2,Y2）…（Xn,Yn），（X1,Y1）.
三、矢量数据组织方法
• 点实体数据结构：P60 • 线实体数据结构： • 面实体数据结构：
线实体数据结构
唯一 线标 起始 终止 坐标 显示 非几 非几 非几 非几
• 缺点：
• 1、对于邻域函数运算、消除无用 边、处理岛状信息及检查拓扑关系 等方面较为困难。
• 2、编码表均需要人工方式建立， 工作量大，容易出错。
四、拓扑关系及其应用
• 通过一幅地图，我们可以了解地理要 素的区域信息、属性信息和空间信息。
• 而在计算机中，地理信息可以用坐标 对表示，属性信息以一组特征码的数 字或字符形式存储。而空间关系只能 靠拓扑结构来定义。
地理信息系统GIS—第3章矢量数据
空间关系及其表达
绝对空间关系：坐标、角度、方位、距离等 相对空间关系：相邻、包含、关联（连接）
等
相对空间关系的类型
拓扑空间关系：描述空间对象的相邻、包含、关联 关系等。
顺序空间关系：描述空间对象在空间上的排列次序 ，如前后、左右、东、西、南、北等。
地图、遥感影像上的空间关系是通过图形识别的， 在GIS中的空间关系则必须显式的进行定义和表达
地理信息系统
第三章 矢量数据模型
第二章内容回顾
1、什么叫坐标系？ 2、为什么要建立坐标系？ 3、为什么要建立地球的坐标系？ 4、如何建立地球的坐标系统？ 5、坐标系统与地图绘制有什么关系？
第二章内容回顾
1. 什么是地图投影？ 2. 地图投影主要有几种分类方法？ 3. 中国、美国的地图投影主要有哪几种？ 4. 在地图投影过程中需要设置哪两部分内容？需要设
3.2 拓扑
Topology一词来自希腊文，它的原意是“形状 的研究”。拓扑学属于数学中几何学的内容， 最早由德国数学家莱布尼茨1679年提出。历 史上著名的哥尼斯堡七桥问题、多面体的欧 拉定理、四色问题等都是拓扑学发展史的重 要问题。
3.2 拓扑-哥尼斯堡七桥问题
问：能不能每座桥都 只走一遍，最后又回 到原来的位置？
空间数据结构
数据结构的概念：
数据结构即指数据组织的形式，是适于计算机存 储、管理和处理的数据逻辑结构。
对空间数据而言，数据结构则是地理实体的空间 排列方式和相互关系的抽象描述。
在地理系统中描述地理要素和地理现象的空间数 据主要包括：空间位置、拓扑关系和属性三个方 面的内容。
常用的空间数据结构
ArcGIS中的矢量数据模型
Coverage Shapefile
第三章 矢量数据模型
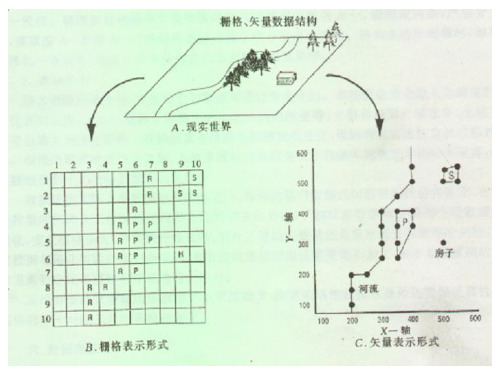
3.3.2 拓扑矢量数据
• 拓扑数据模型定义：不仅表达几何位置和属 性，还表示空间拓扑关系的矢量数据模型。 • 拓扑关系具体可由4个关系表来表示：
– （1）结点—弧段关系 – （2）弧段—结点关系 – （3）弧段—多边形关系 – （4）多边形—弧段关系
结点-弧
1
A b a 3 2
c
B e D 6 C 5 7
线：位置： (x1,y1),(x2,y2),„,(xn,yn) 属性：符号—形状、颜色、尺寸
面：位置： (x1,y1),(x2,y2),„,(xi,yi),„,(xn,yn) 属性：符号变化 等值线
点
抽象的点, 有位置，无宽度和长度；
美国佛罗里达洲地震监测站2002年9月该洲可 能的500个地震位置
1)关联性
• 关联性： 不同 类要素之间关 系
– 结点与弧段 如V9与L5,L6,L3 – 多边形与弧段 如P2与L3,L5,L2
2)邻接性
• 邻接性：同类元素 之间关系
– 多边形之间、结 点之间。 – 邻接矩阵 ： 重叠：-- 邻接：1 不邻接：0
P1 P2 P3 P4 P -1 1 1 P2 1 -1 0 P3 1 1 -0 P4 1 0 0 --
5 6
表中数字前负号为相反方向
7
B
—
空间拓扑关系表达：面与弧
1
A b a 3 2 c B
多边形-弧拓扑
e
D 7
面号
6
弧号 -1,-2,3 2,-7,5,0,-6 -3,-5,4 6
A B
C
5
4
d
a: 结点号 1: 弧段号
A: 多边形号 弧段数字化方向
C D
表中数字前负号为相反方向
第五章 矢量数据的空间分析方法
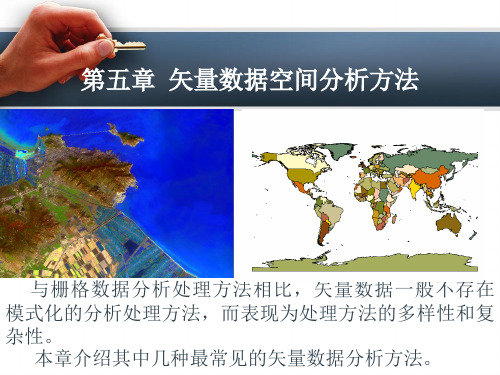
第五章 矢量数据空间分析方法
5.2 矢量数据的包含分析 在包含分析的具体算法中，点与点，点与线的包含分 析一般均可以分别通过先计算点到点，点到线之间的距离， 然后利用最小距离阈值判断包含的结果。 点与面之间的包含分析，或者称为Point-Polygon分析， 具有较为典型的意义。
5.2 矢量数据的包含分析
5.4 矢量数据的叠置分析
通过点与多边形叠置，可以计算出每个多边形类型里 有多少个点，不但要区分点是否在多边形内，还要描述在 多边形内部的点的属性信息。 例如将油井与行政区划叠置可以得到除油井本身的属 性如井位、井深、出油量等外，还可以得到行政区划的目 标标识，行政区名称，行政区首长姓名等。
5.4 矢量数据的叠置分析
8/37
5.1 矢量数据
(2)线状数据的拓扑关系 线状数据的拓扑关系 一条线段叫做一条弧段，由节点的连线组成。 一条线段叫做一条弧段，由节点的连线组成。开始点称为始 节点，结束点称为终节点。 节点，结束点称为终节点。 弧段-节点清单 列出了弧段-节点的关系 节点清单” “弧段 节点清单”列出了弧段 节点的关系 弧段-坐标清单 显示组成每条弧段的x、 坐标 坐标清单” “弧段 坐标清单”显示组成每条弧段的 、y坐标
第五章 矢量数据空间分析方法
5.4 矢量数据的叠置分析
其基本的处理方法是：根据两组多边形边界的交点来建立具有 多重属性的多边形或进行多边形范围内的属性特性的统计分析。 其中，前者叫做地图内容的合成叠置，如左图。后者称为地图 内容的统计叠置，如右图。
5.4 矢量数据的叠置分析
合成叠置的目的，是通过 区域多重属性的模拟，寻找和 确定同时具有几种地理属性的 分布区域。 或者按照确定的地理目标， 对叠置后产生的具有不同属性 多边形进行重新分类或分级， 因此叠置的结果为新的多边形 数据文件。
矢量和栅格数据模型介绍课件
在环境监测中，栅格数据模型可以用 于分析空气质量、水质、土壤状况等 环境要素的空间分布和变化趋势。
在城市规划中，栅格数据模型可以用 于城市空间布局规划、交通规划、公 共设施布局等方面。
矢量和栅格数据模型的比 较
数据精度比 较
矢量数据模型
矢量数据模型通过记录坐标点之间的几何关系来表达空间实 体，能够精确表示点、线、面等几何要素的位置和形状。因 此，矢量数据模型在表示复杂几何形状和细节方面具有较高 的精度。
栅格数据模型
栅格数据模型通过将空间划分为规则的格网或像素来表达空 间实体，每个像素或格网表示一个离散的地理空间单元。栅 格数据模型的精度取决于格网的大小，格网越小，精度越高。
数据结构比较
矢量数据模型
矢量数据模型的数据结构通常包括要素类和特征类，分别用于表示空间实体和 几何要素。矢量数据模型的数据结构相对简单，但表达的空间关系和属性信息 较为丰富。
栅格数据模型
栅格数据模型的数据结构通常包括网格矩阵和栅格地图，分别用于表示地理空 间单元和地表覆盖信息。栅格数据模型的数据结构相对复杂，但表达的空间信 息和属性信息较为有限。
数据处理速度比较
矢量数据模型
矢量数据模型的数据处理速度通 常较快，因为矢量数据模型的数 据结构相对简单，可以进行高效 的几何运算和空间分析。
02
矢量数据模型以离散方式表示空 间信息，每个几何对象都有明确 的坐标信息，可以精确表示地理 实体的位置和形状。
矢量数据模型特点
数据精度高
数据结构紧凑
由于矢量数据模型基于几何对象表示，可 以精确表示地理实体的位置和形状，因此 具有较高的数据精度。
矢量数据模型采用高效的数据压缩和编码 技术，使得数据存储和传输更加紧凑，节 省存储空间和网络带宽。
Ch04VECTORDATAMODEL
• spatial data structure 空间数据结构——是指适合于计算机系统 存储、管理和处理的地学图形的逻辑结构，是地理实体 的空间排列 方式和相互关系的抽象描述。
• digital description approach:
（1）explicit expression 显式描述—— raster data 栅格数据结构 （2）implicit expression 隐式描述—— vector data 矢量数据结构
4.2 Vector Data Structure 矢量数据结构类型
4.3 Vector Data Encoding 矢量数据结构编码
2
-Geosciences & GIS- Peng Kui
USTB
4.1 Spatial Objects and Their Digital Descriptions 空间对象及其数字化描述
4.2.2 Vector Data Structure 矢量数据结构类型
(1) Data Models for simple features 简单要素数据结构
(2) Data Models for topology 拓扑数据结构
(3) Data Models for Composite Features 复合要素数据模型
Spatial object
空间对象(实体）一般按地形维数进行归类划分 Point 点：零维 Line 线：一维 Polygon 面：二维 Volume 体：三维 Time 时间：通常以第四维表达，但目前GIS还很
难处理时间属性。
空间对象的维数与比例尺是相关的
-Geosciences & GIS- Peng Kui
• Can display more rapidly on monitors
• digital description approach:
（1）explicit expression 显式描述—— raster data 栅格数据结构 （2）implicit expression 隐式描述—— vector data 矢量数据结构
4.2 Vector Data Structure 矢量数据结构类型
4.3 Vector Data Encoding 矢量数据结构编码
2
-Geosciences & GIS- Peng Kui
USTB
4.1 Spatial Objects and Their Digital Descriptions 空间对象及其数字化描述
4.2.2 Vector Data Structure 矢量数据结构类型
(1) Data Models for simple features 简单要素数据结构
(2) Data Models for topology 拓扑数据结构
(3) Data Models for Composite Features 复合要素数据模型
Spatial object
空间对象(实体）一般按地形维数进行归类划分 Point 点：零维 Line 线：一维 Polygon 面：二维 Volume 体：三维 Time 时间：通常以第四维表达，但目前GIS还很
难处理时间属性。
空间对象的维数与比例尺是相关的
-Geosciences & GIS- Peng Kui
• Can display more rapidly on monitors
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
地理相关数据模型 基于对象数据模型
4
Copyright © The McGraw Hill Companies, Inc. Permission required for reproduction or display.
4.1 Georelational Data Model 地理相关数据模型
• Geographically referenced data: 地理参照数据：
• Vector data model 矢量数据模型 – Uses x, y coordinates of points to represent points, lines, areas 用点的 x, y 坐标来代表点、线、面 – Organizes geometric objects thus represented into digital data files 将如此表示的几何对象组织成数字化数据文件
复合要素数据模型
2
Copyright © The McGraw Hill Companies, Inc. Permission required for reproduction or display.
How does a computer “see” map features? 计算机如何“看”地图要素？(请看课本第72页)
Vector Data Model 矢量数据模型
1
Copyright © The McGraw Hill Companies, Inc. Permission required for reproduction or display.
CHAPTER 4: VECTOR DATA MODEL 第 4 章 矢量数据模型
– Uses geometric objects of point, line, area to represent spatial features
– 用点、线、面等几何对象表示空间要素
Figure 3.3 Point, line, and area features.
7
Copyright © The McGraw Hill Companies, Inc. Permission required for reproduction or display.
– Spatial and attribute components 空间和属性组分
• Georelational data model 地理相关数据模型
– Stores spatial and attribute data separately with a link in a split system 空间数据和属性数据分别贮存在链接的分离系统
Figure 3.2 Based on the georelational data model, an ArcInfo coverage has two components: graphic files for spatial data and INFO files for attribute data. The label connects the two components.
例如：井、建筑物、测量标记
8
Copyright © The McGraw Hill Companies, Inc. Permission required for reproduction or display.
Line
• One-dimensional • Properties of length and location • Defined by x, y coordinates of its end
• 4.1 Georelational data model 地理关系数据模型
• 4.2 Representation of Simple Features 简单要素的表示
4.3 Topology 拓扑 • 4.4 Nontopological Vector Data 非拓扑矢量数据 • 4.5 Data Models for Composite Features
– Called relational database 所谓关系数据库
• Object-based data model stores spatial and attribute data together, not a split system
基于对象数据模型将空间数据和属性数据贮存在一起
5
Copyright © The McGraw Hill Companies, Inc. Permission required for reproduction or display.
Point
• Zero dimensions • No length, width or height, only location
implied • Defined by x, y coordinates • Also called a node or vertex • Examples: wells, buildings, survey markers
3
Copyright © The McGraw Hill Companies, Inc. Permission required for reproduction or display.
Evolution of Vector Data Model 矢量数据模型的演变
• ESRI, Inc.
– Arc/Info: coverages – ArcView: shapefiles – ArcGIS: geodMcGraw Hill Companies, Inc. Permission required for reproduction or display.
4.2 Representation of Simple Features
简单要素的表示
• Vector data model 矢量数据模型