实验一 基本信号
数字信号处理实验报告
实验一 信号、系统及系统响应一、实验目的1、熟悉理想采样的性质，了解信号采样前后的频谱变化，加深对时域采样定理的理解。
2、熟悉离散信号和系统的时域特性。
3、熟悉线性卷积的计算编程方法：利用卷积的方法，观察、分析系统响应的时域特性。
4、掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对离散信号、系统及其系统响应进行频域分析。
二、 实验原理1.理想采样序列：对信号x a (t)=A e −αt sin(Ω0t )u(t)进行理想采样，可以得到一个理想的采样信号序列x a (t)=A e −αt sin(Ω0nT ),0≤n ≤50，其中A 为幅度因子，α是衰减因子，Ω0是频率，T 是采样周期。
2.对一个连续时间信号x a (t)进行理想采样可以表示为该信号与一个周期冲激脉冲的乘积，即x ̂a (t)= x a (t)M(t),其中x ̂a (t)是连续信号x a (t)的理想采样；M(t)是周期冲激M(t)=∑δ+∞−∞(t-nT)=1T ∑e jm Ωs t +∞−∞,其中T 为采样周期，Ωs =2π/T 是采样角频率。
信号理想采样的傅里叶变换为X ̂a (j Ω)=1T ∑X a +∞−∞[j(Ω−k Ωs )],由此式可知：信号理想采样后的频谱是原信号频谱的周期延拓，其延拓周期为Ωs =2π/T 。
根据时域采样定理，如果原信号是带限信号，且采样频率高于原信号最高频率分量的2倍，则采样以后不会发生频率混叠现象。
三、简明步骤产生理想采样信号序列x a (n),使A=444.128，α=50√2π，Ω0=50√2π。
（1） 首先选用采样频率为1000HZ ，T=1/1000，观察所得理想采样信号的幅频特性，在折叠频率以内和给定的理想幅频特性无明显差异，并做记录；（2） 改变采样频率为300HZ ，T=1/300，观察所得到的频谱特性曲线的变化，并做记录；（3） 进一步减小采样频率为200HZ ，T=1/200，观察频谱混淆现象是否明显存在，说明原因，并记录这时候的幅频特性曲线。
信号与信号实验
信号与信号实验MATLAB 部分实验一：基本信号在MATLAB 中的表示和运算 一、 实验目的;1、学会用MATLAB 表示常用连续信号的方法；2、学会用MATLAB 进行信号基本运算的方法；3、学会用MATLAB 实现连续时间信号的卷积的方法。
二、 实验内容：1、绘出下列信号的时域波形(1)f(t)=(2-e-2t)u(t) (2)f(t)=cos(πt)[u(t)-u(t-1)] (3)f(t)=u(-3t+2) (4)f(t)= -(1/2)tu(t+2) 解：t1=0:0.01:5; y1=(2-exp(-2*t1)).*(t1>0); subplot(221);plot(t1,y1);grid; title('f(t)=(2-e-2t)u(t)'); t2=0:0.01:5; y2=cos(pi*t2).*((t2>0)-(t2>1)); subplot(222);plot(t2,y2);grid; title('f(t)=cos(πt)[u(t)-u(t-1)]'); t3=-2:0.01:5; y3=(-3*t3+2>0); subplot(223);plot(t3,y3);grid; title('f(t)=u(-3t+2)'); t4=-3:0.01:5; y4=(-1/2)*t4.*(t4>-2); subplot(224);plot(t4,y4);grid; title('f(t)=-(1/2)tu(t+2)');00.511.52f(t)=(2-e-2t)u(t)图 1-1f(t)=cos(πt)[u(t)-u(t-1)]图1-200.51f(t)=u(-3t+2)图1-3f(t)=-(1/2)tu(t+2)图 1-42、用MATLAB 绘出下列信号的卷积积分f1(t)*f2(t)的时域波形(1) f1(t)=tu(t), f2(t)=u(t) (2) f1(t)=u(t)-u(t-4), f2(t)=sin(πt)u(t) (3) f1(t)= e-2t u(t), f2(t)= e-t u(t) (4) f1(t)= e-t u(t), f2(t)=u(t) 解：（1）fs=1000; t=-1:1/fs:4; x1=stepfun(t,0); x2=x1.*t; y=conv(x1,x2)/fs; n=length(y1); tt=(0:n-1)/fs-2; subplot(311),plot(t,x1),grid; title('f1(t)=tu(t)'); subplot(312),plot(t,x2),grid; title(' f2(t)=u(t)'); subplot(313),plot(tt,y),grid on; title('f1(t) * f2(t)');（2）fs=1000; t=-1:1/fs:4; x1=(t>0)-(t>4); x2=sin(pi*t).*(t>0); x=conv(x1,x2)/fs; n=length(x); tt=(0:n-1)/fs-2; subplot(311);plot(t,x1);grid; title('f1(t)=u(t)-u(t-4))'); subplot(312);plot(t,x2);grid; title('f2(t)=sin(πt)u(t)'); subplot(313);plot(tt,x);grid; title('f1(t) * f2');（3）t=0:1/fs:4; x1=exp(-2*t).*(t>0); x2=exp(-t).*(t>0); x=conv(x1,x2)/fs; n=length(x); tt=(0:n-1)/fs-0; subplot(311);plot(t,x1);grid; title('f1(t)= e-2t u(t)'); subplot(312);plot(t,x2);grid; title('f2(t)= e-t u(t)'); subplot(313);plot(tt,x);grid; title('f1(t) * f2(t)');（4）t=0:1/fs:2; x1=exp(-2*t).*(t>0); x2=(t>0); x=conv(x1,x2)/fs; n=length(x); tt=(0:n-1)/fs-0; subplot(311);plot(t,x1);grid; title(' f1(t)= e-t u(t))'); subplot(312);plot(t,x2);grid; title('f2(t)=u(t)'); subplot(313);plot(tt,x);grid; title('f1(t)*f2(t)');0.51 1.52 2.53 3.540.51 1.52 2.53 3.5412345678-1 -0.5 00.51 1.52 2.53 3.54? 2-1 -1 -0.5 00.51 1.52 2.53 3.54? 2-2 -2-112 3 4 5678? 2-3实验二：连续时间LTI 系统的时域分析一、实验目的：学会用MATLAB 求解连续系统的零状态响应、冲击响应和阶跃响应。
实验- 基本信号在 MATLAB中的表示和运算
实验一基本信号在 MATLAB中的表示和运算一、[实验目的]1．学会常用连续信号的MATLAB表示方法；2．学会用MATLAB进行信号的基本运算，为信号分析和滤波器设计奠定基础；3. 通过信号的求导，观察信号在跳变点处的导数；4. 通过卷积积分运算，观察两个时限信号的卷积积分结果所具有的特点；5. 掌握信号相关与卷积的关系；6. 通过实验熟悉自相关和互相关性质在周期信号识别、延迟信号检测等场合中的应用。
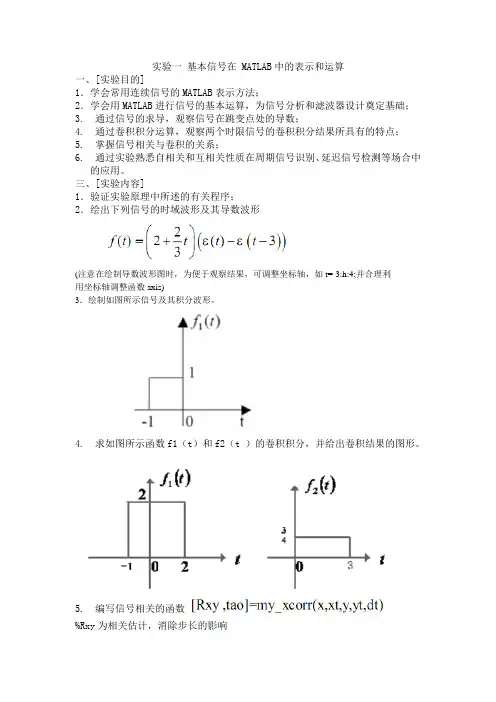
三、[实验内容]1．验证实验原理中所述的有关程序；2．绘出下列信号的时域波形及其导数波形(注意在绘制导数波形图时，为便于观察结果，可调整坐标轴，如t=-3:h:4;并合理利用坐标轴调整函数axis)3．绘制如图所示信号及其积分波形。
4. 求如图所示函数f1（t）和f2（t ）的卷积积分，并给出卷积结果的图形。
5. 编写信号相关的函数%Rxy为相关估计，消除步长的影响%tao为相关估计Rxy的序号向量%x为参加相关的信号,xt为信号 x的序号向量%y为需反转的信号,yt为 y的序号向量%dt为xt 或yt的步长（xt,yt的步长要一致）%信号反转可利用：ytf=fliplr(-yt);yf=fliplr(y);6.已知两信号x=rectpuls(t-0.5,1); y=rectpuls(t+0.5,1) ;调用自编函数[Rxy,tao]=my_xcorr(x,xt,y,yt,dt)计算 x 与 y 的时延差，即Rxy 取得最大值的时刻。
7. 已知频率为10Hz的余弦信号，分别求：（1）不带噪声的余弦信号的自相关；（2）分别求带有白噪声干扰的频率为 10Hz 的余弦信号和白噪声信号的自相关函数并进行比较，得出相应的结论。
主要信号如下：N=1000;Fs=500; %数据长度和采样频率n=0:N-1; t=n/Fs; %时间序列x=cos(2*pi*10*t); %频率为10Hz的余弦信号xz=cos(2*pi*10*t)+0.6*randn(1,length(t)); %带有白噪声干扰的频率为10Hz 的余弦信号noise_sig=randn(1,length(x)); %产生一与 x长度一致的随y=cos(2*pi*20*t); %频率为20Hz的余弦信号xy=x+y; 频率为10Hz, 20Hz的余弦信号的叠加信号…..调用 MATLAB 提供的函数[Rxx,tao]=xcorr(x,Lags,'unbiased')完成三个自相关运算。
《信号分析与处理》实验报告
序号：号项目名称：《信号分析与处理》实验报告学生学院：信息工程学院专业班级：学生学号：学生姓名：指导老师：朱铮涛2013年12月25日目录实验一、基本信号的产生和时频域抽样实验 (1)一、实验目的 (1)二、实验内容及所得图表 (1)三、思考题解答 (15)实验二、连续和离散系统分析 (16)一、实验目的 (16)二、实验内容和要求 (16)三、思考题解答 (22)实验三、用FFT实现谱分析实验 (23)一、实验目的 (23)二、实验原理 (23)三、实验内容及实验得到的结果 (23)四、实验结论 (26)五、思考题解答 (26)实验四、IIR数字滤波器设计和应用 (27)一、实验目的 (27)二、实验原理 (27)三、实验内容和结果 (27)四、思考题解答 (33)实验五、FIR数字滤波器设计和应用 (34)一、实验目的 (34)二、FIR数字滤波器的设计基本原理 (34)三、实验内容和实验结果 (37)四、思考题解答 (40)实验一、基本信号的产生和时频域抽样实验一、实验目的1、学习使用matlab产生基本信号波形、实现信号的基本运算；2、熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定理的理解;3、加深理解频谱离散化过程中的数学概念和物理概念，掌握频域抽样定理的基本内容。
二、实验内容及所得图表1、用Matlab产生以下序列的样本，并显示其波形：(a):()(0.9)cos(0.2/3),020nx n n nππ=+≤≤(b):)20()5()(---=nununx(c):)*5.0exp()(n nx-=(d):(e):(f):)()sin()(t u tAetx taΩ=-α2 设（a）：求其傅里叶变换；对进行采样，求出采样所得离散时间信号的傅里叶变（b）：用频率Fs=5000Hz对进行采样，求出采样所得离散时间信号的傅里叶变换；换；再用频率Fs=1000Hz（c）：分别针对（b）中采样所得离散时间信号和，重建出对应的连续时间信号和，并分别与原连续时间信号进行比较；根据抽样定理（即Nyquist定理）的知识，说明采样频率对信号重建的影响。
信号与系统实验(MATLAB版) (1)
《信号与系统MATLAB实现》实验指导书电气信息工程学院2014年2月长期以来，《信号与系统》课程一直采用单一理论教学方式，同学们依靠做习题来巩固和理解教学内容，虽然手工演算训练了计算能力和思维方法，但是由于本课程数学公式推导较多，概念抽象，常需画各种波形，作题时难免花费很多时间，现在，我们给同学们介绍一种国际上公认的优秀科技应用软件MA TLAB，借助它我们可以在电脑上轻松地完成许多习题的演算和波形的绘制。
MATLAB的功能非常强大，我们此处仅用到它的一部分，在后续课程中我们还会用到它，在未来地科学研究和工程设计中有可能继续用它，所以有兴趣的同学，可以对MATLAB 再多了解一些。
MATLAB究竟有那些特点呢？1．高效的数值计算和符号计算功能，使我们从繁杂的数学运算分析中解脱出来；2．完备的图形处理功能，实现计算结果和编程的可视化；3．友好的用户界面及接近数学表达式的自然化语言，易于学习和掌握；4．功能丰富的应用工具箱，为我们提供了大量方便实用的处理工具；MATLAB的这些特点，深受大家欢迎，由于个人电脑地普及，目前许多学校已将它做为本科生必须掌握的一种软件。
正是基于这些背景，我们编写了这本《信号与系统及MATLAB实现》指导书，内容包括信号的MA TLAB表示、基本运算、系统的时域分析、频域分析、S域分析、状态变量分析等。
通过这些练习，同学们在学习《信号与系统》的同时，掌握MATLAB的基本应用，学会应用MATLAB的数值计算和符号计算功能，摆脱烦琐的数学运算，从而更注重于信号与系统的基本分析方法和应用的理解与思考，将课程的重点、难点及部分习题用MATLAB进行形象、直观的可视化计算机模拟与仿真实现，加深对信号与系统的基本原理、方法及应用的理解，为学习后续课程打好基础。
另外同学们在进行实验时，最好事先预习一些MATLAB的有关知识，以便更好地完成实验，同时实验中也可利用MATLAB的help命令了解具体语句以及指令的使用方法。
信号实验报告
第一部分正文实验一常用信号观察一、实验目的：1．了解常用波形的输出和特点；2．了解相应信号的参数；3．了解示波器与函数发生器的使用；4．了解常用信号波形的输出与特点。
二、实验原理：描述信号的方法有很多可以是数学表达式（时间的函数），也可以是函数图形（即为信号的波形）。
信号的产生方式有多种，可以是模拟量输出，也可以是数字量输出。
本实验由数字信号发生器产生，是数字量输出，具体原理为数字芯片将数字量通过A/D 转换输出，可以输出广泛频率范围内的正弦波、方波、三角波、锯齿波等等。
示波器可以暂态显示所观察到的信号波形，并具有信号频率、峰值测量等功能。
三、实验内容：1．由数字信号发生器产生正弦波、三角波、方波以及锯齿波并输入示波器观察其波形。
2．使用示波器读取信号的频率与幅值。
四、实验设备：1．函数信号发生器一台2．数字示波器一台。
五、实验步骤：1．接通函数发生器的电源，连接示波器。
2．利用函数发生器产生各种基本信号波形，并将波形结果导入计算机中，保存图像，写出各种信号的数学表达式。
六、实验结果：根据实验测量的数据，绘制各个信号的波形图，并写出相应的数学函数表达式。
该试验包括交流：① 该正弦信号的数学表达式为：)1001sin(4t y π=图1-1输入正弦波（Hz 504，V ±） ② 该方波的数学表达式为： )]02.001.0()02.0([4∑∞-∞=----=k k t u k t u y图1-2 输入方波（Hz 504，V ±） ③ 该三角波的数学表达式为：∑∞-∞=-------+-----=k k t u k t u k t k t u k t u k t y )]}02.002.0()02.001.0()][02.0(02.0[800)]02.001.0()02.0()[02.0(800{图1-3 输入三角波（Hz 504，V ±） ④ 该锯齿波的数学表达式为：∑∞-∞=-----=k k t u k t u k t y )]}02.002.0()02.0()[02.0(400{图1-4 输入锯齿波（Hz 504，V ±） 实验的一些问题：数字信号发生器的示值与示波器测量有一定的误差。
信号分析实验一内容
实验一连续时间信号的时域和频域分析一. 实验目的：1. 熟悉MATLAB 软件平台。
2. 掌握MATLAB 编程方法、常用语句和可视化绘图技术。
3. 编程实现常用信号及其运算MATLAB 实现方法。
4. 编程实现常用信号的频域分析。
二. 实验原理：1、连续时间信号的描述：（1）向量表示法连续信号是指自变量的取值范围是连续的，且对于一切自变量的取值，除了有若干个不连续点之外，信号都有确定的值与之对应。
严格来说，MATLAB 并不能处理连续信号，而是用等时间间隔点的样值来近似表示连续信号。
当取样时间间隔足够小时，这些离散的样值就能较好地近似连续信号。
矩阵是MATLAB 进行数据处理的基本单元，矩阵运算是MATLAB 最重要的运算。
通常意义上的数量（也称为标量）在MATLAB 系统中是作为1×1 的矩阵来处理的，而向量实际上是仅有一行或者一列的矩阵。
通常用向量表示信号的时间取值范围，如t = -5:5，但信号x(t)、向量t 本身的下标都是从1 开始的，因此必须用一个与向量x 等长的定位时间变量t，以及向量x，才能完整地表示序列x(t)。
在MATLAB 可视化绘图中，对于以t 为自变量的连续信号，在绘图时统一用plot 函数；而对n 为自变量的离散序列，在绘图时统一用stem 函数。
（2）符号运算表示法符号对象(Symbolic Objects 不同于普通的数值计算)是Matlab 中的一种特殊数据类型，它可以用来表示符号变量、表达式以及矩阵，利用符号对象能够在不考虑符号所对应的具体数值的情况下能够进行代数分析和符号计算(symbolic math operations)，例如解代数方程、微分方程、进行矩阵运算等。
符号对象需要通过sym 或syms 函数来指定, 普通的数字转换成符号类型后也可以被作为符号对象来处理.我们可以用一个简单的例子来表明数值计算和符号计算的区别: 2/5+1/3 的结果为0.7333(double 类型数值运算), 而sym(2)/sym(5)+sym(1)/sym(3)的结果为11/15, 且这里11/15 仍然是属于sym 类型, 是符号数。
实验一 常用基本信号的MATLAB表示和运算
一．实验目的1.学会用MATLAB 表示常用连续信号的方法；2.学会用MATLAB 进行信号基本运算的方法； 二．实验原理与步骤 原理：1.信号的MATLAB 表示 （1）向量表示法对于连续时间信号()f t ,可以用两个行向量f 和t 来表示，其中向量t 是用形如12::t t p t =的命令定义的时间范围向量，其中，1t 为信号起始时间，2t 为终止时间，p 为时间间隔。
向量f 为连续信号f(t)在向量t 所定义的时间点上的样值。
例如：对于连续信号sin()()()t f t Sa t t==，同时用绘图命令plot()函数绘制其波形。
其程序如下： t2=-10:0.1:10; %定义时间t 的取值范围：-10~10，取样间隔为0.1，%则t2是一个维数为201的行向量 f2=sin(t2)./t2; %定义信号表达式，求出对应采样点上的样值 %同时生成与向量t2维数相同的行向量f2 figure(2); %打开图形窗口2Plot(t2,f2); %以t2为横坐标，f2为纵坐标绘制f2的波形 运行结果如下：（2）符号运算表示法如果一个信号或函数可以用符号表达式来表示，那么我们就可以用前面介绍的符号函数专用绘图命令ezplot()等函数来绘出信号的波形。
例如：对于连续信号sin()()()t f t Sa t t==，我们也可以用符号表达式来表示它，同时用ezplot()命令绘出其波形。
其MATLAB 程序如下： Syms t; %符号变量说明f=sin （t ）/t; %定义函数表达式ezplot （f,[-10,10]）; %绘制波形，并且设置坐标轴显示范围 运行结果如下：（3）常见信号的MATLAB 表示 单位阶跃信号：方法一：调用Heaviside(t)函数首先定义函数Heaviside(t)的m函数文件，该文件名应与函数名同名即Heaviside.m。
%定义函数文件，函数名为Heaviside,输入变量为x,输出变量为yfunction y=Heaviside（t）y=(t>0);%定义函数体，即函数所执行指令%此处定义t>0时y=1,t<=0时y=0,注意与实际的阶跃信号定义的区别。
信号与检验实验一
信号与测试技术实验一姓名：xxxx学号：xxxxxxxx班级：xxxxxxxx2016年5月实验目的1、掌握基本信号的时域和频域的分析方法。
2、掌握信号的自相关和互相关分析，了解其应用。
实验原理（1）信号的时域和频域转换目的：研究分析信号的时域特征（如持续时间、幅值、周期等）和信号的频域特征（如是否含有周期性信号、信号的频率带宽等）转换方法：时域的连续周期信号←→频域的离散信号：傅里叶级数时域的连续非周期信号←→频域的连续信号：傅里叶变换时域非周期序列←→频域连续周期信号：序列傅里叶变换时域有限长序列←→频域有限长序列：离散傅里叶变换（2）信号相关性相关是用来描述一个随机过程自身在不同时刻的状态间，或者两个随机过程在某个时刻状态间线性依从关系的数字特征。
自相关函数定义为：互相关函数定义为：实验内容1.产生不同的周期信号包括正弦信号、方波信号、锯齿波信号，在时域分析这些波形特征（幅值、频率）。
在Matlab 中产生随机噪声、阶跃信号、矩形脉冲。
信号进行Fourier 变换，在频域分析信号的特征，并说明方波信号和锯齿波信号的信号带宽。
1.1正弦信号dtt x t x T R TT xx ⎰+=∞→0)()(1lim )(ττdtt y t x T R TT xy ⎰+=∞→0)()(1lim )(ττ时域分析：信号频率f=50Hz，幅值为1的正弦信号。
频域分析：信号频谱为离散频谱。
由图易知，f=50Hz的时候达到最大值。
1.2方波信号时域分析：信号频率f=50Hz,幅值为2。
频域分析：信号频谱是离散的。
易知，在基频（f=50Hz）的奇数倍频（150Hz,250Hz）有振幅值，且幅值递减趋近于0。
信号带宽为10f0，即500Hz。
1.3 锯齿波信号时域分析：频率为50Hz，幅值为2。
频域分析：信号频谱是离散的。
易知，在基频（50Hz）的整数倍频有（100Hz，150Hz等）有振幅值。
幅值逐步递减趋近于0。
实验1 信号的时域描述与运算
实验1 信号的时域描述与运算一、实验目的1、掌握信号的MATLAB 表示及其可视化方法。
2、掌握信号基本时域运算的MATLAB 实现方法。
3、利用MATLAB 分析常用信号，加深对信号时域特性的理解。
二、实验原理1、连续时间信号的MATLAB 表示在MATLAB 中连续时间信号可以用两种方法来表示，即向量表示法和符号对象表示法。
在MATLAB 中连续时间信号是用信号等时间间隔采样后的采样值来近似表示的，当采样间隔足够小时，这些采样值就可以很好的近似表示出连续时间信号，这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量，其中一个向量用于表示信号的时间范围，另一个向量表示连续时间信号在该时间范围内的采样值。
例如一个正弦信号可以表示如下：>>t=0:0.01:10; >>x=sin(t); 利用plot(t,x)命令可以绘制上述信号的时域波形。
如果连续时间信号可以用表达式来描述，则还可以用符号表达式来表示信号。
例如对于上述正弦信号，可以用符号对象表示如下：>>syms t; >>x=sin(t); 利用ezplot(x)命令可以绘制上述信号的时域波形。
2、连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分，以及移位、反转、尺度变换等。
（1）相加和相乘对于两个采用向量表示的可以直接使用算术运算的运算符“+”和“*”来计算，此时要求表示两信号的向量时间范围和采样间隔相同。
采用符号对象表示的两个信号，可以直接根据符号对象的运算规则运算。
（2）微分和积分对于向量表示法表示的连续时间信号，可以通过数值计算的方法计算信号的微分和积分。
这里微分是用差分来近似求取的，由时间向量[t 1,t 2,⋯,t N ]和采样值向量[x 1,x 2,⋯,x N ]表示的连续时间信号，其微分可以下式实现1()|,1,2,,1k k k t t x xx t k N t+=-'≈=-∆其中∆t 表示采样间隔。
实验一 常用信号分类与观察山东交通学院
实验一 常用信号分类与观察一、实验目的1、观察常用信号的波形，了解其特点及产生方法。
2、学会用示波器测量常用波形的基本参数，了解信号及信号的特性。
二、实验仪器1 1块2、双踪示波器 1台三、实验原理对于一个系统特性的研究，其中重要的一个方面是研究它的输入输出关系，即在一特定的输入信号下，系统对应的输出响应信号。
因而对信号的研究是对系统研究的出发点，是对系统特性观察的基本手段与方法。
在本实验中，将对常用信号和特性进行分析、研究。
信号可以表示为一个或多个变量的函数，在这里仅对一维信号进行研究，自变量为时间。
常用信号有：指数信号、正弦信号、指数衰减正弦信号、抽样信号、钟形信号、脉冲信号等。
1、指数信号：指数信号可表示为atKe t f )(。
对于不同的a 取值，其波形表现为不同的形式，如图1-1所示：图1-1 指数信号2、指数衰减正弦信号：其表达式为 )0( )sin()0( 0)(⎩⎨⎧><=-t t Ket t f atω ， 其波形如图1-2所示：图1-2 指数衰减正弦信号3、抽样信号： 其表达式为：ttt S a sin )(=。
)(t S a 是一个偶函数，t =±π,±2π,…,±n π时，函数值为零。
该函数在很多应用场合具有独特的运用。
其信号如图1-3所示：图1-3 抽样信号4、钟形信号（高斯函数）： 其表达式为：2)t()(τ-=Eet f ，其信号如图1-4所示：图1-4钟形信号5、脉冲信号：其表达式为)()()(T t u t u t f --=，其中)(t u 为单位阶跃函数。
6、方波信号：信号周期为T ，前2T 期间信号为正电平信号，后2T期间信号为负电平信号。
TP1测试点可观测的常见信号主要有：指数信号（增长）、指数信号（衰减）、指数正弦信号（增长）、指数正弦信号（衰减）、抽样信号以及钟形信号。
观测前首先需将拨码开关SW1拨为00000001，规信号观测功能；然后通过设置S3对应选择常规信号类型，如下表所示：四、实验步骤任务一常用信号的波形观测预备工作：将拨码开关SW1置为“00000001”（开关拨上为1，拨下为0）, 打开实验箱及模块电源，按下复位键S2加载常用信号观测功能。
数字基带信号实验报告
数字基带信号实验报告指导老师：李敏姓名：学号：试验一数字基带信号一、试验目的1、了解单极性码、双极性码、归零码、不归零码等基带信号波形特点。
2、掌控AMI、HDB3码的编码规章。
3、掌控从HDB3码信号中提取位同步信号的方法。
4、掌控集中插入帧同步码时分复用信号的帧结构特点。
5、了解HDB3〔AMI〕编译码集成电路CD22103。
二、试验内容1、用示波器观测单极性非归零码〔NRZ〕、传号交替反转码〔AMI〕、三阶高密度双极性码〔HDB3〕、整流后的AMI码及整流后的HDB3码。
2、用示波器观测从HDB3码中和从AMI码中提取位同步信号的电路中有关波形。
3、用示波器观测HDB3、AMI译码输出波形。
三、试验步骤本试验运用数字信源单元和HDB3编译码单元。
1、熟识数字信源单元和HDB3编译码单元的工作原理。
接好电源线，打开电源开关。
2、用示波器观测数字信源单元上的各种信号波形。
用信源单元的FS作为示波器的外同步信号，示波器探头的地端接在试验板任何位置的GND点均可，进行以下观测：〔1〕示波器的两个通道探头分别接信源单元的NRZ-OUT和BS-OUT，对比发光二极管的发光状态，判断数字信源单元是否已正常工作〔1码对应的发光管亮，0码对应的发光管熄〕；〔2〕用开关K1产生代码×1110010〔×为任意代码，1110010为7位帧同步码〕，K2、K3产生任意信息代码，观测本试验给定的集中插入帧同步码时分复用信号帧结构，和NRZ码特点。
3、用示波器观测HDB3编译单元的各种波形。
仍用信源单元的FS信号作为示波器的外同步信号。
〔1〕示波器的两个探头CH1和CH2分别接信源单元的NRZ-OUT和HDB3单元的AMI-HDB3，将信源单元的K1、K2、K3每一位都置1，观测全1码对应的AMI码〔开关K4置于左方AMI端〕波形和HDB3码〔开关K4置于右方HDB3端〕波形。
再将K1、K2、K3置为全0，观测全0码对应的'AMI 码和HDB3码。
通信原理实验讲义
实验一数字基带信号系统实验一、实验目的1、了解插入帧同步码信号的帧结构特点。
2、了解数字绝对波形输出特点。
3、了解单极性码、归零码、不归零码等基带信号波形特点。
二、实验原理数字信源块是整个实验系统的发终端，模块内部只使用+5V电压，其原理方块图如图1-1所示。
本单元产生NRZ信号，信号码速率约为170.5KB,帧结构如图1-2所示。
帧长为24位，其中首位无定义，第2位到第8位是帧同步码（7位巴克码1110010），另外16位为2路数据信号，每路8位。
此NRZ信号为集中插入帧同步码时分复用信号，实验电路中数据码用红色发光二极管指示，帧同步码及无定义位用绿色发光二极管指示。
发光二极管亮状态表示1码，熄状态表示0码。
图1-1 数字信源方框图图1-2帧结构MAR-OUTFS图1-3 FS、NRZ-OUT波形三、实验内容用示波器观察数字信源中晶振信号试点，信源位同步信号，信源帧同步信号，NRZ信号（绝对码）。
本模块有以下测试点及输入输出点：CLK 晶振信号测试点BS—OUT 信源位同步信号输出点/测试点(2个)FS 信源帧同步信号输出点/测试点NRZ—OUT（AK） NRZ信号（绝对码）输出点/测试点（4个）四、实验步骤本实验使用数字信源单元。
1、熟悉数字信源单元的工作原理，检查直流稳压电源输出正常的+5V，+12V、-12V电压，关直流稳压电源。
将与直流稳压电源相连（若未连接好请通知指导教师）的实验专用的电源四芯插头正确的插入实验板左上角的四芯插座中。
打开直流稳压电源，实验中不再改变电源输出参数。
（以后的实验中接通电源均照此操作！）2、用示波器观察数字信源单元上的各种信号波形。
01110010 11110000 00001111(1.)示波器的两个通道探头分别接信源单元的NRZ—OUT和BS—OUT，对照发光二极管的发光状态，判断数字信源单元是否已正常工作（1码对应的发光管亮，0码对应的发光管熄。
）(2.)用开关K1产生代码X1110010（X为任意代码，1110010为7位帧同步码），K2、K3产生任意信息代码，观察本实验给定的集中插入帧同步码时分复用信号帧结构，和NRZ码特点。
信号与系统实验
信号与系统实验
信号与系统实验是指通过实验手段来研究和验证信号与系统的原理、性质、特性以及处理方法等内容。
它是信号与系统学科教学中非常重要的一部分，可以帮助学生深入理解信号与系统的原理和方法，并提高他们的实验能力和创新能力。
信号与系统实验通常包括以下几个方面：
1. 基本信号的产生和分析：产生基本信号（如正弦波、方波、锯齿波等）并对其进行分析，如频域特性、时域特性等。
2. 线性系统的模拟和测量：通过外部输入信号以及系统的输出信号来验证系统的线性性质，并测量系统的频率响应、阻抗等参数。
3. 卷积的实验验证：通过卷积的实验验证卷积的性质，并研究其应用于信号处理的例子。
4. 连续时间信号的采样和重构：通过模拟信号采样和重构实验来验证采样定理，以及研究采样率等相关内容。
5. FFT算法的实现和应用：通过实现快速傅里叶变换算法，研究其原理和应用于频域分析的例子。
综上所述，信号与系统实验对于学生理解和掌握信号与系统原理和应用方法具有重要的意义，通过实验可以更加深入地了解和掌握信号与系统的基本概念、算法以及应用技术。
信号产生实验实验报告
信号产生实验实验报告信号产生实验实验报告引言：在现代科学技术的发展中，信号产生是一项十分重要的实验。
无论是通信领域、电子工程还是生物医学等领域，信号产生都扮演着至关重要的角色。
本实验旨在通过实际操作，探索信号产生的原理和方法，以及对信号的性质和特点进行分析和研究。
一、实验目的本实验的主要目的是掌握信号产生的基本原理和方法，了解信号的性质和特点，并能够运用所学知识进行实际应用。
二、实验器材和原材料1. 信号发生器2. 示波器3. 电阻、电容、电感等元件4. 电源5. 连接线等三、实验步骤1. 准备工作：检查实验器材的正常工作状态，确保实验环境安全。
2. 连接信号发生器和示波器：使用连接线将信号发生器和示波器连接起来，确保信号的输出能够被示波器正确地接收和显示。
3. 选择信号类型：在信号发生器上选择所需的信号类型，如正弦波、方波、三角波等。
4. 调节信号参数：通过调节信号发生器上的频率、幅度等参数，改变信号的特性，观察示波器上信号的变化。
5. 添加电阻、电容等元件：通过在信号发生器和示波器之间添加电阻、电容等元件，改变信号的波形，观察信号的变化。
6. 记录观察结果：根据实验过程中的观察结果，记录信号的特性和变化规律，分析信号产生的原理和机制。
四、实验结果和分析通过实验观察和记录，我们发现信号的产生与频率、幅度、波形等参数密切相关。
当我们改变信号发生器上的频率时，示波器上的信号波形也会相应地发生变化。
当频率较低时，信号呈现出较为缓慢的变化，而当频率较高时，信号则呈现出较为快速的变化。
此外，当我们改变信号发生器上的幅度时，示波器上的信号振幅也会相应地发生变化。
通过添加电阻、电容等元件，我们还可以改变信号的波形，例如将正弦波转换为方波或三角波。
五、实验总结通过本次实验，我们深入了解了信号产生的原理和方法，掌握了信号的性质和特点。
信号产生在现代科学技术中具有广泛的应用，例如在通信领域中，信号的产生和传输是实现信息交流的基础；在电子工程中，信号的产生和处理是实现电路功能的关键；在生物医学领域中，信号的产生和检测是实现生物信号分析和诊断的重要手段。
信号与系统实验指导书
信号与系统实验指导书实验一：信号与系统实验指导书实验目的：本实验旨在通过对信号与系统的实际应用，加深对信号与系统理论知识的理解和掌握程度。
具体实验目标如下：1. 学习使用示波器和信号发生器进行信号的产生与观测；2. 熟悉信号与系统实验中常用的信号类型，如正弦信号、方波信号等；3. 掌握信号的频谱分析方法，如傅里叶变换和功率谱估计；4. 理解系统的时域和频域特性，如冲激响应、单位脉冲响应和传递函数。
实验器材：1. 示波器（型号：XXXX）2. 信号发生器（型号：XXXX）3. 实验信号源（型号：XXXX）4. 电缆、连接线等实验辅助器材实验步骤：注意：在进行实验之前，请确保所有仪器设备连接正确，且电源线接地良好。
第一步：信号发生与观测1. 将信号发生器的输出端与示波器的输入端连接，在信号发生器上选择合适的信号类型和频率进行输出。
2. 调节示波器的触发模式和水平控制，使得信号在示波器屏幕上显示清晰。
3. 改变信号发生器的输出参数，观察示波器上信号的变化，并记录观测结果。
第二步：信号频谱分析1. 使用信号发生器产生一个频率为f的正弦信号，并将信号输入示波器。
2. 切换示波器的测量模式为频谱分析模式，选择傅里叶变换作为频谱分析方法。
3. 记录示波器上显示的频谱图像，并分析频谱图像中各谐波分量的相对强度和频率。
第三步：系统时域特性测量1. 使用信号发生器产生一个单位冲激信号，并将信号输入系统。
2. 通过示波器观测系统的响应信号，并记录系统对单位冲激信号的响应情况。
3. 切换示波器的触发模式，选择单次触发模式，以便更好地观察系统的响应。
第四步：系统频域特性测量1. 使用信号发生器产生一个频率为f的正弦信号，并将信号输入系统。
2. 通过示波器观测系统的输出信号，并记录观测结果。
3. 将示波器的触发模式设置为频谱分析模式，进行系统输出信号的频谱分析。
4. 根据频谱分析结果，分析系统在不同频率下的增益特性和相位特性。
实验一典型电信号的观察与测量
七、实验报告
1.整理实验中显示的各种波形，绘制有代表性的波形。
2.总结实验中所用仪器的使用方法及观测电信号的方法。
3心得体会及其它。
实验二 电路元件伏安特性的测绘
一、实验目的
1.学会识别常用电路元件的方法
2.掌握线性电阻、非线性电阻元件伏安特性的逐点测试法
3.掌握实验台上直流电工仪表和设备的使用方法。
UR（V）
0
2
4
6
8
10
I（mA）
2.测定非线性白炽灯泡的伏安特性
将图2-2中的R换成一只12V，0.1A的灯泡，重复1的测量。数据记录于表2，UL为灯泡的端电压。
表2白炽灯泡伏安特性实验数据
UL（V）
0.1
0.5
1
2
3
4
5
I（mA）
3.测定半导体二极管的伏安特性
按图2-3接线，R为限流电阻器。测二极管的正向特性时，其正向电流不得超过35mA，二极管D的正向压降UD+可在0～0.75V之间取值。在0.5～0.75V之间应多取几个测量点。测反向特性时，只需将图2-3中的二极管D反接，且其反向电压UD－可加到30V。
图1-1软件主界面
如果USB采集卡驱动没有装好或者USB线没有连接到虚拟示波器接口箱，启动时都会弹出警告对话框，如图1-2所示界面。此时应关闭软件，连接好USB电缆后，再重新启动软件。
图1-2错误警告
2.2虚拟示波器界面介绍
打开软件，进入虚拟示波器界面，如图1-1所示。虚拟示波器界面中，左边栏是示波器显示窗口，右面是参数设置和操作区，下面是参数显示窗口。用户可以通过右键快捷菜单，参数设置和操作区按钮，完成对虚拟示波器的操作。
CH1耦合方式：包括直流耦合方式、交流耦合方式和接地。
信号与系统实验教学大纲
信号与系统实验教学大纲一、实验目的本实验旨在帮助学生深入了解信号与系统的基本概念和原理，并通过实际操作加深对信号与系统的理解和应用能力。
具体目的包括：1. 掌握信号与系统的基本概念和定义；2. 理解常见信号的分类和特性；3. 熟悉信号与系统的数学表示方法；4. 学习使用仪器和工具进行信号与系统的实际测量与分析；5. 培养学生的实验设计和解决问题的能力。
二、实验内容1. 基本信号的生成与分析实验1.1 正弦信号的产生和观测1.2 方波信号的产生和观测1.3 单位阶跃信号和单位冲激信号的产生和观测2. 信号与系统的线性特性实验2.1 线性系统的特性分析2.2 线性时不变（LTI）系统的特性分析2.3 线性时变系统的特性分析3. 时域和频域分析实验3.1 时域分析方法的学习与应用3.2 傅里叶变换及其性质的学习与应用3.3 频谱分析实验4. 常用滤波器的设计与应用实验4.1 低通滤波器的设计与应用4.2 高通滤波器的设计与应用4.3 带通滤波器的设计与应用4.4 带阻滤波器的设计与应用5. 采样和量化实验5.1 采样定理及抽样方式的实验验证5.2 量化误差的分析与实验验证三、实验要求1. 掌握实验的基本原理和方法，理解实验的实际应用场景；2. 完成实验报告的撰写和实验数据的分析；3. 在实验过程中严格遵守实验守则，注意实验安全；4. 鼓励学生进行探索和创新，提出自己的实验设计方案。
四、实验器材和软件1. 示波器2. 函数发生器3. 信号源4. 滤波器5. 计算机及相关软件（如MATLAB等）五、实验评分实验报告和实验操作将共同作为评分的主要依据，其中实验报告占60%的权重，实验操作占40%的权重。
实验报告的评分标准包括实验目的的明确性、实验内容的完整性、实验数据的准确性以及实验结论的合理性。
实验操作的评分标准包括实验装置的正确搭建、实验数据的准确采集和实验操作的规范性。
六、参考资料1. 《信号与系统实验教程》2. 《信号与系统实验导论》3. 《信号与系统实验教程及案例》4. 《MATLAB在信号与系统实验中的应用》5. 《信号与系统实验方法与技巧》本大纲根据信号与系统实验教学的实际需求和课程目标制定，重点培养学生的实际动手能力和问题解决能力。
实验一信号基本运算的MATLAB实现
实验一信号基本运算的MATLAB实现MATLAB是一种用于数值计算和数据可视化的高级编程语言和环境。
它提供了丰富的函数和工具箱来处理信号。
在MATLAB中，我们可以进行一系列信号的基本运算，包括信号的加法、乘法、平移、取反等。
下面将介绍几种常见的信号基本运算的MATLAB实现方法。
1.信号的加法：信号的加法可以使用MATLAB的"+"操作符来实现。
例如，我们有两个信号x1和x2，它们的采样点分别存储在向量x1和x2中，我们可以使用以下代码将它们相加，并将结果存储在向量y中：```matlabx1=[1,2,3];x2=[4,5,6];y=x1+x2;disp(y); % 输出结果：5 7 9```2.信号的乘法：信号的乘法可以使用MATLAB的"\*"操作符来实现。
与信号的加法类似，我们可以将要相乘的信号存储在向量中，并使用"\*"操作符进行乘法运算。
例如，两个信号x1和x2的乘积可以用以下代码实现：```matlabx1=[1,2,3];x2=[4,5,6];y=x1.*x2;disp(y); % 输出结果：4 10 18```3.信号的平移：信号的平移是将信号在时间上移动一定的步长。
在MATLAB中，我们可以使用向量索引来实现信号的平移。
例如，我们有一个信号x，要将其向右平移3个单位，可以使用以下代码实现：```matlabx=[1,2,3,4,5];shift = 3;y = [zeros(1, shift), x];disp(y); % 输出结果：0 0 0 1 2 3 4 5```在上述代码中，我们使用了`zeros`函数生成了一个长度为平移步长的零向量，并将其与信号x进行拼接。
4.信号的取反：信号的取反是将信号的每个采样点的值取相反数。
在MATLAB中，我们可以使用"-"操作符来实现信号的取反。
例如，我们有一个信号x，要将其取反，可以使用以下代码实现：```matlabx=[1,-2,3,-4,5];y=-x;disp(y); % 输出结果：-1 2 -3 4 -5```在上述代码中，我们使用了"-"操作符来实现信号的取反。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验一基本信号一、实验目的利用MATLAB 产生基本信号、绘制信号波形；二、实验原理本实验主要使用MATLAB 内部向量程序来产生信号。
用MATLAB 的stem 指令绘出离散时间信号。
下面的MATLAB 代码产生31点离散时间正弦信号。
nn=0:30; %时间标号向量 sinus=sin(nn/2+1);依据MATLAB 编址约定，标号0n n =必须对应nn(1);同样，sinus （1）是正弦信号的第一个数值。
Stem 指令产生离散时间信号图形。
使用stem 指令绘出正弦波。
stem(nn,sinus);必须给定向量的第一个参数以得到正确的n 轴。
1、冲激信号最简单的信号是单位冲激信号：0001[](3.1)0n n n n n n δ=⎧-=⎨≠⎩在MATLAB 中产生冲激信号，必须先确定所关注信号部分的长度。
2、正弦信号另一个非常基本的信号是正弦信号。
一般，完备的描述实正弦信号需要三个参数：振幅A 、频率0ω和相位ϕ。
0[]cos()(3.2)x n A n ωϕ=+3、指数信号（1）衰减的指数信号是数字信号处理中的基本信号。
因为它是线性常微分差分方程的解。
（2）指数序列在信号处理中常出现的另一个原因是，时移并不改变其信号特征。
（3）可以用差分方程给出的递归表示式来产生指数信号。
当输入[]x n 是一个冲激信号的时候，信号[][]ny n a u n =是下面差分方程的解：[][1][],y n ay n x n --=初始条件y-1=0(3.3)由于假定差分方程以因果方式递归（即n 增大），1n =-的初始条件是必须的。
用MATLAB 的filter 函数可实现差分方程。
函数filter 的用法如下所示(,,)yout filter b a xin =假设描述离散时间系统输入与输出关系的线性常系数差分方程为()()n nkkk k a y n k b x n k ==-=-∑∑那么01[,,]M b b b b = 和01[,,]N a a a a =是差分方程中的系数组成的向量，xin 是输入信号向量（filter （）函数只向y 返回与x 中样本个数一样多的样本）。
4、复值信号复值信号通常是非常有用的。
通过把信号配对，分别作为复数的实部与虚部，再将此信号对与其他复值信号依据复数运算规则进行运算处理来实现。
以这种方式使用信号对是许多信号处理系统的重要部分，尤其是那些涉及调制的系统。
在MATLAB 中，real 函数和image 函数分别提取复数的实部和虚部。
画复向量时，plot 指令和stem 指令的缺省设置容易使人困惑。
如果z 是复数，那么plot （z ）指令绘出z 实部与虚部的对应点；plot （n,z ）指令绘出z 实部与n 的对应点（连线），stem （z ）指令既标注实部又标注虚部。
如果想同时看到绘出的实部与虚部，在stem 指令之前的subplot 可将屏分成几部分。
5、复指数信号实指数信号表示式可以扩展成包含正弦和余弦信号的复指数信号形式。
这些信号构成了傅里叶变换的基础。
（1）．在MATLAB 中，复信号是实指数信号的自然扩展。
复指数信号表示为：00(ln )0[]()(cos jsin )(3.4)z j z n n n j n n x n z e r e r n n θθθ+∠====+此处0j n z re r θθ==∠。
（2）式（3.4）不足以产生所有复指数信号的通式，通式为：()0[cos()sin()]n j n j n n j n n Gz Ae r e Ar e Ar n j n ϕθθϕθϕθϕ+===+++这里0n j Gz Ae A ϕϕ==∠是复指数信号的复振幅。
（3）复指数信号也可由一阶差分方程（利用filter 函数）产生：0[][1][](3.5)y n z y n x n =-+滤波器系数0j z re θ=是复数，容易看出序列中连续项之比为0z ;但是正确的振幅和相位必须由选择激励差分方程的冲激信号的复振幅（即[][]x n G n δ=）来设置。
三、实验内容 1、冲激信号：产生并绘出下面的序列。
在每种情形下，水平n 轴应该只在指定的区间展开并相应标注。
使用stem 指令使每个序列显示成离散时间信号。
1234[]0.9[5]120[]0.8[]1525[] 1.5[333]300350[] 4.5[7]100x n n n x n n n x n n n x n n n δδδδ=-≤≤=-≤≤=-≤≤=+-≤≤m 文件：function imp=delta(L1,L2,n0,a) % generate an impulse signal% useage: imp=a*delta(L1,L2,n0,a) % a: the impulse amplitude % (L1,L2): display range% n0: impulse coordinatenn=L1:L2; %时间向量imp=zeros(L2-L1+1,1); %产生L2-L1+1行的单列零矩阵 imp(n0-L1+1)=a; %n=n0处幅度为a,其他位置为0 stem(nn,imp) %产生图形 end在命令窗口输入：subplot(2,2,1) %把屏分成四部分，在第一部分显示 x1=delta(1,20,5,0.9); %生成x1 ylabel('x1'),gtext('n') %标注x 、y 轴subplot(2,2,2) %在第二部分显示 x2=delta(-15,15,0,0.8); %生成x2 ylabel('x2'),gtext('n')subplot(2,2,3) %在第三部分显示 x3=delta(300,350,333,1.5); %生成x3 ylabel('x3'),gtext('n')subplot(2,2,4) %在第四部分显示 x4=delta(-10,0,-7,4.5); %生成x4 ylabel('x4'),gtext('n')实验结果：x1(n)=0.9*delta(n-5)x 1(n )nx 2(n )nx 3(n )nx4(n)=4.5*delta(n+7)x 4(n )n单位冲激信号图1-12、正弦信号产生并绘出下列每一个序列。
使用MATLAB 的向量功能求解此问题，将向量参数赋予余弦或正弦函数，再利用一个函数调用。
在每种情形下，水平n 轴应该只在指定的区间展开并相应标注。
使用stem 指令使每个序列显示成离散时间信号。
1234()sin(/17)025()sin(/17)1525()sin(3/2)1010()cos(/050x n n n x n n n x n n n x n n n πππππ=≤≤=-≤≤=+-≤≤=≤≤不利用三角函数来给出3()x n 较简单的表示式。
解释为什么4()x n 不是周期序列。
m 文件：function sinus=gensin(A,w0,fai,L1,L2) %GENEXP generate a sinusoidal signal%A ：正弦信号的振幅 %w0:角频率 %fai:相位% L1,L2:显示的区间nn=L1:L2; %时间向量 sinus=A*sin(w0*nn+fai); %产生正弦信号 stem(nn,sinus) %显示图形 end在命令窗口输入：subplot(2,2,1) %把屏分成4部分，在第一部分显示 x1=gensin(1,pi/17,0,0,25); %生成x1 title('x1(n)=sin(pi*n/17)'),ylabel('x1(n)');gtext('n') subplot(2,2,2)x2=gensin(1,pi/17,0,-15,25); %生成x2 title('x2(n)=sin(pi*n/17)'),ylabel('x2(n)');gtext('n') subplot(2,2,3)x3=gensin(1,pi*3,pi/2,-10,10); %生成x3 title('x3(n)=sin(3*pi*n+pi/2)'),ylabel('x3(n)');gtext('n') subplot(2,2,4)x4=gensin(1,pi/sqrt(23),pi/2,0,50); %生成x4 title('x4(n)=cos(pi*n/sqrt(23))'),ylabel('x4(n)');gtext('n')实验结果：图1-2 结果分析:从上图可以看出4()x n不是周期序列，因为由周期序列的定义，当2NMπω=为有理数时，序列是周期的，而这里2πω==3、指数信号a.绘制指数信号[](0.9)020nx n n=≤≤b.对(a)中产生的指数信号求和，验证11,1(3.6)1LLnnaa aa-=-=≠-∑c.证明一有限长指数信号满足移位关系：[][1],11(3.7)y n ay n n L=-≤≤-比较向量(2:L)y和*(1:1)a y L-。
d.使用filter函数产生与（a）部分中信号相同的信号（即a=0.9）。
（一）、问题a、b、c三个问题写在同一m文件里，如下：m文件：x1(n)nx3(n)nx4(n)nx2(n)n正弦信号function y=genexp(b,n0,L)%GENEXP generate an exponential signal:b^n% useage: Y=genexp(A,B,N0,L)% B: input scalar giving signal ratio between terms% N0:starting index(integer)% L:length of generated signal% Y:output signal Y(1:L)if(L<=0)error('GENEXP:length not positive')endnn=n0+[1:L]'-1;y=b.^nn; % 得到指数序列y=b^n,n范围[0,L-1]subplot(2,1,1) %把屏分成两部分stem(nn,y) % 画出y的图形s=sum(y) % 对产生的指数序列求和t=b*[0y]; % 把序列y(n)右移一位，得到t=b*y(n-1)，n范围[0,L]y1=t(1:L); % 得到y1=b*y(n-1),n范围[0,L-1]subplot(2,1,2)stem(nn,y1) % 画出y1的图形end在命令窗口输入：genexp(0.9,0,21)得到结果：s =8.9058ans=1.00000.90000.81000.72900.65610.59050.53140.47830.43050.38740.34870.31380.28240.25420.22880.20590.18530.16680.15010.13510.1216实验结果：图1-3-abc结果分析：（1） 可知，对[](0.9)020nx n n =≤≤的求和结果为s =8.9058，按式（3.6）的计算结果也为s=8.9058,可见结果相同。