4托勒密定理与西姆松定理
托勒密定理和西姆松定理(一)

【例3】⑵由△ABC外接圆的弧BC上一点P分别向边BC、AC 与AB作垂线PK、PL和PM。 BC AC AB 求证: 求 PK PL PM
3
1
【例1】⑶等腰梯形一条对角线的平方,等于一腰的平方加上 两底之积。已知,梯形ABCD,AD=BC,AB∥ CD,求证: BD2=BC2+AB·CD。
【例2】⑵如图,已知圆的内接正五边形ABCDE,P为 BC 上 的一点,则 的 点,则PA+PABCD中,∠ABC=60°,∠BAD= ∠BCD=90°, ,AB=2,CD=1,对角线AC、BD 交于点O,如图,求sin∠AOB。
【例1】⑴证明 明托勒密定 托勒密定理及其逆定理。 及其逆定 ①四边形ABCD内接于圆, 求证: AC·BD=AD·BC+AB·CD。
(
【例1】⑴证明托勒密定理及其逆定理。 ②四边形ABCD满足, AC·BD=AD·BC+AB·CD,求 证:四边形ABCD 是圆内接四边形。
【例1】⑵如图,已知P为正△ABC外接圆 BC 上一点, 求证: PA=PB+PC
托勒密定理和西姆松定理(一)
托勒密定理 托勒密定 托勒密定理:圆内接四边形两条对角线乘积等于两组对边乘积 圆内接 边形两条对角线乘积等 两组对边乘积 之和。 逆定理:一个凸四边形的两组对边乘积的和等于其对角线的乘 积,那么该四边形内接于一个圆 积,那么该四边形内接于 个圆(或者说该四边形的四个顶点共 圆) 广义定理 对于 般的四边形ABCD,有 广义定理:对于一般的四边形 有AB·CD+ AD·BC≥AC·BD,当且仅当ABCD是圆内接四边形时等号成立。
第14讲 托勒密定理和西姆松定理(一)

第十四讲托勒密定理和西姆松定理(一)托勒密定理:圆内接四边形两条对角线乘积等于对边乘积之和.逆定理:一个凸四边形的两组对边乘积的和等于其对角线的乘积,那么该四边形内接于一个圆(或者说该四边形的四个顶点共圆)广义定理:对于一般的四边形ABCD,有AB·CD+AD·BC≥AC·BD,当且仅当ABCD是圆内接四边形时等号成立.【例1】(1)证明托勒密定理及其逆定理.①四边形ABCD内接于圆,求证:AC·BD=AD·BC+AB·CD②四边形ABCD满足,AC·BD=AD·BC+AB·CD,求证:四边形ABCD是圆内接四边形.(2)如图,已知P为正△ABC外接圆»BC上一点.求证:P A=PB+PC.(3)等腰梯形一条对角线的平方,等于一腰的平方加上两底之积.已知梯形ABCD,AD=BC,AB∥CD.求证:BD2=BC2+AB·CD.【例2】(1)在△ABC中,已知∠A:∠B:∠C=1:2:4.求证:111 AB AC BC+=.(2)如图,已知圆的内接正五边形ABCDE,P为»BC上的一点,则P A+PD+PB=PE+PC.(3)若a、b、x、y是正实数,且a2+b2=1,x2+y2=1.求证:ab+by≤1.【例3】(1)凸四边形ABCD中,∠ABC=60°,∠BAD=∠BCD=90°,AB=2,CD=1,对角线AC、BD交于点O,如图,求sin∠AOB.(2)由△ABC外接圆的弧BC上一点分别向边BC、AC与AB作垂线PK、PL、PM.求证:BC AC AB PK PL PM=+.。
第15讲 托勒密定理和西姆松定理(二)

第十五讲托勒密定理和西姆松定理(二)
西姆松定理
西姆松定理:如图,从△ABC外接圆上任一点P向三边AB、BC、CA所在直线引垂线,设垂足分别为D、E、F,则D、E、F共线.
逆定理:由△ABC外一点P向其三边AB、BC、CA所在直线引垂线,垂足为D、E、F,若D、E、F共线,则P点必在△ABC的外接圆上.
【例1】(1)证明西姆松定理及逆定理.
(2)四边形ABCD是圆内接四边形,且∠D是直角,若从B作直线AC、AD的垂线,垂足分别为E、F,则直线EF平分线段BD.
【例2】(1)在△ABC中,过点A作∠ABC的内、外角平分线BE,BF的垂线,垂足为E、F;再过点A 作∠ACB的内外角的平分线CG、CD的垂线,垂足为G、D,试证明:F、G、E、D共线.
【例3】(1)如图,设P为△ABC外接圆上»BC内一点,过P作PD⊥BD,垂足为D,PF⊥AB,垂足为F.设
H为△ABC的垂心,延长PD至P’,是PD=PD’.
求证:HP’∥DF.
(2)设H为△ABC的垂心,P为△ABC的外接圆上一点,则从点P引出的三角形的西姆松线平分PH.。
托勒密定理及圆的其它定理

托勒密定理及圆的其它定理托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理提出定理的内容。
摘出并完善后的托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
定理表述:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理内容指圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在任意凸四边形ABCD中(如右图),作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD,连接DE.则△ABE∽△ACD所以 BE/CD=AB/AC,即BE·AC=AB·CD (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD,所以△ABC∽△AED.BC/ED=AC/AD,即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、CD、AD、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到复数恒等式: (a−b)(c−d) + (a−d)(b−c) = (a−c)(b −d) ,两边取模,运用三角不等式得。
初等几何五大ZB定理
初等几何五大ZB定理某日,燕尾模型讲毕,一六年级学霸级学生说,其可用燕尾模型证梅涅劳斯定理,大惊,问其如何得之,其说:一老师讲的。
六年级学生学梅涅劳斯定理,ZB大于实用。
既然学生感兴趣,咱就一装到底。
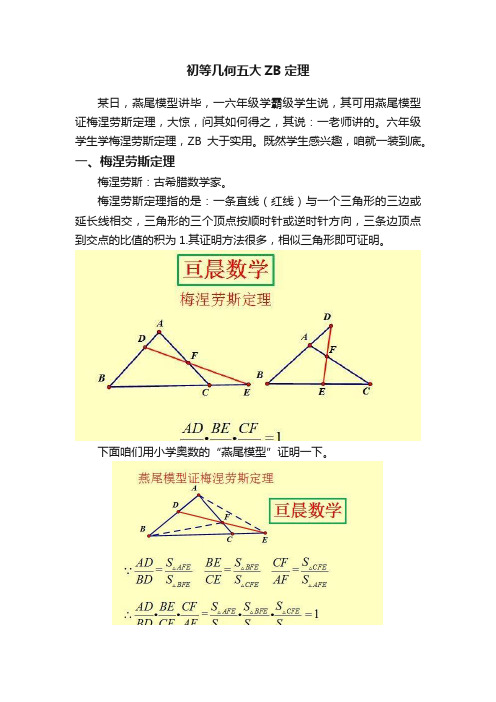
一、梅涅劳斯定理梅涅劳斯:古希腊数学家。
梅涅劳斯定理指的是:一条直线(红线)与一个三角形的三边或延长线相交,三角形的三个顶点按顺时针或逆时针方向,三条边顶点到交点的比值的积为1.其证明方法很多,相似三角形即可证明。
下面咱们用小学奥数的“燕尾模型”证明一下。
二、塞瓦定理塞瓦:意大利数学家、水利工程师,该定理于1678年发表于《直线论》一书。
塞瓦定理:可以简单记为三线共点的充要条件是:顺时针或逆时针的分线段的比值积为1.该定理可以用上面的梅涅劳斯定理证明。
三、斯坦纳定理斯坦纳:瑞士几何学家斯坦纳定理:两内角平分线相等的三角形必为等腰三角形。
早在2000多年前,《几何原本》就有定理:等腰三角形的两底角平分线的长相等。
可是它的逆定理书上却只字未提,估计作者也不会,呵呵。
直到1840年,莱默斯请求斯图姆给予纯几何证明,可斯图姆也不会,最后斯坦纳给出了证明,因此该定理也称作:斯坦纳——莱默斯定理。
现在很多高中生也能证明。
大家可以试试有没有难度。
四、托勒密定理托勒密定理:圆内接凸四边形的对边积的和等于对角线的积。
用相似可以证明五、西姆松定理西姆松定理:过三角形外接圆上异于三角形顶点的任意一点作三边所在直线垂线,则三垂足在一点直线上,这条直线我们称作西姆松线。
这些定理一般的中考都不考,一和四和中学的相似联系比较紧密,尽量掌握,培优课上可能会有,感兴趣的同学可以看看。
各种圆定理总结(包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆)

各种圆定理总结(包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆)-标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理的提出一般几何教科书中的“托勒密定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。
证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在任意四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD因为△ABE∽△ACD所以 BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE,,∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、CD、A D、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到复数恒等式: (a− b)(c− d) + (a− d)(b− c) = (a− c)(b− d) ,两边取模,运用三角不等式得。
等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
四点不限于同一平面。
四个重要定理(梅涅劳斯_塞瓦_托勒密_西姆松)
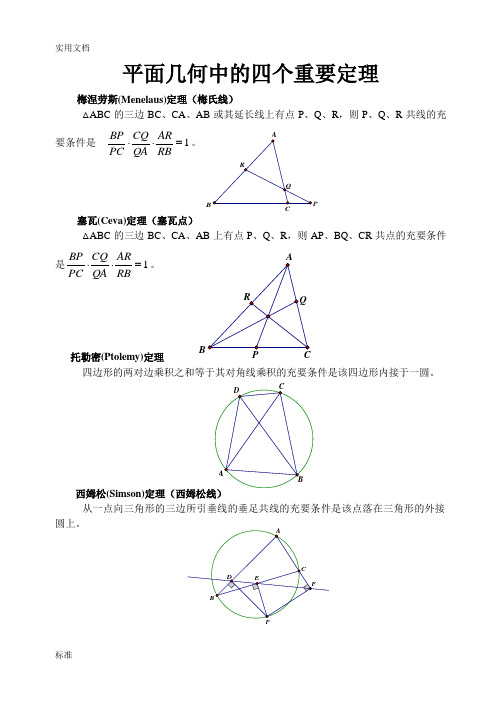
B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理(梅氏线)△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ,则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。
塞瓦(Ceva)定理(塞瓦点)△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题:1、设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。
求证:FBAF 2ED AE =。
【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行线。
2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交CB 于D 。
求证:1FACFEA BE =+。
【分析】连结并延长AG 交BC 于M ,则M 为BC 的中点。
DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅(梅氏定理)DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅(梅氏定理)∴FA CF EA BE +=MDAG )DC DB (GM ⋅+⋅=MD GM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上,λ===EACEFB AF DC BD ,AD 、BE 、CF 交成△LMN 。
求S △【分析】【评注】梅氏定理4、以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。
求证:AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5、已知△ABC 中,∠B=2∠C 。
各种圆定理总结包括托勒密定理塞瓦定理西姆松定理梅涅劳斯定理圆幂定理和四点共圆

托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理的提出一般几何教科书中的“定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。
证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在任意四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ACD因为△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE,,∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、C D、AD、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到:(a? b)(c? d) + (a? d)(b? c) = (a? c)(b?d) ,两边取,运用得。
等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
四点不限于同一。
平面上,托勒密不等式是三角不等式的形式。
二、设ABCD是。
在BC上,∠BAC = ∠BDC,而在AB上,∠ADB = ∠ACB。
在AC上取一点K,使得∠ABK = ∠CBD;因为∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD,所以∠CBK = ∠ABD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§4托勒密定理与西姆松定理
托勒密(Ptolemy)定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).
即:
E
D
C
B
A
一、直接应用托勒密定理
例1、 如图2,P是正△ABC外接圆的劣弧
上任一点(不与B、C重合),
求证:PA=PB+PC.
分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗.
若借助托勒密定理论证,则有PA·BC=PB·AC+PC·AB,
∵AB=BC=AC.
∴PA=PB+PC.
二、完善图形 借助托勒密定理
例2 、证明“勾股定理”:在Rt△ABC中,∠B=90°,求证:AC2=AB2+BC2
证明:如图,作以Rt△ABC的斜边AC为一对角线的矩形ABCD,显然ABCD 是圆内接四边形.由托勒密定理有
AC·BD=AB·CD+AD·BC. ①又∵ABCD是矩形,∴AB=CD,AD=BC,AC=BD. ②
把②代人①,得AC2=AB2+BC2.
例3 、如图,在△ABC中,∠A的平分线交外接圆于D,连结BD,
求证:AD·BC=BD(AB+AC).
证明:连结CD,依托勒密定理有
AD·BC=AB·CD+AC·BD.
∵∠1=∠2,∴ BD=CD.
故 AD·BC=AB·BD+AC·BD=BD(AB+AC).
三、构造图形 借助托勒密定理
例4 若a、b、x、y是实数,且a2+b2=1,x2+y2=1.求证:ax+
by≤1.
证明:如图作直径AB=1的圆,在AB两边任作Rt△ACB和Rt△ADB, 使AC =a,BC=b,
BD=x,AD=y.
由勾股定理知a、b、x、y是满足题设条件的.
据托勒密定理有
AC·BD+BC·AD=AB·CD.
∵CD≤AB=1,∴ax+by≤1.
四、巧变原式 妙构图形,借助托勒密定理
例5、已知a、b、c是△ABC的三边,且a2=b(b+c),求证:∠A=2∠B.分析:将a2=b(b+c)变形为a·a=b·b+bc,从而联想到托勒密定理,进而构造一个等腰
梯形,使两腰为b,两对角线为a,一底边为c.
证明:如图,作△ABC的外接圆,以A为圆心,BC为半径作弧交圆于D,连结BD、DC、
DA.∵AD=BC,∴∠ABD=∠BAC.
又∵∠BDA=∠ACB(对同弧),∴∠1=∠2.
依托勒密定理有
BC·AD=AB·CD+BD·AC. ①
而已知a2=b(b+c),即a·a=b·c+b2. ②
∴∠BAC=2∠ABC.
五、巧变形 妙引线 借肋托勒密定理
例6 、在△ABC中,已知∠A∶∠B∶∠C=1∶2∶4,
分析:将结论变形为AC·BC+AB·BC=AB·AC,把三角形和圆联系起来,可联想到托勒密
定理,进而构造圆内接四边形.
如图,作△ABC的外接圆,作弦BD=BC,连结AD、CD.
在圆内接四边形ADBC中,由托勒密定理有
AC·BD+BC·AD=AB·CD
易证AB=AD,CD=AC,∴AC·BC+BC·AB=AB·AC,
练习1.已知△ABC中,∠B=2∠C。
求证:AC2=AB2+AB·BC。
【分析】过A作BC的平行线交△ABC的外接圆于D,连结BD。
则CD=DA=AB,AC=BD。
由托勒密定理,AC·BD=AD·BC+CD·AB。
西姆松(Simson)定理(西姆松线)
注:
例7、
例8、
例9、
例10、
作业:
1.设AD是△ABC的边BC上的中线,直线CF交AD于F。
求证:。
2.过△ABC的重心G的直线分别交AB、AC于E、F,交CB于D。
求证:。
3.D、E、F分别在△ABC的BC、CA、AB边上,
, AD、BE、CF交成△LMN。
求S△LMN。
4.以△ABC各边为底边向外作相似的等腰△BCE、
△CAF、△ABG。
求证:AE、BF、CG相交于一点。
5.已知正七边形A1A2A3A4A5A6A7。
求证:。
6.△ABC的BC边上的高AD的延长线交外接圆于P,作PE⊥AB
于E,延长ED交AC延长线于F。
求证:BC·EF=BF·CE+BE·CF。
7.正六边形ABCDEF的对角线AC、CE分别被内分点M、N分成的
比为AM:AC=CN:CE=k,且B、M、N共线。
求k。
(23-IMO-5)
8.O为△ABC内一点,分别以d a、d b、d c表示O到BC、CA、
AB的距离,以R a、R b、R c表示O到A、B、C的距离。
求证:(1)a·R a≥b·d b+c·d c;
(2) a·R a≥c·d b+b·d c;
(3) R a+R b+R c≥2(d a+d b+d c)。
9.△ABC中,H、G、O分别为垂心、重心、外心。
求证:H、G、O三点共线,且HG=2GO。
(欧拉线)
10.⊙O1和⊙O2与ΔABC的三边所在直线都相切,E、F、 G、H为切点,EG、FH的延长线交于P。
求证:PA⊥BC。
11.如图,在四边形ABCD中,对角线AC平分∠BAD。
在CD 上取一点E,BE与AC相交于F,延长DF交BC于G。
求证:∠GAC=∠EAC。
1.分析:CEF截△ABD→
(梅氏定理)
评注:也可以添加辅助线证明:过A、B、D之一 作CF的平行线。
2.分析:连结并延长AG交BC于M,则M为BC的中点。
DEG截△ABM→
(梅氏定理)
DGF截△ACM→
(梅氏定理)
∴
=
=
=1
评注:梅氏定理
3. 梅氏定理
4. 塞瓦定理
5.评注:托勒密定理
6.评注:西姆松定理(西姆松线)
7.评注:面积法
8.评注:面积法
9.评注:同一法
10. 评注:同一法
11. 证明:连结BD交AC于H。
对△BCD用塞瓦定理,可得
因为AH是∠BAD的角平分线,由角平分线定理,
可得
,故。
过C作AB的平行线交AG的延长线于I,过C作AD的
平行线交AE的延长线于J。
则
,
所以
,从而CI=CJ。
又因为CI//AB,CJ//AD,故∠ACI=π-∠BAC=π-∠DAC=∠ACJ。
因此,△ACI≌△ACJ,从而∠IAC=∠JAC,即∠GAC=∠EAC。
