基于蒙特卡洛仿真的项目风险评估分析
金融经济中基于蒙特卡罗模拟的风险评估

金融经济中基于蒙特卡罗模拟的风险评估第一章:引言金融风险评估是金融经济领域中的一项重要任务。
在金融市场中,各种风险因素不断涌现,如利率、汇率、信用、市场等风险。
在这个背景下,风险评估成为了必要的手段。
蒙特卡罗模拟方法在风险评估领域中得到越来越广泛的应用。
本文将详细介绍基于蒙特卡罗模拟的金融风险评估方法。
第二章:蒙特卡罗模拟方法蒙特卡罗模拟方法是一种利用计算机模拟真实随机事件的方法。
其原理是随机数模拟,通过大量的重复试验得到随机事件的结果,从而对实际风险进行评估。
其基本流程包括以下几个步骤:1. 确定模型:确定所需要评估的风险模型。
2. 设定输入参数:确定模型的输入参数,并对其进行概率分析。
3. 生成随机数:根据概率分布生成随机数。
4. 模拟结果:模拟输入参数和随机数的组合,得到输出结果。
5. 统计分析:对模拟结果进行统计分析,得出相应的风险指标。
蒙特卡罗模拟方法因为其可靠性高、适用性强等优点,已经被广泛应用于金融风险评估领域。
第三章:蒙特卡罗模拟在金融领域中的应用基于蒙特卡罗模拟的金融风险评估方法可以应用于以下领域:1. 信用风险评估:通过蒙特卡罗模拟,根据公司历史数据和市场数据进行信用评估,估计出公司违约概率。
2. 收益风险评估:通过蒙特卡罗模拟,对股票、债券等资产组合进行收益风险评估。
3. 利率风险评估:通过蒙特卡罗模拟,模拟利率波动,对债券投资进行利率风险评估。
4. 波动率风险评估:通过蒙特卡罗模拟,模拟资产价格波动,对股票、证券等进行波动率风险评估。
5. 经济风险评估:通过蒙特卡罗模拟,模拟宏观经济情况,对公司的财务状况进行评估。
6. 商品价格风险评估:通过蒙特卡罗模拟,模拟商品价格的波动,对商品投资进行风险评估。
以上应用领域只是冰山一角,蒙特卡罗模拟在金融领域中的应用还有很多,需要根据实际情况进行选择和应用。
第四章:基于蒙特卡罗模拟的风险评估实例以收益风险评估为例,通过蒙特卡罗模拟对某公司的股票投资进行风险评估。
财务风险评估中蒙特卡洛模拟与风险值分析方法

财务风险评估中蒙特卡洛模拟与风险值分析方法在现代商业环境中,财务风险评估是企业决策过程中至关重要的一环。
蒙特卡洛模拟和风险值分析是财务风险评估中常用的两种方法。
本文将简要介绍这两种方法的原理和应用,并探讨它们在财务风险评估中的作用。
1. 蒙特卡洛模拟蒙特卡洛模拟是一种基于随机数的计算方法,被广泛应用于现代金融风险管理。
它的基本原理是通过多次模拟随机变量的取值,对风险事件发生概率及其对结果的影响进行估计。
在财务风险评估中,蒙特卡洛模拟的主要步骤如下:1.1 确定风险事件和相关变量首先,需要确定和描述需要评估的风险事件,并识别与这些事件相关的重要变量。
这些变量可以是价格、成本、利率、汇率等等。
1.2 设定变量的概率分布和相关参数第二步,需要对这些变量进行概率分布的设定,并确定相应的参数,如均值、标准差等。
这些参数可以通过历史数据、市场研究或专家意见获得。
1.3 进行蒙特卡洛模拟接下来,进行大量的模拟,生成随机数,并根据设定的概率分布得出每个变量的取值。
根据这些取值,可以计算出对应的风险事件发生情况及其对结果的影响。
1.4 收集模拟结果并进行分析最后,将模拟得到的结果进行汇总和分析。
可以计算出每个风险事件的发生概率、影响程度以及整体风险水平。
同时,还可以通过敏感性分析探索不同变量对结果的影响程度。
蒙特卡洛模拟方法的优点在于可以较为全面地考虑不同变量之间的关联性,并且能够提供结果的分布情况,从而帮助管理者更好地理解风险。
然而,也需要注意到该方法的一些限制性因素,例如对参数的设定敏感性,以及对大量模拟数据的需求。
2. 风险值分析风险值分析是一种通过一定的统计方法来衡量风险的方法。
它主要用于评估在给定置信水平下的最大可能损失。
在财务风险评估中,风险值分析的主要步骤如下:2.1 选择风险值水平首先,需要确定评估的风险值水平,常见的风险值包括VaR(Value-at-Risk)和CVaR(Conditional Value-at-Risk)。
基于重要性采样的蒙特卡洛仿真在风险评估中的应用

基于重要性采样的蒙特卡洛仿真在风险评估中的应用蒙特卡洛仿真是一种基于统计学原理的数值模拟方法,常用于评估不确定性问题和风险分析。
在风险评估过程中,准确地计算和评估风险指标非常关键。
然而,由于不确定性因素的存在,风险评估往往具有高度复杂性和困难。
基于重要性采样的蒙特卡洛仿真是一种有效的方法,可以帮助我们应对这类复杂问题。
重要性采样是一种通过抽样技术对参数空间进行加权抽样的方法。
在风险评估中,我们常常需要估计一个随机变量的期望或方差等特征。
传统的蒙特卡洛仿真方法是通过简单随机抽样进行模拟,但当模拟目标随机变量的分布函数是高度非线性、复杂或多模态的情况下,传统方法效率较低。
基于重要性采样的蒙特卡洛仿真则可以通过引入一个辅助的抽样分布函数,将原本低频事件的抽样转换为高频事件,从而提高模拟的效率。
在风险评估中,我们通常需要考虑多个随机变量之间的关系,这些随机变量可能代表着不同的风险因素或输入参数。
基于重要性采样的蒙特卡洛仿真可以帮助我们对多个随机变量进行联合抽样和联合分析,从而更全面地评估系统的风险。
通过确定适当的抽样分布函数,将模拟过程集中在关键的参数空间,我们可以获得更准确的风险评估结果。
在实际应用中,基于重要性采样的蒙特卡洛仿真常被用于评估金融风险、工程风险以及自然灾害等方面。
例如,在金融领域,我们常需要计算投资组合的风险价值和价值以 VaR(Value at Risk)和 CVaR(Conditional Value at Risk)等指标。
基于重要性采样的蒙特卡洛仿真可以帮助我们对不同资产之间的关联性进行建模,并评估整个投资组合的风险水平。
在工程领域,我们可以使用基于重要性采样的蒙特卡洛仿真来评估不同设计参数对结构安全性的影响,从而指导工程决策。
在自然灾害方面,比如地震、洪水等,我们可以利用基于重要性采样的蒙特卡洛仿真来评估地质和气候等因素对风险的影响,从而优化防灾措施。
基于重要性采样的蒙特卡洛仿真方法虽然在风险评估中有着广泛的应用,但也存在一些限制和注意事项。
基于蒙特卡罗模拟方法的项目工程造价风险分析

基于蒙特卡罗模拟方法的项目工程造价风险分析[摘要]本文主要通过蒙特卡罗模拟方法来定量进行工程造价风险分析并预测风险性造价。
按照蒙特卡罗的原理,结合工程造价管理的方法给出造价风险模拟的关键步骤,最后以一个项目实例进行验证该方法的可行性。
[关键词]蒙特卡罗模拟;工程造价;风险分析1引言目前我国工程项目造价估算方法依然是根据设计文件以及定额或经验数据,计算出一个总的确定的数值,工程承包企业便以此定值为依据投标报价并制订成本计划。
但实际上,工程项目在实施过程中往往受到诸如自然、劳动生产率、施工管理水平、市场等众多不确定因素的影响,各工序的成本具有较大的不确定性,并非是能事先确知的定值,而是服从某种概率分布的一个随机变量,因此构成的工程项目总造价也是一个随机变量,而应用蒙特卡罗模拟技术可以预测工程项目的总造价并进行风险分析。
工程实施过程中遇到各种风险因素对不同分项工作的影响程度是不同的,且有些风险因素之间还存在关联,难以用数学方法准确表示它们各自对工程造价成本的影响,但在各种因素的共同作用下,对工程某分项工作的总体综合影响是可知的,在工程施工时,在各种随机因素的共同作用下,各分项工程的成本值在某一范围内变化,而某分项工程的单位成本分布于一个区间内,有最大、最小值,在此区间内的分布也不均匀,存在一个最可能值,并且在进行大量的施工实践(模拟)后,它们会呈现出一定的规律性,服从某种统计规律,虽然不能确切地知道该值,但可以用数学方法对它们的分布情况加以描述,因此,可以依据工程项目的历史成本资料,考虑时间因素,计算出各分项工程的分布参数;可用蒙特卡罗法逐步模拟出拟建工程的可能成本区间以及实现某一计划成本值的可能性,以便为施工企业下一步风险决策、控制提供科学的理论依据。
2蒙特卡罗原理蒙特卡罗(Monte Carlo)方法亦称为随机模拟(Random simulation)方法,有时也称为随机抽样(Random sampling)技术。
基于蒙特卡罗模拟法的项目风险分析
各项费用
统计分布或计算标准
年收益 R( 万元)
正态分布,均值 2500,标准差 200
年支出 C( 万元)
均匀分布,最大值 1500,最小值 1300
折现率 i
正态分布,均值 10%,标准差 1%
寿命 n( 年)
10 年
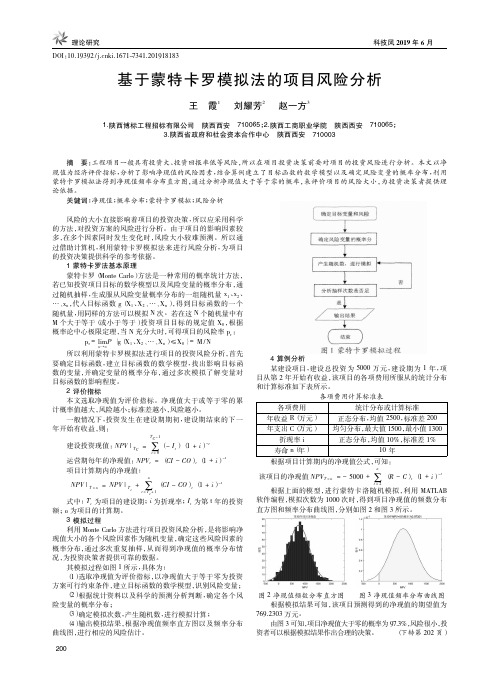
根据项目计算期内的净现值公式,可知:
n
∑ 该项目的净现值 NPVT = n = - 5000 +
数的变量,并确定变量的概率分布,通过多次模拟了解变量对
目标函数的影响程度。
2 评价指标
本文选取净现值为评价指标。净现值大于或等于零的累
计概率值越大,风险越小; 标准差越小,风险越小。
一般情况下,投 资 发 生 在 建 设 期 期 初,建 设 期 结 束 的 下 一
年开始有收益,则:
TC-1
∑ 建设投资现值:
5 结语
高校科研实验室管理并不仅仅只有文章中提到的四个方 面,它还有实验室安全的管理,实验室信息产权的管理,实验室 空间布局的建设等等,每一条都影响着一个实验室是否能为一 流实验室的评判标准。想要进一步提高管理水平,只有通过管 理人员不断摸索,提高自身管理水平,发挥创造力,结合实际, 推成出新,推出一套行之有效并且更加有利于高校科研实验室 发展的全面性,系统性的管理体系,为高校建设“双一流”提供 坚实的基石。
关键词: 净现值; 概率分布; 蒙特卡罗模拟; 风险分析
风险的大小直接影响着项目的投资决策,所以应采用科学
的方法,对投资方案的风险进行分析。由于项目的影响因素较
多,在多个因素 同 时 发 生 变 化 时,风 险 大 小 较 难 预 测。所 以 通
过借助计算机,利用蒙特卡罗模拟法来进行风险分析,为项目
基于蒙特卡罗模拟法的项目风险分析

基于蒙特卡罗模拟法的项目风险分析项目风险无处不在,它可能会影响项目成本、时间进度、和最终结果的成功。
由于项目的不确定性,项目管理人员需要在项目周期的早期就开始识别和评估风险,并采取相应的措施来减轻或消除风险,以确保项目成功。
蒙特卡罗模拟法是一种评估项目风险并制定风险管理策略的有效工具。
蒙特卡罗模拟法是一种利用随机抽样的方法来模拟某些过程的统计方法。
在项目风险分析中,蒙特卡罗模拟法通常用于估算项目成本或时间进度的概率分布,以确定项目完成时间或成本的可能范围和概率。
这种方法在风险较大或风险未知的情况下很有用,它可以帮助项目管理人员评估风险并制定风险应对策略。
蒙特卡罗模拟法的过程包括以下步骤:1. 确定项目范围和目标,确定项目任务的各个子任务,并为每项任务估计时间和成本。
2. 确定每项任务的风险因素,并为每个风险因素分配概率分布。
这些风险因素可以是技术上的挑战,设备故障,特定资源的延迟或变化,或其它不确定因素。
3. 对每一个任务的成本或时间进行蒙特卡罗模拟。
每项任务的模拟包括从相应的风险因素的概率分布中产生随机数字。
4. 计算所需成本或时间的概率分布,这是所有任务模拟的结果之和。
5. 根据所得到的概率分布,确定项目完成时间或成本的可能范围和概率,并制定应对策略。
蒙特卡罗模拟法的优点在于它可以考虑许多因素对风险评估的影响。
此外,它可以为项目管理人员提供真实的数据,以帮助他们做出明智的决策。
最后,它还可以为项目提供多个可能的方案,并提供概率分布,以帮助项目管理人员选取最优的方案。
在实际应用中,蒙特卡罗模拟法需要使用计算机程序进行模拟,这些程序具有很高的计算能力,可以快速处理大量数据并进行概率分析。
此外,蒙特卡罗模拟法还需要精确的数据和可靠的概率分布,这些数据和分布通常需要通过历史数据或专家意见得出。
总之,蒙特卡罗模拟法是一种强大的工具,可帮助项目管理人员评估项目风险并制定风险管理策略。
通过模拟多个可能情况的概率分布,项目管理人员可以更好地了解项目风险,并在发生问题时采取更好的决策。
基于蒙特卡洛方法的金融风险评估模型研究

基于蒙特卡洛方法的金融风险评估模型研究金融风险评估是金融领域中的重要问题之一,对于投资者、金融机构和政府机构来说至关重要。
在过去的几十年里,蒙特卡洛方法已被广泛应用于金融风险评估模型的研究中。
本文将基于蒙特卡洛方法,探讨金融风险评估模型的相关研究。
首先,我们需要了解蒙特卡洛方法的基本原理。
蒙特卡洛方法是一种基于随机模拟的计算方法,通过随机抽样生成大量的数据点,并利用这些数据点进行数值计算和统计分析。
在金融风险评估中,蒙特卡洛方法可以用于模拟金融资产价格的未来变动,并通过建立模型来评估金融市场的风险。
在金融风险评估模型的研究中,蒙特卡洛方法可以应用于不同的方面。
首先,可以利用蒙特卡洛方法研究金融资产的价格波动性。
通过对金融资产价格进行随机抽样和模拟,可以得到不同时间点上的资产价值,并以此为基础计算风险价值和价值-at-risk等指标,来评估金融风险的大小。
这种方法尤其适用于复杂金融产品和市场中的非线性风险。
其次,蒙特卡洛方法可以应用于金融风险模型的参数估计。
在实际应用中,金融风险模型的参数通常是通过历史数据进行估计的。
然而,由于金融市场的复杂性和不确定性,历史数据并不能完全反映未来的风险。
通过蒙特卡洛方法,可以生成大量的模拟数据,并利用这些数据来估计模型参数的不确定性。
通过分析这些参数的分布情况,可以得到更准确的风险估计。
另外,蒙特卡洛方法还可以应用于金融风险模型的模型选择和验证。
在金融风险评估中,存在不同的风险模型,如波动性模型、利率模型和违约模型等。
通过蒙特卡洛方法,可以对不同的风险模型进行模拟比较,并选择最优的模型来评估风险。
此外,蒙特卡洛方法还可以用于验证风险模型的有效性和鲁棒性,通过与实际观察值进行对比,评估模型对真实数据的拟合程度。
在实际应用中,基于蒙特卡洛方法的金融风险评估模型还需要解决一些挑战和问题。
首先,模型中的假设和参数选择需要合理和准确,否则将影响风险估计的准确性。
其次,在模拟结果中存在一定的随机性,需要通过统计分析方法进行稳定性和可靠性的检验。
基于蒙特卡罗方法的软件估算风险分析

武警 浙江省 总 队司令部 信 息化 处 陈菊萍
[ 摘
周 劫功
,
要] 蒙特卡 罗方法应用在 软件估 算模 型 中, 将 通过按 照一定分布规律随机 产生输入值 , 然后依 照模 型进行计 算 得 到 输 出 结果 , 将这个过程进行 多次重复得 出一组输 出值 , 最后 对输 出值进 行统计分析 以得 出结论 。这种 方法能够 自动分析不 同的输入对输 出所 造成的影响 , 出软件估算工作量 与进度 的风险分析结果。 得 [ 关键 词] 软件估 算 风 险 蒙特卡 罗 蒙特卡罗模 拟方法概 述 蒙特卡 罗模 拟是一种随机 模拟方法 , 它经 常被用在有效 的统计 实 验 中。这 种方法 的基本思想 是人为地造 出一种概率模型 , 它的某些 使 参数恰好重合于所需计算 的量 ; 又可 以通过实验 , 用统计方法求出这些 参数的估值 ; 把这些估值作 为要求 的量 的近似值 1 。 蒙特卡 罗方法应用在软件 估算模型 中 , 能够 自动分析不 同的输人 对输 出所 造成的影 响 , 给出风险分析结 果。通过按照一定分 布规律随 机产生输 入值 , 然后依 照模 型进行计算 , 到输出结果 , 得 将这 个过程进 行多次重复得出一组输 出值 , 最后对输 出值进行统计Y- 以得出结 论。 ) N: 从理论上来说 , 蒙特卡罗方法需要大量的实验。实验次数越多 , 所 得 到 的结果 才越精确 。计算机 技术的发展 , 使得 蒙特卡罗方法在 最近 1 年得到快速 的普及 。借助计算机 的高速运转能力 , O 能够使得原 本费
i ” -
一
z
S
promots en nh
㈩
其 中 E是全 面开发工作 量( 人月)D ; 是产 品复杂度 ; C 是有效技术 常数 ; S是有效组 件规模 ( 等效代码行数 ) 。 开发进度计算公式 如下 :
