蒙特卡罗模方法与项目风险案例分析
蒙特卡罗模拟在项目风险分析中的应用研究

蒙特 卡 罗 分析 法 是 14 代 , 美 国军 方研 制 原 90年 在
子 弹 的“ 哈 顿项 目” 曼 中开发 出来 的一 种利 用 随机 数模
但 是它不 能准 确 描 述 最 终 检验 变 量 的概 率 分 布 , 这 而 种概 率分 布 对 于决 策者 极 为 重 要 。 由 最好/ 差分 析 最 法可 以扩 展到情 景分 析法 。在 最 好 和最 差 中加 入 一个 中间值 , 这样 就 组 成 三 种 情 况 , 果 有 两 个 随 机 变 量 , 如
种 模拟 方法 在 全球 得 以推广 应用 。
些问题的提出促使管理者在项 目投资前期必须对其进
行 充分 的风 险分析 。
二 、 目风 险分 析技术 的 比较 项
有几 种技 术可 以用来 进 行 项 目风 险 分析 。最 常 见
的是“ 最好/ 差分析 ” “ 最 、 假设 分 析 ” “ 和 模拟 ” 。
收稿 日期 :0 1 0 0 2 1 — 9— 3
作者简 介 : 常海 申( 9 3一 ) 河北保 定人 , 18 , 云南 财经大学 经济研究 院硕士研究 生 , 专业 为世 界经 济 , 究方 向为国 研
际投资 。
通讯作 者简介 : 陆亚琴 (9 2一 )女 , 17 , 云南大t A.经济学博士 , J ,  ̄ 云南 财经 大学 经济研究院 国际 贸易研究所 副教授 , 研究方 向为 国际投资 、 国际 贸易 与环境 。
采 用 蒙特 卡罗 模 拟 时 , 终 检 验 变 量 的 方差 不 会 随着 最 随机 变量 数量 的增 加 而 迅 速 增 加 , 使 得模 拟 输 出 的 这 结 果 具有 实 际有 用性 。 . 三 、 特卡 罗模 拟在 项 目风 险 分析 中的典 型应 用 蒙 C sl a 给 出了五 种视 图输 出 , 文列 出第一 种 y aB l r t l 本 视 图。从 概率 分布 图上可 以看 出 N V大 致服从 正态 分 P 布 , 目 N V有 7 .5 的 可 能 性 大 于零 。其 它 四 种 项 P 54%
蒙特卡罗方法在风险评估中的应用

蒙特卡罗方法在风险评估中的应用蒙特卡罗方法是一种基于随机抽样的数值计算方法,通过随机抽样来解决实际问题中的复杂计算和模拟,被广泛应用于金融、工程、科学等领域。
在风险评估中,蒙特卡罗方法可以帮助分析人员更准确地评估风险,制定相应的风险管理策略。
本文将探讨蒙特卡罗方法在风险评估中的应用,介绍其原理和优势,并结合实际案例进行说明。
一、蒙特卡罗方法原理蒙特卡罗方法是一种基于随机抽样的数值计算方法,其基本原理是通过大量的随机抽样来模拟问题的不确定性因素,从而得出问题的解或结果。
在风险评估中,蒙特卡罗方法可以用来模拟不同的风险因素,如市场波动、自然灾害等,通过大量的模拟实验来评估风险的概率分布和可能的损失情况。
二、蒙特卡罗方法在风险评估中的优势1. 考虑不确定性因素:风险评估中存在许多不确定性因素,传统的计量方法往往难以全面考虑这些因素。
蒙特卡罗方法通过随机抽样的方式,可以全面考虑各种不确定性因素,更准确地评估风险。
2. 灵活性强:蒙特卡罗方法适用于各种类型的风险评估问题,可以根据具体情况灵活调整模型和参数,适用性广泛。
3. 结果可靠性高:通过大量的随机抽样和模拟实验,蒙特卡罗方法可以得出较为可靠的结果,有助于决策者更好地理解和应对风险。
三、蒙特卡罗方法在风险评估中的应用案例以金融领域为例,假设某投资机构要评估某种金融产品的市场风险。
首先,需要确定影响市场风险的各种因素,如利率变动、汇率波动、市场需求等。
然后,利用蒙特卡罗方法进行模拟实验,通过大量的随机抽样来模拟这些因素的变动情况,得出不同情况下的市场风险概率分布和可能的损失情况。
最后,根据模拟结果,评估产品的整体风险水平,制定相应的风险管理策略。
通过蒙特卡罗方法的应用,投资机构可以更全面地了解产品的市场风险,为决策提供科学依据。
同时,还可以根据模拟结果进行风险敞口管理,降低风险带来的损失。
四、结语蒙特卡罗方法作为一种强大的数值计算方法,在风险评估中发挥着重要作用。
基于蒙特卡罗模拟法的项目风险分析
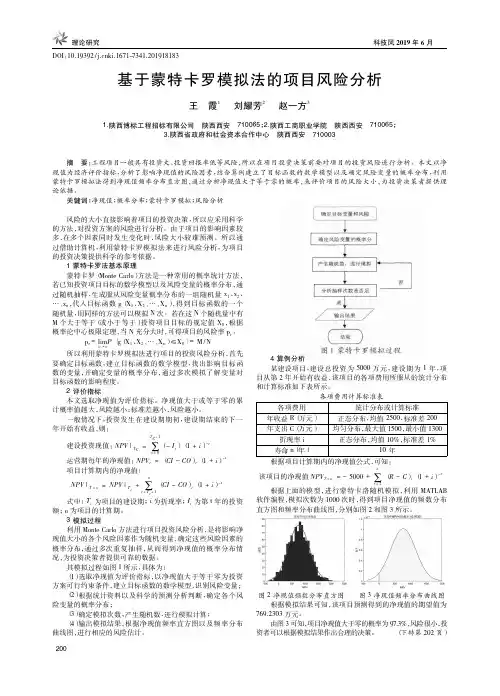
各项费用
统计分布或计算标准
年收益 R( 万元)
正态分布,均值 2500,标准差 200
年支出 C( 万元)
均匀分布,最大值 1500,最小值 1300
折现率 i
正态分布,均值 10%,标准差 1%
寿命 n( 年)
10 年
根据项目计算期内的净现值公式,可知:
n
∑ 该项目的净现值 NPVT = n = - 5000 +
数的变量,并确定变量的概率分布,通过多次模拟了解变量对
目标函数的影响程度。
2 评价指标
本文选取净现值为评价指标。净现值大于或等于零的累
计概率值越大,风险越小; 标准差越小,风险越小。
一般情况下,投 资 发 生 在 建 设 期 期 初,建 设 期 结 束 的 下 一
年开始有收益,则:
TC-1
∑ 建设投资现值:
5 结语
高校科研实验室管理并不仅仅只有文章中提到的四个方 面,它还有实验室安全的管理,实验室信息产权的管理,实验室 空间布局的建设等等,每一条都影响着一个实验室是否能为一 流实验室的评判标准。想要进一步提高管理水平,只有通过管 理人员不断摸索,提高自身管理水平,发挥创造力,结合实际, 推成出新,推出一套行之有效并且更加有利于高校科研实验室 发展的全面性,系统性的管理体系,为高校建设“双一流”提供 坚实的基石。
关键词: 净现值; 概率分布; 蒙特卡罗模拟; 风险分析
风险的大小直接影响着项目的投资决策,所以应采用科学
的方法,对投资方案的风险进行分析。由于项目的影响因素较
多,在多个因素 同 时 发 生 变 化 时,风 险 大 小 较 难 预 测。所 以 通
过借助计算机,利用蒙特卡罗模拟法来进行风险分析,为项目
基于蒙特卡罗模拟法的项目风险分析

基于蒙特卡罗模拟法的项目风险分析项目风险无处不在,它可能会影响项目成本、时间进度、和最终结果的成功。
由于项目的不确定性,项目管理人员需要在项目周期的早期就开始识别和评估风险,并采取相应的措施来减轻或消除风险,以确保项目成功。
蒙特卡罗模拟法是一种评估项目风险并制定风险管理策略的有效工具。
蒙特卡罗模拟法是一种利用随机抽样的方法来模拟某些过程的统计方法。
在项目风险分析中,蒙特卡罗模拟法通常用于估算项目成本或时间进度的概率分布,以确定项目完成时间或成本的可能范围和概率。
这种方法在风险较大或风险未知的情况下很有用,它可以帮助项目管理人员评估风险并制定风险应对策略。
蒙特卡罗模拟法的过程包括以下步骤:1. 确定项目范围和目标,确定项目任务的各个子任务,并为每项任务估计时间和成本。
2. 确定每项任务的风险因素,并为每个风险因素分配概率分布。
这些风险因素可以是技术上的挑战,设备故障,特定资源的延迟或变化,或其它不确定因素。
3. 对每一个任务的成本或时间进行蒙特卡罗模拟。
每项任务的模拟包括从相应的风险因素的概率分布中产生随机数字。
4. 计算所需成本或时间的概率分布,这是所有任务模拟的结果之和。
5. 根据所得到的概率分布,确定项目完成时间或成本的可能范围和概率,并制定应对策略。
蒙特卡罗模拟法的优点在于它可以考虑许多因素对风险评估的影响。
此外,它可以为项目管理人员提供真实的数据,以帮助他们做出明智的决策。
最后,它还可以为项目提供多个可能的方案,并提供概率分布,以帮助项目管理人员选取最优的方案。
在实际应用中,蒙特卡罗模拟法需要使用计算机程序进行模拟,这些程序具有很高的计算能力,可以快速处理大量数据并进行概率分析。
此外,蒙特卡罗模拟法还需要精确的数据和可靠的概率分布,这些数据和分布通常需要通过历史数据或专家意见得出。
总之,蒙特卡罗模拟法是一种强大的工具,可帮助项目管理人员评估项目风险并制定风险管理策略。
通过模拟多个可能情况的概率分布,项目管理人员可以更好地了解项目风险,并在发生问题时采取更好的决策。
基于蒙特卡罗模拟法的项目风险分析

基于蒙特卡罗模拟法的项目风险分析项目管理是一门复杂的学科,它需要项目经理在整个项目周期中不断地管理和控制各种风险。
项目风险分析是项目管理中至关重要的一环,它可以帮助项目团队更好地理解项目中可能发生的风险,并采取相应的措施来降低风险并确保项目的成功完成。
而基于蒙特卡罗模拟法的项目风险分析是一种有效的工具,可以帮助项目团队更精准地评估项目中的风险,并提供决策支持,以便在项目中做出正确的决策。
蒙特卡罗模拟法是20世纪40年代飞行员约翰·冯·诺伊曼和斯坦尼斯拉夫·乌拉姆在洛斯阿拉莫斯国家实验室为解决核爆炸的放射性衰变问题而发明的一种数值计算方法。
通过随机抽样的方法,蒙特卡罗模拟法能够模拟出大量可能的结果,从而提供对风险事件发生的概率分布的估计。
在项目风险分析中,蒙特卡罗模拟法可以帮助项目团队更好地理解项目中各种不确定性因素的影响,并基于概率和统计数据进行决策。
进行基于蒙特卡罗模拟法的项目风险分析需要收集和整理项目相关的各种数据,包括项目的工期、成本、资源需求、技术风险、市场风险、政策风险等。
这些数据可以通过对历史数据的分析和专家的访谈来获取,从而建立项目的风险模型。
将收集到的数据输入到蒙特卡罗模拟软件中,通过随机抽样的方法生成大量可能的项目结果。
在模拟过程中,需要考虑项目中各种不确定性因素的影响,例如工期延误、成本增加、资源短缺等。
这些因素可以通过统计分布来描述,例如正态分布、均匀分布、泊松分布等。
通过模拟的方法,可以得到项目完成时间、成本和其他关键指标的概率分布。
接下来,需要对模拟结果进行分析和评估,以确定项目的风险水平和关键风险因素。
通过对模拟结果的统计分析,可以得出项目完成时间、成本等指标的均值、方差、置信区间等统计量。
通过对这些统计量的分析,可以确定项目的风险水平和不确定性程度,从而为项目决策提供参考和支持。
在基于蒙特卡罗模拟法的项目风险分析中,需要对风险事件的概率和影响进行评估,并制定相应的风险应对策略。
蒙特卡洛模拟技术应用的项目风险分析

模拟过程
一、确定风险变量的概率分布:选取建设投资、经营成本、销售收入这三个最为敏感的 因素作为风险变量 (1)(1)建设投资的概率分布。建设投资的概率分布采用三角形分布,邀请专家根据项 目初步设计概算情况对项目投资进行预测,估计项目投资的最乐观值、最大可能值、最 悲观值,求取专家意见的平均值,并计算标准差和离散系数,离散系数满足专家一致性 要求时,经测算估计最后确定三角形分布模型,结果为:乐观值34181万元,最大 可能值采用概算值40213.75万元,悲观值44235万元。 (2)经营成本和销售收入的概率分布。经营成本和销售收入的概率分布均采用正态分布, 邀请专家对经营成本和销售收入的期望值、分布范围和范围内概率进行估计。 选取三位专家对经营成本的估计结果进行计算示例如下:1.专家认为经营成本的期望值 为3000万元,在2760~3240万元范围内的概率为90% ,即在2760—3240万 元范围外的概率为10% ,小于2760万元(或大于3240万元)的概率为5% 。即比期望值 3000万元减少240万元的概率为5% ,查标准正态分布概率表或通过计算机程序计算 得离差为-1.645,即相当于期望值偏离了-1.6450,于是标准差δ=240/1.645=146万元。 同理计算其他专家对经营成本的期望值与标准差的估计值,结果见表1。专家估计结果 标准差的平均值为164万元,方差为247,离散系数为9.58% ,满足专家一致性要求, 从而确定经营成本的概率分布服从N(3037,164² )的正态分布。采用同样的方法,经专 家估计确定销售收入的概率分布服从N (6570,380²)的正态分布。
污水处理厂项目可行性分析
-蒙特卡洛模拟技术
• 小组成员:李汝强 • 许心田 • 宋金鑫 • 李选松
201010905116 201010905112 201010905118 201010905121
基于蒙特卡罗模拟法的项目风险分析
基于蒙特卡罗模拟法的项目风险分析随着市场竞争的加剧和商业环境的不断变化,项目的风险管理变得越来越重要。
项目风险分析是评估项目面临的不确定性和风险的过程,通过识别、评估和监控项目风险,可以帮助项目团队预测和减轻潜在的损失。
在项目管理中,蒙特卡罗模拟法是一种常用的风险分析工具,它可以帮助项目团队更好地了解项目风险,并制定相应的风险管理策略。
蒙特卡罗模拟法是一种基于概率统计的数学方法,通过模拟随机变量的分布和相互关系,可以对项目风险进行定量分析。
在蒙特卡罗模拟中,通过随机生成大量可能的情景,并对这些情景进行模拟和仿真,从而得出项目可能面临的不同风险情况和概率分布,进而为项目决策和风险管理提供依据。
在进行基于蒙特卡罗模拟法的项目风险分析时,首先需要明确分析的目标和范围。
确定分析的范围和关键影响因素是非常重要的,因为这将直接影响到模拟的准确性和可靠性。
需要收集和整理项目相关的数据和信息,包括项目的时间、成本、质量、资源、市场、技术等方面的信息。
这些数据将作为模拟的输入,直接影响到模拟结果的准确性。
接下来,通过建立项目的概率模型和随机变量模型,对项目的不确定性进行建模和分析。
这一步通常涉及到对项目的关键参数和影响因素进行概率分布的假设和参数估计,包括正态分布、指数分布、泊松分布等等。
通过模拟这些概率分布,可以得出项目可能的风险情况和结果分布。
通过分析蒙特卡罗模拟的结果,可以得出项目面临的不同风险情况的概率分布和可能的损失情况。
还可以进行风险敏感性分析,确定项目的关键风险因素和影响因素,从而制定相应的风险管理策略和应对措施。
这将帮助项目团队更好地预测和减轻潜在的损失,提高项目的成功率和效益。
蒙特卡罗模拟优化与风险决策分析的应用研究
蒙特卡罗模拟优化与风险决策分析的应用研究一、概览随着科学技术和经济社会的发展,复杂系统和大型项目越来越普遍。
这些系统的规模和复杂性使得传统的决策方法和工具难以满足需求,因此基于随机性模拟与风险决策技术的蒙特卡罗方法应运而生,并在众多领域得到广泛应用。
本文将围绕“蒙特卡罗模拟优化与风险决策分析的应用研究”,针对工程实践中经常遇到的问题,从蒙特卡罗模拟的基本原理出发,进而深入探讨如何利用该方法进行优化决策和提高风险管理水平。
蒙特卡罗模拟是一种运用概率统计原理对不确定性进行建模和测试的方法,其基本思想是通过大量重复试验,输出某一信号参数的统计分布特性,从而来了解系统的性能和特性。
自从20世纪50年代,纽约的著名数学家约翰莫勒首次提出这一方法以来,蒙特卡罗模拟已经发展成为一种重要的经济和工程概率分析工具。
在实际问题中,许多涉及随机性和不确定性的领域,如金融、工程、物理学、环境科学等,都可以运用蒙特卡罗模拟技术进行求解。
通过采集和分析数据,决策者可以对系统的内在规律有更深入的理解,从而做出更加明智的决策。
为了更好地应用蒙特卡罗模拟优化与风险决策分析,本文将从以下几个方面展开讨论:首先介绍了蒙特卡罗模拟的基本原理;探讨了蒙特卡罗模拟在优化问题中的应用;再次,分析了蒙特卡罗模拟在风险决策中的应用;总结了蒙特卡罗模拟的重要价值和意义。
本文的研究目的是通过对蒙特卡罗模拟的应用研究和案例分析,为决策者提供实用的参考和指导。
1. 背景和意义在本论文中,首先介绍了研究的背景和意义。
蒙特卡罗方法在许多领域得到了广泛应用,如物理学、化学、工程、金融、经济学等。
尤其在金融领域,蒙特卡罗模拟已经成为一种重要的风险管理工具,帮助投资者制定投资策略并进行资产配置。
蒙特卡罗模拟在优化与决策方面的应用仍然面临着许多挑战,例如如何提高模拟的效率和准确性,以及如何将模拟结果应用于实际问题等。
本文将深入探讨蒙特卡罗模拟在优化与决策领域的应用,并结合具体案例,分析其在解决实际问题中的优势和局限性。
基于蒙特卡罗模拟的PPP项目投资风险分析
基于蒙特卡罗模拟的PPP项目投资风险分析蒙特卡罗模拟是一种常用的投资风险分析方法,通过随机模拟多个可能的投资情景,来评估项目的风险和潜在回报。
本文将结合蒙特卡罗模拟的方法,对PPP项目投资风险进行分析。
一、PPP项目投资风险分析的背景和意义PPP项目(即政府与社会资本合作项目)是一种公私合作的投资模式,具有分散风险、提高效率、降低成本等优势。
由于PPP项目多涉及国家战略、市场需求、政策环境等多个因素,其投资风险较大。
通过风险分析来评估PPP项目的投资风险,可以帮助投资者制定科学的投资策略,提高投资的成功率。
1. 确定关键变量和参数:在PPP项目投资风险分析中,关键变量可包括市场需求、项目运营成本、政策环境等。
参数则是这些变量的数值或概率分布。
2. 构建模型:根据项目特点和投资需求,构建相应的投资模型,建立项目收益和风险之间的关系。
3. 确定概率分布:根据历史数据、专家咨询或经验判断,确定关键变量的概率分布。
常见的概率分布包括正态分布、均匀分布、指数分布等。
4. 进行模拟实验:通过蒙特卡罗模拟,随机抽取关键变量的数值,代入模型中,得出模拟结果。
重复多次实验,得到一系列可能的结果。
5. 分析模拟结果:对模拟结果进行统计分析,计算平均值、方差、置信区间等指标。
通过对结果的分析,评估项目的风险和潜在回报。
三、蒙特卡罗模拟在PPP项目投资风险分析中的应用蒙特卡罗模拟在PPP项目投资风险分析中具有广泛的应用。
1. 评估项目的风险暴露程度:通过蒙特卡罗模拟,可以得出不同概率下的投资回报率,从而评估项目的风险暴露程度。
投资者可以根据不同风险偏好,制定相应的投资策略。
2. 优化投资组合:蒙特卡罗模拟可以模拟多个相关的项目,并分析它们的风险和收益之间的关系。
通过优化投资组合,可以降低整体风险,提高综合回报。
3. 确定项目关键风险因素:通过对模拟结果的分析,可以确定对项目回报率影响最大的关键风险因素。
投资者可以针对这些风险因素采取相应的风险管理措施,减少投资风险。
系统集成项目管理案例分析教程 案例二蒙特卡罗分析
案例二蒙特卡罗分析阅读以下关于信息系统项目管理过程中风险管理和蒙特卡罗分析方面问题的叙述,回答问题1至问题3。
8.2.1案例场景某公司实施CRM工程,实施过程中进行风险量化,其中的进度仿真采用蒙特卡罗分析,如图8-2所示。
需求调研阶段,发现功能需求15个,非功能需求12个;需求复审阶段,有10个用户参与复审,所有复审者都有相同解释的需求数目是24个。
项目开发过程中,应用功能点法则,分解出的系统功能点有346开发过程中发现23个错误,提交后又发现3个错误。
测试过程中,采用植入故障法估算程序中原有故障总数,人为植入的故障数是10个,经过一段时间的测试后发现的播种故障数是4个,在测试中又发现原有的故障数是2个。
产品发布时,发布模块总数是46个,和以前相比,变动6个模块,新添加7个模块,删除6个模块。
【问题1】(8分)解释案例中分析图的含义,简述进度仿真中,为什么不用传统的数学分析技术(不超过250字)。
【问题2】(8分)请用500字之内阐述项目质量管理中蒙特卡罗模拟方法的一般步骤。
【问题3】(9分)根据案例中的数据,分别计算整体缺陷清除率、需求解释一致性、程序中原有的故障数和软件成熟度。
8.2.2案例分析【问题1】本题考查考生在进度仿真中对蒙特卡罗仿真结果进行分析的能力。
要想回答好该题,考生需要了解蒙特卡罗曲线的实际意义。
风险量化的目的是形成有关需要追逐的机遇和需要注意的威胁的清单,建立有关项目团队有意识地接受或忽略的那些风险源和风险事件,以及谁决定这么做的文档。
进行风险量化的常用方法包括:期望的货币价值、统计综合、风险仿真、决策树等。
其中风险仿真除了量化风险以外,还可以制定项目进度计划。
风险仿真使用系统的表示法或模型来分析系统的行为或性能。
项目最常用的仿真形式,是使用项目网络作为项目模型的进度仿真。
大多数进度仿真是基于某种形式的蒙特卡罗(Monte Carlo)分析,该方法是一种模拟方法,通过多次“执行”目标项目,从而给出计算结果的统计分布,可以用来量化风险、计算在不同活动假设下的多个项目的持续时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
▪ Monte Carlo方法在求解一个问题是,总是需要根据 问题的要求构造一个用于求解的概率统计模型,常见
的模型把问题的解化为一个随机变量 X 的某个参数
的估计问题。
▪ 要估计的参数 通常设定为 X 的数学期望(亦平均
值,即 E(X ) )。按统计学惯例, 可用 X 的样
本( X1, X 2,...X n ) 的平均值来估计,即
Presentation_ID
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
4
蒙特卡罗方法的基本思想
▪ 蒙特卡罗方法又称计算机随机模拟方法。它是以概率统 计理论为基础的一种方法。
▪ 由蒲丰试验可以看出,当所求问题的解是某个事件的概 率,或者是某个随机变量的数学期望,或者是与概率、 数学期望有关的量时,通过某种试验的方法,得出该事 件发生的频率,或者该随机变量若干个具体观察值的算 术平均值,通过它得到问题的解。这就是蒙特卡罗方法 的基本思想。
Honeywell Confidential
12
随机数表
▪ 随机数表是由0,1,2,…,9十个数字组成,每个数字以0.1的 概率出现,数字之间相互独立。
▪ 方法:如果要得到n位有效数字的随机数,只需将表中每 n个相邻的随机数字合并在一起,且在最高位的前边加上 小数点即可。
例如:某随机数表第一行数字为7634258910…,要想得到三位有效数字 的随机数依次为:0.763,0.425,0.891
⑤程序结构简单,易于实现 。
缺点 ①收敛速度慢。 ②误差具有概率性。
③进行模拟的前提是 各输入变量是相互独 立的。
Presentation_ID
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
18
①能够比较逼真地描述具有随机性质的事物的特点及物理实 验过程
Presentation_ID
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
6
计算机模拟试验过程
计算机模拟试验过程,就是将试验过程(如投针问 题)化为数学问题,在计算机上实现。
Presentation_ID
加,除了增加相应的计算量外,不影响问题的误差。这一特点,
决定了蒙特卡罗方法对多维问题的适应性。
Presentation_ID
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
21
程序结构简单,易于实现
▪ 在计算机上进行蒙特卡罗方法计算时,程序结构简单, 分块性强,易于实现。
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
17
蒙特卡罗方法的特点
优点
①能够比较逼真地描述具有 随机性质的事物的特点及物 理实验过程。
②受几何条件限制小。
③收敛速度与问题的维数无 关。
④误差容易确定。
8
例子
某投资项目每年所得盈
利额A由投资额P、劳动
生产率L、和原料及能
源价格Q三个因素。
N
1
A aP bL2 cQ 2 d
根据历史数据,预测未来。
1
A aP bL2 cQ 2 d
收集P,L,Q数据,确定分布函 数 f (P), f (L), f (Q)
模拟次数N;根据分
其中作为当时的代表性工作便是在第二次世界大战期间,为解 决原子弹研制工作中,裂变物质的中子随机扩散问题,美国数学家 冯.诺伊曼(Von Neumann)和乌拉姆(Ulam)等提出蒙特卡罗模 拟方法。 由于当时工作是保密的,就给这种方法起了一个代号叫蒙 特卡罗,即摩纳哥的一个赌城的名字。用赌城的名字作为随机模拟 的名称,既反映了该方法的部分内涵,又易记忆,因而很快就得到 人们的普遍接受。
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
7
①建立概率统计模型
N
②收集模型中风险变量的数据 , 确定风 ⑤根据随机数在各风
险因数的分布函数
险变量的概率分布中
随机抽样,代入第一
步中建立的数学模型
N
N
布函数,产生随机数
产生 N个A值
N
抽取 P,L,Q一 组随机 数,带 入模型
统计分析,估计 均值,标准差
Presentation_ID
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
9
X
模型建立的两点说明
ba
a (b a)r1
f [a (b a)r1] f (m)r2 br 1 a s 1
m r,s为r函数s 参2数
Presentation_ID
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
X
1 n
n k 1
Xk
Presentation_ID
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
10
收集模型中风险变量的数据 , 确定 风险因数的分布函数
▪ 这时就必须采用主观概率,即由专家做出主观估计得到的概 率。
▪ 另一方面,在对估测目标的资料与数据不足的情况下,不可能 得知风险变量的真实分布时,根据当时或以前所收集到的类 似信息和历史资料,通过专家分析或利用德尔菲法还是能够 比较准确地估计上述各风险因素并用各种概率分布进行描 述的。
▪ Crystal ball软件对各种概率分布进行拟合以选取最合适的 分布。
15
常用概率分布的抽样公式
分布名称 [a,b]均匀分布
指数分布 正态分布
三角分布
分布
抽样公式
注
a b a r
ln r
12
ri
6
i1
a bacar,0r ca
ba
b b ab c1 r, c a r 1 a,b,c为三角分布的参数
蒙特卡罗模拟方法 与项目风险案例分析
Honeywell Confidential
1
Monte Carlo方法的发展历史
▪ 早在17世纪,人们就知道用事件发生的“频率”来决定 事件的“概率”。从方法特征的角度来说可以一直追溯 到18世纪后半叶的蒲丰(Buffon)随机投针试验,即著 名的蒲丰问题。
1707-1788
Presentation_ID
③根据风险分N 析的精度要求,确 N
定模拟次数
④建立对随机变量的抽样 方法,产生随机数。
⑥ N个样本值
⑦统计分析,估计均 值,标准差
Presentation_ID
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
Presentation_ID
© 2008 Honeywell Systems, Inc. All rights reserved.
Honeywell Confidential
3
20世纪四十年代,由于电子计算机的出现,利用电子计算机可 以实现大量的随机抽样的试验,使得用随机试验方法解决实际问题 才有了可能。
16
三角分布 三角形概率分布是一种应用较广连续型概率分布,
它是一种3点估计: 特别适用于对那些风险变量缺乏历 史统计资料和数据,但可以经过咨询专家意见,得出各参 数变量的最乐观值( a) ,最可能出现的中间值( b)以及最 悲观值(m ) ,这3个估计值( a,b, m )构成一个三角形分 布。
Presentation_ID
g 0 g(r) f (r)dr
从机变分量布通的密过值度某g函种(r数1试),f验(rg),中(r2得抽),到取…NN,个个g观子(rN察样)的值算r1,术r1,r平2,r均2,…值…,,rN,rN()用,概将率相语应言的来N说个,随
1 N
g N N i1 g(ri )
作为积分的估计值(近似值)。
Honeywell Confidential
ห้องสมุดไป่ตู้
20
③收敛速度与问题的维数无关
▪ 由误差定义可知,在给定置信水平情况下,蒙特卡罗方法的收敛
速度为
,与问题本身的维数无关O。(N维数1/的2 )变化,只引起
抽样时间及估计量计算时间的变化,不影响误差。也就是说,使
用蒙特卡罗方法时,抽取的子样总数N与维数s无关。维数的增
Honeywell Confidential
19
②受几何条件限制小
▪ 在计算s维空间中的任一区 域Ds上的积分,无论区域 Ds的形状多么特殊,只要 能给出描述Ds的几何特征 的条件,就可以从Ds中均 匀产生N个点
4 2
-4
-2
-2
-4
2
4
Presentation_ID
© 2008 Honeywell Systems, Inc. All rights reserved.
