高考数学正余弦定理1精编版
高三高考数学复习课件4-6正弦定理余弦定理

题型一 利用正弦定理、余弦定理解三角形
【例 1】 (1)在△ABC 中,已知 a=2,b= 6,A=45°,
则满足条件的三角形有( )
A.1 个
B.2 个
C.0 个
D.无法确定
(2)在△ABC 中,已知 sin A∶sin B= 2∶1,c2=b2+ 2bc, 则三内角 A,B,C 的度数依次是________.
π A= 3 .
由题意得21bcsin A=3sain2 A,a=3,所以 bc=8. 由余弦定理得 b2+c2-bc=9, 即(b+c)2-3bc=9.由 bc=8,得 b+c= 33. 故△ABC 的周长为 3+ 33.
【思维升华】 (1)对于面积公式 S=21absin C=21acsin B=12 bcsin A,一般是已知哪一个角就使用哪一个公式.
π 又 0<B<π,∴B= 3 . (2)因为 a=2,c= 2, 所以由正弦定理可知,sin2 A=sin2C, 故 sin A= 2sin C.
又B=π-(A+C), 故sin B+sin A(sin C-cos C) =sin(A+C)+sin Asin C-sin Acos C =sin Acos C+cos Asin C+sin Asin C-sin Acos C =(sin A+cos A)sin C =0. 又C为△ABC的内角, 故sin C≠0, 则sin A+cos A=0,即tan A=-1.
又 A∈(0,π),所以 A=3π 4 .
从而
sin
C=
1 2sin
A=
22×
22=12.
由 A=3π 4 知 C 为锐角,故 C=π6 .
故选 B.
π 【答案】 (1) 3 (2)B
正弦定理、余弦定理及其应用-高考数学【解析版】

专题24 正弦定理、余弦定理及其应用近几年高考对解三角形问题考查,大多放在解答题的第一题,主要利用三角形的内角和定理,正、余弦定理、三角形面积公式等知识解题,解题时要灵活利用三角形的边角关系进行“边转角”“角转边”,另外要注意22,,a c ac a c ++三者的关系. 高考中经常将三角变换与解三角形知识综合起来命题,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理实现边角互化;以上特征都不明显时,则要考虑两个定理都有可能用到.而三角变换中主要是“变角、变函数名和变运算形式”,其中的核心是“变角”,即注意角之间的结构差异,弥补这种结构差异的依据就是三角公式.与平面几何相结合的问题,要注重几何图形的特点的利用.由于新教材将正弦定理、余弦定理列入平面向量的应用,与平面向量相结合的命题将会出现.另外,“结构不良问题”作为实验,给予考生充分的选择空间,充分考查学生对数学本质的理解,引导中学数学在数学概念与数学方法的教学中,重视培养数学核心素养,克服“机械刷题”现象.同时,也增大了解题的难度.【重点知识回眸】(一)正弦、余弦定理1.在△ABC 中,若角A ,B ,C 所对的边分别是a ,b ,c ,R 为△ABC 的外接圆半径,则 定理正弦定理余弦定理内容2sin sin sin a b cR A B C=== a 2=b 2+c 2-2bc cos A ;b 2=c 2+a 2-2ca cos B ; c 2=a 2+b 2-2ab cos C 变形(1)a =2R sin A ,b =2R sin B , c =2R sin C ;(2)a ∶b ∶c =sin A ∶sin B ∶sin C ; (3)a +b +c sin A +sin B +sin C =asin A=2R cos A =b 2+c 2-a 22bc ;cos B =c 2+a 2-b 22ac ;cos C =a 2+b 2-c 22ab2. 正弦定理的主要作用是方程和分式中的边角互化.其原则为关于边、或是角的正弦值是否具备齐次的特征.如果齐次则可直接进行边化角或是角化边,否则不可行(1)222222sin sin sin sin sin A B A B C a b ab c +-=⇔+-= (2)cos cos sin cos sin cos sin b C c B a B C C B A +=⇒+=(恒等式) (3)22sin sin sin bc B C a A=3.余弦定理的变式应用:公式通过边的大小(角两边与对边)可以判断出A 是钝角还是锐角 当222b c a +>时,cos 0A >,即A 为锐角;当222b c a +=(勾股定理)时,cos 0A =,即A 为直角; 当222b c a +<时,cos 0A <,即A 为钝角 (二)三角形常用面积公式 (1)S =12a ·h a (h a 表示边a 上的高);(2)S =12ab sin C =12ac sin B =12bc sin A ;(3)S =12r (a +b +c )(r 为内切圆半径).(三)常用结论 1.三角形内角和定理在△ABC 中,A +B +C =π;变形:A +B 2=π2-C2.2.三角形中的三角函数关系(1)sin(A +B )=sin C ;(2)cos(A +B )=-cos C ; (3)sinA +B 2=cosC 2;(4)cos A +B 2=sin C2. 3.三角形中的射影定理在△ABC 中,a =b cos C +c cos B ;b =a cos C +c cos A ;c =b cos A +a cos B . 4.三角形中的大角对大边在△ABC 中,A >B ⇔a >b ⇔sin A >sin B . 5.海伦公式:()()()()1,2S p p a p b p c p a b c =---=++ 6.向量方法:()()2212S a ba b=⋅-⋅ (其中,a b 为边,a b 所构成的向量,方向任意)证明:()2222222111sin sin 1cos 244S ab C S a b C a b C =⇒==- ()()221cos 2S ab ab C ∴=-cos a b ab C ⋅=∴ ()()2212S a b a b =⋅-⋅坐标表示:()()1122,,,a x y b x y =,则122112S x y x y =- 7.三角形内角和A B C π++=(两角可表示另一角).()sin()sin sin A B C C π+=-= ()cos()cos cos A B C C π+=-=-8.三角形的中线定理与角平分线定理(1)三角形中线定理:如图,设AD 为ABC 的一条中线,则()22222AB AC AD BD +=+ (知三求一)证明:在ABD 中2222cos AB AD BD AD BD ADB =+-⋅ ① 2222cos AC AD DC AD DC ADC =+-⋅ ②D 为BC 中点 BD CD ∴=ADB ADC π∠+∠= cos cos ADB ADC ∴=-∴ ①+②可得:()22222AB AC AD BD +=+(2)角平分线定理:如图,设AD 为ABC 中BAC ∠的角平分线,则AB BDAC CD=证明:过D 作DE ∥AC 交AB 于EBD BEDC AE∴= EDA DAC ∠=∠ BBEAD 为BAC ∠的角平分线EAD DAC ∴∠=∠ EDA EAD ∴∠=∠EAD ∴为等腰三角形 EA ED ∴= BD BE BEDC AE ED ∴==而由BED BAC 可得:BE ABED AC=AB BDAC CD ∴=(四)测量中的几个常用术语术语名称术语意义图形表示仰角与俯角在目标视线与水平视线(两者在同一铅垂平面内)所成的角中,目标视线在水平视线上方的叫做仰角,目标视线在水平视线下方的叫做俯角方位角从某点的指北方向线起按顺时针方向到目标方向线之间的夹角叫做方位角,方位角θ的范围是[0°,360°)方向角正北或正南方向线与目标方向线所成的锐角,通常表达为北(南)偏东(西)α例:(1)北偏东α:(2)南偏西α:坡角与坡度坡面与水平面所成锐二面角叫坡角(θ为坡角);坡面的垂直高度与水平宽度之比叫坡度(坡比),即i =hl=tan θ135°的始边是指北方向线,始边顺时针方向旋转135°得到终边;方向角南偏西30°的始边是指南方向线,向西旋转30°得到终边.【典型考题解析】热点一 利用正、余弦定理解三角形【典例1】(2021·全国·高考真题(文))在ABC 中,已知120B =︒,19AC 2AB =,则BC =( ) A .1 B 2C 5D .3【答案】D 【解析】 【分析】利用余弦定理得到关于BC 长度的方程,解方程即可求得边长. 【详解】设,,AB c AC b BC a ===,结合余弦定理:2222cos b a c ac B =+-可得:21942cos120a a c =+-⨯⨯⨯, 即:22150a a +-=,解得:3a =(5a =-舍去), 故3BC =. 故选:D.【典例2】(2020·山东·高考真题)在ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若222sin a b c ab C +=+,且sin cos +a B C 2sin cos c B A =,则tan A 等于( ) A .3 B .13- C .3或13-D .-3或13【答案】A 【解析】 【分析】利用余弦定理求出tan 2C =,并进一步判断4C π>,由正弦定理可得22sin()sin A C B +=⇒=,最后利用两角和的正切公式,即可得到答案; 【详解】222sin cos tan 222a b c CC C ab +-==⇒=,4C π∴>,2sin sin sin a b cR A B C===, 2sin sin cos sin sin cos A B C C B A B ∴⋅⋅+⋅⋅=, 22sin()sin A C B ∴+=⇒=4B π∴=, tan 1B ∴=,∴tan tan tan tan()31tan tan B CA B C B C+=-+=-=-⋅,故选:A.【典例3】(2022·全国·高考真题(文))记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ﹐已知()()sin sin sin sin C A B B C A -=-. (1)若2A B =,求C ;(2)证明:2222a b c =+ 【答案】(1)5π8; (2)证明见解析. 【解析】 【分析】(1)根据题意可得,()sin sin C C A =-,再结合三角形内角和定理即可解出;(2)由题意利用两角差的正弦公式展开得()()sin sin cos cos sin sin sin cos cos sin C A B A B B C A C A -=-,再根据正弦定理,余弦定理化简即可证出. (1)由2A B =,()()sin sin sin sin C A B B C A -=-可得,()sin sin sin sin C B B C A =-,而π02B <<,所以()sin 0,1B ∈,即有()sin sin 0C C A =->,而0π,0πC C A <<<-<,显然C C A ≠-,所以,πC C A +-=,而2A B =,πA B C ++=,所以5π8C =. (2)由()()sin sin sin sin C A B B C A -=-可得,()()sin sin cos cos sin sin sin cos cos sin C A B A B B C A C A -=-,再由正弦定理可得,cos cos cos cos ac B bc A bc A ab C -=-,然后根据余弦定理可知,()()()()22222222222211112222a c b b c a b c a a b c +--+-=+--+-,化简得: 2222a b c =+,故原等式成立.【总结提升】1.解三角形的常用方法:(1)直接法:观察题目中所给的三角形要素,使用正余弦定理求解(2)间接法:可以根据所求变量的个数,利用正余弦定理,面积公式等建立方程,再进行求解 2.解三角形的常见题型及求解方法(1)已知两角A ,B 与一边a ,由A +B +C =π及a sin A =b sin B =c sin C ,可先求出角C 及b ,再求出c .(2)已知两边b ,c 及其夹角A ,由a 2=b 2+c 2-2bc cos A ,先求出a ,再求出角B ,C . (3)已知三边a ,b ,c ,由余弦定理可求出角A ,B ,C .(4)已知两边a ,b 及其中一边的对角A ,由正弦定理a sin A =bsin B 可求出另一边b 的对角B ,由C =π-(A +B ),可求出角C ,再由a sin A =c sin C 可求出c ,而通过a sin A =bsin B 求角B 时,可能有一解或两解或无解的情况.热点二 三角形面积问题【典例4】(2022·浙江·高考真题)在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知345,cos 5a c C ==. (1)求sin A 的值;(2)若11b =,求ABC 的面积. 【答案】5(2)22. 【解析】 【分析】(1)先由平方关系求出sin C ,再根据正弦定理即可解出;(2)根据余弦定理的推论222cos 2a b c C ab+-=以及45a c =可解出a ,即可由三角形面积公式in 12s S ab C =求出面积. (1)由于3cos 5C =, 0πC <<,则4sin 5C =.因为45a c =, 由正弦定理知4sin 5A C ,则55sin A C ==(2)因为45a c =,由余弦定理,得2222221612111355cos 22225a a a abc C ab a a +--+-====, 即26550a a +-=,解得5a =,而4sin 5C =,11b =, 所以ABC 的面积114sin 51122225S ab C ==⨯⨯⨯=. 【典例5】(2022·全国·高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,分别以a ,b ,c 为边长的三个正三角形的面积依次为123,,S S S ,已知123313S S S B -+==. (1)求ABC 的面积; (2)若2sin sin A C =,求b .【答案】2 (2)12 【解析】 【分析】(1)先表示出123,,S S S ,再由1233S S S -+=2222a c b +-=,结合余弦定理及平方关系求得ac ,再由面积公式求解即可;(2)由正弦定理得22sin sin sin b acB AC =,即可求解.(1)由题意得222212313333,,2S a S S =⋅===,则2221233333S S S -+==即2222a c b +-=,由余弦定理得222cos 2a c b B ac+-=,整理得cos 1ac B =,则cos 0B >,又1sin 3B =,则2122cos 13B ⎛⎫=- ⎪⎝⎭132cos ac B ==12sin 2ABCS ac B ==(2)由正弦定理得:sin sin sin b a c B A C ==,则223294sin sin sin sin sin 42b a c ac B A C A C =⋅===,则3sin 2b B =,31sin 22b B ==. 【规律方法】 1.求三角形面积的方法(1)若三角形中已知一个角(角的大小或该角的正、余弦值),结合题意求解这个角的两边或该角的两边之积,代入公式求面积.(2)若已知三角形的三边,可先求其一个角的余弦值,再求其正弦值,代入公式求面积.总之,结合图形恰当选择面积公式是解题的关键. 2.已知三角形面积求边、角的方法(1)若求角,就寻求夹这个角的两边的关系,利用面积公式列方程求解. (2)若求边,就寻求与该边(或两边)有关联的角,利用面积公式列方程求解. 热点三 三角形的周长问题【典例6】(2022·北京·高考真题)在ABC 中,sin 23C C =. (1)求C ∠;(2)若6b =,且ABC 的面积为3ABC 的周长. 【答案】(1)6π(2)663 【解析】 【分析】(1)利用二倍角的正弦公式化简可得cos C 的值,结合角C 的取值范围可求得角C 的值; (2)利用三角形的面积公式可求得a 的值,由余弦定理可求得c 的值,即可求得ABC 的周长. (1)解:因为()0,C π∈,则sin 0C >32sin cos C C C =, 可得3cos C =,因此,6C π=.(2)解:由三角形的面积公式可得13sin 6322ABCSab C a ===3a = 由余弦定理可得22232cos 4836243612c a b ab C =+-=+-⨯=,23c ∴= 所以,ABC 的周长为36a b c ++=.【典例7】(2022·全国·高考真题(理))记ABC 的内角,,A B C 的对边分别为,,a b c ,已知sin sin()sin sin()C A B B C A -=-.(1)证明:2222a b c =+; (2)若255,cos 31a A ==,求ABC 的周长. 【答案】(1)见解析 (2)14 【解析】 【分析】(1)利用两角差的正弦公式化简,再根据正弦定理和余弦定理化角为边,从而即可得证; (2)根据(1)的结论结合余弦定理求出bc ,从而可求得b c +,即可得解. (1)证明:因为()()sin sin sin sin C A B B C A -=-,所以sin sin cos sin sin cos sin sin cos sin sin cos C A B C B A B C A B A C -=-,所以2222222222222a c b b c a a b c ac bc ab ac bc ab +-+-+-⋅-⋅=-⋅, 即()22222222222a cb a bc b c a +-+--+-=-, 所以2222a b c =+; (2)解:因为255,cos 31a A ==, 由(1)得2250b c +=,由余弦定理可得2222cos a b c bc A =+-, 则50502531bc -=, 所以312bc =, 故()2222503181b c b c bc +=++=+=, 所以9b c +=,所以ABC 的周长为14a b c ++=. 【规律方法】求边,就寻求与该边(或两边)有关联的角,利用已知条件列方程求解.【典例7】反映的“整体代换”思想,具有一定的技巧性. 热点四 判断三角形的形状【典例8】(2020·海南·高考真题)在①3ac ①sin 3c A =,①3=c b 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的值;若问题中的三角形不存在,说明理由. 问题:是否存在ABC ,它的内角,,A B C 的对边分别为,,a b c ,且sin 3sin A B ,6C π=,________?注:如果选择多个条件分别解答,按第一个解答计分. 【答案】详见解析 【解析】 【分析】方法一:由题意结合所给的条件,利用正弦定理角化边,得到a ,b 的比例关系,根据比例关系,设出长度长度,由余弦定理得到c 的长度,根据选择的条件进行分析判断和求解. 【详解】[方法一]【最优解】:余弦定理 由sin 3sin AB 可得:3ab=()3,0a m b m m ==>, 则:22222232cos 323c a b ab C m m m m m =+-=+-⨯=,即c m =. 若选择条件①:据此可得:2333ac m m m =⨯==1m ∴=,此时1c m ==. 若选择条件②:据此可得:222222231cos 222b c a m m m A bc m +-+-===-, 则:213sin 12A ⎛⎫=-- ⎪⎝⎭3sin 3c A m ==,则:23c m ==若选择条件③: 可得1c mb m==,c b =,与条件3=c b 矛盾,则问题中的三角形不存在. [方法二]:正弦定理 由,6C A B C ππ=++=,得56A B π=-. 由sin 3sin A B ,得5sin 36B B π⎛⎫-= ⎪⎝⎭,即13cos 32B B B =, 得3tan B =.由于0B π<<,得6B π=.所以2,3b c A π==.若选择条件①:由sin sin a c A C=,得2sin sin 36a cππ=,得3a c =. 解得1,3c b a ===.所以,选条件①时问题中的三角形存在,此时1c =. 若选择条件②: 由sin 3c A =,得2sin33c π=,解得3c =23b c == 由sin sin a c A C=,得2sin sin 36a cππ=,得36a c ==. 所以,选条件②时问题中的三角形存在,此时23c =.若选择条件③:由于3c b 与b c =矛盾,所以,问题中的三角形不存在. 【整体点评】方法一:根据正弦定理以及余弦定理可得,,a b c 的关系,再根据选择的条件即可解出,是本题的通性通法,也是最优解;方法二:利用内角和定理以及两角差的正弦公式,消去角A ,可求出角B ,从而可得2,,36b c A B C ππ====,再根据选择条件即可解出.【典例9】(2020·全国·高考真题(文))△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知25cos ()cos 24A A π++=.(1)求A ; (2)若3b c -=,证明:△ABC 是直角三角形. 【答案】(1)3A π=;(2)证明见解析【解析】 【分析】(1)根据诱导公式和同角三角函数平方关系,25cos cos 24A A π⎛⎫++= ⎪⎝⎭可化为251cos cos 4A A -+=,即可解出;(2)根据余弦定理可得222b c a bc +-=,将3b c -=代入可找到,,a b c 关系, 再根据勾股定理或正弦定理即可证出. 【详解】(1)因为25cos cos 24A A π⎛⎫++= ⎪⎝⎭,所以25sin cos 4A A +=,即251cos cos 4A A -+=, 解得1cos 2A =,又0A π<<, 所以3A π=;(2)因为3A π=,所以2221cos 22b c a A bc +-==, 即222b c a bc +-=①, 又3b c -=②, 将②代入①得,()2223b c b c bc +--=,即222250b c bc +-=,而b c >,解得2b c =, 所以3a c =, 故222b a c =+, 即ABC 是直角三角形. 【总结提升】1.判定三角形形状的两种常用途径2.判定三角形的形状的注意点在判断三角形的形状时一定要注意解是否唯一,并注重挖掘隐含条件.另外,在变形过程中要注意角A ,B ,C 的范围对三角函数值的影响,在等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解. 3.确定三角形要素的条件: (1)唯一确定的三角形:① 已知三边(SSS ):可利用余弦定理求出剩余的三个角② 已知两边及夹角(SAS ):可利用余弦定理求出第三边,进而用余弦定理(或正弦定理)求出剩余两角 ③ 两角及一边(AAS 或ASA ):利用两角先求出另一个角,然后利用正弦定理确定其它两条边 (2)不唯一确定的三角形① 已知三个角(AAA ):由相似三角形可知,三个角对应相等的三角形有无数多个.由正弦定理可得:已知三个角只能求出三边的比例:::sin :sin :sin a b c A B C =② 已知两边及一边的对角(SSA ):比如已知,,a b A ,所确定的三角形有可能唯一,也有可能是两个.其原因在于当使用正弦定理求B 时,sin sin sin sin a b b A B A B a =⇒=,而0,,22B πππ⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝⎭时,一个sin B 可能对应两个角(1个锐角,1个钝角),所以三角形可能不唯一.(判定是否唯一可利用三角形大角对大边的特点)热点五 正弦定理、余弦定理实际应用【典例10】(2021·全国·高考真题(理))魏晋时刘徽撰写的《海岛算经》是有关测量的数学著作,其中第一题是测海岛的高.如图,点E ,H ,G 在水平线AC 上,DE 和FG 是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG 称为“表距”,GC 和EH 都称为“表目距”,GC 与EH 的差称为“表目距的差”则海岛的高AB =( )A .⨯+表高表距表目距的差表高B .⨯-表高表距表目距的差表高C .⨯+表高表距表目距的差表距D .⨯表高表距-表目距的差表距【答案】A 【解析】 【分析】利用平面相似的有关知识以及合分比性质即可解出. 【详解】 如图所示:由平面相似可知,,DE EH FG CGAB AH AB AC==,而 DE FG =,所以 DE EH CG CG EH CG EHAB AH AC AC AH CH--====-,而 CH CE EH CG EH EG =-=-+, 即CG EH EG EG DE AB DE DE CG EH CG EH-+⨯=⨯=+--=+⨯表高表距表高表目距的差. 故选:A.【典例11】(2021·全国·高考真题(理))2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m ),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A ,B ,C 三点,且A ,B ,C 在同一水平面上的投影,,A B C '''满足45ACB ∠'''=︒,60A BC ''∠'=︒.由C 点测得B 点的仰角为15︒,BB '与CC '的差为100;由B 点测得A 点的仰角为45︒,则A ,C 两点到水平面A B C '''的高度差AA CC ''-3 1.732≈)( )A .346B .373C .446D .473【答案】B 【解析】 【分析】通过做辅助线,将已知所求量转化到一个三角形中,借助正弦定理,求得''A B ,进而得到答案. 【详解】过C 作'CH BB ⊥,过B 作'BD AA ⊥,故()''''''100100AA CC AA BB BH AA BB AD -=--=-+=+, 由题,易知ADB △为等腰直角三角形,所以AD DB =. 所以''100''100AA CC DB A B -=+=+. 因为15BCH ∠=︒,所以100''tan15CH C B ==︒在'''A B C 中,由正弦定理得:''''100100sin 45sin 75tan15cos15sin15A B C B ===︒︒︒︒︒,而62sin15sin(4530)sin 45cos30cos 45sin 30-︒=︒-︒=︒︒-︒︒=, 所以210042''100(31)27362A B ⨯==≈-,所以''''100373AA CC A B -=+≈. 故选:B .【典例12】(2022·上海·高考真题)如图,矩形ABCD 区域内,D 处有一棵古树,为保护古树,以D 为圆心,DA 为半径划定圆D 作为保护区域,已知30AB =m ,15AD =m ,点E 为AB 上的动点,点F 为CD 上的动点,满足EF 与圆D 相切.(1)若∠ADE 20︒=,求EF 的长;(2)当点E 在AB 的什么位置时,梯形FEBC 的面积有最大值,最大面积为多少? (长度精确到0.1m ,面积精确到0.01m²) 【答案】(1)23.3m(2)当8.7AE =时,梯形FEBC 的面积有最大值,最大值为255.14 【解析】 【分析】(1)设EF 与圆D 相切于对点H ,连接DH ,则DH EF ⊥,15DH AD ==,在直角HED △和直角FHD △中分别求出,EH HF ,从而得出答案.(2)先求出梯形AEFD 的面积的最小值,从而得出梯形FEBC 的面积的最大值. (1)设EF 与圆D 相切于对点H ,连接DH ,则DH EF ⊥,15DH AD == 则AE EH =,所以直角ADE 与直角HED △全等 所以20ADE HDE ∠=∠=︒在直角HED △中,tan2015tan20EH DH =︒=︒90250HDF ADE ∠=︒-∠=︒在直角FHD △中,tan5015tan50HF AD =︒=︒()sin 20sin5015tan 20tan5015cos20cos50EF EH HF ︒︒⎛⎫=+=︒+︒=+ ⎪︒︒⎝⎭()sin 2050sin 20cos50cos20sin501515cos20cos50cos20cos50︒+︒︒︒︒+︒︒=⨯=⨯︒︒︒︒sin 70151523.3cos 20cos50cos50︒=⨯=≈︒︒︒(2)设ADE θ∠=,902HDF θ∠=︒-,则15tan AE θ=,()15tan 902FH θ=︒- ()115151515tan 15tan 90215tan 222tan 2EFDS EF DH θθθθ⎛⎫=⨯⨯=⎡+︒-⎤=+ ⎪⎣⎦⎝⎭ 11515tan 22ADESAD AE θ=⨯⨯=⨯ 所以梯形AEFD 的面积为215152251tan 30tan 2tan 2tan 222tan ADEDEFS S Sθθθθθ⎛⎫-⎛⎫=+=+=+ ⎪ ⎪⎝⎭⎝⎭2251225122533tan 23tan 4tan 4tan 2θθθθ⎛⎫=+≥⨯⨯= ⎪⎝⎭ 当且当13tan tan θθ=,即3tan θ=时取得等号,此时315tan 15538.7AE θ===≈ 即当3tan θ=时,梯形AEFD 2253则此时梯形FEBC 的面积有最大值22531530255.14⨯≈ 所以当8.7AE =时,梯形FEBC 的面积有最大值,最大值为255.14 热点五 平面几何中的解三角形问题【典例13】(2021·浙江·高考真题)在ABC 中,60,2B AB ∠=︒=,M 是BC 的中点,23AM =AC =___________,cos MAC ∠=___________. 【答案】 13239【解析】 【分析】由题意结合余弦定理可得=8BC ,进而可得AC ,再由余弦定理可得cos MAC ∠. 【详解】由题意作出图形,如图,在ABM 中,由余弦定理得2222cos AM AB BM BM BA B =+-⋅⋅,即21124222BM BM =+-⨯⨯,解得=4BM (负值舍去),所以=2=2=8BC BM CM ,在ABC 中,由余弦定理得22212cos 464228522AC AB BC AB BC B =+-⋅⋅=+-⨯⨯⨯=, 所以13AC =在AMC 中,由余弦定理得222239cos 2223213AC AM MC MAC AM AC +-∠=⋅⨯⨯. 故答案为:213239【典例14】(2020·江苏·高考真题)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知3,2,45a c B ===︒.(1)求sin C 的值;(2)在边BC 上取一点D ,使得4cos 5ADC ∠=-,求tan DAC ∠的值. 【答案】(1)5sin C (2)2tan 11DAC ∠=.【解析】 【分析】(1)方法一:利用余弦定理求得b ,利用正弦定理求得sin C .(2)方法一:根据cos ADC ∠的值,求得sin ADC ∠的值,由(1)求得cos C 的值,从而求得sin ,cos DAC DAC ∠∠的值,进而求得tan DAC ∠的值. 【详解】(1)[方法一]:正余弦定理综合法由余弦定理得22222cos 922325b a c ac B =+-=+-⨯=,所以5b = 由正弦定理得sin 5sin sin sin c b c B C C B b =⇒==. [方法二]【最优解】:几何法过点A 作AE BC ⊥,垂足为E .在Rt ABE △中,由2,45c B,可得1AE BE ==,又3a =,所以2EC =.在Rt ACE 中,225AC AE EC =+5sin 5C ==(2)[方法一]:两角和的正弦公式法由于4cos 5ADC ∠=-,,2ADC ππ⎛⎫∠∈ ⎪⎝⎭,所以23sin 1cos 5ADC ADC ∠=-∠=.由于,2ADC ππ⎛⎫∠∈ ⎪⎝⎭,所以0,2C π⎛⎫∈ ⎪⎝⎭,所以225cos 1sin C C =- 所以()sin sin DAC DAC π∠=-∠()sin ADC C =∠+∠sin cos cos sin ADC C ADC C =∠⋅+∠⋅325452555⎛⎫=-= ⎪⎝⎭. 由于0,2DAC π⎛⎫∠∈ ⎪⎝⎭,所以2115cos 1sin DAC DAC ∠=-∠=所以sin 2tan cos 11DAC DAC DAC ∠∠==∠. [方法二]【最优解】:几何法+两角差的正切公式法在(1)的方法二的图中,由4cos 5ADC ∠=-,可得4cos cos()cos 5ADE ADC ADC π∠=-∠=-∠=,从而4sin 4sin cos ,tan 5cos 3DAE DAE ADE DAE DAE ∠∠=∠=∠==∠.又由(1)可得tan 2EC EAC AE ∠==,所以tan tan 2tan tan()1tan tan 11EAC EAD DAC EAC EAD EAC EAD ∠-∠∠=∠-∠==+∠⋅∠.[方法三]:几何法+正弦定理法在(1)的方法二中可得1,2,5AE CE AC === 在Rt ADE △中,45,cos sin 3AE AD ED AD ADE ADE ===∠=∠,所以23CD CE DE =-=. 在ACD △中,由正弦定理可得25sin sin CD DAC C AD ∠=⋅=, 由此可得2tan 11DAC ∠=. [方法四]:构造直角三角形法如图,作AE BC ⊥,垂足为E ,作DG AC ⊥,垂足为点G .在(1)的方法二中可得1,2,5AE CE AC ===由4cos 5ADC ∠=-,可得243cos ,sin 1cos 55ADE ADE ADE ∠=∠=-∠.在Rt ADE △中,22542,,sin 333AE AD DE AD AE CD CE DE ADE ==-==-=∠.由(1)知5sin C =Rt CDG △中,222545sin DG CD C CG CD DG =⋅==-=,从而115AG AC CG =-=在Rt ADG 中,2tan 11DG DAG AG ∠==. 所以211DAC ∠=. 【整体点评】(1)方法一:使用余弦定理求得5b =sin C ;方法二:抓住45°角的特点,作出辅助线,利用几何方法简单计算即得答案,运算尤其简洁,为最优解;(2)方法一:使用两角和的正弦公式求得DAC ∠的正弦值,进而求解;方法二:适当作出辅助线,利用两角差的正切公式求解,运算更为简洁,为最优解;方法三:在几何法的基础上,使用正弦定理求得DAC ∠的正弦值,进而得解;方法四:更多的使用几何的思维方式,直接作出含有DAC ∠的直角三角形,进而求解,也是很优美的方法. 【典例15】(2021·北京·高考真题)在ABC 中,2cos c b B =,23C π=.(1)求B ;(2)再从条件①、条件②、条件③这三个条件中选择一个作为已知,使ABC 存在且唯一确定,求BC 边上中线的长. 条件①:2c b =;条件②:ABC 的周长为423+ 条件③:ABC 33【答案】(1)6π;(2)答案不唯一,具体见解析. 【解析】 【分析】(1)由正弦定理化边为角即可求解; (2)若选择①:由正弦定理求解可得不存在;若选择②:由正弦定理结合周长可求得外接圆半径,即可得出各边,再由余弦定理可求; 若选择③:由面积公式可求各边长,再由余弦定理可求. 【详解】(1)2cos c b B =,则由正弦定理可得sin 2sin cos C B B =, 23sin 2sin 3B π∴==23C π=,0,3B π⎛⎫∴∈ ⎪⎝⎭,220,3B π⎛⎫∈ ⎪⎝⎭,23B π∴=,解得6B π=;(2)若选择①:由正弦定理结合(1)可得3sin 231sin 2c Cb B=== 与2c b =矛盾,故这样的ABC 不存在; 若选择②:由(1)可得6A π=,设ABC 的外接圆半径为R , 则由正弦定理可得2sin 6a b R R π===,22sin33c R R π=, 则周长23423a b c R R ++==+ 解得2R =,则2,23a c ==由余弦定理可得BC 边上的中线的长度为:()222312231cos76π+-⨯⨯⨯若选择③:由(1)可得6A π=,即a b =,则211333sin 22ABCSab C a ===,解得3a = 则由余弦定理可得BC 边上的中线的长度为:22233212cos 3322342a a b b π⎛⎫+-⨯⨯⨯++⨯= ⎪⎝⎭【总结提升】与平面图形有关的解三角形问题的关键及思路求解平面图形中的计算问题,关键是梳理条件和所求问题的类型,然后将数据化归到三角形中,利用正弦定理或余弦定理建立已知和所求的关系. 具体解题思路如下:(1)把所提供的平面图形拆分成若干个三角形,然后在各个三角形内利用正弦、余弦定理求解; (2)寻找各个三角形之间的联系,交叉使用公共条件,求出结果.【精选精练】一、单选题1.(2022·贵州贵阳·高三开学考试(文))“云楼”是白云区泉湖公园的标志性建筑,也是来到这里必打卡的项目之一,它端坐于公园的礼仪之轴,建筑外形主体木质结构,造型独特精巧,是泉湖公园的“阵眼”和“灵魂”,同时也是泉湖历史与发展变化的资料展示馆.小张同学为测量云楼的高度,如图,选取了与云楼底部D 在同一水平面上的A ,B 两点,在A 点和B 点测得C 点的仰角分别为45°和30°,测得257AB =150ADB ∠=︒,则云楼的高度CD 为( )A .20米B .25米C .7D .257【答案】B【分析】设CD x =,由锐角三角函数得到AD x =,3BD x =,再在ABD △中利用余弦定理求出x ,即可得解.【详解】解:依题意45CAD ︒∠=,30CBD ︒∠=, 设CD x =,在Rt ACD △、Rt BCD 中,tan 1CD CAD AD∠==,3tan 3CD CBD BD ∠==,所以AD x =,3BD x =,在ABD △中由余弦定理2222cos AB AD BD AD BD ADB =+-⋅∠, 即()()22232573232x x x x ⎛⎫=+-⋅⋅- ⎪ ⎪⎝⎭,解得25x =或25x =-(舍去), 所以云楼的高度CD 为25米; 故选:B2.(2022·河南·郑州四中高三阶段练习(文))在ABC 中,角,,A B C 的对边分别为,,a b c ,已知三个向量,cos 2A m a ⎛⎫= ⎪⎝⎭,,cos ,,cos 22B C n b p c ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭共线,则ABC 的形状为( )A .等边三角形B .钝角三角形C .有一个角是6π的直角三角形 D .等腰直角三角形【答案】A【分析】由向量共线的坐标运算可得cos cos 22B Aa b =,利用正弦定理化边为角,再展开二倍角公式整理可得sinsin 22A B=,结合角的范围求得A B =,同理可得B C =,则答案可求. 【详解】向量(,cos )2A m a =,(,cos )2B n b =共线,cos cos 22B A a b ∴=,由正弦定理得:sin cos sin cos 22B A A B =, 2sincos cos 2sin cos cos 222222A A B B B A ∴=,则sin sin 22A B=, 022A π<<,022B π<<,∴22A B =,即A B =.同理可得B C =.ABC ∴形状为等边三角形.故选:A .3.(2022·安徽蚌埠·一模)圭表是我国古代通过观察记录正午时影子长度的长短变化来确定季节变化的一种天文仪器,它包括一根直立的标杆(称为“表”)和一把呈南北方向水平固定摆放的与标杆垂直的长尺(称为“圭”).当正午阳光照射在表上时,影子就会落在圭面上,圭面上影子长度最长的那一天定为冬至,影子长度最短的那一天定为夏至.如图是根据蚌埠市(北纬32.92)的地理位置设计的圭表的示意图,已知蚌埠市冬至正午太阳高度角(即ABC ∠)约为33.65,夏至正午太阳高度角(即ADC ∠)约为80.51.圭面上冬至线和夏至线之间的距离(即BD 的长)为7米,则表高(即AC 的长)约为( )(已知229tan33.65,tan80.5135≈≈)A .4.36米B .4.83米C .5.27米D .5.41米【答案】C【分析】由题意可求出35,229BC AC CD AC ==,再由BD 的长为7米,求出AC ,即可得出答案. 【详解】由图可知229tan33.65,tan80.5135AC AC BC CD =≈=≈, 所以35,229BC AC CD AC ==, 得3577587 5.272295811BD AC AC AC ⎛⎫=-==⇒=≈ ⎪⎝⎭. 故选:C. 二、多选题4.(2022·吉林·延边第一中学高一期中)下列命题错误的是( ) A .三角形中三边之比等于相应的三个内角之比 B .在ABC 中,若sin sin A B >,则A B >C .在ABC 的三边三角共6个量中,知道任意三个,均可求出剩余三个D .当2220b c a +->时,ABC 为锐角三角形;当2220b c a +-=时,ABC 为直角三角形;当2220b c a +-<时,ABC 为钝角三角形 【答案】ACD【分析】对于ACD ,举例判断,对于B ,利用正弦定理结果合三角形的性质判断.【详解】对于A ,等腰直角三角形的三边比为1:1:2,而三个内角的比为1:1:2,所以A 错误, 对于B ,在ABC 中,当sin sin A B >时,由正弦定理可得a b >,因为在三角形中大边对大角,所以A B >,所以B 正确,对于C ,在ABC 中,若三个角,,A B C 确定,则这样的三角形三边无法确定,这样的三角形有无数个,所以C 错误,对于D ,在ABC 中,2220b c a +->时,由余弦定理可知角A 为锐角,而角,B C 的大小无法判断,所以三角形的形状无法判断,所以D 错误, 故选:ACD5.(2021·黑龙江黑河·高二阶段练习)在ABC 中,已知2,3,AB AC AD ==是角A 的平分线,则AD 的长度可能为( ) A .2.1 B .2.2 C .2.3 D .2.4【答案】ABC【分析】过C 作//CE AB 交AD 延长线于E ,由题设可得3AC EC ==且ADB EDC ,进而有23AD ED =,令2AD x =并在ACE 中应用余弦定理求x 范围,即可得AD 范围. 【详解】过C 作//CE AB 交AD 延长线于E ,又AD 是角A 的平分线,得CAE BAE E ∠=∠=∠,故3AC EC ==, 而ADB EDC ,则23AD AB ED EC ==, 令2AD x =,则5AE x =,在ACE 中,22221825cos (1,1)218AC EC AE x ACE AC EC +--∠==∈-⋅, 可得605x <<,则122(0,)5AD x =∈,故A 、B 、C 满足要求.故选:ABC6.(2022·吉林·长春市第二实验中学高一期末)中国南宋时期杰出的数学家秦九韶在《数书九章》中提出了“三斜求积术”,即以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一为从隅,开平方得积.把以上文字写成公式,即222222142c a b S c a ⎡⎤⎛⎫+-=-⎢⎥ ⎪⎢⎥⎝⎭⎣⎦S 为三角形的面积,a 、b 、c 为三角形的三边).现有ABC 满足::2:7a b c =ABC 的面积63ABC S =△列结论正确的是( ) A .ABC 的最短边长是2 B .ABC 的三个内角满足2A B C +=C .ABC 221D .ABC 的中线CD 的长为32【答案】BC【分析】依题意设2a t =,3b t =,7c t =(0t >),利用面积公式求出t ,即可求出边长,从而判断A ,再由余弦定理求出C ,即可判断B ,利用正弦定理求出外接圆的半径,即可判断C ,最后由数量积的运算律求出中线CD ,即可判断D.【详解】解:由::2:3:7a b c =,设2a t =,3b t =,7c t =(0t >),因为63ABC S =△,所以2222221749637442t t t t t ⎡⎤⎛⎫+-=+-⎢⎥ ⎪⎢⎥⎝⎭⎣⎦,解得2t =,则4a =,6b =,27c =,故A 错误;因为2221636281cos 22462a b c C ab +-+-===⨯⨯,所以π3C =,π2ππ233A B C +=-==,故B 正确; 因为π3C =,所以3sin 2C =,由正弦定理得4212sin 3c R C ==,2213R =,故C 正确; ()12CD CA CB =+,所以()22111361624619442CD CA CB ⎛⎫=+=⨯++⨯⨯⨯= ⎪⎝⎭,故19CD =,故D 错误.故选:BC . 三、填空题7.(2022·贵州·贵阳乐湾国际实验学校高三开学考试(理))在ABC 中,角A ,B ,C 所对的边分别为,,a b c ,且42c =B =4π,若ABC 的面积S =2,则b =___________. 【答案】5【分析】先由面积公式计算1a =,再利用余弦定理计算5b =. 【详解】由三角形面积公式,1sin 22S ac B ==, 所以,1a =.由余弦定理,2222cos 25b a c ac B =+-=.所以,5b =. 故答案为:5.8.(2022·全国·高三专题练习)在△ABC 中,若cos cos A bB a=,则△ABC 的形状是________. 【答案】等腰三角形或直角三角形【分析】由已知及余弦定理可得22222()()0a b c a b ---=,即可判断△ABC 的形状.【详解】由余弦定理,222222cos 2cos 2b c a A bbc a c b B aac+-==+-,化简得22222()()0a b c a b ---=, ∴a b =或222c a b =+,∴△ABC 为等腰三角形或直角三角形. 故答案为:等腰三角形或直角三角形 四、解答题9.(2022·云南昆明·高三开学考试)已知ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,3sin cos 0a B b A -=.(1)求A ; (2)若3c =3a =ABC 的面积. 【答案】(1)6A π=(2)338【分析】(1)由正弦定理将已知式子统一成角的形式,然后化简可求出角A ; (2)利用余弦定理求出b ,再利用三角形的面积公式可求得结果. (1)因为3sin cos 0a B b A -=所以由正弦定理得3sin sin sin cos A B B A =, 因为()0,B π∈,所以sin 0B ≠, 所以3sin cos A A =,即3tan 3A =, 又因为()0,A π∈,所以6A π=.(2)。
高考数学正弦定理和余弦定理

课堂考点探究
[解析]在△ABC中,由2cos Csin B=sin A及正弦定理可得2bcos C=a,再利用余弦定理可得2b×=a,可得b=c,则该三角形的形状是等腰三角形,故选B.
A
课堂考点探究
(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,且cos2=,则△ABC的形状为( )A.等边三角形 B.等腰三角形或直角三角形C.等腰直角三角形 D.直角三角形
[思路点拨] 先利用二倍角的余弦公式化简等式,再利用正弦定理边化角,然后利用两角和的正弦公式进行化简,可得C=,进而判断三角形的形状.[解析]由cos2==,得cos A==,即cos Asin C=sin B,所以cos Asin C = sin(A+C),整理得sin Acos C=0,因为0<A<π,所以sin A≠0,所以cos C=0,因为0<C<π,所以C=,故△ABC为直角三角形.故选D.
D
[总结反思]判定三角形的形状的常用途径:(1)角化边:利用正弦、余弦定理化角为边,通过代数恒等变换,求出边与边之间的关系进行判断.(2)边化角:利用正弦、余弦定理化边为角,通过三角恒等变换,得出三角形内角之间的关系进行判断.
课堂考点探究
课堂考点探究
变式题 (1)(多选题)已知△ABC的内角A,B,C所对的边分别为a,b,c,则下列说法中正确的有( )A.若==,则△ABC一定是等边三角形B.若acos A=bcos B,则△ABC一定是等腰三角形C.若bcos C+ccos B=b,则△ABC一定是等腰三角形D.若a2+b2<c2,则△ABC一定是钝角三角形
高中数学正余弦定理

一:基础知识理解1.正弦定理分类定理变形公式解决的问题2.余弦定理分类定理变形公式精品文档正弦定理和余弦定理内容a=b=c= 2R(R 是△ ABC 外接圆的半径 )sin A sin B sin C①a= 2Rsin_A, b=2Rsin_B, c= 2Rsin_C,② sin A∶ sin B∶sin C= a∶ b∶c,③sin A=a, sin B=b, sin C=c2R2R2R①已知两角和任一边,求其他两边和另一角,②已知两边和其中一边的对角,求另一边的对角内容在△ ABC 中,有 a2= b2+c2- 2bccos_A;b2= a2+ c2- 2accos_B; c2= a2+ b2- 2abcos_Ccos A=b2+c2-a2a2+c2- b2; cos B=;2bc2accos C=a2+ b2- c22ab解决的①已知三边,求各角;问题②已知两边和它们的夹角,求第三边和其他两个角3.三角形中常用的面积公式1(1)S=2ah(h 表示边 a 上的高 );111(2)S=2bcsin A=2acsin B=2absin C;1(3)S=2r(a+ b+ c)(r 为三角形的内切圆半径 ).二:基础知识应用演练1. (2012 广·东高考 )在△ ABC 中,若∠ A=60°,∠ B= 45°,BC =32,则 AC= () A.4 3B.2 33C. 3D. 22.在△ ABC 中, a=3, b= 1, c= 2,则 A 等于 ()A .30°B. 45°C.60°D. 75°精品文档A .无解B .两解C.一解 D .解的个数不确定π4. (2012 ·西高考陕 )在△ ABC 中,角 A, B, C 所对边的长分别为a, b, c.若 a= 2, B=, c= 2 3,6则 b= ________.5.△ ABC 中, B= 120 °, AC= 7,AB =5,则△ ABC 的面积为 ________.解析:1选 B由正弦定理得:BC=AC,即32 =AC,所以 AC=3 2×2=2 3.sin A sin B sin 60 °sin 45°3222222 选 C∵cos A= b + c - a=1+4-3=1,又∵ 0°<A<180°,∴ A= 60°.2bc2×1× 2 23选 B∵a=b bsin A=2422,∴ sin B=18sin 45 ,°∴ sin B=3.又∵ a<b,∴ B 有两个.sin A sin B a4由余弦定理得b2= a2+c2-2accos B=4+ 12- 2× 2× 23×3= 4,所以 b=2.答案: 225、解析:设 BC= x,由余弦定理得49=25+ x2- 10xcos 120 °,整理得 x2+5x- 24= 0,即 x= 3.113=153153因此 S ABC= AB× BC× sin B=×3× 5×. 答案:△22244小结:(1) 在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ ABC 中, A>B? a>b? sin A>sin B.(2) 在△ ABC 中,已知a、 b 和 A 时,解的情况如下:A 为钝角A为锐角或直角图形关系式a= bsin A bsin A<a<b a≥ b a>b解的个数一解两解一解一解三、典型题型精讲( 1)利用正弦、余弦定理解三角形[例 1] (2012 浙·江高考 )在△ ABC 中,内角 A, B, C 的对边分别为a, b, c,且 bsin A= 3acos B.(1)求角 B 的大小;(2) 若 b= 3, sin C=2sin A,求 a, c 的值.精品文档解析: (1) 由 bsin A= 3acos B 及正弦定理a=b,得 sin B=3cos B,所以 tan B=πsin A3,所以 B=.sin B3a =c,得 c= 2a.由 b= 3 及余弦定理 b2= a2+ c2- 2accos B,(2)由 sin C= 2sin A 及sin A sin C得 9=a2+c2-ac. 所以 a= 3, c= 2 3.思考一下:在本例 (2) 的条件下,试求角 A 的大小.方法小结:1.应熟练掌握正、余弦定理及其变形.解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.2.已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的有界性和大边对大角定理进行判断.试题变式演练1.△ ABC 的三个内角A, B, C 所对的边分别为a, b, c,asin Asin B+ bcos2A=2a.b(1)求a;(2)若 c2= b2+3a2,求 B.解: (1) 由正弦定理得,sin2 Asin B+ sin Bcos2A=2sin A,即 sin B(sin 2A+cos2A)= 2sin A.故 sin B= 2sin A,所以b= 2. a(2)由余弦定理和 c2= b2+3a2,得 cos B=1+ 3 a.2c由 (1)知 b2= 2a2,故 c2= (2+ 3)a2.可得 cos2B=1,2又 cos B>0,故 cos B=2,所以 B= 45°. 2精品文档( 2)利用正弦、余弦定理判定三角形的形状[例 2] 在△ ABC 中 a ,b , c 分别为内角 A , B ,C 的对边,且 2asin A = (2b +c)sin B + (2c + b)sin C.(1)求 A 的大小;(2)若 sin B + sin C =1,试判断△ ABC 的形状.[解析 ] (1)由已知,根据正弦定理得2a 2=(2b + c) ·b + (2c + b)c ,即 a 2= b 2+ c 2+ bc.由余弦定理得 a 2=b 2+c 2-2bccos A ,故 cos A =-12,∵ 0<A<180°,∴ A = 120°.(2)由 (1) 得 sin 2A = sin 2B + sin 2C +sin Bsin C =3 1 4又 sin B + sin C = 1,解得 sin B =sin C = .2∵ 0°<B<60°, 0°<C<60°,故 B = C ,∴△ ABC 是等腰的钝角三角形.方法小结: 依据已知条件中的边角关系判断三角形的形状时,主要有如下两种方法:(1)利用正、余弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而判断出三角形的形状,此时要注意应用A +B +C = π这个结论.[注意 ] 在上述两种方法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.试题变式演练 (2012 ·安徽名校模拟 )已知△ ABC 的三个内角 A , B , C 所对的边分别为a ,b ,c ,向量A7m = (4,- 1), n = cos 2 2, cos 2A ,且 m ·n = 2.(1)求角 A 的大小;(2)若 b + c = 2a = 2 3,试判断△ ABC 的形状.精品文档解: (1) ∵ m = (4,- 1), n = cos2A,cos 2A , 21+ cos A -(2cos 2A - 1)=- 2cos 2A +2cos A + 3.又∵ m ·n = 7, ∴ m ·n = 4cos 2A - cos 2A = 4·2 22 ∴- 2cos 2 A + 2cos A +3= 7,解得 cos A =1 π .∵ 0<A<π,∴ A = .2231 (2)在△ ABC 中, a 2= b 2+ c 2- 2bccos A ,且 a =3,∴ (3)2= b 2+ c 2- 2bc ·= b 2+ c 2-bc.①2又∵ b + c = 2 3, ∴ b = 2 3- c ,代入①式整理得 c 2- 2 3c + 3= 0,解得 c = 3,∴ b =3,于是 a= b = c = 3,即△ ABC 为等边三角形.( 3)与三角形面积有关的问题[ 例 3] (2012 新·课标全国卷)已知 a , b , c 分别为△ ABC 三个内角 A ,B ,C 的对边, acos C + 3asin C -b -c = 0.(1)求 A ;(2)若 a = 2,△ ABC 的面积为 3,求 b , c.[解 ] (1)由 acos C + 3asin C - b - c =0 及正弦定理得 sin Acos C + 3sin Asin C - sin B -sin C = 0.因为 B = π- A - C , 所以 3sin Asin C -cos Asin C - sin C = 0.由于 sin C ≠ 0,所以 sin A -ππ=1. 又 0<A < π,故 A = .6231(2)△ ABC 的面积 S = 2bcsin A = 3,故 bc = 4. 而 a 2= b 2+ c 2- 2bccos A ,故 b 2+c 2= 8. 解得 b = c = 2.方法小结:1.正弦定理和余弦定理并不是孤立的.解题时要根据具体题目合理选用,有时还需要交替使用.1 112.在解决三角形问题中,面积公式S =2absin C =2bcsin A = 2acsin B 最常用,因为公式中既有边也有角,容易和正弦定理、余弦定理结合应用.试题变式演练 (2012 ·江西重点中学联考 )在△ ABC 中, 1 cos 2A = cos 2A -cos A.2(1)求角 A 的大小;△精品文档解: (1) 由已知得1221 π2(2cos A - 1)= cos A - cos A ,则 cos A = 2.因为 0<A<π,所以 A = 3.b =c ,可得sin B =b= 2, 即 b = 2c.(2)由 sin Bsin Csin C cb 2+c 2- a 24c 2+ c 2- 9 1所以 cos A = 2bc =4c 2=2, 解得 c = 3, b = 2 3,1 bcsin A = 1 ×2 3× 3×3 3 3所以 S △ ABC = 2 = 2.2 2课后强化与提高练习(基础篇 -必会题)1.在△ ABC 中, a 、 b 分别是角 A 、 B 所对的边,条件 “a<b ”是使 “ cosA>cos B ”成立的 ( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件π2.(2012 泉·州模拟 )在△ ABC 中, a , b , c 分别是角 A ,B ,C 所对的边.若 A = 3,b =1,△ ABC 的面积为3,则 a 的值为 ()2A .1B .23C. 2D. 33. (2013 “· 江南十校 ”联考 )在△ ABC 中,角 A ,B , C 所对的边分别为 a , b , c ,已知 a = 2 3, c =tan A =2c,则 C =()2 2, 1+ tan B bA .30°B .45°C .45°或 135 °D .60°4. (2012 陕·西高考 )在△ ABC 中 ,角 A , B , C 所对边的长分别为 a , b ,c ,若 a 2+ b 2= 2c 2,则 cos C的最小值为 ()3 2 A. 2B. 21 1C.2D .-25. (2012 上·海高考 )在△ ABC 中,若 sin 2 A + sin 2B<sin 2C ,则△ ABC 的形状是 () A .锐角三角形 B .直角三角形 C .钝角三角形D .不能确定6.在△ ABC 中,角 A 、B 、 C 所对的边分别是 a 、 b 、 c.若 b = 2asin B ,则角 A 的大小为 ________. 解析: 由正弦定理得 sin B = 2sin Asin B ,∵ sin B ≠ 0,π7.在△ ABC 中,若 a = 3, b = 3, A =3,则 C 的大小为 ________.π,5sin C=5,则 c= ________; a= ________.1,则 b= ________.9. (2012 北·京高考 )在△ ABC 中,若 a= 2, b+ c= 7, cos B=-410.△ ABC 的内角 A,B, C 的对边分别为a, b, c, asin A+ csin C- 2asin C= bsin B.(1)求 B;(2)若 A= 75°, b= 2,求 a, c.11. (2013 北·京朝阳统考)在锐角三角形ABC 中, a,b,c 分别为内角A,B,C 所对的边,且满足3a-2bsin A= 0.(1)求角 B 的大小;uuur uuur(2)若 a+ c= 5,且 a>c,b=7,求AB·AC的值.12. (2012 ·东高考山 )在△ ABC 中,内角A,B, C 所对的边分别为a, b, c,已知 sin B(tan A+ tan C)(1)求证: a ,b , c 成等比数列;(2)若 a = 1,c = 2,求△ ABC 的面积 S.课后强化与提高练习(提高篇-选做题)1. (2012 湖·北高考 )设△ ABC 的内角 A ,B ,C 所对的边分别为a ,b , c.若三边的长为连续的三个正整数,且 A>B>C , 3b = 20acos A ,则 sin A ∶ sin B ∶ sin C 为 ()A .4∶ 3∶2B .5∶6∶7C .5∶ 4∶ 3D . 6∶5∶ 42. (2012 长·春调研 )在△ ABC 中,角 A , B ,C 的对边分别为 a ,b , c ,已知 4sin2A+ B- cos 2C = 7,2 2且 a + b = 5, c = 7,则△ ABC 的面积为 ________.3.在△ ABC 中,角 A ,B , C 的对边分别为a ,b ,c ,且满足 (2b - c)cos A -acos C =0.(1)求角 A 的大小;(2)若 a = 3, S △ABC =3 4 3,试判断△ ABC 的形状,并说明理由.选做题1.已知 a ,b ,c 分别是△ ABC 的三个内角A ,B ,C 所对的边.若 a = 1,b = 3,A + C =2B ,则 sin C精品文档= ________.2.在△ ABC 中, a = 2bcos C ,则这个三角形一定是 ()A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形3.在△ ABC 中,角 A ,B , C 所对的边分别为a ,b ,c ,已知1cos 2C =- 4.(1)求 sin C 的值;(2)当 a = 2,2sin A = sin C 时,求 b 及 c 的长.4.设△ ABC 的内角 A ,B , C 所对的边长分别为 a , b , c ,且 cos B = 45, b =2.(1)当 A = 30°时,求 a 的值;(2)当△ ABC 的面积为 3 时,求 a + c 的值.课后强化与提高练习(基础篇-必会题)解析1 解析: 选 C a<b? A<B? cos A>cos B.2 解析:选 D由已知得 1 1 π 3,解得 c = 2,则由余弦定理可得 a 2= 4+ 1-bcsin A = × 1× c × sin =2223π a = 3.2× 2× 1× cos = 3?33解析:选 Btan A=2c和正弦定理得cos Asin B + sin Acos B = 2sin Ccos A ,由 1+tan B b即 sin C =2sin Ccos A ,所以 cos A =12,则 A = 60°.由正弦定理得 sin 2 3A =sin 2 2C ,则 sin C = 22,又 c<a ,则 C<60°,故 C = 45°.4 解析:选 C由余弦定理得22 2 21221 2 2a +b -c =2abcos C ,又 c = (a+ b ),得 2abcos C =(a+ b ),即 cos22a 2+b 2 2ab 1.精品文档6 解析: 选 C 由正弦定理得a 2+b 2<c 2,所以 cos C = a 2+ b 2- c 22ab <0,所以 C 是钝角,故△ ABC 是钝角三角形.∴ sin A = 1,∴ A = 30°或 A = 150°.答案: 30°或 150°2π7 解析:由正弦定理可知 sin B =bsin A= 3sin 3 1π 5π π a =2,所以 B = 或 6 ( 舍去 ),所以 C = π-A - B = π- -3 63π π π= .答案:26 28b =c ,则 c = bsin C = 22,再由余弦定理得b 2= a 2+c 2- 2accos B ,即解析: 根据正弦定理得 sin B sin Csin Ba 2 -4a - 12=0, (a + 2)(a - 6)= 0,解得 a = 6 或 a =- 2(舍去 ). 答案: 2 2 69 解析: 根据余弦定理代入b 2= 4+ (7- b) 2- 2×2× (7- b)× -1,解得 b = 4.答案: 4410 解: (1) 由正弦定理得 a 2+ c 2- 2ac = b 2.由余弦定理得 b 2= a 2+ c 2- 2accos B.故 cos B = 2,因此 B = 45°.2(2)sin A = sin(30 +°45°)= sin 30 cos ° 45 +°cos 302+ 6sin ° 45 =° 4 .故 a =b ×sin A = 2+ 6 3, c = b × sin C sin 60°sin B = 1+= 2×sin 45=6.2sin B °11 解: (1)因为 3a -2bsin A = 0,所以3sin A -2sin Bsin A = 0,因为 sin A ≠ 0,所以 sin B =3π2 .又 B 为锐角,所以B = 3.π(2)由 (1) 可知, B = 3.因为 b = 7.π根据余弦定理,得7= a 2+ c 2- 2accos 3,整理,得 (a + c)2- 3ac = 7.由已知 a + c = 5,得 ac = 6.又 a>c ,故 a = 3, c = 2.b 2+c 2- a 27+4-9 7于是 cos A =2bc= 4 7 = 14 ,uuur uuur = | uuur uuur所以 AB · AB · |cos A =cbcos AAC | |AC = 2× 7× 7=1.1412 解: (1) 证明:在△ ABC 中,由于 sin B(tan A + tan C)= tan Atan C ,sin A + sin C = sin A sin C, 所以 sin Bcos C ·cos A cos A cos C因此 sin B(sin Acos C + cos Asin C)= sin Asin C ,所以 sin Bsin(A +C)= sin Asin C.又 A + B + C = π,.精品文档所以 sin(A+C)= sin B,因此 sin2B= sin Asin C.由正弦定理得b2=ac,即 a,b, c 成等比数列.(2)因为 a= 1, c= 2,所以 b=2,由余弦定理得cos B=a2+ c2- b212+ 22- 23,2ac==42× 1×2因为 0<B<π,所以 sin B=1- cos 2B=7,4故△ ABC 的面积 S=1acsin B=1× 1× 2×7=7.2244课后强化与提高练习(提高篇-选做题)解析1解析:选 D由题意可得 a>b>c,且为连续正整数,设c= n, b= n+ 1, a= n+ 2(n>1,且 n∈ N* ),则由余弦定理可得3(n+1)= 20(n+n+ 1 2+ n2- n+ 2 27n2- 13n-60= 0,n∈ N*,解得 n= 4,2) ·,化简得2n n+ 1由正弦定理可得sin A∶sin B∶ sin C= a∶b∶ c= 6∶5∶ 4.2 解析:因为 4sin2A+B- cos 2C=7,所以 2[1 - cos(A+B)]- 2cos2C+ 1=7,222711.根据余弦定理有1=a2+ b2- 7,2+ 2cos C- 2cos2C+ 1=,cos2C- cos C+= 0,解得 cos C=cos C=2ab2422ab= a2+ b2- 7,3ab= a2+ b2+ 2ab- 7= (a+ b)2-7= 25- 7= 18, ab= 6,所以△ ABC 的面积 S△ABC=121× 6×33333absin C=2=2.答案:223 解: (1)法一:由 (2b- c)cos A- acos C= 0 及正弦定理,得(2sin B- sin C)cos A-sin Acos C=0,∴ 2sin Bcos A- sin(A+ C)= 0,1πsin B(2cos A- 1)=0. ∵ 0<B<π,∴ sin B≠ 0,∴ cos A=2.∵ 0<A<π,∴ A=3.法二:由 (2b- c)cos A-acos C=0,及余弦定理,得b2+ c2- a2a2+b2- c2(2b- c) ·-a·= 0,2bc2ab整理,得 b2+ c2- a2= bc,∴ cos A=b2+ c2-a21,∵π=0<A<π,∴ A= .2bc23133(2)∵ S△ABC=2bcsin A=4,1π 33,∴ bc= 3,①∵ a2= b2+ c2- 2bccos A, a=π即 bcsin =43,A=,233∴b2+ c2= 6,②由①②得 b= c= 3,∴△ ABC 为等边三角形.选择题解析.精品文档1 解析: 在△ ABC 中, A + C = 2B ,∴ B = 60°.又∵ sin A =asin B= 1,∴ A =30°或 150°(舍 ),∴ C = 90°, b 2∴ sin C = 1.答案: 12 解析: 选 A法一: (化边为角 )由正弦定理知:sin A = 2sin Bcos C ,又 A = π- (B +C),∴ sin A = sin(B +C)= 2sin Bcos C.∴ sin Bcos C + cos Bsin C = 2sin Bcos C ,∴ sin Bcos C - cos Bsin C = 0,∴ sin(B - C) =0.又∵ B 、 C 为三角形内角,∴ B = C.法二: (化角为边 )由余弦定理知cos C =a 2 +b 2 -c 2,2aba 2+b 2-c 2 a 2+ b 2- c 2∴ a = 2b · 2ab= a ,∴ a 2= a 2+ b 2- c 2,∴ b 2= c 2,∴ b = c.13 解: (1)因为 cos 2C =1- 2sin 2C =- 4,且 0<C<π, 所以 sin C =104.(2)当 a = 2,2sin A = sin C 时,由正弦定理a =c,得 c = 4.由 cos 2C = 2cos 2C - 1=-1,及 0<C<πsin A sin C4得 cos C = ± 6.4由余弦定理 c 2= a 2+ b 2- 2abcos C ,得 b 2± 6b - 12= 0,解得 b = 6或 2 6,b = 6,或b = 2 6,所以c = 4.c = 4434 解: (1) 因为 cos B =,所以 sin B = .55由正弦定理a= b,可得 a =105sin A,所以 a = .sin Bsin 30 °3 313,所以3(2)因为△ ABC 的面积 S = 2ac ·sin B , sin B = 510ac = 3, ac = 10.由余弦定理得b 2=a 2+c 2-2accos B ,得 4= a 2+ c 2-8ac = a 2+ c 2- 16,即 a 2+ c 2= 20.5所以 ( a + c ) 2- 2ac = 20, ( a + c ) 2= 40. 所以 a +c = 210..。
2024全国高考真题数学汇编:正弦定理与余弦定理

2024全国高考真题数学汇编正弦定理与余弦定理一、单选题1.(2024全国高考真题)在ABC 中,内角,,A B C 所对的边分别为,,a b c ,若π3B =,294b ac =,则sin sin A C +=()A B C D 二、解答题2.(2024天津高考真题)在ABC 中,角,,A B C 所对的边分别为,,a b c ,已知92cos 5163a Bbc ===,.(1)求a ;(2)求sin A ;(3)求()cos 2B A -的值.3.(2024全国高考真题)记ABC 的内角A 、B 、C 的对边分别为a ,b ,c ,已知sin C B =,222a b c +-=(1)求B ;(2)若ABC 的面积为3c .4.(2024全国高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin 2A A =.(1)求A .(2)若2a =sin sin 2C c B =,求ABC 的周长.5.(2024北京高考真题)在ABC 中,,,A B C 的对边分别为,,a b c ,A ∠为钝角,7a =,sin 2cos B B =.(1)求A ∠;(2)从条件①、条件②、条件③这三个条件中选择一个作为已知,使得ABC 存在,求ABC 的面积.条件①:7b =;条件②:13cos 14B =;条件③:sin c A =注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.参考答案1.C【分析】利用正弦定理得1sin sin 3A C =,再利用余弦定理有22134a c ac +=,由正弦定理得到22sin sin A C +的值,最后代入计算即可.【详解】因为29,34B b ac π==,则由正弦定理得241sin sin sin 93A CB ==.由余弦定理可得:22294b ac ac ac =+-=,即:22134a c ac +=,根据正弦定理得221313sin sin sin sin 412A C A C +==,所以2227(sin sin )sin sin 2sin sin 4A C A C A C +=++=,因为,A C 为三角形内角,则sin sin 0A C +>,则sin sin 2A C +=.故选:C.2.(1)4(3)5764【分析】(1)2,3a t c t ==,利用余弦定理即可得到方程,解出即可;(2)法一:求出sin B ,再利用正弦定理即可;法二:利用余弦定理求出cos A ,则得到sin A ;(3)法一:根据大边对大角确定A 为锐角,则得到cos A ,再利用二倍角公式和两角差的余弦公式即可;法二:直接利用二倍角公式和两角差的余弦公式即可.【详解】(1)设2,3a t c t ==,0t >,则根据余弦定理得2222cos b a c ac B =+-,即229254922316t t t t =+-⨯⨯⨯,解得2t =(负舍);则4,6a c ==.(2)法一:因为B 为三角形内角,所以sin 16B =,再根据正弦定理得sin sin a b A B =,即4sin A =sin 4A =,法二:由余弦定理得2222225643cos 22564b c a A bc +-+-===⨯⨯,因为()0,πA ∈,则sin 4A ==(3)法一:因为9cos 016B =>,且()0,πB ∈,所以π0,2B ⎛⎫∈ ⎪⎝⎭,由(2)法一知sin B =因为a b <,则A B <,所以3cos 4A ==,则3sin 22sin cos 24A A A ===2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭()9157cos 2cos cos 2sin sin 216816864B A B A B A -=+=⨯+⨯=.法二:3sin 22sin cos 24A A A ===,则2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭,因为B 为三角形内角,所以sin 16B ===,所以()9157cos 2cos cos 2sin sin 216864B A B A B A -=+=⨯=3.(1)π3B =(2)【分析】(1)由余弦定理、平方关系依次求出cos ,sin C C ,最后结合已知sin C B =得cos B 的值即可;(2)首先求出,,A B C ,然后由正弦定理可将,a b 均用含有c 的式子表示,结合三角形面积公式即可列方程求解.【详解】(1)由余弦定理有2222cos a b c ab C +-=,对比已知222a b c +-=,可得222cos 2a b c C ab +-===因为()0,πC ∈,所以sin 0C >,从而sin 2C =,又因为sin C B =,即1cos 2B =,注意到()0,πB ∈,所以π3B =.(2)由(1)可得π3B =,cos 2C =,()0,πC ∈,从而π4C =,ππ5ππ3412A =--=,而5πππ1sin sin sin 124622224A ⎛⎫⎛⎫==+⨯+⨯= ⎪ ⎪⎝⎭⎝⎭,由正弦定理有5πππsin sin sin 1234a b c==,从而,a b ===,由三角形面积公式可知,ABC的面积可表示为21113sin 222228ABC S ab C c c ==⋅= ,由已知ABC的面积为32338c =所以c =4.(1)π6A =(2)2+【分析】(1)根据辅助角公式对条件sin 2A A =进行化简处理即可求解,常规方法还可利用同角三角函数的关系解方程组,亦可利用导数,向量数量积公式,万能公式解决;(2)先根据正弦定理边角互化算出B ,然后根据正弦定理算出,b c 即可得出周长.【详解】(1)方法一:常规方法(辅助角公式)由sin 2A A =可得1sin 122A A +=,即sin()1π3A +=,由于ππ4π(0,π)(,)333A A ∈⇒+,故ππ32A +=,解得π6A =方法二:常规方法(同角三角函数的基本关系)由sin 2A A =,又22sin cos 1A A +=,消去sin A得到:224cos 30(2cos 0A A A -+=⇔=,解得cos 2A =,又(0,π)A ∈,故π6A =方法三:利用极值点求解设()sin (0π)f x x x x =<<,则π()2sin (0π)3f x x x ⎛⎫=+<< ⎪⎝⎭,显然π6x =时,max ()2f x =,注意到π()sin 22sin(3f A A A A =+==+,max ()()f x f A =,在开区间(0,π)上取到最大值,于是x A =必定是极值点,即()0cos sin f A A A '==,即tan 3A =,又(0,π)A ∈,故π6A =方法四:利用向量数量积公式(柯西不等式)设(sin ,cos )a b A A ==,由题意,sin 2a b A A ⋅==,根据向量的数量积公式,cos ,2cos ,a b a b a b a b ⋅==,则2cos ,2cos ,1a b a b =⇔= ,此时,0a b =,即,a b 同向共线,根据向量共线条件,1cos sin tan 3A A A ⋅=⇔=,又(0,π)A ∈,故π6A =方法五:利用万能公式求解设tan 2A t =,根据万能公式,2222)sin 211t t A A t t-+==+++,整理可得,2222(2(20((2t t t -+==-,解得tan22A t ==22tan 13t A t ==-,又(0,π)A ∈,故π6A =(2)由题设条件和正弦定理sin sin 2sin 2sin sin cos C c B B C C B B =⇔=,又,(0,π)B C ∈,则sin sin 0B C ≠,进而cos B =π4B =,于是7ππ12C A B =--=,sin sin(π)sin()sin cos sin cos 4C A B A B A B B A =--=+=+=,由正弦定理可得,sin sin sin a b cA B C==,即2ππ7πsin sin sin 6412bc==,解得b c ==故ABC的周长为2+5.(1)2π3A =;(2)选择①无解;选择②和③△ABC【分析】(1)利用正弦定理即可求出答案;(2)选择①,利用正弦定理得3B π=,结合(1)问答案即可排除;选择②,首先求出sin 14B =,再代入式子得3b =,再利用两角和的正弦公式即可求出sin C ,最后利用三角形面积公式即可;选择③,首先得到5c =,再利用正弦定理得到sin 14C =,再利用两角和的正弦公式即可求出sin B ,最后利用三角形面积公式即可;【详解】(1)由题意得2sin cos cos B B B =,因为A 为钝角,则cos 0B ≠,则2sin 7B =,则7sin sin sin b a BA A ==,解得sin 2A =,因为A 为钝角,则2π3A =.(2)选择①7b =,则sin 7B ==2π3A =,则B 为锐角,则3B π=,此时πA B +=,不合题意,舍弃;选择②13cos 14B =,因为B为三角形内角,则sin B ,则代入2sin 7B =得2147⨯=,解得3b =,()2π2π2πsin sin sin sin cos cos sin 333C A B B B B⎛⎫=+=+=+ ⎪⎝⎭131142⎛⎫=+-⨯ ⎪⎝⎭,则11sin 7322ABC S ab C ==⨯⨯选择③sin c A =2c ⨯=5c =,则由正弦定理得sin sin a c A C =5sin C,解得sin 14C =,因为C为三角形内角,则11cos 14C ==,则()2π2π2πsin sin sin sin cos cos sin 333B A C C C C ⎛⎫=+=+=+⎪⎝⎭111142⎛⎫=+-⨯ ⎪⎝⎭,则11sin 7522ABC S ac B ==⨯⨯=△。
高考数学复习正弦定理和余弦定理
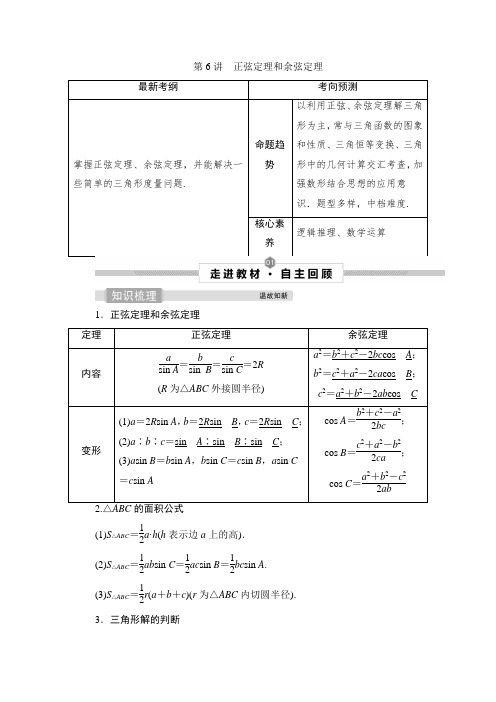
第6讲正弦定理和余弦定理最新考纲考向预测掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.命题趋势以利用正弦、余弦定理解三角形为主,常与三角函数的图象和性质、三角恒等变换、三角形中的几何计算交汇考查,加强数形结合思想的应用意识.题型多样,中档难度.核心素养逻辑推理、数学运算1.正弦定理和余弦定理定理正弦定理余弦定理内容asin A=bsin B=csin C=2R(R为△ABC外接圆半径)a2=b2+c2-2bc cos__A;b2=c2+a2-2ca cos__B;c2=a2+b2-2ab cos__C变形(1)a=2R sin A,b=2R sin__B,c=2R sin__C;(2)a∶b∶c=sin__A∶sin__B∶sin__C;(3)a sin B=b sin A,b sin C=c sin B,a sin C=c sin Acos A=b2+c2-a22bc;cos B=c2+a2-b22ca;cos C=a2+b2-c22ab(1)S△ABC=12a·h(h表示边a上的高).(2)S△ABC=12ab sin C=12ac sin B=12bc sin A.(3)S△ABC=12r(a+b+c)(r为△ABC内切圆半径).3.三角形解的判断A为锐角A为钝角或直角图形关系式a=b sin A b sin A<a<b a≥b a>b解的个数一解两解一解一解[注意]上表中A为锐角时,a<b sin A,无解.A为钝角或直角时,a=b,a<b均无解.常用结论1.在△ABC中,两边之和大于第三边,两边之差小于第三边,A>B⇔a>b⇔sin A>sin B⇔cos A<cos B.2.三角形中的三角函数关系(1)sin(A+B)=sin C.(2)cos(A+B)=-cos C.(3)sin A+B2=cosC2.(4)cos A+B2=sinC2.3.三角形中的射影定理在△ABC中,a=b cos C+c cos B;b=a cos C+c cos A;c=b cos A+a cos B.常见误区1.在△ABC中,已知a,b和A,利用正弦定理时,会出现解的不确定性,应注意根据“大边对大角”来取舍.2.在判断三角形的形状时,等式两边一般不要约去公因式,应移项提取公因式,以免漏解.1.判断正误(正确的打“√”,错误的打“×”)(1)三角形中三边之比等于相应的三个内角之比.( ) (2)在△ABC 中,若sin A >sin B ,则A >B .( )(3)在△ABC 中的六个元素中,已知任意三个元素可求其他元素.( ) 答案:(1)× (2)√ (3)×2.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若A =60°,a 2=bc ,则sin B sin C =( )A.12 B.32 C.35D.34解析:选D.因为a 2=bc ,所以sin 2A =sin B sin C .因为A =60°,所以sin B sin C =sin 2A =34.故选D.3.(多选)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =4,sin A =45,cos C =210,则下列结论正确的是( )A .cos A =±35 B .B =π4C .b =522D .△ABC 的面积为7 2解析:选BC.由sin A =45,得cos A =±35,由cos C =210,得sin C =7210,若cos A =-35,则sin B =sin(A +C )=-17250<0,与sin B >0矛盾,故cos A =35,A 错误,则sin(A +C )=22,由sin A =45,cos C =210,得A >π4,C >π4,所以A +C >π2,所以A +C =3π4,故B =π4,B 正确.由正弦定理a sin A =b sin B ,得b =522,C 正确,所以△ABC 的面积为12×4×522×7210=7,D 错误.4.(易错题)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知C =60°,b =6,c =3,则A =________.解析:由题意得,b sin B =c sin C ,即sin B =b sin C c =6×323=22,结合b <c可得B =45°,则A =180°-B -C =75°.答案:75°利用正、余弦定理解三角形(2020·高考天津卷节选)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知a =22,b =5,c =13.(1)求角C 的大小; (2)求sin A 的值.【解】 (1)在△ABC 中,由余弦定理及a =22,b =5,c =13,有cos C =a 2+b 2-c 22ab =22.又因为C ∈(0,π),所以C =π4.(2)在△ABC 中,由正弦定理及C =π4,a =22,c =13,可得sin A =a sin Cc =21313.(1)正、余弦定理的选用①利用正弦定理可解决两类三角形问题:一是已知两角和一角的对边,求其他边或角;二是已知两边和一边的对角,求其他边或角;②利用余弦定理可解决两类三角形问题:一是已知两边和它们的夹角,求其他边或角;二是已知三边求角.由于这两种情形下的三角形是唯一确定的,所以其解也是唯一的.(2)三角形解的个数的判断已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的有界性和大边对大角定理进行判断.1.在△ABC 中,已知b =40,c =20,C =60°,则此三角形的解的情况是( ) A .有一解C .无解D .有解但解的个数不确定解析:选C.由正弦定理得b sin B =csin C , 所以sin B =b sin Cc =40×3220=3>1.所以角B 不存在,即满足条件的三角形不存在.2.(2020·广东省七校联考)若△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,已知2b sin 2A =3a sin B ,且c =2b ,则ab =( )A.32 B. 2 C.43D. 3解析:选B.由2b sin 2A =3a sin B ,及正弦定理可得4sin B sin A cos A =3sin A sin B .由于sin A ≠0,sin B ≠0,所以cos A =34,又c =2b ,所以a 2=b 2+c 2-2bc cos A =b 2+4b 2-2b ×2b ×34=2b 2,所以ab =2,故选B.3.(2019·高考全国卷Ⅰ改编)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,设(sin B -sin C )2=sin 2A -sin B sin C .(1)求A ;(2)若2a +b =2c ,求C .解:(1)由已知得sin 2B +sin 2C -sin 2A =sin B sin C ,故由正弦定理得b 2+c 2-a 2=bc .由余弦定理得cos A =b 2+c 2-a 22bc =12. 因为0°<A <180°,所以A =60°.(2)由(1)知B =120°-C ,由题设及正弦定理得2sin A +sin(120°-C )=2sin C ,即62+32cos C +12sin C =2sin C ,可得cos(C +60°)=-22.由于0°<C <120°,所以C +60°=135°,判断三角形的形状(1)(一题多解)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,则△ABC 的形状为( )A .直角三角形B .锐角三角形C .钝角三角形D .不确定(2)在△ABC 中,若c -a cos B =(2a -b )cos A ,则△ABC 的形状为________. 【解析】 (1)方法一:因为b cos C +c cos B =b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac =2a 22a =a ,所以a sin A =a 即sin A =1,故A =π2,因此△ABC 是直角三角形.方法二:因为b cos C +c cos B =a sin A , 所以sin B cos C +sin C cos B =sin 2 A , 即sin(B +C )=sin 2 A ,所以sin A =sin 2 A , 故sin A =1,即A =π2,因此△ABC 是直角三角形.(2)因为c -a cos B =(2a -b )cos A ,所以由正弦定理得sin C -sin A cos B =2sin A cos A -sin B cos A ,所以sin(A +B )-sin A cos B =2sin A cos A -sin B cos A , 故cos A (sin B -sin A )=0, 所以cos A =0或sin A =sin B , 即A =π2或A =B ,故△ABC 为等腰三角形或直角三角形. 【答案】 (1)A (2)等腰三角形或直角三角形【引申探究】 (变条件)若将本例(1)条件改为“2sin A cos B =sin C ”,试判断△ABC 的形状.解:方法一:由已知得2sin A cos B =sin C =sin(A +B )=sin A cos B +cos A sin B ,即sin(A -B )=0,因为-π<A -B <π,所以A =B ,故△ABC 为等腰三角形.方法二:由正弦定理得2a cos B =c ,再由余弦定理得2a ·a 2+c 2-b 22ac =c ⇒a 2=b 2⇒a =b , 故△ABC 为等腰三角形.判定三角形形状的两种常用途径[提醒] “角化边”后要注意用因式分解、配方等方法得出边的相应关系;“边化角”后要注意用三角恒等变换公式、三角形内角和定理及诱导公式推出角的关系.1.在△ABC 中,a ∶b ∶c =3∶5∶7,那么△ABC 是( ) A .直角三角形 B .钝角三角形 C .锐角三角形D .非钝角三角形解析:选B.因为a ∶b ∶c =3∶5∶7,所以可设a =3t ,b =5t ,c =7t ,由余弦定理可得cos C =9t 2+25t 2-49t 22×3t ×5t =-12,所以C =120°,△ABC 是钝角三角形,故选B.2.(多选)已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,则下列四个命题中正确的是( )A .若a cos A =b cosB =ccos C ,则△ABC 一定是等边三角形 B .若a cos A =b cos B ,则△ABC 一定是等腰三角形 C .若b cos C +c cos B =b ,则△ABC 一定是等腰三角形 D .若a 2+b 2-c 2>0,则△ABC 一定是锐角三角形解析:选AC.由a cos A =b cos B =c cos C 及正弦定理得,sin A cos A =sin B cos B =sin Ccos C ,即tan A =tan B =tan C ,所以A =B =C ,所以△ABC 是等边三角形,A 正确.由a cos A =b cos B 及正弦定理得,sin A cos A =sin B cos B ,解得sin 2A =sin 2B ,则2A =2B 或2A +2B =π,所以△ABC 是等腰三角形或直角三角形,B 不正确.由b cos C +c cos B =b 及正弦定理得,sin B cos C +sin C cos B =sin B ,即sin(B +C )=sin B ,所以sin A =sin B ,则A =B ,所以△ABC 是等腰三角形,C 正确.由余弦定理得,cos C =a 2+b 2-c 22ab >0,所以角C 为锐角.而角A ,B 不一定是锐角,故D 不正确.故选AC.与三角形面积有关的问题 角度一 计算三角形的面积(1)(2020·高考全国卷Ⅰ改编)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知B =150°.若a =3c ,b =27,则△ABC 的面积为________.(2)(2020·福建五校第二次联考)在△ABC 中,A ,B ,C 所对的边分别为a ,b ,c ,已知a 2+b 2-c 2=3ab ,且ac sin B =23sin C ,则△ABC 的面积为________.【解析】 (1)由题设及余弦定理得28=3c 2+c 2-2×3c 2×cos 150°. 解得c =-2(舍去),c =2,从而a =2 3. △ABC 的面积为12×23×2×sin 150°= 3.(2)因为a 2+b 2-c 2=3ab ,所以由余弦定理得cos C =a 2+b 2-c 22ab =3ab 2ab =32,又0<C <π,所以C =π6.因为ac sin B =23sin C ,结合正弦定理可得abc =23c ,所以ab =2 3.故S △ABC =12ab sin C =12×23sin π6=32.【答案】 (1)3 (2)32求三角形面积的方法(1)若三角形中已知一个角(角的大小或该角的正、余弦值),结合题意求解这个角的两边或该角的两边之积,代入公式求面积;(2)若已知三角形的三边,可先求其中一个角的余弦值,再求其正弦值,代入公式求面积,总之,结合图形恰当选择面积公式是解题的关键.角度二 已知三角形的面积解三角形(2020·广州市调研检测)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知c sin ⎝ ⎛⎭⎪⎫A +π3-a sin C =0.(1)求角A 的值;(2)若△ABC 的面积为3,周长为6,求a 的值. 【解】 (1)因为c sin ⎝ ⎛⎭⎪⎫A +π3-a sin C =0, 所以由正弦定理得sin C ⎝ ⎛⎭⎪⎫12sin A +32cos A -sin A ·sin C =0.因为sin C >0,所以32cos A -12sin A =0,即tan A =3, 因为A ∈(0,π),所以A =π3.(2)因为△ABC 的面积为3,所以12bc sin A =3,得bc =4.由余弦定理a 2=b 2+c 2-2bc cos A ,得a 2=b 2+c 2-bc =(b +c )2-3bc =(b +c )2-12,因为△ABC 的周长为6,即a +b +c =6, 所以a 2=(6-a )2-12, 所以a =2.已知三角形面积求边、角的方法(1)若求角,就寻求这个角的两边的关系,利用面积公式列方程求解; (2)若求边,就寻求与该边(或两边)有关联的角,利用面积公式列方程求解. [注意] 正弦定理、余弦定理与三角函数性质的综合应用中,要注意三角函数公式的工具性作用.1.(2020·福州市质量检测)在钝角△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知c =7,b =1,若△ABC 的面积为62,则a 的长为________.解析:因为△ABC 的面积S =12bc sin A ,所以62=12×1×7sin A ,所以sin A=67,所以cos A=±77,当cos A=77时,由a2=b2+c2-2bc cos A得a=6,此时△ABC为直角三角形(舍去);当cos A=-77时,由a2=b2+c2-2bc cos A得a=10,经检验,a=10符合题意.综上,a=10.答案:102.(2020·合肥第一次教学检测)在△ABC中,内角A,B,C所对的边分别为a,b,c,若a=2,a cos C+c cos A+2b cos B=0.(1)求B;(2)若BC边的中线AM长为5,求△ABC的面积.解:(1)在△ABC中,asin A=bsin B=csin C,且a cos C+c cos A+2b cos B=0,所以sin A cos C+sin C cos A+2sin B cos B=0,所以sin B·(1+2cos B)=0,又sin B≠0,所以cos B=-2 2.因为B是三角形的内角,所以B=3π4.(2)在△ABM中,BM=1,AM=5,B=3π4,AB=c,由余弦定理AM2=c2+BM2-2c·BM·cos B,得c2+2c-4=0,因为c>0,所以c= 2.在△ABC中,a=2,c=2,B=3π4,所以△ABC的面积S=12ac sin B=1.高考新声音系列4解三角形中的结构不良型开放型问题新高考卷Ⅰ第17题别具匠心地设计了开放性试题,设问方式追求创新,补充已知条件(三选一)并解答,条件不同,结论不同,不同的选择会有不同的结论,难度也会有区别.(2020·新高考卷Ⅰ)在①ac =3,②c sin A =3,③c =3b 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的值;若问题中的三角形不存在,说明理由.问题:是否存在△ABC ,它的内角A ,B ,C 的对边分别为a ,b ,c ,且sin A =3sin B ,C =π6,________________?【解】 方案一:选条件①.由C =π6和余弦定理得a 2+b 2-c 22ab =32. 由sin A =3sin B 及正弦定理得a =3b . 于是3b 2+b 2-c 223b 2=32,由此可得b =c . 由①ac =3,解得a =3,b =c =1.因此,选条件①时问题中的三角形存在,此时c =1. 方案二:选条件②.由C =π6和余弦定理得a 2+b 2-c 22ab =32. 由sin A =3sin B 及正弦定理得a =3b .于是3b 2+b 2-c 223b 2=32,由此可得b =c ,B =C =π6,A =2π3. 由②c sin A =3,所以c =b =23,a =6.因此,选条件②时问题中的三角形存在,此时c =2 3. 方案三:选条件③.由C =π6和余弦定理得a 2+b 2-c 22ab =32.由sin A =3sin B 及正弦定理得a =3b . 于是3b 2+b 2-c 223b 2=32,由此可得b =c . 由③c =3b ,与b =c 矛盾.因此,选条件③时问题中的三角形不存在.本题以解三角形为背景命制,给定了若干条件(在这些条件下三角形并不能随之确定),在此基础上让学生在另外给出的几个条件中自主选择,在所选条件下,若问题中的三角形存在,求解三角形;若问题中的三角形不存在,说明理由.在①sin B=32,②cos B=34,③cos C=-79这三个条件中选择一个,补充在下面的问题中,并判断三角形是否有解.若有解,求出a的值;若无解,请说明理由.在△ABC中,已知a,b,c分别是角A,B,C的对边,且满足C=2B,b +c=10,________.解:若选择①sin B=32,则B=60°或B=120°,因为C=2B,所以C=120°或C=240°,显然矛盾,此时三角形无解.若选择②cos B=3 4,则由正弦定理可得cb=sin Csin B=sin 2Bsin B=2sin B cos Bsin B=2cos B=2×34=32,又b+c=10,所以c=6,b=4.由余弦定理b2=a2+c2-2ac cos B,可得16=a2+36-9a,解得a=4或a=5.若a=4,则由b=4知A=B,又C=2B,所以B+B+2B=180°,解得B=45°,这与cos B=34矛盾,舍去.经检验知,当a=5时适合题意.故a的值为5.若选择③cos C=-7 9,因为C=2B,所以cos 2B=-7 9,即2cos2B-1=-79,得cos B=13,此时cb=sin Csin B=sin 2Bsin B=2cos B=23<1,所以c<b,这与C=2B矛盾,此时三角形无解.[A 级 基础练]1.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若a =2,c =23,cos A =32且b <c ,则b =( )A .3B .2 2C .2D . 3解析:选C.由余弦定理b 2+c 2-2bc cos A =a 2,得b 2-6b +8=0,解得b =2或b =4,因为b <c =23,所以b =2.选C.2.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,已知b =7,c =4,cos A =74,则△ABC 的面积为( )A .37B .372C .9D .92解析:选B.因为cos A =74,则sin A =34,所以S △ABC =12×bc sin A =372,故选B.3.(2020·湖北八校第一次联考)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且sin B -sin A (sin C +cos C )=0,a =2,c =2,则角C =( )A.5π6B.π6C.π4D.π3解析:选B.因为A +C =π-B ,所以sin B =sin(A +C )=sin A cos C +cos A sin C ,因为sin B -sin A (sin C +cos C )=0,所以cos A sin C -sin A sin C =0,因为C ∈(0,π),所以sin C >0,所以cos A =sin A ,又A ∈(0,π),所以A =π4,由正弦定理得a sin π4=c sin C ,又a =2,c =2,所以sin C =12,因为a >c ,所以C =π6,故选B.4.(多选)在△ABC 中,根据下列条件解三角形,其中有一解的是( ) A .b =7,c =3,C =30° B .b =5,c =4,B =45° C .a =6,b =33,B =60° D .a =20,b =30,A =30°解析:选BC.对于A ,因为b =7,c =3,C =30°,所以由正弦定理可得sin B =b sin C c =7×123=76>1,无解;对于B ,b =5,c =4,B =45°,所以由正弦定理可得sin C =c sin Bb =4×225=225<1,且c <b ,有一解;对于C ,因为a =6,b =33,B =60°,所以由正弦定理可得sin A =a sin B b =6×3233=1,A =90°,此时C =30°,有一解; 对于D ,因为a =20,b =30,A =30°,所以由正弦定理可得sin B =b sin Aa =30×1220=34<1,且b >a ,所以B 有两解,故选BC.5.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .若C =π4,a =4,S △ABC=2,则2a +3c -b2sin A +3sin C -sin B=( )A . 5B .2 5C .27D .213解析:选B.因为C =π4,a =4,S △ABC =2,所以S △ABC =12ab sin π4=12×4×b ×22=2,解得b = 2.由余弦定理可得c 2=b 2+a 2-2ba cos π4=10,c =10.由正弦定理可得2a +3c -b 2sin A +3sin C -sin B =c sin C =1022=25,故选B.6.在△ABC 中,A =60°,AC =4,BC =23,则△ABC 的面积为________. 解析:因为23sin 60°=4sin B , 所以sin B =1,所以B =90°,所以AB =2,所以S △ABC =12×2×23=2 3. 答案:2 37.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a =4,c =2,B =60°,则b =________,C =________.解析:因为a =4,c =2,B =60°,所以由余弦定理得b 2=a 2+c 2-2ac cos B =16+4-2×4×2×12=20-8=12,则b =2 3.由正弦定理b sin B =c sin C ,可得sin C =c sin Bb =2×3223=12,因为c <b ,故C 为锐角,所以C =30°. 答案:23 30°8.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若B =π3,c =2,且sin A =3sin C .AC 的中点为D ,则BD =________.解析:sin A =3sin C .由正弦定理得,a =3c ,所以a =6. 由余弦定理得,b 2=62+22-2×2×6×cos 60°=28, 所以b =27.所以cos A =b 2+c 2-a 22bc =(27)2+22-622×2×27=-714.因为D 是AC 的中点,所以AD =7.所以BD 2=AB 2+AD 2-2AB ·AD cos A =22+(7)2-2×2×7×⎝ ⎛⎭⎪⎫-714=13.所以BD =13. 答案:139.(2020·高考全国卷Ⅱ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos 2⎝ ⎛⎭⎪⎫π2+A +cos A =54.(1)求A ;(2)若b -c =33a ,证明:△ABC 是直角三角形. 解:(1)由已知得sin 2A +cos A =54, 即cos 2A -cos A +14=0. 所以⎝ ⎛⎭⎪⎫cos A -122=0, cos A =12. 由于0<A <π,故A =π3.(2)证明:由正弦定理及已知条件可得sin B -sin C =33sin A . 由(1)知B +C =2π3,所以sin B -sin ⎝ ⎛⎭⎪⎫2π3-B =33sin π3.即12sin B -32cos B =12,sin ⎝ ⎛⎭⎪⎫B -π3=12.由于0<B <2π3,故B =π2.从而△ABC 是直角三角形.10.(2020·成都市诊断性检测)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且b 2+c 2-a 2=423bc .(1)求sin A 的值;(2)若△ABC 的面积为2,且2sin B =3sin C ,求△ABC 的周长. 解:(1)因为b 2+c 2-a 2=2bc cos A , 所以2bc cos A =423bc , 所以cos A =223,所以在△ABC 中,sin A =1-cos 2 A =13.(2)因为△ABC 的面积为2,所以12bc sin A =16bc =2, 所以bc =6 2.因为2sin B =3sin C ,所以由正弦定理得2b =3c , 所以b =32,c =2,所以a 2=b 2+c 2-2bc cos A =6,所以a = 6. 所以△ABC 的周长为2+32+ 6.[B 级 综合练]11.在△ABC 中,已知2a cos B =c, sin A sin B (2-cos C )=sin 2C 2+12,则△ABC 为( )A .等边三角形B .等腰直角三角形C .锐角非等边三角形D .钝角三角形解析:选B.将已知等式2a cos B =c 利用正弦定理化简得2sin A cos B =sin C , 因为sin C =sin ()A +B =sin A cos B +cos A sin B , 所以2sin A cos B =sin A cos B +cos A sin B , 即sin A cos B -cos A sin B =sin(A -B )=0, 因为A 与B 都为△ABC 的内角, 所以A -B =0,即A =B .因为sin A sin B (2-cos C )=sin 2C 2+12,所以sin A sin B (2-cos C )=12(1-cos C )+12=1-12cos C , 所以-12[]cos ()A +B -cos (A -B )(2-cos C )=1-12cos C , 所以-12(-cos C -1)(2-cos C )=1-12cos C , 即(cos C +1)(2-cos C )=2-cos C ,整理得cos 2C -2cos C =0,即cos C (cos C -2)=0,所以cos C =0或cos C =2(舍去),所以C =90°,则△ABC 为等腰直角三角形,故选B.12.(多选)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若b =c cos A ,角A 的平分线交BC 于点D ,AD =1,cos A =18,则以下结论正确的是( )A .AC =34 B .AB =8C .CD BD =18D .△ABD 的面积为374解析:选ACD.在△ABC 中,根据余弦定理得,cos A =b 2+c 2-a 22bc =bc ,即b 2+a 2=c 2,所以C =π2,由二倍角公式得cos ∠BAC =2cos 2∠CAD -1=18,解得cos ∠CAD =34.在Rt △ACD 中,AC =AD cos ∠CAD =34,故选项A 正确;在Rt △ABC 中,cos ∠BAC =AC AB =18,解得AB =6,故选项B 错误;S △ACD S △ADB =12CD ·AC 12BD ·AC =12AC ·AD ·sin ∠CAD 12AB ·AD ·sin ∠BAD ,则CD BD =AC AB =18,故选项C 正确; 在△ABD 中,由cos ∠BAD =34得,sin ∠BAD =74,所以S △ABD =12AD ·AB ·sin ∠BAD =12×1×6×74=374,故选项D 正确.13.(2020·沈阳市教学质量监测(一))△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a cos B +b cos A =77ac ,sin 2A =sin A . (1)求A 及a ;(2)若b -c =2,求BC 边上的高. 解:(1)因为a cos B +b cos A =77ac ,所以由正弦定理得sin A cos B +sin B cos A =77a sin C ,所以sin(A +B )=77a sin C ,又A +B =π-C ,所以sin C =77a sin C ,又sin C >0,所以a =7.因为sin 2A =sin A ,所以2sin A cos A =sin A ,又sin A >0,所以cos A =12, 因为A ∈(0,π),所以A =π3.(2)由(1)及余弦定理a 2=b 2+c 2-2bc cos A , 得b 2+c 2-bc =7.将b =c +2,代入b 2+c 2-bc =7,得c 2+2c -3=0, 解得c =1或c =-3(舍去),所以b =3. 因为a sin A =c sin C ,所以sin C =c sin A a =2114, 设BC 边上的高为h ,则h =b sin C =32114.14.在①(2a +b )sin A +(2b +a )sin B =2c sin C ,②a =3c sin A -a cos C ,③△ABC 的面积S △ABC =34(a 2+b 2-c 2)这三个条件中任选一个,补充在下面的问题中,作为问题的条件,再解答这个问题.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若c =3,且________,探究三角形ABC 的周长l 是否存在最大值?若存在,求出l 的最大值;若不存在,说明理由.解:若选①,因为(2a +b )sin A +(2b +a )sin B =2c sin C , 所以由正弦定理可得(2a +b )a +(2b +a )b =2c 2, 即a 2+b 2-c 2=-ab ,所以cos C =a 2+b 2-c 22ab =-12,因为C ∈(0,π),所以C =2π3.又c =3,所以由正弦定理可得a sin A =b sin B =332=2,所以a =2sin A ,b =2sin B ,则l =a +b +c =2sin A +2sin B +3=2sin A +2sin ⎝ ⎛⎭⎪⎫π3-A +3=sin A +3cos A +3=2sin ⎝ ⎛⎭⎪⎫A +π3+3, 因为0<A <π3,所以23<2sin ⎝ ⎛⎭⎪⎫A +π3+3≤2+3,即△ABC 的周长l 存在最大值,且最大值为2+ 3. 若选②,因为a =3c sin A -a cos C ,所以由正弦定理可得sin A =3sin C sin A -sin A cos C , 因为sin A ≠0,所以3sin C -cos C =1, 所以sin ⎝ ⎛⎭⎪⎫C -π6=12,又0<C <π,故C =π3,又c =3,所以由正弦定理可得a sin A =b sin B =332=2,所以a =2sin A ,b =2sin B ,则l =a +b +c =2sin A +2sin B +3=2sin A +2sin ⎝ ⎛⎭⎪⎫2π3-A +3=3sin A +3cos A +3=23sin ⎝ ⎛⎭⎪⎫A +π6+3,因为0<A <2π3,所以23<23sin ⎝ ⎛⎭⎪⎫A +π6+3≤33,即△ABC 的周长l 存在最大值,且最大值为3 3. 若选③,因为△ABC 的面积S △ABC =34(a 2+b 2-c 2),所以12ab sin C =34(a 2+b 2-c 2),所以sin C =3×a 2+b 2-c 22ab ,由余弦定理可得sin C =3cos C ,即tan C =3, 又因为0<C <π,故C =π3,又c =3,所以由正弦定理可得a sin A =b sin B =332=2,所以a =2sin A ,b =2sin B ,则l =a +b +c =2sin A +2sin B +3=2sin A +2sin ⎝ ⎛⎭⎪⎫2π3-A +3=23sin ⎝ ⎛⎭⎪⎫A +π6+3, 因为0<A <2π3,所以23<23sin ⎝ ⎛⎭⎪⎫A +π6+3≤33,即△ABC 的周长l 存在最大值,且最大值为3 3.[C 级 创新练]15.(2020·河南豫南九校联考)我国南宋著名数学家秦九韶提出了由三角形三边求三角形面积的“三斜求积”公式.设△ABC 三个内角A ,B ,C 所对的边分别为a ,b ,c ,面积为S ,则“三斜求积”公式为S =14⎣⎢⎡⎦⎥⎤a 2c 2-⎝ ⎛⎭⎪⎫a 2+c 2-b 222.若a 2sin C =2sin A ,(a +c )2=6+b 2,则用“三斜求积”公式求得的△ABC 的面积为( )A . 3B .1C .32D .12解析:选C.因为a 2sin C =2sin A ,所以a 2c =2a .又a >0,所以ac =2. 因为(a +c )2=6+b 2,所以a 2+c 2+2ac =6+b 2,所以a 2+c 2-b 2=6-2ac =6-4=2.所以△ABC 的面积为S =14×⎣⎢⎡⎦⎥⎤22-⎝ ⎛⎭⎪⎫222=32.故选C. 16.(2020·山东潍坊月考)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若1tan A ,1tan B ,1tan C 依次成等差数列,则下列结论中不一定成立的是( )A .a ,b ,c 依次成等差数列 B.a ,b ,c 依次成等差数列 C .a 2,b 2,c 2依次成等差数列 D .a 3,b 3,c 3依次成等差数列解析:选ABD.在△ABC 中,若1tan A ,1tan B ,1tan C 依次成等差数列,则2tan B =1tan A +1tan C .所以2cos B sin B =cos A sin A +cos Csin C .利用正弦定理和余弦定理得,2·a 2+c 2-b 22abc =b 2+c 2-a 22abc +a 2+b 2-c 22abc ,整理得2b 2=a 2+c 2,即a 2,b 2,c 2依次成等差数列.此时对等差数列a2,b2,c2的每一项取相同的运算得到数列a,b,c或a,b,c或a3,b3,c3,这些数列一般都不可能是等差数列,除非a=b =c.故都不一定成立.故选ABD.第6讲正弦定理和余弦定理最新考纲考向预测掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.命题趋势以利用正弦、余弦定理解三角形为主,常与三角函数的图象和性质、三角恒等变换、三角形中的几何计算交汇考查,加强数形结合思想的应用意识.题型多样,中档难度.核心素养逻辑推理、数学运算1.正弦定理和余弦定理定理正弦定理余弦定理内容asin A=bsin B=csin C=2R(R为△ABC外接圆半径)a2=b2+c2-2bc cos__A;b2=c2+a2-2ca cos__B;c2=a2+b2-2ab cos__C变形(1)a=2R sin A,b=2R sin__B,c=2R sin__C;(2)a∶b∶c=sin__A∶sin__B∶sin__C;(3)a sin B=b sin A,b sin C=c sin B,a sin C=c sin Acos A=b2+c2-a22bc;cos B=c2+a2-b22ca;cos C=a2+b2-c22ab(1)S△ABC=12a·h(h表示边a上的高).(2)S△ABC=12ab sin C=12ac sin B=12bc sin A.(3)S△ABC=12r(a+b+c)(r为△ABC内切圆半径).3.三角形解的判断A为锐角A为钝角或直角图形关系式a=b sin A b sin A<a<b a≥b a>b解的个数一解两解一解一解[注意]上表中A为锐角时,a<b sin A,无解.A为钝角或直角时,a=b,a<b均无解.常用结论1.在△ABC中,两边之和大于第三边,两边之差小于第三边,A>B⇔a>b⇔sin A>sin B⇔cos A<cos B.2.三角形中的三角函数关系(1)sin(A+B)=sin C.(2)cos(A+B)=-cos C.(3)sin A+B2=cosC2.(4)cos A+B2=sinC2.3.三角形中的射影定理在△ABC中,a=b cos C+c cos B;b=a cos C+c cos A;c=b cos A+a cos B.常见误区1.在△ABC中,已知a,b和A,利用正弦定理时,会出现解的不确定性,应注意根据“大边对大角”来取舍.2.在判断三角形的形状时,等式两边一般不要约去公因式,应移项提取公因式,以免漏解.1.判断正误(正确的打“√”,错误的打“×”)(1)三角形中三边之比等于相应的三个内角之比.( ) (2)在△ABC 中,若sin A >sin B ,则A >B .( )(3)在△ABC 中的六个元素中,已知任意三个元素可求其他元素.( ) 答案:(1)× (2)√ (3)×2.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若A =60°,a 2=bc ,则sin B sin C =( )A.12 B.32 C.35D.34解析:选D.因为a 2=bc ,所以sin 2A =sin B sin C .因为A =60°,所以sin B sin C =sin 2A =34.故选D.3.(多选)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =4,sin A =45,cos C =210,则下列结论正确的是( )A .cos A =±35 B .B =π4C .b =522D .△ABC 的面积为7 2解析:选BC.由sin A =45,得cos A =±35,由cos C =210,得sin C =7210,若cos A =-35,则sin B =sin(A +C )=-17250<0,与sin B >0矛盾,故cos A =35,A 错误,则sin(A +C )=22,由sin A =45,cos C =210,得A >π4,C >π4,所以A +C >π2,所以A +C =3π4,故B =π4,B 正确.由正弦定理a sin A =b sin B ,得b =522,C 正确,所以△ABC 的面积为12×4×522×7210=7,D 错误.4.(易错题)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知C =60°,b =6,c =3,则A =________.解析:由题意得,b sin B =c sin C ,即sin B =b sin C c =6×323=22,结合b <c可得B =45°,则A =180°-B -C =75°.答案:75°利用正、余弦定理解三角形(2020·高考天津卷节选)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知a =22,b =5,c =13.(1)求角C 的大小; (2)求sin A 的值.【解】 (1)在△ABC 中,由余弦定理及a =22,b =5,c =13,有cos C =a 2+b 2-c 22ab =22.又因为C ∈(0,π),所以C =π4.(2)在△ABC 中,由正弦定理及C =π4,a =22,c =13,可得sin A =a sin Cc =21313.(1)正、余弦定理的选用①利用正弦定理可解决两类三角形问题:一是已知两角和一角的对边,求其他边或角;二是已知两边和一边的对角,求其他边或角;②利用余弦定理可解决两类三角形问题:一是已知两边和它们的夹角,求其他边或角;二是已知三边求角.由于这两种情形下的三角形是唯一确定的,所以其解也是唯一的.(2)三角形解的个数的判断已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的有界性和大边对大角定理进行判断.1.在△ABC 中,已知b =40,c =20,C =60°,则此三角形的解的情况是( ) A .有一解C .无解D .有解但解的个数不确定解析:选C.由正弦定理得b sin B =csin C , 所以sin B =b sin Cc =40×3220=3>1.所以角B 不存在,即满足条件的三角形不存在.2.(2020·广东省七校联考)若△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,已知2b sin 2A =3a sin B ,且c =2b ,则ab =( )A.32 B. 2 C.43D. 3解析:选B.由2b sin 2A =3a sin B ,及正弦定理可得4sin B sin A cos A =3sin A sin B .由于sin A ≠0,sin B ≠0,所以cos A =34,又c =2b ,所以a 2=b 2+c 2-2bc cos A =b 2+4b 2-2b ×2b ×34=2b 2,所以ab =2,故选B.3.(2019·高考全国卷Ⅰ改编)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,设(sin B -sin C )2=sin 2A -sin B sin C .(1)求A ;(2)若2a +b =2c ,求C .解:(1)由已知得sin 2B +sin 2C -sin 2A =sin B sin C ,故由正弦定理得b 2+c 2-a 2=bc .由余弦定理得cos A =b 2+c 2-a 22bc =12. 因为0°<A <180°,所以A =60°.(2)由(1)知B =120°-C ,由题设及正弦定理得2sin A +sin(120°-C )=2sin C ,即62+32cos C +12sin C =2sin C ,可得cos(C +60°)=-22.由于0°<C <120°,所以C +60°=135°,判断三角形的形状(1)(一题多解)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,则△ABC 的形状为( )A .直角三角形B .锐角三角形C .钝角三角形D .不确定(2)在△ABC 中,若c -a cos B =(2a -b )cos A ,则△ABC 的形状为________. 【解析】 (1)方法一:因为b cos C +c cos B =b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac =2a 22a =a ,所以a sin A =a 即sin A =1,故A =π2,因此△ABC 是直角三角形.方法二:因为b cos C +c cos B =a sin A , 所以sin B cos C +sin C cos B =sin 2 A , 即sin(B +C )=sin 2 A ,所以sin A =sin 2 A , 故sin A =1,即A =π2,因此△ABC 是直角三角形.(2)因为c -a cos B =(2a -b )cos A ,所以由正弦定理得sin C -sin A cos B =2sin A cos A -sin B cos A ,所以sin(A +B )-sin A cos B =2sin A cos A -sin B cos A , 故cos A (sin B -sin A )=0, 所以cos A =0或sin A =sin B , 即A =π2或A =B ,故△ABC 为等腰三角形或直角三角形. 【答案】 (1)A (2)等腰三角形或直角三角形【引申探究】 (变条件)若将本例(1)条件改为“2sin A cos B =sin C ”,试判断△ABC 的形状.解:方法一:由已知得2sin A cos B =sin C =sin(A +B )=sin A cos B +cos A sin B ,即sin(A -B )=0,因为-π<A -B <π,所以A =B ,故△ABC 为等腰三角形.方法二:由正弦定理得2a cos B =c ,再由余弦定理得2a ·a 2+c 2-b 22ac =c ⇒a 2=b 2⇒a =b , 故△ABC 为等腰三角形.判定三角形形状的两种常用途径[提醒] “角化边”后要注意用因式分解、配方等方法得出边的相应关系;“边化角”后要注意用三角恒等变换公式、三角形内角和定理及诱导公式推出角的关系.1.在△ABC 中,a ∶b ∶c =3∶5∶7,那么△ABC 是( ) A .直角三角形 B .钝角三角形 C .锐角三角形D .非钝角三角形解析:选B.因为a ∶b ∶c =3∶5∶7,所以可设a =3t ,b =5t ,c =7t ,由余弦定理可得cos C =9t 2+25t 2-49t 22×3t ×5t =-12,所以C =120°,△ABC 是钝角三角形,故选B.2.(多选)已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,则下列四个命题中正确的是( )A .若a cos A =b cosB =ccos C ,则△ABC 一定是等边三角形 B .若a cos A =b cos B ,则△ABC 一定是等腰三角形 C .若b cos C +c cos B =b ,则△ABC 一定是等腰三角形 D .若a 2+b 2-c 2>0,则△ABC 一定是锐角三角形解析:选AC.由a cos A =b cos B =c cos C 及正弦定理得,sin A cos A =sin B cos B =sin Ccos C ,即tan A =tan B =tan C ,所以A =B =C ,所以△ABC 是等边三角形,A 正确.由a cos A =b cos B 及正弦定理得,sin A cos A =sin B cos B ,解得sin 2A =sin 2B ,则2A =2B 或2A +2B =π,所以△ABC 是等腰三角形或直角三角形,B 不正确.由b cos C +c cos B =b 及正弦定理得,sin B cos C +sin C cos B =sin B ,即sin(B +C )=sin B ,所以sin A =sin B ,则A =B ,所以△ABC 是等腰三角形,C 正确.由余弦定理得,cos C =a 2+b 2-c 22ab >0,所以角C 为锐角.而角A ,B 不一定是锐角,故D 不正确.故选AC.与三角形面积有关的问题 角度一 计算三角形的面积(1)(2020·高考全国卷Ⅰ改编)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知B =150°.若a =3c ,b =27,则△ABC 的面积为________.(2)(2020·福建五校第二次联考)在△ABC 中,A ,B ,C 所对的边分别为a ,b ,c ,已知a 2+b 2-c 2=3ab ,且ac sin B =23sin C ,则△ABC 的面积为________.【解析】 (1)由题设及余弦定理得28=3c 2+c 2-2×3c 2×cos 150°. 解得c =-2(舍去),c =2,从而a =2 3. △ABC 的面积为12×23×2×sin 150°= 3.(2)因为a 2+b 2-c 2=3ab ,所以由余弦定理得cos C =a 2+b 2-c 22ab =3ab 2ab =32,又0<C <π,所以C =π6.因为ac sin B =23sin C ,结合正弦定理可得abc =23c ,所以ab =2 3.故S △ABC =12ab sin C =12×23sin π6=32.【答案】 (1)3 (2)32求三角形面积的方法(1)若三角形中已知一个角(角的大小或该角的正、余弦值),结合题意求解这个角的两边或该角的两边之积,代入公式求面积;(2)若已知三角形的三边,可先求其中一个角的余弦值,再求其正弦值,代入公式求面积,总之,结合图形恰当选择面积公式是解题的关键.角度二 已知三角形的面积解三角形(2020·广州市调研检测)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知c sin ⎝ ⎛⎭⎪⎫A +π3-a sin C =0.(1)求角A 的值;(2)若△ABC 的面积为3,周长为6,求a 的值. 【解】 (1)因为c sin ⎝ ⎛⎭⎪⎫A +π3-a sin C =0, 所以由正弦定理得sin C ⎝ ⎛⎭⎪⎫12sin A +32cos A -sin A ·sin C =0.因为sin C >0,所以32cos A -12sin A =0,即tan A =3, 因为A ∈(0,π),所以A =π3.(2)因为△ABC 的面积为3,所以12bc sin A =3,得bc =4.由余弦定理a 2=b 2+c 2-2bc cos A ,得a 2=b 2+c 2-bc =(b +c )2-3bc =(b +c )2-12,因为△ABC 的周长为6,即a +b +c =6, 所以a 2=(6-a )2-12, 所以a =2.已知三角形面积求边、角的方法(1)若求角,就寻求这个角的两边的关系,利用面积公式列方程求解; (2)若求边,就寻求与该边(或两边)有关联的角,利用面积公式列方程求解. [注意] 正弦定理、余弦定理与三角函数性质的综合应用中,要注意三角函数公式的工具性作用.1.(2020·福州市质量检测)在钝角△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知c =7,b =1,若△ABC 的面积为62,则a 的长为________.解析:因为△ABC 的面积S =12bc sin A ,所以62=12×1×7sin A ,所以sin A=67,所以cos A=±77,当cos A=77时,由a2=b2+c2-2bc cos A得a=6,此时△ABC为直角三角形(舍去);当cos A=-77时,由a2=b2+c2-2bc cos A得a=10,经检验,a=10符合题意.综上,a=10.答案:102.(2020·合肥第一次教学检测)在△ABC中,内角A,B,C所对的边分别为a,b,c,若a=2,a cos C+c cos A+2b cos B=0.(1)求B;(2)若BC边的中线AM长为5,求△ABC的面积.解:(1)在△ABC中,asin A=bsin B=csin C,且a cos C+c cos A+2b cos B=0,所以sin A cos C+sin C cos A+2sin B cos B=0,所以sin B·(1+2cos B)=0,又sin B≠0,所以cos B=-2 2.因为B是三角形的内角,所以B=3π4.(2)在△ABM中,BM=1,AM=5,B=3π4,AB=c,由余弦定理AM2=c2+BM2-2c·BM·cos B,得c2+2c-4=0,因为c>0,所以c= 2.在△ABC中,a=2,c=2,B=3π4,所以△ABC的面积S=12ac sin B=1.高考新声音系列4解三角形中的结构不良型开放型问题新高考卷Ⅰ第17题别具匠心地设计了开放性试题,设问方式追求创新,补充已知条件(三选一)并解答,条件不同,结论不同,不同的选择会有不同的结论,难度也会有区别.(2020·新高考卷Ⅰ)在①ac =3,②c sin A =3,③c =3b 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的值;若问题中的三角形不存在,说明理由.问题:是否存在△ABC ,它的内角A ,B ,C 的对边分别为a ,b ,c ,且sin A =3sin B ,C =π6,________________?【解】 方案一:选条件①.由C =π6和余弦定理得a 2+b 2-c 22ab =32. 由sin A =3sin B 及正弦定理得a =3b . 于是3b 2+b 2-c 223b 2=32,由此可得b =c . 由①ac =3,解得a =3,b =c =1.因此,选条件①时问题中的三角形存在,此时c =1. 方案二:选条件②.由C =π6和余弦定理得a 2+b 2-c 22ab =32. 由sin A =3sin B 及正弦定理得a =3b .于是3b 2+b 2-c 223b 2=32,由此可得b =c ,B =C =π6,A =2π3. 由②c sin A =3,所以c =b =23,a =6.因此,选条件②时问题中的三角形存在,此时c =2 3. 方案三:选条件③.由C =π6和余弦定理得a 2+b 2-c 22ab =32.由sin A =3sin B 及正弦定理得a =3b . 于是3b 2+b 2-c 223b 2=32,由此可得b =c . 由③c =3b ,与b =c 矛盾.因此,选条件③时问题中的三角形不存在.本题以解三角形为背景命制,给定了若干条件(在这些条件下三角形并不能随之确定),在此基础上让学生在另外给出的几个条件中自主选择,在所选条件下,若问题中的三角形存在,求解三角形;若问题中的三角形不存在,说明理由.在①sin B=32,②cos B=34,③cos C=-79这三个条件中选择一个,补充在下面的问题中,并判断三角形是否有解.若有解,求出a的值;若无解,请说明理由.在△ABC中,已知a,b,c分别是角A,B,C的对边,且满足C=2B,b +c=10,________.解:若选择①sin B=32,则B=60°或B=120°,因为C=2B,所以C=120°或C=240°,显然矛盾,此时三角形无解.若选择②cos B=3 4,则由正弦定理可得cb=sin Csin B=sin 2Bsin B=2sin B cos Bsin B=2cos B=2×34=32,又b+c=10,所以c=6,b=4.由余弦定理b2=a2+c2-2ac cos B,可得16=a2+36-9a,解得a=4或a=5.若a=4,则由b=4知A=B,又C=2B,所以B+B+2B=180°,解得B=45°,这与cos B=34矛盾,舍去.经检验知,当a=5时适合题意.故a的值为5.若选择③cos C=-7 9,因为C=2B,所以cos 2B=-7 9,即2cos2B-1=-79,得cos B=13,此时cb=sin Csin B=sin 2Bsin B=2cos B=23<1,所以c<b,这与C=2B矛盾,。
高考数学一轮复习---正弦定理和余弦定理(一)

高考数学一轮复习---正弦定理和余弦定理(一)一、基础知识1.正弦定理a sin A =b sin B =c sin C=2R (R 为△ABC 外接圆的半径).正弦定理的常见变形:(1)a =2R sin A ,b =2R sin B ,c =2R sin C ; (2)sin A =a 2R ,sin B =b 2R ,sin C =c 2R; (3)a ∶b ∶c =sin A ∶sin B ∶sin C ;(4)a +b +c sin A +sin B +sin C =a sin A . 2.余弦定理a 2=b 2+c 2-2bc cos A ; b 2=c 2+a 2-2ca cos B ; c 2=a 2+b 2-2ab cos C .3.三角形的面积公式(1)S △ABC =12ah a (h a 为边a 上的高); (2)S △ABC =12ab sin C =12bc sin A =12ac sin B ; (3)S =12r (a +b +c )(r 为三角形的内切圆半径). 二、常用结论汇总1.三角形内角和定理在△ABC 中,A +B +C =π;变形:A +B 2=π2-C 2. 2.三角形中的三角函数关系(1)sin(A +B )=sin C ; (2)cos(A +B )=-cos C ;(3)sin A +B 2=cos C 2; (4)cos A +B 2=sin C 2. 3.三角形中的射影定理在△ABC 中,a =b cos C +c cos B ;b =a cos C +c cos A ;c =b cos A +a cos B .4.用余弦定理判断三角形的形状在△ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,当b 2+c 2-a 2>0时,可知A 为锐角;当b 2+c 2-a 2=0时,可知A 为直角;当b 2+c 2-a 2<0时,可知A 为钝角.三、考点解析考点一 利用正、余弦定理解三角形考法(一) 正弦定理解三角形例.(1)在△ABC 中,a =3,b =2,A =30°,则cos B =________.(2)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若a =3,sin B =12,C =π6,则b =________.考法(二) 余弦定理解三角形例.(1)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若b cos A +a cos B =c 2,a =b =2,则△ABC 的周长为( )A .7.5B .7C .6D .5(2)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且c -b 2c -a =sin A sin B +sin C,则角B =________.跟踪训练1.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若b 2=ac ,c =2a ,则cos C =( )A.24 B .-24 C.34 D .-34 2.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知sin B +sin A (sin C -cos C )=0,a =2,c =2,则C =( )A.π12B. π6C.π4D.π33.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知sin 2B +sin 2C =sin 2A +sin B sin C .(1)求角A 的大小;(2)若cos B =13,a =3,求c 的值. 考点二 判定三角形的形状例、(1)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,则△ABC 的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .不确定(2)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若sin A sin B =a c,(b +c +a )(b +c -a )=3bc ,则△ABC 的形状为( )A .直角三角形B .等腰非等边三角形C .等边三角形D .钝角三角形变式练习1.(变条件)若本例(1)条件改为“a sin A +b sin B <c sin C ”,那么△ABC 的形状为________.2.(变条件)若本例(1)条件改为“c -a cos B =(2a -b )cos A ”,那么△ABC 的形状为________.3.(变条件)若本例(2)条件改为“cos A cos B =b a =2”,那么△ABC 的形状为________. 课后作业1.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .若sin A a =cos B b,则B 的大小为( ) A .30° B .45° C .60° D .90°2.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知b =40,c =20,C =60°,则此三角形的解的情况是( )A .有一解B .有两解C .无解D .有解但解的个数不确定3.在△ABC 中,cos B =a c(a ,b ,c 分别为角A ,B ,C 的对边),则△ABC 的形状为( ) A .直角三角形 B .等边三角形 C .等腰三角形 D .等腰三角形或直角三角形4.在△ABC 中,a ,b ,c 分别是内角A ,B ,C 的对边.若b sin A =3c sin B ,a =3,cos B =23,则b =( ) A .14 B .6 C.14 D.65.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若a sin B cos C +c sin B cos A =12b ,且a >b ,则B =( )A.π6B.π3C.2π3D.5π66.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若2(b cos A +a cos B )=c 2,b =3,3cos A =1,则a =( ) A. 5 B .3 C.10 D .47.在△ABC 中,AB =6,A =75°,B =45°,则AC =________.8.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a =2,cos C =-14,3sin A =2sin B ,则c =________. 9.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a =7,b =2,A =60°,则sin B =________,c =________.10.在△ABC 中,a ,b ,c 分别为角A ,B ,C 所对的边,sin A ,sin B ,sin C 成等差数列,且a =2c ,则cos A =________.11.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且A =2B .(1)求证:a =2b cos B ;(2)若b =2,c =4,求B 的值.12.在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b +c )sin B +(2c +b )sin C .(1)求A 的大小;(2)若sin B +sin C =1,试判断△ABC 的形状.提高训练1.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若2c os 2A +B 2-cos 2C =1,4sin B =3sin A ,a -b =1,则c 的值为( ) A.13 B.7 C.37 D .62.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且c =3,2sin A a =t a n C c,若sin(A -B )+sin C =2sin 2B ,则a +b =________.3.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且2a cos C -c =2b .(1)求角A 的大小;(2)若c =2,角B 的平分线BD =3,求a .。
高考数学一轮总复习课件:正、余弦定理(一)

状元笔记
三角形形状的判定方法 (1)通过正弦定理和余弦定理,化边为角(如a=2RsinA,a2+ b2-c2=2abcosC等),利用三角变换得出三角形内角之间的关系 进行判断.此时注意一些常见的三角等式所体现的内角关系, 如sinA=sinB⇔A=B;sin(A-B)=0⇔A=B;sin2A=sin2B⇔A
方法二:同方法一可得2a2cosAsinB=2b2cosBsinA. 由正、余弦定理,得a2bb2+2cb2c-a2=b2aa2+2ca2c-b2. ∴a2(b2+c2-a2)=b2(a2+c2-b2). 即(a2-b2)(c2-a2-b2)=0. ∴a=b或c2=a2+b2. ∴△ABC为等腰三角形或直角三角形. 【答案】 等腰三角形或直角三角形 【误区警示】 方法一:本题容易由sin2A=sin2B只得出2A=2B 而漏掉2A=π-2B. 方法二:对于(a2-b2)(c2-a2-b2)=0.容易只得出a2=b2而漏解.
余弦定理
a2=___b2_+__c2_-_2_b_c_co_s_A___;b2=__a_2+__c_2-__2_ac_c_os_B____;
c2=__a_2_+_b_2_-_2_a_b_co_s_C___.
b2+c2-a2
a2+c2-b2
变式:cosA=____2_b_c____;cosB=_____2a_c_____;
授人以渔
题型一 利用正、余弦定理解三角形
例1 (1)在△ABC中,已知a= 2 ,b= 3 ,A=45°,求
角B,C及边c. 【解析】 方法一:由正弦定理,得sinaA=sibnB.
∴sinB=basinA=
32·sin45°=
3· 2
22=
23.
∵b>a,∴B>A=45°,∴有两解B=60°或120°.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦、余弦定理一. 教学内容:正弦、余弦定理二. 教学重、难点: 1. 重点:正弦、余弦定理。
2. 难点:运用正、余弦定理解决有关斜三角形问题。
【典型例题】[例1] 已知在ABC ∆中,︒=∠45A ,2=a ,6=c 解此三角形。
解:由正弦定理得23222645sin 26sin =⋅=︒⋅=C∵ 6sin =A c 322=⨯2=a ,6=c ,623<<∴ 有两解,即︒=∠60C 或︒=∠120C︒=︒-︒-︒=∠754560180B 或︒=︒-︒-︒=∠1545120180B由B A ab sin sin =得13+=b 或13-=b∴ 13+=b ,︒=∠60C ,︒=∠75B 或13-=b ,︒=∠120C ,︒=∠15B[例2] 不解三角形,判断下列三角形解的个数。
(1)5=a ,4=b ,︒=120A (2)7=a ,14=b ,︒=150A (3)9=a ,10=b ,︒=60A(4)50=c ,72=b ,︒=135C 解:(1)232354120sin sin <⨯=︒=a b B ,∴ ABC ∆有一解。
(2)1150sin sin =︒=a bB ∴ ABC ∆无解(3)93523910sin sin =⨯==A a bB 而193523<<∴ 当B 为锐角时,满足935sin =B 的︒<<︒9060B ,故对应的钝角B 有︒<<︒12090B ,也满足A+B ︒<180,故ABC ∆有两解。
(4)22sin sin 5072sin sin =>==C C c C b B∴ ︒>45B ∴ ︒>+180C B ∴ ABC ∆无解[例3] 已知在ABC ∆中,︒=∠45A ,2=a ,6=c 解此三角形。
解:由余弦定理得:445cos 62)6(22=︒⋅-+b b ∴ 02322=+-b b ∴ 13±=b又 C b b cos 222)6(222⨯-+= ∴ 21cos ±=C ,︒=∠60C 或︒=∠120C∴ ︒=∠75B 或︒=∠15B ∴ 13+=b ,︒=∠60C ,︒=∠75B 或13-=b ,︒=∠120C ,︒=∠15B[例4] 已知a 、b 、c 是ABC ∆中,A ∠、B ∠、C ∠的对边,S 是ABC ∆的面积,若4=a ,5=b ,35=S ,求c 的长度。
解:∵ 4=a ,5=b ,35sin 21==C ab S∴23sin =C ∴ ︒=60C 或︒120∴ 当︒=60C 时,21222=-+=ab b a c ∴ 21=c当︒=120C 时,61222=++=ab b a c ∴ 61=c[例5] 在ABC ∆中,A 、B 、C 成等差数列,1=b ,求证:21≤+<c a证明:方法一:由正弦定理:C cB b A a sin sin sin == 得C B bA B b c a sin sin sin sin +⋅=+)]120sin([sin 332)sin (sin 332A A C A -︒+=+=)30sin(2︒+=A∵ ︒<<︒1200A ∴ ︒<︒+<︒1503030A ∴ 2)30sin(21≤︒+<A方法二:∵ ︒=60B ,1=b ∴ ︒=-+60cos 2222ac b c a∴ ac c a =-+122 ∴ 122=-+ac c a ∴4)(3)(22=-++c a c a ∴ 22)(34)(c a c a --=+∵ 1||0<-≤c a ∴ 3)(302<-≤c a ∴ 4)(342≤--c a 即4)(2≤+c a ∴ 2≤+c a 又1>+c a ∴ 21≤+<c a[例6] 在ABC ∆中,已知)13(-=a b ,︒=30C ,求A 、B 。
解:由余弦定理,ab c b a C 22330cos cos 222-+==︒=∴)13(3)324(2222-=--+a c a a ∴ 22)32(a c -= ∴aa c 21332-=-=由正弦定理:︒-=-=30sin 213sin )13(sin aB a A a ∴2230sin 2sin =︒=B∵ b a > ∴ B A > ∴ B 为锐角 ∴ ︒=45B ∴ ︒=︒+︒-︒=105)3045(180A[例7] 已知ABC ∆中,B b a C A sin )()sin (sin 2222-=-,外接圆半径为2。
(1)求C ∠(2)求ABC ∆面积的最大值 解:(1)由B b a C A sin )()sin (sin 2222-=-∴R b b a R c R a 2)()44(22222-=-2 ∴ 2=R ∴ 222b ab c a -=- ∴ ab c b a =-+222∴212cos 222=-+=ab c b a C又 ︒<<︒1800C ∴ ︒=60C(2)B A abC ab S sin sin 322321sin 21=⨯==)sin 120cos cos 120(sin sin 32)120sin(sin 32A A A A A ︒-︒=-︒⋅=232cos 232sin 23sin 3cos sin 32+-=+=A A A A A23)302sin(3+︒-=A∴ 当︒=1202A 即︒=60A 时,233max =S[例8] 在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c 依次成等比数列,求BB B y cos sin 2sin 1++=的取值范围。
解:∵ ac b =2∴2121)(2122cos 22222≥-+=-+=-+=a c c a acacc a acb c a B∴30π≤<B)4sin(2cos sin cos sin )cos (sin cos sin 2sin 12π+=+=++=++=B B B B B B B B B B y∵ πππ12744<+<B ∴ 1)4sin(22≤+<πB ∴ 21≤<y[例9] 在ABC ∆中,若三边长为连续三个正整数,最大角是钝角,求此最大角。
解:设1-=k a ,k b =,1+=k c ,*N k ∈且1>k∵ C 是钝角 ∴ 0)1(242cos 222<--=-+=k k ab c b a C解得41<<k ∵ *N k ∈ ∴ 2=k 或3当2=k 时,1cos -=C (舍去)当3=k 时,41cos -=C ∴ )41arccos(-=c∴ 最大角为)41arccos(-【模拟试题】(答题时间:60分钟)一. 选择题:1. 在ABC ∆中,一定成立的等式是( ) A. B b A a sin sin = B. B b A a cos cos = C. A b B a sin sin =D. A b B a cos cos =2. 在ABC ∆中,若a bB A =cos cos ,则ABC ∆是( )A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰或直角三角形 3. 已知ABC ∆中,AB=1,BC=2,则C ∠的取值范围是( )A.]6,0(πB.)2,0(πC. ]2,6(ππ D. ]3,6(ππ4. ABC ∆中,若A b a sin 23=,则B 为( )A. 3πB. 6πC. 3π或π32D. 6π或π655. ABC ∆的三边满足ab c b a c b a 3))((=-+++,则C ∠等于( )A. ︒15B. ︒30C. ︒45D. ︒606. 在ABC ∆中,AB=3,BC=13,AC=4,则边AC 上的高为( )A. 223B. 233C. 23D. 337. ABC ∆中,“B A sin sin =”是“A=B ”的( )条件A. 充分不必要B. 必要不充分C. 充要D. 既不充分也不必要8. ABC ∆中,C C B B A 222sin sin sin sin sin ++=,则A 等于( )A. ︒30B. ︒60C. ︒120D. ︒1509. ABC ∆中,︒=30B ,350=b ,150=c ,则这个三角形是( ) A. 等边三角形 B. Rt 三角形 C. 等腰三角形 D. 等腰或直角三角形10. 在ABC ∆中,kC cB b A a ===sin sin sin ,则k =( )A. 2RB. RC. 4RD. 21R二. 填空:1. 在ABC ∆中,已知7=a ,8=b ,1413cos =C ,则最大角的余弦值为 。
2. 在ABC ∆中,C B A sin cos 2sin =,则三角形为 。
3. 在ABC ∆中,:6:)13(::+=c b a 2,则最小角为 。
4. 若)(341222a c b S -+=∆,则A= 。
三. 解答题:1. 在ABC ∆中,BC=a ,b AC =,a ,b 是02322=+-x x 的两个根,且)cos(2B A +=1,求(1)角C 的度数 (2)AB 的长 (3)ABC ∆的面积。
2. 在ABC ∆中,10=c ,︒=45A ,︒=30C ,求a 、b 和B 。
3. 若2,3,x 为三边组成一个锐角三角形,求x 的范围。
4. 在ABC ∆中,若C B A cos sin 2sin =,C B A 222sin sin sin +=,试判断ABC ∆形状。
【试题答案】一.1. C2. D3. A4. C5. D6. B7. C8. C9. D 10. A 二.1.71-2. 等腰三角形3. ︒454. ︒30三.1. 解:(1)21)cos()](cos[cos -=+-=+-=B A B A C π ∴ ︒=120C(2)∵ a 、b 是02322=+-x x 的两个根 ∴ ⎩⎨⎧=⋅=+232b a b a∴ 10)(cos 2222222=-+=++=⋅⋅-+=ab b a ab a b C BC AC BC AC AB ∴ 10=AB(3)23sin 21=⋅=∆C b a S ABC2. 解:∵ C c A a sin sin =∴21030sin 45sin 10sin sin =︒︒⋅==C A c a︒=+-︒=105)(180C A B ∴ C cB b sin sin =∴ )26(5105sin 20+=︒=b3. 解:∵ ABC ∆为锐角∆ ∴ ⎪⎩⎪⎨⎧>>>0cos 0cos 0cos C B A 且51<<x∴ ⎪⎪⎩⎪⎪⎨⎧<<>-+>-+>-+51032023032222222222x x x x ∴⎪⎩⎪⎨⎧<<><5151322x x x ∴135<<x4. 解:∵ C B A 222sin sin sin +=∴ 222c b a += ∴ ABC ∆为∆Rt 且︒=∠90A∴ ︒=+90C B ,C B -︒=90 ∴ C B cos sin =由C B A cos sin 2sin ⋅= ∴ B 2sin 21= ∴21sin 2=B∵ B 为锐角 ∴22sin =B ∴ ︒=45B ∴ ︒=45C∴ ABC ∆是等腰直角三角形。
