唐山2016高三二模理科数学答案
河北省唐山市2016届高三第二次模拟考试理综试题

试卷类型:A 唐山市2015-2016学年度高三年级第二次模拟考试理科综合能力测试第I卷本卷共21小题,每小题6分,共1 26分。
一、选择题(本题包括13小题,每小题只有一个选项符合题意)1.下列有关人体细胞结构和功能的叙述,正确的是A.成熟红细胞代谢过程中可产生C02B。
衰老细胞核内可进行DNA复制C.B细胞可分泌免疫活性物质D.神经细胞轴突末梢可形成多个突触小体2.胰腺细胞中某种酶能催化肽键形成,该酶经蛋白酶处理后活性不受影响,下列叙述错误的是A.该酶在细胞核中形成 B.该酶的活性不受酸碱影响C.该酶在核糖体中发挥作用 D.该酶的单体是核糖核苷酸3.科研小组将分离得到的某动物细胞膜放在特制的槽中央,左侧加入5%葡萄糖溶液,右侧加入蒸馏水。
一段时间后,从右侧取少量溶液用斐林试剂检测呈蓝色。
将动物细胞的细胞质基质加到左侧后,发现右侧用斐林试剂检测呈砖红色。
下列有关实验叙述错误的是A.细胞质基质提供了运输葡萄糖的载体 B,用斐林试剂检测时需要水浴加热C.水分子在膜两侧双向移动 D.葡萄糖跨膜运输需要能量4. 一对染色体正常的夫妇生了一个性染色体组成为XXY的孩子,产生这种现象的原因不可能是A.父方减数第一次分裂同源染色体未分离B.母方减数第一次分裂同源染色体未分离C.父方减数第二次分裂姐妹染色单体未分离D.母方减数第二次分裂姐妹染色单体未分离5.给正常家兔静脉注射较高剂量的胰高血糖素后,家兔体内不会发生的变化是A.胰岛A细胞分泌量减少 B,胰岛B细胞分泌量增多C.肝脏、肌肉中糖原的分解加快 D。
抗利尿激素分泌增多6.图l为某池塘生态系统中4种生物的食物网,图2为不同体长D种群的食性相对值,下列叙述错误的是A.C和D之间的种间关系是竞争和捕食B.若体长为6.5 cm的D种群增重lkg,至少需要消耗第一营养级生物l0kgC.若池塘中投放大量体长小于2.8cm的D种群,一定时间内A、B数量会增加D.池塘中的植物能实现水体净化,体现了生物多样性的直接价值29.(10分)将长势相同的A. B.C三组水稻幼苗,分别培养在成分相同、营养充足的培养液中。
2016年高考理科数学全国卷2(含详细答案)
数学试卷 第1页(共39页) 数学试卷 第2页(共39页) 数学试卷 第3页(共39页)绝密★启用前2014年普通高等学校招生全国统一考试(全国新课标卷2)理科数学使用地区:海南、宁夏、黑龙江、吉林、新疆、云南、内蒙古、青海、贵州、甘肃、西藏注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,{0}1,2M =,2{|320}N x x x =-+≤,则M N = ( )A .{1}B .{2}C .{0,1}D .{1,2}2.设复数1z ,2z 在复平面内的对应点关于虚轴对称,12i z =+,则12z z =( )A .5-B .5C .4i -+D .4i -- 3.设向量a ,b 满足|a +b||a -b|=则a b =( )A .1B .2C .3D .5 4.钝角三角形ABC △的面积是12,1AB =,BC =,则AC =( )A .5BC .2D .15.某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( )A .0.8B .0.75C .0.6D .0.456.如图,网格纸上正方形小格的边长为1(表示1 cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm ,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A .1727B .59 C .1027D .137.执行如图的程序框图,如果输入的x ,t 均为2,则输出的S =( )A .4B .5C .6D .7 8.设曲线ln(1)y ax x =-+在点(0,0)处的切线方程为2y x =,则a =( ) A .0 B .1 C .2D .39.设x ,y 满足约束条件70,310,350,x y x y x y +-⎧⎪-+⎨⎪--⎩≤≤≥则2z x y =-的最大值为( )A .10B .8C .3D .210.设F 为抛物线C :23y x =的焦点,过F 且倾斜角为30的直线交C 于A ,B 两点,O 为坐标原点,则OAB △的面积为 ( )ABC .6332D .94 11.直三棱柱111ABC A B C -中,90BCA ∠=,M ,N 分别是11A B ,11AC 的中点,1BC CA CC ==,则BM 与AN 所成角的余弦值为( )A .110B .25 CD12.设函数π()3sin x f x m,若存在()f x 的极值点0x 满足22200[()]x f x m +<,则m 的取值范围是( )A .(,6)(6,)-∞-+∞B .(,4)(4,)-∞-+∞C .(,2)(2,)-∞-+∞D .(,1)(1,)-∞-+∞第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13.10()x a +的展开式中,7x 的系数为15,则a = (用数字填写答案). 14.函数()sin(2)2sin cos()f x x x ϕϕϕ=+-+的最大值为 .15.已知偶函数()f x 在[0,)+∞上单调递减,(2)0f =,若(1)0f x ->,则x 的取值范围是 .16.设点0(,1)M x ,若在圆O :221x y +=上存在点N ,使得45OMN ∠=,则0x 的取值范围是 .三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知数列{}n a 满足11a =,131n n aa +=+.(Ⅰ)证明:1{}2n a +是等比数列,并求{}n a 的通项公式;(Ⅱ)证明:1211132n a a a ++⋅⋅⋅+<.-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页(共39页) 数学试卷 第5页(共39页) 数学试卷 第6页(共39页)18.(本小题满分12分)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点. (Ⅰ)证明:PB平面AEC ;(Ⅱ)设二面角D AE C --为60,1AP =,AD =求三棱锥E ACD -的体积.19.(本小题满分12分)某地区2007年至2013年农村居民家庭人均纯收入y (单位:千元)的数据如下表:(Ⅰ)求y 关于t 的线性回归方程;(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.附:回归直线的斜率和截距的最小二乘估计公式分别为:121()()ˆ()nii i ni i tt y y bt t ==--=-∑∑,ˆˆay bt =-.20.(本小题满分12分)设1F ,2F 分别是椭圆C :22221(0)x y a b a b+=>>的左、右焦点,M 是C 上一点且2MF 与x 轴垂直,直线1MF 与C 的另一个交点为N . (Ⅰ)若直线MN 的斜率为34,求C 的离心率;(Ⅱ)若直线MN 在y 轴上的截距为2,且1||5||MN F N =,求a ,b .21.(本小题满分12分)已知函数()e e 2x xf x x -=--. (Ⅰ)讨论()f x 的单调性;(Ⅱ)设()(2)4()g x f x bf x =-,当0x >时,()0g x >,求b 的最大值; (Ⅲ)已知1.4142 1.4143<,估计ln2的近似值(精确到0.001).请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时填写试题号.22.(本小题满分10分)选修4—1:几何证明选讲如图,P 是O 外一点,PA 是切线,A 为切点,割线PBC 与O 相交于点B ,C ,2PC PA =,D 为PC 的中点,AD 的延长线交O 于点E .证明:(Ⅰ)BE EC =; (Ⅱ)22AD DE PB =.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,半圆C 的极坐标方程为2cos ρθ=,π0,2θ⎡⎤∈⎢⎥⎣⎦.(Ⅰ)求C 的参数方程;(Ⅱ)设点D 在C 上,C 在D 处的切线与直线l :2y +垂直,根据(Ⅰ)中你得到的参数方程,确定D 的坐标.24.(本小题满分10分)选修4—5:不等式选讲设函数1()||(0)f x x x a a a =++->.(Ⅰ)证明:()2f x ≥;(Ⅱ)若(3)5f <,求a 的取值范围.3 / 132016年普通高等学校招生全国统一考试(全国新课标卷2)【解析】集合A B {0,1,2,3}=A B 的值.【解析】向量a(4,m),b(3,2)-,a b (4,m ∴+=-又(a b)b +⊥,12∴-【提示】求出向量a b +的坐标,根据向量垂直的充要条件,构造关于m 的方程,解得答案.【解析】输入的数学试卷第10页(共39页)数学试卷第11页(共39页)数学试卷第12页(共39页)5 / 13:πcos 4⎛- ⎝:π2cos 4⎛⎫-α= ⎝【提示】方法1:利用诱导公式化22π1n 1,π∴=解得e 2=.1数学试卷第16页(共39页)数学试卷第17页(共39页)数学试卷第18页(共39页)(Ⅰ)某保险的基本保费为7 / 13数学试卷 第22页(共39页)数学试卷 第23页(共39页) 数学试卷 第24页(共39页)(Ⅰ)ABCD 是菱形,AC BD ⊥,则,AC 6=,AEOD 1AO=,则, ,又OHEF H =,为坐标原点,建立如图所示空间直角坐标系,AB 5=,C(1,3,0),D (0,0,3)',AB (4,3,0)=,AD (1,3,3)'=-,AC (0,6,0)=,设平面的一个法向量为n (x,y,z)=11n AB 0n AD 0⎧=⎪⎨'=⎪⎩,得3y 03y 3z 0=⎧⎨+=3=,得n (3,4,5)∴=-同理可求得平面AD '的一个法向量n (3,01)=,的平面角为θ,122n n 9255210n n +==,∴二面角9 / 13为坐标原点,建立如图所示空间直角坐标系,由已知求得所用点的坐标,得到AB 、AD '、AC的一个法向量n 、n ,设二面角221234k +,由2212121k 413k 341kk =+⎛⎫++- ⎪⎝⎭,由AM =22212121k434k 3k k=+++, 整理可得2(k 1)(4k k 4)0--+=,由24k -212144134⎫=⎪+⎭轴对称,由MA ⊥数学试卷 第28页(共39页)数学试卷 第29页(共39页) 数学试卷 第30页(共39页)226t 3tk +,26t t 3k k+, AN ,可得2226t 6t 21k 1kt 3tk 3k k+=+++, 整理得26k 3kt -=,由椭圆的焦点在x 轴上,11 / 13 当2)(2,)-+∞2)和(2,-+∞x 2e f (0)=2>x 2e a 2⎫+⎪⎭a ∈x x 2(x)e 2-=的值域为t 2e a 2=-,只需t 2e 02≤0,可得t ∈t t 2e e 2t 2=+t e (t +22.【答案】(Ⅰ)DF CE ⊥,Rt DFC Rt EDC ∴△∽△,DF CF ED CD∴=, DE DG =,CD BC =,DF CF DG BC∴=,又GDF DEF BCF ∠=∠=∠, GDF BCF ∴△∽△,CFB DFG ∴∠=∠,GFB GFC CFB GFC DFG DFC 90∴∠=∠+∠=∠+∠=∠=,GFB GCB 180∴∠+∠=,B ∴,C ,G ,F 四点共圆;(Ⅱ)E 为AD 中点,A B 1=,1DG CG DE 2∴===,数学试卷 第34页(共39页)数学试卷 第35页(共39页) 数学试卷 第36页(共39页)∴在Rt DFC △中,1GF CD GC 2==,连接GB ,Rt BCG Rt BFG △≌△, BCG BCGF 111S 2S =21=222∴=⨯⨯⨯△四边形.【提示】(Ⅰ)证明B ,C ,G ,F 四点共圆可证明四边形BCGF 对角互补,由已知条件可知BCD 90∠=,因此问题可转化为证明GFB 90∠=;(Ⅱ)在Rt DFC △中,1GF CD GC ==,因此可得BCG BFG △≌△,则BCG BCGF S 2S =△四边形,据此解答.(Ⅰ)圆,22x ρ=+(Ⅱ)直线x α, l C (6,0)-,13 / 13 【考点】圆的标准方程,直线与圆相交的性质24.【答案】(Ⅰ)当1x 2<-时,不等式f (x)2<可化为:11x x 222---<,解得x 1>-, 11x 2∴-<<-, 当11x 22-≤≤时,不等式f (x)2<可化为:11x x 1222-+-=<,此时不等式恒成立, 11x 22∴-≤≤,当1x 2>时,不等式f (x)2<可化为:11x x 222++-<,解得x 1<, 1x 12∴<<,综上可得M (1,1)=-; (Ⅱ)当a ,b M ∈时,22(a 1)(b 1)0-->,即2222a b 1a b +>+,即2222a b 2ab 1a 2ab b +++>++, 即22(ab 1)(a b)+>+,即a b ab 1+<+.【提示】(Ⅰ)分当1x 2<-时,当11x 22-≤≤时,当1x 2>时三种情况,分别求解不等式,综合可得答案; (Ⅱ)当a ,b M ∈时,22(a 1)(b 1)0-->,即2222a b 1a b +>+,配方后,可证得结论. 【考点】绝对值不等式的解法。
唐山市2016届高三下学期二模 理综答案

唐山市2015—2016学年度高三年级第二次模拟考试理科综合能力测试参考答案及评分参考生物部分(共90分)A卷 1.D 2.B 3.A 4.C 5.C 6.DB卷 1.A 2.B 3.C 4.C 5.D 6.D参考答案1-6 DBACCD29.(共10分,每空2分)(1)主动运输(2)渗透吸水(3)叶绿素(部分)气孔关闭暗反应30.(共10分,每空2分)(1)两只正常小鼠连体共生(2)甲状腺低等于(3)反馈31.(共9分,除注明外,每空2分)(1)增长型(1分)不会(2)男性死亡率(3)B 出生率32.(共10分,每空2分)(1)F2中高茎:矮茎=3:1(2)10 1/7(3)全为矮茎紫花矮茎紫花:矮茎白花=9:739.(共15分,除注明外,每空2分)(1)大量元素、微量元素细胞分裂素(2)先升高后下降乙烯 2.0 抑制 6-BA 1.0mg/L+IAA0.5mg/L(3)微生物(1分)40.(共15分,除注明外,每空2分)(1)灭活的(仙台)病毒流动(2)人-人融合细胞鼠-鼠融合细胞(3)有丝分裂 106(4)甲、丙(5)B(1分)唐山市2015—2016学年度高三年级第二次模拟考试理科综合能力测试参考答案及评分参考(一)NaCl(1分);NO2-+H2O HNO2+OH-(2分)(二)(1)可以控制反应的发生与停止(1分)(2)Cu +4HNO3(浓)=Cu(NO3)2+2NO2↑+2H2O (2分)C(2分)防止水蒸气进入(1分)(3)① bc 2分)② 6H++2MnO4-+5NO2-=2Mn2++5NO3-+3H2O (2分)③ 69% (2分)27.(14分)(每空2分)(1)MnO2+2Fe2++4H+=Mn2++2Fe3++2H2O;(2)Fe(OH)3和过量的MnO2(3)使Cu2+完全沉淀为Cu(OH)2(4)Mn2+ + 2HCO3-= MnCO3↓+ CO2↑+H2O(5)加热浓缩,降温结晶(其它合理答案也给分)(6)7.0(1分)pH等于7.0时反应速率最快,且MnCO3产率最高(7)NH4Cl(1分)28.(14分)(除标明外每空2分)(1)乙(1分)(2)①0.015 mol·L-1 ·min-1 (1分)0.56 (或9/16)②bc ③降低(1分)< (1分)(3)2NH3(g)+CO2(g)=CO(NH2)2(s)+H2O(l) ΔH=–87.0 kJ·mol-1(4)2NH3+6OH-– 6e-=N2 + 6H2O 0.6 mol36.【化学——选修2化学与技术】(15分)(1)2Cl-+2H2O电解Cl2↑+H2↑+2OH-(2分); C (2分)(2)2FeTiO3+6C+7 Cl2高温2FeCl3+2TiCl4+6CO (2分);14 (2分)(3)CH 3OH+8OH -– 6e -=CO 32-+6H 2O (2分)(4)保护气作用 (1分)(5)①CO(g)+2H 2(g)=CH 3OH(l) ΔH =–128.6 kJ/mol (2分) ② 112 (2分) 37.【化学——选修3物质结构与性质】(15分)(除标注外其余每空2分) (1)[Ar]3d 64s 2 (1分) (2)3s 2 (1分)(3)①C<O<N ②4 ③sp 2杂化、 sp 3杂化 7 (4)MgO 晶体所含离子半径小,电荷数多,晶格能大 (1分)(5)正四面体 (1分) SO 3或者BF 3 (1分)(其它合理答案也给分) (6)38.【化学——选修5有机化学基础】(15分) (1)CH 3Cl(2分); 羧基;取代反应 (各1分)(2)4 (2分) (3)2HCl SO OCH 2CH 2CClClSOCl 2CH 2CH 2COOHCl(2分)(4) 6 (2分) (5)B (2分)(6)3COOCCH 2CH2CH 2CH 2COOCH 3CH OHHOOCCH 2CH 2CH 2CH 2COOHHOH 5C 2OOC)2CHCH 2CH 2CH(COOC 2H 5)2CH 2(COOC 2H 5)2ClCH 2CH 2Cl 2CH 2=CH 2(3分)唐山市2015—2016学年度高三年级第二次模拟考试理科综合能力测试参考答案及评分参考物理部分(110分)D 22. (1) 相同(2分) (2) L 2 (2分)h s kb4(2分) 23.(1)不可行,电流表量程太大不利于读数,只要合理可得分。
2017年唐山二模理科数学答案

P(X=3200)=()2=,P(X=500)=C××(×)=,
P(X=200)=C××(×)=,
P(X=-2800)=(×)2=.…10分
X的分布列为:
X
3800
3500
3200
500
200
-2800
P
E(X)=3800×+3500×+3200×+500×+200×+(-2800)×
=(1,0,2),=+λ=(1-3λ,2,0).
平面ABCD的一个法向量m=(0,0,1),
设平面PAM的法向量为n=(x,y,z),
由·n=0,·n=0得,
令x=2,得n=(2,3λ-1,-1).…8分
由题意可得,|cosm,n|===,
解得,λ=.…10分
所以四棱锥P-ABCM的体积VP-ABCM=S梯形ABCM×PE=.…12分
因为AB⊥EC,所以FM⊥AB.
由PE⊥平面ABCD,FM平面ABCD,
得PE⊥FM,又FM⊥AB,PE∩AB=E,
得FM⊥平面PAB,又FM平面PFM,
所以,平面PFM⊥平面PAB…5分
(Ⅱ)以E为坐标原点,EB,EC,EP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,则A(-1,0,0),P(0,0,2),C(0,2,0),D(-3,2,0),
①-②得,Tn=1+()1+()2+…+()n-1-n()n=)解:
(Ⅰ)记每台仪器不能出厂为事件A,则
P(A)=(1-)(1-)=,…2分
所以每台仪器能出厂的概率P()=1-=.…3分
(Ⅱ)生产一台仪器利润为1600元的概率P=(1-)×=.…6分
(Ⅲ)X可取3800,3500,3200,500,200,-2800.
2016年高考理科数学全国卷2(含详细答案)

数学试卷 第1页(共39页) 数学试卷 第2页(共39页) 数学试卷 第3页(共39页)绝密★启用前2014年普通高等学校招生全国统一考试(全国新课标卷2)理科数学使用地区:海南、宁夏、黑龙江、吉林、新疆、云南、内蒙古、青海、贵州、甘肃、西藏注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,{0}1,2M =,2{|320}N x x x =-+≤,则M N = ( )A .{1}B .{2}C .{0,1}D .{1,2}2.设复数1z ,2z 在复平面内的对应点关于虚轴对称,12i z =+,则12z z =( )A .5-B .5C .4i -+D .4i -- 3.设向量a ,b 满足|a +b||a -b|=则a b =( )A .1B .2C .3D .5 4.钝角三角形ABC △的面积是12,1AB =,BC =,则AC =( )A .5BC .2D .15.某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( )A .0.8B .0.75C .0.6D .0.456.如图,网格纸上正方形小格的边长为1(表示1 cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm ,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A .1727B .59 C .1027D .137.执行如图的程序框图,如果输入的x ,t 均为2,则输出的S =( )A .4B .5C .6D .7 8.设曲线ln(1)y ax x =-+在点(0,0)处的切线方程为2y x =,则a =( ) A .0 B .1 C .2D .39.设x ,y 满足约束条件70,310,350,x y x y x y +-⎧⎪-+⎨⎪--⎩≤≤≥则2z x y =-的最大值为( )A .10B .8C .3D .210.设F 为抛物线C :23y x =的焦点,过F 且倾斜角为30的直线交C 于A ,B 两点,O 为坐标原点,则OAB △的面积为 ( )ABC .6332D .94 11.直三棱柱111ABC A B C -中,90BCA ∠=,M ,N 分别是11A B ,11AC 的中点,1BC CA CC ==,则BM 与AN 所成角的余弦值为( )A .110B .25 CD12.设函数π()3sin x f x m,若存在()f x 的极值点0x 满足22200[()]x f x m +<,则m 的取值范围是( )A .(,6)(6,)-∞-+∞B .(,4)(4,)-∞-+∞C .(,2)(2,)-∞-+∞D .(,1)(1,)-∞-+∞第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13.10()x a +的展开式中,7x 的系数为15,则a = (用数字填写答案). 14.函数()sin(2)2sin cos()f x x x ϕϕϕ=+-+的最大值为 .15.已知偶函数()f x 在[0,)+∞上单调递减,(2)0f =,若(1)0f x ->,则x 的取值范围是 .16.设点0(,1)M x ,若在圆O :221x y +=上存在点N ,使得45OMN ∠=,则0x 的取值范围是 .三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知数列{}n a 满足11a =,131n n aa +=+.(Ⅰ)证明:1{}2n a +是等比数列,并求{}n a 的通项公式;(Ⅱ)证明:1211132n a a a ++⋅⋅⋅+<.-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页(共39页) 数学试卷 第5页(共39页) 数学试卷 第6页(共39页)18.(本小题满分12分)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点. (Ⅰ)证明:PB平面AEC ;(Ⅱ)设二面角D AE C --为60,1AP =,AD =求三棱锥E ACD -的体积.19.(本小题满分12分)某地区2007年至2013年农村居民家庭人均纯收入y (单位:千元)的数据如下表:(Ⅰ)求y 关于t 的线性回归方程;(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.附:回归直线的斜率和截距的最小二乘估计公式分别为:121()()ˆ()nii i ni i tt y y bt t ==--=-∑∑,ˆˆay bt =-.20.(本小题满分12分)设1F ,2F 分别是椭圆C :22221(0)x y a b a b+=>>的左、右焦点,M 是C 上一点且2MF 与x 轴垂直,直线1MF 与C 的另一个交点为N . (Ⅰ)若直线MN 的斜率为34,求C 的离心率;(Ⅱ)若直线MN 在y 轴上的截距为2,且1||5||MN F N =,求a ,b .21.(本小题满分12分)已知函数()e e 2x xf x x -=--. (Ⅰ)讨论()f x 的单调性;(Ⅱ)设()(2)4()g x f x bf x =-,当0x >时,()0g x >,求b 的最大值; (Ⅲ)已知1.4142 1.4143<,估计ln2的近似值(精确到0.001).请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时填写试题号.22.(本小题满分10分)选修4—1:几何证明选讲如图,P 是O 外一点,PA 是切线,A 为切点,割线PBC 与O 相交于点B ,C ,2PC PA =,D 为PC 的中点,AD 的延长线交O 于点E .证明:(Ⅰ)BE EC =; (Ⅱ)22AD DE PB =.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,半圆C 的极坐标方程为2cos ρθ=,π0,2θ⎡⎤∈⎢⎥⎣⎦.(Ⅰ)求C 的参数方程;(Ⅱ)设点D 在C 上,C 在D 处的切线与直线l :2y +垂直,根据(Ⅰ)中你得到的参数方程,确定D 的坐标.24.(本小题满分10分)选修4—5:不等式选讲设函数1()||(0)f x x x a a a =++->.(Ⅰ)证明:()2f x ≥;(Ⅱ)若(3)5f <,求a 的取值范围.3 / 132016年普通高等学校招生全国统一考试(全国新课标卷2)【解析】集合A B {0,1,2,3}=A B 的值.【解析】向量a(4,m),b(3,2)-,a b (4,m ∴+=-又(a b)b +⊥,12∴-【提示】求出向量a b +的坐标,根据向量垂直的充要条件,构造关于m 的方程,解得答案.【解析】输入的数学试卷第10页(共39页)数学试卷第11页(共39页)数学试卷第12页(共39页)5 / 13:πcos 4⎛- ⎝:π2cos 4⎛⎫-α= ⎝【提示】方法1:利用诱导公式化22π1n 1,π∴=解得e 2=.1数学试卷第16页(共39页)数学试卷第17页(共39页)数学试卷第18页(共39页)(Ⅰ)某保险的基本保费为7 / 13数学试卷 第22页(共39页)数学试卷 第23页(共39页) 数学试卷 第24页(共39页)(Ⅰ)ABCD 是菱形,AC BD ⊥,则,AC 6=,AEOD 1AO=,则, ,又OHEF H =,为坐标原点,建立如图所示空间直角坐标系,AB 5=,C(1,3,0),D (0,0,3)',AB (4,3,0)=,AD (1,3,3)'=-,AC (0,6,0)=,设平面的一个法向量为n (x,y,z)=11n AB 0n AD 0⎧=⎪⎨'=⎪⎩,得3y 03y 3z 0=⎧⎨+=3=,得n (3,4,5)∴=-同理可求得平面AD '的一个法向量n (3,01)=,的平面角为θ,122n n 9255210n n +==,∴二面角9 / 13为坐标原点,建立如图所示空间直角坐标系,由已知求得所用点的坐标,得到AB 、AD '、AC的一个法向量n 、n ,设二面角221234k +,由2212121k 413k 341kk =+⎛⎫++- ⎪⎝⎭,由AM =22212121k434k 3k k=+++, 整理可得2(k 1)(4k k 4)0--+=,由24k -212144134⎫=⎪+⎭轴对称,由MA ⊥数学试卷 第28页(共39页)数学试卷 第29页(共39页) 数学试卷 第30页(共39页)226t 3tk +,26t t 3k k+, AN ,可得2226t 6t 21k 1kt 3tk 3k k+=+++, 整理得26k 3kt -=,由椭圆的焦点在x 轴上,11 / 13 当2)(2,)-+∞2)和(2,-+∞x 2e f (0)=2>x 2e a 2⎫+⎪⎭a ∈x x 2(x)e 2-=的值域为t 2e a 2=-,只需t 2e 02≤0,可得t ∈t t 2e e 2t 2=+t e (t +22.【答案】(Ⅰ)DF CE ⊥,Rt DFC Rt EDC ∴△∽△,DF CF ED CD∴=, DE DG =,CD BC =,DF CF DG BC∴=,又GDF DEF BCF ∠=∠=∠, GDF BCF ∴△∽△,CFB DFG ∴∠=∠,GFB GFC CFB GFC DFG DFC 90∴∠=∠+∠=∠+∠=∠=,GFB GCB 180∴∠+∠=,B ∴,C ,G ,F 四点共圆;(Ⅱ)E 为AD 中点,A B 1=,1DG CG DE 2∴===,数学试卷 第34页(共39页)数学试卷 第35页(共39页) 数学试卷 第36页(共39页)∴在Rt DFC △中,1GF CD GC 2==,连接GB ,Rt BCG Rt BFG △≌△, BCG BCGF 111S 2S =21=222∴=⨯⨯⨯△四边形.【提示】(Ⅰ)证明B ,C ,G ,F 四点共圆可证明四边形BCGF 对角互补,由已知条件可知BCD 90∠=,因此问题可转化为证明GFB 90∠=;(Ⅱ)在Rt DFC △中,1GF CD GC ==,因此可得BCG BFG △≌△,则BCG BCGF S 2S =△四边形,据此解答.(Ⅰ)圆,22x ρ=+(Ⅱ)直线x α, l C (6,0)-,13 / 13 【考点】圆的标准方程,直线与圆相交的性质24.【答案】(Ⅰ)当1x 2<-时,不等式f (x)2<可化为:11x x 222---<,解得x 1>-, 11x 2∴-<<-, 当11x 22-≤≤时,不等式f (x)2<可化为:11x x 1222-+-=<,此时不等式恒成立, 11x 22∴-≤≤,当1x 2>时,不等式f (x)2<可化为:11x x 222++-<,解得x 1<, 1x 12∴<<,综上可得M (1,1)=-; (Ⅱ)当a ,b M ∈时,22(a 1)(b 1)0-->,即2222a b 1a b +>+,即2222a b 2ab 1a 2ab b +++>++, 即22(ab 1)(a b)+>+,即a b ab 1+<+.【提示】(Ⅰ)分当1x 2<-时,当11x 22-≤≤时,当1x 2>时三种情况,分别求解不等式,综合可得答案; (Ⅱ)当a ,b M ∈时,22(a 1)(b 1)0-->,即2222a b 1a b +>+,配方后,可证得结论. 【考点】绝对值不等式的解法。
河北省唐山市高三数学第二次模拟考试参考答案 理

理科数学参考答案一、选择题A 卷:BDCAB CBABD CA B 卷:DABCC ABDAD BD 二、填空题(13)54 (14)6 (15)100π (16)100 三、解答题 (17)解:由余弦定理得,a 2-b 2=c 2-2bc cos A ,将已知条件代入上式,得ac =3bc -c 2,则3b -c =a ,再由正弦定理,3sin B -sin C =sin π6.…4分又sin C =sin (5π6-B )= 1 2cos B +32sin B ,所以32sin B - 1 2cos B = 1 2,即sin (B - π 6)= 1 2. (10)分因为- π 6<B - π 6<5π6,所以B - π 6= π 6,即B = π3. (12)分(18)解:因为K 2=800(160×640×200×600≈16.667>10.828,所以能在犯错概率不超过0.001的前提下认为该校学生母语对于学习和掌握一门外语有关系. …5分(Ⅱ)由已知数据,语文、外语两科成绩至少一科为优秀的频率是 38.则X ~B (3, 3 8),P (X =k )=C k 8( 3 8)k ( 58)8-k,k =0,1,2,3.X 的分布列为…10分 E (X )=3× 3 8= 98. (12)分(19)解:(Ⅰ)连接B 1C 交BC 1于点P ,连接PQ .因为直线AB 1∥平面BC 1Q ,AB 1⊂平面AB 1C ,平面BC 1Q ∩平面AB 1C =PQ , 所以AB 1∥PQ .因为P 为B 1C 的中点,且AB 1∥PQ , 所以,Q 为AC 的中点. …4分(Ⅱ)如图建立空间直角坐标系.设AB =BC =a ,BB 1=b ,则 面BC 1C 的法向量为m =(1,0,0).B (0,0,0),C 1(0,a ,b ),Q (34a , 14a ,0), BC 1→=(0,a ,b ),QC 1→=(-34a , 3 4a ,b ). 因QC 1与面BC 1C 所成角的正弦值为24, 故|m ·QC 1→|___________|m |·|QC 1→|=34a ___________√________ 3 4a 2+b 2=24,解得b =3 2a .…8分设平面C 1BQ 的法向量n =(x ,y ,z ),则⎩⎨⎧n ·QC 1→=0,n ·BC 1→=0,即⎩⎪⎨⎪⎧-3 4ax + 3 4ay +32az =0,ay +32az =0,取n =(1,-3,2). (10)分所以有cos 〈m ,n 〉=m ·n |m |·|n |=24.故二面角Q -BC 1-C 的余弦值为24.…12分(20)解:(Ⅰ)f '(x )=ln x +1-ax .f (x )单调递减当且仅当f '(x )≤0,即∀x ∈(0,+∞), a ≥ln x +1x.①设g (x )=ln x +1x ,则g '(x )=-ln x x2.当x ∈(0,1)时,g '(x )>0,g (x )单调递增; 当x ∈(1,+∞)时,g '(x )<0,g (x )单调递减.所以g (x )≤g (1)=1,故a 的最小值为1. …5分 (Ⅱ)(1)由(Ⅰ)知,当a ≥1时,f (x )没有极值点.(2)当a ≤0时,f '(x )单调递增,f '(x )至多有一个零点,f (x )不可能有两个极值点.A…7分(3)当0<a <1时,设h (x )=ln x +1-ax ,则h '(x )= 1x-a .当x ∈(0, 1a)时,h '(x )>0,h (x )单调递增;当x ∈( 1a,+∞)时,h '(x )<0,h (x )单调递减.…9分因为f '( 1 a )=h ( 1 a )=ln 1 a >0,f '( 1 e )=h ( 1 e )=- ae<0,所以f (x )在区间( 1 e , 1a )有一极小值点x 1. (10)分由(Ⅰ)中的①式,有1≥ln x +1x ,即ln x ≤x -1,则ln 1 a ≤ 1a-1,故f '( 2 a 2)=h ( 2 a 2)=ln 2+2ln 1 a +1- 2 a ≤l n 2+2( 1 a -1)+1- 2a=ln 2-1<0.所以f (x )在区间( 1 a , 2a2)有一极大值点x 2.综上所述,a 的取值范围是(0,1). (12)分(21)解:(Ⅰ)依题意,曲线E 是以(0,m )为焦点,以y =-m 为准线的抛物线.曲线E 的方程为x 2=4my . …2分设动圆圆心为A (a ,a 24m ),则圆C 方程为(x -a )2+(y -a 24m )2=(a 24m +m )2,令y =0,得(x -a )2=a 22+m 2.当a =0时,圆C 被x 轴截得弦长取得最小值2m ,于是m = 12,故曲线E 的方程为x 2=2y . …5分(Ⅱ)假设存在题设的公共点B (b , 1 2b 2).圆C 方程为(x -a )2+(y - 1 2a 2)2=( 1 2a 2+ 1 2)2,将点B 坐标代入上式,并整理,得(b -a )2[1+ 1 4(a +b )2]= 1 4(a 2+1)2.① (7)分对y = 1 2x 2求导,得y '=x ,则曲线E 在点B 处的切线斜率为b .又直线AB 的斜率k = 1 2b 2- 1 2a 2b -a = 12(a +b ).由圆切线的性质,有 12(a +b )b =-1.② (8)分由①和②得b 2(b 2-8)=0.显然b ≠0,则b =±22. …9分 所以存在题设的公共点B ,其坐标为(±22,4),公切线方程为y =22(x -22)+4或y =-22(x +22)+4,即y =±22x -4. …12分(22)证明:(Ⅰ)连接BD ,因为D 为BC ︵的中点,所以BD =DC . 因为E 为BC 的中点,所以DE ⊥BC . 因为AC 为圆的直径,所以∠ABC =90︒,所以AB ∥DE . …5分(Ⅱ)因为D 为BC ︵的中点,所以∠BAD =∠DAC , 又∠BAD =∠DCB ,则∠DAC =∠DCB .又因为AD ⊥DC ,DE ⊥CE ,所以△DAC ∽△ECD .所以AC CD =ADCE,AD ·CD =AC ·CE ,2AD ·CD =AC ·2CE , 因此2AD ·CD =AC ·BC .…10分(23)解:(Ⅰ)将椭圆C 的参数方程化为普通方程,得x 24+y 23=1.a =2,b =3,c =1,则点F 坐标为(-1,0).l 是经过点(m ,0)的直线,故m =-1. …4分(Ⅱ)将l 的参数方程代入椭圆C 的普通方程,并整理,得(3cos 2α+4sin 2α)t 2-6t cos α-9=0.设点A ,B 在直线参数方程中对应的参数分别为t 1,t 2,则|FA |·|FB |=|t 1t 2|=93cos 2α+4sin 2α=93+sin 2α. 当sin α=0时,|FA |·|FB |取最大值3;当sin α=±1时,|FA |·|FB |取最小值 94. (10)分(24)解:(Ⅰ)当a =2时,f (x )=2(|x -2|-|x +4|)=⎩⎪⎨⎪⎧12,x <-4,-4x -4,-4≤x ≤2,-12,x >2.当x <-4时,不等式不成立;当-4≤x ≤2时,由-4x -4<2,得- 32<x ≤2;当x >2时,不等式必成立.综上,不等式f (x )<2的解集为{x |x >- 32}.…6分(Ⅱ)因为f (x )=|ax -4|-|ax +8|≤|(ax -4)-(ax +8)|=12, 当且仅当ax ≤-8时取等号. 所以f (x )的最大值为12.故k 的取值范围是[12,+∞).…10分。
(完整word版)2016年新课标全国卷2高考理科数学试题及答案
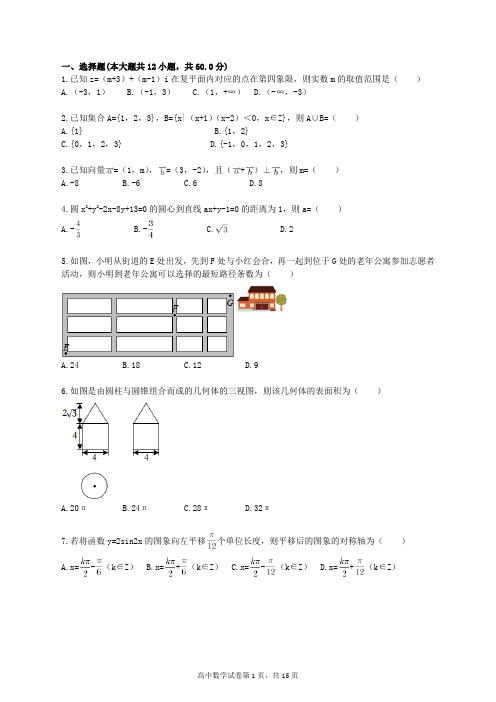
一、选择题(本大题共12小题,共60.0分)1.已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是()A.(-3,1)B.(-1,3)C.(1,+∞)D.(-∞,-3)2.已知集合A={1,2,3},B={x|(x+1)(x-2)<0,x∈Z},则A∪B=()A.{1}B.{1,2}C.{0,1,2,3}D.{-1,0,1,2,3}3.已知向量=(1,m),=(3,-2),且(+)⊥,则m=()A.-8B.-6C.6D.84.圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1,则a=()A.-B.-C.D.25.如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为()A.24B.18C.12D.96.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A.20πB.24πC.28πD.32π7.若将函数y=2sin2x的图象向左平移个单位长度,则平移后的图象的对称轴为()A.x=-(k∈Z)B.x=+(k∈Z)C.x=-(k∈Z)D.x=+(k∈Z)8.中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=()A.7B.12C.17D.349.若cos(-α)=,则sin2α=()A. B. C.- D.-10.从区间[0,1]随机抽取2n个数x1,x2,…,x n,y1,y2,…,y n构成n个数对(x1,y1),(x2,y2)…(x n,y n),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为()A. B. C. D.11.已知F1,F2是双曲线E:-=1的左、右焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=,则E的离心率为()A. B. C. D.212.已知函数f(x)(x∈R)满足f(-x)=2-f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(x m,y m),则(x i+y i)=()A.0B.mC.2mD.4m二、填空题(本大题共4小题,共20.0分)13.△ABC的内角A,B,C的对边分别为a,b,c,若cosA=,cosC=,a=1,则b= ______ .14.α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题是 ______ (填序号)15.有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 ______ .16.若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b= ______ .三、解答题(本大题共8小题,共94.0分)17.S n为等差数列{a n}的前n项和,且a1=1,S7=28,记b n=[lga n],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1.(Ⅰ)求b1,b11,b101;(Ⅱ)求数列{b n}的前1000项和.18.某保险的基本保费为a(单位:元),继续购买该保险的投保人成为续保人,续保人本年度的保费与其上年度出险次数的关联如下:上年度出险0 1 2 3 4 ≥5次数保费0.85a a 1.25a 1.5a 1.75a 2a设该险种一续保人一年内出险次数与相应概率如下:一年内出险0 1 2 3 4 ≥5次数概率0.30 0.15 0.20 0.20 0.10 0.05(Ⅰ)求一续保人本年度的保费高于基本保费的概率;(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;(Ⅲ)求续保人本年度的平均保费与基本保费的比值.19.如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF=,EF交于BD于点M,将△DEF沿EF折到△D′EF的位置,OD′=.(Ⅰ)证明:D′H⊥平面ABCD;(Ⅱ)求二面角B-D′A-C的正弦值.20.已知椭圆E:+=1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.(Ⅰ)当t=4,|AM|=|AN|时,求△AMN的面积;(Ⅱ)当2|AM|=|AN|时,求k的取值范围.21.(Ⅰ)讨论函数f(x)=e x的单调性,并证明当x>0时,(x-2)e x+x+2>0;(Ⅱ)证明:当a∈[0,1)时,函数g(x)=(x>0)有最小值.设g(x)的最小值为h(a),求函数h(a)的值域.22.如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.(Ⅰ)证明:B,C,G,F四点共圆;(Ⅱ)若AB=1,E为DA的中点,求四边形BCGF的面积.23.在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.(Ⅰ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;(Ⅱ)直线l的参数方程是(t为参数),l与C交与A,B两点,|AB|=,求l的斜率.24.已知函数f(x)=|x-|+|x+|,M为不等式f(x)<2的解集.(Ⅰ)求M;(Ⅱ)证明:当a,b∈M时,|a+b|<|1+ab|.2016年全国统一高考数学试卷(新课标Ⅱ)(理科)答案和解析【答案】1.A2.C3.D4.A5.B6.C7.B8.C9.D 10.C 11.A 12.B13.14.②③④15.1和316.1-ln217.解:(Ⅰ)S n为等差数列{a n}的前n项和,且a1=1,S7=28,7a4=28.可得a4=4,则公差d=1.a n=n,b n=[lgn],则b1=[lg1]=0,b11=[lg11]=1,b101=[lg101]=2.(Ⅱ)由(Ⅰ)可知:b1=b2=b3=…=b9=0,b10=b11=b12=…=b99=1.b100=b101=b102=b103=…=b999=2,b10,00=3.数列{b n}的前1000项和为:9×0+90×1+900×2+3=1893.18.解:(Ⅰ)∵某保险的基本保费为a(单位:元),上年度出险次数大于等于2时,续保人本年度的保费高于基本保费,∴由该险种一续保人一年内出险次数与相应概率统计表得:一续保人本年度的保费高于基本保费的概率:p1=1-0.30-0.15=0.55.(Ⅱ)设事件A表示“一续保人本年度的保费高于基本保费”,事件B表示“一续保人本年度的保费比基本保费高出60%”,由题意P(A)=0.55,P(AB)=0.10+0.05=0.15,由题意得若一续保人本年度的保费高于基本保费,则其保费比基本保费高出60%的概率:p2=P(B|A)===.(Ⅲ)由题意,续保人本年度的平均保费与基本保费的比值为:=1.23,∴续保人本年度的平均保费与基本保费的比值为1.23.19.(Ⅰ)证明:∵ABCD是菱形,∴AD=DC,又AE=CF=,∴,则EF∥AC,又由ABCD是菱形,得AC⊥BD,则EF⊥BD,∴EF⊥DH,则EF⊥D′H,∵AC=6,∴AO=3,又AB=5,AO⊥OB,∴OB=4,∴OH=,则DH=D′H=3,∴|OD′|2=|OH|2+|D′H|2,则D′H⊥OH,又OH∩EF=H,∴D′H⊥平面ABCD;(Ⅱ)解:以H为坐标原点,建立如图所示空间直角坐标系,∵AB=5,AC=6,∴B(5,0,0),C(1,3,0),D′(0,0,3),A(1,-3,0),,,设平面ABD′的一个法向量为,由,得,取x=3,得y=-4,z=5.∴.同理可求得平面A D′C的一个法向量,设二面角二面角B-D′A-C的平面角为θ,则|cosθ|=.∴二面角B-D′A-C的正弦值为sinθ=.20.解:(Ⅰ)t=4时,椭圆E的方程为+=1,A(-2,0),直线AM的方程为y=k(x+2),代入椭圆方程,整理可得(3+4k2)x2+16k2x+16k2-12=0,解得x=-2或x=-,则|AM|=•|2-|=•,由AN⊥AM,可得|AN|=•=•,由|AM|=|AN|,k>0,可得•=•,整理可得(k-1)(4k2-k+4)=0,由4k2-k+4=0无实根,可得k=1,即有△AMN的面积为|AM|2=(•)2=;(Ⅱ)直线AM的方程为y=k(x+),代入椭圆方程,可得(3+tk2)x2+2t k2x+t2k2-3t=0,解得x=-或x=-,即有|AM|=•|-|=•,|AN|═•=•,由2|AM|=|AN|,可得2•=•,整理得t=,由椭圆的焦点在x轴上,则t>3,即有>3,即有<0,可得<k<2,即k的取值范围是(,2).21.解:(1)证明:f(x)=f'(x)=e x()=∵当x∈(-∞,-2)∪(-2,+∞)时,f'(x)>0∴f(x)在(-∞,-2)和(-2,+∞)上单调递增∴x>0时,>f(0)=-1即(x-2)e x+x+2>0(2)g'(x)==a∈[0,1]由(1)知,当x>0时,f(x)=的值域为(-1,+∞),只有一解使得,t∈[0,2]当x∈(0,t)时,g'(x)<0,g(x)单调减;当x∈(t,+∞),g'(x)>0,g(x)单调增;h(a)===记k(t)=,在t∈(0,2]时,k'(t)=>0,故k(t)单调递增,所以h(a)=k(t)∈(,].22.(Ⅰ)证明:∵DF⊥CE,∴Rt△DFC∽Rt△EDC,∴=,∵DE=DG,CD=BC,∴=,又∵∠GDF=∠DEF=∠BCF,∴△GDF∽△BCF,∴∠CFB=∠DFG,∴∠GFB=∠GFC+∠CFB=∠GFC+∠DFG=∠DFC=90°,∴∠GFB+∠GCB=180°,∴B,C,G,F四点共圆.(Ⅱ)∵E为AD中点,AB=1,∴DG=CG=DE=,∴在Rt△DFC中,GF=CD=GC,连接GB,Rt△BCG≌Rt△BFG,∴S四边形BCGF=2S△BCG=2××1×=.23.解:(Ⅰ)∵圆C的方程为(x+6)2+y2=25,∴x2+y2+12x+11=0,∵ρ2=x2+y2,x=ρcosα,y=ρsinα,∴C的极坐标方程为ρ2+12ρcosα+11=0.(Ⅱ)∵直线l的参数方程是(t为参数),∴直线l的一般方程y=tanα•x,∵l与C交与A,B两点,|AB|=,圆C的圆心C(-6,0),半径r=5,∴圆心C(-6,0)到直线距离d==,解得tan2α=,∴tanα=±=±.∴l的斜率k=±.24.解:(I)当x<时,不等式f(x)<2可化为:-x-x-<2,解得:x>-1,∴-1<x<,当≤x≤时,不等式f(x)<2可化为:-x+x+=1<2,此时不等式恒成立,∴≤x≤,当x>时,不等式f(x)<2可化为:-+x+x+<2,解得:x<1,∴<x<1,综上可得:M=(-1,1);证明:(Ⅱ)当a,b∈M时,(a2-1)(b2-1)>0,即a2b2+1>a2+b2,即a2b2+1+2ab>a2+b2+2ab,即(ab+1)2>(a+b)2,即|a+b|<|1+ab|.【解析】1. 解:z=(m+3)+(m-1)i在复平面内对应的点在第四象限,可得:,解得-3<m<1.故选:A.利用复数对应点所在象限,列出不等式组求解即可.本题考查复数的几何意义,考查计算能力.2. 解:∵集合A={1,2,3},B={x|(x+1)(x-2)<0,x∈Z}={0,1},∴A∪B={0,1,2,3}.故选:C.先求出集合A,B,由此利用并集的定义能求出A∪B的值.本题考查并集的求法,是基础题,解题时要认真审题,注意并集定义的合理运用.3. 解:∵向量=(1,m),=(3,-2),∴+=(4,m-2),又∵(+)⊥,∴12-2(m-2)=0,解得:m=8,故选:D.求出向量+的坐标,根据向量垂直的充要条件,构造关于m的方程,解得答案.本题考查的知识点是向量垂直的充要条件,难度不大,属于基础题.4. 解:圆x2+y2-2x-8y+13=0的圆心坐标为:(1,4),故圆心到直线ax+y-1=0的距离d==1,解得:a=,故选:A.求出圆心坐标,代入点到直线距离方程,解得答案.本题考查的知识点是圆的一般方程,点到直线的距离公式,难度中档.5. 解:从E到F,每条东西向的街道被分成2段,每条南北向的街道被分成2段,从E到F最短的走法,无论怎样走,一定包括4段,其中2段方向相同,另2段方向相同,每种最短走法,即是从4段中选出2段走东向的,选出2段走北向的,故共有C42=6种走法.同理从F到G,最短的走法,有C31=3种走法.∴小明到老年公寓可以选择的最短路径条数为6×3=18种走法.故选:B.从E到F最短的走法,无论怎样走,一定包括4段,其中2段方向相同,另2段方向相同,每种最短走法,即是从4段中选出2段走东向的,选出2段走北向的,由组合数可得最短的走法,同理从F到G,最短的走法,有C31=3种走法,利用乘法原理可得结论.本题考查排列组合的简单应用,得出组成矩形的条件和最短走法是解决问题的关键,属基础题6. 解:由三视图知,空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是2,∴在轴截面中圆锥的母线长是=4,∴圆锥的侧面积是π×2×4=8π,下面是一个圆柱,圆柱的底面直径是4,圆柱的高是4,∴圆柱表现出来的表面积是π×22+2π×2×4=20π∴空间组合体的表面积是28π,故选:C.空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是2,在轴截面中圆锥的母线长使用勾股定理做出的,写出表面积,下面是一个圆柱,圆柱的底面直径是4,圆柱的高是4,做出圆柱的表面积,注意不包括重合的平面.本题考查由三视图求表面积,本题的图形结构比较简单,易错点可能是两个几何体重叠的部分忘记去掉,求表面积就有这样的弊端.7. 解:将函数y=2sin2x的图象向左平移个单位长度,得到y=2sin2(x+)=2sin(2x+),由2x+=kπ+(k∈Z)得:x=+(k∈Z),即平移后的图象的对称轴方程为x=+(k∈Z),故选:B.利用函数y= A sin(ωx+ φ)(A>0,ω>0)的图象的变换及正弦函数的对称性可得答案.本题考查函数yy= A sin(ωx+ φ)(A>0,ω>0)的图象的变换规律的应用及正弦函数的对称性质,属于中档题.8. 解:∵输入的x=2,n=2,当输入的a为2时,S=2,k=1,不满足退出循环的条件;当再次输入的a为2时,S=6,k=2,不满足退出循环的条件;当输入的a为5时,S=17,k=3,满足退出循环的条件;故输出的S值为17,故选:C根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,可得答案.本题考查的知识点是程序框图,当循环次数不多,或有规律可循时,可采用模拟程序法进行解答.9. 解:∵cos(-α)=,∴sin2α=cos(-2α)=cos2(-α)=2cos2(-α)-1=2×-1=-,故选:D.利用诱导公式化sin2α=cos(-2α),再利用二倍角的余弦可得答案.本题考查三角函数的恒等变换及化简求值,熟练掌握诱导公式化与二倍角的余弦是关键,属于中档题.10. 解:由题意,,∴π=.故选:C.以面积为测度,建立方程,即可求出圆周率π的近似值.古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积和体积的比值得到.11.解:设|MF1|=x,则|MF2|=2a+x,∵MF1与x轴垂直,∴(2a+x)2=x2+4c2,∴x=∵sin∠MF2F1=,∴3x=2a+x,∴x=a,∴=a,∴a=b,∴c=a,∴e==.故选:A.设|MF1|=x,则|MF2|=2a+x,利用勾股定理,求出x=,利用sin∠MF2F1=,求得x=a,可得=a,求出a=b,即可得出结论.本题考查双曲线的定义与方程,考查双曲线的性质,考查学生分析解决问题的能力,比较基础.12. 解:函数f(x)(x∈R)满足f(-x)=2-f(x),即为f(x)+f(-x)=2,可得f(x)关于点(0,1)对称,函数y=,即y=1+的图象关于点(0,1)对称,即有(x1,y1)为交点,即有(-x1,2-y1)也为交点,(x2,y2)为交点,即有(-x2,2-y2)也为交点,…则有(x i+y i)=(x1+y1)+(x2+y2)+…+(x m+y m)=[(x1+y1)+(-x1+2-y1)+(x2+y2)+(-x2+2-y2)+…+(x m+y m)+(-x m+2-y m)]=m.故选B.由条件可得f(x)+f(-x)=2,即有f(x)关于点(0,1)对称,又函数y=,即y=1+的图象关于点(0,1)对称,即有(x1,y1)为交点,即有(-x1,2-y1)也为交点,计算即可得到所求和.本题考查抽象函数的运用:求和,考查函数的对称性的运用,以及化简整理的运算能力,属于中档题.13. 解:由cosA=,cosC=,可得sinA===,sinC===,sinB=sin(A+C)=sinAcosC+cosAsinC=×+×=,由正弦定理可得b===.故答案为:.运用同角的平方关系可得sinA,sinC,再由诱导公式和两角和的正弦公式,可得sinB,运用正弦定理可得b=,代入计算即可得到所求值.本题考查正弦定理的运用,同时考查两角和的正弦公式和诱导公式,以及同角的平方关系的运用,考查运算能力,属于中档题.14. 解:①如果m⊥n,m⊥α,n∥β,那么α∥β,故错误;②如果n∥α,则存在直线l⊂α,使n∥l,由m⊥α,可得m⊥l,那么m⊥n.故正确;③如果α∥β,m⊂α,那么m与β无公共点,则m∥β.故正确④如果m∥n,α∥β,那么m,n与α所成的角和m,n与β所成的角均相等.故正确;故答案为:②③④根据空间直线与平面的位置关系的判定方法及几何特征,分析判断各个结论的真假,可得答案.本题以命题的真假判断与应用为载体,考查了空间直线与平面的位置关系,难度中档.15. 解:根据丙的说法知,丙的卡片上写着1和2,或1和3;(1)若丙的卡片上写着1和2,根据乙的说法知,乙的卡片上写着2和3;∴根据甲的说法知,甲的卡片上写着1和3;(2)若丙的卡片上写着1和3,根据乙的说法知,乙的卡片上写着2和3;又甲说,“我与乙的卡片上相同的数字不是2”;∴甲的卡片上写的数字不是1和2,这与已知矛盾;∴甲的卡片上的数字是1和3.故答案为:1和3.可先根据丙的说法推出丙的卡片上写着1和2,或1和3,分别讨论这两种情况,根据甲和乙的说法可分别推出甲和乙卡片上的数字,这样便可判断出甲卡片上的数字是多少.考查进行简单的合情推理的能力,以及分类讨论得到解题思想,做这类题注意找出解题的突破口.16. 解:设y=kx+b与y=lnx+2和y=ln(x+1)的切点分别为(x1,kx1+b)、(x2,kx2+b);由导数的几何意义可得k==,得x1=x2+1再由切点也在各自的曲线上,可得联立上述式子解得;从而kx1+b=lnx1+2得出b=1-ln2.先设切点,然后利用切点来寻找切线斜率的联系,以及对应的函数值,综合联立求解即可本题考查了导数的几何意义,体现了方程思想,对学生综合计算能力有一定要求,中档题17.(Ⅰ)利用已知条件求出等差数列的公差,求出通项公式,然后求解b1,b11,b101;(Ⅱ)找出数列的规律,然后求数列{b n}的前1000项和.本题考查数列的性质,数列求和,考查分析问题解决问题的能力,以及计算能力.18.(Ⅰ)上年度出险次数大于等于2时,续保人本年度的保费高于基本保费,由此利用该险种一续保人一年内出险次数与相应概率统计表根据对立事件概率计算公式能求出一续保人本年度的保费高于基本保费的概率.(Ⅱ)设事件A表示“一续保人本年度的保费高于基本保费”,事件B表示“一续保人本年度的保费比基本保费高出60%”,由题意求出P(A),P(AB),由此利用条件概率能求出若一续保人本年度的保费高于基本保费,则其保费比基本保费高出60%的概率.(Ⅲ)由题意,能求出续保人本年度的平均保费与基本保费的比值.本题考查概率的求法,是中档题,解题时要认真审题,注意对立事件概率计算公式、条件概率计算公式的合理运用.19.(Ⅰ)由底面ABCD为菱形,可得AD=CD,结合AE=CF可得EF∥AC,再由ABCD是菱形,得AC⊥BD,进一步得到EF⊥BD,由EF⊥DH,可得E F⊥D′H,然后求解直角三角形得D′H⊥OH,再由线面垂直的判定得D′H⊥平面ABCD;(Ⅱ)以H为坐标原点,建立如图所示空间直角坐标系,由已知求得所用点的坐标,得到的坐标,分别求出平面ABD′与平面AD′C的一个法向量,设二面角二面角B-D′A-C的平面角为θ,求出|cosθ|.则二面角B-D′A-C的正弦值可求.本题考查线面垂直的判定,考查了二面角的平面角的求法,训练了利用平面的法向量求解二面角问题,体现了数学转化思想方法,是中档题.20.(Ⅰ)求出t=4时,椭圆方程和顶点A,设出直线AM的方程,代入椭圆方程,求交点M,运用弦长公式求得|AM|,由垂直的条件可得|AN|,再由|AM|=|AN|,解得k=1,运用三角形的面积公式可得△AMN的面积;(Ⅱ)直线AM的方程为y=k(x+),代入椭圆方程,求得交点M,可得|AM|,|AN|,再由2|AM|=|AN|,求得t,再由椭圆的性质可得t>3,解不等式即可得到所求范围.本题考查椭圆的方程的运用,考查直线方程和椭圆方程联立,求交点,以及弦长公式的运用,考查化简整理的运算能力,属于中档题.21.从导数作为切入点探求函数的单调性,通过函数单调性来求得函数的值域,利用复合函数的求导公式进行求导,然后逐步分析即可该题考查了导数在函数单调性上的应用,重点是掌握复合函数的求导,以及导数代表的意义,计算量较大,中档题.22.(Ⅰ)证明B,C,G,F四点共圆可证明四边形BCGF对角互补,由已知条件可知∠BCD=90°,因此问题可转化为证明∠GFB=90°;(Ⅱ)在Rt△DFC中,GF=CD=GC,因此可得△GFB≌△GCB,则S四边形BCGF=2S△BCG,据此解答.本题考查四点共圆的判断,主要根据对角互补进行判断,注意三角形相似和全等性质的应用.23.(Ⅰ)把圆C的标准方程化为一般方程,由此利用ρ2=x2+y2,x=ρcosα,y=ρsinα,能求出圆C 的极坐标方程.(Ⅱ)由直线l的参数方程求出直线l的一般方程,再求出圆心到直线距离,由此能求出直线l的斜率.本题考查圆的极坐标方程的求法,考查直线的斜率的求法,是中档题,解题时要认真审题,注意点到直线公式、圆的性质的合理运用.24.(I)分当x<时,当≤x≤时,当x>时三种情况,分别求解不等式,综合可得答案;(Ⅱ)当a,b∈M时,(a2-1)(b2-1)>0,即a2b2+1>a2+b2,配方后,可证得结论.本题考查的知识点是绝对值不等式的解法,不等式的证明,难度中档.。
河北省唐山市开滦二中2016届高三12月月考数学(理)试卷带答案

唐山市开滦二中2015年高三年级12月月考理 科 数 学 试 卷一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项符合题目要求.)1.已知集合{}{}02,1log 22<-+=<=x x x B x x A ,则B A ( )A .()2,∞-B .()1,0C .()2,2-D .()1,∞-2.若复数z 满足)1(21i z i +-=⋅,则z 的共轭复数的虚部是( ) A .21- B .21 C.i 21- D .i 21 3.已知()()062:,11:<--+<<-x x q m x m p ,且q 是p 的必要不充分条件,则m 的取值范围是( )A .35m << B .35m ≤≤ C .53m m ><或 D .53m m ≥≤或4. 执行如图所示的程序框图,若输出的结果是8,则输入的数是( )A.2或22B.22或22-C.2-或22-D.2或22-5.设变量y x ,满足约束条件00220x x y x y ≥⎧⎪-≥⎨⎪--≤⎩则y x z 23-=的最大值为( )A .6B .4C .2D .09.设四边形ABCD为平行四边形,46==.若点N M ,满足NC DN MC BM 2,3==,则⋅=().A. 6 B. 9 C. 15 D. 20( ) A.π16B.π12C.π8D.π411.已知A 是双曲线22221(0,0)x y a b a b-=>>的左顶点,12,F F 分别为双曲线的左、右焦点,P 为双曲线上一点,G 是12PF F ∆的重心,若1GA PF λ= ,则双曲线的离心率为( )24二、填空题:(本大题共4小题,每小题5分,共20分.把答案填写在答题纸上.)三、解答题:(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)设数列{}n a 的前n 项和为n S ,11=a ,0>n a ,()()*∈+=N n a S n n 214.⑴求数列{}n a 的通项公式;⑵求数列⎭⎬⎫⎩⎨⎧n na 2的前n 项和n T . 18.(本小题满分12分)由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检査得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:若视力测试结果不低于5.0,则称为“好视力”.⑴求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;⑵以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记ξ表示抽到“好视力”学生的人数,求ξ的分布列及数学期望.20.(本小题满分12分)已知椭圆()01:2222>>=+b a b y a x C 的离心率为22,以原点为圆心,椭圆的短半轴长为半径的圆与直线02=+-y x 相切.⑴求椭圆C 的方程;⑵若过点()0,2M 的直线与椭圆C 相交于两点B A ,,设P 为椭圆上一点,且满足t =+(O 为坐标原点)352<-时,求实数t 取值范围 21.(本小题满分12分)已知函数.1,ln )1(21)(2>-+-=a x a ax x x f ⑴讨论函数()f x 的单调性; ⑵证明:若5<a ,则对任意21,x x ∈(0,)+∞,21x x ≠,有()()12121->--x x x f x f . 请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.答题时在答题纸上注明所选题目的题号.22.(本小题满分10分) 选修4—1;几何证明选讲.已知AB 为半圆O 的直径,C AB ,4=为半圆上一点,过点C 作半圆的切线CD ,过点A 作CD AD ⊥于D ,交圆于点1,=DE E . ⑴求证:AC 平分BAD ∠;⑵求BC 的长.23.(本小题满分10分)选修4—4;坐标系与参数方程.⑴求曲线的直角坐标方程;⑵求直线被曲线所截得的弦长.24.(本小题满分10分)选修4—5;不等式选讲.已知0,0>>b a ,且2922=+b a ,若m b a ≤+恒成立, ⑴求m 的最小值;⑵若b a x x +≥+-12对任意的b a ,恒成立,求实数x 的取值范围.唐山市开滦二中2015年高三年级12月月考理科数学参考答案一、二.选择题、填空题:CABDB ACDBC BA (13)97-,(14)53,(15(16)22或4 三、解答题:17. 解⑴(),142+=n n a S ()().214211≥+=∴--n a S n n ()()()2114212≥+-+=∴-n a a a n n n , ()()()20211≥=--+∴--n a a a a n n n n ,………2分0>n a ,()201≥>+∴-n a a n n , ()221≥=-∴-n a a n n ,∴数列{}n a 是以1为首项,2为公差的等差数列,………4分 ()12121-=-+=∴n n a n .………………6分 ⑵,2122n n n n a -=n n n T 21225232132-++++=∴ ,① 132212232232121+-+-+++=∴n n n n n T ,② 由①-②得1113221221121412212122222222121+++--⎪⎪⎪⎪⎭⎫ ⎝⎛--+=--+++=n n n n n n n T 1123223232121+++-=+-+=n n n n ,………………10分 .323n n n T +-=∴………12分19.⑴证明: 菱形ABCD 中,=∠=60,ABC BC AB ,ABC ∆∴是等边三角形, E 是BC 的中点,BC AE ⊥∴,AD BC // ,AD AE ⊥∴, ⊥PA 平面ABCD ,⊂AE 平面ABCD ,AE PA ⊥∴,A AD PA = ,⊥∴AE 平面PAD ,PD AE ⊥∴. ………………5分 ⑵解:由⑴⊥EA 平面PAD 于点A , EH 平面H PAD =,AH ∴是EH 在平面PAD 的射影,AHE ∠∴是EH 与平面PAD 所成的角AH AE AHE =∠∴tan ,且AB AE 23=∴当AH 最短即PD AH ⊥时,26t a n =∠A H E ,此时AB AH 22=,AB PA =∴,…………7分 以点A 为坐标原点,分别以直线AP AD AE ,,为x 轴,y 轴,z 轴建立空间直角坐标系xyz A -,令2=AB ,则()()()⎪⎪⎭⎫ ⎝⎛1,21,23,0,1,3,0,0,3,0,0,0F C E A ,()0,0,3,1,21,23=⎪⎪⎭⎫ ⎝⎛=∴AE AF ,设平面AEF 的法向量为()z y x n ,,1=, 则⎩⎨⎧⊥⊥AE n AF n 11,⎪⎩⎪⎨⎧==⋅=++=⋅∴030212311x n z y x AF n ,令2=y ,解得0,1=-=x z , ∴平面AEF 的一个法向量为()1,2,01-=n ,同理平面ACF 的一个法向量为()0,3,12-=n ,…………9分515311432-=+⋅+-=∴,…………11分 ∴二面角C AF E --的余弦值为515……………………12分.20解:(1)由题意知:所以又故所求椭圆的方程为 ……………………………… 4分(2) 由题意知直线的斜率存在.设其方程为:, 由得.,设,,,∴,. (6分) ∵,∴,,.∵点在椭圆上,∴,∴( 8分) ∵<,∴,∴即 ∴ 得: ∴ ………10分又∴或 ,故实数t 的取值范围是…12分 21⑴解:函数()x f 的定义域为()+∞,0,()()[]()xx a x x a a x x f 111'---=-+-=, ①当21<<a 时,110<-<a , 由()0'<x f ,解得11<<-x a ,由()0'>x f ,解得10-<<a x 或1>x ;②当2=a 时,11=-a ,()0'≥x f 在()+∞,0恒成立;③当2>a 时,11>-a ,由()0'<x f ,解得11-<<a x ,由()0'>x f ,解得10<<x 或1->a x .……… 4分 综上可得,当21<<a 时,函数()x f 在()1,1-a 上单调递减,在()1,0-a ,()+∞,1单调递增;当2=a 时,函数()x f 在()+∞,0单调递增;当2>a 时,函数()x f 在()1,1-a 上单调递减,在()1,0,()+∞-,1a 单调递增……………………… 5分()()()()051141,512<--=---=∆∴<<a a a a a , ()0'>∴x F 在()+∞,0恒成立,()x F ∴在()+∞,0上单调递增,………………… 9分①当021>>x x 时,()()21x F x F >,即()()2211x x f x x f +>+,()()12121->--∴x x x f x f ; ②当210x x <<时,()()21x F x F <,即()()2211x x f x x f +<+,()()12121->--∴x x x f x f ; 综上可得,若51<<a ,则对任意()+∞∈,0,21x x ,21x x ≠,有()()12121->--x x x f x f .… 12分 22⑴证明:连结AC ,OCA OAC OC OA ∠=∠∴=, 2分⑵要使恒成立,须且只须或或或…………。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
…12 分
高三理科数学答案第 1 页
共4页
(19)解: (Ⅰ) ∵直角三角形 ABC 中, ∠BAC=60°, AC=4, 1 ∴AB=8,AF= AB=2,由余弦定理得 CF=2 3且 4 CF⊥AB.
z
E
D ∵AD⊥平面 ABC,CF平面 ABC,∴AD⊥CF, C M 又 AD∩AB=A,∴CF⊥平面 DABE, B y ∴CF⊥DF,CF⊥EF. ∴∠DFE 为二面角 D-CF-E 的平面角. F A 又 AF=2,AD=3,BE=4,BF=6, x 故 Rt△ADF∽Rt△BFE.∴∠ADF=∠BFE, ∴∠AFD+∠BFE=∠AFD+∠ADF=90º , ∴∠DFE=90º ,D-CF-E 为直二面角. ∴平面 CDF⊥平面 CEF. …6 分 (Ⅱ)以 C 为坐标原点,建立如图所示的空间直角坐标系 C-xyz,则 C(0,0,0), B(0,4 3,0),E(0,4 3,4),F(3, 3,0),M(0,a,0), (0≤a≤4 3)
唐山市 2015—2016 学年度高三年级第二次模拟考试
理科数学参考答案
一、选择题 A 卷:BCCAD BACAB DC B 卷:BCBAD BADAB CC 二、填空题 5 (13) (14)14 2
(15)36π
(16)(-∞,2]
三、解答题 (17)解: (Ⅰ)由题设,2Sn=(n+1)2an-n2an+1,2Sn+1=(n+2)2an+1-(n+1)2an+2, 两式相减得(n+1)2(an+2+an)=2(n+1)2an+1, 由于(n+1)2>0,所以 an+2+an=2an+1,即{an}为等差数列. …4 分 由于 2S1=4a1-a2=2a1,可得 a2=2a1=4,所以{an}的公差为 2, 故 an=2n. …6 分 a a + (Ⅱ)由题设,bnbn+1=λ·2 n,bn+1bn+2=λ·2 n 1, 两式相除可得 bn+2=4bn, 即{b2n}和{b2n-1}都是以 4 为公比的等比数列. …8 分 a1 因 b1b2=λ·2 =4λ,b1=1,所以 b2=4λ, 1 2 由 b3=4b1=4 及 b2 =b1b3 得 4λ2=1,又 λ>0,所以 λ= . 2 - - - - 所以 b2n=2·4 n 1=22n 1,b2n-1=22n 2,即 bn=2n 1,则 bn+1=2bn. 1 因此存在 λ= ,使得数列{bn}为等比数列. …12 分 2 (18)解: (Ⅰ)由已知:x =6,y =10, ∑ xiyi=242, ∑ x2 i =220,
y
{
}
-1 -2
O
1 3
x
因为 m<0, 1 所以- |x+1|≥|x-1|-2, m 在同一直角坐标系中画出 1 y=|x-1|-2 及 y=- |x+1|的图像, m 1 根据图像性质可得- ≥1,即-1≤m<0, m 故 m 的最小值为-1.
…10 分
高三理科数学答案第 4 页
共4页
∴→ CF =(3, 3,0),→ EM =(0,a-4 3,-4), 1 ∵异面直线 CF 与 EM 所成角的余弦值为 , 4 |→ CF ·→ EM| 3(4 3-a) 1 → → ∴|cos CF , EM | = = = , 2 4 → → | CF || EM | 2 3· (4 3-a) +16 解得 a= (20)解: 8 3 8 3 ,故 CM= . 3 3 …12 分
i=1 i=1 5 5
^ b=
i=1 n
-∑ xiyi-nx y
i=1
n
∑
-2பைடு நூலகம்x2 i -nx
=-1.45,a ˆ =y -^ bx =18.7;
…6 分
所以回归直线的方程为^ y =-1.45x+18.7 (Ⅱ)z=y-w=-1.45x+18.7-(0.05x2-1.75x+17.2) =-0.05x2+0.3x+1.5 =-0.05(x-3)2+1.95 所以预测当 x=3 时,销售利润 z 取得最大值.
(
) (
)
(
)
|
|
|
| |
|
(
)
高三理科数学答案第 2 页
共4页
法二: x2 x2 (x0-x1)2 x0 x0 1 1 直线 BD 的方程为 y= (x-x1)+ ,yM= (x0-x1)+ ,得 yM-y0= . 2 4 2 4 4 3 |x0-x1| 则 S△ABD=2S△ABM= , 4 设直线 AB:y=kx+1,代入 x2=4y 得 x2-4kx-4=0, 则|x0-x1|=4 k2+1≥4,故 S△ABD≥16(k=0 时等号成立) . (21)解: x0ln x0+a=x0, (Ⅰ)f (x)=ln x+1,设切点为(x0,x0ln x0+a),得 ln x0+1=1, 解得 x0=1,a=1. …4 分 - - (Ⅱ)证明:xex 1[f (x)-2]+f (x)≥0xex 1(xln x-1)+(xln x+1)≥0, - - - - xex 1(xln x+1)+(xln x+1)≥2xex 1(xex 1+1)(xln x+1)≥2xex 1 1 - (ln x+ )(x+e1 x)≥2. …6 分 x 1 1 1 - - 设 g (x)=ln x+ ,h (x)=x+e1 x,则 g (x)= - 2 ,h (x)=1-e1 x, x x x 所以 g (x)在(0,1)上单调递减,在(1,+∞)上单调递增, 即 g (x)的最小值为 g (1)=1; …9 分 h (x)在(0,1)上单调递减,在(1,+∞)上单调递增, 即 h (x)的最小值为 h (1)=2, …11 分 1 1-x 所以(ln x+ )(x+e )≥2, (x=1 时等号成立) x 故原不等式成立. …12 分 (22)解: (Ⅰ)因为 AE 与圆 O 相切于点 A,所以∠CAE=∠CBA; 因为四边形 ABCD 内接于圆 O,所以∠CBA=∠ADE; 又已知∠ADE=∠BDC,所以∠BDC=∠CAE, 故 A,E,D,F 四点共圆. …5 分 (Ⅱ)由(Ⅰ)得∠ADE=∠AFE=∠BDC, 又∠BDC=∠BAC(同弧所对的圆周角相等) , 所以∠AFE=∠BAC,故 AB∥EF. …10 分 (23)解: x=1+cos φ, (Ⅰ)由 (φ 为参数,0<φ<π)得(x-1)2+y2=1(0<y≤1) , y=sin φ. π 所以曲线 C1 的极坐标方程为 ρ=2cos θ(0<θ < ) . …5 分 2 π (Ⅱ)由题意可设 A(ρ1,θ),C(2,θ)(0<θ < ) , 2 则|AC|=2-ρ1=2-2cos θ,|BC|=2+ρ1=2+2cos θ, 所以|AC|·|BC|=4sin2θ∈(0,4). …10 分
高三理科数学答案第 3 页
共4页
(24)解:
1-3x, x<-1, (Ⅰ)当 m=2 时,f (x)=3-x, -1≤x≤1, 3x-1, x>1. 5 由 f (x)的单调性及 f ( )=f (-1)=4, 3 5 得 f (x)<4 的解集为 x|-1<x< . 3 …5 分 (Ⅱ)由 f (x)≥2m 得|x+1|≥m (2-|x-1|),
2 x2 x2 x2 0 1 (Ⅰ)设 A x0, ,B x1, ,D x2, . (x0>0) 4 4 4 x1+x2 x1+x2 x x0 x0 x1+x2 由 y' = 得 kBD= ,又 kBD= ,所以 = ,即 x0= =xM. 2 2 4 2 4 2 故 AM 与 y 轴平行. …4 分 (Ⅱ)法一: 由 A,B,F 共线可得 kAF=kBF,所以(x0x1+4)(x0-x1)=0, 4 因 x0-x1≠0,所以 x0x1=-4,即 x1=- . …6 分 x0 2 2 x1 x0x 4 x0 4 x0 直线 BD 的方程为 y= (x-x1)+ = + 2+2,所以 yM= + 2+2. …8 分 2 4 2 x0 2 x0 2 x2 x 4 0 0 由(Ⅰ)得 S△ABD=2S△ABM= + 2+2- ×|x1-x0| 2 x0 4 x2 4 4 1 4 3 0 = + 2+2 × x0+ = x0+ ≥16, 4 x0 x0 4 x0 4 当且仅当 x0= 即 x0=2 时等号成立,故 S 的最小值为 16. …12 分 x0
