最新2019年七年级下册数学单元测试题-三角形的初步认识测试题(含标准答案)
最新版精选2019年七年级下册数学单元测试题-三角形的初步认识考核题完整版(含参考答案)

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1.如图,CD 是△ABC 的中线,DE 是△ACD 的中线,BF 是△ADE 的中线,若△AEF 的面积是 1cm 2,则△ABC 的面积是( )A . 4cm 2B .5 cm 2C . 6 cm 2D .8 cm 2答案:D2.如图,AD 是△ABC 的角平分线,DE 是△ABD 的高,DF 是△ACD 的高,则( )A . ∠B=∠CB . ∠EDB=∠FDC C .∠ADE=∠ADFD . ∠ADB=∠ADC答案:C3.若AD 是△ABC 的中线,则下列结论中,错误的是( )A .AD 平分∠BACB .BD =DC C .AD 平分BC D .BC =2DC 答案:A4. 如图,点P 是∠BAC 的平分线AD 上一点,PE ⊥AC 于点E .已知PE =3,则点P 到AB 的距离是( )A .3B .4C .5D .6答案:A5.如图,直线123,,l l l 表示三条相互交叉的公路,现要建造一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A .一处B .两处C .三处D .四处答案:D6.如图所示,A ,B 是数轴上的两点,C 是AB 的中点,则0C 等于( )A.34OB B.1()2OB OA-C.1()2OA OB+D.以上都不对答案:C7.下列说法中,正确的个数有()①延长直线AB;②取线段AB的中点C;③以0为圆心作弧;④已知∠α,作∠α的余角的一半.A.0个B.1个C.2个D.3个答案:C8.如图所示,已知∠A=∠D,∠l=∠2,那么,要得到△ABC≌△DEF,还应给出的条件是()A.∠E=∠B B.ED=BC C.AB=EF D.AF=CD答案:D9.如图所示,已知△ABC≌△DCB,那么下列结论中正确的是()A.∠ABC=∠CDB,∠BAC=∠DCB,∠ACB=∠DBCB.∠ABC=∠DCB,∠BAC=∠CDB,∠ACB=∠ABDC.∠ABC=∠DCB,∠BAC=∠CDB,∠ACB=∠DBCD.∠ABC=∠DBC,∠BAC=∠CDB,∠ACB=∠ACD答案:C10.如图所示,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是()A 10° B.20° C.30° D.40°答案:B11.如图所示是跷跷板的示意图,支柱0C与地面垂直,点0是横板AB的中点,AB可以绕着点0上下转动,当A端落地时,∠0AC=20°.跷跷板上下可转动的最大角度(即∠A′OA)是()A.800 B.60°C.40°D.20°答案:C12.下列条件中不能判定两个直角三角形全等的是()A.两条直角边对应相等B.直角边和斜边对应相等C.两个锐角对应相等D.斜边和锐角对应相等答案:C二、填空题13.如图,AC、BD相交于点O,∠A=∠D,,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是 .解析:AO = DO或AB = DC或BO=CO14.如图所示,已知∠C=∠B,AC=AB,请写出一个与点D有关的正确结论:.解析:AD=AE等15.仔细观察下图:(1)图中的△ABC与△A′B′C′全等吗? .(2)由图中的信息,你可以得到的重要结论是:.解析:(1)不全等;(2)有两边及其中一边的对角对应相等的两个三角形不一定全等16.如图所示,△ABC 中,BC=16 cm,AB,AC边上的中垂线分别交BC于E,F,则△AEF的周长是 cm.解析:1617.如图,若把△ABC绕A点旋转一定角度就得到△ADE,那么对应边AB= ,AC= ,BC= ;对应角∠CAB= ,∠B= ,∠C= .解析:AD,AE,DE,∠EAD,∠D,∠E18.如图所示,已知点D,E,F分别是BC,AC,DC的中点,△EFC的面积为6 cm2,则△ABC的面积为.解析:48cm219.如果三角形的三个内角都相等,那么这个三角形是三角形.解析:等边20.在△ABC中,(1)∠C=85°,∠A=25°,则∠B= ;(2)∠A+∠B=90°,则∠C= ;(3)∠A=∠B=∠C,则∠A= ;(4)∠A=∠B,∠C=80°,则∠B= .解析:(1)70°;(2)90°;(3)60°;(4)50°21.等腰三角形两边长分别是7cm和3 cm,则第三边长是.解析:7 cm三、解答题22.求各边长互不相等且都是整数、周长为24的三角形共有多少个?解析:⎪⎩⎪⎨⎧===,7,8,9c b a ⎪⎩⎪⎨⎧===,6,8,10c b a ⎪⎩⎪⎨⎧===,6,7,11c b a ⎪⎩⎪⎨⎧===,5,9,10c b a ⎪⎩⎪⎨⎧===,5,8,11c b a ⎪⎩⎪⎨⎧===,4,9,11c b a ⎪⎩⎪⎨⎧===.3,10,11c b a由此知符合条件的三角形一共有7个.23.如图,在△ABC 中,已知∠ABC=66°,∠ACB=54°,BE 是AC 上的高,CF 是AB 上的高,H 是BE 和CF 的交点,求∠ABE 、∠ACF 和∠BHC 的度数.解析:∠ABE=30°,∠ACF=30°, ∠BHC=120°.24.如图,四边形ABCD 是一防洪堤坝的横截面,AE ⊥CD ,BF ⊥CD ,且AE=BF ,∠D=∠C ,问:AD 与BC 是否相等?说明你的理由.解: AE ⊥CD∴∠AED=BF ⊥CD∴∠BFC=∴ =在△ADE 和△BCF 中,()()()⎪⎩⎪⎨⎧=∠=∠=∠_____________________________________________________________________AE AED D ∴△ADE ≌△BCF( )∴AD=BC( )90 º ,90 º,∠AED ,∠BFC ,∠C ,已知,BFC ,已证,BF , 已知,AAS ,全等三角形的对应边相等.解析:25.如图所示,以Rt△ABC的两直角边AB,BC为边向外作正△ABE和正△BCF,连结EF,EC,请说明EF=EC.解析:略26.如图所示,已知△ABC≌△DCB,其中AB=DC,试说明∠ABD=∠ACD的理由.解析:略27.如图所示,在△ABC中,∠ABC=60°,∠ACB=72°,BD,CE分别是AC,AB上的高,BD交CE于点0.求:(1)∠A的度数;(2)∠ACE的度数;(3)∠BOC的度数.解析:(1)48°;(2)42°;(3)132°28.如图所示,在△ABC中,AD是高,CE是角平分线,它们相交于点P.已知∠APE=55°,∠AEP=80°,求△ACB各个内角的度数.解析:∠B=45°,∠ACB=70°,∠BAC=6529.如图所示,在△ABC中,∠B=35°,∠C=75°,AD是△ABC的角平分线.(1)∠BAC等于多少度?(2)∠ADC等于多少度?解析:(1)70°;(2)70°30.如图所示,在Rt△ABC中,∠A=∠B,CD是∠ACB的平分线,请判定CD与AB的位置关系,并说明理由.解析:CD⊥AB,理由略。
精选新版2019年七年级下册数学单元测试题《三角形的初步认识》完整考试题(含答案)

2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1.下列选项中的三角形全等的是()A.两角及其夹边对应相等的两个三角形B.有两个角对应相等的两个三角形C.面积相等的两个三角形D.都是锐角三角形的两个三角形答案:A2.下列说法错误的是()A.有一个外角是锐角的三角形是钝角三角形B.有两个角互余的三角形是直角三角形C.直角三角形只有一条高D.任何一个三角形中,最大角不小于60度答案:C3.如图,△ABC≌△BAD,A与B,C与D是对应点,若AB=4cm,BD=4.5cm,AD=1.5cm,则BC的长为()A.4cm B.4.5cm C.1.5cm D.不能确定答案:C4.如图,△ABC≌△DCB,AB=5cm,AC=7 cm,BC=8 cm,那么DC的长是()A.8 cm B.7 cm C.6cm D.5 cm答案:D5.如图,已知0A=OC,OB=OD,那么根据“SAS”能直接判定三角形全等的对数为()A.1对B.2对C.3对D.4对答案:B6.如图,△ABD≌△CDB,∠ABD=40°,∠C=110°,则∠CBD等于()A.20°B.30°C.40°D.50°答案:B7.如图所示,△ABC≌△BAD.A与B,C与D是对应顶点,若AB=4cm,BD=4.5 cm,AD=1.5 cm,则BC的长为()A 4.5 cm B.4 cm C.1.5 cm D.不能确定答案:C8.如图所示,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是()A 10° B.20° C.30° D.40°答案:B9.如图所示,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE内部时,则∠A 与∠l+∠2之间有一种数量关系始终保持不变,你认为该规律是()A.∠A=∠l+∠2 B.2∠A=∠l+∠2C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)答案:B二、填空题10.三角形两个外于第三个内角的 4倍,则第三个内角等于 .解析:60°11.如图,在△ABC中,AB=AC=10cm,DE是AB的中垂线,△BDC 的周长为 16 cm,则 BC 的长为 .解析:6cm12.Rt△ABC中,∠C=Rt∠,∠A=30°,AB的中垂线交AB于D,交AC于E,若△ADE的面积是8,EC=3,BC=4,则△ABC的面积为.解析:2213.如图,∠1∶∠2∶∠3=1∶2∶3,则∠4=.72 º解析:14.如图所示,已知AB=DC,AD=BC,E,F是BD上两点,且BE=DF.若∠AEB=100°,∠ADB=30°,则∠BCF= .解析:70°15.如图所示:(1)若△ABD≌△ACE,AB=AC,则对应边还有,对应角有.(2)若△BOE≌△COD,则0E的对应边是,∠EB0的对应角是;(3)若△BEC≌△CDB,则相等的边有.解析: (3)BE=CD,CE=BD,BC=CB (1)AD与AE,BD与CE;∠A与∠A,∠ABD与∠ACE,∠ADB与∠AEC;(2)OD,∠DCO;16.如图所示,已知点D,E,F分别是BC,AC,DC的中点,△EFC的面积为6 cm2,则△ABC的面积为.解析:48cm217.已知三角形的两条边的长分别是3和5,第三条边的长为a,则a的长度在和之间.解析:2,8三、解答题18.如图,已知 AB=DC,AD=BC,说出下列判断成立的理由:(1)△ABC≌△ACD; (2)∠B=∠D.解析:略19.如图,AD平分∠BAC,AB=AC,则BD=CD,试说明理由.解析:△ABD≌△ACD(SAS),则BD=CD.20.如图所示,已知∠α,线段a,b,求作一个三角形,使其两边长分别为a,a+b,两边的夹角等于∠α.解析:略21.画一个三角形,使两个内角分别为45°和60°,它们的夹边为2.5cm.解析:略22.如图①所示,长方形通过剪切可以拼成直角三角形,方法如下:仿照上图,用图示的方法,解答下列问题:(1)如图②所示,已知直角三角形,设计一种方案,将它分成若干块,再拼成一个与之等面积的长方形;(2)如图③所示,对任意一个三角形,设计一种方案,把它分成若干块,再拼成一个与它等面积的长方形.解析:(1)(2)23.如图所示,已知∠BAC=∠DAE,∠B=∠C,BD=CE.证明:AB=AC,AD=AE.解析:略24.如图所示,A,D,F,B在同一直线上,AD=BF,AE=BC,且∠A=∠B,说明下列各式成立的理由.(1)△AEF≌△BCD;(2)∠BFE=∠ADC.解析:略25.三角形的三条中线、三条高、三条角平分线都分别交于一点,其中交点可能不在三角形内部的是哪种线段?请通过画图说明.解析:高线的交点可以在三角形的外部、内部及其顶点上26.如图所示,画出△ABC的角平分线BD,AB边上的高CE,BC边上的中线AF.解析:略27.一个三角形有两条边相等,它的最长的边比最短的边多2,已知这个三角形的周长为8,求它的三条边长.解析:103,103,4328.如图所示,在Rt△ABC中,∠A=∠B,CD是∠ACB的平分线,请判定CD与AB的位置关系,并说明理由.解析:CD⊥AB,理由略29.已知,如图所示,△ABC中,∠B=30°,∠C=40°,D为BC上一点,∠1=∠2,求∠BAD的度数.解析:∠l=∠2=70°,∠1=∠B+∠BAD,得∠BAD=40°30.(1)为了求出四边形的内角和,你能根据图中的两种添线方法,分别求出四边形的内角和吗?(2)请你用类似的方法求出五边形、六边形的内角和,比较一下,你发现了什么规律?(3)利用你发现的规律,可以求得20边形的内角和为度.解析:(1)360°;(2)规律:n边形的内角和为(n-2)·180°;(3)3240。
精选最新版2019年七年级下册数学单元测试题-三角形的初步认识完整题(含参考答案)

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1.如图,把图形沿BC 对折,点A 和点D 重合,那么图中共有全等三角形( )A . 1对B .2对C .3对D .4对答案:C2.如图,在△ABC 中,∠ABC 与∠ACB 的角平分线交于点0,且∠BOC=α,则∠A 的度数是 ( )A .180°-αB .2α-180°C .180°-2αD .12α答案:B3.已知AD 是△ABC 的角平分线,则下列结论正确的个数有( )①BD =CD ,②BC =2CD ,③AD 平分BC ,④∠BAC =2∠DACA .一个B .二个C .三个D . 四个答案:A4.下面三种说法:①两个能够重合的三角形是全等三角形;②全等三角形的形状和大小相同;③全等三角形的面积相等.其中正确的个数有 ( )A .3个B .2个C .1个D .0个答案:A5.如图,AC=AD ,BC=BD ,则图中全等三角形的对数是( )A .6对B .3对C .2对D .1对答案:B6.如图,M 是AB 的中点,∠C=∠D ,∠1=∠2,说明AC=BD 的理由.解: M 是AB 的中点,∴ AM =在BMD AMC ∆∆和中∴ ≌ ( )∴AC=BD ( )解析:BM ,∠C ,∠D ,已知,∠1,∠2,已知,BM ,ΔAMC ,ΔBMD ,AAS ,全等三角形的对应边相等.7.作△ABC 的高AD ,中线AE ,角平分线AF ,三者中有可能画在△ABC 外的是( )A .中线AEB .高ADC .角平分线AFD .都有可能 答案:B8.如图所示,A ,B 是数轴上的两点,C 是AB 的中点,则0C 等于( )A .34OB B .1()2OB OA - C .1()2OA OB + D .以上都不对答案:C9.如图所示,BA=BD ,BC=BE ,根据“边角边”条件得到△ABE △DBC ,则需要增加条件 ( )A .∠A=∠DB .∠E=∠C C .∠A=∠CD .∠l=∠2答案:D10.如图所示,已知△ABC ≌△DCB ,那么下列结论中正确的是( )A .∠ABC=∠CDB ,∠BAC=∠DCB ,∠ACB=∠DBCB .∠ABC=∠DCB ,∠BAC=∠CDB ,∠ACB=∠ABDC .∠ABC=∠DCB ,∠BAC=∠CDB ,∠ACB=∠DBCD .∠ABC=∠DBC ,∠BAC=∠CDB ,∠ACB=∠ACD答案:C)(21M D C B A ()()________________________________________________________AM ⎧=⎪⎪=⎨⎪=⎪⎩二、填空题11.如图,在△ABC 和△CDA 中,((______(________)AB DC BC DA =⎧⎪=⎨⎪=⎩已知)已知), 所以△ABC ≌△CDA( ).解析:AC ,CA ,公共边,SSS12.如图所示,△ABC 中,DE 是AC 的中垂线,AE=5,△ABC 的周长为30,则△ABD 的周长是 .解析:2013.如图所示,△ABC 中,BC=16 cm ,AB ,AC 边上的中垂线分别交BC 于E ,F ,则△AEF 的周长是 cm .解析:1614.已知△ABC ≌△A ′B ′C ′,AB+AC=18 cm ,BC=7 cm ,则△A ′B ′C ′的周长是 .解析:25 cm15.如图所示,点E ,F 在△ABC 的BC 边上,点D 在BA 的延长线上,则∠DAC= + ,∠AFC=∠B+ =∠AEF+ .解析:∠B ,∠C ,∠BAF ,∠EAF16.如图所示,△ABC 中,∠B=∠C ,FD ⊥BC 于D ,DE ⊥AB 于E ,∠AFD=155°,则∠EDF= .解析:65°17.已知三角形的两条边的长分别是3和5,第三条边的长为a ,则a 的长度在 和 之间.解析:2,8三、解答题18.2008年 10月 18 日上午 10时,经过中国铁建十六局集团和中铁隧道局集团2000多名员工4年零2个月的顽强拼搏,被誉为世界级工程难题的宜万铁路野三关隧道Ⅱ线胜利贯通. 如图,这是工程建设中一个山峰的平面图,施工队在施工之前需要先测量出隧道AB 的长度,请你利用三角形全等的知识设计一种测量方法,并说明理由.解析:利用全等三角形的判定(AAS ,SAS ,ASA)来设计完成19.如图,AC =AE ,∠BAM =∠BND =∠EAC , 图中是否存在与△ABE 全等的三角形?并说明理由.A D M CB EN解析:存在△ABE≌△ADC,理由略20.如图,在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB 上的高,H是BE和CF的交点,求∠ABE、∠ACF和∠BHC的度数.解析:∠ABE=30°,∠ACF=30°,∠BHC=120°.21.如图所示,已知线段a,c,求作Rt△ABC,使BC=a,AB=c.解析:提示:两种情况22.如图所示,已知AD=AE,∠l=∠2.请说明OB=OC成立的理由.解析:略23.三月三,放风筝,如图所示是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH.请你运用所学知识给予说明.解析:提示:连结DH24.如图所示,△ABC与△DFE全等,AC与DE是对应边.(1)找出图中相等的线段和相等的角;(2)若BE=14 cm,FC=4 cm,求出EC的长.解析:(1)BF=CE,AC=DE,AB=DF,BC=EF,∠A=∠D,∠B=∠EFD,∠ACB=∠E;(2)5 cm25.如图所示,在△ABC中,∠ABC=60°,∠ACB=72°,BD,CE分别是AC,AB上的高,BD交CE于点0.求:(1)∠A的度数;(2)∠ACE的度数;(3)∠BOC的度数.解析:(1)48°;(2)42°;(3)132°26.三角形的三条中线、三条高、三条角平分线都分别交于一点,其中交点可能不在三角形内部的是哪种线段?请通过画图说明.解析:高线的交点可以在三角形的外部、内部及其顶点上27.一个三角形有两条边相等,它的最长的边比最短的边多2,已知这个三角形的周长为8,求它的三条边长.解析:103,103,4328.如图所示,在△ABC中,∠BAC=90°,画出BC边上的中线AM,分别量出AM,BC的长,并比较AM与12BC的大小.再画一个锐角△ABC及其中线AM,此结论还成立吗?对于钝角三角形呢?解析:对于Rt△ABC,AM=12BC,对于其他三角形此结论不成立29.如图所示,在△ABC中,∠A=∠ACB,CD是∠ACB的平分线,CE⊥AB于E.(1)试说明∠CDB=3∠DCB;(2)若∠DCE=48°,求∠ACB的度数.解析:(1)略;(2)28°30.如图所示,一张三个内角都相等的三角形纸片ABC,∠CBP=20°(图①).现将纸片沿射线BP折叠成图②的形状,BP交AC于点E,BC′交AC于点D.求图②中∠ADC′,∠AEC′的度数.解析:∠ADC′=80°,∠AEC′=20°。
精选最新2019年七年级下册数学单元测试题-三角形的初步认识考核题(含参考答案)

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1.若AD 是△ABC 的中线,则下列结论中,错误的是( )A .AD 平分∠BACB .BD =DC C .AD 平分BC D .BC =2DC 答案:A2.如图,PD ⊥AB ,PE ⊥AC ,垂足分别为D ,E ,且AP 平分∠BAC ,则△APD 与△APE 全等的理由是( )A .AASB .ASAC .SSSD .AAS答案:D3.如图△ABC 中,AB 的中垂线交AC 于D ,AB =10,AC =8,△DBC 的周长是a ,则BC 等于 ( )A . a -6B .a -8C .a -10D .10-a答案:B4.如图,AD 、AE 分别是△ABC 的高和角平分线,∠DAE=20°,∠B=65°,则∠C 等于( )A .25°B .30°C .35°D .40°答案:A5.如图,123,,∠∠∠的大小关系为( )A .213>>∠∠∠B .132>>∠∠∠C .321>>∠∠∠D .123>>∠∠∠ 答案:D6.如图所示,A ,B 是数轴上的两点,C 是AB 的中点,则0C 等于( )A .34OB B .1()2OB OA - C .1()2OA OB + D .以上都不对答案:C7.如图所示,△ABC 中,AB=AC ,BE=CE ,则由“SSS”可直接判定( )A.△ABD≌△ACD B.△ABE≌△ACE C.△BED≌△CED D.以上答案都不对答案:B8.如图所示,已知△ABC≌△DCB,那么下列结论中正确的是()A.∠ABC=∠CDB,∠BAC=∠DCB,∠ACB=∠DBCB.∠ABC=∠DCB,∠BAC=∠CDB,∠ACB=∠ABDC.∠ABC=∠DCB,∠BAC=∠CDB,∠ACB=∠DBCD.∠ABC=∠DBC,∠BAC=∠CDB,∠ACB=∠ACD答案:C9.如图所示,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是()A 10° B.20° C.30° D.40°答案:B10.下列说法中正确的是()A.从三角形一个顶点向它对边所在直线画垂线,此垂线就是三角形的高B.三角形的角平分线是一条射线C.直角三角形只有一条高D.钝角三角形的三条高所在的直线的交点在此三角形的外部答案:D11.如图所示,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE内部时,则∠A 与∠l+∠2之间有一种数量关系始终保持不变,你认为该规律是()A.∠A=∠l+∠2 B.2∠A=∠l+∠2C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)答案:B二、填空题12.有两条边相等的三角形中已知一边长为 5,另一边长 6,则这个三角形的周长 .解析:16或1713.一个三角形中最多有个内角是钝角,最多可有个角是锐角.解析:1,314.已知ABC DEF20cm,那么△DEF中EF==,△ABC的面积是2BC EF△≌△,5cm边上的高是__________cm.解析:815.如图所示,△ABC 中,BC=16 cm,AB,AC边上的中垂线分别交BC于E,F,则△AEF的周长是 cm.解析:1616.如图所示,已知点D,E,F分别是BC,AC,DC的中点,△EFC的面积为6 cm2,则△ABC的面积为.解析:48cm217.直角三角形的两个锐角的平分线AD,BE交于点0,则∠AOB= .解析:135°18.在△ABC中,(1)∠C=85°,∠A=25°,则∠B= ;(2)∠A+∠B=90°,则∠C= ;(3)∠A=∠B=∠C,则∠A= ;(4)∠A=∠B,∠C=80°,则∠B= .解析:(1)70°;(2)90°;(3)60°;(4)50°19.如图所示,∠1=135°,∠2=75°,则∠3的度数是 .解析:30°20.(1)自行车用脚架撑放比较稳定的原因是 .(2)若AABC 的三边长都为整数,周长为11,有一边长为4,且任何两边都不相等,则这个三角形的最大边长为 .解析:(1)三角形的稳定性;(2)5三、解答题21.看图按要求完成问题:(1)画ABC ∆边BC 的中线和B ∠的平分线;(2)分别指出直角三角形DE 和EF 边上的高线;(3)画钝角三角形OP 边上的高线.解析:略 22.如图所示,已知线段a ,b 和∠α,用直尺和圆规作△ABC ,使∠B=∠α,AB=a ,BC=b .Q P O F E D C B A (2) (1) (3)解析:略23.如图所示,已知AD=AE,∠l=∠2.请说明OB=OC成立的理由.解析:略24.如图所示,以Rt△ABC的两直角边AB,BC为边向外作正△ABE和正△BCF,连结EF,EC,请说明EF=EC.解析:略25.如图所示,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点,说出AF是CD的中垂线的理由.解:连结AC,AD,在△ABC和△AED中,AB=AE(已知),∠B=∠E(已知),BC=ED(已知),∴△ABC≌△AED(SAS).∴AC=AD(全等三角形的对应边相等).请把后面的过程补充完整:解析:略26.如图所示,已知△ABD≌△ACE,AD=6 cm,AC=4 cm,∠ABD=50°,∠E=30°.求BE的长和∠COD的度数.解析:BE=2 cm,∠COD=20°27.把大小为4×4的正方形方格图形分割成两个全等图形,如右图所示,请在下图中,沿着虚线再画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形解析:略28.如图所示,在△ABC中,∠ABC=60°,∠ACB=72°,BD,CE分别是AC,AB上的高,BD交CE于点0.求:(1)∠A的度数;(2)∠ACE的度数;(3)∠BOC的度数.解析:(1)48°;(2)42°;(3)132°29.在△ABC中,∠A+∠C=120°,∠B+∠C=110°,求三角形各内角的度数.解析:∠A=70°,∠B=60°,∠C=50°30.如图所示,在Rt △ABC中,∠ACB为直角,∠CAD的平分线交BC的延长线于点E,若∠B=35°,求∠BAE和∠E的度数.解析:∠E=27.5°,∠BAF=117.5°。
新版精选2019年七年级下册数学单元测试题《三角形的初步认识》完整题(含参考答案)

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1.下列说法错误的是( )A .有一个外角是锐角的三角形是钝角三角形B .有两个角互余的三角形是直角三角形C .直角三角形只有一条高D .任何一个三角形中,最大角不小于60度答案:C2.一块试验田的形状是三角形(设其为ABC △),管理员从BC 边上的一点D 出发,沿DC CA AB BD →→→的方向走了一圈回到D 处,则管理员从出发到回到原处在途中身体( )A .转过90B .转过180C .转过270D .转过360答案:D3.如图,123,,∠∠∠的大小关系为( )A .213>>∠∠∠B .132>>∠∠∠C .321>>∠∠∠D .123>>∠∠∠ 答案:D4.如图所示,BA=BD ,BC=BE ,根据“边角边”条件得到△ABE △DBC ,则需要增加条件 ( )A .∠A=∠DB .∠E=∠C C .∠A=∠CD .∠l=∠2答案:D5.任意一个三角形被一条中线分成两个三角形,则这两个三角形:①形状相同,②面积相同,③全等.上述说法正确的有( )A .0个B .1个C .2个D .3个答案:B6.△ABC 中,∠A :∠B :∠C=1:2:3,则△ABC 为( )A .锐角三角形B .直角三角形C .钝角三角形D .锐角或钝角三角形答案:B7.如图所示,在直角三角形ABC 中,AC ≠AB ,AD 是斜边BC 上的高,DE ⊥AC ,DF ⊥AB ,垂足分别是E ,F ,则 图中与∠C (除°C 外)相等的角的个数是( )A .2个B .3个C .4个D .5个答案:B8.下列叙述中正确的个数是( )①三角形的中线、角平分线都是射线;②三角形的中线、角平分线都在三角形内部;③三角形的中线就是过一边中点的线段;④三角形三条角平分线交于一点.A .0个B .1个C .2个D .3个答案:C9.现有两根木棒,它们的长度分别是20 cm 和30 cm .如果不改变木棒的长度,要钉成一个三角形木架,那么应在下列四根木棒中选取( )A .10 cm 的木棒B .20 cm 的木棒C .50 cm 的木棒D .60 cm 的木捧 答案:B二、填空题10.如图,在△ABC 和△CDA 中,((______(________)AB DC BC DA =⎧⎪=⎨⎪=⎩已知)已知), 所以△ABC ≌△CDA( ).解析:AC ,CA ,公共边,SSS11.如图,,已知OA=OB ,OC=OD ,D 和BC 相交于点E ,则图中全等三角形有 对.解析:412.一个三角形中最多有个内角是钝角,最多可有个角是锐角.解析:1,313.如图,在△ABC中,AB=AC=10cm,DE是AB的中垂线,△BDC 的周长为 16 cm,则 BC 的长为 .解析:6cm14.如图,长方形ABCD中(AD>AB),M为CD上一点,若沿着AM折叠,点N恰落在BC上,∠ANB+∠MNC=____________.解析:90°15.如图,△ABC是不等边三角形,DE=BC,以D ,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出_______个.解析:416.如图所示,已知点C是∠AOB角平分线上的一点,点P,P′分别在边0A,OB上,如果要得到OP=OP′,需添加以下条件中的某一个即可,请你写出所有可能结果的序号:.①∠0CP=∠OCP′;②∠0PC=∠OP′C;③PC=P′C;④PP′⊥0C;⑤PC⊥OA,P′C ⊥OB.解析:①②④⑤17.如图所示,△ABC中,DE是AC的中垂线,AE=5,△ABC的周长为30,则△ABD 的周长是.解析:2018.如图所示,在△ABC中,AD是角平分线,已知∠B=66°,∠C=38°,那么∠ADB= ,∠ADC= .解析:76°,l04°19.已知△ABC三边为a,b,c,且a,b满足2-+-=,c 为整数,则c的取值a b1(3)0为.解析:3三、解答题20.如图,已知BE=CF,AB=CD,∠B=∠C,则AF=DE吗?请说明理由.解析:利用SAS说明△ABF≌△DCE21.如图所示,已知线段a,b,c,用直尺和圆规作△ABC,使AB=c,BC=a,AC=b.解析:略22.画一个三角形,使两个内角分别为45°和60°,它们的夹边为2.5cm.解析:略23.如图所示,以Rt△ABC的两直角边AB,BC为边向外作正△ABE和正△BCF,连结EF,EC,请说明EF=EC.解析:略24.如图所示,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点,说出AF是CD的中垂线的理由.解:连结AC,AD,在△ABC和△AED中,AB=AE(已知),∠B=∠E(已知),BC=ED(已知),∴△ABC≌△AED(SAS).∴AC=AD(全等三角形的对应边相等).请把后面的过程补充完整:解析:略25.请你在如图所示的方格纸中,画一个与左上角已有图形全等的图形.解析:略26.如图所示,把△ACB沿着AB翻转,点C与点D重合,请用符号表示图中所有的全等三角形.解析:△ACE≌△ADE,△BCE≌△BDE,△ACB≌△ADB27.如图所示,在四边形ABCD中,E,F分别为AD,BC的中点.已知四边形ABCD的面积为l,求四边形DEBF的面积.解析:1228.如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,求∠DAE的大小.解析:18°29.已知,如图所示,△ABC中,∠B=30°,∠C=40°,D为BC上一点,∠1=∠2,求∠BAD的度数.解析:∠l=∠2=70°,∠1=∠B+∠BAD,得∠BAD=40°30.在△ABC中,已知∠A+∠B=70°,∠C=2∠A,求∠A,∠B,∠C的度数.解析:∠A=55°,∠B=15°,∠C=110°。
最新2019年七年级下册数学单元测试题《三角形的初步认识》完整考试题(含答案)

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1.如果一个三角形有一个角是99°,那么这个三角形是( )A .锐角三角形B .钝角三角形C .直角三角形D .钝角三角形或直角三角形答案:B2.下列长度的三条线段,能组成三角形的是( )A .224,,B .225,,C .236,,D .245,,答案:D3.如图所示,△ABD ≌△CDB ,∠ABD=40°,∠CBD=30°,则∠C 等于 ()A .20°B .100°C .110°D .115°答案:C4.△ABC 中,∠A :∠B :∠C=1:2:3,则△ABC 为( )A .锐角三角形B .直角三角形C .钝角三角形D .锐角或钝角三角形答案:B5.关于三角形的高的位置,下列判断中正确的是( )A .必在三角形内B .必在三角形外C .不在三角形内,就在三角形外D .以上都不对答案:D6.以下列各组线段的长为边,能构成三角形的是( )A .4 cm ,5 cm ,6 cmB .2 cm ,3 cm ,5 cmC .4 cm ,4 cm 。
9 cmD .12 cm ,5 cm ,6 cm答案:A7.下列说法中:①如果两个三角形可以依据“AAS”来判定全等,那么一定也可以依据“ASA”来判定它们全等;②如果两个三角形都和第三个三角形不全等,那么这两个三角形也一定不全等;③要判断两个三角形全等,给出的条件中至少要有一对边对应相等.正确的是()A.①和②B.②和③C.①和③D.①②③答案:C二、填空题8.如图,∠A=80°,∠2=130°,则∠l= .解析:130°9.如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠+∠=.AOC DOB解析:180°10.在ΔABC中, ∠C=90°,BD平分∠ABC,交AC于D,若AB=5,CD=2, 则ΔABD的面积是 .解析:511.如图所示,已知AB=DC,AD=BC,E,F是BD上两点,且BE=DF.若∠AEB=100°,∠ADB=30°,则∠BCF= .解析:70°12.如图所示,四边形ABCD为正方形,它被虚线分成了9个小正方形,则△DBE与△DEC的面积之比为.解析:1:213.如图所示,△ABC中,D,E是BC边上的两点,且BD=DE=EC,则AD是三角形的中线,AE是三角形的中线.解析:ABE,ACD14.如图所示.(1)AD是△ABC的角平分线,则∠BAC=2 =2 ;(2)AE是△ABC的中线,则 = 2BE=2 .解析:(1)∠BAD,∠CAD;(2)BC,CE15.如图所示.(1)图中共有个三角形,分别是;(2)∠CDB是的内角,是的外角;(3)在AACD中,∠A是边和的夹角,边AC是的对边.解析:(1)3;△ACD,△BCD,△ABC;(2)△BDC,△ACD;(3)AD,AC,∠ADC 16.四条长度分别是2,3,4,5的线段,任选3条可以组成个三角形.解析:317.(1)自行车用脚架撑放比较稳定的原因是.(2)若AABC的三边长都为整数,周长为11,有一边长为4,且任何两边都不相等,则这个三角形的最大边长为.解析:(1)三角形的稳定性;(2)5三、解答题18.如图,把4×4的正方形方格图形分割成两个全等图形,请在下图中,沿虚线画出四种不同的分法,把4×4的正方形分割成两个全等图形.解析:19.如图,在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB 上的高,H是BE和CF的交点,求∠ABE、∠ACF和∠BHC的度数.解析:∠ABE=30°,∠ACF=30°,∠BHC=120°.20.如图,AB⊥BD于B,DE⊥BD于D,已知AB=CD,BC=ED,求∠ACE的度数.解析:△ABC≌△CDE(SAS),则∠ACB=∠E,由于∠ACB+∠ACE =∠E+∠D, 则∠ACE=∠D=90°.21.如图,已知线段AC=8,BD=6.(1)已知线段AC⊥BD于0.设图①,图②,图③中的四边形ABCD的面积分别为S1,S2,S3,则 S1= ,S2= ,S3= ;(2)如图④,对于线段AC与线段BD垂直相交(垂足O不与A,B,C,D重合)的任意情况,请你猜想四边形ABCD的面积,并说明你的猜想是正确的;(3)当线段BD与AC(或CA)的延长线垂直相交时,猜想顺次连结点A,B,C,D,A所围成的封闭图形的面积是多少;请画出图形,并说明你的猜想是正确的.解析:(1)S1=24,S2=24,S3=24;(2)面积为24,411111()8624 22222S BD AO BD CO BD AO CO BD AC=⋅+⋅=+=⋅=⨯⨯=;(3)图略,原理类似于(2),面积为2422.如图所示,已知线段a,c,求作Rt△ABC,使BC=a,AB=c.解析:提示:两种情况23.如图所示,已知线段a,b和∠α,用直尺和圆规作△ABC,使∠B=∠α,AB=a,BC=b.解析:略24.如图所示,已知AD=AE,∠l=∠2.请说明OB=OC成立的理由.解析:略25.如图所示,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点,说出AF是CD的中垂线的理由.解:连结AC,AD,在△ABC和△AED中,AB=AE(已知),∠B=∠E(已知),BC=ED(已知),∴△ABC≌△AED(SAS).∴AC=AD(全等三角形的对应边相等).请把后面的过程补充完整:解析:略26.如图所示,已知△ABE≌△ACE,D是BC的中点,你能说明△BDE≌△CDE吗?解析:略27.如图所示,已知AB=AC,D是BC的中点,说明AD⊥BC的理由.解:∵D是BC的中点( ),∴ (中点的定义).在△和△中,= ( ),= (已证),= ( ),∴△≌△ ( ),∴∠l=∠2( )∴∠+∠2= ,∴∠l=∠2= ,即AD⊥BC.解析:已知,BD=CD,ABD,ACD,AB,AC,已知,BD,CD,AD,AD,公共边,ABD,ACD,SSS,全等三角形对应角相等,l80°,90°28.请你在如图所示的方格纸中,画一个与左上角已有图形全等的图形.解析:略29.如图所示,已知△ABD≌△ACE,AD=6 cm,AC=4 cm,∠ABD=50°,∠E=30°.求BE的长和∠COD的度数.解析:BE=2 cm,∠COD=20°30.如图所示,画出△ABC的角平分线BD,AB边上的高CE,BC边上的中线AF.解析:略。
最新精选2019年七年级下册数学单元测试题-三角形的初步认识完整考题(含标准答案)
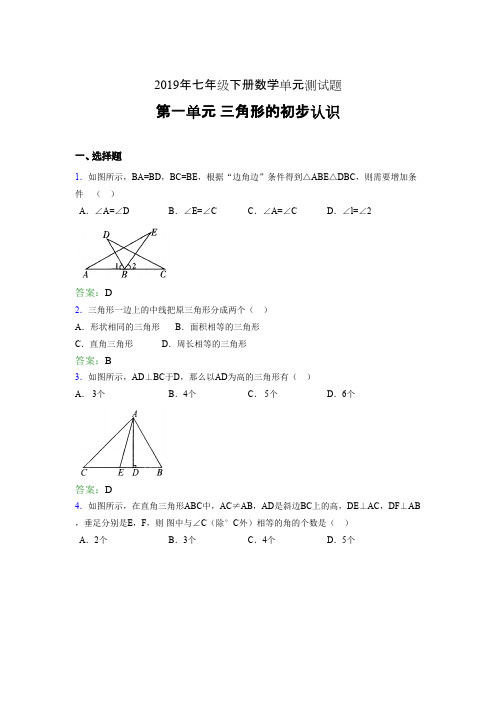
仿照上图,用图示的方法,解答下列问题: (1)如图②所示,已知直角三角形,设计一种方案,将它分成若干块,再拼成一个与之等面 积的长方形;
(2)如图③所示,对任意一个三角形,设计一种方案,把它分成若干块,再拼成一个与它等 面积的长方形.
解析:(1) (2) 27.已知,如图所示,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.试判断 ∠B与∠DEC是否相等,并说明理由.
A.2个
B.3个
C.4个
D.5个
答案:B
5.如图所示是跷跷板的示意图,支柱0C与地面垂直,点0是横板AB的中点,AB可以绕着
点0上下转动,当A端落地时,∠0AC=20°.跷跷板上下可转动的最大角度(即∠A′OA
)是( )
A.800
B.60°
C.40°
D.20°
答案:C
6.如图所示,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是( ) A 10° B.20° C.30° D.40°
(1)经过线段中点的直线是线段的中垂线. ( )
(2)以AB为直径可以作一个圆. ( )
(3)已知两条边和一个角可以作唯一的三角形. ( )
(4)已知两角一边可以作唯一的三角形. ( )
解析:(1)× (2)√ (3)× (4)×
19.如图所示,∠1=∠2,∠ABC=∠DCB,AC,BD相交于O,请将下列说明AB=DC的理 由的过程补充完整.
解析:CD⊥AB,理由略
解析:∠B=∠DEC,理由略 28.请你在如图所示的方格纸中,画一个与左上角已有图形全等的图形.
解析:略 29.怎样作一条线,就能使如图所示的正五角星成为两个全等的图形?这样的线共有几条?
解析:5 30.如图所示,在Rt△ABC中,∠A=∠B,CD是∠ACB的平分线,请判定CD与AB的位置 关系,并说明理由.
精选新版2019年七年级下册数学单元测试题《三角形的初步认识》考核题完整版(含参考答案)
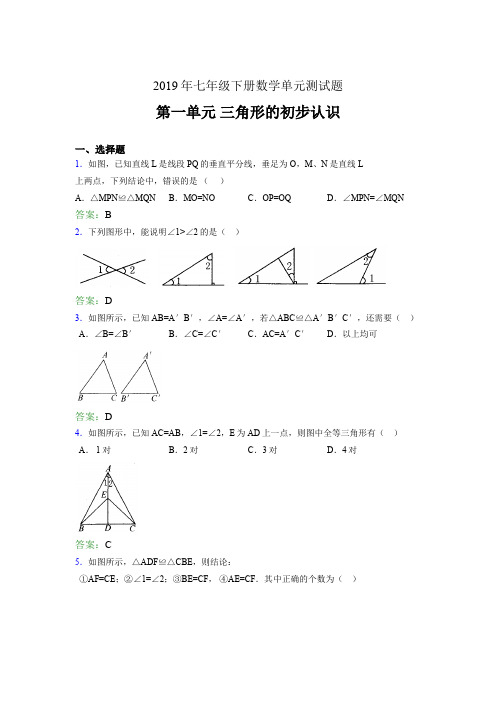
2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1.如图,已知直线L是线段PQ的垂直平分线,垂足为O,M、N是直线L上两点,下列结论中,错误的是()A.△MPN≌△MQN B.MO=NO C.OP=OQ D.∠MPN=∠MQN答案:B2.下列图形中,能说明∠1>∠2的是()答案:D3.如图所示,已知AB=A′B′,∠A=∠A′,若△ABC≌△A′B′C′,还需要() A.∠B=∠B′B.∠C=∠C′C.AC=A′C′D.以上均可答案:D4.如图所示,已知AC=AB,∠1=∠2,E为AD上一点,则图中全等三角形有()A. 1对B.2对C.3对D.4对答案:C5.如图所示,△ADF≌△CBE,则结论:①AF=CE;②∠1=∠2;③BE=CF,④AE=CF.其中正确的个数为()A.1个B.2个C.3个D.4个答案:C6.△ABC中,∠A:∠B:∠C=1:2:3,则△ABC为()A.锐角三角形B.直角三角形C.钝角三角形D.锐角或钝角三角形答案:B7.关于三角形的高的位置,下列判断中正确的是()A.必在三角形内B.必在三角形外C.不在三角形内,就在三角形外D.以上都不对答案:D8.下列叙述中正确的个数是()①三角形的中线、角平分线都是射线;②三角形的中线、角平分线都在三角形内部;③三角形的中线就是过一边中点的线段;④三角形三条角平分线交于一点.A.0个B.1个C.2个D.3个答案:C9.在△ABC和△A′B′C′中,①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠8′;⑥∠C=∠C′,则下列条件中不能使△ABC≌△A′B′C′的是()A.②④⑤B.①②③C.①③⑤D.①②⑤答案:C10.如图,已知BC=BD,∠ABE=∠CBD,∠ADB=∠BCE.要说明BA=BE,则只要先说明()A.△ABE≌△DBC B.△ABD≌△EBC C.△BDG≌△BEH D.△ABG≌△BCH答案:B11.下列长度的三条线段,能够组成三角形的是()A.2.5,2.5,5 B. l,6,6 C.2,8,4 D.10,7,2答案:B二、填空题12.如图,AD=AE,DB=EC,则图中一共有对全等三角形.解析:413.如图,∠1∶∠2∶∠3=1∶2∶3,则∠4=.72 º解析:14.判断正误,对的打“√”,错的打“×”.(1)经过线段中点的直线是线段的中垂线. ( )(2)以AB为直径可以作一个圆. ( )(3)已知两条边和一个角可以作唯一的三角形. ( )(4)已知两角一边可以作唯一的三角形. ( )解析:(1)× (2)√ (3)× (4)×15.要使△ABC≌△A′B′C′,已知AB=A′B′,∠B=∠B′,如果利用“ASA”,要补充条件,如果利用“AAS”,要补充条件.解析:∠A=∠A′,∠=∠C′16.如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃.最省事的办法是带去,理由是.解析:③,可根据③中的两角及夹边画出一个与之全等的三角形17.如图所示,直线AD交△ABC的BC边于D点,且AB=AC.(1)若已知D为BC中点,则可根据,说明△ABD≌△ACD;(2)若已知AD平分∠BAC,可以根据说明△ABD≌△ACD;(3)若AD是BC的中垂线,则可以根据,说明△ABD≌△ACD,还可以根据说明△ABD≌△ACD.解析:(1)SSS;(2)SAS;(3)SAS,SSS18.如图所示:(1)若△ABD≌△ACE,AB=AC,则对应边还有,对应角有.(2)若△BOE≌△COD,则0E的对应边是,∠EB0的对应角是;(3)若△BEC≌△CDB,则相等的边有.解析: (3)BE=CD,CE=BD,BC=CB (1)AD与AE,BD与CE;∠A与∠A,∠ABD与∠ACE,∠ADB与∠AEC;(2)OD,∠DCO;19.木材加工厂堆放木料的方式如图所示:依此规律可以得出第六堆木料的根数是根.解析:2820.如图所示,△ABC三条中线AD、BE、CF交于点0,S△ABC=l2,则S△ABD= ,S△AOF= .解析:6,221.如图所示,△ABC中,D,E是BC边上的两点,且BD=DE=EC,则AD是三角形的中线,AE是三角形的中线.解析:ABE ,ACD22.如图所示,∠1=135°,∠2=75°,则∠3的度数是 .解析:30°23.四条长度分别是2,3,4,5的线段,任选3条可以组成 个三角形. 解析:3三、解答题24.如图 ,AB=AD ,∠BAD=∠CAE ,AC=AE ,试说明CB=ED.解析:可证△ABC ≌△ADB ,然后说明CB =ED25.如图,DF ⊥AB ,∠A=430,∠D=42°,求∠ACB 的度数.E B DF C AF E DC B A ∠ACB=89 º.解析:26.如图,BD =CD ,∠ABD =∠ACD ,DE 、DF 分别垂直于AB 及AC 交延长线于E 、F .求证:DE =DF .解析:∠ABD=∠ACD ,则∠E+∠BDE =∠F+∠CDF, 由于 ∠E=∠F ,∴∠BDE =∠CDF ,∴△BED ≌△CFD(AAS),∴DE=DF .27.根据条件作图:(1)任意画一个Rt △ABC ,使∠C=90°;(2)画∠CAB 的平分线交对边于D ;(3)画出点D 到Rt △ABC 的斜边的垂线段DE .解析:略28.请你在如图所示的方格纸中,画一个与左上角已有图形全等的图形.解析:略29.如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,求∠DAE的大小.解析:18°30.已知△ABC中,以点A为顶点的外角为120°,∠B=30°,求∠C的度数.解析:∠C=90°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年七年级下册数学单元测试题
第一单元三角形的初步认识
一、选择题
1.如图,点D、E分别在AC、AB上,已知AB=AC,添加下列条件,不能说明ΔABD≌ΔACE的是()
A.∠B=∠C B.AD=AE C.∠BDC=∠CEB D.BD=CE
答案:D
2.下列条件中,不能作出唯一
..三角形的是()
A.已知两边和夹角
B.已知两边和其中一边的对角
C.已知两角和夹边
D.已知两角和其中一角的对边
答案:B
3.如图所示,BA=BD,BC=BE,根据“边角边”条件得到△ABE△DBC,则需要增加条件()
A.∠A=∠D B.∠E=∠C C.∠A=∠C D.∠l=∠2
答案:D
4.如图所示,在直角三角形ABC中,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别是E,F,则图中与∠C(除°C外)相等的角的个数是()
A.2个B.3个C.4个D.5个
答案:B
5.三角形一边上的中线把原三角形分成两个()
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
答案:B
6.下列叙述中正确的个数是()
①三角形的中线、角平分线都是射线;②三角形的中线、角平分线都在三角形内部;③三角形的中线就是过一边中点的线段;④三角形三条角平分线交于一点.
A.0个B.1个C.2个D.3个
答案:C
7.三角形的三边长都是整数,并且唯一的最长边是5,则这样的三角形共有()
A 1个 B.2个 C.3个 D.4个
答案:D
8.下列长度的三条线段,能组成三角形的是()
A.6,3,3 B.4,8,8 C.3,4,8 D.8,l5,7
答案:B
二、填空题
9.如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是.
解析:A0=D0或B0=C0或AB=CD或∠ACB=∠DBC
10.如图,已知任意三角形的内角和为180°,试利用多边形中过某一点的对角线条数,寻求多边形内角和的公式.
根据上图所示,①一个四边形可以分成2个三角形,于是四边形的内角和为度;②一个五边形可以分成3个三角形,于是五边形的内角和为度;……,③按此规律,n边形可以分成个三角形,于是n边形的内角和为度.
解答题
解析: 360,540,(n-2),180(n-2)
11.如图,OP平分∠EOF,PA⊥OE于点A.已知PA=2cm,求点P到OF的距离
为.
解析:2cm
12.要使△ABC≌△A′B′C′,已知AB=A′B′,∠B=∠B′,如果利用“ASA”,要补充条件,如果利用“AAS”,要补充条件.
解析:∠A=∠A′,∠=∠C′
13.如图所示,△ABC 中,BC=16 cm,AB,AC边上的中垂线分别交BC于E,F,则△AEF的周长是 cm.
解析:16
14.如图所示:
(1)若△ABD≌△ACE,AB=AC,则对应边还有,对应角有.
(2)若△BOE≌△COD,则0E的对应边是,∠EB0的对应角是;
(3)若△BEC≌△CDB,则相等的边有.
解析: (3)BE=CD,CE=BD,BC=CB (1)AD与AE,BD与CE;∠A与∠A,∠ABD与∠ACE,∠ADB与∠AEC;(2)OD,∠DCO;
15.△ABC与△DEF全等,AB=DE,若∠A=50°,∠B=60°,则∠D= .
解析:50°或60°
16.如图所示,△ABC三条中线AD、BE、CF交于点0,S△ABC=l2,则S△ABD= ,S△AOF= .
解析:6,2
17.如图所示,已知点D,E,F分别是BC,AC,DC的中点,△EFC的面积为6 cm2,则△ABC的面积为.
解析:48cm2
18.如图所示.
(1)图中共有个三角形,分别是;
(2)∠CDB是的内角,是的外角;
(3)在AACD中,∠A是边和的夹角,边AC是的对边.
解析:(1)3;△ACD,△BCD,△ABC;(2)△BDC,△ACD;(3)AD,AC,∠ADC 19.在Rt△ABC中,∠C=90°,其中∠A,∠B的平分线的交点为E,则∠AEB的度数为.
解析:135°
三、解答题
20.已知:△ABC的周长为 18 cm,AB边比AC边短2 cm,BC边是AC边的一半,求△ABC三边的长.
解析:AB=6 cm,BC=4cm,AC=8cm
21.如图.在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件.请你在其中选三个作为已知条件,余下的一个作为结论,写出—个正确的结论,并说明理由.
①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF.
已知:
结沦:
理由:
解析:①③④,②,BE=CF,则BC=EF,ΔABC≌ΔDEF(SAS).
22.如图,AD平分∠BAC,AB=AC,则BD=CD,试说明理由.
解析:△ABD≌△ACD(SAS),则BD=CD.
23.如图所示,已知线段a,b,c,用直尺和圆规作△ABC,使AB=c,BC=a,AC=b.
解析:略
24.如图所示,已知∠E=∠F=90°,∠B=∠C,AE=AF,则以下结论有哪些是成立的?并挑选一个将理由补充完整.
①∠1=∠2;②BE=CF;③CD=FN;④△AEM≌△AFN.
成立的有:.我选,理由如下:
解析:①②④,以下略
25.如图所示,已知AB=AE,∠BAE=∠CAD,AC=AD,说出下列结论成立的理由.
(1)△ABC≌△AED;
(2)BC=ED.
解析:略
26.如图所示,△ABC与△DFE全等,AC与DE是对应边.
(1)找出图中相等的线段和相等的角;
(2)若BE=14 cm,FC=4 cm,求出EC的长.
解析:(1)BF=CE,AC=DE,AB=DF,BC=EF,∠A=∠D,∠B=∠EFD,∠ACB=∠E;(2)5 cm
27.已知三角形的周长是46 cm,其中一边比最短边长2 cm,比最长边短3 cm,求三角形三
边的长.
解析:13 cm,15 cm,18 cm
28.如图所示,一张三个内角都相等的三角形纸片ABC,∠CBP=20°(图①).现将纸片沿射线BP折叠成图②的形状,BP交AC于点E,BC′交AC于点D.求图②中∠ADC′,∠AEC′的度数.
解析:∠ADC′=80°,∠AEC′=20°
29.如图所示,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC,∠l=∠2,根据上述条件,请在图中找出一对全等三角形,并证明你的结论.
解析:略
30.如图,从建筑物顶端A处拉一条宣传标语条幅到地面C处,为了测量条幅AC的长,在地面另一处选一点D,使D、C、B(B为建筑物的底部)三点在同一直线上,并测得
∠D=40°,∠ACB=80°,求∠DAC的度数.
A
B
D
C
解析:40°。
