七、直线和圆
第七章(直线与圆)过关测试

高三数学练习十九一、填空题:(每小题5分,共70分)1.已知直线m 的倾斜角是直线0333=--y x 的倾斜角的2倍,且直线m 在x 轴上的截距是3-,则直线m 的方程是2.圆1C :222880x y x y +++-=与圆2C 224420x y x y +-+-=的位置关系是3.如果直线0121=+-ay x l :与直线07642=-+y x l :平行,则a 的值为4.到直线3410x y --=的距离为2的直线方程是5.与直线01:2=--y m mx l 垂直于点(2,1)P 的直线方程是6.与圆8)3()3(22=-+-y x 相切,且在y x 、轴上截距相等的直线有 条7.过原点的直线与圆03422=+++x y x 相切,若切点在第三象限,则该直线的方程是8.若直线:10 (0,0)l ax by a b ++=>>始终平分圆M :228210x y x y ++++=的周长,则14a b+的最小值为 9. 设,x y 满足约束条件04312x y x x y ≥⎧⎪≥⎨⎪+≤⎩,则231x y x +++取值范围是 10. 00(,)M x y 为圆222x y a+=()0a >内异于圆心的一点,则直线200x x y y a +=与该圆的位置关系是11.已知圆的方程是x 2+y 2=1,则在y 轴上截距为2的切线方程为 12.圆心在直线270x y --=上的圆C 与y 轴交于两点(0,4)A -,(0,2)B -,则圆C 的方程为13.已知实数x 、y 满足方程22410x y x +-+=,则xy 的最大值为 14.如图,已知()4,0A 、()0,4B ,从点()2,0P 射出的光线经直线AB 反向后再射到直线OB 上,最后经直线OB 反射后又回到P 点,则光线所经过的路程是二、解答题:本大题共6小题,共90分.15. (14分)求经过两条直线04:1=-+y x l 和02:2=+-y x l 的交点,且分别与直线012=--y x (1)平行, (2)垂直的直线方程.16. (14分)圆的方程为x 2+y 2-6x -8y =0,过坐标原点作长为8的弦,求弦所在的直线方程.17. (14分)一圆与y 轴相切,圆心在直线03=-y x 上,在x y =上截得的弦长为72,求此圆的方程.18. (16分)已知关于x ,y 的方程C :04222=+--+m y x y x .(1)当m 为何值时,方程C 表示圆.(2)若圆C 与直线l :x +2y -4=0相交于M ,N 两点,且MN =,求m 的值19. (16分)设有半径为3km 的圆形村落,A 、B 两人同时从村落中心出发,B 向北直行,A 先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B 相遇.设A 、B 两人速度一定,其速度比为3:1,问两人在何处相遇?20. (16分)已知可行域0,20,0,y x y ≥⎧⎪+≥⎨+-≤的外接圆C 与x 轴交于点1A 、2A ,椭圆1C 以线段12A A为长轴,离心率2e =. (1)求圆C 及椭圆1C 的方程;(2)设椭圆1C 的右焦点为F ,点P 为圆C 上异于1A 、2A 的动点,过原点O 作直线PF的垂线交直线x =Q ,判断直线PQ 与圆C 的位置关系,并给出证明.。
第七章直线和圆的方程复习

A B1 C1 1 l1、l2重合 A2 B2 C2
A B1 1 l1、l2 相交 A2 B2
二、两直线的位置关系
(考虑直线斜率均存在) 1、平行 k1=k2且b1≠b2
2、垂直
k 1· k2= -1
注 2:
1、与直线 Ax+By+C1=0平行的直线
方程:Ax+By+C2=0 ( C1≠ C2 ) 2、与直线 Ax+By+C1=0垂直的直线方程:Bx-Ay+C2=0
若Ax+By+C ≥ 0 (或 ≤ 0) ,则边界应画成实线
2、画图时应非常准确,否则将得不到正确结果
2.简单的线性规划有关概念
设 z = 2x + y 且变量 x、y 满足下列条件 x 4 y 3 3 x 5 y 25 x 1 求z 的最大值和最小值
由x,y 的不等式(或方程)组成的不等式组称为x,y 的 约束条件。关于x,y 的一次不等式或方程组成的不等 式组称为x,y 的线性约束条件。欲达到最大值或最小 值所涉及的变量x,y 的解析式称为目标函数。关于x, y 的一次目标函数称为线性目标函数
典例解读 10.已知动圆过定点P(1,0),且与定直 线 l : x 1 相切, 求动圆圆心的轨迹M的方程;
典例解读
11.已知点A(2, 0), B(0, 6),O为坐标原点 若点C 在线段OB上,且BAC 求ABC的面积
4
,
; / 奇迹私发网 ; 2019.1
(1)两圆外离 (2)两圆外切 (3)两圆相交 (4)两圆内切 (5)两圆内含 d>R+r d=R+r R-r<d<R+r d=R-r d<R-r
直线与圆的关系

直线与圆的关系
直线和圆是数学中的重要概念,它们之间的关系被应用于解决各种问题,并在
不同的研究领域中发挥着重要作用。
直线是指任意给定两点之间的最短路径,它是一个平行四边形中所有顶点的连线。
而圆即一个由一个点为中心,由某一距离为半径的闭合曲线形成的球面。
圆的方程可以表示为:x²+y²=r²,圆的方程的参数包括圆的半径r和圆心位置(h,k)。
直线和圆之间的关系是十分重要的。
通常情况下,直线可以与圆有四种关系:
穿过圆心、与圆相切、穿过圆、相交。
第一种关系是直线穿过圆心,这意味着圆心落在直线上,满足直线方程
y=mx+b,圆方程可以表示为(x-h)²+(y-k)²=r²。
第二种情况是直线与圆相切,此时直线满足直线方程y=mx+b,圆方程可以表
示为(x-h)²+(y-k)²=r²,这意味着直线的斜率等于半径的平方根。
第三种情况是直线穿过圆,这意味着直线满足直线方程y=mx+b,而圆方程可
以表示为(x-h)²+(y-k)²=r²,此时,斜率不等于半径的平方根。
第四种情况是直线与圆相交,满足直线方程y=mx+b,圆方程可以表示为(x-h)²+(y-k)²=r²,斜率可以大于,小于或等于半径的平方根。
在总结以上,我们可以看出,直线和圆之间的关系是一个复杂的问题,有四个
基本的关系,所有的情况都取决于斜率以及圆半径的大小。
因此,要求学生了解直线和圆之间的关系和方程,从而判断他们之间的不同关系,尤其是线与圆相交和线与圆相切等情况,这需要深入研究和分析。
最新高职高专考数学科复习7.直线和圆

第七章 直线和圆一 直线(一)直线的独立图形:1.定义:),0[πα∈,2121tan x x y y k --==α 2.方程:题型是求直线方程(1) 点斜式)(00x x k y y -=-不能表示斜率不存在的直线,如右图(2) 斜截式y kx b =+不能表示斜率不存在的直线,如右图(3) 两点式 121121x x x x y y y y --=-- 不能表示和坐标轴平行的直线,如右图(4) 截距式1x y a b+= 不能表示与坐标轴平行的直线以及过原点的直线,如图(5) 一般0C =++By Ax 能表示所有直线(二)直线与其他图的位置关系1.位置关系的判定(1) 点与直线位置关系y kx b y kx b y kx b =+⎧⎪>+⎨⎪<+⎩在直线上在直线上方在直线下方(2) 两直线平行的判定11111122222200A x B y C A B C A x B y C A B C ++=⎧=≠⎨++=⎩ 这两条直线平行的等价条件是 11121222y k x b k k b b y k x b =+⎧=≠⎨=+⎩ 这两条直线平行的等价条件是 且(3) 两直线垂直1111212222000A xB yC A A B B A x B y C ++=⎧+=⎨++=⎩ 这两条直线垂直的等价条件是 1112221y k x b k k y k x b =+⎧=-⎨=+⎩ 这两条直线垂直的等价条件是2.求量(1)、点与线不同位置关系的求量问题a.点()00,x y 到直线A B C 0x y ++=的距离为:2200B A C By Ax d +++=b.点()00,x y 关于直线A B C 0x y ++=的对称点(),x y 的求法:⎪⎪⎩⎪⎪⎨⎧=++++=--0220000C y y B x x A A B x x y y(2)、线与线不同位置关系的求量问题a.⎩⎨⎧=++=++0021C By Ax C By Ax 两条平行线的距离:2221B A C C d +-=二.圆(一)圆的独立图形1.定义: 主要考定义中轨迹一词求轨迹题型:(1)直接求a.设点),(y xb.列关于y x ,的等式c.把所有未知量全转化为y x 、(2)、间接求a.设点),(y x 和必须联系的点),(00y xb.列关于),(y x ,),(00y x 的等式c.解出),(0y x f x =,),(0y x f y =d.把00,y x 代入满足的方程(3)、根据平面几何的结论和曲线定义直接写出轨迹2.圆的方程:标准方程: 222)()(r b y a x =-+-一般式: 022=++++F Ey Dx y x题型:求方程,相当于求方程里字母取值(1)F E D ,,(已知圆上三点坐标)(2)r b a ,,(其他情况)求方程就是求三个系数,需要列出关于系数的等式。
高中数学竞赛试题汇编七《直线与圆》讲义

高中数学竞赛试题汇编七《直线与圆》一、知识清单1. 求轨迹方程的步骤:建(系),设(点),限(制条件),代(入坐标),化(简).2.直线方程的几种形式:一般/点斜/斜截/截距/两点式.3.l 1//l 2的充要条件是k 1=k 2;l 1l 2的充要条件是k 1k 2=-1。
4.两点P 1(x 1, y 1)与P 2(x 2, y 2)间的距离公式:|P 1P 2|=221221)()(y y x x -+-。
5.点P(x 0, y 0)到直线l: Ax+By+C=0的距离公式:2200||B A C By Ax d +++=。
6.圆的标准方程为(x-a)2+(y-b)2=r 2;圆的一般方程:x 2+y 2+Dx+Ey+F=0(D 2+E 2-4F>0)圆的参数方程为⎩⎨⎧+=+=θθsin cos r b y r a x 二、试题汇编1. 与圆()2221x y -+=相切,且在两坐标轴上截距相等的直线有 (A) 2条 (B) 3条 (C) 4条 (D) 6条2. 已知221a b +=,且c a b <+恒成立,则c 的取值范围是(A) (,2)-∞- (B) (,-∞ (C) ( (D) (-∞3. P 是圆2236x y +=上的动点,A (20,0)线段PA 的中点M 的轨迹方程为4. 已知点P 是直线40kx y ++=,PA ,PB 是圆C: 2220x y y +-=的两条切线,A 、B 是切点,若四边形PACB 的最小面积是2,则k 的值为 .5. 若集合: {}221(,)lg(1)1lg()S x y x y x y =++≤++ {}222(,)lg(2)2lg()S x y x y x y =++≤++则2S 的面积与1S 的面积之比为 .6. 在直角坐标xoy 中,曲线235x y +=所围成的图形的面积是 .7. 直线10ax by -+=平分圆222410x y x y ++-+=的周长,则ab 的取值范围为 .8. 点P 在圆2225x y +=上,A (1,2)、B (4,1),则△PAB 面积最大值是 .9. 已知[0,2)θπ∈,则θθs i n 2c o s 3-+=y 的取值范围是 .10. 方程1x -=表示的曲线是 .11. 函数()2f x x =+的值域是 .。
高考数学专题7解析几何之直线与圆
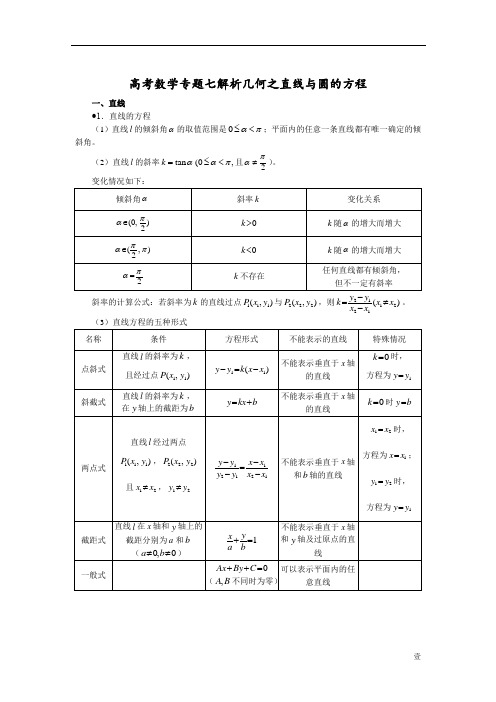
壹高考数学专题七解析几何之直线与圆的方程一、直线 ●1.直线的方程(1)直线l 的倾斜角α的取值范围是0απ≤<;平面内的任意一条直线都有唯一确定的倾斜角。
(2)直线l 的斜率tan (0,k ααπ=≤<且2πα≠)。
变化情况如下:斜率的计算公式:若斜率为k 的直线过点111(,)P x y 与222(,)P x y ,则211221()k x x x x =≠-。
(3)直线方程的五种形式贰●2.两条直线位置关系(1)设两条直线111:l y k x b =+和222:l y k x b =+,则有下列结论:1212//l l k k ⇔=且12b b ≠; 12121l l k k ⊥⇔⋅=-。
(2)设两条直线111111:0(,l A x B y C A B ++=不全为0)和2222:0l A x B y C ++=22(,A B ,不全为0),则有下列结论:12//l l ⇔12210A B A B -=且12210BC B C -≠或12210A B A B -=且12210AC A C -≠; 12l l ⊥⇔12120A A B B +=。
(3)求两条直线交点的坐标:解两条直线方程所组成的二元一次方程组而得解。
(4)与直线0Ax By C ++=平行的直线一般可设为0Ax By m ++=;与直线0Ax By C ++=垂直的直线一般可设为0Bx Ay n -+=。
(5)过两条已知直线1112220,0A x B y C A x B y C ++=++=交点的直线系:111222222()0(0)A x B y C A x B y C A x B y C λ+++++=++=其中不包括直线●3.中点公式:平面内两点111(,)P x y 、222(,)P x y ,则12,P P 两点的中点(,)P x y 为1212,22y y x x x y ++==。
●4.两点间的距离公式:平面内两点111(,)P x y ,222(,)P x y ,则12,PP两点间的距离为:12PP 。
直线与圆的位置关系 属于什么阶段知识点

直线与圆的位置关系属于什么阶段知识点
直线与圆的位置关系是初中数学中的一个知识点,主要涉及平面几何的内容。
具体来说,这一知识点通常出现在初中数学七年级和八年级的课程中,特别是在学习点和直线的距离、圆的性质和圆与直线的位置关系等章节时。
这个知识点要求学生理解直线与圆的基本性质,掌握判断直线与圆的位置关系的方法,例如通过圆心到直线的距离与圆的半径的比较来判断。
此外,学生还需要了解直线与圆的位置关系在日常生活中的应用,例如在几何图形、工程制图和地理测量等领域的应用。
在学习这一知识点时,学生需要通过观察、操作和推理等活动,培养自己的几何直觉和空间观念,提高自己的逻辑推理和证明能力。
同时,学生还需要掌握基本的数学工具和技能,如使用量角器和圆规等工具进行测量和作图。
总之,直线与圆的位置关系是初中数学中的一个重要知识点,对于培养学生的几何思维和空间观念具有重要意义。
直线与圆知识点总结

直线与圆知识点总结1. 直线与圆的位置关系:- 直线与圆可能相交于两个点,这种情况称为相交。
- 直线与圆可能与圆外部割线相切于一点,这种情况称为相切。
- 直线可能与圆没有交点,这种情况称为相离。
2. 判断直线与圆的位置关系:- 使用勾股定理可以判断直线与圆是否相交。
设直线的方程为ax + by + c = 0,圆的方程为(x - h)² + (y - k)² = r²,其中(h, k)为圆心的坐标,r为半径。
将直线的方程代入圆的方程,计算方程的解。
若方程的解为实数,且解满足直线的方程,则直线与圆相交;若方程的解为实数,但解不满足直线的方程,则直线与圆相离;若方程的解为复数,则直线与圆相切。
- 使用两点式可以判断直线与圆的位置关系。
设直线上两点为(x₁, y₁)和(x₂, y₂),圆的方程为(x - h)² + (y - k)² = r²,其中(h, k)为圆心的坐标,r为半径。
计算直线的斜率m = (y₂ - y₁) / (x₂ - x₁),若直线的斜率存在且非零,则直线与圆相交或相离;若直线的斜率不存在或为0,则直线可能与圆相切或相离。
将直线的方程代入圆的方程,计算方程的解。
若方程的解为实数,且解满足直线的方程,则直线与圆相交;若方程的解为实数,但解不满足直线的方程,则直线与圆相离;若方程的解为复数,则直线与圆相切。
3. 求直线与圆的交点:- 设直线的方程为ax + by + c = 0,圆的方程为(x - h)² + (y - k)²= r²,其中(h, k)为圆心的坐标,r为半径。
将直线的方程代入圆的方程,得到一个关于x的二次方程。
解这个方程即可得到直线与圆的交点的x坐标。
将得到的x坐标代入直线的方程,可以求得对应的y坐标。
4. 求直线与圆的切点:- 设直线的方程为ax + by + c = 0,圆的方程为(x - h)² + (y - k)²= r²,其中(h, k)为圆心的坐标,r为半径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学概念、方法、题型、易误点总结(七)班级 姓名七、直线和圆1、直线的倾斜角:(1)定义:在平面直角坐标系中,对于一条与x 轴相交的直线l ,如果把x 轴绕着交点按逆时针方向转到和直线l 重合时所转的最小正角记为α,那么α就叫做直线的倾斜角。
当直线l 与x 轴重合或平行时,规定倾斜角为0;(2)倾斜角的范围[)π,0。
如(1)直线023cos =-+y x θ的倾斜角的范围是__ __; (2)过点),0(),1,3(m Q P -的直线的倾斜角的范围m 那么],32,3[ππα∈值的范围是__2、直线的斜率:(1)定义:倾斜角不是90°的直线,它的倾斜角的正切值叫这条直线的斜率k ,即k =tan α(α≠90°);倾斜角为90°的直线没有斜率;(2)斜率公式:经过两点111(,)P x y 、222(,)P x y 的直线的斜率为()212121x x x x y y k ≠--=;(3)直线的方向向量(1,)a k =,直线的方向向量与直线的斜率有何关系?(4)应用:证明三点共线: AB BC k k =。
如(1) 两条直线钭率相等是这两条直线平行的____________条件; (2)实数,x y 满足3250x y --= (31≤≤x ),则xy的最大值、最小值分别为______3、直线的方程:(1)点斜式:已知直线过点00(,)x y 斜率为k ,则直线方程为00()y y k x x -=-,它不包括垂直于x 轴的直线。
(2)斜截式:已知直线在y 轴上的截距为b 和斜率k ,则直线方程为y kx b =+,它不包括垂直于x 轴的直线。
(3)两点式:已知直线经过111(,)P x y 、222(,)P x y 两点,则直线方程为121121x x x x y y y y --=--,它不包括垂直于坐标轴的直线。
(4)截距式:已知直线在x 轴和y 轴上的截距为,a b ,则直线方程为1=+bya x ,它不包括垂直于坐标轴的直线和过原点的直线。
(5)一般式:任何直线均可写成0Ax By C ++=(A,B 不同时为0)的形式。
如(1)经过点(2,1)且方向向量为v=(-1,3)的直线的点斜式方程是___________; (2)直线(2)(21)(34)0m x m y m +----=,不管m 怎样变化恒过点______;(3)若曲线||y a x =与(0)y x a a =+>有两个公共点,则a 的取值范围是_______提醒:(1)直线方程的各种形式都有局限性.(如点斜式不适用于斜率不存在的直线,还有截距式呢?);(2)直线在坐标轴上的截距可正、可负、也可为0.直线两截距相等⇔直线的斜率为-1或直线过原点;直线两截距互为相反数⇔直线的斜率为1或直线过原点;直线两截距绝对值相等⇔直线的斜率为1±或直线过原点。
如过点(1,4)A ,且纵横截距的绝对值相等的直线共有___条4.设直线方程的一些常用技巧:(1)知直线纵截距b ,常设其方程为y kx b =+;(2)知直线横截距0x ,常设其方程为0x my x =+(它不适用于斜率为0的直线); (3)知直线过点00(,)x y ,当斜率k 存在时,常设其方程为00()y k x x y =-+,当斜率k 不存在时,则其方程为0x x =;(4)与直线:0l Ax By C ++=平行的直线可表示为10Ax By C ++=; (5)与直线:0l Ax By C ++=垂直的直线可表示为10Bx Ay C -+=.提醒:求直线方程的基本思想和方法是恰当选择方程的形式,利用待定系数法求解。
5、点到直线的距离及两平行直线间的距离: (1)点00(,)P x y 到直线0Ax By C ++=的距离d =;(2)两平行线1122:0,:0l Ax By C l Ax By C ++=++=间的距离为d =。
6、直线1111:0l A x B y C ++=与直线2222:0l A x B y C ++=的位置关系: (1)平行⇔12210A B A B -=(斜率)且12210B C B C -≠(在y 轴上截距); (2)相交⇔12210A B A B -≠;(3)重合⇔12210A B A B -=且12210B C B C -=。
提醒:(1)111222A B C A B C =≠、1122A B A B ≠、111222A B CA B C ==仅是两直线平行、相交、重合的充分不必要条件!为什么?(2)在解析几何中,研究两条直线的位置关系时,有可能这两条直线重合,而在立体几何中提到的两条直线都是指不重合的两条直线;(3)直线1111:0l A x B y C ++=与直线2222:0l A x B y C ++=垂直⇔12120A A B B +=。
如(1)设直线1:60l x my ++=和2:(2)320l m x y m -++=,当m =_______时1l ∥2l ; 当m =________时1l ⊥2l ;当m _________时1l 与2l 相交;当m =_________时1l 与2l 重合; (2)已知直线l 的方程为34120x y +-=,则与l 平行,且过点(—1,3)的直线方程是______;(3)两条直线40ax y +-=与20x y --=相交于第一象限,则实数a 的取值范围是____;(4)设,,a b c 分别是△ABC 中∠A 、∠B 、∠C 所对边的边长,则直线sin 0x A ay c ++=与sin sin 0bx y B C -+=的位置关系是____;(5)已知点111(,)P x y 是直线:(,)0l f x y =上一点,222(,)P x y 是直线l 外一点,则方程1122(,)(,)(,)f x y f x y f x y ++=0所表示的直线与l 的关系是____;(6)直线l 过点(1,0),且被两平行直线360x y +-=和330x y ++=所截得的线段长为9,则直线l 的方程是________7、到角和夹角公式:(1)1l 到2l 的角是指直线1l 绕着交点按逆时针方向转到和直线2l 重合所转的角θ,θ()π,0∈且tan θ=21121k k k k +-(121k k ≠-);(2)1l 与2l 的夹角是指不大于直角的角,(0,]2πθθ∈且tan θ=︱21121k k k k +-︱(121k k ≠-)。
提醒:解析几何中角的问题常用到角公式或向量知识求解。
如已知点M 是直线240x y --=与x 轴的交点,把直线l 绕点M 逆时针方向旋转45°,得到的直线方程是______8、对称(中心对称和轴对称)问题——代入法:如(1)已知点(,)M a b 与点N 关于x 轴对称,点P 与点N 关于y 轴对称,点Q 与点P 关于直线0x y +=对称,则点Q 的坐标为_______;(2)已知直线1l 与2l 的夹角平分线为y x =,若1l 的方程为0(0)ax by c ab ++=>,那么2l 的方程是___________;(3)点A(4,5)关于直线l 的对称点为B(-2,7),则l 的方程是_________; (4)已知一束光线通过点A(-3,5),经直线l :3x -4y+4=0反射。
如果反射光线通过点B(2,15),则反射光线所在直线的方程是_________;(5)已知ΔABC 顶点A(3,-1),AB边上的中线所在直线的方程为6x+10y -59=0,∠B 的平分线所在的方程为x -4y+10=0,求BC边所在的直线方程;(6)直线2x ―y ―4=0上有一点P,它与两定点A(4,-1)、B(3,4)的距离之差最大,则P的坐标是______;(7)已知A x ∈轴,:B l y x ∈=,C (2,1),ABC ∆周长的最小值为______。
提醒:在解几中遇到角平分线、光线反射等条件常利用对称求解。
9、简单的线性规划:(1)二元一次不等式表示的平面区域:①法一:先把二元一次不等式改写成y kx b >+或y kx b <+的形式,前者表示直线的上方区域,后者表示直线的下方区域;法二:用特殊点判断;②无等号时用虚线表示不包含直线l ,有等号时用实线表示包含直线l ;③设点11(,)P x y ,22(,)Q x y ,若11Ax By C ++与22Ax By C ++同号,则P ,Q 在直线l 的同侧,异号则在直线l 的异侧。
如已知点A (—2,4),B (4,2),且直线:2l y kx =-与线段AB 恒相交,则k 的取值范围是__________(2)线性规划问题中的有关概念:①满足关于,x y 的一次不等式或一次方程的条件叫线性约束条件。
②关于变量,x y 的解析式叫目标函数,关于变量,x y 一次式的目标函数叫线性目标函数; ③求目标函数在线性约束条件下的最大值或最小值的问题,称为线性规划问题; ④满足线性约束条件的解(,x y )叫可行解,由所有可行解组成的集合叫做可行域; ⑤使目标函数取得最大值或最小值的可行解叫做最优解; (3)求解线性规划问题的步骤是什么?①根据实际问题的约束条件列出不等式;②作出可行域,写出目标函数; ③确定目标函数的最优位置,从而获得最优解。
如(1)线性目标函数z=2x -y 在线性约束条件{||1||1x y ≤≤下,取最小值的最优解是____;(2)点(-2,t )在直线2x -3y+6=0的上方,则t 的取值范围是_________;(3)不等式2|1||1|≤-+-y x 表示的平面区域的面积是_________;(4)如果实数y x ,满足2040250x y x y x y -+≥⎧⎪+-≥⎨--≤⎪⎩,则|42|-+=y x z 的最大值_________(5)4个茶杯和5包茶叶的价格之和小于22元,而6个茶杯与3包茶叶的价格之和大于24元,则2个茶杯与3包茶叶的价格比较(A )2个茶杯贵, (B )3包茶叶贵, (C )二者相同, (D )无法确定。
(4)在求解线性规划问题时要注意:①将目标函数改成斜截式方程;②寻找最优解时注意作图规范。
10、圆的方程:⑴圆的标准方程:()()222x a y b r -+-=。
⑵圆的一般方程:22220(D E 4F 0)+-x y Dx Ey F ++++=>,特别提醒:只有当22D E 4F 0+->时,方程220x y Dx Ey F ++++=才表示圆心为(,)22D E --(二元二次方程220Ax Bxy Cy Dx Ey F +++++=表示圆的充要条件是什么?(0,A C =≠且0B =且2240D E AF +->));⑶圆的参数方程:{cos sin x a r y b r θθ=+=+(θ为参数),其中圆心为(,)a b ,半径为r 。
