2012年第十届四年级走美杯试题详解
2012走美杯第十届五年级模拟

第十届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛模拟卷注意事项:1. 考生要按要求在密封线内填好考生的有关信息.2. 不允许使用计算器.小学五年级试卷一、填空题(共5题,每题8分,共40分)1、 算式:1÷(2÷3)÷(3÷4)÷(4÷5)的计算结果是________________2、 2、用大小两辆火车运煤,大货车运了 9 次,小货车运了 12 次 ,一共运了 180 吨。
大货车的载重量等于小货车载重量的 2 倍,大货车的载重量为 吨,小货车的载重量为 吨3、三个正方形如图放置,中心都重合,它们的边长一次是 1cm 、3cm 、5cm ,图中阴影部分的面积是____平方厘米。
4、有两根同样长的绳子,第一根平均剪成 5 段,第二根平均剪成 9 段。
第一根剪成的每段比第二根剪成的每段长 10 米。
原来的每根绳子长____米。
5、观察一组式,41409,25247,13125,543222222222222=+=+=+=+……根据以上规律,请你写出第7组的式子:__________________二、填空题(共5题,每题10分)6、右图的两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,四位数 ABCD =____。
7、A 、B 、C 、D 、E 五个盒子中依次放有 2、4、6、8、10 个小球。
第一个小朋友找到放球最多的盒子,从中拿出 4 个放在其他盒子中各一个球。
第二个小朋友也找到放球最多的盒子,从中拿出 4 个放在其他盒子中各一个球,依次类推,… ,当 2011 个小朋友放完后,A 盒中放有___个球。
8、右图是一个 6×6 的方格表,现在将格线将它分割成 N 个面积各不相等的长方形(含正方形)。
N 最大是___。
9、五个连续的自然数,每个数都是合数,这五个连续自然数的和最小是____。
小学奥数杯赛真题1312

1.小泉做一道除数是一位数的除法时,误把除数9看成6,结果算出的商是7,余数是3。
你知道正确的结果是(2012世奥(中国区)选拔赛三年级A卷)2.杨阳是班里有名的小马虎,这次在做(200×9-□)÷25+13时,又没看到题里的括号,算的结果是1788,正确的结果应该是 (2012世奥数浙江赛区四年级)。
3.袋子里有若干个球,每次拿出其中的一半又一个球,这样共操作了4次,袋中还有5个球。
袋中原有____个球(2012年第十届走美杯三年级)。
4.盒子里有若干个球。
小明每次拿出盒中的一半再放回一个球。
这样共操作了7次,袋中还有3个球。
袋中原有个球(2010年走美杯三年级)。
5.抽屉里有若干个玻璃球, 小军每次操作都取出抽屉中球数的一半再放回一个球。
如此操作了2012次后, 抽屉里还剩有2个球。
那么原来抽屉里有个球(第十七届华杯赛小中组复赛)。
6.黑板上写有一个数,男同学从黑板前走过时,把他乘以3再减去14,擦去原数,换上答案,女同学从黑板前走过时,把他乘以2再减去7,擦去原数,换上答案。
全班25名男同学和15名女同学都走过后,老师把最后的数乘以5,减去5,结果是30。
那么,黑板上最初的数字是(湖北第七届创新杯)。
7.豆豆和苗苗各有一盒玻璃球,共108粒,豆豆给了苗苗10粒,豆豆剩下的玻璃比苗苗还多8粒。
原来苗苗有粒玻璃球(2010年第八届走美杯三年级)。
8.甲、乙、丙三人的平均年龄为42岁,若将甲的岁数增加7岁,乙的岁数扩大2倍,丙的岁数缩小2倍,则三人岁数相等。
丙的年龄为________岁(第四届迎春杯)。
9.甲、乙、丙、丁四人一共做了370个零件,如果把甲做的个数加上10个,乙做的个数减去20个,丙做的个数乘以2,丁做的个数除以2,四人做的零件数就正好相等。
那么乙实际做了_____ 个零件(第二届迎春杯)。
10.甲、乙、丙三所小学的学生人数的总和为1999。
已知甲校学生人数的2倍和乙校学生人数减去3人与丙校学生人数加上4人都相等。
走美杯

1.“走美杯”的重要性“走美”是小学奥数竞赛中覆盖年级数最多的杯赛,从小学三年级到初中二年级的学生都可以通过参加“走进美妙的数学花园”杯赛活动。
“走美”作为数学竞赛中的后起之秀,凭借其新颖的考试形式以及较高的竞赛难度取得了非常迅速的发展,近年来在重点中学选拔中引起了广泛的关注。
客观地说“走美”一、二等奖对小升初作用非常大,三等奖作用不大。
中低年级是学生参加杯赛考试的最佳时期。
学生的数学竞赛实力不是一朝一夕之间就可以轻易锻炼出来的,低年级从不接触竞赛而等到六年级再拿到含金量高的杯赛成绩是不切实际的想法与做法。
所以,孩子从学习奥数开始就应该为各种杯赛作好应战的准备,其中“走美”是中低年级同学的一次绝佳竞赛锻炼机会。
获得奖可以增强孩子信心、提高孩子兴趣、积累成绩证书。
考试失败也可以锻炼孩子应考能力、总结考试经验、促进学习动力。
中低年级的所有杯赛准备都是为了高年级时向更高杯赛奖项冲击,这是一个非常必要的提高过程。
五六年级的“走美”奖项都是小升初中被各重点中学看中的含金量非常高的杯赛奖项之一。
尤其被北大附、清华附、四中、实验等重视学生综合素质的重点中学看重。
因为“走美”作为奥数杯赛的一个重要特点就是试题不偏不刁、难度适中,强调考察学生的数学基本能力,奥数基础知识。
所以受到众多重点中学选拔综合型学生的青睐,成为录取的最佳参考标准之一。
2.“走美杯”难度指数有多高走美杯03年起办,12年为第10届。
“走美”作为奥数杯赛的一个重要特点就是试题不偏不刁、难度适中,强调考察学生的数学基本能力,奥数基础知识。
走美成绩管理很好,且透明度高,应该有说服力。
走美的透明度和速度,成绩名次张榜公布,考完后迅速出成绩,不拖泥带水。
较之其他杯赛,走美是比较透明清晰的。
只要比赛公平透明,结果就会有说服力。
获奖人数较多,是因总参加人数多。
走美是按比例设奖的:5%一等,10%二等,15%三等。
3.“走美杯”的特色和优势1、“走美”是四大杯赛中唯一一个只考一次就评选最后奖项的竞赛。
9数的整除2(学生)

第九讲数的整除(2)知识概述一、常见数字的整除判定方法1.一个数的末位能被2或5整除,这个数就能被2或5整除;一个数的末两位能被4或25整除,这个数就能被4或25整除;一个数的末三位能被8或125整除,这个数就能被8或125整除。
2.一个数各位数数字和能被3整除,这个数就能被3整除;一个数各位数数字和能被9整除,这个数就能被9整除。
3.如果一个整数的奇数位上的数字之和与偶数位上的数字之和的差能被11整除,那么这个数能被11整除。
4.如果一个整数的末三位与末三位以前的数字组成的数之差能被7、11或13整除,那么这个数能被被7、11或13整除。
二、整除的性质1.如果数a和数b都能被数c整除,那么它们的和或差也能被c整除。
2.如果数a能被数b整除,b又能被数c整除,那么a也能被c整除。
3.如果数a能被数b与数c的积整除,那么a也能被b或c整除。
4.如果数a能被数b整除,也能被数c整除,且数b和数c互素,那么a一定能被b与c的乘积整除。
5.如果数a能被数b整除,那么am也能被bm整除。
(m为非0整数)6.如果数a能被数b整除,数c能被数d整除,那么bd也能被ac整除。
例题精讲【例1】判断下面11个数的整除性:23487,3568,8875,6765,5880,7538,198954,6512,93625,864,407⑴这些数中,有哪些数能被4整除?有哪些数能被8整除?⑵这些数中,哪些数能被25整除?哪些数能被125整除?⑶这些数中,哪些数能被3整除?哪些数能被9整除?⑷这些数中,哪些数能被11整除?【拓展】五位数abcde是9的倍数,其中abcd是4的倍数,那么abcde的最小值是。
【拓展】(2013年第十一届“小机灵杯”四年级决赛)把一个三位数的百位与个位上的两个数字交换,十位数不变,所得的新数与原数相等,这样的数共有()个,其中能被4整除的有()个。
【例2】(2011年第九届“小机灵杯”四年级决赛)某三位数是9的倍数,而且在300~400之间,它的百位与个位数字和为10,问这个数是()。
2012年第十届走美杯初赛小学五年级(含解析)
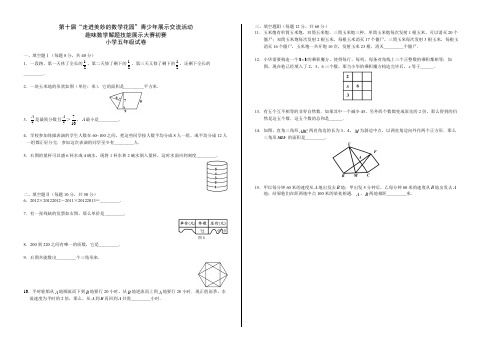
第十届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学五年级试卷一、填空题Ⅰ(每题8分,共40分)1.一段路,第一天休了全长的12,第二天修了剩下的12,第三天又修了剩下的12,还剩下全长的_________.2.一块玉米地的形状如图(单位:米).它的面积是_________平方米.3.7A 是最简分数且7A >710,A 最小是_________.4.学校参加体操表演的学生人数在60~100之间,把这些同学按人数平均分成8人一组,或平均分成12人一组都正好分完.参加这次表演的同学至少有_________人.5.右图的量杯可以盛6杯水或4碗水,现将1杯水和2碗水倒入量杯,这时水面应到刻度_________.二、填空题Ⅱ(每题10分,共50分)6.2012×20122012-2011×20122013=_________.7.有一张残缺的发票如右图,那么单价是_________.8.200到220之间有唯一的质数,它是_________.9.右图共能数出_________个三角形来.10.平时轮船从A 地顺流而下到B 地要行20小时,从B 地逆流而上到A 地要行28小时.现正值雨季,水流速度为平时的2倍,那么,从A 到B 再回到A 共需_________小时.三、填空题Ⅲ(每题12分,共60分)11.玉米炮有单筒玉米炮、双筒玉米炮、三筒玉米炮三种,单筒玉米炮每次发射1根玉米,可以消灭20个僵尸;双筒玉米炮每次发射2根玉米,每根玉米消灭17个僵尸,三筒玉米每次发射3根玉米,每根玉 消灭16个僵尸,玉米炮一共开炮10次,发射玉米23根,消灭_________个僵尸.12.小华需要构造一个33 的乘积魔方,使得每行、每列、每条对角线上三个正整数的乘积都相等;如图,现在他已经填入了2,3,6三个数,那当小华的乘积魔方构造完毕后,x 等于______.13.有五个互不相等的非零自然数.如果其中一个减少45,另外四个数都变成原先的2倍,那么得到的仍然是这五个数.这五个数的总和是______.14.如图,直角三角形ABC 两直角边的长为3、4,M 为斜边中点,以两直角边向外作两个正方形.那么三角形MEF 的面积是_________.15.甲以每分钟60米的速度从A 地出发去B 地;甲出发5分钟后,乙每分钟80米的速度从B 地出发去A 地;结果他们在距两地中点100米的某处相遇.A 、B 两地相距_________米.第十届“走进美妙的数学花园”青少年展示交流活动图3趣味数学解题技能展示大赛初赛 小学五年级试卷参考答案1 2 3 4 5 6 7 8 18 85 5 72 4 20120001 1.36 2119 10 11 12 13 14 153252.5382369312.251000或3800参考解析一、填空题Ⅰ(每题8分,共40分)1.一段路,第一天休了全长的12,第二天修了剩下的12,第三天又修了剩下的12,还剩下全长的________.【考点】分数应用题 【难度】☆ 【答案】18【解析】相当于每天将剩余的减少到12,共减少了3次,共减少到11112228⨯⨯=.2.一块玉米地的形状如图(单位:米).它的面积是_________平方米.【考点】几何 【难度】☆【答案】87【解析】分成一个三角形和一个平行四边形,其面积为6827987⨯÷+⨯=.3.7A 是最简分数且7A >710,A 最小是_________.【考点】最值问题 【难度】☆☆ 【答案】5【解析】两边乘以7得到494.910A >=,所以所求的最小值为5.4.学校参加体操表演的学生人数在60~100之间,把这些同学按人数平均分成8人一组,或平均分成12人一组都正好分完.参加这次表演的同学至少有_________人. 【考点】数论整除 【难度】☆☆【答案】72【解析】8和12的最小公倍数为24,其倍数依次为:48、72、108、……所以为72.5.右图的量杯可以盛6杯水或4碗水,现将1杯水和2碗水倒入量杯,这时水面应到刻度_________.【考点】几何【难度】☆☆☆【答案】4【解析】每杯水相当于661÷=个刻度,每碗水相当于64 1.5÷=个刻度,所以1杯水和2碗水相当于12 1.54+⨯=个刻度.二、填空题Ⅱ(每题10分,共50分)6.2012×20122012-2011×20122013=_________. 【考点】速算巧算 【难度】☆☆☆【答案】20120001【解析】原式201220120000201220122011201200002011201320120001=⨯+⨯-⨯-⨯=.7.有一张残缺的发票如右图,那么单价是_________.【考点】数论弃九法 【难度】☆☆☆【答案】1.36【解析】可观察到个位数字为7,由于72是9的倍数,可得其数字和为9的倍数,百分位为2.经检验,符合题意:97.9272 1.36÷=.8.200到220之间有唯一的质数,它是_________. 【考点】质数合数 【难度】☆☆☆【答案】211【解析】依次划去所有2、3、5、7、11的倍数可得其为211.9.右图共能数出_________个三角形来.【考点】几何计数 【难度】☆☆☆【答案】32【解析】小正三角形有6个,大正三角形有2个,以大正六边形的边为底的等腰三角形有6个,以大正六边形的两条相邻的边为腰的等腰三角形有6个,直角三角形有12个,共32个.10.平时轮船从A地顺流而下到B地要行20小时,从B地逆流而上到A地要行28小时.现正值雨季,水流速度为平时的2倍,那么,从A到B再回到A共需_________小时.【考点】行程问题【难度】☆☆☆【答案】52.5【解析】设全程为1,每小时顺水行驶的距离为1720140=,逆水行驶的距离为1528140=,则观察到水速增加后,每小时顺水行驶的距离和逆水行驶的距离分别为8140和4140,所求的时间为140140+=52.584小时.三、填空题Ⅲ(每题12分,共60分)11.玉米炮有单筒玉米炮、双筒玉米炮、三筒玉米炮三种,单筒玉米炮每次发射1根玉米,可以消灭20个僵尸;双筒玉米炮每次发射2根玉米,每根玉米消灭17个僵尸,三筒玉米每次发射3根玉米,每根玉米消灭16个僵尸,玉米炮一共开炮10次,发射玉米23根,消灭_________个僵尸.【考点】鸡兔同笼【难度】☆☆☆【答案】382【解析】三种玉米炮每发射一次分别消灭20个,34个,48个僵尸,成等差数列.也就是说,无论哪种玉米炮,发射一次,消灭的僵尸数等于玉米数146⨯+.多次发射后,消灭的僵尸数应该等于总玉米数14⨯+发射次数6⨯.那么,总共发射了10次,所以消灭的僵尸数等于2314106382⨯+⨯=.12.小华需要构造一个33⨯的乘积魔方,使得每行、每列、每条对角线上三个正整数的乘积都相等;如图,现在他已经填入了2,3,6三个数,那当小华的乘积魔方构造完毕后,x等于______.【考点】幻方【难度】☆☆【答案】36【解析】幻积等于中间数6的立方,所以362336x=÷÷=.13.有五个互不相等的非零自然数.如果其中一个减少45,另外四个数都变成原先的2倍,那么得到的仍然是这五个数.这五个数的总和是______.【考点】数论倍数约数【难度】☆☆☆【答案】93【解析】如果一开始的五个数分别是1、2、4、8、16,则将16减少15后,将其他四个数都乘以2,可以仍然得到这5个数.而45153÷=,所以原来的五个数是1、2、4、8、16的3倍,总和为313=93⨯.14.如图,直角三角形ABC两直角边的长为3、4,M为斜边中点,以两直角边向外作两个正方形.那么三角形MEF的面积是_________.【考点】几何【难度】☆☆☆【答案】12.25【解析】1(43)4142BEFS=⨯+⨯=△,1(43)310.52CBFS=⨯+⨯=△,以EF为底,则MEF△的高是BEF△和CEF△的高的平均值,所以面积也是它们的平均值,等于12.25.15.甲以每分钟60米的速度从A地出发去B地;甲出发5分钟后,乙每分钟80米的速度从B地出发去A地;结果他们在距两地中点100米的某处相遇.A、B两地相距_________米.【考点】行程问题【难度】☆☆☆【答案】1000或3800【解析】设两地相距2x米,则有10010056080x x+-=+或10010056080x x-+=+,得到500x=或1900x=,则答案为1000或3800.。
四年级走美自测题 教师版

四年级走美杯自测卷填空题Ⅰ(每题8分,共40分)1、2000年后为三个连续自然数乘积的第一个年份是 。
【解析】:11×12×13=1716,12×13×14=2184。
2、将正整数1,2,3,4,5,6,…,10000排成一行。
若一个数不能表示成两个合数的和,则将此数划去。
例如要划去1,但是因为8=4+4,8就不能划去。
根据上面规定划掉所有能划掉的数之后,将剩下的由小到达排列,这时从左数第2016个数是 。
【解析】:从8开始往后的偶数可以拆成两个偶合数的和;从13开始的奇数可以拆成9+2n 的形式(n 大于等于2),而1、2、3、4、5、6、7、9、11要划去,所以剩下的数列为8、10、12、13、14、15……,第2016项即为2025。
3、图中共有 个三角形。
【解析】:①由1个小三角形构成的三角形有24个;②由2个小三角形构成的三角形有20个;③由3个小三角形构成的三角形有8个;④由4个小三角形构成的三角形有8个;⑤由5个小三角形构成的三角形有4个;⑥由6个小三角形构成的三角形有4个;⑦由7个小三角形构成的三角形有4个;所以图中共有三角形24+20+8+8+4+4+4=72个。
4、四位数abcd 与cdab 的和为3636,差为396,那么四位数abcd 为 。
【解析】:100abcd ab cd =+,100cdab cd ab =+。
当ab cd >时: ()1001003636100100396ab cd cd ab ab cd cd ab ⎧+++=⎪⎨+-+=⎪⎩ 整理得36ab cd +=,4ab cd -=,所以20ab =,16cd =,2016abcd =。
同理,ab cd <时,1620abcd =。
5、A、B、C、D四个箱子中分别装有一些小球,现将A箱中的部分小球按如下要求转移到其他三个箱子中:该箱中原有几个小球,就再放入几个小球,此后,按照同样的方法依次把B、C、D箱中的小球转移到其他箱子中,此时,四个箱子都各有16个小球,那么开始时装有小球最多的是______箱,其中装有______小球个。
走美杯四年级试题及答案

走美杯四年级试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是正确的?A. 地球是平的B. 太阳是宇宙的中心C. 地球围绕太阳转D. 月亮是地球的卫星答案:C2. 哪个国家被称为“千岛之国”?A. 中国B. 日本C. 印度尼西亚D. 印度答案:C3. 下列哪个选项是数学中的“奇数”?A. 2B. 4C. 5D. 8答案:C4. 以下哪种动物是哺乳动物?A. 蛇B. 鳄鱼C. 鲸鱼D. 乌龟答案:C5. 世界上最高的山峰是?A. 珠穆朗玛峰B. 乞力马扎罗山C. 富士山D. 阿尔卑斯山答案:A二、填空题(每题2分,共10分)1. 一年有______个季节。
答案:四2. 地球上最大的陆地动物是______。
答案:非洲象3. 光年是长度单位,表示光在一年内通过的距离,大约是______公里。
答案:9.46万亿4. 人体最大的器官是______。
答案:皮肤5. 世界上最大的海洋是______。
答案:太平洋三、简答题(每题5分,共20分)1. 简述地球的自转和公转。
答案:地球的自转是指地球围绕自己的轴线旋转,周期约为24小时,导致了昼夜交替。
地球的公转是指地球围绕太阳的轨道运动,周期约为365.25天,导致了季节更替。
2. 请解释什么是生态系统。
答案:生态系统是由生物群落和其所在的非生物环境相互作用而形成的一个统一整体,包括了生产者、消费者和分解者等生物组成部分以及水、土壤、空气等非生物组成部分。
3. 请列举三种常见的哺乳动物。
答案:猫、狗、牛4. 描述一下水循环的过程。
答案:水循环是指地球上水分子在大气、陆地和海洋之间不断循环的过程,包括蒸发、凝结、降水和径流等环节。
四、计算题(每题10分,共20分)1. 如果一个长方形的长是8米,宽是5米,求其面积。
答案:面积 = 长× 宽 = 8米× 5米 = 40平方米2. 一个班级有40名学生,如果每名学生需要2本练习册,那么总共需要多少本练习册?答案:总练习册数 = 学生数× 每人练习册数= 40 × 2 = 80本五、阅读理解题(每题5分,共10分)阅读以下短文,回答后面的问题。
10届2012初赛A卷走美杯的答案

第十届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛初赛注意事项:1.考生要按要求在密封线内填好考生的有关信息.总分2.不允许使用计算器.小学四年级试卷(A卷)一、填空题Ⅰ(每题8分,共40分)1.125×16+2×2×3= (2012)2.如果m#n=m+n÷2,那么 19#18= (28)3.今天是星期日,再过100天是星期。
(二)4.下图一笔画是不可能的,最少添上条连线就可以一笔画成了。
(2)5.如图,一个正方形被分成了5个相同的长方形,每个长方形的周长都是24厘米,则原来正方形的周长是厘米。
(40)二、填空题Ⅱ(每题10分,共50分)6.某年7月恰有4个星期一和4个星期四,这月的15号是星期。
(五)7.从正整数1~N中去掉一个数,剩下的N-1个数的平均值是16.3;去掉的数是。
(7)8.葛大财主请园艺师为其整修花园,要求一个月完成,3月1日开始31日结束,每天的工钱为一钱黄金。
葛大财主是出了名的守财奴,园艺师要求每天结束时结算工钱,葛大财主恰有一块31钱的金条。
聪明绝顶的葛大财主只做了次(填最少次数)切割,就解决了这个问题。
(4)====Word 行业资料分享--可编辑版本--双击可删==== 源-于-网-络-收-集 9. 小华需要构造一个3×3的乘积魔方,使得每行、每列、每条 对角线上三个正整数的乘积都相等;现在他已经填入了2,3, 6三个数,那当小华的乘积魔方构造完毕后,x 等 于 .(36)10. 十进制下的三位数TWO 和四位数FOUR 满足:TWO+TWO=FOUR, 其中不同的字母代表不同的数字,FOUR 的最小可能的值是 . (1468)三、填空题Ⅲ(每题12分,共60分)11. 今年,丹丹和父亲、母亲、弟弟的年龄和是120岁.当父亲的年龄是丹丹年龄的3倍时,母亲的年龄恰好也是弟弟年龄的3倍,当时弟弟12岁.那么丹丹今年 岁.(18)12. 玉米炮有单筒玉米炮、双筒玉米炮、三筒玉米炮三种.单筒玉米炮每炮发射一根玉米,可以消灭20个僵尸;双筒玉米炮每次发射2根玉米,每根玉米消灭17个僵尸,三筒玉米炮每次发射三根玉米,每根玉米消灭16个僵尸.玉米炮一共开炮10次,发射玉米23根,消灭 个僵尸.(382 20×10 + 14×13 = 382)13. 如图,大正六边形的面积是24平方厘米,其中放了三个一样的小正六边形.阴影面积是 平方厘米.(18)14. 甲、乙、丙三人同时同向骑车,各自的速度都保持不变,乙在甲、丙的正中间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年第十届走美杯四年级试题
一、填空题Ⅰ(每题8分,共40分)
1.2012+2011+2010+……+1007-1006-1005-1004-……-1=__________。
2.某年7月恰有4个星期一和四个星期四,这月的15号是星期________。
3.从正整数1~N中去掉一个数,剩下的N~1个数的平均值是16.3;去掉的数是_______。
4.葛大财主请园艺师为其整修花园,要求一个月完成,3月1日开始31日结束,每天的工
钱为一钱黄金。
葛大财主是出了名的守财奴,园艺师要求每天结束时结算工钱,葛大财主恰有一块31钱的金条。
聪明绝顶的葛大财主只做了______次(填最少次数)切割,就解决了这个问题。
5.在台球“斯诺克”比赛中,有红球15个,黄、绿、棕、蓝、粉、黑球各一个,其中红球落袋积1分,黄、绿、棕、蓝、粉、黑球落袋分别积2、3、4、5、6、7分。
比赛中,第一阶段先要将15个红球全击落袋,而每击落1个红球后必须再击落1个其他颜色的球,红球落袋不拿回,而其它颜色球在此阶段被击落袋后再放回台面;第二阶段要按黄、绿、棕、蓝、粉、黑的顺序依次将这些球击落袋。
那么,“斯诺克”比赛中最高能得______分。
二、填空题Ⅱ(每题10分,共50分)
6.小华需要构造一个3×3的乘积魔方,使得每行、每列、每条对角线上三个正整数的乘积都相等;现在他已经填入了2,3,6三个数,那当小华的乘积魔方构造完毕后,x等于______。
7.十进制下的三位数TWO和四位数FOUR满足:TWO+TWO=FOUR,其中不同的字母代表不同的数字,FOUR的最小可能的值是______。
8.今年,丹丹和父亲、母亲和弟弟的年龄和是120岁。
当父亲的年龄是丹丹年龄的3倍时,母亲的年龄恰好也是弟弟年龄的3倍,当时弟弟12岁。
那么丹丹今年______岁。
9.玉米炮有单筒玉米炮、双筒玉米炮、三筒玉米炮三种。
单筒玉米炮每次发射1根玉米,可以消灭20个僵尸;双筒玉米炮每次发射2根玉米,每根玉米消灭17个僵尸,三筒玉
米炮每次发射3根玉米,每根消灭16个僵尸。
玉米炮一共开炮10次,发射23根玉米,消灭______个僵尸。
10.有五个互不相等的非零自然数。
如果其中一个减少45,另外四个数都变成原先的2倍,那么得到的仍然是这五个数。
这五个数的总和是______。
11.如图,大正六边形的面积是24平方厘米,其中放了三个一样的小正六边形。
阴影面积是_____平方厘米。
12.甲、乙、丙三人同时同向骑车,各自的速度都保持不变,乙在甲、丙的正中间。
甲20分钟追上乙,又过10分钟追上丙。
再过______分钟乙追上丙。
三、填空题Ⅲ(每题12分,共60分
13.六位数2□012□个为上填_______时,万位上无论填入0~9中哪一个数,都不能被11整除。
14.1个4×4的棋盘,在每个小方格上染上黑白两色之一,染法与国际象棋盘的染法相同。
允许任意选择一个矩形(矩形的边都在格子上),被选中的矩形中的内个小正方格改变颜色(黑变白,白变黑)。
至少需要______次上述操作,才能使棋盘上的格子都同色。
15.将一个5×5×5的正方体分割成若干个3×3×3,2×2×2和1×1×1的小正方体。
1×1×1的小正方体最少有________个。
2012年第十届走美杯四年级答案详解。
