同角三角函数的基本关系式与诱导公式
同角三角函数基本关系式及诱导公式
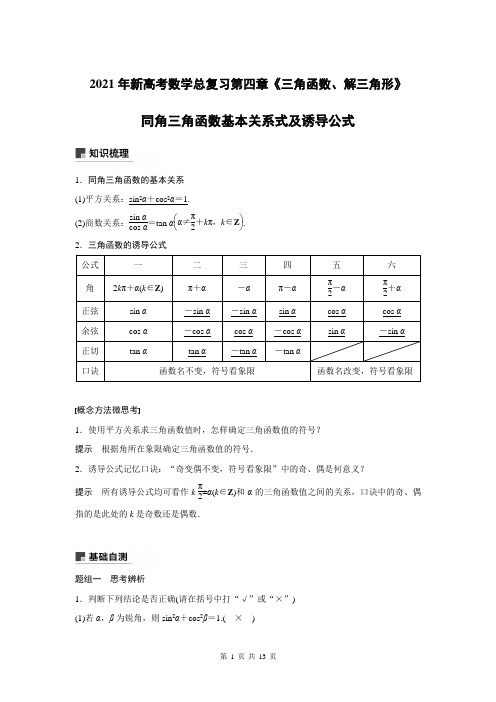
2021年新高考数学总复习第四章《三角函数、解三角形》同角三角函数基本关系式及诱导公式1.同角三角函数的基本关系 (1)平方关系:sin 2α+cos 2α=1.(2)商数关系:sin αcos α=tan α⎝⎛⎭⎫α≠π2+k π,k ∈Z . 2.三角函数的诱导公式 公式 一 二 三 四 五 六 角 2k π+α(k ∈Z )π+α -α π-α π2-α π2+α 正弦 sin α -sin α -sin α sin α cos α cos α 余弦 cos α -cos α cos α -cos α sin α -sin α 正切 tan αtan α-tan α-tan α口诀 函数名不变,符号看象限 函数名改变,符号看象限概念方法微思考1.使用平方关系求三角函数值时,怎样确定三角函数值的符号? 提示 根据角所在象限确定三角函数值的符号.2.诱导公式记忆口诀:“奇变偶不变,符号看象限”中的奇、偶是何意义?提示 所有诱导公式均可看作k ·π2±α(k ∈Z )和α的三角函数值之间的关系,口诀中的奇、偶指的是此处的k 是奇数还是偶数.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)若α,β为锐角,则sin 2α+cos 2β=1.( × )(2)若α∈R ,则tan α=sin αcos α恒成立.( × )(3)sin(π+α)=-sin α成立的条件是α为锐角.( × ) (4)若sin(k π-α)=13(k ∈Z ),则sin α=13.( × )题组二 教材改编 2.若sin α=55,π2<α<π,则tan α= . 答案 -12解析 ∵π2<α<π,∴cos α=-1-sin 2α=-255,∴tan α=sin αcos α=-12.3.已知tan α=2,则sin α+cos αsin α-cos α的值为 .答案 3解析 原式=tan α+1tan α-1=2+12-1=3.4.化简cos ⎝⎛⎭⎫α-π2sin ⎝⎛⎭⎫5π2+α·sin(α-π)·cos(2π-α)的结果为 .答案 -sin 2α解析 原式=sin αcos α·(-sin α)·cos α=-sin 2α.题组三 易错自纠5.已知sin θ+cos θ=43,θ∈⎝⎛⎭⎫0,π4,则sin θ-cos θ的值为 . 答案 -23解析 ∵sin θ+cos θ=43,∴sin θcos θ=718.又∵(sin θ-cos θ)2=1-2sin θcos θ=29,θ∈⎝⎛⎭⎫0,π4, ∴sin θ-cos θ=-23. 6.(2018·成都诊断)已知α为锐角,cos ⎝⎛⎭⎫32π+α=45,则cos(π+α)= .。
第十八讲:同角三角函数基本关系与诱导公式

共 57 页
5
考点陪练
1.α 是第四象限角,tanα=-152,则 sinα=(
)
1 A.5
B.-15
5 C.13
D.-
5 13
解析:由 tanα=csoinsαα=-152,sin2α+cos2α=1,及 α 是第四象
限角,解得csionsαα==-11231.53,
)
A.1
B.0
C.-1
1 D.2
解析:原式=cotαta-nαco-sαco-sαs3inα2=ctaontααtan2α=1.
❖ 答案:A
共 57 页
9
4.cos-769π的值为(
A.-12
1 B.2
)
C.-
3 2
3 D. 2
解析:cos-769π=cos769π=cos13π+π6=-cosπ6=- 23,故 选 C.
由
tanα=2 知
sinα=
2 ,又 5
cosα=13,
∵sin2α+cos2α≠1,∴B 错.
由 sinα=12得 cosα=± 23,∴tanα=± 33,
当 α 为第一象限角时有 tanα= 33,故选 C.
❖ 答案:C
共 57 页
8
3.化简cotα- tan4ππ+·cαos·cαo+s3π-·sαin-2πα-3π的结果是(
共 57 页
27
❖ [点评] (1)掌握诱导公式,关键掌握函数名及 符号,口诀“奇变偶不变,符号看象限”.
❖ (2)k是奇数还是偶数,直接影响到用哪组诱导公 式.
共 57 页
28
❖ 类型四 同角三角函数基本关系式与诱导公式 的综合应用
同角三角函数基本关系式、三角函数的诱导公式

一、知识概述1、同角三角函数的基本关系式同角三角函数基本关系可概括为平方关系,商数关系和倒数关系,如考虑sinα,cos α,tanα,cotα与secα,cscα六个函数,还可借助如下图表形象记忆:(1)对角线上两个函数的积为1(倒数关系)(2)任一顶点的函数等于与其相邻两个顶点的函数的积(商数关系)(3)阴影部分,顶角两个函数的平方和等于底角函数的平方(平方关系)由此图可得出公式的变形形式或其他同角函数关系式.平方关系:sin2α+cos2α=1,sec2α=1+tan2α,csc2α=1+cot2α.商数关系:倒数关系:tanα·cotα=1,sinα·cscα=1,cosα·secα=1.注:课本上只介绍了其中两个重要的关系式,事实上,掌握好其余的五个关系式能在有关解题中节省过程,带来方便.2、三角函数的诱导公式公式一:sin(α+k·)=sinαcos(α+k·)=cosαtan(α+k·)=tanα其中k∈Z.公式二:sin(+α)=-sinαcos(+α)=-cosαtan(+α)=tanα公式三:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanα公式四:sin(-α)=sinαcos(-α)=-cosαtan(-α)=-tanα总结:α+k·2(k∈Z),-α,±α的三角函数,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号。
公式五:sin(-α)=cosαcos(-α)=sinα公式六:sin(+α)=cosαcos(+α)=-sinα总结:±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号.二、重、难点知识归纳及讲解(一)利用诱导公式可以把任意角的三角函数转化为锐角三角函数,即:例1、求值:.分析:运用诱导公式,对于cot,可先求出sin,cos,然后由商数关系可求出cot.解:原式例2、设的值为()A.B.C.-1 D.1分析:利用诱导公式将条件等式和欲求式都化到α的同名三角函数上去,再利用同角三角函数基本关系式求解.解答:(二)同角三角函数关系式在求值、化简、证明中的应用.1、已知角α的某一三角函数值,可求出α的其余三角函数值.例3、已知tanα=2,求2sin2α-3sinαcosα-2cos2α的值.分析:由平方关系知1=sin2α+cos2α,可把式子的分母看成sin2α+cos2α,然后分子分母同除以cos2α,可得.解:2、利用同角三角函数关系式进行化简:化简结果的基本要求:(1)函数个数尽可能少;(2)次数尽可能低;(3)项数尽可能少;(4)尽可能地去掉根号;(5)尽可能地不含分母;(6)能求出值的要求出值来.例4、若sinαcosα<0,sinαtanα<0,化简:.分析:要想去掉根号,就应考虑将被开方数配成完全平方的形式.解:∵sinαcosα<0,sinαtanα<0.∴α是第二象限角.故是第一或第三象限角.原式若是第一象限角,此时1±sin>0,cos>0. 原式=若是第三象限角,此时1±sin>0,cos<0. 原式=.3、利用同角关系式进行三角恒等式的证明.证明三角恒等式的方法较多,既可由一边证向另一边,也可先证得另一个等式成立,从而得出要证的等式,还可用比较法证明等,关键是要依题而定。
同角三角函数的基本关系及诱导公式-高考复习

)
√2
A.6
(2)已知 sin
√2
B.
6
2√5
α= 5 ,则
2
C.3
5π
+)
2
5π
cos ( -)
2
sin (
tan(π+α)+
=
2
D.
3
.
答案 (1)D
5
5
(2) 或2
2
解析 (1)sin2θ+sin(3π-θ)cos(2π+θ)-√2cos2θ
sin
θ-2cos2θ=
=
,
2
2
2
sin +cos
tan +1
4+2-2
θ=2,故原式=
4+1
=
4
.
5
解题心得 1.利用 sin2α+cos2α=1 可以实现角 α 的正弦、余弦的互化,利用
tan
sin
α=cos
≠ π +
π
,∈Z
2
可以实现角 α 的弦切互化.
2.“1”的灵活代换:1=cos α+sin α=(sin α+cos α) -2sin αcos
解题心得1.利用诱导公式化简三角函数的基本思路:(1)分析结构特点,选择
恰当公式;(2)利用公式化成单角三角函数;(3)整理得最简形式.
2.化简要求:(1)化简过程是恒等变形;(2)结果要求项数尽可能少,次数尽可
能低,结构尽可能简单,能求值的要求出值.
3.用诱导公式求值时,要善于观察所给角之间的关系,利用整体代换的思想简
【例 1】 (1)若
1
同角三角函数的基本关系与诱导公式-高考数学复习

3
θ= ,
5
cos
π
θ<0,所以可得θ∈( ,π),
2
sin θ cos
θ)2=1-2
sin θ+ cos
4
θ=- ,tan
5
1
θ= ,可得
25
sin θ cos
1
θ=- ,
5
sin θ cos θ
49
θ= ,所以
25
sin θ- cos
sin θ
7
θ= ,联
5
3
θ=- ,故B错误,C正确.
4
目录
高中总复习·数学
可求解;
(2)若齐次式为二次整式,可将其视为分母为1的分式,然后将分母
1用 sin 2α+ cos 2α替换,再将分子与分母同除以 cos 2α,化为只
含有tan α的式子,代入tan α的值即可求解.
目录
高中总复习·数学
考向3 “ sin α±cos α, sin α cos α”之间关系的应用
可以知一求二.
目录
高中总复习·数学
1. 若 sin θ+ cos
2 3
θ=
,则
3
解析:由 sin θ+ cos
θ cos
1
θ= ,∴
6
sin 4θ+ cos 4θ=(
2 3
θ=
,平方得1+2
3
)
sin θ cos
4
θ= ,∴
3
sin
sin 4θ+ cos 4θ=( sin 2θ+ cos 2θ)2-2 sin 2θ cos 2θ
(1)思路:①分析结构特点,选择恰当的公式;②利用公式化成单
(4) sin α=tan α cos
同角三角函数的基本关系式与诱导公式

课堂互动讲练
考点一
诱导公式的应用
应用诱导公式进行化简或证明时, 首先根据题意选准公式再用,一般是负 变正、大变小的思想.
在使用诱导公式时,α可为任意角, 并不一定要为锐角,只不过是在运用的 过程中把它“看作”是锐角而已.“奇 变偶不变,符号看象限”同样适用于正 切和余切.如tan(270°-α)=cotα等.
cos2x-1 sin2x=
cos2x+sin2x cos2x-sin2x
,想法
使分
子分
母都出现 tanx 即可.
课堂互动讲练
【解】 (1)法一:联立方程:
sinx+cosx=15, sin2x+cos2x=1.
① 2分
②
①式两边平方得:sin2x+cos2x+2sinxcosx
=215,
∴2sinxcosx=-2245.4 分 ∵-π2<x<0,∴sinx<0,cosx>0. ∴sinx-cosx=- sin2x-2sinxcosx+cos2x
三基能力强化
5.已知scions2θθ++14=2,那么(cosθ + 3)(sinθ+1)的值为________.
解析:∵scions2θθ++14=2,∴sin2θ+4= 2cosθ+2,
∴cos2θ+2cosθ-3=0,解得 cosθ= 1 或 cosθ=-3(舍去),由 cosθ=1 得 sinθ =0,∴(cosθ+3)(sinθ+1)=4.
规律方法总结
公式中 k·π2+α 的整数 k 来讲的.“象
限”指在 k·π2+α 中,将 α 看作锐角时 k·π2+
α
所在的象限,如将
cos(32π+α)写成
π cos(3·2
同角三角函数的基本关系式与诱导公式

第二节 同角三角函数的基本关系与诱导公式 1,.同角三角函数的基本关系倒数关系:tan α∙cot α=1 商数关系:ααcos sin =tan α,ααsin cos =cot α 平方关系:sin ²α+cos ²α=1注意:同角三角函数的关系式的基本用途:根据一个角的某一个三角函数值,求出该角的其他三角函数值,化解同角的三角函数式,证明同角的三角恒等式 2,诱导公式 x sinx cosx tanx cotx -α-sin α cos α-tan α-cot αα±2πcos αsin ααcottan απ±α sin α-cos α ±tan α±cot α23π±α -cos α±sin αcot αtan α2π±α±sin αcos α±tan α±cot α记忆规律:奇变偶不变,符号看象限。
其中奇变偶不变中的奇,偶分别是指2π的奇数倍和偶数倍,变与不变指的是函数名称的变化 3,求值题型已知一个角的某一个三角函数值,求这个角的其他三角函数值,这类问题用同角三角函数的基本关系式求解,一般分成三种情况:(1)一个角的某一个三角函数值和这个角所在的象限或终边所在位置都是已知的,此类情况只有一组解.(2)一个角的某一个三角函数值是已知的,但这个角所在的象限或终边所在位置没有给出,解答这类问题,首先要根据已知的三角函数值确定这个角所在的象限或终边所在位置,然后分不同的情况求解(3)一个角的某一个三角函数值是用字母给车的,或用一个角的某一个三角函数值来表示这个角的其他三角函数值,此类情况需对字母进行讨论或对角α所在象限进行讨论,并注意对分类标准适当选取,一般有两组解`例题1,(1)已知sin α=31,且α为第二象限角,求tan α. (2)已知sin α=m(m 0≠,m 1±≠),求tan α4.化解题型:化简三角函数式的一般要求是:能求出值的要求出值来;函数种类尽可能少;化解后的式子项数最少,次数最低,尽可能不含根号 例题1化解(1).︒︒︒︒-10-10sin 10cos 10sin 21sin2(2)若角α的终边落在直线x+y=0上,则ααααcos 11sin cos sin 22-+-的值等于( A )A.2B.-2C.1D.05,已知tan α的值,求sin α和cos α构成的齐次式(或能化为齐次式)的值例题1,已知11tan tan -=-αα,求下列各式的值(1)ααααcos sin cos 3sin +-; (2)2cos sin sin 2++ααα6.利用方程思想解三角题对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,已知其中一个式子的值,可以求出其余两个式子的值,如:(sin α+cos α)²=1+2sin αcos α. (sin α-cos α)²=1-2sin αcos α.(sin α+cos α)²+(sin α-cos α)²=2 典型例题在△ABC 中,sinA+cosA=22,AC=2,AB=3, 求tanA 的值和△ABC 的面积二、 例题讲解【例1】化简sin tan tan (cos sin )cot s c c ααααααα+-++分析:切割化弦是解本题的出发点.解:原式sin sin sin (cos sin )cos sin cos 1cos sin sin ααααααααααα+-=+=+.【例2】化简(1)sin()cos()44ππαα-++; (2)已知32,cos(9)5παπαπ<<-=-,求11cot()2πα-的值. 解:(1)原式sin()cos[()]424πππαα=-++-sin()sin()044ππαα=---=.(2)3cos()cos(9)5απαπ-=-=-,∴3cos 5α=,∵2παπ<<,∴4sin 5α=-,sin 4tan cos 3ααα==, ∴1134cot()cot()tan 223ππααα-=--=-=.【例3】(1) 若tan 2α=,求值①cos sin cos sin αααα+-;②222sin sin cos cos αααα-+.(2)求值66441sin cos 1sin cos x xx x----.解:(1)①原式sin 112cos 322sin 121cos αααα++===----. ②∵2211cos 1tan 3αα==+,∴原式2221cos (2tan tan 1)3ααα+=-+=. (2)∵66224224sin cos (sin cos )(sin sin cos cos )x x x x x x x x +=+-⋅+2222222(sin cos )3sin cos 13sin cos x x x x x x =+-⋅=-⋅.又∵442222222sin cos (sin cos )2sin cos 12sin cos x x x x x x x x +=+-⋅=-⋅.∴原式66441sin cos 31sin cos 2x x x x --==--.【例4】已知sin ,cos θθ是方程244210x mx m -+-=的两个根,322πθπ<<,求角θ. 解:∵2sin cos 21sin cos 416(21)0m m m m θθθθ+=⎧⎪-⎪⋅=⎨⎪⎪∆=-+≥⎩,代入2(sin cos )12sin cos θθθθ+=+⋅,得132m ±=,又322πθπ<<,∴21sin cos 04m θθ-⋅=<, 13sin cos 2m θθ-+==,∴31sin ,cos 22θθ-==,又∵322πθπ<<, ∴56πθ=.【例5】(2010²大连模拟)已知cos(π4+α)=-12,则sin(π4-α)=( )A .-12 B.12 C .-22 D.22解析:sin(π4-α)=cos[π2-(π4-α)]=cos(π4+α)=-12.答案:A【例6】已知A =sin(k π+α)sin α+cos(k π+α)cos α(k ∈Z),则A 的值构成的集合是 ( )A .{1,-1,2,-2}B .{-1,1}C .{2,-2}D .{1,-1,0,2,-2} 解析:当k 为偶数时,A =sin αsin α+cos αcos α=2;k 为奇数时,A =-sin αsin α-cos αcos α=-2. 答案:C【例7】已知tan x =sin(x +π2),则sin x = ( ) A.-1±52 B.3+12 C.5-12 D.3-12解析:∵tan x =sin(x +π2), ∴tan x =cos x ,∴sin x =cos 2x ,∴sin 2x +sin x -1=0, 解得sin x =5-12(或-1-52<-1,舍去). 答案:C【例8】已知α∈(π2,3π2),tan(α-7π)=-34,则sin α+cos α的值为 ( )A .±15B .-15 C.15 D .-75解析:tan(α-7π)=tan α=-34,∴α∈(π2,π),sin α=35,cos α=-45,∴sin α+cos α=-15.【例9】已知f (x )=a sin(πx +α)+b cos(πx -β),其中α、β、a 、b 均为非零实数,若f (2 010)=-1,则f (2 011)等于 ( )A .-1B .0C .1D .2 解析:由诱导公式知f (2 010)=a sin α+b cos β=-1, ∴f (2 011)=a sin(π+α)+b cos(π-β) =-(a sin α+b cos β)=1. 答案:C【例10】已知sin(2π+θ)tan(π+θ)tan(3π-θ)cos(π2-θ)tan(-π-θ)=1,则3sin 2θ+3sin θcos θ+2cos 2θ的值是( )A .1B .2C .3D .6 解析:∵sin(2π+θ)tan(π+θ)tan(3π-θ)cos(π2-θ)tan(-π-θ)=sin θtan θtan(π-θ)-sin θtan(π+θ)=-sin θtan θtan θ-sin θtan θ=tan θ=1,∴3sin 2θ+3sin θcos θ+2cos 2θ=3sin 2θ+3cos 2θsin 2θ+3sin θcos θ+2cos 2θ =3tan 2θ+3tan 2θ+3tan θ+2=3+31+3+2=1. 答案:A【例11】若cos(2π-α)=53,且α∈(-π2,0),则sin(π-α)=________. 解析:cos(2π-α)=cos α=53,又α∈(-π2,0), 故sin(π-α)=sin α=-1-(53)2=-23. 答案:-23【例12】若cos α+2sin α=-5,则tan α=________.解析:法一:将已知等式两边平方得cos 2α+4sin 2α+4sin αcos α=5(cos 2α+sin 2α),化简得sin 2α-4sin αcos α+4cos 2α=0,则(sin α-2cos α)2=0,故tan α=2. 法二:由cos α+2sin α=-5可知,cos α≠0,两边同时除以cos α得1+2tan α=-5sec α,平方得(1+2tan α)2=5sec 2α=(1+tan 2α),∴tan 2α-4tan α+4=0,解得tan α=2. 答案:2三、巩固练习1、若(cos )cos 2f x x =,(sin15)f =( D )()A 12 ()B 12- ()C 32 ()D 32- 2、已知1sin cos (0)5αααπ+=-≤≤,则tan α=34-.3、已知sin α是方程5x 2-7x -6=0的根,α是第三象限角,则 sin(-α-32π)cos(32π-α)cos(π2-α)sin(π2+α)²tan 2(π-α)=________.4、已知sin α=255,求tan(α+π)+sin(5π2+α)cos(5π2-α).5、(1)若角α是第二象限角,化简tan α1sin 2α-1; (2)化简: 1-2sin130°cos130°sin130°+1-sin 2130°. 6、sin585的值为 ( ) A.22-B.22C.32-D.327、已知3cos(),,tan 222ππϕϕϕ+=<=且则( ) A.33-B.33C.3-D.3 8、若2sin cos tan 2,sin 2cos ααααα-=+则的值为( )A.0B.34 C.1 D.549、已知tan 2tan 1αα=-,求下列各式的值: (1)sin 3cos sin cos αααα-+(2)22222sin 3cos 4sin 9cos αααα-- (3)224sin 3sin cos 5cos αααα--。
高考数学一轮复习考点知识专题讲解27---同角三角函数基本关系式及诱导公式

高考数学一轮复习考点知识专题讲解 同角三角函数基本关系式及诱导公式考点要求1.理解同角三角函数的基本关系式sin 2α+cos 2α=1,sin αcos α=tan α.2.掌握诱导公式,并会简单应用.知识梳理1.同角三角函数的基本关系 (1)平方关系:sin 2α+cos 2α=1.(2)商数关系:sin αcos α=tan α⎝ ⎛⎭⎪⎫α≠π2+k π,k ∈Z .2.三角函数的诱导公式公式一 二三四五 六角2k π+α(k ∈Z )π+α-απ-απ2-απ2+α 正弦sin α-sin α-sin αsin α cos α cos α余弦cos α-cos α cos α-cos αsin α-sin α正切tan αtan α-tan α-tan α口诀奇变偶不变,符号看象限常用结论同角三角函数的基本关系式的常见变形 sin 2α=1-cos 2α=(1+cos α)(1-cos α); cos 2α=1-sin 2α=(1+sin α)(1-sin α); (sin α±cos α)2=1±2sin αcos α. 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”) (1)若α,β为锐角,则sin 2α+cos 2β=1.(×) (2)若α∈R ,则tan α=sin αcos α恒成立.(×) (3)sin(π+α)=-sin α成立的条件是α为锐角.(×) (4)若sin ⎝⎛⎭⎪⎫3π2-α=13,则cos α=-13.(√)教材改编题1.已知α是第二象限角,sin α=55,则cos α的值为. 答案-255解析∵sin α=55,α是第二象限角, ∴cos α=-1-sin 2α=-255.2.已知sin α-2cos α3sin α+5cos α=-5,那么tan α的值为.答案-2316解析由sin α-2cos α3sin α+5cos α=-5,知cos α≠0,等式左边分子、分母同时除以cos α,可得tan α-23tan α+5=-5,解得tan α=-2316.3.化简cos ⎝⎛⎭⎪⎫α-π2sin ⎝ ⎛⎭⎪⎫5π2+α·sin(α-π)·cos(2π-α)的结果为.答案-sin 2α解析原式=sin αcos α·(-sin α)·cos α=-sin 2α.题型一 同角三角函数基本关系 例1(1)已知cos α=-513,则13sin α+5tan α=. 答案0解析∵cos α=-513<0且cos α≠-1, ∴α是第二或第三象限角.①若α是第二象限角, 则sin α=1-cos 2α=1-⎝ ⎛⎭⎪⎫-5132=1213, ∴tan α=sin αcos α=1213-513=-125.此时13sin α+5tan α=13×1213+5×⎝ ⎛⎭⎪⎫-125=0. ②若α是第三象限角, 则sin α=-1-cos 2α=-1-⎝ ⎛⎭⎪⎫-5132=-1213,∴tan α=sin αcos α=-1213-513=125,此时,13sin α+5tan α=13×⎝ ⎛⎭⎪⎫-1213+5×125=0.综上,13sin α+5tan α=0.(2)已知tan α=12,则sin α-3cos αsin α+cos α=;sin 2α+sin αcos α+2=.答案-53135解析已知tan α=12,所以sin α-3cos αsin α+cos α=tan α-3tan α+1=-53.sin 2α+sin αcos α+2 =sin 2α+sin αcos αsin 2α+cos 2α+2=tan 2α+tan αtan 2α+1+2=⎝ ⎛⎭⎪⎫122+12⎝ ⎛⎭⎪⎫122+1+2=135.(3)已知sin θ+cos θ=713,θ∈(0,π),则tan θ=. 答案-125解析由sin θ+cos θ=713,得sin θcos θ=-60169, 因为θ∈(0,π),所以sin θ>0,cos θ<0, 所以sin θ-cos θ=1-2sin θcos θ=1713,联立⎩⎪⎨⎪⎧sin θ+cos θ=713,sin θ-cos θ=1713,解得⎩⎪⎨⎪⎧sin θ=1213,cos θ=-513,所以tan θ=-125. 教师备选1.(2022·平顶山联考)已知sin α+3cos α3cos α-sin α=5,则cos 2α+12sin2α等于()A.35 B .-35C .-3D .3答案A解析由sin α+3cos α3cos α-sin α=5,得tan α+33-tan α=5,可得tan α=2,则cos 2α+12sin2α=cos 2α+sin αcos α=cos 2α+sin αcos αcos 2α+sin 2α=1+tan α1+tan 2α=35. 2.若α∈(0,π),sin(π-α)+cos α=23,则sin α-cos α的值为() A.23 B .-23 C.43 D .-43 答案C解析由诱导公式得sin(π-α)+cos α=sin α+cos α=23, 所以(sin α+cos α)2=1+2sin αcos α=29,则2sin αcos α=-79<0,因为α∈(0,π),所以sin α>0, 所以cos α<0,所以sin α-cos α>0, 因为(sin α-cos α)2=1-2sin αcos α=169,所以sin α-cos α=43.思维升华 (1)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二. (2)注意公式逆用及变形应用:1=sin 2α+cos 2α,sin 2α=1-cos 2α,cos 2α=1-sin 2α.跟踪训练1(1)(2021·新高考全国Ⅰ)若tan θ=-2,则sin θ(1+sin2θ)sin θ+cos θ等于()A .-65B .-25 C.25 D.65答案C解析方法一因为tan θ=-2, 所以角θ的终边在第二或第四象限, 所以⎩⎪⎨⎪⎧sin θ=25,cos θ=-15或⎩⎪⎨⎪⎧sin θ=-25,cos θ=15,所以sin θ(1+sin2θ)sin θ+cos θ=sin θ(sin θ+cos θ)2sin θ+cos θ=sin θ(sin θ+cos θ) =sin 2θ+sin θcos θ =45-25=25. 方法二(弦化切法)因为tan θ=-2, 所以sin θ(1+sin2θ)sin θ+cos θ=sin θ(sin θ+cos θ)2sin θ+cos θ=sin θ(sin θ+cos θ) =sin 2θ+sin θcos θsin 2θ+cos 2θ=tan 2θ+tan θ1+tan 2θ=4-21+4=25.(2)已知α是三角形的内角,且tan α=-13,则sin α+cos α的值为.答案-105解析由tan α=-13,得sin α=-13cos α,将其代入sin 2α+cos 2α=1,得109cos 2α=1, 所以cos 2α=910,易知cos α<0, 所以cos α=-31010,sin α=1010,故sin α+cos α=-105. 题型二 诱导公式例2(1)已知sin ⎝ ⎛⎭⎪⎫α-π4=13,则cos ⎝ ⎛⎭⎪⎫π4+α的值为()A.223 B .-223 C.13 D .-13答案D解析cos ⎝⎛⎭⎪⎫π4+α=cos ⎣⎢⎡⎦⎥⎤π2+⎝ ⎛⎭⎪⎫α-π4 =-sin ⎝⎛⎭⎪⎫α-π4=-13. 延伸探究本例(1)改为已知θ是第二象限角,且sin ⎝⎛⎭⎪⎫θ+π4=45,则tan ⎝ ⎛⎭⎪⎫θ-π4=. 答案34解析∵θ是第二象限角,且sin ⎝⎛⎭⎪⎫θ+π4=45, ∴θ+π4为第二象限角,∴cos ⎝ ⎛⎭⎪⎫θ+π4=-35,∴tan ⎝⎛⎭⎪⎫θ-π4=sin ⎝⎛⎭⎪⎫θ-π4cos ⎝ ⎛⎭⎪⎫θ-π4=sin ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫θ+π4-π2cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫θ+π4-π2=-cos ⎝⎛⎭⎪⎫θ+π4sin ⎝ ⎛⎭⎪⎫θ+π4=-⎝ ⎛⎭⎪⎫-3545=34.(2)tan(π-α)cos(2π-α)sin⎝⎛⎭⎪⎫-α+3π2cos(-α-π)sin(-π-α)的值为()A.-2B.-1C.1D.2 答案B解析原式=-tanα·cosα·(-cosα)cos(π+α)·[-sin(π+α)]=tanα·cos2α-cosα·sinα=-sinαcosα·cosαsinα=-1.教师备选1.已知函数f(x)=a x-2+2(a>0且a≠1)的图象过定点P,且角α的始边与x轴的正半轴重合,终边过点P,则cos⎝⎛⎭⎪⎫11π2-αsin⎝⎛⎭⎪⎫9π2+α+sin2αcos⎝⎛⎭⎪⎫π2+αsin(-π-α)等于()A.23B.-23C.32D.-32答案B解析易知函数f(x)=a x-2+2(a>0且a≠1)的图象过定点P(2,3),故tanα=3 2,则cos⎝⎛⎭⎪⎫11π2-αsin⎝⎛⎭⎪⎫9π2+α+sin2αcos⎝⎛⎭⎪⎫π2+αsin(-π-α)=cos ⎝ ⎛⎭⎪⎫3π2-αsin ⎝ ⎛⎭⎪⎫π2+α+sin2αcos ⎝ ⎛⎭⎪⎫π2+αsin α =-sin αcos α+2sin αcos α-sin αsin α=-cos αsin α=-1tan α=-23. 2.若sin x =3sin ⎝ ⎛⎭⎪⎫x -π2,则cos x ·cos ⎝⎛⎭⎪⎫x +π2等于() A.310 B .-310 C.34 D .-34答案A解析易知sin x =3sin ⎝⎛⎭⎪⎫x -π2=-3cos x , 所以tan x =-3,所以cos x cos ⎝⎛⎭⎪⎫x +π2 =-sin x cos x =-sin x cos x sin 2x +cos 2x=-tan x tan 2x +1=310. 思维升华 (1)诱导公式的两个应用①求值:负化正,大化小,化到锐角为终了;②化简:统一角,统一名,同角名少为终了.(2)诱导公式的应用步骤任意负角的三角函数―――――→利用诱导公式三或一任意正角的三角函数――――――→利用诱导公式一0~2π内的角的三角函数――――――→利用诱导公式二或四或五或六锐角三角函数.跟踪训练2(1)已知cos(75°+α)=13,求cos(105°-α)+sin(15°-α)=. 答案0解析因为(105°-α)+(75°+α)=180°,(15°-α)+(α+75°)=90°,所以cos(105°-α)=cos[180°-(75°+α)]=-cos(75°+α)=-13, sin(15°-α)=sin[90°-(α+75°)]=cos(75°+α)=13. 所以cos(105°-α)+sin(15°-α)=-13+13=0. (2)(2022·盐城南阳中学月考)设tan(5π+α)=2,则sin (-3π+α)+cos (α-π)cos ⎝ ⎛⎭⎪⎫α-112π+sin ⎝ ⎛⎭⎪⎫9π2+α=. 答案3解析由已知tan(5π+α)=tan α=2,sin (-3π+α)+cos (α-π)cos ⎝ ⎛⎭⎪⎫α-112π+sin ⎝ ⎛⎭⎪⎫9π2+α=sin (π+α)+cos (π-α)cos ⎝ ⎛⎭⎪⎫α+π2+sin ⎝ ⎛⎭⎪⎫π2+α =-sin α-cos α-sin α+cos α=sin α+cos αsin α-cos α=tan α+1tan α-1=3. 题型三 同角三角函数基本关系式和诱导公式的综合应用例3已知f (α)=sin (α-3π)cos (2π-α)sin ⎝ ⎛⎭⎪⎫-α+3π2cos (-π-α)sin (-π-α). (1)化简f (α);(2)若α=-31π3,求f (α)的值; (3)若cos ⎝ ⎛⎭⎪⎫-α-π2=15,α∈⎣⎢⎡⎦⎥⎤π,3π2,求f (α)的值. 解(1)f (α)=sin (α-3π)cos (2π-α)sin ⎝ ⎛⎭⎪⎫-α+3π2cos (-π-α)sin (-π-α)=-sin α×cos α×(-cos α)-cos α×sin α=-cos α.(2)若α=-31π3, 则f (α)=-cos ⎝⎛⎭⎪⎫-31π3=-cos π3=-12. (3)由cos ⎝⎛⎭⎪⎫-α-π2=15, 可得sin α=-15, 因为α∈⎣⎢⎡⎦⎥⎤π,3π2, 所以cos α=-265, 所以f (α)=-cos α=265. 教师备选设f (α)=2sin (π+α)cos (π-α)-cos (π+α)1+sin 2α+cos ⎝ ⎛⎭⎪⎫3π2+α-sin 2⎝ ⎛⎭⎪⎫π2+α(1+2sin α≠0). (1)化简f (α);(2)若α=-23π6,求f (α)的值. 解(1)f (α)=(-2sin α)·(-cos α)-(-cos α)1+sin 2α+sin α-cos 2α=2sin αcos α+cos α2sin 2α+sin α=cos α(2sin α+1)sin α(2sin α+1)=cos αsin α=1tan α. (2)当α=-23π6时,f (α)=f ⎝ ⎛⎭⎪⎫-23π6=1tan ⎝ ⎛⎭⎪⎫-23π6=1tan ⎝⎛⎭⎪⎫-4π+π6 =1tan π6=133= 3. 思维升华 (1)利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活使用公式进行变形.(2)注意角的范围对三角函数符号的影响.跟踪训练3(1)(2022·聊城模拟)已知α为锐角,且2tan(π-α)-3cos ⎝ ⎛⎭⎪⎫π2+β+5=0,tan(π+α)+6sin(π+β)-1=0,则sin α的值是()A.355B.377C.31010D.13答案C解析由已知得⎩⎨⎧ 3sin β-2tan α+5=0,tan α-6sin β-1=0.消去sin β,得tan α=3,∴sin α=3cos α,代入sin 2α+cos 2α=1, 化简得sin 2α=910,则sin α=31010(α为锐角). (2)已知-π<x <0,sin(π+x )-cos x =-15,则sin2x +2sin 2x 1-tan x=. 答案-24175解析由已知,得sin x +cos x =15, 两边平方得sin 2x +2sin x cos x +cos 2x =125, 整理得2sin x cos x =-2425. ∴(sin x -cos x )2=1-2sin x cos x =4925, 由-π<x <0知,sin x <0,又sin x cos x =-1225<0, ∴cos x >0,∴sin x -cos x <0,故sin x -cos x =-75. ∴sin2x +2sin 2x 1-tan x =2sin x (cos x +sin x )1-sin x cos x=2sin x cos x (cos x +sin x )cos x -sin x=-2425×1575=-24175. 课时精练1.cos ⎝ ⎛⎭⎪⎫-19π3等于()A .-32 B .-12 C.12 D.32答案C解析cos ⎝ ⎛⎭⎪⎫-19π3=cos 19π3=cos ⎝ ⎛⎭⎪⎫6π+π3=cos π3=12.2.若cos165°=a ,则tan195°等于()A.1-a 2B.1-a 2a C .-1-a 2a D .-a 1-a 2答案C解析若cos165°=a ,则cos15°=cos(180°-165°)=-cos165°=-a ,sin15°=1-a 2,所以tan195°=tan(180°+15°)=tan15°=sin15°cos15°=-1-a 2a .3.若cos ⎝ ⎛⎭⎪⎫α-π5=513,则sin ⎝ ⎛⎭⎪⎫7π10-α等于()A .-513 B .-1213 C.1213 D.513 答案D解析因为7π10-α+⎝ ⎛⎭⎪⎫α-π5=π2,所以7π10-α=π2-⎝⎛⎭⎪⎫α-π5, 所以sin ⎝ ⎛⎭⎪⎫7π10-α=cos ⎝⎛⎭⎪⎫α-π5=513. 4.(2022·天津西青区模拟)已知sin α+cos α=-2,则tan α+1tan α等于()A .2 B.12 C .-2 D.-12答案A解析由已知得1+2sin αcos α=2,∴sin αcos α=12,∴tan α+1tan α=sin αcos α+cos αsin α=sin 2α+cos 2αsin αcos α=112=2.5.在△ABC 中,下列结论不正确的是()A .sin(A +B )=sin CB .sin B +C 2=cos A 2C .tan(A +B )=-tan C ⎝ ⎛⎭⎪⎫C ≠π2D .cos(A +B )=cos C答案D解析在△ABC 中,有A +B +C =π,则sin(A +B )=sin(π-C )=sin C ,A 正确.sin B +C 2=sin ⎝ ⎛⎭⎪⎫π2-A 2=cos A 2,B 正确. tan(A +B )=tan(π-C )=-tan C ⎝⎛⎭⎪⎫C ≠π2,C 正确. cos(A +B )=cos(π-C )=-cos C ,D 错误.6.已知α∈(0,π),且sin α+cos α=15,给出下列结论: ①π2<α<π; ②sin αcos α=-1225; ③cos α=35; ④cos α-sin α=-75. 其中所有正确结论的序号是()A .①②④B .②③④C .①②③D .①③④答案A解析∵sin α+cos α=15, 等式两边平方得(sin α+cos α)2=1+2sin αcos α=125, 解得sin αcos α=-1225,故②正确; ∵α∈(0,π),sin αcos α=-1225<0,∴α∈⎝ ⎛⎭⎪⎫π2,π, ∴cos α<0,故①正确,③错误;cos α-sin α<0,且(cos α-sin α)2=1-2sin αcos α=1-2×⎝ ⎛⎭⎪⎫-1225=4925, 解得cos α-sin α=-75,故④正确. 7.sin 21°+sin 22°+sin 23°+…+sin 289°=________.答案44.5解析∵sin1°=cos89°,sin2°=cos88°,…,sin89°=cos1°, ∴sin 21°+sin 22°+sin 23°+…+sin 289°=44.5.8.设f (θ)=2cos 2θ+sin 2(2π-θ)+sin ⎝ ⎛⎭⎪⎫π2+θ-32+2cos 2(π+θ)+cos (-θ),则f ⎝ ⎛⎭⎪⎫17π3=. 答案-512解析∵f (θ)=2cos 2θ+sin 2θ+cos θ-32+2cos 2θ+cos θ=cos 2θ+cos θ-22cos 2θ+cos θ+2, 又cos 17π3=cos ⎝⎛⎭⎪⎫6π-π3 =cos π3=12,∴f ⎝ ⎛⎭⎪⎫17π3=14+12-212+12+2=-512.9.(1)(2022·郑州模拟)已知sin θ=45,求sin (π-θ)cos ⎝ ⎛⎭⎪⎫π2+θcos (π+θ)sin ⎝ ⎛⎭⎪⎫π2-θ的值. 解∵sin θ=45, ∴cos 2θ=1-sin 2θ=925, 则sin (π-θ)cos ⎝ ⎛⎭⎪⎫π2+θcos (π+θ)sin ⎝ ⎛⎭⎪⎫π2-θ=sin θ(-sin θ)(-cos θ)cos θ =sin 2θcos 2θ=169. (2)已知sin x +cos x =-713(0<x <π),求cos x -2sin x 的值. 解∵sin x +cos x =-713(0<x <π), ∴cos x <0,sin x >0,即sin x -cos x >0,把sin x +cos x =-713, 两边平方得1+2sin x cos x =49169, 即2sin x cos x =-120169,∴(sin x -cos x )2=1-2sin x cos x =289169, 即sin x -cos x =1713, 联立⎩⎪⎨⎪⎧ sin x +cos x =-713,sin x -cos x =1713,解得sin x =513,cos x =-1213, ∴cos x -2sin x =-2213. 10.(2022·衡水模拟)已知角α的终边经过点P (3m ,-6m )(m ≠0).(1)求sin (α+π)+cos (α-π)sin ⎝ ⎛⎭⎪⎫α+π2+2cos ⎝⎛⎭⎪⎫α-π2的值; (2)若α是第二象限角,求sin 2⎝ ⎛⎭⎪⎫α+3π2+sin(π-α)·cos α-cos ⎝ ⎛⎭⎪⎫π2+α的值. 解(1)∵m ≠0,∴cos α≠0,即sin (α+π)+cos (α-π)sin ⎝ ⎛⎭⎪⎫α+π2+2cos ⎝⎛⎭⎪⎫α-π2 =-sin α-cos αcos α+2sin α=-tan α-11+2tan α. 又∵角α的终边经过点P (3m ,-6m )(m ≠0),∴tan α=-6m 3m=-2,故sin (α+π)+cos (α-π)sin ⎝ ⎛⎭⎪⎫α+π2+2cos ⎝⎛⎭⎪⎫α-π2 =-tan α-11+2tan α=2-11+2×(-2)=-13. (2)∵α是第二象限角,∴m <0,则sin α=-6m (3m )2+(-6m )2 =-6m 35|m |=255, cos α=3m (3m )2+(-6m )2=3m 35|m |=-55, ∴sin 2⎝ ⎛⎭⎪⎫α+3π2+sin(π-α)cos α-cos ⎝ ⎛⎭⎪⎫π2+α =cos 2α+sin αcos α+sin α=⎝ ⎛⎭⎪⎫-552+255×⎝ ⎛⎭⎪⎫-55+255 =-1+255.11.已知角α满足sin α·cos α≠0,则表达式sin (α+k π)sin α+cos (α+k π)cos α(k ∈Z )的取值可能为()A .-2或0B .-1或1C .2或-2D .-2或2或0答案C解析当k 为奇数时,原式=-sin αsin α+-cos αcos α=(-1)+(-1)=-2; 当k 为偶数时,原式=sin αsin α+cos αcos α=1+1=2. ∴原表达式的取值可能为-2或2.12.(2022·河北六校联考)若sin α是方程5x 2-7x -6=0的根,则sin ⎝ ⎛⎭⎪⎫-α-3π2sin ⎝ ⎛⎭⎪⎫3π2-αtan 2(2π-α)cos ⎝ ⎛⎭⎪⎫π2-αcos ⎝ ⎛⎭⎪⎫π2+αsin (π+α)等于() A.35 B.53 C.45 D.54答案B解析方程5x 2-7x -6=0的两根为x 1=-35,x 2=2,则sin α=-35. 原式=cos α(-cos α)tan 2αsin α(-sin α)(-sin α)=-1sin α=53. 13.曲线y =e x +x 2-23x 在x =0处的切线的倾斜角为α,则sin ⎝⎛⎭⎪⎫2α+π2=. 答案45解析由题意得y ′=f ′(x )=e x +2x -23, 所以f ′(0)=e 0-23=13, 所以tan α=13, 所以α∈⎝⎛⎭⎪⎫0,π2, 所以cos α=310, 所以sin ⎝⎛⎭⎪⎫2α+π2 =cos2α=2cos 2α-1=2×910-1=45. 14.函数y =log a (x -3)+2(a >0且a ≠1)的图象过定点Q ,且角α的终边也过点Q ,则3sin 2α+2sin αcos α=.答案75解析由题意可知点Q (4,2),所以tan α=12, 所以3sin 2α+2sin αcos α=3sin 2α+2sin αcos αsin 2α+cos 2α=3tan 2α+2tan α1+tan 2α=3×14+2×121+14=75.15.已知f (x )是定义在R 上的偶函数,且在[0,+∞)上单调递增,若a =f ⎝⎛⎭⎪⎫sin 12π7,b =f ⎝ ⎛⎭⎪⎫cos 5π7,c =f ⎝⎛⎭⎪⎫tan 2π7,则() A .a >b >c B .c >a >bC .b >a >cD .c >b >a答案B解析根据题意,sin12π7=sin ⎝ ⎛⎭⎪⎫2π-2π7 =-sin2π7, cos 5π7=cos ⎝⎛⎭⎪⎫π-2π7=-cos 2π7, 又由函数f (x )是定义在R 上的偶函数,则a =f ⎝ ⎛⎭⎪⎫sin 12π7=f ⎝ ⎛⎭⎪⎫-sin 2π7=f ⎝⎛⎭⎪⎫sin 2π7, b =f ⎝ ⎛⎭⎪⎫cos 5π7=f ⎝ ⎛⎭⎪⎫-cos 2π7=f ⎝⎛⎭⎪⎫cos 2π7, 又由π4<2π7<π2, 则有0<cos 2π7<sin 2π7<1<tan 2π7, 又由函数在[0,+∞)上单调递增,则有c >a >b .16.已知关于x 的方程2x 2-(3+1)x +m =0的两根分别是sin θ和cos θ,θ∈(0,2π),求:(1)sin 2θsin θ-cos θ+cos θ1-tan θ的值; (2)m 的值;(3)方程的两根及此时θ的值.解(1)原式=sin 2θsin θ-cos θ+cos θ1-sin θcos θ=sin 2θsin θ-cos θ+cos 2θcos θ-sin θ=sin 2θ-cos 2θsin θ-cos θ=sin θ+cos θ.由已知得sin θ+cos θ=3+12, 所以sin 2θsin θ-cos θ+cos θ1-tan θ=3+12. (2)由已知得sin θcos θ=m2, 因为1+2sin θcos θ=(sin θ+cos θ)2,所以1+m =⎝ ⎛⎭⎪⎫3+122, 解得m =32. (3)联立⎩⎪⎨⎪⎧ sin θ+cos θ=3+12,sin θcos θ=34,解得⎩⎪⎨⎪⎧ sin θ=32,cos θ=12或⎩⎪⎨⎪⎧ sin θ=12,cos θ=32.因为θ∈(0,2π),所以θ=π3或π6.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
sinα+cosα +cos2α=( sinα-cosα
)
16 B.- 5 D.- 8 5
解析
sinα+cosα sinα+cosα cos2α 2 +cos α= + sinα-cosα sinα-cosα sin2α+cos2α
tanα+1 1 16 = + 2 = .故选 A. tanα-1 tan α+1 5
4.sin(π+α)=-sinα 成立的条件是 α 为锐角.( × ) 5.六组诱导公式中的角 α 可以是任意角.( √ ) 1 1 6.若 cos(nπ-θ)= (n∈Z),则 cosθ= .( × ) 3 3 1 1 7.已知 sin(α-37° )= ,则 cos(α+53° )=- .( √ ) 3 3
π 3π 又因为 α∈2, 2 ,所以 α 为第三象限的角, π 4 所以 sinα+2=cosα=- . 5
5π 1 π π (2)[2016· 衡水模拟]已知 cos12+α= ,且-π<a<- ,则 cos12-α等于( 2 3
)
A.
2 2 3
1 B. 3
C.-
1 3
D.-
2 2 3
解析
5 π π π π π 5π π 因为 12π+α + 12-α = ,所以 cos 12-α =sin - 12-α =sin 12+α.因为-π<α<- , 2 2 2
(2)由已知条件及(1)可知
sinx+cosx=1, 5 7 sinx-cosx=-5 ,
3 ∴tanx=- . 4
sinx=-3, 5 解得 cosx=4 , 5
sin2x+cos2x 1 又∵ 2 = cos x-sin2x cos2x-sin2x sin2x+cos2x tan2x+1 cos2x 1 25 = 2 . 2 = 2 ,∴ 2 2 = cos x-sin x 1-tan x cos x-sin x 7 cos2x
[解析]
5π π tan 6 +α =tan π- 6-α
π =- 2. - α =-tan 6
利用诱导公式化简求值的思路 (1)给角求值问题,关键是利用诱导公式把任意角的三角函数值转化为锐角的三角函数值求解.转化过 程中注意口诀“奇变偶不变,符号看象限”的应用. (2)在对给定的式子进行化简或求值时,要注意给定的角之间存在的特定关系,充分利用给定的关系结 合诱导公式来将角进行转化.特别要注意每一个角所在的象限,防止符号及三角函数名称搞错.
cosα
tanα
-cosα
-tanα
[必会结论] 1.特殊角的三角函数值 α sinα 0 0 π 6 1 2 3 2 3 3 π 4 2 2 2 2 1 π 3 3 2 1 2 3 π 2 1 0 不存在 π 0 -1 0 3π 2 -1 0 不存在
cosα 1 tanα 0
π 2.诱导公式可简记为:奇变偶不变,符号看象限.“奇”与“偶”指的是诱导公式 k·+α 中的整数 k 2 是奇数还是偶数.“变”与“不变”是指函数的名称的变化,若 k 是奇数,则正、余弦互变;若 k 为偶数, π π 则函数名称不变.“符号看象限”指的是在 k·+α 中,将 α 看成锐角时 k·+α 所在的象限. 2 2
sin239° · tan149° =sin(270° -31° )· tan(180° -31° )=(-cos31° )· (-tan31° )=sin31° = 1-a2.
(2)[2016· 淮南模拟]已知 f(x)=
-1 21π ,则 f- 4 =________. 11 cos3π-x· sin 2 π-x
第 2讲
同角三角函数的基本关系式与诱导公式
1.理解同角三角函数的基本关系式:sin2α+cos2α=1,
sinα =tanα. cosα
π 2.能利用单位圆中的三角函数线推导出 ± α,π±α 的正弦、余弦、正切的诱导公 2 式.
板块一 知识梳理· 自主学习
[必备知识] 考点1 同角三角函数的基本关系式 sin2α+cos2α=1 1.平方关系:___________________.
考向 的,在高考中常以选择题、解答题的形式出现. 命题角度 1 例2 1 -a 2 A. a a2-1 C. a
[解析]
利用诱导公式化简求值
利用诱导公式、同角三角函数关系式化简求值是高考的重点,常与三角恒等变换结合,达到化简的目 利用诱导公式化简三角函数式 )
(1)[2016· 厦门模拟]已知 cos31° =a,则 sin239° · tan149° 的值是( B. 1-a2 D.- 1-a2
7 ∴sinx-cosx=- . 5
1 解法二:∵sinx+cosx= , 5
1 ∴(sinx+cosx)2=52,
1 即 1+2sinxcosx= , 25 24 ∴2sinxcosx=- . 25 ∵(sinx-cosx)2=sin2x-2sinxcosx+cos2x 24 49 =1-2sinxcosx=1+ = .① 25 25 π 又∵- <x<0,∴sinx<0,cosx>0, 2 ∴sinx-cosx<0.② 7 由①②可知 sinx-cosx=- . 5
9 3 tan x+tanx 16-4 3 = = =- . 2 9 25 tan x+1 +1 16的应用 (1)利用 sin2α+cos2α=1 可以实现角 α 的正弦、 余弦的互化, 利用 sinα =tanα 可以实现角 α 的弦切互化. cosα
(2)应用公式时注意方程思想的应用: 对于 sinα+cosα, sinαcosα, sinα-cosα 这三个式子, 利用(sinα± cosα)2 =1± 2sinαcosα,可以知一求二. (3)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α. (4)关于 sinα,cosα 的齐次式,往往转化为关于 tanα 的式子求解.
解析 原式=
cosθ+cosθ 2cosθ = cosθ-sinθ cosθ-sinθ
2 2 = = 1-tanθ 1-2 =-2.
板块二 典例探究· 考向突破
考向 例1
同角三角函数基本关系式的应用
π 1 [2016· 杭州模拟]已知- <x<0,sinx+cosx= . 2 5
(1)求 sinx-cosx 的值;
延伸探究 1 sinx-2cosx 的值. 4sinx+cosx 3 - -2 sinx-2cosx tanx-2 4 11 解 = = = . 4sinx+cosx 4tanx+1 -3+1 8 在本例条件下,求
延伸探究 2 在本例条件下,求 sin2x+sinxcosx 的值.
2 sin x+sinxcosx 2 解 sin x+sinxcosx= sin2x+cos2x
2.[2016· 泰安模拟]sin600° 的值为( A.- C. 1 2 1 2 B.- D. 3 2 3 2
)
解析
sin600° =sin(360° +240° )=sin240° =sin(180° +60° )=-sin60° =-
3 . 2
π 3 π 3π 3.[2015· 辽宁五校联考]已知 cos 2+α = ,且 α∈2, 2 ,则 tanα=( 5
sinα tanα= cosα 2.商数关系:______________.
考点2 六组诱导公式 角函 数 正弦 余弦 正切 2kπ+α(k∈Z) π+α -α π -α π -α 2 π +α 2
sinα
-sinα -cosα
tanα
-sinα cosα
-tanα
sinα
cosα
sinα —
cosα -sinα —
【变式训练 1】 A.- C.- 1 5 5 5
(1)若 α 是第二象限角,且 tanα=-2,则 cosα=( B.- 2 5 2 5 5
)
D.-
解析 由 tanα=-2,得 sinα=-2cosα,代入平方关系得 5cos2α=1,因为 cosα<0,所以 cosα=-
5 . 5
(2)若 tanα=2,则 16 A. 5 C. 8 5
)
3 7 7
解析 sin2α= 9 . 10
由 tan(π-α)+3=0 得 tanα=3,即
sinα =3,sinα=3cosα,所以 sin2α=9(1-sin2α),10sin2α=9, cosα
3 又因为 α 为锐角,所以 sinα= 10. 10
π sin 2+θ-cosπ-θ -2 5.[课本改编]已知 tanθ=2,则 =________. π sin2-θ-sinπ-θ
[双基夯实] 一、疑难辨析 判断下列结论的正误.(正确的打“√”,错误的打“×”) 1.若 α,β 为锐角,则 sin2α+cos2β=1.( × ) 2.若 α∈R,则 tanα= 4 3.已知 sinα= ,α∈ 5 sinα 恒成立.( × ) cosα
π 3 ,π,则 cosα= .( × ) 5 2
)
A.
4 3 3 4
3 B. 4
3 D .± 4 π 3 3 4 3 解析 因为 cos 2+α= ,所以 sinα=- .显然 α 在第三象限,所以 cosα=- ,故 tanα= . 5 5 4 5 C.-
4.[2016· 梅州模拟]已知 α 为锐角,且 tan(π-α)+3=0,则 sinα 的值是( A. C. 1 3 3 B. 10 10 D. 3 5 5
【变式训练 2】 A. C. 4 5 B.- 4 5 3 5
π 3π π 3 (1)[2016· 成都月考]已知 tan(α-π)= ,且 α∈ 2, 2 ,则 sin α+2=( 4
