辅助圆专题
定弦定角构造辅助圆

专题25 定弦定角构造辅助圆1.如图,点P 是正六边形ABCDEF 内一点,4AB =,当90APB ∠=︒时,连接PD ,则线段PD 的最小值是( )A .2B .2-C .6D .【解答】解:4AB =,90APB ∠=︒,∴点P 在以AB 为直径的圆弧上,如图,取AB 的中点O ,连接OD ,当O 、P 、D 三点共线时,PD 有最小值, 连接BD ,过点C 作CH BD ⊥于点H ,点O 为AB 的中点,422OA OB OP ∴===÷=,正六边形的每个内角为180(62)6120︒⨯-÷=︒,CD CB =,(180120)230CBD ∴∠=︒-︒÷=︒,2BD BH =,1203090OBD ∴∠=︒-︒=︒,在Rt CBH ∆中,122CH CB ==,BH =BD ∴=在Rt OBD ∆中,OD ,PD ∴的最小值为2OD OP -=.故选:B .2.如图,在平面直角坐标系中,线段AB 在x 轴上移动,在运动过程中,直线y =上的点P 如果满足30APB ∠=︒,则点P 为好点,当AB 在x 轴上运动到某一位置时,好点P 的个数最多有()A.1个B.2个C.3个D.4个【解答】解:如图,当AB在x轴的正半轴时,构建等边三角形ABC,以C为圆心,以CA 为半径作辅助圆C,直线y=与C的交点就是点P,此时1302APB ACB∠=∠=︒,∴好点P最多有两个,同理在x轴的负半轴时,也存在两个好点P,故选:B.3.如图,BC是O的直径,BC=,M、N是半圆上不与B、C重合的两点,且120MON∠=︒,ABC∆的内心为E点,当点A在MN上从点M运动到点N时,点E运动的路径长是()A.23πB.43πC.83πD.163π【解答】解:如图,连接BE 、CE ,90BAC ∠=︒,E 是内心,135BEC ∴∠=︒,∴点E 在以P 为圆心的PC 为半径的圆上运动(轨迹是)GH ,在P 上取一点M ',连接BM '、CM ',则18013545M ∠'=︒-︒=︒,290BPC M ∠=∠'=︒,BCP ∴∆是等腰直角三角形, 4BC =,4PB PC ∴==,122HPC HBC NBC NOC ∠=∠=∠=∠,同理12GPB MOB ∠=∠, 1()302HPC GPB NOC MOB ∴∠+∠=∠+∠=︒, 60GPH ∴∠=︒, ∴点E 运动的路径长是60441803ππ⋅=, 故选:B .4.如图,在平面直角坐标系中,等边OAB ∆的边OB 在x 轴正半轴上,点(3,)A m ,0m >,点D 、E 分别从B 、O 以相同的速度向O 、A 运动,连接AD 、BE ,交点为F ,M 是y 轴上一点,则FM 的最小值是( )A .3 B1 C.2 D.6-【解答】解:如图,OAB ∆是等边三角形,60AOB ABD ∴∠=∠=︒,OB AB =,点D 、E 分别从B 、O 以相同的速度向O 、A 运动,BD OE ∴=,在OBE ∆和DAB ∆中,60OE BD BOE ABD OB AB =⎧⎪∠=∠=︒⎨⎪=⎩,()OBE DAB SAS ∴∆≅∆,OBE BAD ∴∠=∠,60ABE BAD ABE OBE ABO ∴∠+∠=∠+∠=∠=︒180()120AFB ABE BAD ∴∠=︒-∠+∠=︒,∴点F 是经过点A ,B ,F 的圆上的点,记圆心为O ',在O '上取一点N ,使点N 和点F 在弦AB 的两侧,连接AN ,BN ,18060ANB AFB ∴∠=︒-∠=︒,连接O A ',O B ',2120AO B ANB '∴∠=∠=︒,O A O B ''=,ABO BAO ''∴∠=∠,11(180)(180120)3022ABO AO B ''∴∠=︒-∠=︒-︒=︒, 60ABO ∠=︒,90OBO '∴∠=︒,AOB ∆是等边三角形,(3,)A m ,23AB OB ∴==⨯,m =过点O '作O G AB '⊥,132BG AB ∴==, 在Rt △BO G '中,30ABO '∠=︒,3BG =,3cos cos30BG O B ABO '∴==='∠︒, (6O '∴,,设(0,)M n ,O M '∴=FM O M O F ''∴=-=,只有0n -=时,(n -最小为06.当0n -=时,即:n =时,FM 最小,6FM ∴=-的最小值.故选:D .5.如图,正方形ABCD 中,2AB =,动点E 从点A 出发向点D 运动,同时动点F 从点D 出发向点C 运动,点E 、F 运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF 、BE 相交于点P ,则线段DP1 .【解答】解:如图:, 动点F ,E 的速度相同,DF AE ∴=,又正方形ABCD 中,2AB =,AD AB ∴=,在ABE ∆和DAF ∆中,AB AD BAE ADF AE DF =⎧⎪∠=∠⎨⎪=⎩,ABE DAF ∴∆≅∆,ABE DAF ∴∠=∠.90ABE BEA ∠+∠=︒,90FAD BEA ∴∠+∠=︒,90APB ∴∠=︒,点P 在运动中保持90APB ∠=︒,∴点P 的路径是一段以AB 为直径的弧,设AB 的中点为G ,连接CG 交弧于点P ,此时CP 的长度最小, 112AG BG AB ===.在Rt BCG ∆中,DG =1PG AG ==,1DP DG PG ∴=-=即线段DP 1,1.6.如图,正方形ABCD ,以B 为圆心,BC 长为半径画弧,点E 在圆弧上,EH BC ⊥于点H ,P 是EHB ∆的内心,2AB =,则AP 的最小值为【解答】解:连接PE 、PC 、PB .P 是EHB ∆的内心,90EHB ∠=︒,1180()1352EPB HEB HBE ∴∠=︒-∠+∠=︒, BC BE =,PBC PBE ∠=∠,PB PB =,PBC PBE ∴∆≅∆,135BPC BPE ∴∠=∠=︒(定角), ∴点P 的运动轨迹是圆弧,以BC 为斜边在BC 的下方作等腰直角三角形BCO ,连接OP 、OA .则以点O 为圆心,OB 为半径的O 是点P 的轨迹,AP AO OP -,∴当O 、P 、A 共线时,PA 的值最小,作OM AB ⊥于M .易知OB ,1OF BF ==,OA =PA ∴-7.如图,在矩形ABCD 中,AB a =,BC b =,点P 是BC 上的一个动点,连接AP ,把PAB ∆沿着AP 翻折到△PB C '(点B '在矩形的内部),连接B C ',B D '.点P 在整个运动过程中,若存在唯一的位置使得△B CD '为直角三角形,则a ,b 之间的数量关系是 b = .【解答】解:如图,以CD 为直径作O ,当点A 到O 的最小距离等于AB 时,使得△B CD '为直角三角形且唯一,在Rt ADO ∆中,222AD OD OA +=,22211()()22b a a a ∴+=+, 整理得222b a =,0a >,0b >,b ∴=.8.如图,O 的直径为4,C 为O 上一个定点,30ABC ∠=︒,动点P 从A 点出发沿半圆弧AB 向B 点运动(点P 与点C 在直径AB 的异侧),当P 点到达B 点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.CD.(1)在点P的运动过程中,线段CD长度的取值范围为43(2)在点P的运动过程中,线段AD长度的最大值为.【解答】解:(1)如图1中,AB=AB是直径,30∠=︒,4ABCAC=,A P∠=∠=︒,2∴∠=︒,60ACB90⊥,CD PC=⋅︒,CD PC90∴∠=︒,tan60PCD=,==,PC的最大值为直径4ACPC的最小值2∴的最小值为CD点P与点C在直径AB的异侧∴.CD43CD.故答案为43(2)如图2中,在Rt PCDP∠=︒,60∠=︒,PCD∆中,90PDC∴∠=︒,30∴点D在以BC为弦的O'(红弧线)上运动,∴当A、O'、D共线时,AD的值最大.连接CO'、BO'.'=',∠'=∠=︒,O C O BBO C CDB260'是等边三角形,∴△O BC∴'==60BO BC∠'=︒,CBO∠=︒,30ABC∴∠'=︒,90ABOAO∴'=AD AO O D∴='+'=∴的最大值为AD故答案为9.如图,AB是O的直径,C为圆上一点,且120∠=︒,O的半径为2,P为圆上AOC一动点,Q为AP的中点,则CQ的长的最大值是1+【解答】解:如图,连接OQ,作CH AB⊥于H.AQ QP =,OQ PA ∴⊥,90AQO ∴∠=︒,∴点Q 的运动轨迹为以AO 为直径的K ,连接CK ,当点Q 在CK 的延长线上时,CQ 的值最大,在Rt OCH ∆中,60COH ∠=︒,2OC =,112OH OC ∴==,CH =,在Rt CKH ∆中,CK =CQ ∴的最大值为1+10.如图,P 是矩形ABCD 内一点,4AB =,2AD =,AP BP ⊥,则当线段DP 最短时,CP =【解答】解:以AB 为直径作半圆O ,连接OD ,与半圆O 交于点P ',当点P 与P '重合时,DP 最短,122AO OP OB AB ='===, 2AD =,90BAD ∠=︒,OD ∴=,45ADO AOD ODC ∠=∠=∠=︒,2DP OD OP ∴'=-'=,过P '作P E CD '⊥于点E ,则22P E DE DP '=='=,2CE CD DE ∴=-=,CP ∴'=故答案为:11.在平面直角坐标系中,已知点(0,2)A -、(0,3)B ,点C 是x 轴正半轴上的一点,当45BCA ∠=︒时,点C 的坐标为 (6,0) .【解答】解:如图,作ABC ∆的外接圆P ,过P 作EP BA ⊥,PF OC ⊥于F , AE BE ∴=,点(0,2)A -、(0,3)B ,5AB ∴=,1(0,)2E ∴, 45ACB ∠=︒,90APB ∴∠=︒,1522PE AB ∴==, 5(2P ∴,1)2,在Rt PBE ∆中,52PE BE ==,由勾股定理得:PB ,在Rt PFC ∆中,12PF =,PC PB =72FC = 57622OC OF CF ∴=+=+=, ∴点C 坐标为(6,0),故答案为(6,0).12.如图,正方形ABCD中,2AB=,动点E从点A出发向点D运动,同时动点F从点D 出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD MP+的最小值为【解答】解:如图作点D关于BC的对称点D',连接PD',由轴对称的性质可知:MD D M=',2='=CD CD∴+=+'='PM DM PM MD PD过点P作PE垂直DC,垂足为G,易证AF BE⊥,故可知P的轨迹为以AB为直径的四分之一圆弧上,当点E与点D重合,点F与点C重合时,PG和GD'均最短,∴此时,PD'最短.四边形ABCD为正方形,112PG AD ∴==,112GC DC ==. 3GD ∴'=.在Rt PGD ∆'中,由勾股定理得:PD '===13.如图,边长为4的正方形ABCD 外有一点E ,90AEB ∠=︒,F 为DE 的中点,连接CF ,则CF 的最大值为 1 .【解答】解:解法一:如图,以AB 为直径作圆H ,90AEB ∠=︒,∴点E 在这个H 上,延长DC 至P ,使CD PC =,连接BE ,EH ,PH ,过H 作HM CD ⊥于M , EF DF =,CD PC =,12CF PE ∴=, Rt AEB ∆中,H 是AB 的中点,122EH AB ∴==,Rt PHM ∆中,由勾股定理得:PH ==2PE EH PH +=+,当P ,E ,H 三点共线时,PE 最大,CF 最大,CF ∴1;解法二:连接BD ,取BD 、AD 的中点为H 、G ,连接FH 、GF ,F 为DE 的中点,FH ∴是BDE ∆的中位线,FG 是ADE ∆的中位线,//FH BE ∴,//FG AE ,HFD BED ∴∠=∠,GFD AED ∠=∠,90AEB ∠=︒,90BED AED ∴∠+∠=︒,90HFD GFD ∴∠+∠=︒,90HFG ∴∠=︒,∴点F 在以GH 为直径的半圆上运动,取GH 的中点I ,则CF 最大时,是经过圆心I , GH 是ABD ∆的中位线,114222GH AB ∴==⨯=, 1GI ∴=,过I 作IM CD ⊥于M ,在Rt CIM ∆中,413CM =-=,2IM =,由勾股定理得:CI ==1CF ∴'=,1.14.如图,正方形ABCD 中,4AB =,动点E 从点A 出发向点D 运动,同时动点F 从点D 出发向点C 运动,点E 、F 运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF 、BE 相交于点P ,M 是线段BC 上任意一点,则MD MP +的最小值为【解答】解:如图作点D 关于BC 的对称点D ',连接PD ',由轴对称的性质可知:MD D M =',4CD CD ='=,PM DM PM MD PD ∴+=+'='过点P 作PE 垂直DC ,垂足为G ,易证AF BE ⊥,故可知P 的轨迹为以AB 为直径的四分之一圆弧上,当点E 与点D 重合,点F 与点C 重合时,PG 和GD '均最短,∴此时,PD '最短.四边形ABCD 为正方形,122PG AD ∴==,122GC DC ==. 6GD ∴'=.在Rt PGD ∆'中,由勾股定理得:PD '===.故答案为三.解答题(共4小题)15.在平行四边形ABCD 中,AD =,2AB =,45A ∠=︒,问AB 边上是否存在一个点P ,使得45DPC ∠=︒?若存在,请求出AP 的长;若不存在,请说明理由.【解答】解:存在.理由如下,如图,作DM AB ⊥于M .在Rt ADM ∆中,2AD =45A ∠=︒,1AM DM ∴==, 2AB =,1AM BM DM ∴===,90ADB ∴∠=︒,//AD CB ,90DBC ADB ∴∠=∠=︒,ADB ∆,DBC ∆的是等腰直角三角形,BD BC AD ∴==以B 为圆心BC 画圆交AB 于P ,此时1452DPC DBC ∠=∠=︒,PB BC ∴==2AP AB PB ∴=-=16.已知线段2BC =,用尺规作ABC ∆,使45A ∠=︒,你能作出多少个满足条件的三角形?【解答】解:如图,当2BC =,90BOC ∠=︒时,点A 在优弧BC 上, 1452A BOC ∠=∠=︒, 45A A A ∴∠'=∠''=∠=︒,∴满足条件的点A 有无数个.17.如图,在四边形ABCD 中,2AB =,BC =1CD =,90ABC BCD ∠=∠=︒,点E 、点P 是四边形内的动点,且150AED ∠=︒,求PC PB PE ++的最小值.【解答】解:过点A 作AG CD ⊥于点G ,90ABC BCD ∠=∠=︒,∴四边形ABCG 是矩形,2CG AB ∴==,AG BC ==211DG ∴=-=,Rt AGD ∆中,tan AG AHD GD∠==, 60ADG ∴∠=︒,2AD =,延长DG 至点O ,使得2OD AD ==,OAD ∴∆是等边三角形,以点O 为圆心,OA 为半径作圆,∴优AD 的度数为300︒,150AED ∠=︒,∴点E 在O 上,BPC ∆绕着点B 顺时针旋转60︒至△BP C '',BP BP ∴=',PC P C =',60PBP ∠'=︒,BP PP ∴=',PC PB PE P C PP PE ∴++='+'+,而OE 是定值,∴求P C PP PE '+'+最短,就是求P C PP PE OE '+'++最短,当O 、E 、P 、C '四点共线时,P C PP PE OE '+'++最短,最短值就是OC '的长, 过点C '作C F OC '⊥于点F ,BCC ∆'是等边三角形,12C F BC ∴'=,32CF F '=,OC ∴'=,P C PP PE OE ∴'+'++P C PP PE ∴'+'+2,PC PB PE ∴++2.18.如图1,已知四边形ABCD 是平行四边形,AC BC ⊥且AC BC =,以BC 、AC 所在直线为坐标轴建立平面直角坐标系(6,0)B -,直线3y x b =+过点D 且与x 轴交于点M .(1)请直接写出点D ,b 的值及点M 的坐标;(2)如图2,点E 是线段AB 上的一点,点F 是线段AC 上的一点,且45CEF ∠=︒,若CEF ∆为等腰三角形,求线段AE 的长;(3)如图3,点G 为y 轴正半轴上的一点,当45BGM ∠=︒时,求线段AG 的长.【解答】解:(1)如图1,(6,0)B -,6BC ∴=,AC BC =,6AC ∴=,四边形ABCD 是平行四边形,且AC BC ⊥,6AD BC ∴==,AD AC ⊥,(6,6)D ∴,把(6,6)D 代入3y x b =+中得:636b =⨯+,12b =-,312y x ∴=-,当0y =时,3120x -=,4x =,(4,0)M ∴;(2)若CEF ∆为等腰三角形,分三种情况讨论:①当CE CF =时,如图2,则CEF CFE ∠=∠,45CEF ∠=︒,E ∴与B 重合,F 与A 重合,AE AB ∴==;②当CE EF =时,如图3,过E 作EH AC ⊥于H ,则CEH FEH ∠=∠, 45CEF ∠=︒,14522.52CEH ∴∠=⨯︒=︒, 9022.567.5ECH ∴∠=︒-︒=︒,在AEC ∆中,45BAC ∠=︒,1804567.567.5AEC ∴∠=︒-︒-︒=︒,AEC ECH ∴∠=∠,6AE AC ∴==;③当EF CF =时,如图4,设EF x =,EF FC x ==,45CEF ∠=︒,45EFC CEF ∴∠=∠=︒,90EFC ∴∠=︒,90ACB ∠=︒,AFE ACB ∴∠=∠,//EF BC ∴, ∴EF AF BC AC=, AC BC =,EF AF ∴=,6x x ∴=-,3x =,3EF AF ∴==,∴=,AE综上所述:AE的长为6或(3)如图5,作BM的中垂线交AB于E,交BM于P,过E作EF y⊥轴于F,连接EM、GE,EB EM∴=,∠=︒,45ABC∴∠=∠=︒,ABC EMB45∴∠=︒,BEM90∠=︒,BGM45∆的外接圆的圆心,∴点E是BGM∴==,EG EB EMCM=,BC=,46∴=,BM10∴==,BP PE5∴==,BE∴=,EGEF=-=,651∴,7GF∴=+-=+-=.AG GF FC AC7566。
专题16 构造辅助圆(隐圆)解题的几种常见模型-2023年中考数学二轮复习核心考点拓展训练(解析版)

专题16 构造辅助圆(隐圆)解题的几种常见模型(解析版)类型一定点定长模型典例1(威海中考)如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )A.68°B.88°C.90°D.112°思路引领:如图,作辅助圆;首先运用圆周角定理证明∠CAD=2∠CBD,∠BAC=2∠BDC,结合已知条件∠CBD=2∠BDC,得到∠CAD=2∠BAC,即可解决问题.解:如图,∵AB=AC=AD,∴点B、C、D在以点A为圆心,以AB的长为半径的圆上;∵∠CBD=2∠BDC,∠CAD=2∠CBD,∠BAC=2∠BDC,∴∠CAD=2∠BAC,而∠BAC=44°,∴∠CAD=88°,故选:B.总结提升:该题主要考查了圆周角定理及其推论等几何知识点及其应用问题;解题的方法是作辅助圆,将分散的条件集中;解题的关键是灵活运用圆周角定理及其推论等几何知识点来分析、判断、推理或解答.针对训练1.(苏州期中)如图,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD2的值为( )A.14B.15C.18D.12思路引领:作AM⊥BC于点M,AN⊥BD于点N,根据题给条件及等腰三角形的性质证明△ABN≌△BAM,继而求出AN的值,在Rt△ABN中,利用勾股定理求解即可.解:作AM⊥BC于点M,AN⊥BD于点N,∵AC=AB,∴△ABC为等腰三角形,∴AM也是△ABC的中线和角平分线(三线合一),∴∠CAM=∠BAM,∴△ABM≌△ACM,∵AB∥CD,AC=AD,∴∠ADC=∠ACD=∠CAB,∵∠ADB=∠ABD=∠CDB,∴∠ADB=12∠ADC=∠MAB,∴∠MAB=∠DBA,又∵AB=AB,∴△ABN≌△BAM(AAS),∴AN=12BC=12,∵AB=2,∴BN2=AB2﹣AN2=15 4,∴BD2=4BN2=15.故选:B.总结提升:本题考查了梯形的知识,同时涉及了等腰三角形的性质和勾股定理的知识,难度适中,解题关键是正确作出辅助线.2.(2021春•牧野区校级期中)如图,在矩形ABCD中,E为AB的中点,P为BC边上的任意一点,把△PBE 沿PE折叠,得到△PFE,连接CF.若AB=10,BC=12,当CF取最小值时,BP的值等于 .思路引领:点F在以E为圆心EA为半径的圆上运动,当E、F、C共线时时,此时FC的值最小,根据勾股定理求出CE,根据折叠的性质可知BE=EF=5,即可求出CF,再利用勾股定理即可解决问题.解:如图所示,点F在以E为圆心EA为半径的圆上运动,当E、F、C共线时时,此时CF的值最小,根据折叠的性质,△EBP≌△EFP,∴EF⊥PF,EB=EF,∵E是AB边的中点,AB=10,∴AE=EF=5,∵AD=BC=12,∴CE=BE2+BC2=13,∴CF=CE﹣EF=13﹣5=8.由折叠可知:FP=BP,∴CP=BC﹣BP=12﹣BP,在Rt△CFP中,根据勾股定理得:CF2+FP2=CP2,∴82+BP2=(12﹣BP)2,解得BP=10 3.故答案为:10 3.总结提升:本题考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用,熟练掌握折叠的性质是解题的关键.类型二对角互补模型典例2 (2018•汉阳区模拟)如图,在菱形ABCD中,点P是BC边上一动点,P和C不重合,连接AP,AP 的垂直平分线交BD于点G,交AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )A.变大B.先变大后变小C.先变小后变大D.不变思路引领:连接AC交BD于O,连接EO、AG,根据菱形的性质得出∠AOB=90°,AO=CO,求出A、E、G、O四点共圆,得出∠PAG=∠EOB,∠APG=∠PAG,求出∠APG=∠EOB=∠DBC,即可求出答案.解:连接AC交BD于O,连接EO、AG,∵四边形ABCD是菱形,∴∠AOB=90°,∵EG是AP的垂直平分线,∴AG=PG,∠AEG=∠AOB=90°,∴A、E、G、O四点共圆,∴∠PAG=∠EOB,∠APG=∠PAG,∴∠EOG=∠APG,∵四边形ABCD是菱形,∴OA=OC,∵AE=PE,∴OE∥BC,∴∠EOB =∠DBC =12∠ABC ,∵菱形ABCD 固定,∴∠ABC 的度数固定,即∠APG 的度数不变,故选:D .总结提升:本题考查了菱形的性质,线段垂直平分线性质,圆内接四边形性质等知识点,能正确作出辅助线是解此题的关键.变式训练1.(2018•碑林区校级一模)如图,在△ABC 中,∠ACB =120°,AC =BC =2,D 是AB 边上的动点,连接CD ,将△BCD 绕点C 沿顺时针旋转至△ACE ,连接DE ,则△ADE 面积的最大值= .思路引领:设BD 为a ,表示线段AE ,AD ,用a 表示△ADE 的面积表达式,从而利用二次函数的极值属性求出极值.解:设BD 为a∵∠ACB =120°,AC =BC =2∴AB =23∴AD =23―a∵AE =BD ,∠B =∠CAE =30°,BC =AC∴△BDC ≌△AEC (SAS )作EF ⊥AB ,垂足为F在Rt △AEF 中∠FAE =60°,AE =BD =a∴AF =12a ,EF =123a ∴△ADE 的面积=12×(23―a)×123a =―34a 2+32a 即当a =3,△ADE 的面积有最大值为343故答案为343总结提升:本题考查了数形结合的数学思想,将几何问题转化为函数问题,利用函数关系式获得极值.2.(2020•淮阴区模拟)在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2,O为AC的中点,过O作OE⊥OF,OE、OF分别交射线AB,BC于E、F,则EF的最小值为 .思路引领:首先过点O分别作OM⊥AB于M,ON⊥BC于N,易证四边形OMBN为矩形,则OM∥BC,ON∥AB,由直角三角形中30°角性质,可得AC的长,进而求得BC长.又O为AC中点,可求得OM 与ON的长,由勾股定理可得MN的长.又由垂线段最短,可得当OE与OM重合,OF与ON重合时,EF最短.得解.解:∵∠ABC=90°,∠ACB=30°,AB=2.∴AC=2AB=4.过点O分别作OM⊥AB于M,ON⊥BC于N.∵∠B=90°,∴四边形OMBN为矩形,∴OM∥BC,ON∥AB.∴△AOM∽△ACB,△CON∽△CAB,∴OM:CB=OA:CA,ON:AB=OC:AC.∵O为AC中点,则OB=12AC=2=MN,由垂线段最短,可得当OE与OM重合,OF与ON重合时,EF最短.∴EF的最小值为2.故答案为:2.总结提升:本题考查了矩形的判定和性质,相似三角形的判定与性质,勾股定理以及垂线段最短的知识,难度适中,注意数形结合思想的运用.3.如图,在平面直角坐标系xOy中,A(0,2),点P在直线y=33x上,连接AP,过点P作PQ⊥AP,交x轴于点Q,连接AQ.求∠QAP的度数.思路引领:分点P在第三象限、点P在第一象限的线段OH上、点P在第一象限的线段OH的延长线上三种情况,用四点共圆求解.解:①当点P在第三象限时,如图2,由∠QPA=∠QOA=90°,可得Q、P、O、A四点共圆,∴∠PAQ=∠POQ=30°;②当点P在第一象限的线段OH上时,如图3,由∠QPA=∠QOA=90°可得Q、P、O、A四点共圆,∴∠PAQ+∠POQ=180°,又此时∠POQ=150°,∴∠PAQ=180°﹣∠POQ=30°;③当点P在第一象限的线段OH的延长线上时,由∠QPA=∠QOA=90°可得∠APQ+∠AOQ=180°,∴Q、P、O、A四点共圆,∴∠PAQ=∠POQ=30°.总结提升:本题为一次函数综合题,涉及到四点共圆、等腰三角形性质,分类讨论求解是解决此题关键.类型三定边定角模型(1)定边对直角典例3东西湖区模拟)如图,已知A(2,6)、B(8,﹣2),C为坐标轴上一点,且△ABC是直角三角形,则满足条件的C点有( )个.A.6B.7C.8D.9思路引领:过点A作AB的垂线,交x轴于点C1,交y轴于点C2;过点B作AB的垂线,交x轴于点C3,交y轴于点C4;根据直径所对的圆周角为直角,以AB为直径作圆,根据A和B的坐标求出AB的长度,即为圆的直径,可得出半径的长,进而判断得出圆与y轴相切,可得出圆与y轴有1个交点,与x 轴交于2点.所以满足条件的点共有7个.解:分三种情况考虑:①当A为直角顶点时,过A作AC⊥AB,交x轴于点C1,交y轴于点C2,此时满足题意的点为C1,C2;②当B为直角顶点时,过B作BC⊥AB,交x轴于点C3,交y轴于点C4,此时满足题意的点为C3,C4;③当C为直角顶点时,以AB为直径作圆,由A(2,6)、B(8,﹣2),可得此圆与y轴相切,则此圆与y轴有1个交点,与x轴有2个交点,分别为C5,C6,C7.综上,所有满足题意的C有7个.故选:B.总结提升:此题考查了圆周角定理,直角三角形以及坐标与图形性质,利用了分类讨论及数形结合的思想.注意:若△ABC是直角三角形,则它的任意一个顶点都有可能为直角顶点.针对训练1.(2021•内乡县一模)(1)【学习心得】于彤同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.例如:如图1,在△ABC中,AB=AC,∠BAC=90°,D是△ABC外一点,且AD=AC,求∠BDC的度数.若以点A为圆心,AB为半径作辅助⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC 是圆周角,从而可容易得到∠BDC= °.(2)【问题解决】如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=25°,求∠BAC的度数.(3)【问题拓展】如图3,如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 5―1 .思路引领:(1)利用同弦所对的圆周角是所对圆心角的一半求解.(2)由A、B、C、D共圆,得出∠BDC=∠BAC,(3)根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE和△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△ADG和△CDG 全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,取AB的中点O,连接OH、OD,根据直角三角形斜边上的中线等于斜边的一半可得OH=12AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.解:(1)如图1,∵AB=AC,AD=AC,∴以点A为圆心,AB为半径作圆A,点B、C、D必在⊙A上,∵∠BAC是⊙A的圆心角,而∠BDC是圆周角,∴∠BDC=12∠BAC=45°,故答案是:45;(2)如图2,取BD的中点O,连接AO、CO.∵∠BAD=∠BCD=90°,∴点A、B、C、D共圆,∴∠BDC=∠BAC,∵∠BDC=25°,∴∠BAC=25°,(3)如图3,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,在△ABE和△DCF中,AB=CD∠BAD=∠CDAAE=DF,∴△ABE≌△DCF(SAS),∴∠1=∠2,在△ADG和△CDG中,AD=CD∠ADG=∠CDGDG=DG,∴△ADG≌△CDG(SAS),∴∠2=∠3,∴∠1=∠3,∵∠BAH+∠3=∠BAD=90°,∴∠1+∠BAH=90°,∴∠AHB=180°﹣90°=90°,取AB的中点O,连接OH、OD,则OH=AO=12AB=1,在Rt△AOD中,OD=AO2+AD2=12+22=5,根据三角形的三边关系,OH+DH>OD,∴当O、D、H三点共线时,DH的长度最小,最小值=OD﹣OH=5―1.(解法二:可以理解为点H是在Rt△AHB,AB直径的半圆AB上运动当O、H、D三点共线时,DH长度最小)故答案为:5―1.总结提升:本题主要考查了圆的综合题,需要掌握垂径定理、圆周角定理、等腰直角三角形的性质以及勾股定理等知识,难度偏大,解题时,注意辅助线的作法.(2)定边对定角典例4(2021秋•如皋市期中)如图,△ABC 为等边三角形,AB =3.若P 为△ABC 内一动点,且满足∠PAB =∠ACP ,则线段PB 长度的最小值为( )A .1.5B .3C .433D .2思路引领:由等边三角形的性质得出∠ABC =∠BAC =60°,AC =AB =3,求出∠APC =120°,当O 、P 、B 共线时,PB 长度最小,由等边三角形的性质得出AD =CD =12AC =32,∠PAC =∠ACP =30°,求出PD 和BD 的长,可得PB 的长,即可得出答案.解:∵△ABC 是等边三角形,∴∠ABC =∠BAC =60°,AC =AB =3,∵∠PAB =∠ACP ,∴∠PAC +∠ACP =60°,∴∠APC =120°,∴点P 的运动轨迹是AC ,设AC 所在圆的圆心为O ,当O 、P 、B 共线时,PB 长度最小,设OB 交AC 于D ,如图所示:此时PA=PC,OB⊥AC,则AD=CD=12AC=32,∠PAC=∠ACP=30°,∠ABD=12∠ABC=30°,∴PD=32,BD=332,∴PB=BD﹣PD=332―32=3.故选:B.总结提升:本题考查了等边三角形的性质、等腰三角形的性质、三角形内角和定理、勾股定理等知识;作辅助线构建圆是解决问题的关键.典例5(2021秋•白云区期中)在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.(1)求∠A+∠C的度数;(2)连接BD,探究AD,BD,CD三者之间的数量关系,并证明;(3)若点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求∠BEC的度数.思路引领:(1)在四边形ABCD中,由四边形内角和定理即可得出结果;(2)以BD为边向下作等边△BDQ,连接CQ,由等边三角形的性质得出∠DBQ=60°,BD=BQ,证出∠ABD=∠CBQ,证明△ABD≌△CBQ,得出AD=CQ,∠A=∠BCQ,证出∠DCQ=90°,再由勾股定理即可得出结论;(3)根据旋转的性质作辅助线,构建全等三角形,利用勾股定理的逆定理和等边三角形的判定和性质可得结论.解:(1)在四边形ABCD中,∵∠A+∠B+∠C+∠D=360°,∠B=60°,∠D=30°,∴∠A+∠C=360°﹣60°﹣30°=270°;(2)结论:CD2+AD2=BD2,理由:以BD为边向下作等边△BDQ,连接CQ,则∠DBQ=60°,BD=BQ,∵∠ABC=∠DBQ=60°,∴∠ABD=∠CBQ,在△ABD和△CBQ中,AB=BC∠ABD=∠CBQ,BD=BQ∴△ABD≌△CBQ(SAS),∴AD=CQ,∠A=∠BCQ,∴∠A+∠BCD=∠BCQ+∠BCD=270°,∴∠DCQ=90°,∴CD2+CQ2=DQ2,∵CQ=AD,DQ=BD,∴CD2+AD2=BD2;(3)如图2,∵AB=BC,∠ABC=60°,∴将△ABE绕点B顺时针旋转60°得到△CBE',∴△ABE≌△CBE,∴BE=BE',AE=CE',∠EBE'=60°,∴△EBE'是等边三角形,∴EE'=BE,∠BEE'=60°,∵AE2=BE2+CE2,∴CE'2=E'E2+CE2,∴∠CEE'=90°,∵∠BEE'=60°,∴∠BEC=60°+90°=150°.总结提升:本题是四边形的综合题,考查了四边形内角和定理、等边三角形的判定和性质、勾股定理以及逆定理、全等三角形的判定与性质、解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.针对训练1.(广州中考)如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.(1)求∠A+∠C的度数;(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.思路引领:(1)利用四边形内角和定理计算即可;(2)连接BD.以BD为边向下作等边三角形△BDQ.想办法证明△DCQ是直角三角形即可解决问题;(3)如图3中,连接AC,将△ACE绕点A顺时针旋转60°得到△ABR,连接RE.想办法证明∠BEC=150°即可解决问题;解:(1)如图1中,在四边形ABCD中,∵∠A+∠B+∠C+∠D=360°,∠B=60°,∠D=30°,∴∠A+∠C=360°﹣60°﹣30°=270°.(2)如图2中,结论:DB2=DA2+DC2.理由:连接BD.以BD为边向下作等边三角形△BDQ.∵∠ABC=∠DBQ=60°,∴∠ABD=∠CBQ,∵AB=BC,DB=BQ,∴△ABD≌△CBQ(SAS),∴AD=CQ,∠A=∠BCQ,∵∠A+∠BCD=∠BCQ+∠BCD=270°,∴∠DCQ=90°,∴DQ2=DC2+CQ2,∵CQ=DA,DQ=DB,∴DB2=DA2+DC2.(3)如图3中,连接AC,将△ACE绕点A顺时针旋转60°得到△ABR,连接RE.则△AER是等边三角形,∵EA2=EB2+EC2,EA=RE,EC=RB,∴RE2=RB2+EB2,∴∠EBR=90°,∴∠RAE+∠RBE=150°,∴∠ARB+∠AEB=∠AEC+∠AEB=210°,∴∠BEC=150°,∴点E的运动轨迹在O为圆心的圆上,在⊙O上取一点K,连接KB,KC,OB,OC,∵∠K+∠BEC=180°,∴∠K=30°,∠BOC=60°,∵OB=OC,∴△OBC是等边三角形,∴OB=OC=BC=1,∴点E的运动路径=60⋅π⋅1180=π3.总结提升:本题考查四边形综合题、等边三角形的判定和性质、勾股定理以及逆定理、弧长公式等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题2.如图,在△ABC中,∠C=120°,则△ABC所在的平面上是否存在点M,使△ABM的面积等于△ABC 的面积,且∠AMB=60°?若存在,画出该点的位置,若不存在,请说明理由.思路引领:构造等边三角形ABE,作等边△ABE的外接圆⊙O,过点C作AB的平行线交⊙O于点M1和M2,由同底等高三角形面积相等可知△ABM1和△ABM2的面积与△ABC的面积相等,由同弧所对的圆周角相等可知∠AM1B=∠AM2B=∠E=60°,故M1和M2是符合题意的点,分别作M1和M2关于AB 的对称点M3和M4也符合题意.解:存在点M,如图,构造等边三角形ABE,作等边△ABE的外接圆⊙O,过点C作AB的平行线交⊙O于点M1和M2,∴∠AM1B=∠AM2B=∠E=60°,∵M1M2∥AB,∴S△ABM1=S△ABM2=S△ABC,∴M1和M2是符合题意的点,分别作M1和M2关于AB的对称点M3和M4,则点M3和M4也符合题意,故符合题意的点有4个,分别为M1、M2、M3和M4.总结提升:本题考查了三角形的综合知识,掌握圆周角定理和同底等高三角形面积相等是解决问题的关键.。
专题15:《辅助圆》

中考核心知识点专题练习(辅助圆)德化第五中学:罗文平添加辅助圆解平面几何题,虽远不如辅助(直)线那么为人们所熟知,但许多直线形问题,若辅助圆添加得合理,则能收到化难为易,事半功倍的效果.一、根据圆的定义作辅助圆例1 如图,四边形ABCD中,AB∥CD,AB=AC=AD=p,BC=q,求BD的长.解析:以点A为圆心、AB为半径作⊙A.因为AB=AC=AD,所以B、C、D三点在⊙A上.延长BA交⊙A于点E,连结DE.因为DC∥EB,所以弧ED=弧BC,所以ED=BC=q.在Rt△BDE中,根据勾股定理,得BD =.例2 如图, PA=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,求AD·DC的值.解析:以点P为圆心、PB为半径的作⊙P.因为PA=PB,∠APB=2∠ACB,所以点A、B、C在⊙P上.此时⊙P的直径BE=10,DE=8,DB=2,由相交弦定理,得AD·DC=DE·DB=8×2=16二、作三角形的外接圆例3 如图,D、E为△ABC边BC上的两点,且BD=CE,∠BAD=∠CAE,求证:AB=AC.解析:作△ADE的外接圆,分别交AB、AC于点M、N,连结MD、NE.因为∠BAD=∠CAE,所以∠BAD+∠DAE=∠CAE+∠DAE,即∠NAD=∠MAE.因为∠BDM=∠MAE,∠CEN=∠NAD,所以∠BDM=∠CEN.又BD=CE,DM=EN,所以△BDM≌△CEN,所以∠B=∠C,即AB=AC.例4 如图,△ABC中,BF、CE交于点D,BD=CD,∠BDE=∠A,求证:BE=CF.解析:作△ABC的外接⊙O,延长CE交⊙O于G,连接BG.因为∠G=∠A,∠BDE=∠A,所以∠G=∠BDE,所以BG=BD.又BD=CD,所以BG=CD.又因为∠G=∠CDF,∠GBE=∠DCF,所以△GBE≌△DCF.所以BE=CF.例5 如图,在△ABC中,AB=AC,∠BAC=100°,∠B的平分线交AC于D,求证:BC=BD+AD.教学设计解析:作△ABD的外接圆交BC于E,连结DE.因为BD是∠ABC的平分线,所以弧AD=弧DE,所以AD=DE.在△BDE中,∠DBE=20°,∠BED=180°―100°=80°,所以∠BDE=80°,所以BE=BD.在△DEC中,∠EDC=80°―40°=40°,所以EC=DE.所以BC=BE+EC=BD+AD.三、结论类似于圆幂定理的形式时作辅助圆例6 如图,在△ABC中,AB=AC=,D是边BC上的一点,且AD=1,求BD·DC的值.解析:以点A为圆心、AB为半径作⊙A,交直线AD于点E、F,则点C在⊙A上,DE=,DF=.由相交弦定理,得BD·DC=DE·DF==2.例7 如图,在△ABC中,∠DAB=∠C,∠B的平分线BN交AD于M.求证:(1)AM=AN;(2)AB 2-AN 2=BM·BN.解析:(1)略;(2)由(1),得AM=AN.以点A为圆心、AM为半径作⊙A,交AB于E,交BA的延长线于F,则N在⊙A 上,且AE=AF=AN.由割线定理,得BM·BN=BE·BF=(AB-AE)(AB+AF)=(AB―AN)(AB+AN)=AB 2-AN 2,即AB 2-AN 2=BM·BN.四、探究动点对定线段所张的角时作辅助圆例8 如图,在直角梯形ABCD中,AB∥DC,∠B=90°,设AB=a,DC=b,AD=c,当a、b、c之间满足什么关系时,在直线BC上存在点P,使AP⊥PD?解析:以AD为直径作⊙O,根据直径所对的圆周角是直角,当⊙O与直线BC有公共点(相切或相交)时,在直线BC上存在点P,使AP⊥PD.因为⊙O的半径r=,圆心O到直线BC的距离d=.所以,当d≤r,即a+b≤c时,在直线BC上存在点P,使AP⊥PD.例9 如图,在平面直角坐标系xOy中,给定y轴正半轴上的两点A (0,2)、B(0,8),试在x轴正半轴上求一点C,使∠ACB取得最大值。
中考数学几何最值模型 专题03 辅助圆模型(学生版+解析版)

辅助圆模型模型讲解一、定点定长1、O为定点,OA=OB,且长度固定,那么O、A、B三点可以确定一个圆,动点P在圆弧AB上运动,如图所示,Q为圆外一定点,当P运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,PQ最小。
二、定弦定角2、线段AB固定,Q为动点,且∠AQB为定值,那么Q、A、B三点可以确定一个圆,动点Q在圆弧AB上运动,如图所示,R为圆外一定点,当Q运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,RQ最小。
方法点拨一、题型特征:①动点的运动轨迹为圆②圆外一点到圆上一点的距离最短:即圆外一点与圆心连线与圆的交点③常见确定圆的模型:定点定长、定弦定角。
二、模型本质:两点之间,线段最短。
例题演练1.如图,已知AB=AC=BD=6,AB⊥BD,E为BC的中点,则DE的最小值为()A.3﹣3B.3C.3﹣3D.2【解答】解:取AB的中点O,连接AE,OE,OD.∵AB=AC,BE=EC,∴AE⊥BC,∴∠AEB=90°,∵OA=OB,∴OE=AB=3,∵AB⊥BD,∴∠OBD=90°,∵OB=3,BD=6,∴OD===3,∵DE≥OD﹣OE,∴DE≥3﹣3,∴DE的最小值为3﹣3,故选:C.强化训练1.如图,矩形ABCD中,AB=3,BC=8,点P为矩形内一动点,且满足∠PBC =∠PCD,则线段PD的最小值为()A.5B.1C.2D.3 2.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE ⊥BE,则线段CE的最小值为.3.如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠P AB =∠ACP,则线段PB长度的最小值为.4.如图,在矩形ABCD中,AB=4,BC=6,E是平面内的一个动点,且满足∠AEB=90°,连接CE,则线段CE长的最大值为.5.如图1,P是⊙O外的一点,直线PO分别交⊙O于点A,B,则P A是点P 到⊙O上的点的最短距离.(1)探究一:如图2,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是.(2)探究二:如图3,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.(3)探究三,在正方形ABCD中,点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=4,试求出线段CP的最小值.1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.辅助圆模型模型讲解一、定点定长1、O为定点,OA=OB,且长度固定,那么O、A、B三点可以确定一个圆,动点P在圆弧AB上运动,如图所示,Q为圆外一定点,当P运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,PQ最小。
九年级数学上册第24章: 辅助圆(隐圆)专题练习(无答案)
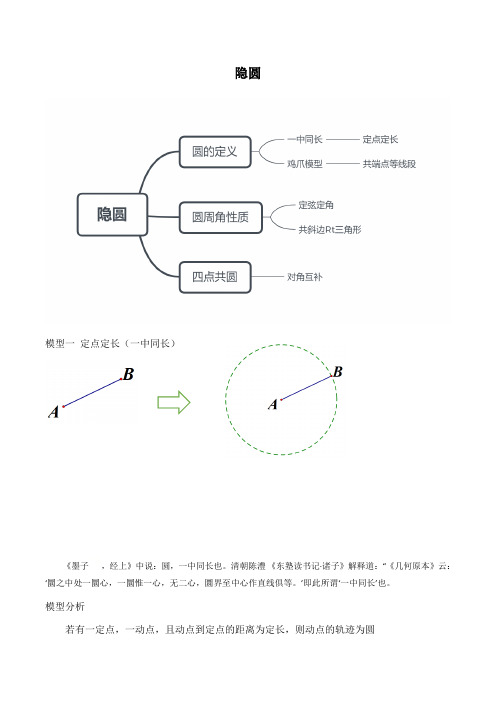
隐圆模型一定点定长(一中同长)《墨子,经上》中说:圆,一中同长也。
清朝陈澧《东塾读书记·诸子》解释道:“《几何原本》云:‘圜之中处一圜心,一圜惟一心,无二心,圜界至中心作直线俱等。
’即此所谓‘一中同长’也。
模型分析若有一定点,一动点,且动点到定点的距离为定长,则动点的轨迹为圆模型实例如图,在矩形ABCD中,AB=4,AD=8,点E是AB中点,点F是BC 上一点,把△BEF沿着EF翻折,点B落在点B'处,求B'D的最小值.练习:如图,OA⊥OB,P、Q分别是射线OA、OB上两个动点,C是线段PQ的中点,且PQ=4,则在线段PQ滑动的过程中,点C运动形成的路径长为_________2、如图,在Rt△ABC中,∠C=90°,AC=6,∠A=60°,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是_________3图2图BC OABC OAABC O图13、如图,在矩形ABCD 中,AB=4,BC=8,P 、Q 分别是直线BC 、AB 上的两个动点,AE=2,△AEQ 沿EQ 翻折形成△FEQ ,连接PF ,PD ,则PF+PD 的最小值是_________.模型二 共端点,等线段模型(鸡爪模型)12BCA D模型分析(1)若有共端点的三条等线段,可考虑构造辅助圆; (2)构造辅助圆是方便利用圆的性质快速解决角度问题。
模型典例如图 1,四边形 ABCD 中,AB=AC=AD ,若∠CAD=76°,则∠CBD=__________度。
练习1、如图,△ABC 和△ACD 都是等腰三角形,AB=AC ,AC=AD ,连接BD 。
求证:∠1+∠2=90°。
2、如图,在△ABC 内有一点 D,使得 DA=DB=DC,若∠DAB=20°,则∠ACB=__________模型三定弦定角模型分析若有一固定线段AB及线段AB所对的角(∠C)固定,则点C可以看作是以AB为弧的圆上运动.模型典例如图在△ABC中,BC=2,∠A=45°,求△ABC的面积最大值.练习1、如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,P为一动点,且PA⊥PC,连接BP,则BP的最大值为_____2、如图,△ABC中,AB=AC=2,BC=2√3,D点是△ABC所在平面上的一个动点,且∠BDC=60°,则△DBC面积的最大值是E BCADF模型四 共斜边的直角三角形模型分析:(1)共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆;(2)四点共圆后可以根据圆周角定理得到角度相等,完成角度等量关系的转化,是证明角相等重要的途径之一。
中考复习专题之构造辅助圆

9/13/2024
D A
C
30°
B
2. (2012青海中考) 如图,四边形A BCD是正方形,点E是边BC的中点, ∠AEF=90,EF交正方形外角的平分线C F于 F。求证:AE=EF。(人教版八年 级下册第69页)
A
D
F
BE
CG
一题多解
证法1 AE=EF 证法2
A
D
A
D
M
F
F
BE
CG
图 18
∠BCA=45°时,点C的坐标为
.
定张角
定线段
9/13/2024
探究3.在平面直角坐标系中,已知点A(4,0)、
B(﹣6,0),点C是y轴上的一个动点,当
∠BCA=45°时,点C的坐标为
.
变式1:如果把∠BCA=45°改成∠BCA=30°, 还会做吗?
9/13/2024
探究3.在平面直角坐标系中,已知点A(4,0)、
A
BE
图 19
D
证法5
F
BE
CG
P
图 22
CG
N
ADQ源自BEC图 21
证法3
A
D
F
B
E
H
CG 图 20
F 证法4
G
3.(2014年山东淄博市中考数学)如图,点A与 点B的坐标分别是(1,0),(5,0),点P是 该直角坐标系内的一个动点。
(1)使∠APB=30°的点P有 个; (2)若点P在y轴上且∠APB=30°, 求满足条件的点P的坐标;
B(﹣6,0),点C是y轴上的一个动点,当
∠BCA=45°时,点C的坐标为
.
变式2:如果把“∠BCA=45°”改成“∠ BCA=θ° 还能做吗?
初中辅助圆专题最值问题

在初中数学中,辅助圆是一个常见的工具,用于解决与圆有关的问题。
在辅助圆专题中,最值问题是一个重要的部分,涉及到在特定条件下找到某个量的最大值或最小值。
解决这类问题的一般步骤包括:
理解题意:首先,需要清楚地理解题目的要求和条件,确定需要找到哪个量的最值。
构造辅助圆:根据题目的条件,构造合适的辅助圆。
这个辅助圆可能与题目中给出的圆有关,也可能是一个新的圆。
应用几何性质:利用圆的几何性质,如半径、直径、弧长、弦长等,以及点与圆、直线与圆的位置关系,进行分析和推理。
建立方程或不等式:根据题目条件和几何性质,建立方程或不等式。
这个方程或不等式通常与需要找到的最值有关。
求解方程或不等式:解方程或不等式,找到需要求的最值。
这可能涉及到代数运算、几何图形的分析等。
检验解:最后,需要检验解是否符合题目的条件和要求。
如果符合,那么这个解就是题目的答案。
需要注意的是,每个最值问题都有其独特的特点和解决方法。
因此,在解决这类问题时,需要灵活运用所学的数学知识,结合题目的具体条件进行分析和推理。
同时,也需要多做一些练习,提高自己的解题能力和思维水平。
图中无圆,心中有圆——构造辅助圆解决最值问题

图中无圆,心中有圆——构造辅助圆解决最值问题圆,规范简约且具有丰富的性质。
尽管在许多几何问题的条件中可能并不明确涉及到圆,但是如果能够根据问题的条件和图形的特点构造一个圆,转机或许因此出现。
这就需要我们有明亮的眼光、明锐的视角发现图中的“隐形圆”,充分利用圆的众多性质,为解决问题铺设“桥梁”。
本文讲述两种常用的构造辅助圆的模型:(1)定点定长构造辅助圆;(2)定弦定角构造辅助圆。
一、模型介绍类型一:定点定长构造辅助圆平面内,点A为定点,点B为动点,且AB长度固定,则点B的轨迹在以点A 为圆心,AB长为半径的圆上(如图1).依据的是圆的定义:圆是所有到定点的距离等于定长的点的集合。
图1经典例题如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是______分析:CF为定长,翻折得PF=CF,故无论E点如何运动,点P随着点E的运动而始终在以点F为圆心,1为半径的圆上,将问题转化为⊙F上一点到直线AB 的距离的最小值。
解:如图,构造以F为圆心,CF为半径的圆。
过F作FG⊥AB于点G,交⊙F 于点P,此时PG的值最小,最小值为AF×sinA-1=2×-1=.模型总结:利用“定点定长”构造辅助圆的关键在于寻找一个定点,使目标动点到该定点的距离为定值。
类型二:定弦定角构造辅助圆固定的线段只要对应固定的角度,那么这个角的顶点轨迹为圆的部分。
在⊙O中,若弦AB长度固定,则弦AB所对的圆周角都相等。
如图2,若有一固定线段AB及线段AB所对的∠C固定,根据圆的知识可知点C不唯一。
当∠C <90°时,点C在优弧上运动;当∠C=90°时,点C在半圆上运动,且线段AB 是圆的直径;当∠C>90°时,点C在劣弧上运动。
图2经典例题如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点P为一动点,且PA⊥PC,连结BP,则BP的最大值为____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新东方 王昊龙
• 辅助圆是一种思想,是一个工具!不利用辅 助圆我们照样可以完成题目,但是利用辅助 圆可以方便我们完成题目!
基本类型
1、利用定义:等线段,共端点。
O C
A B
基本类型
1、利用定义:等线段,共端点。
O C
A B
• 如图,在边长为2的菱形中,∠A=60°,M是AD 边上的中点,N是AB边上的一个动点,将△AMN 沿着MN所在的直线翻折,得到△A’MN,连接 A’C,则A’C长度的最小值是多少?
如图,E,F 是正方形 ABCD 的边 AD 上两个动点,满足 AE=DF.连接 CF 交 BD 于 G,连接 BE 交 AG 于点 H. 若正方形的边长为 2,则线段 DH 长度的最小值是____.
H
o
O M
基本类型
3、(1)对角互补 (2)同弦等角
基本类型
3、(1)对角互补 (2)同弦等角
• (2)求△ABC面积的最大值。
• 如图,在锐角△ABC中,∠ACB=45°,AB=1,分别以 A、B为直角顶点,向△ABC外作等腰直角三角形ACE和 等腰直角三角形BCF,再分别过点E、F作边AB所在直线 的垂线,垂足为M、N。
• (2)求△ABC面积的最大值。
O
D
如图,E,F 是正方形 ABCD 的边 AD 上两个动点,满足 AE=DF.连接 CF 交 BD 于 G,连接 BE 交 AG 于点 H. 若正方形的边长为 2,则线段 DH 长度的最小值是____.
如图等边△PQR 内接于正方形 ABCD,其中点 P、Q、R 分别在边 AD、AB、DC 上,M 是 QR 的中点, 求证:不论等边△PQR 怎样运动,点 M 为不动点.
已知:在△ABC 中,∠ABC=∠ACB=α,点 D 是 AB 边上 任意一点,将射线 DC 绕点 D 逆时针旋转 α 与过点 A 且 平行于 BC 边的直线交于点 E.当 α=45°时,判断线段 BD 与 AE 之间的数量关系
• 如图,在边长为2的菱形中,∠A=60°,M是AD 边上的中点,N是AB边上的一个动点,将△AMN 沿着MN所在的直线翻折,得到△A’MN,连接 A’C,则A’C长度的最小值是多少?
E
A’
•
D
•
D
D
基本类型
2、三点共圆:定角度对定线段。
C O
A
B
• 如图,正方形ABCD的中心为O,面积为
AP
DAP
D
E
B(E)
C(F) B
F
C
在矩形 ABCD 中,点 P 在 AD 上,AB=2,AP=1,将三角板绕点 P 顺时针旋转,当点 E 与点 A 重合时停止,在这个过程中:∠PEF 的大 小是否发生变化?请说明理由
AP
DAP
D
E
B(E)
C(F) B
C
如图等边△PQR 内接于正方形 ABCD,其中点 P、Q、R 分别在边 AD、AB、DC 上,M 是 QR 的中点, 求证:不论等边△PQR 怎样运动,点 M 为不动点.
• 已知等腰直角三角形ABC中,∠A=90°,D为BC中 点,E、F分别为AB、AC上的点,且满足 ∠EDF=90°。
• 求证:DE=DF
• 已知等腰直角三角形ABC中,∠A=90°,D为BC中 点,E、F分别为AB、AC上的点,且满足 ∠EDF=90°。
• 求证:DE=DF
在矩形 ABCD 中,点 P 在 AD 上,AB=2,AP=1,将三角板绕点 P 顺时针旋转,当点 E 与点 A 重合时停止,在这个过程中:∠PEF 的大 小是否发生变化?请说明理由
如图,等边三角形ABC的边长为6,点D在AB 边上,从A匀速运动到B。点E在BC边上,以 相同的速度从B匀速运动到C。AE和CD相交于 点P, 求动点P所走过的路径长。
O
E
练习
已知:△AOB 中,AB=OB=2,△COD 中,CD=OC=3,∠ABO 2 ∠ABO=∠DCO.点 M、N、P 分别为 OA、OD、BC 的中点. 若 A、O、C 三点在同一直线上,请证明:△PMN∽△BAO
已知:在△ABC 中,∠ABC=∠ACB=α,点 D 是 AB 边上 任意一点,将射线 DC 绕点 D 逆时针旋转 α 与过点 A 且 平行于 BC 边的直线交于点 E.当 α=45°时,判断线段 BD 与 AE 之间的数量关系
F
如图,等边三角形ABC的边长为6,点D在AB 边上,从A匀速运动到B。点E在BC边上,以 相同的速度从B匀速运动到C。AE和CD相交于 点P, 求动点P所走过的路径长。
练习
已知:△AOB 中,AB=OB=2,△COD 中,CD=OC=3,∠ABO 2 ∠ABO=∠DCO.点 M、N、P 分别为 OA、OD、BC 的中点. 若 A、O、C 三点在同一直线上,请证明:△PMN∽△BAO
1989cm2,P为正方形内一点,且∠OPB=45°,
PA:PB=5:14,则PB的长
为
.
• 如图,正方形ABCD的中心为O,面积为
1989cm2,P为正方形内一点,且∠OPB=45°,
PA:PB=5:14,则PB的长
为
.
42
• 如图,在锐角△ABC中,∠ACB=45°,AB=1,分别以 A、B为直角顶点,向△ABC外作等腰直角三角形ACE和 等腰直角三角形BCF,再分别过点E、F作边AB所在直线 的垂线,垂足为M、N。
