圆的训练题1
人教版六年级上册第五单元圆综合训练(一)(含答案)

人教版六上第五单元圆综合训练(一)一、选择题(满分16分)1.下面几种说法中正确的是()A.圆周率表示圆的周长B.圆周率表示圆的周长与它直径的比的比值C.圆周率表示π保留两位小数的近似值2.大圆周长和直径的比()小圆周长和直径的比.A.大于B.小于C.等于D.不确定3.一个长方形的长是4厘米,宽是2厘米,在长方形内画一个最大的圆,圆的直径长是()厘米.A.4 B.1.25 C.2.5 D.24.以下四个图形中阴影部分面积最大的一个是()A.B.C.D.5.利用半径为5厘米的圆形纸片剪一个面积最大的正方形,此正方形的面积为()A..60平方厘米B.、55平方厘米C..50平方厘米6.在一个边长是8厘米的正方形里面画一个最大的圆,这个圆的半径是()厘米.A.4 B.8 C.167.在正方形内画一个最大的圆,若此圆周长是12.56厘米,则正方形面积是()A.16平方厘米B.16π平方厘米C.4平方厘米D.4π平方厘米8.如图中圆的直径是6厘米,则正方形的面积是()A.9.42cm2B.18cm2C.25cm2D.28.26cm2二、填空题(满分16分)9.一条线段长4cm,以它的中点为圆心画出的圆的周长是(______)cm,面积是(______)cm2。
10.一个圆形花坛的直径是3米,它的周长是(________)米,面积是(________)平方米。
11.用一条长20m的绳子绕一根圆柱形柱子6圈还余下1.16m这根圆柱形柱子底面的周长是(________)m,直径是(________)m。
12.推导圆的面积公式时,把圆剪成若干等份后拼成一个近似长方形,长方形的长是18.84分米,这个圆的半径是(________)分米,面积是(________)平方分米。
13.用一张正方形纸片剪成一个最大的圆,若正方形的周长是40cm。
剪成的圆的面积是(________)cm2。
14.如图长方形的长为12厘米,长方形的宽是(________)cm,两个等圆的半径是(________)cm。
(必考题)小学数学六年级上册第五单元《圆》测试(有答案解析)(1)

(必考题)小学数学六年级上册第五单元《圆》测试(有答案解析)(1) 一、选择题1.同圆中扇形甲的弧长是扇形乙的弧长的,那么扇形乙的面积是扇形甲面积的()A. 36倍 B. 12倍 C. 6倍 D. 3倍2.把一个直径10厘米圆分成两个相等的半圆,两个半圆的周长的和是()A. 31.4B. 62.8C. 41.4D. 51.4 3.下图的周长是()A. (π+1)dB. πd+dC. dD. πd4.已知一个圆的半径是R,且R满足3:R=R:4,则这个圆的面积为()A. 7πB. 7C. 12πD. 无法求出5.半径是3cm的圆,下列关于这个圆的数据正确的是()A. 直径9cmB. 周长18.84cmC. 周长9.42cmD. 面积113.04cm26.计算如图阴影部分面积,正确的列式是()A. 62×3.14﹣()×3.14B. ×62×3.14﹣()2×3.14C. ×[62×3.14﹣()2×3.14]D. ×(6×2×3.14﹣6×3.14)7.一个圆的半径由4厘米增加到9厘米,面积增加了()平方厘米.A. 25πB. 16πC. 65πD. 169π8.如图,沿半圆形草坪外围铺一条4m宽的小路.求小路的面积,正确的列式是()A. 3.14×42÷2B. 3.14×202÷2C. 3.14×(202﹣42)÷2D. 3.14×242÷2﹣3.14×202÷2 9.一个圆的周长扩大3倍,它的面积就扩大()倍.A. 3B. 6C. 910.在圆内剪去一个圆心角为45的扇形,余下部分的面积是剪去部分面积的()倍.A. 9 B. 8 C. 711.把一个直径是2cm的圆平分成2个半圆后,每个半圆的周长是()。
五年级数学下册试题 一课一练《圆的认识》习题 苏教版(含答案)

《圆的认识》习题一、选择题1、下面图形的阴影部分是扇形的是()A.B.C.D.2、“车轮的形状为什么选择圆形?”,下面的解释中最合理的是()A.圆形很美观B.圆的周长是直径的π倍C.圆是曲线图形D.圆有无数条半径,而且都相等3、下面各圆中的阴影部分,()是扇形.A.B.C.D.4、如图,下面说法正确的是()A.线段AC是这个圆的直径B.线段AB是这个圆的半径C.线段OD是这个圆的直径D.OA OD=5、下列图形中,涂色部分不是扇形的是()A.B.C.6、下面()的阴影部分面积是扇形.A.B.C.D.7、1张圆形纸片至少对折()次,才能找到圆心.A.1 B.2 C.3 D.08、在一张长7分米,宽4分米的长方形纸上画一个最大的圆,这个圆的半径是()分米.A.2 B.3.5 C.4二、填空题9、在边长是12cm的正方形中画一个最大的圆,这个圆的半径是cm.10、以14圆为弧的扇形的圆心角是度.11、(1)半圆的直径是,半径是.(2)大圆的直径是,小圆的半径是.12、在一个圆里有条直径,直径的长度是半径的倍.13、圆的与的比是一个固定数,我们把它叫做圆周率.14、圆的位置由决定;圆的半径决定圆的.三、判断题15、我国古代名著《墨经》中记载:“圆,一中同长也.”意思是:圆有一个中心(圆心),圆上各点到圆心的距离(半径)都相等.()16无论圆的大小如何,圆的周长与各自的直径的比值均为π.()17、大圆的圆周率与小圆的圆周率相等.()18、圆的周长与它直径的比值是3.14.()19、两个圆的半径相等,它们的直径也相等.()20、圆的周长与它直径的比就是圆周率,用字母“π”表示.()四、应用题21、如图,在长方形中有两个大小相等的圆,已知这个长方形的宽是10cm,圆半径是多少厘米?长方形的周长是多少厘米?22、小华在一个直径10厘米的圆中画了一个圆心角是120︒的扇形.这个扇形的大小是圆的()().要使扇形的大小正好是圈的16,它的圆心角应是︒.23、一张圆形纸片,圆内画有一条线段AB,请你想办法判断这条线段是不是该圆半径.五、操作题24.(2018秋•郑州期末)这是小明在用测量的方法确定没有圆心的圆的直径,他做得对吗?依据是什么?25、(2014秋•龙沙区校级期末)找出如图的圆心,并用字母表示.26、用你喜欢的两种颜色分别描出下面各圆的半径、直径.27、画出圆的圆心,并量出圆的半径.六、解答题28、找出下面图中的圆心角,在横线里画“ ”.29、看图填空.(单位:厘米)30、有一个长方形的长是9dm,宽是6dm,在这个长方形中画一个最大的半圆,这个半圆的直径是多少?半径是多少?31、用铅笔分别描出下列圆的直径和半径.参考答案一、选择题1、解:图形的阴影部分是扇形的是;故选:C.2、解:把车轮做成圆形,车轴定在圆心,是因为圆形易滚动,而且车轮上各点到车轴即圆心的距离都等于半径,当车轮在平面上滚动时,车轴与平面的距离保持不变.故选:D.3、解:图A,顶点不在圆心上,不是圆心角,所以不是扇形;图B,由圆心角的两条半径和圆心角所对的弧围成的图形,所以是扇形;图C,只是圆的一部分,所以不是扇形;图D,角的顶点在圆上不是圆心角,所以不是扇形.故选:B.4、解:A、线段AC是这个圆的直径,说法错误;B、线段AB是这个圆的半径,说法错误;C、线段OD是这个圆的直径,说法错误;=,说法正确;D、OA OD故选:D.5、解:由扇形的意义可知,选项A、B都是扇形,选项C两条线段不经过圆心,不是半径,所以不是扇形;故选:C.6、解:由两条半径,和连接两条半径的一段弧组成的图形叫做扇形.所以4个选项中,A中的阴影部分面积是扇形.故选:A.7、解:1张圆形纸片至少对折2次,才能找到圆心.故选:B.8、解:在一张长7分米,宽4分米的长方形纸上画一个最大的圆÷=(分米)这个圆的半径是422答:这个圆的半径是2分米. 故选:A . 二、填空题9、解:由分析得出:圆的半径为:1226÷=(厘米) 答:圆的半径是6厘米. 故答案为:6.10、解:以圆为弧的扇形的圆心角是:360490︒÷=︒ 故答案为:90.11、解:(1)5210⨯=(厘米) 半圆的直径是10厘米,半径是5厘米.(2)1064-=(厘米),422÷=(厘米) 大圆的直径是6厘米,小圆的半径是2厘米.故答案为:10厘米,5厘米;6厘米,2厘米.12、解:在一个圆里有无数条直径,直径的长度是半径的2倍; 故答案为:无数,2.13、解:圆的周长与它的直径的比是一个固定数,我们把它叫做圆周率; 故答案为:周长,它的直径.14、解:圆的位置由圆心决定;圆的半径决定圆的大小; 故答案为:圆心,大小. 三、判断题15、解:我国古代名著《墨经》中记载:“圆,一中同长也.”意思是:圆有一个中心(圆心),圆上各点到圆心的距离(半径)都相等,说法正确;故答案为:√.16、由分析知:任意一个圆,其周长和直径的比值都是圆周率,圆周率不随圆的大小的改变而改变;所以无论圆的大小如何,圆的周长与各自的直径的比值均为π,说法正确.故答案为:√.17、解:因为任意圆的圆周率=圆的周长÷圆的直径,圆周率是一个定值,用π表示,所以大圆的圆周率与小圆的圆周率相等.故判断为:√.18、解:圆的周长与直径的比值是圆周率π, 3.14π≈,所以原题说法错误;故答案为:⨯.19、解:由分析可知,两个圆的半径相等,那么它们的直径也一定相等.原题说法正确.故答案为:√.20、解:任意一个圆的周长与它的直径的比值都是一个固定的数,我们把它叫做圆周率,用字母π表示.所以圆周率是比值,不是比,原题说法错误.故答案为:⨯.四、应用题21、解:1025÷=(厘米)长:10220⨯=(厘米)(2010)2+⨯302=⨯60=(厘米)答:圆的半径是5厘米,长方形的周长是60厘米.22、解:1 1203603︒÷︒=1 360606︒⨯=︒答:这个扇形的大小是圆的13.要使扇形的大小正好是圈的16,它的圆心角应是60 .故答案为:13,60.23、解:从圆心到圆上任意一点的线段叫做半径,所以圆内的线段AB若符合圆半径的定义就是圆半径,否则不是.五、操作题24、解:小明在用测量的方法确定没有圆心的圆的直径,他做得对,依据是:直径是圆内最长的线段.25、解:26、解:如图直径涂红色,半径用蓝色;27、解:六、解答题28、解:根据圆心角的意义可得:29、解:①6r cm =;2612d cm =⨯= ② 4.3r cm =;2 4.38.6d cm =⨯= ③9d cm =;92 4.5r cm =÷=; ④长方形的长是:2.537.5⨯=(厘米) 宽是:2.525⨯=(厘米) (7.55)225+⨯=(厘米)故答案为:6、12,4.3、8.6,4.5、9,25.30、解:根据题干分析可得这个最大的半圆的直径是9分米, 92 4.5÷=(分米)答:这个半圆的直径是9分米,半径是4.5分米. 32、解:。
1.2圆的认识(一)练习题及答案

1
不夯实基础,难建成高楼。
1. 填一填。
(1)画圆能够明白,必须明白()与(),()决定所画圆的位置,()决定所画圆的大小。
(2)画圆时,把圆规的两脚分开,定好的两脚间的距离,即是该圆()的长度。
2. 判一判。
(1)在一个正方形中能够画一个最大的圆。
()
(2)同一个圆中只能画一条半径和一条直径。
()
3. 观看下面各圆里的线段,是直径的涂上红色,是半径的涂上蓝色。
4.
重点难点,一网打尽。
5. 画一画。
(1)分不以点A和点C为圆心画两个圆。
(2)画一个直径是3 cm的圆。
(3)以点O为圆心画一个半径为1.4厘米的圆。
(4)以点O为圆心画一个直径为4.4厘米的圆。
6. 在下面两个正方形内分不画出最大的圆和半圆。
7. 右图是由三个半径相等的圆组成的平面图形。
依次连接三个圆心的线段所围成的三角形中,任意一个角是多少度?
举一反三,应用创新,方能一显身手!
8.
第2课时
1. (1)圆心半径圆心半径(2)半径
2. (1) √(2) ×
3. 略
4. 略
5. 略
6. 略
7. 60°
8.。
《常考题》小学数学六年级上册第五单元《圆》检测(有答案解析)(1)
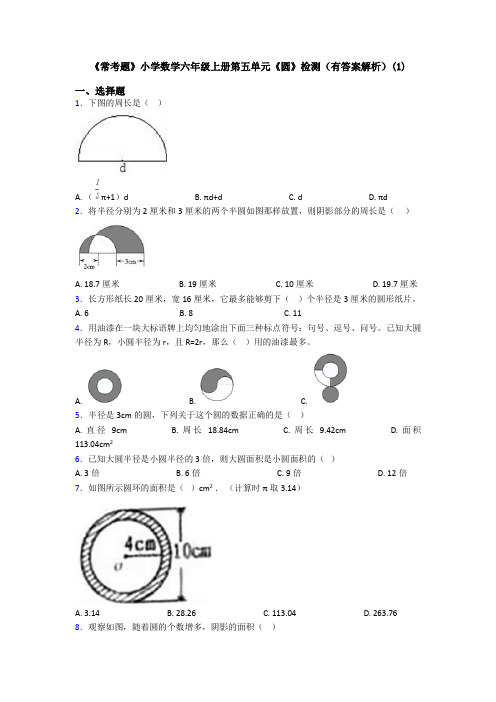
3.长方形纸长 20 厘米,宽 16 厘米,它最多能够剪下( )个半径是 3 厘米的圆形纸片。
A. 6
B. 8
C. 11
4.用油漆在一块大标语牌上均匀地涂出下面三种标点符号:句号、逗号、问号。已知大圆
半径为 R,小圆半径为 r,且 R=2r,那么( )用的油漆最多。
A.
B.
C.
5.半径是 3cm 的圆,下列关于这个圆的数据正确的是( )
《常考题》小学数学六年级上册第五单元《圆》检测(有答案解析)(1)
一、选择题
1.下图的周长是( )
A. ( π+1)d
B. πd+d
C. d
D. πd
2.将半径分别为 2 厘米和 3 厘米的两个半圆如图那样放置,则阴影部分的周长是( )
A. 18.7 厘米
B. 19 厘米
C. 10 厘米
D. 19.7 厘米
10.A
解析: A
【解析】【解答】解: ×5×2÷2+5×2=5 +10(cm)。
故答案为:A。
【分析】半圆的周长包括所在圆周长的一半加上直径的长度,由此根据周长公式计算即
可。
11.C
解析: C
【解析】【解答】解:设直径是 1,则周长是: ×1+1,(
)÷1=
。
故答案为:C。
【分析】半圆的周长是圆周长的一半加上直径的长度,设直径是 1,计算出半圆的周长,
24.街心花园有一个圆形花坛,花坛的直径是 10m。要在花坛的外围修一条宽 1.5m 的小 路,这条小路的面积是多少平方米? 25.在一个长 20cm、宽 10cm 的长方形里,剪一个最大的圆,这个圆的周长是多少?面积 是多少? 26.求下图中阴影部分的周长和面积。
圆的面积计算 练习题 (1)

圆的面积计算练习题之答禄夫天创作创作时间:贰零贰壹年柒月贰叁拾日一、填空1.一个圆形桌面的直径是 2米,它的面积是()平方米。
2.已知圆的周长,求d=(),求r=()。
3.圆的半径扩大2倍,直径就扩大()倍,周长就扩大()倍,面积就扩大()倍。
4.环形面积S=()。
5.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是()厘米,画出的这个圆的面积是()平方厘米。
6.大圆半径是小圆半径的4倍,大圆周长是小圆周长的()倍,小圆面积是大圆面积的()。
7.圆的半径增加,圆的周长增加(),圆的面积增加()。
8.一个半圆的周长是20.56分米,这个半圆的面积是()平方分米。
9.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是()平方厘米。
10.在一个面积是16平方厘米的正方形内画一个最大的圆,这个圆的面积是()平方厘米;再在这个圆内画一个最大的正方形,正方形的面积是()平方厘米。
11.大圆半径是小圆半径的3倍,大圆面积是84.78平方厘米,则小圆面积为()平方厘米。
12.大圆半径是小圆半径的2倍,大圆面积比小圆面积多12平方厘米,小圆面积是()平方厘米。
13.鼓楼中心岛是半径 10米的圆,它的占地面积是()平方米。
14.小华量得一根树干的周长是75.36厘米,这根树干的横截面大约是()平方厘米15.一只羊栓在一块草地中央的树桩上,树桩到羊颈的绳长是 3米。
这只羊可以吃到()平方米地面的草。
16.一根 2米长的铁丝,围成一个半径是30厘米的圆,(接头处不计),还多()米,围成的面积是()17.用一根 10.28米的绳子,围成一个半圆形,这个半圆的半径是(),面积是()18.从一个长8分米,宽5分米的长方形木板上锯下一个最大的圆,这个圆的面积是()19.大圆的半径等于小圆的直径,大圆的面积是小圆面积的()20.一个圆的周长扩大3倍,面积就扩大()倍。
2021年中考数学《圆综合压轴题》模拟训练题集(一)

2021年中考数学《圆综合压轴题》模拟训练题集(一)1.如图,在△ABC中,AB=AC,∠A=30°,AB=10,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接CP、OP.(1)求证:点D为BC的中点;(2)求AP的长度;(3)求证:CP是⊙O的切线.2.已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.(1)求证:DE=OE;(2)若CD∥AB,求证:BC是⊙O的切线;(3)在(2)的条件下,求证:四边形ABCD是菱形.3.如图,AB是⊙O的直径,C、G是⊙O上两点,且C是弧AG的中点,过点C的直线CD⊥BG的延长线于点D,交BA的延长线于点E,连接BC,交OD于点F.(1)求证:CD是⊙O的切线;(2)若=,求证:AE=AO;(3)连接AD,在(2)的条件下,若CD=2,求AD的长.4.如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F(1)求证:ED是⊙O的切线;(2)求证:△CFP∽△CPD;(3)如果CF=1,CP=2,sin A=,求O到DC的距离.5.如图1,▱AOBC的顶点A、B、C在⊙O上,点D、E分别在BO、AO的延长线上,且OD=2OB,OE=2OA,连接DE.(1)求∠AOB的度数;(2)求证:DE是⊙O的切线;(3)如图2,设直线DE与⊙O相切于点F,连接AD、BF,判断线段AD与BF的位置关系和数量关系,并证明你的结论.6.如图,AB是⊙O的直径,D是的中点,DE⊥AB于E,交CB于点F.过点D作BC的平行线DM,连接AC 并延长与DM相交于点G.(1)求证:GD是⊙O的切线;(2)求证:GD2=GC•AG;(3)若CD=6,AD=8,求cos∠ABC的值.7.如图1,⊙O是△ABC的外接圆,AB是直径,OD∥AC,OD交⊙O于点E,且∠CBD=∠COD.(1)求证:BD是⊙O的切线;(2)若点E为线段OD的中点,判断以O、A、C、E为顶点的四边形的形状并证明;(3)如图2,作CF⊥AB于点F,连接AD交CF于点G,求的值.8.如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.(1)如图2,当PD∥AB时,求PD的长;(2)如图3,当=时,延长AB至点E,使BE=AB,连接DE.①求证:DE是⊙O的切线;②求PC的长.9.如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的⊙O与AE交于点F.(1)求证:四边形AOCE为平行四边形;(2)求证:CF与⊙O相切;(3)若F为AE的中点,求∠ADF的大小.10.已知AM是⊙O直径,弦BC⊥AM,垂足为点N,弦CD交AM于点E,连按AB和BE.(1)如图1,若CD⊥AB,垂足为点F,求证:∠BED=2∠BAM;(2)如图2,在(1)的条件下,连接BD,若∠ABE=∠BDC,求证:AE=2CN;(3)如图3,AB=CD,BE:CD=4:7,AE=11,求EM的长.11.⊙O是△ABC的外接圆,AB是直径,过的中点P作⊙O的直径PG交弦BC于点D,连接AG、CP、PB.(1)如图1,若D是线段OP的中点,求∠BAC的度数;(2)如图2,在DG上取一点K,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;(3)如图3,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.12.如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.(1)求∠FDE的度数;(2)试判断四边形F ACD的形状,并证明你的结论;(3)当G为线段DC的中点时,①求证:FD=FI;②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.13.如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.(1)求证:AH是⊙O的切线;(2)若OB=4,AC=6,求sin∠ACB的值;(3)若=,求证:CD=DH.14.如图,⊙O与AB,AC分别相切于D,E两点,AB=AC,AO交⊙O于点F,交BC于点G,BC与⊙O交于点P,Q连接EQ(1)求证:AG⊥BC;(2)若DE平分OF,求证:△ADE是等边三角形;(3)在(2)的条件下,若AD=PQ,EQ=2,求BP的长.15.如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接DE.(1)求证:直线DE是⊙O的切线;(2)连接OC交DE于点F,若OF=CF,①判断以O、E、C、D为顶点的四边形的形状,并说明理由;②求tan∠ACO的值.16.如图,在△ABC中,AB=BC,以BC为直径作⊙O交AB于点E、交AC于点F,连结EF、BF、CE,BF与CE相交于点D,点G是EF的中点,连结OG.(1)判断OG与EF的位置关系,直接写出你的结论(不需证明);(2)求证:EF=CF;(3)若BF=2+,OG•FD=8﹣,求⊙O的面积.17.如图,AB、ED是⊙O的直径,点C在ED延长线上,且∠CBD=∠F AB.点F在⊙O上,且AB⊥DF.连接AD并延长交BC于点G.(1)求证:BC是⊙O的切线;(2)求证:BD•BC=BE•CD;(3)若⊙O的半径为r,BC=3r,求tan∠CDG的值.18.如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P 从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t ≤5).以P为圆心,P A长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.(1)求当t为何值时,点Q与点D重合?(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.19.如图,四边形ABCD内接于⊙O,已知直径AD=4,∠ABC=120°,∠ACB=45°,连接OB交AC于点E.(1)求AC的长;(2)求CE:AE的值;(3)在CB的延长线上取一点P,使PB=2BC,试判断直线P A和⊙O的位置关系,并证明你的结论.20.如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AO交BC于点O,以O为圆心,OC长为半径作⊙O,⊙O交AO所在的直线于D、E两点(点D在BC左侧).(1)求证:AB是⊙O的切线;(2)连接CD,若AC=AD,求tan∠D的值;(3)在(2)的条件下,若⊙O的半径为5,求AB的长.21.如图,点C是等边△ABD的边AD上的一点,且∠ACB=75°,⊙O是△ABC的外接圆,连结AO并延长交BD于E、交⊙O于F.(1)求证:∠BAF=∠CBD;(2)过点C作CG∥AE交BD于点G,求证:CG是⊙O的切线;(3)在(2)的条件下,当AF=2时,求的值.22.如图,平行四边形ABCD中,AC=BC,过A、B、C三点的⊙O与AD相交于点E,连接CE.(1)证明:AB=CE;(2)证明:DC与⊙O相切;(3)若⊙O的半径r=5,AB=8,求sin∠ACE的值.23.如图,⊙O是△ABC的外接圆,AB为⊙O的直径,过点C作∠BCD=∠BAC交AB的延长线于点D,过点O 作直径EF∥BC,交AC于点G.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为2,∠BCD=30°;①连接AE、DE,求证:四边形ACDE是菱形;②当点P是线段AD上的一动点时,求PF+PG的最小值.24.如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.(1)求证:△ECF∽△GCE;(2)求证:EG是⊙O的切线;(3)延长AB交GE的延长线于点M,若tan∠G=,AH=3,求EM的值.25.如图,线段AB是⊙O的直径,C、D是半圆的三等分点,过点C的直线与AD的延长线垂直,垂足为点E,与AB的延长线相交于点F,连接OE,交AC于点G.(1)求证:FC是⊙O的切线;(2)连接DC、CO,判断四边形ADCO的形状,并证明;(3)求OG与GE的比值.26.如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.(1)证明:∠E=∠C;(3)设DE交AB于点G,若DF=4,cos B=,E是的中点,求EG•ED的值.27.如图,AB为⊙O的直径,AB=4,P为AB上一点,过点P作⊙O的弦CD,设∠BCD=m∠ACD.(1)已知=,求m的值,及∠BCD、∠ACD的度数各是多少?(2)当=时,是否存在正实数m,使弦CD最短?如果存在,求出m的值,如果不存在,说明理由;(3)在(1)的条件下,且=,求弦CD的长.28.如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.(1)求证:CF是⊙O的切线;(2)求证:△ACM∽△DCN;(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=,求BN的长.29.如图1,AB为⊙O的直径,点C为⊙O上一点,CD平分∠ACB交⊙O于点D,交AB于点E.(1)求证:△ABD为等腰直角三角形;(2)如图2,ED绕点D顺时针旋转90°,得到DE′,连接BE′,证明:BE′为⊙O的切线;(3)如图3,点F为弧BD的中点,连接AF,交BD于点G,若DF=1,求AG的长.30.如图,△BCD内接于⊙O,直径AB经过弦CD的中点M,AE交BC的延长线于点E,连接AC,∠EAC=∠ABD =30°.(1)求证:△BCD是等边三角形;(2)求证:AE是⊙O的切线;(3)若CE=2,求⊙O的半径.31.如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB,⊙O及CB延长线交于点F、G、M.(1)求证:四边形ABCD为矩形;(2)若N为MF中点,求证:NB是⊙O的切线;(3)若F为GE中点,且DE=6,求⊙O的半径.32.如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.(1)求证:DE为⊙O切线;(2)若⊙O的半径为3,sin∠ADP=,求AD;(3)请猜想PF与FD的数量关系,并加以证明.33.如图,AB为半圆O的直径,OD⊥AB,与弦BC延长线交于点D,与弦AC交于点E.(1)求证:△AOE∽△DOB;(2)若点F为DE的中点,连接CF,求证:CF为⊙O的切线;(3)在(2)的条件下,若CF=3,tan A=,求AB的长.34.如图,在Rt△ABC中,∠C=90°,BD为∠ABC的平分线,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相交于点M,过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连结FN.(1)求证:AC是⊙O的切线;(2)若AF=4,tan∠N=,求⊙O的半径长;(3)在(2)的条件下,求MN的长.35.如图1,四边形ABCD内接于⊙O,AC为⊙O的直径,AC与BD交于点E,且AE=AB,DA=DB.(1)求证:AB=CB;(2)如图2,△ABC绕点C逆时针旋转30°得到△FGC,点A经过的路径为,若AC=4,求图中阴影部分面积S;(3)在(2)的条件下,连接FB,求证:FB为⊙O的切线.36.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.(1)求证:AC平分∠DAB;(2)求证:PC=PF;(3)若tan∠ABC=,AB=14,求线段PC的长.37.如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连EC,CD (1)试猜想直线AB于⊙O的位置关系,并说明理由;(2)求证:BC2=BD•BE;(3)若tan∠CED=,⊙O的半径为3,求△OAB的面积.38.如图,⊙O中,FG,AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为.(1)分别求出线段AP、CB的长;(2)如果OE=5,求证:DE是⊙O的切线;(3)如果tan∠E=,求DE的长.39.已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是的中点,连结BD并延长交EC的延长线于点G,连结AD,分别交CE、BC于点P、Q.(1)求证:AP=CP;(2)若tan∠ABC=,CF=8,求CQ的长;(3)求证:(FP+PQ)2=FP•FG.40.如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.(1)求证:DH是圆O的切线;(2)若A为EH的中点,求的值;(3)若EA=EF=1,求圆O的半径.41.如图,AB是⊙O的直径,点C在⊙O上,点E在线段OA上运动,DE⊥AB,垂足为E,DE交AC于点G,DC是⊙O的切线,交AB的延长线于点F.(1)求证:∠D=2∠A;(2)如图(2),若点E是OA的中点,点H是DE与⊙O的交点,OH∥BC,求证:△DCG是等边三角形;(3)如图(1),若CD=CF,且BF=1,CF=2,求CG的长.42.如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.(1)求证:∠BME=∠MAB;(2)求证:BM2=BE•AB;(3)若BE=,sin∠BAM=,求线段AM的长.43.如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E作直线l∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=4,DF=3,求AF的长.44.如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为的中点,连接OE交CD于点F,连接BE交CD 于点G.(1)求证:AB=AG;(2)若DG=DE,求证:GB2=GC•GA;(3)在(2)的条件下,若tan D=,EG=,求⊙O的半径.45.如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.(1)求证:BD=CD;(2)若AE=6,BF=4,求⊙O的半径;(3)在(2)条件下判断△ABC的形状,并说明理由.46.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH•EA;(3)若⊙O的半径为5,sin A=,求BH的长.47.如图,⊙O是△ABC的外接圆,AF平分∠BAC交BC于点E,交⊙O于点F,BD平分∠ABC交AF于点D,过点F作FH∥BC.(1)求证:FH是⊙O的切线;(2)求证:BF=DF;(3)若EF=3,DE=4,求线段AD的长.48.如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F 作射线BC的垂线,垂足为H,连接AC.(1)试判断BE与FH的数量关系,并说明理由;(2)求证:∠ACF=90°;(3)连接AF,过A、E、F三点作圆,如图2,若EC=4,∠CEF=15°,求的长.49.如图,P A为⊙O的切线,A为切点,直线PO交⊙O与点E,F过点A作PO的垂线AB垂足为D,交⊙O与点B,延长BO与⊙O交于点C,连接AC,BF.(1)求证:PB与⊙O相切;(2)试探究线段EF,OD,OP之间的数量关系,并加以证明;(3)若AC=12,tan∠F=,求cos∠ACB的值.50.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的三边,交点分别是G,E,F点.EG与CD交点为M.(1)求证:∠GEF=∠A;(2)求证:△OME∽△EMC;(3)若ME=4,MD:CO=2:5,求⊙O面积.。
2023年人教版初中数学中考第八章 圆(基础)专题训练(一)打印版含答案

2023年人教版初中数学中考第八章 圆(基础)专题训练时间:45分钟 满分:80分一、选择题(每题4分,共32分)1.已知⊙O 的直径为10,点P 到点O 的距离大于8,那么点P 的位置( )A .一定在⊙O 的内部B .一定在⊙O 的外部C .一定在⊙O 上D .不能确定2.如图,△ABC 内接于圆,弦BD 交AC 于点P ,连接AD .下列角中,AB ︵所对的圆周角是( )(第2题)A .∠APBB .∠ABDC .∠ACBD .∠BAC3.已知一个扇形的半径是1,圆心角是120°,则这个扇形的弧长是( ) A.π6 B .π C.π3 D.2π34.如图,⊙O 的直径AB =8,弦CD ⊥AB 于点P ,若BP =2,则CD 的长为( )A .2 5B .4 2C .4 3D .8 2(第4题) (第5题) (第6题)5.如图,AB是⊙O的直径,CD是⊙O的弦,若∠ACD=65°,则∠BAD的度数为()A.25°B.30°C.35°D.40°6.如图,在⊙O中,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E的度数为()A.40°B.50°C.55°D.60°7.如图,以边长为2的等边三角形ABC的顶点A为圆心,一定的长为半径画弧,恰好与BC边相切,分别交边AB,AC于点D,E,则图中阴影部分的面积是()A.3-π4B.23-πC.(6-π)33 D.3-π2 (第7题)(第8题)8.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是()A.12B.1 C.32D.2二、填空题(每题4分,共16分)9.已知圆的半径是3,则该圆的内接正六边形的边长是________.10.如图,四边形ABCD内接于⊙O,∠A=110°,则∠BOD=________°.(第10题)(第11题)11.如图,P A,PB与⊙O相切于A,B两点,点C在⊙O上,若∠C=70°,则∠P=________°.12.已知圆锥的母线长为5,底面半径为3,则圆锥的侧面展开图的面积为________.三、解答题(共32分)13.(10分)如图,四边形ABCD是⊙O的内接四边形,连接AC,BD,延长CD 至点E.(1)若AB=AC,求证:∠ADB=∠ADE;(2)若BC=3,⊙O的半径为2,求sin∠BAC.(第13题)14. (10分)如图,⊙O是△ABC的外接圆,连接OC,过点A作AD∥OC交BC的延长线于点D,∠ABC=45°.(1)求证:AD是⊙O的切线;(2)若sin ∠CAB=35,⊙O的半径为522,求AB的长.(第14题)15.(12分)如图,在Rt △ABC 中,∠C =90°,BC 与⊙O 相切于点D ,且⊙O 分别交AB ,AC 于点E ,F .(1)求证:AD 平分∠CAB ;(2)当AD =2,∠CAD =30°时,求AD ︵的长.(第15题)答案一、1.B 2.C 3.D 4.C 5.A 6.A 7.D 8.A 二、9.3 10.140 11.40 12.15π三、13.(1)证明:∵四边形ABCD 是⊙O 的内接四边形,∴∠ABC +∠ADC =180°.∵∠ADC +∠ADE =180°,∴∠ADE =∠ABC . ∵AB =AC ,∴∠ABC =∠ACB .∵∠ACB =∠ADB ,∴∠ADB =∠ADE .(2)解:如图,连接CO 并延长交⊙O 于点F ,连接BF , 则∠FBC =90°.由题意得在Rt △BCF 中CF =4,BC =3,(第13题)∴sin F =BC CF =34.∵∠F =∠BAC ,∴sin ∠BAC =sin F =34.14.(1)证明:如图,连接OA .∵∠ABC =45°, ∴∠AOC =2∠ABC =90°.∵AD ∥OC ,∴∠DAO +∠AOC =180°,∴∠DAO =90°,即OA ⊥AD .又∵OA 是⊙O 的半径,∴AD 是⊙O 的切线.(2)解:如图,过点C 作CE ⊥AB 于点E .由(1)知∠AOC =90°.∵AO =OC =522,∵CE ⊥AB ,∴∠AEC =∠CEB =90°,∴sin ∠CAB =CE AC =35, ∴CE =3,∴AE =AC 2-CE 2=4.∵∠CEB =90°,∠ABC =45°,∴∠BCE =45°, ∴CE =BE =3,∴AB =AE +BE =7.(第14题)15.(1)证明:如图,连接OD .∵BC 与⊙O 相切于点D ,∴OD ⊥BC ,即∠ODB =90°.∵∠C =90°,∴OD ∥AC ,∴∠ODA =∠CAD .∵OD =OA ,∴∠OAD =∠ODA ,∴∠CAD =∠OAD ,∴AD 平分∠CAB .(2)解:如图,连接DE .∵AE 为⊙O 的直径,∴∠ADE =90°.∵∠CAD =30°,∠OAD =∠ODA =∠CAD , ∴∠OAD =∠ODA =30°,∴∠AOD =120°. 在Rt △ADE 中,AE =AD cos ∠EAD =232=43 3,∴⊙O 的半径为23 3, ∴AD ︵的长=120π×23 3180=49 3π.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F. (1)求证:直线EF是⊙O的切线; (2)当直线DF与⊙O相切时,求⊙O的半径 2、如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E. (1)求证:直线BD与⊙O相切;(2)若AD:AE=4:5,BC=6,求⊙O的直径. 3、如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C. (1)求证:OD⊥AC;(2)若AE=8,tanA=43,求OD的长. 4、已知,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,
PC=5,PT为⊙O的切线,切点为T.
(1)如图(1),当C点运动到O点
时,求PT的长;
(2)如图(2),当C点运动到A点时
,连接PO、BT,求证:PO∥BT
5、如图,在⊙S中,AB是直径,AC,BC是弦,D是⊙S外一点,且DC与⊙S相切于点C,
连接DS,DB,其中DS交BC于E,交⊙S于F,F为⌒BC 的中点.
(1)求证:DB=DC;
(2)若AB=10,AC=6,P是线段DS上的动点.设DP
长为x,四边形ACDP面积为y.
①求y与x的函数关系式;
②求△PAC周长的最小值,并确定这时x的值.
6、如图,AB是⊙O的直径,CD是⊙O的切线,切点为C.延长AB交CD于点E.连接AC
,作∠DAC=∠ACD,作AF⊥ED于点F,交⊙O于
点G.
(1)求证:AD是⊙O的切线;
(2)如果⊙O的半径是6cm,EC=8cm,求GF的长.
7、已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧 上取一点E使∠EBC=∠DEC,延长
BE依次交AC于点G,交⊙O于H.
(1)求证:AC丄BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.
8、如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过
C作CD丄PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
9、如图,AB是半径O的直径,AB=2.射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半
圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相
交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.
(1)求证:△ABC∽△OFB;
(2)当△ABD与△BFO的面枳相等时,求BQ的长;
(3)求证:当D在AM上移动时(A点除外),点Q始
终是线段BF的中点.
10、如图1,已知在⊙O中,点C为劣弧AB上的中点,连接AC并延长至D,使CD=CA,
连接DB并延长DB交⊙O于点E,连接AE.
(1)求证:AE是⊙O的直径;
(2)如图2,连接EC,⊙O半径为5,AC的长为4,求阴影部分的面积之和.(结果保留π
与根号)
11、如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点
P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的
时间为t s.
(1)当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
(2)已知⊙O为△ABC的外接圆.若⊙P与⊙O相切,求t的值.
