中国粮食生产函数模型
特定要素模型

特定要素模型
图 3-2: 劳动的边际产量
MPLM
MPLM LM
特定要素模型
图3-3: 特定要素模型中的PPF
食品的生产函数 Output of food, QF (increasing 1'
F
)
PPF
QF =QF(K, LF)
Q2
2' 3'
Labor input in food, LF (increasing ) 劳动资源配置
PF X MPLF (粮食部门的劳动 需求曲线) PM X MPLM (制造品部门的 劳动需求曲线)
制造品部门使用 的劳动, LM L1M 劳动总供给, L L1F
粮食部门使用的劳动 , LF
特定要素模型
MPLMPM=PF MPLF =w -MPLF/MPLM = -PM/PF (3-7)
左边是生产可能性边界在某一特定生产点上的斜率, 右边是负的制造品的相对价格
引言
贸易对国家内部的收入分配有显著影响 原因如下:
资源不可能马上也不可能无成本地在部门间转移 各部门对生产要素的需求有所不同
特定要素模型引入了收入分配问题。 特定要素模型
特定要素模型
假设 生产两种产品:制造品和粮食 三种生产要素: 劳动 (L), 资本 (K) 和土地 (T). 生产制造品需要投入劳动和资本 生产粮食需要投入劳动和土地
特定要素模型中的国际贸易
图 3-11: 贸易和相对价格
制造品的相对价格, 制造品的相对价格 PM /PF RSA RSWORLD (PM /PF )A (PM /PF )W (PM /PF )J RDWORLD 制造品的相对产量, 制造品的相对产量 QM/QF RSJ
经济学之粮食生产模型

一、粮食生产模型1、选择变量和模型的关系形式研究目的:研究我国近十年粮食产量与主要影响因素之间的定量关系。
(1)确定模型应包含的变量被解释变量:粮食总产量(万吨),y解释变量:X1农用化肥施用量(万公斤)X2粮食播种面积(千公顷)X3成灾面积(千公顷)X4农业机械劳动力(万千瓦)X5农业劳力(万人)变量选择依据:国家粮食政策对粮食生产的积极扶持作用,在样本区间内具有一致性;我国粮食统一平价收购,,农民面临的是“无限的需求”。
因此,影响粮食产量的主要因素是:资本和劳动力农业生产的特点决定了资本主要是:土地和化肥考虑到我国的传统农业耕作方式有一定的变革,一方面从事非农产业的农民增加;另一方面,农业机械化水平有所提高,表示劳动力的变量为:农机动力和农业劳动力。
(2)确定模型的数学形式和参数范围被解释变量和解释变量之间的关系是投入产出关系,因此选用C-D生产函数,设定模型为:lnY=a0+a1lnX1+a2lnX2++++u解释变量的个数从2~5个,可根据实际情况选择最有结果;偏回归系数为相应变量的产出弹性,理论值应介于0~1之间;截距a0为常熟虚拟变量,包含政策、气候等难以量化的影响因素;u为随即扰动项,描述模型之外的因素对模型的干扰。
2、采集样本数据本模型使用时间序列数据,数据来源于《中国农村统计年鉴》(1984——1996)(见表2.10.1)其中:由于统计数据没有粮食生产的专用数据,农用化肥施用量(万公斤)、成灾面积(千公顷)、农业机械总动力(万千瓦)、农业劳力(万人)均为农业总体数据,尤其是农业劳力(万人)为农林牧副渔也总劳动力,只有几个年份有种植业、农业劳力数据,占农林牧副渔也劳力的比重为0.8~0.85之间。
表2.10.1obs Y粮食总产量(万吨)X1农用化肥施用量(万公斤)X2粮食播种面积(千公顷)X3成灾面积(千公顷)X4农业机械劳动力(万千瓦)X5农业劳力(万人)1983387281659.811404716209.31802231645.1 1984407311739.8112884152641949731685 1985379111775.810884522705.32091330351.5 1986391511930.6110933236562295030467 1987402981999.311126820393.72483630870 1988394082141.511012323944.72657531455.7 1989407552357.111220524448.72806732440.5 1990446242590.311346617819.32870833330.4 1991435292805.1112314278142938934186.3 1992442662930.211056025894.73030834037 1993456493151.9110509231333181733258.2 1994445103317.9109544313833380232690.3 1995466623593.7110060222673611832334.5 1996504543827.91125482123438546.932260.4将原始数据格式转换为文本文件格式,并保存为:f:\sq\lzn2101.txt(记住样本区间、各列对应的变量名称)38728 1659.8 114047 16209.3 18022 31645.140731 1739.8 112884 15264 19497 3168537911 1775.8 108845 22705.3 20913 30351.539151 1930.6 110933 23656 22950 3046740298 1999.3 111268 20393.7 24836 3087039408 2141.5 110123 23944.7 26575 31455.740755 2357.1 112205 24448.7 28067 32440.544624 2590.3 113466 17819.3 28708 33330.443529 2805.1 112314 27814 29389 34186.344266 2930.2 110560 25894.7 30308 3403745649 3151.9 110509 23133 31817 33258.244510 3317.9 109544 31383 33802 32690.346662 3593.7 110060 22267 36118 32334.550454 3827.9 112548 21234 38546.9 32260.4进入TSP窗口,进行如下操作:Create a 1983 1996Read(o) F:\sq\ lzn2101.txt y x1 x2 x3 x4 x5write(o) F:\sq\ lzn2101.txt y x1 x2 x3 x4 x5save F:\sq\ lzn2101.txtload F:\sq\ lzn2101.txt3、参数估计结果及统计检验(1)ls lny c lnx23 lnx5 lnx123 lnx423把化肥施用量改为单位面积化肥施用量、农机劳力改为单位面积农机劳力,能够在一定程度上避免可能的多重共线性。
中国粮食生产短期预测模型研究

作物 播种 面 积所 占份 额是 非 负 的 。并且 小 于 1 。也不 能 保证 所 有 作 物 播 种 面 积 所 占份 额 之 和 为 1 。而 由
领 域相 对 于 其 它 领 域 投 资 报 酬 率 的 函数 。在 西 方 农
业 经 济 研 究 的文 献 中 ,Nelv ( 9 6 9 8 提 出 r e 15 。15 ) o 的单 方 程 部 分 调 整 模 型 , 由于 考 虑 了农 民对 价 格 的 预期 和生 产 的动 态 调 整 过 程 .在 研 究 产 量 和 播 种 面 积 方 面得 到 广 泛 应 用 ( sa & C mmig.1 7 ) A kr i u n 96 . 本研 究 的准 固定 投 人 ( 食 播 种 面 积 )模 型 ,将 采 粮
T e 16 )提 出 的 分 配 系 统 模 型正 好 可 以 满 足 这 hi 99 l( 些 要求 。该模 型形 式 为 :
L ( )= B n A+ 粗Rj EC n kD n + d , T+  ̄P
n为种 植作 物数 量 。 为某作 物播 种 面积 占总播 种 面积 的份 额 。
总 的粮 食 播 种 面 积是 相对 固定 的 .一种 作 物播 种 面
粮 食 生 产实 际 的决 策是 一个 连 续 的分 阶段 过程 , 在 种 植 季 节 开 始 时 农 民 首先 确定 各 种 作 物 的种 植 面
积 及 其采 用 的 技 术 。即对 播 种 面积 在 各 种 作 物 和 技
粮食产量模型

• 设粮食产量函数为:
Y=β +β X1+β X2+β X3+β X4+μ
(其中X3的符号应为负,其余为正)
二、粮食产量模型的数据收集
通过查阅统计年鉴,我小组得到我国粮食产量从 1983~2011年的数据如下:
引入X4后,虽然拟合优度仍有显著提高,而且也通过了t检验,但因其经济意义 不合理,故应舍弃X4。
序列相关性检验
图示法:e 与e(-1)
• D.W.检验法
• 由计算结果知:D.W.=1.525766 由表查临界值,得 =1.20, =1.65
• 由 若0〈D.W.〈 ,则存在正自相关; 若 〈D.W.〈 ,则不能确定; 若 〈D.W.〈4- ,则无自相关; 若4- 〈D.W.〈,则不能确定; 若4- 〈D.W.〈4,则存在负相关。
谢谢
敬请各位老师 批评指正
异方差检验
如上图所示:显然不是同方差,即存在着异方差。
=29*0.250545=7.265805, =15.51 因为nR^2 <Χ^2 ,所以不存在异方差。
多重共线性
采用逐步回归法(既是检验方法,又是修正方法) Ls y c x1(化肥施用量) 得
Ls c x1(化肥施用量) x2 (粮食播种面积)
• 显然, 〈D.W.〈 , 故不能确定。改用其他方法 检验。
迭代法
Ls y c x1 x2 x3 ar(1) 得:
显然,上表中的D。W。值在 〈D.W.〈4- 之间,故随机干扰项为一阶自回归。 由此,模型应为 Y=-31424.55+4.410307X1+0.591135X2-0.129284X3+0.260639Ц
关于我国粮食生产的单方程计量经济学模型

• 摘������ 要: 以我国改革开放以来1978~ 2002 年的相关数据为依托, 运用计量经济学方法 对影响我国粮食生产的主要因素进行了回 归分析, 最终得出结论: 粮食播种面积对我 国粮食生产的正面影响最大. 同时, 利用模 型对提高我国的粮食产量进行了数量化分 析. • 关键词: 计量经济学; C- D 生产函数; 多重共 线性; 自相关; 异方差; 预测; 评价
文章内容结构
• 一 变量确定与生产函数模型 • 二 数据收集 • 三 模型检验
1、多重共线性的检验与消除 2、自相关的消除 3、异方差的检验 4、经济意义检验 5、模型预测检验
• 四 模型的预测与分析 • 五 政策评价及建议 • 六 模型的进一步改进
变量确定与生产函数模型
一、被解释变量与解释变量的确定
其中
二、数据收集
三、模型检验
• 运用Eviews 软件对模型( 3. 2) 进行估计, 我 们得到估计结果( 见表2) ( 表4~ 表11 分析方 法同表2) :
㈠多重共线性的检验与消除
• 从表2 可以看出, 回归估计的判决系数R ² 很 高, 方程很显著, 但是8 个参数的t 检验值却 只有两个略微显著. 显然, 出现了严重的多 重共线性. • 1、相关系数法 从各解释变量之间的相关系数可以看出X3 与 X4 , X5 , X6 , X7 之间存 在较高的相关系数, 这说明它们之间可能存在 着多重共线性.
模型的进一步改进
在本模型中存在一个很大的缺陷,就是没有 把农民种粮的积极性和粮种的改良因素考虑在 模型中。 但这些因素在本模型中,由于时间和技术的 限制,很难收集到相关的数据,因此我们无法 用计量经济学的方法处理,这样就导致模型的 不足。如若能对这两方面的因素加以处理,那 么这个模型将会变得更加完善,更具有实用价 值。
我国粮食生产与相关投入的计量模型分析

实验三 多元线性回归模型及非线性回归一、多元线性回归模型例题3.2.2 建立2006年中国城镇居民人均消费支出的多元线性回归模型。
数据: 地区 2006年消费支出Y 2006年可支配收入X12005年消费支出X2北京 14825.41 19977.52 13244.2 天津 10548.05 14283.09 9653.3 河北 7343.49 10304.56 6699.7 山西 7170.94 10027.70 6342.6 内蒙古 7666.61 10357.99 6928.6 辽宁 7987.49 10369.61 7369.3 吉林 7352.64 9775.07 6794.7 黑龙江 6655.43 9182.31 6178.0 上海 14761.75 20667.91 13773.4 江苏 9628.59 14084.26 8621.8 浙江 13348.51 18265.10 12253.7 安徽 7294.73 9771.05 6367.7 福建 9807.71 13753.28 8794.4 江西 6645.54 9551.12 6109.4 山东 8468.40 12192.24 7457.3 河南 6685.18 9810.26 6038.0 湖北 7397.32 9802.65 6736.6 湖南 8169.30 10504.67 7505.0 广东 12432.22 16105.58 11809.9 广西 6791.95 9898.75 7032.8 海南 7126.78 9395.13 5928.8 重庆 9398.69 11569.74 8623.3 四川 7524.81 9350.11 6891.3 贵州 6848.39 9116.61 6159.3 云南 7379.81 10069.89 6996.9 西藏 6192.57 8941.08 8617.1 陕西 7553.28 9267.70 6656.5 甘肃 6974.21 8920.59 6529.2 青海 6530.11 9000.35 6245.3 宁夏 7205.57 9177.26 6404.3 新疆 6730.018871.276207.51、 建立模型01122Y X X βββμ=+++2、估计模型 (1)录入数据打开EViews6,点“File ”→“New ”→“Workfile ”选择“Unstructured/Undated”,在Observations 后输入31,如下所示:点“ok”。
我国粮食生产与相关投入计量经济学模型分析
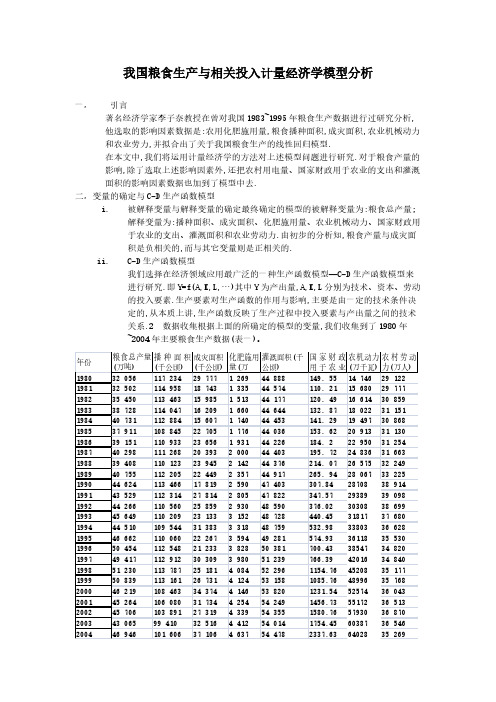
我国粮食生产与相关投入计量经济学模型分析一,引言著名经济学家李子奈教授在曾对我国1983~1995年粮食生产数据进行过研究分析,他选取的影响因素数据是:农用化肥施用量,粮食播种面积,成灾面积,农业机械动力和农业劳力,并拟合出了关于我国粮食生产的线性回归模型.在本文中,我们将运用计量经济学的方法对上述模型问题进行研究.对于粮食产量的影响,除了选取上述影响因素外,还把农村用电量、国家财政用于农业的支出和灌溉面积的影响因素数据也加到了模型中去.二,变量的确定与C-D生产函数模型i.被解释变量与解释变量的确定最终确定的模型的被解释变量为:粮食总产量;解释变量为:播种面积、成灾面积、化肥施用量、农业机械动力、国家财政用于农业的支出、灌溉面积和农业劳动力.由初步的分析知,粮食产量与成灾面积是负相关的,而与其它变量则是正相关的.ii.C-D生产函数模型我们选择在经济领域应用最广泛的一种生产函数模型—C-D生产函数模型来进行研究.即Y=f(A,K,L,…)其中Y为产出量,A,K,L分别为技术、资本、劳动的投入要素.生产要素对生产函数的作用与影响,主要是由一定的技术条件决定的,从本质上讲,生产函数反映了生产过程中投入要素与产出量之间的技术关系.2 数据收集根据上面的所确定的模型的变量,我们收集到了1980年~2004年主要粮食生产数据(表一)。
iii.模型的估计设定:粮食总产量为Y播种面积为X1成灾面积为X2,化肥施用量为X3,灌溉面积为X4,国家财政用于农业资金为X5,农机动力为X6,农村劳动力为X7.由C-D生产函数模型,得模型形式如下:Y t=AX it biεt(i=1,2,…,7)(1)两边取对数并进行变换,得:log Y t =b0+b i logX it+μt (i=1,2,…,7)(2)其中b0=logA,μt=logεt.运用Eviews软件对模型(2)进行OLS估计,我们得到估计结果Dependent Variable: LOG(Y)Method: Least SquaresDate: 06/10/09 Time: 03:55Sample: 1980 2004Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C 3.375895 5.5021110.6135640.5476LOG(X1)0.9587450.279512 3.4300650.0032LOG(X2)-0.1037040.040353-2.5699500.0199LOG(X3)0.4948670.104450 4.7378190.0002LOG(X4)-0.5649730.462026-1.2228180.2381LOG(X5)-0.0143810.074375-0.1933540.8490LOG(X6)0.0183880.1192590.1541820.8793LOG(X7)-0.0694990.137533-0.5053240.6198 R-squared0.963763Mean dependent10.66170varAdjusted R-squared0.948842S.D. dependent var0.127561S.E. of regression0.028852Akaike info criterion-3.998937Sum squared resid0.014151Schwarz criterion-3.608897Log likelihood57.98671F-statistic64.59068Durbin-Watson stat 1.245744Prob(F-statistic)0.000000从表2可以看出,回归估计的判决系数R2很高,方程很显著,但是8个参数的t检验值中,却只有两个略微显著.显然,出现了严重的多重共线性。
我国粮食生产模型的分析报告

我国粮食生产模型的分析报告鉴于粮食是人类赖以生存的必需品,保障粮食生产是每个国家最基本的任务之一。
我国是世界上最大的粮食生产国之一,也是世界上最大的粮食消费国之一。
由于我国的人口众多,生态环境较为复杂,粮食生产模型的分析对于保障粮食安全和实现可持续发展具有重要意义。
我国粮食生产模型主要包括产业链模型、生产要素模型、供给模式模型以及乡村经济模型等四个方面。
其中,产业链模型是连接生产和消费的桥梁,生产要素模型主要解释了我国农业生产的成本和效率,供给模式模型分析了市场供需的情况,乡村经济模型则全面反映了我国农村发展的状况。
首先,产业链模型是粮食生产模型中最基础的模型,它主要包括种粮农户、粮食加工企业和粮食销售商等环节。
在这个模型中,种植粮食是最重要的环节,因此需保证粮食生产的稳定性和质量。
同时,粮食加工企业应当通过先进的生产技术和设备,提高粮食产品的附加值和品质,以增加企业的利润。
粮食销售商则有责任宣传和推广高品质的粮食产品,促进人们对健康和营养的认知。
其次,生产要素模型是解释我国粮食生产状况的模型之一,它包括土地、劳动力、资本和科技等四个要素。
我国的土地资源不足,而且严重受到污染,使得粮食生产受到了严重威胁。
在劳动力方面,虽然有大量的农民从事农业生产,但缺乏先进的农业技术和管理知识,使农业生产成本高,生产效率低下。
在资本方面,资金短缺和银行信贷条件苛刻,导致农民很难获得到贷款和资本。
在科技方面,随着国家投入的不断加强和科技创新的不断推广,农业科技水平逐渐提高。
再者,供给方式模型分析了市场供需的情况。
市场反映了社会经济环境的发展状况。
供给侧主要指生产要素组成,供给总量和供给结构,自身生产障碍等方面,而需求侧主要指居民收入等方面。
近年来,我国进一步加强了相关政策的制定和实施,激发了企业竞争力,提供了更加优质的服务和更高效的生产模式,这有利于减少宏观经济政策对供求的干预。
此外,为满足居民的消费需求,我国还制定了购粮证等一系列政策,有利于保护消费者权益,维护市场秩序和稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国粮食生产函数模型一、引言根据理论和经验分析,影响粮食生产(Y)的主要因素有:农业化肥施用量(X1)、粮食播种面积(X2)、成灾面积(X3)、农业机械总动力(X4)、农业劳动力(X5),其中,成灾面积的符号为负,其余均应是正。
二、数据来源下表列出了中国粮食生产的相关数据,拟建立中国粮食生产函数。
表1 中国粮食生产与相关投入资料年份粮食产量农业化肥施用量粮食播种面积成灾面积农业机械总动力农业劳动力万吨万公斤千公顷公顷万千瓦万人1983 38728 1660 114047 16209 18022 31151 1984 40731 1740 112884 15264 19497 30868 1985 37911 1776 108845 22705 20913 31130 1986 39151 1931 110933 23656 22950 31254 1987 40208 1999 111268 20393 24836 31663 1988 39408 2142 110123 23945 26575 32249 1989 40755 2357 112205 24449 28067 33225 1990 44624 2590 113466 17819 28708 38914 1991 43529 2805 112314 27814 29389 39098 1992 44266 2930 110560 25893 30308 38699 1993 45649 3152 110509 23134 31817 37680 1994 44510 3318 109544 31382 33803 36628 1995 46662 3594 110060 22268 36118 35530 1996 50454 3828 112548 21234 38547 34820 1997 49417 3981 112912 30307 42016 34840 1998 51230 4084 113787 25181 45208 35177 1999 50839 4124 113161 26734 48996 35768 2000 46218 4146 108463 34374 52574 36043 2001 45264 4254 106080 31793 55172 36399 2002 45706 4339 103891 27160 57930 36640 2003 43070 4412 99410 32516 60387 36204 2004 46947 4637 101606 16297 64028 34830 2005 48402 4766 104278 19966 68398 33442 2006 49804 4928 104958 24632 72522 31941 2007 50160 5108 105638 25064 76590 30731 2008 52871 5239 106793 22283 82190 29923 2009 53082 5404 108986 21234 87496 28890 2010 54648 5562 109876 18538 92780 27931 2011 57121 5704 110573 12441 97735 26594 2012 58958 5839 111205 11470 102559 25773资料来源:《中国统计年鉴》(1995,2012)。
三、模型设定设粮食生产函数为=四、模型结果与检验1、用普通最小二乘法估计模型运用Eviews软件进行普通最小二乘回归的结果如下:Dependent Variable: LOG(Y)Method: Least SquaresDate: 03/04/14 Time: 16:55Sample: 1983 2012Included observations: 30Variable Coefficient Std. Error t-Statistic Prob.C -3.399026 1.775984 -1.913883 0.0676LOG(X1) 0.391556 0.049906 7.845954 0.0000LOG(X2) 1.153291 0.115417 9.992351 0.0000LOG(X3) -0.072193 0.013678 -5.277951 0.0000LOG(X4) -0.063170 0.042789 -1.476303 0.1529LOG(X5) -0.099237 0.055146 -1.799520 0.0845R-squared 0.987725 Mean dependent var 10.74426Adjusted R-squared 0.985168 S.D. dependent var 0.118062S.E. of regression 0.014378 Akaike info criterion -5.469319Sum squared resid 0.004962 Schwarz criterion -5.189079Log likelihood 88.03978 Hannan-Quinn criter. -5.379668F-statistic 386.2468 Durbin-Watson stat 1.842639Prob(F-statistic) 0.000000因此,估计的方程为)+1.153log(X2)-0.072log(X3)-0.063log(X4)-0.099log(X5) (-1.91) (7.85) (9.99) (-5.28) (-1.48) (-1.79)R2 =0.9877 =0.9852 F=386.25 D.W.=1.84由于R2 较大且接近于1,而且F=386.25>变量间总体线性关系显著。
但由于其中X4,X5前参数估计值未能通过t检验,而且符号的经济意义也不合理,故认为解释变量间存在多重共线性。
2、检验简单相关系数log(X1),log(X2),log(X3),log(X4),log(X5)的相关系数如下表所示。
表2 相关系数表LOG(X1) LOG(X2) LOG(X3) LOG(X4) LOG(X5)LOG(X1) 1.000000 -0.456032 -0.005288 0.966390 -0.199163 LOG(X2) -0.456032 1.000000 -0.228430 -0.497507 -0.052864 LOG(X3) -0.005288 -0.228430 1.000000 -0.133051 0.657544 LOG(X4) 0.966390 -0.497507 -0.133051 1.000000 -0.393070 LOG(X5) -0.199163 -0.052864 0.657544 -0.393070 1.000000 由表中数据发现log(X1)与log(X2)间存在高度相关性。
3、找出最简单的回归形式分别作log(Y)与log(X1),log(X2),log(X3),log(X4)间的回归:(1)用Eviews作log(Y)与log(X1)间的回归结果如下:Dependent Variable: LOG(Y)Method: Least SquaresDate: 03/04/14 Time: 17:51Sample: 1983 2012Included observations: 30Variable Coefficient Std. Error t-Statistic Prob.C 8.540597 0.200770 42.53911 0.0000LOG(X1) 0.270081 0.024579 10.98839 0.0000R-squared 0.811758 Mean dependent var 10.74426Adjusted R-squared 0.805035 S.D. dependent var 0.118062S.E. of regression 0.052130 Akaike info criterion -3.005801Sum squared resid 0.076092 Schwarz criterion -2.912388Log likelihood 47.08701 Hannan-Quinn criter. -2.975917F-statistic 120.7447 Durbin-Watson stat 0.641647Prob(F-statistic) 0.000000log()=8.541+0.270log(X1)(42.54) (10.99)R2 =0.8118 D.W.=0.6416(2) 用Eviews作log(Y)与log(X2)间的回归结果如下:Dependent Variable: LOG(Y)Method: Least SquaresDate: 03/04/14 Time: 17:59Sample: 1983 2012Included observations: 30Variable Coefficient Std. Error t-Statistic Prob.C 13.65743 7.408742 1.843421 0.0759LOG(X2) -0.251095 0.638580 -0.393209 0.6971R-squared 0.005492 Mean dependent var 10.74426 Adjusted R-squared -0.030027 S.D. dependent var 0.118062 S.E. of regression 0.119822 Akaike info criterion -1.341281 Sum squared resid 0.402004 Schwarz criterion -1.247868 Log likelihood 22.11921 Hannan-Quinn criter. -1.311397 F-statistic 0.154613 Durbin-Watson stat 0.175494 Prob(F-statistic) 0.697143log()=13.657-0.251log(X2)(1.84) (-0.39)R2 =0.0055 D.W.=0.1755(3)用Eviews作log(Y)与log(X3)间的回归结果如下:Dependent Variable: LOG(Y)Method: Least SquaresDate: 03/04/14 Time: 18:03Sample: 1983 2012Included observations: 30Variable Coefficient Std. Error t-Statistic Prob.C 11.94539 0.799292 14.94496 0.0000LOG(X3) -0.119882 0.079748 -1.503264 0.1440R-squared 0.074680 Mean dependent var 10.74426 Adjusted R-squared 0.041633 S.D. dependent var 0.118062 S.E. of regression 0.115579 Akaike info criterion -1.413390 Sum squared resid 0.374036 Schwarz criterion -1.319977 Log likelihood 23.20085 Hannan-Quinn criter. -1.383506 F-statistic 2.259803 Durbin-Watson stat 0.080387 Prob(F-statistic) 0.143967log()=11.945-0.120log(X3)(14.945) (-1.50)R2 =0.0747 D.W.=0.0804(4)用Eviews作log(Y)与log(X4)间的回归结果如下:Dependent Variable: LOG(Y)Method: Least SquaresDate: 03/04/14 Time: 18:07Sample: 1983 2012Included observations: 30Variable Coefficient Std. Error t-Statistic Prob.C 8.630653 0.223791 38.56569 0.0000LOG(X4) 0.197738 0.020913 9.455395 0.0000R-squared 0.761508 Mean dependent var 10.74426Adjusted R-squared 0.752991 S.D. dependent var 0.118062S.E. of regression 0.058677 Akaike info criterion -2.769195Sum squared resid 0.096404 Schwarz criterion -2.675782Log likelihood 43.53792 Hannan-Quinn criter. -2.739311F-statistic 89.40450 Durbin-Watson stat 0.578214Prob(F-statistic) 0.000000log()=8.631-0.198log(X4)(38.566) (9.455)R2 =0.7615 D.W.=0.5782(5)用Eviews作log(Y)与log(X4)间的回归结果如下:Dependent Variable: LOG(Y)Method: Least SquaresDate: 03/04/14 Time: 18:09Sample: 1983 2012Included observations: 30Variable Coefficient Std. Error t-Statistic Prob.C 14.85318 1.951312 7.611892 0.0000LOG(X5) -0.394612 0.187390 -2.105835 0.0443R-squared 0.136723 Mean dependent var 10.74426Adjusted R-squared 0.105891 S.D. dependent var 0.118062S.E. of regression 0.111637 Akaike info criterion -1.482794Sum squared resid 0.348957 Schwarz criterion -1.389380Log likelihood 24.24190 Hannan-Quinn criter. -1.452910F-statistic 4.434539 Durbin-Watson stat 0.191621Prob(F-statistic) 0.044313log()=14.853-0.395log(X5)(7.612) (-2.106)R2 =0.1367 D.W.=0.1916可见,粮食生产受农业化肥施用量的影响最大,与经验相符合,因此选(1)为初始的回归模型。
