计算机控制实验实验三指导--不完全微分PID
计算机控制实验实验三指导--不完全微分PID
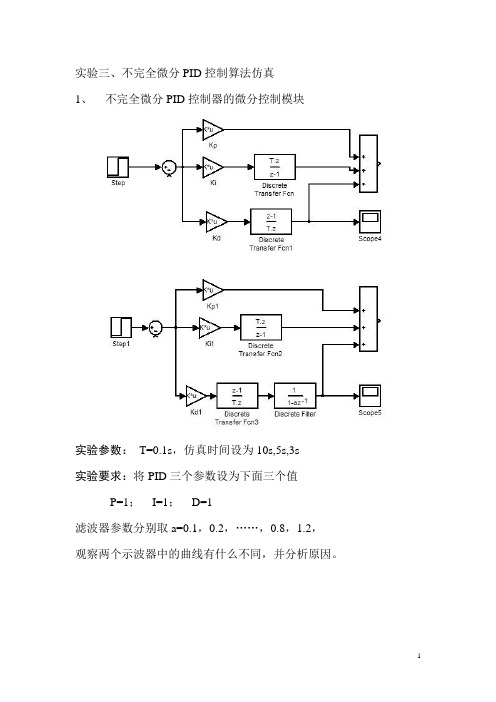
实验三、不完全微分PID控制算法仿真
1、不完全微分PID控制器的微分控制模块
实验参数:T=0.1s,仿真时间设为10s,5s,3s
实验要求:将PID三个参数设为下面三个值
P=1;I=1;D=1
滤波器参数分别取a=0.1,0.2,……,0.8,1.2,
观察两个示波器中的曲线有什么不同,并分析原因。
2、具有不完全微分PID控制器的系统的阶跃响应
实验参数:T =0.1s,饱和限幅u=±2,b为班号1~5,x为学号后2位,1~45
参考值:
(1)b=1,x=1 ,P=1,I=0.4,D=0.5,仿真时间设为20s
(2)b=1,x=45 ,P=5,I=0.2,D=0.5,仿真时间设为200s
滤波器参数分别取.1,0.2,……,0.8,1.2,
实验要求:
(1)画Simulinnk框图
(2)选择不完全微分之滤波器参数a(分别取0.1,0.2,……,0.8,
1.2),设计或凑试PID三个参数,使稳态误差为0,且动态性能
满意
(3)观察阶跃响应,并确定最佳滤波器参数a
实验报告要求
(1)封面见学院网站Word文档(2)给出仿真框架图;
(3)给出PID三个参数值;(4)给出最后的曲线图。
PID控制实验报告

实验二 数字PID 控制计算机控制是一种采样控制,它只能根据采样时刻的偏差值计算控制量。
因此连续PID 控制算法不能直接使用,需要采用离散化方法。
在计算机PID 控制中,使用的是数字PID 控制器。
一、位置式PID 控制算法按模拟PID 控制算法,以一系列的采样时刻点kT 代表连续时间t ,以矩形法数值积分近似代替积分,以一阶后向差分近似代替微分,可得离散PID 位置式表达式:∑∑==--++=⎪⎪⎭⎫ ⎝⎛--++=k j di p k j D I p T k e k e k T j e k k e k k e k e T T j e T T k e k k u 00)1()()()())1()(()()()( 式中,D p d I pi T k k T k k ==,,e 为误差信号(即PID 控制器的输入),u 为控制信号(即控制器的输出)。
在仿真过程中,可根据实际情况,对控制器的输出进行限幅。
二、连续系统的数字PID 控制仿真连续系统的数字PID 控制可实现D/A 及A/D 的功能,符合数字实时控制的真实情况,计算机及DSP 的实时PID 控制都属于这种情况。
1.Ex3 设被控对象为一个电机模型传递函数BsJs s G +=21)(,式中J=0.0067,B=0.1。
输入信号为)2sin(5.0t π,采用PD 控制,其中5.0,20==d p k k 。
采用ODE45方法求解连续被控对象方程。
因为Bs Js s U s Y s G +==21)()()(,所以u dt dy B dty d J =+22,另y y y y ==2,1,则⎪⎩⎪⎨⎧+-==/J)*u ((B/J)y y y y 12221 ,因此连续对象微分方程函数ex3f.m 如下 function dy = ex3f(t,y,flag,para)u=para;J=0.0067;B=0.1;dy=zeros(2,1);dy(1) = y(2);dy(2) = -(B/J)*y(2) + (1/J)*u;控制主程序ex3.mclear all;close all;ts=0.001; %采样周期xk=zeros(2,1);%被控对象经A/D转换器的输出信号y的初值e_1=0;%误差e(k-1)初值u_1=0;%控制信号u(k-1)初值for k=1:1:2000 %k为采样步数time(k) = k*ts; %time中存放着各采样时刻rin(k)=0.50*sin(1*2*pi*k*ts); %计算输入信号的采样值para=u_1; % D/AtSpan=[0 ts];[tt,xx]=ode45('ex3f',tSpan,xk,[],para); %ode45解系统微分方程%xx有两列,第一列为tt时刻对应的y,第二列为tt时刻对应的y导数xk = xx(end,:); % A/D,提取xx中最后一行的值,即当前y和y导数yout(k)=xk(1); %xk(1)即为当前系统输出采样值y(k)e(k)=rin(k)-yout(k);%计算当前误差de(k)=(e(k)-e_1)/ts; %计算u(k)中微分项输出u(k)=20.0*e(k)+0.50*de(k);%计算当前u(k)的输出%控制信号限幅if u(k)>10.0u(k)=10.0;endif u(k)<-10.0u(k)=-10.0;end%更新u(k-1)和e(k-1)u_1=u(k);e_1=e(k);endfigure(1);plot(time,rin,'r',time,yout,'b');%输入输出信号图xlabel('time(s)'),ylabel('rin,yout');figure(2);plot(time,rin-yout,'r');xlabel('time(s)'),ylabel('error');%误差图程序运行结果显示表1所示。
不完全微分pid1

1 引言智能车系统是一个时变且非线性的系统,采用传统PID算法的单一的反馈控制会使系统存在不同程度的超调和振荡现象,无法得到理想的控制效果。
本文将前馈控制引入到了智能车系统的控制中,有效地改善了系统的实时性,提高了系统的反应速度[1];并且根据智能车系统的特点,对数字PID算法进行了改进,引入了微分先行和不完全微分环节,改善了系统的动态特性;同时,利用模糊控制具有对参数变化不敏感和鲁棒性强的特点[2],本文将模糊算法与PID算法相结合,有效地提高了智能车的适应性和鲁棒性,改善了系统的控制性能。
2 改进PID算法智能车的控制是由飞思卡尔公司的S12芯片完成,所以对智能车的控制要采用计算机控制方法。
本文针对智能车控制的特殊性,对传统数字PID算法做了一些改进,这样可以更好地满足智能车控制的需要。
2.1不完全微分PID将微分环节引入智能车的方向和速度控制,明显地改善了系统的动态性能,但对于误差干扰突变也特别敏感,对系统的稳定性有一定的不良影响。
为了克服上述缺点,本文在PID算法中加入了一阶惯性环节[3] ,不完全微分PID算法结构如图1所示。
图1 不完全微分PID算法机构图将一阶惯性环节直接加到微分环节上,可得到系统的传递函数为:(1)将(1)式的微分项推导并整理,得到方程如下:(2)式中,,由系统的时间常数和一阶惯性环节时间常数决定的一个常数。
为了编程方便,可以将2-2式写成如下形式:(3)式中,。
分析式(3)可知,引入不完全微分以后,微分输出在第一个采样周期内被减少了,此后又按照一定比例衰减[3][4]。
实验表明,不完全微分有效克服了智能车的偏差干扰给速度控制带来的不良影响,具有较好的控制效果。
图2为不完全微分PID算法的程序流程图。
2.2 微分先行PID由于智能车在跑道上行驶时,经常会遇到转弯的情况,所以智能车的速度设定值和方向设定值都会发生频繁的变化,从而造成系统的振荡。
为了解决设定值的频繁变化给系统带来的不良影响,本文在智能车的速度和方向控制上引入了微分先行PID算法,其特点是只对输出量进行微分,即只对速度测量值和舵机偏转量进行微分,而不对速度和方向的设定值进行微分。
不完全微分PID算法

不完全微分PID算法不完全微分PID算法是一种改进的PID控制算法,它比传统的PID控制算法有更好的稳定性和鲁棒性。
不完全微分PID算法是在控制系统中引入微分操作的一个改进,通过将差分器的输出与积分因子相乘,得到一个不完全微分PID控制器,从而使系统响应速度更快、误差更小。
PID控制器是由比例项、积分项和微分项组成的。
比例项用来调整控制器的输出与误差之间的线性关系,积分项用来修正系统的稳态误差,微分项用来提高系统的稳定性和响应速度。
然而,传统的PID控制器在实际应用中存在一些不足之处。
比如,微分项通常会引入控制器的噪声放大因子,导致控制器的输出过于敏感,容易产生震荡。
此外,传统的PID控制器在存在大量干扰或参数变化的情况下,容易产生较大的误差。
不完全微分PID算法通过引入微分操作的改进,可以有效地解决传统PID控制器的不足之处。
不完全微分PID算法的核心思想是将差分器的输出与积分因子相乘,得到一个不完全微分PID控制器。
通过不完全微分操作,可以有效地抑制控制器的输出过于敏感,减小系统的震荡。
具体地说,不完全微分PID算法可以通过以下几个步骤来实现:1.根据控制对象的特性和性能指标,确定合适的比例增益、积分增益和微分增益。
2.在传统PID算法的基础上,将微分器的输出与积分因子相乘,得到一个不完全微分项。
3.将不完全微分项与比例项、积分项相加,得到一个新的控制器输出。
4.根据实际系统的反馈信号和期望输出信号,计算系统的误差。
5.根据误差和控制器增益,计算控制器的输出。
通过以上步骤,不完全微分PID算法就可以实现对系统的精确控制。
不完全微分PID算法在很多实际应用中取得了较好的效果,具有较好的稳定性和鲁棒性。
需要注意的是,不完全微分PID算法的实现需要根据具体的系统特性和性能指标进行调整和优化。
此外,不完全微分PID算法也需要根据实际应用的需求进行参数调整,以获得最佳的控制效果。
微分先行PID和不完全微分

5.2.1 微分项的改进
1.不完全微分型PID控制算法: 不完全微分就是用实际PD环节来代替理想PD环节,
使微分作用对于偏差的变化不会有太大的反应. 同时减小理想微分带来的系统剧烈动作. 在比例积分作用的基础上串接一个
令微分部分的传递函数为:
则:
u (s) T s 1
D
D
y(s) TDs 1
1
TD
duD dt
uD
TD
dy dt
y
差分得: duD uD(k) u 1)
dt
T
T uD(k) uD(k 1) u (k) T y(k) y(k 1) y(k)
P
不稳定。
5.1.6 积分调节器
积分作用是指调节器的输出与输入偏差的积分成 比例的作用,其作用是消除静差。
积分方程为:
1
y(t) TI e(t)d (t)
e(t)
积分作用的响应特
0
t
性曲线如右图:
y
0
t
由图中曲线看出积分作用的特点:
只要偏差不为零就会产生对应的控制量并依此影 响被控量。
TD S 1 (TD / KD )S 1
环节。
传递函数框图如下:
图5-2-1 传递函数框图
完全和不完全微分的作用
微分先行PID控制算法及仿真
基本思想:微分先行PID控制的结构如下图所示,其特点是只对输 出量 y(t) 进行微分,而对给定值 r(t)不作微分。这样,在改变给定 值时,输出不会改变,而被控量的变化通常总是比较缓和的。这 种输出量先行微分控制适用于给定值 r(t) 频繁升降的场合,可以 避免给定值升降时所引起的系统振荡,明显地改善了系统的动态 特性。
计算机控制技术3-4

一、防止积分整量化误差的方法•防止积分整量化误差的方法–扩大计算机运算的字长,提高计算精度–当积分项,积分项单独累加,直到产生溢出,溢出值作为积分项的偏差值去进行运算–防止积分整量化误差的程序流程图()I K e k δ<时二、积分饱和及其防止方法•积分饱和及其防止方法–积分饱和的原因和影响–在数字PID 控制系统中,当系统开、停或大幅度变动给定值时,系统输出会出现较大的偏差,经过积分项累积后,可能使控制量–即超过执行机构由机械或物理性能所决定的极限。
实际控制量并不是计算值,而只能取–影响控制效果,主要是积分项的存在,引起了PID 运算的“饱和”,这种饱和称为“积分饱和”max min()()u k u u k u ><或max min()()u k u u k u ==或二、积分饱和及其防止方法•积分饱和的影响–增加了系统的调整时间和超调量二、积分饱和及其防止方法•积分饱和及其防止方法–积分饱和的防止方法减小积分饱和的关键是不使积分项积累过大。
常用的两种方法:•积分分离法当偏差大于某个规定的门限值时,删除积分作用,只有当偏差‘较小时,方引入积分作用,控制量不易进入饱和区,即使进入了,因积分项积累较小,也能较快退出。
•遇限削弱积分法当控制量进入饱和区后,只执行削弱积分项的累加,而不进行增大积分项的累加二、积分饱和及其防止方法•积分分离法–PID 位置式表达式:–其算法框图[]0()()()()(1)1()0()KP L I D j L u k K e k K K e j K e k e k e k K e k εε==++−−≤⎧=⎨>⎩∑,当时,当时二、积分饱和及其防止方法•积分分离法–其算法框图二、积分饱和及其防止方法•遇限削弱积分法当控制量进入饱和区后,只执行削弱积分项的累加,而不进行增大积分项的累加计算u(k)时,先判断u((k-1)是否超过限制范围,若则只累计负偏差;若就只累计正偏差。
计算机控制技术:实验3 温度PID控制系统实验

6 实验步骤
双击“输出板卡设置”按钮,打开输出板卡。
void CPidcontrolDlg::OnButton2() //模拟量输出设备 选择按钮 {
// TODO: Add your control notification handler code here
m_daqao.SelectDevice();//选择模拟量输出设备 m_daqao.SetChannel(0);//通道号0 m_daqao.SetOutputRate(500);//输出频率500ms
}
6 实验步骤
(3) 接通电源 确认硬件连线正确无误后,按照下图所示依次接通实验系 统总电源(图中①)和温控对象电源(图中②)。
6 实验步骤
(4) Visual C++程序设计、调试完毕,运行程序。 ① 程序启动后,首先点击“输入板卡选择”按钮,选择模拟 量输入板卡PCI-1713U、再点击“输出板卡选择”按钮,选择 模拟量输出板卡PCI-1720U。 ② 设置好温度设定值SP、采样周期Ts、比例增益Kp、积分时 间常数Ti、微分时间常数Td。 ③ 点击“开始实验”按钮,系统开始进行数据采集,并在相 应区域显示出温度变化曲线、以及历史采样数据等信息。 ④ 实验中对参数更改时,系统会自动停止运行,参数修改完 毕后,再点击“开始试验”按钮即可重新采集数据。 ⑤ 点击“退出程序”,可退出系统。 ⑥ 实验结束后,关闭程序和计算机,拆除相关系统连线,并 整理好。最后确保所有设备电源均已关闭,离开实验室。
软件开发平台采用VC++6.0,完成模拟量采集与输出、信 息处理、显示、控制等功能。
数字信号 PCI-1720U 模拟量输出卡
工
控 PCI总线插槽
不完全微分PID算法

2 执行机构都存在一个线性工作区。 在此线性区内,它可以线性地跟踪控 制信号,而当控制信号过大,超过这 个线性区,就进入饱和区或截止区, 其特性将变成非线性特性。从而使系 统出现过大的超调和持续振荡,动态 品质变坏。
4 对于具有高频扰动的生产过程, 由于标准PID控制算式中的微分作用 过于灵敏,导致系统控制过程振荡, 降低了调节品质。特别是,对每个 控制回路计算机的输出是快速的, 而执行机构的动作需要一定的时间。 如果输出值较大,在一个采样时间 内执行机构不能到达应到的位置, 会使输出失真。
e] dt
设数字微分调节器的输入 LOGO
为单位阶跃序列 ek 1
普普通通的的数数字字调调节节器器的微分作用
只在第一个采样周期里起作用 不能按照偏差变换的趋势在整个调节 过程中起作用。 微分作用在第一个采样周期时作用很 强,容易溢出。
LOGO
不完全微分PID算法
不完全数字PID
能抑制高频干扰 数字控制器输出的微分作 用能在各个采样周期按照误 差变化的趋势均匀地输出 改善了系统的系能。
输出控制曲线
图一 :不完全微分PID算法输出控制曲线 图二:普通PID算法输出控制曲线
计算得:
在第一个采样周期里 不完全微分数字控制器 的 输出比 完全微分数字控制器 的输出幅度小得 多,而且控制器的输出十分近似于理想的微分控 制器。
由于微分作用容易引进高频干扰,因此,可以
串接一个低通滤波器(一阶惯性环节)来抑制高
频影响。低通滤波器的传递函数为:G
f
(s)
Tf
1 s
1
E(s)
U1(s)
U(s)
PID
Gf(s)
e(t)
u1(t)
u(t)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三、不完全微分PID控制算法仿真
1、不完全微分PID控制器的微分控制模块
实验参数:T=0.1s,仿真时间设为10s,5s,3s
实验要求:将PID三个参数设为下面三个值
P=1;I=1;D=1
滤波器参数分别取a=0.1,0.2,……,0.8,1.2,
观察两个示波器中的曲线有什么不同,并分析原因。
2、具有不完全微分PID控制器的系统的阶跃响应
实验参数:T =0.1s,饱和限幅u=±2,b为班号1~5,x为学号后2位,1~45
参考值:
(1)b=1,x=1 ,P=1,I=0.4,D=0.5,仿真时间设为20s
(2)b=1,x=45 ,P=5,I=0.2,D=0.5,仿真时间设为200s
滤波器参数分别取.1,0.2,……,0.8,1.2,
实验要求:
(1)画Simulinnk框图
(2)选择不完全微分之滤波器参数a(分别取0.1,0.2,……,0.8,
1.2),设计或凑试PID三个参数,使稳态误差为0,且动态性能
满意
(3)观察阶跃响应,并确定最佳滤波器参数a
实验报告要求
(1)封面见学院网站Word文档(2)给出仿真框架图;
(3)给出PID三个参数值;(4)给出最后的曲线图。
